Modern Capabilities of Semi-Airborne UAV-TEM Technology on the Example of Studying the Geological Structure of the Uranium Paleovalley
Abstract
1. Introduction
2. Materials and Methods
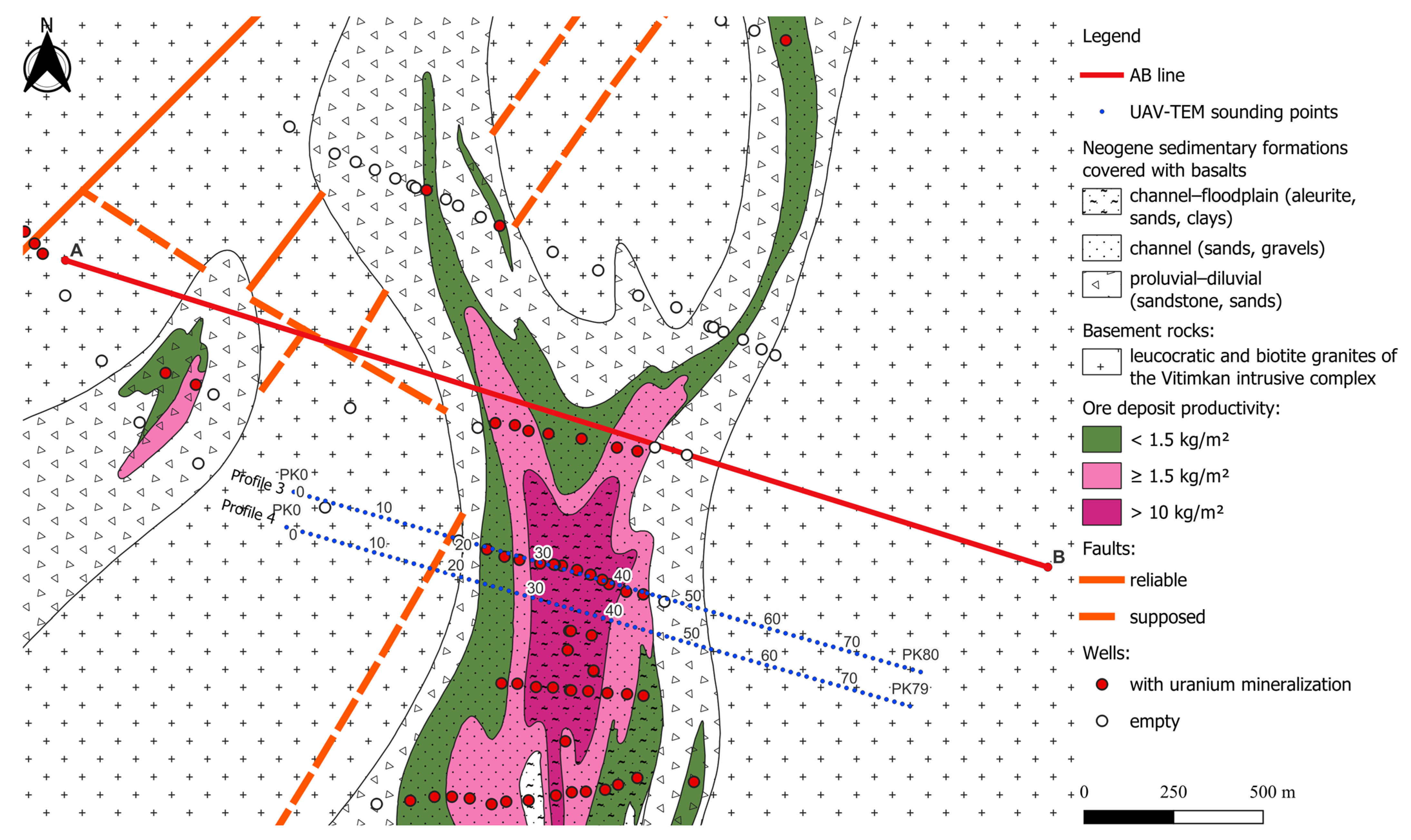
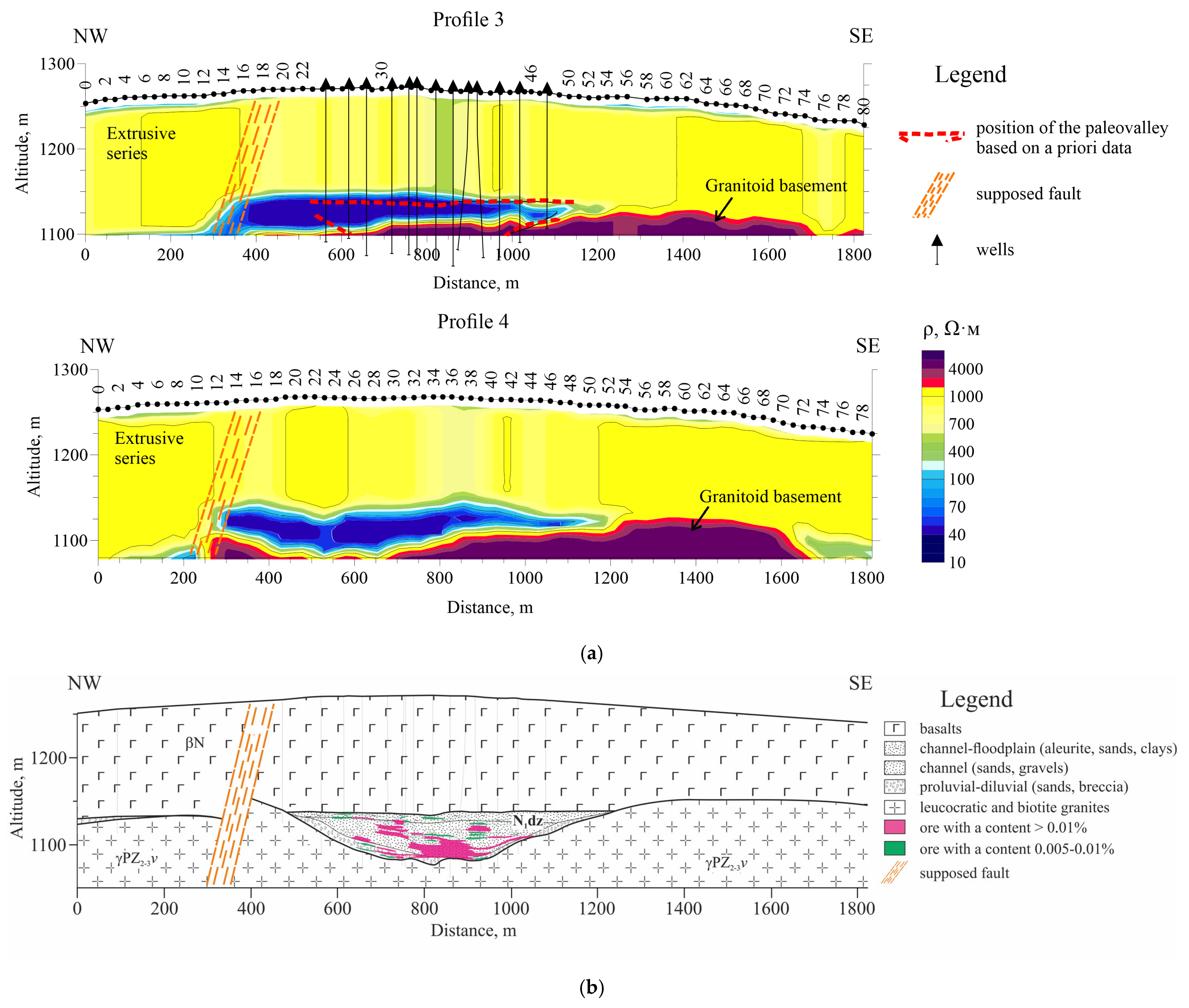
2.1. Geological Model of the Site
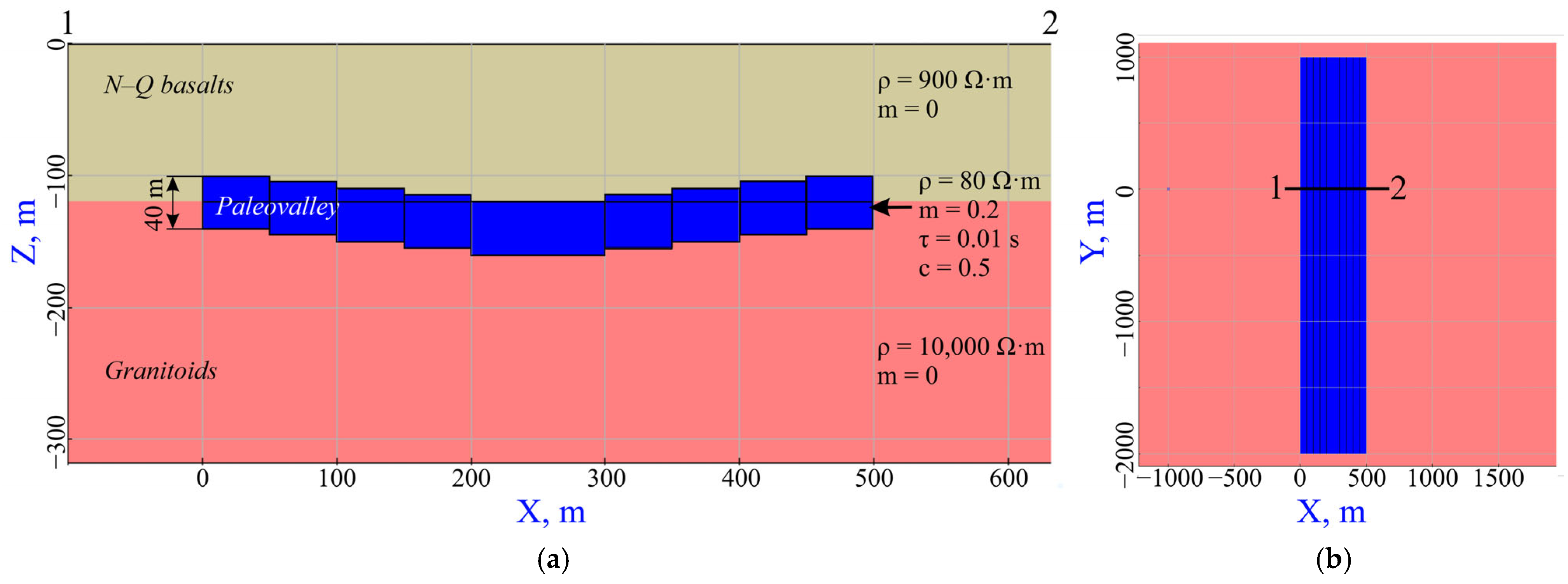
2.2. Physical–Geological Model of the Deposit
- The effusive stratum (several covering layers of basalt separated by interlayers of tuffs and interformational sediments, with an average thickness of 130 m) is characterized by medium density (2.5 g/cm3), high magnetic susceptibility (2.0–230 SI units), high resistivity (900–8000 Ω·m), and medium acoustic velocity (3800 m/s);
- Productive sediments (sands, clays, and grus with a thickness of 40–150 m) have a low density (2.0 g/cm3), weak magnetism (0.24 SI units), low resistivity (40 Ω·m), and low velocity (2150 m/s);
- Crystalline basement rocks (granitoids, diorites, limestone, metamorphic schists, and sandstone) have high density (2.45–2.82 g/cm3), low-to-moderate magnetic susceptibility (0.4–0.73 SI units), a wide range of specific resistivity based on resistivity logging (190–2000 Ω·m), and high acoustic velocity (4300 m/s).
2.3. SibGIS UAV-TEM Technology
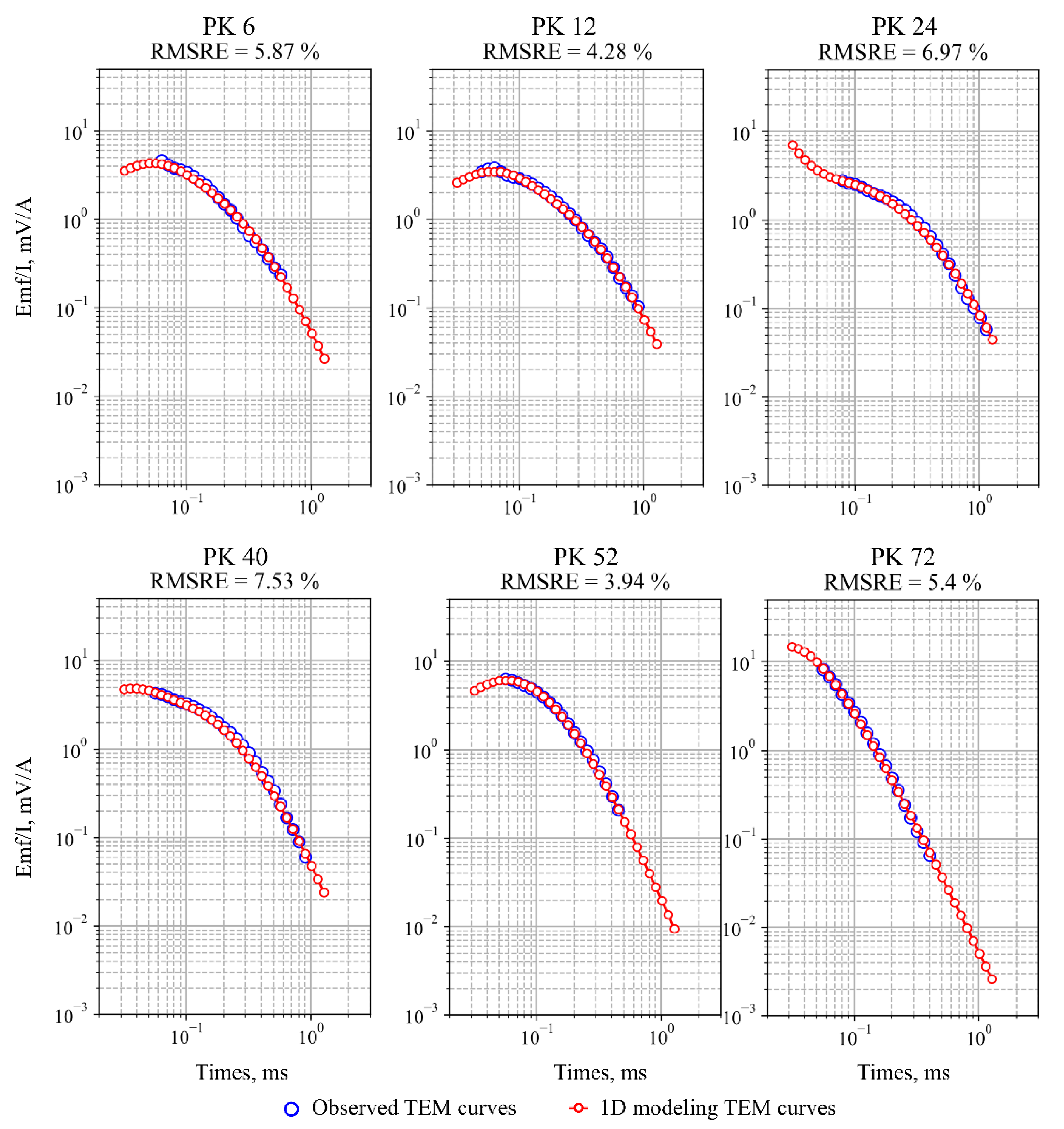
2.4. Solution to the 1D-Inverse Problem
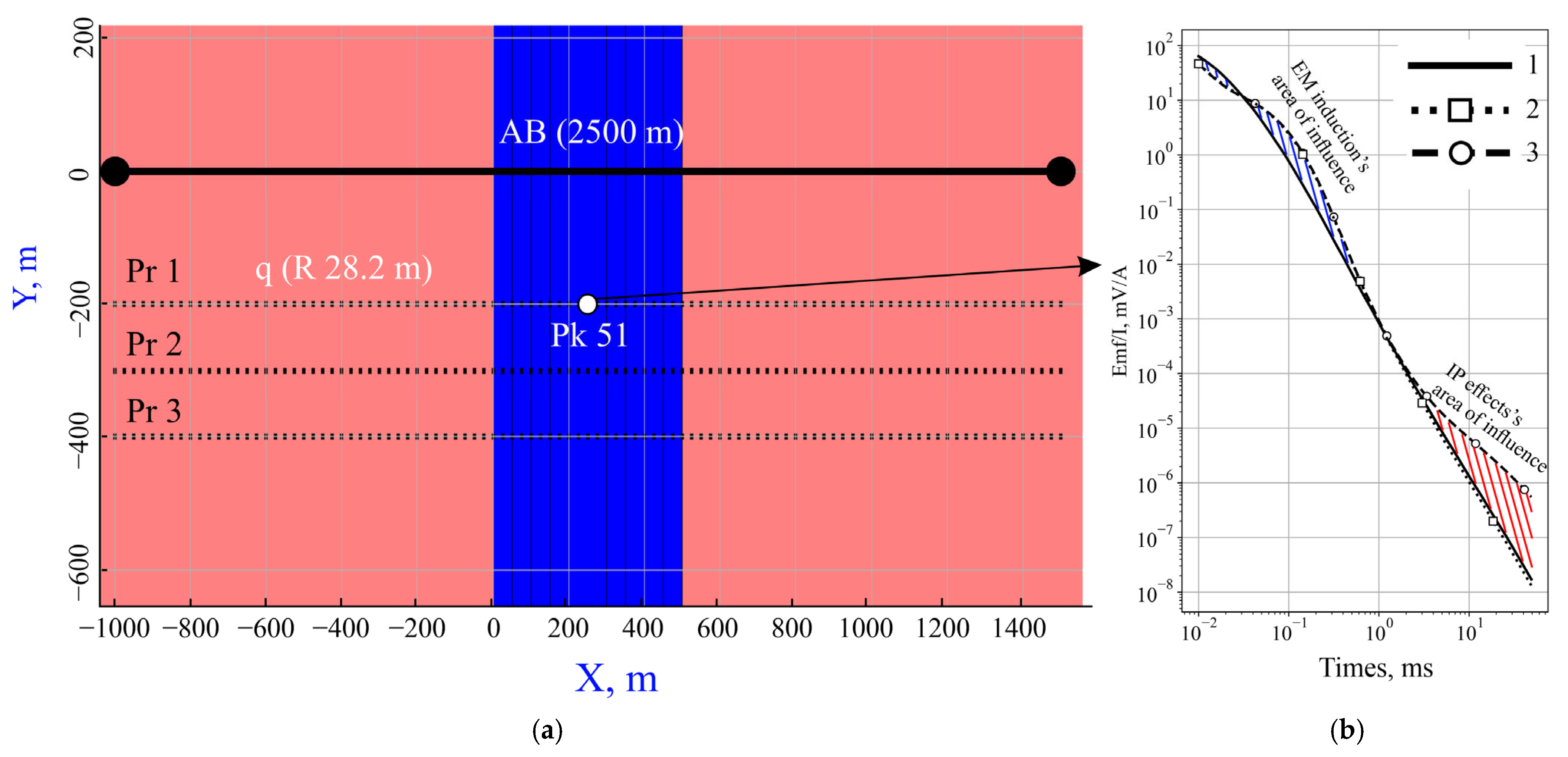
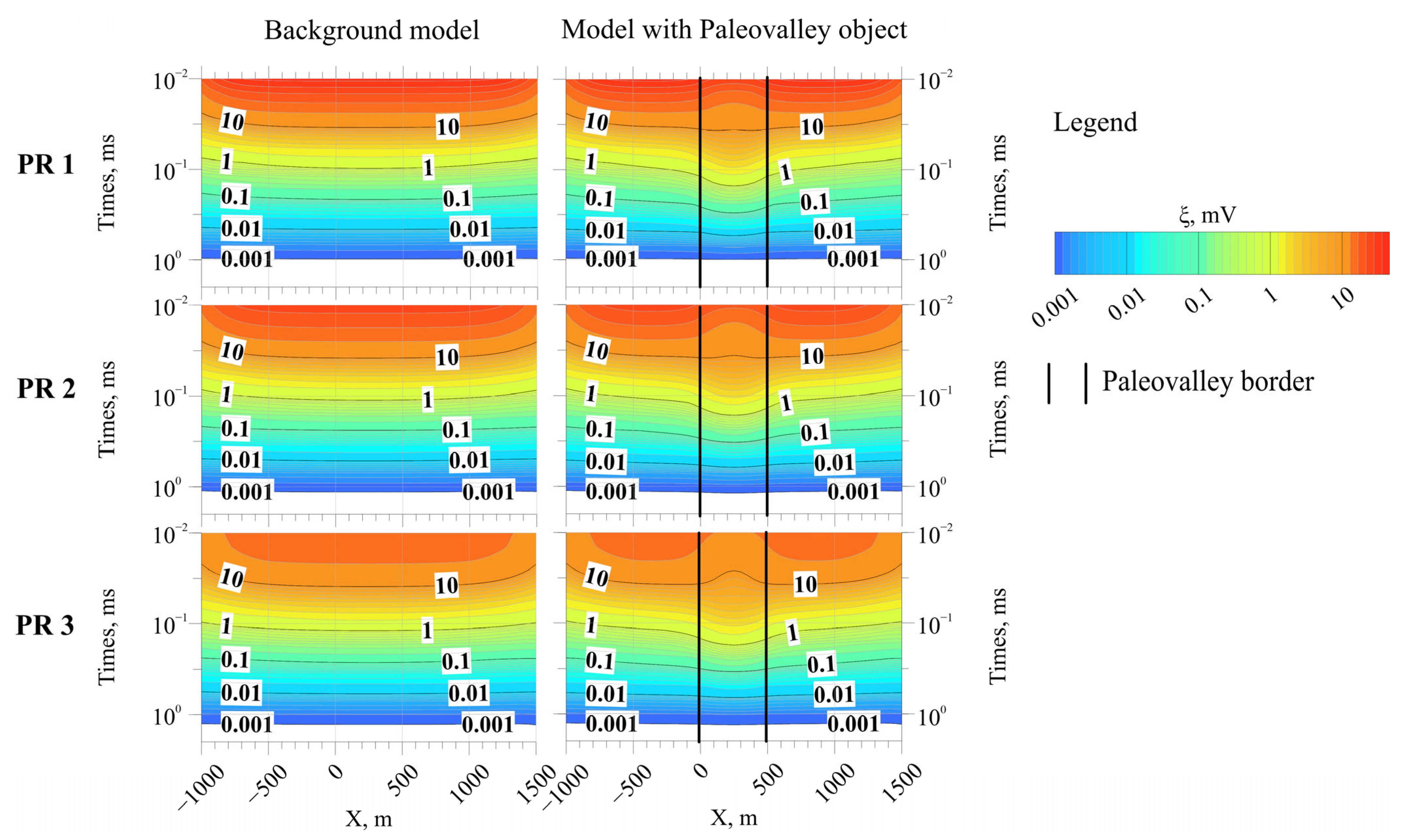
2.5. Numerical Modeling for Sensitivity Assessment
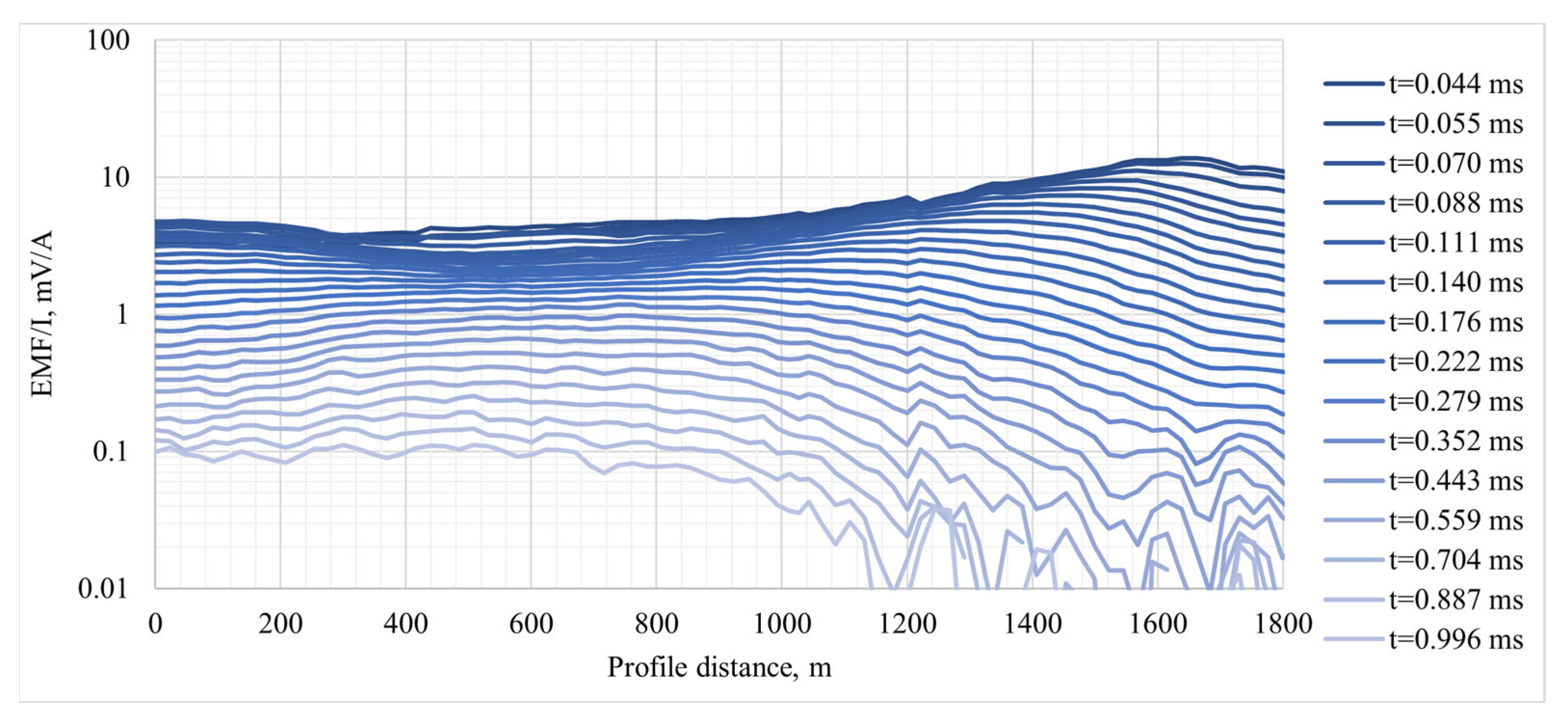
3. Results and Discussion
- Extraction is performed from the initial series of sounding curves at current offsets;
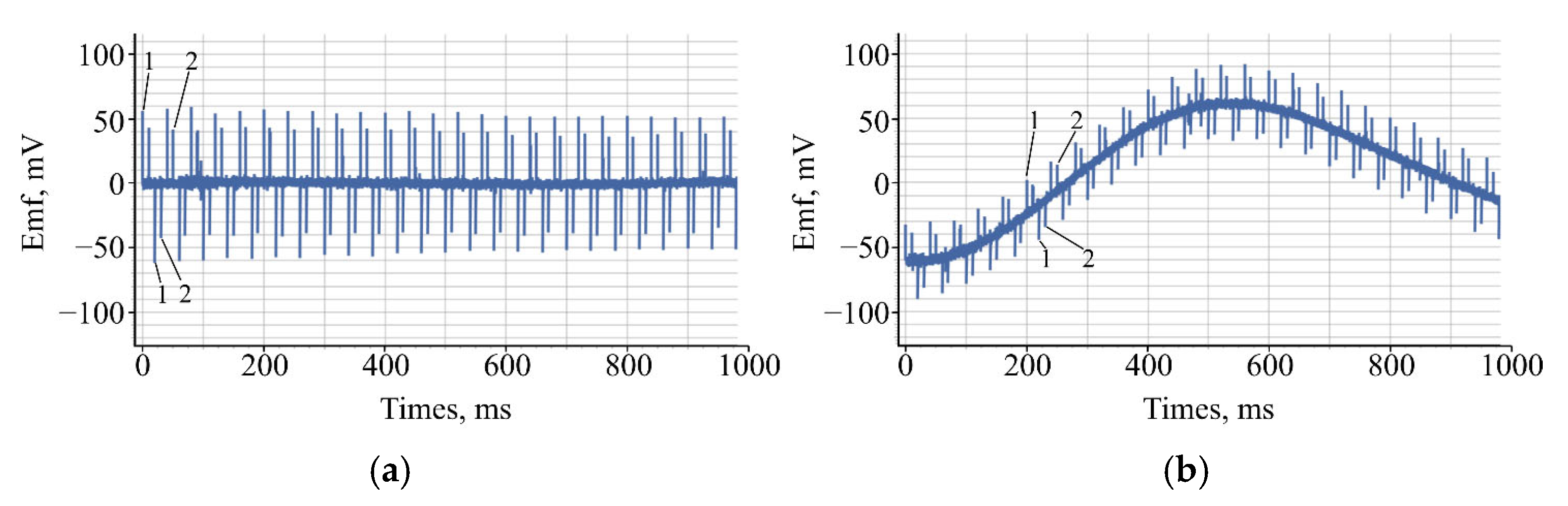
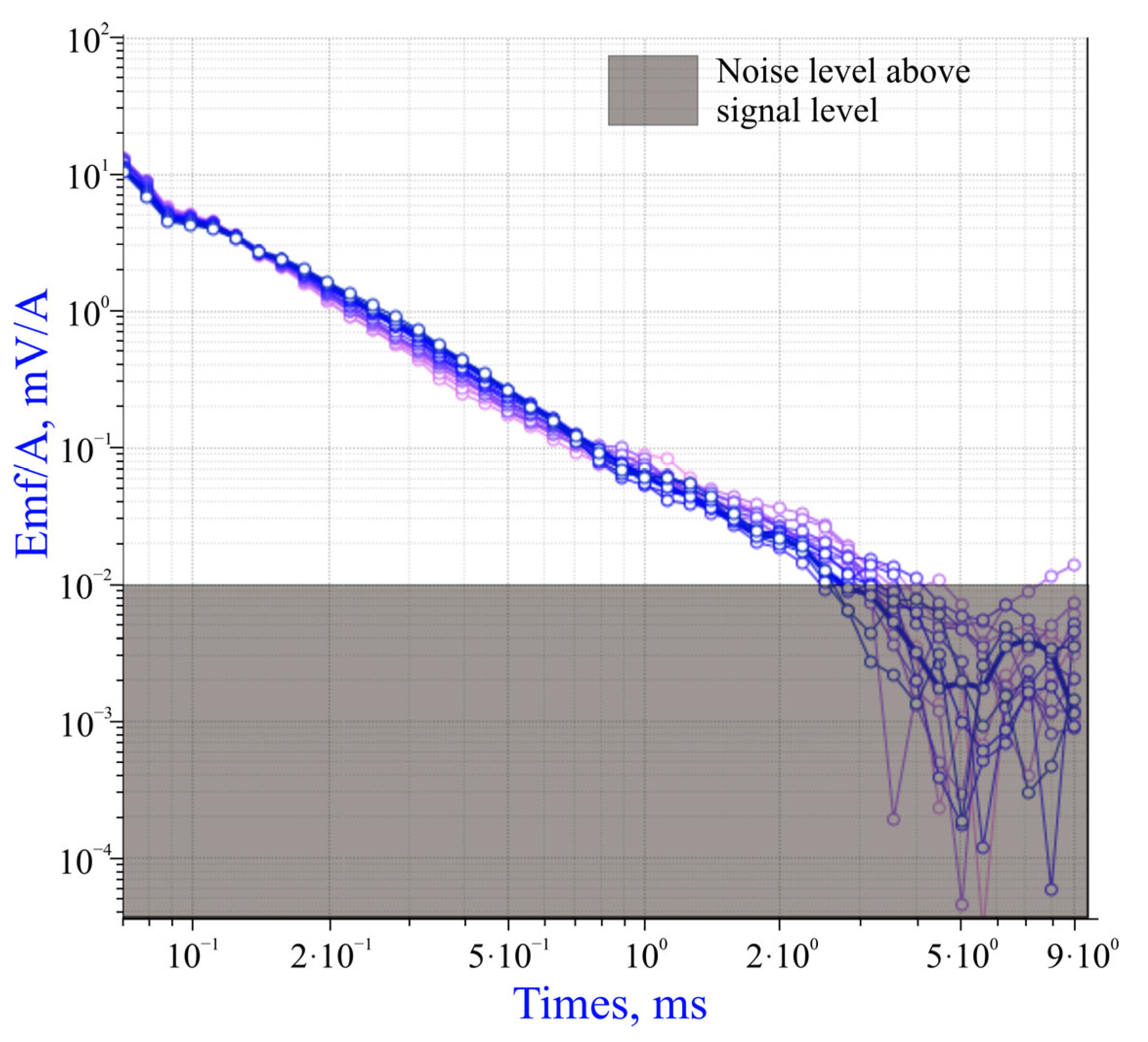
- Drift compensation uses a low-pass filter—this allows distortions like those shown in Figure 5b to be suppressed;
- Robust smoothing using two-dimensional sliding windows is conducted;
- Sounding curves are converted from the arithmetic time step to the logarithmic time step using robust averaging.
4. Conclusions
5. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dadrass Javan, F.; Samadzadegan, F.; Toosi, A.; van der Meijde, M. Unmanned Aerial Geophysical Remote Sensing: A Systematic Review. Remote Sens. 2024, 17, 110. [Google Scholar] [CrossRef]
- Parshin, A.V.; Morozov, V.A.; Blinov, A.V.; Kosterev, A.N.; Budyak, A.E. Low-altitude geophysical magnetic prospecting based on multirotor UAV as a promising replacement for traditional ground survey. Geo-Spat. Inf. Sci. 2018, 21, 67–74. [Google Scholar] [CrossRef]
- Pothuri, R.C.P.; Joseph, C.; Bommu, N.R.; Prabhat, S. Application of UAV-borne Magnetic Survey in Diamond Exploration: A Case Study over Kimberlite-Carbonatite Intrusion from Khaderpet, Eastern Dharwar Craton, South India. J. Geol. Soc. India 2025, 101, 198–207. [Google Scholar] [CrossRef]
- Accomando, F.; Florio, G. Drone-Borne Magnetic Gradiometry in Archaeological Applications. Sensors 2024, 24, 4270. [Google Scholar] [CrossRef]
- Shahsavani, H.; Smith, R.S. Aeromagnetic gradiometry with UAV, a case study on small iron ore deposit. Drone Syst. Appl. 2024, 12, 1–9. [Google Scholar] [CrossRef]
- Molnar, A. Measurement of gamma radiation dose distribution by drone using discrete measurement method. Bull. L.N. Gumilyov Eurasian Natl. Univ. Tech. Sci. Technol. Ser. 2024, 147, 168–187. [Google Scholar] [CrossRef]
- Parshin, A.; Morozov, V.; Snegirev, N.; Valkova, E.; Shikalenko, F. Advantages of Gamma-Radiometric and Spectrometric Low-Altitude Geophysical Surveys by Unmanned Aerial Systems with Small Scintillation Detectors. Appl. Sci. 2021, 11, 2247. [Google Scholar] [CrossRef]
- UAV VLF-EM SYSTEM: Resistivity Mapping Solution. Available online: https://www.gemsys.ca/uav-vlf/ (accessed on 18 February 2021).
- Parshin, A.; Davidenko, Y.; Yakovlev, S.; Vinokurov, V.; Bashkeev, A. Lightweight TEM and VLF systems for low-altitude UAV-based geophysical prospecting. In Proceedings of the NSG2021 27th European Meeting of Environmental and Engineering Geophysics Conference Proceedings, Bordeaux, France, 2 September 2021; Volume 2021, pp. 1–5. [Google Scholar]
- Kotowski, P.O.; Becken, M.; Thiede, A.; Schmidt, V.; Schmalzl, J.; Ueding, S.; Klingen, S. Evaluation of a Semi-Airborne Electromagnetic Survey Based on a Multicopter Aircraft System. Geosciences 2022, 12, 26. [Google Scholar] [CrossRef]
- Stoll, J.; Noellenburg, R.; Kordes, T.; Becken, M.; Tezkan, B.; Yogeshwar, P.; Bergers, R.; Matzander, U. Semi-Airborne electromagnetics using a multicopter. In Proceedings of the International Workshop on Gravity, Electrical & Magnetic Methods and Their Applications, Xi’an, China, 19–22 May 2019. [Google Scholar]
- Vilhelmsen, T.B.; Døssing, A. Drone-towed controlled-source electromagnetic (CSEM) system for near-surface geophysical prospecting: On instrument noise, temperature drift, transmission frequency, and survey set-up. Geosci. Instrum. Methods Data Syst. 2022, 11, 435–450. [Google Scholar] [CrossRef]
- Becken, M.; Nittinger, C.G.; Smirnova, M.; Steuer, A.; Martin, T.; Petersen, H.; Meyer, U.; Mörbe, W.; Yogeshwar, P.; Tezkan, B.; et al. DESMEX: A novel system development for semi-airborne electromagnetic exploration. Geophysics 2020, 85, 253–267. [Google Scholar] [CrossRef]
- Günther, T.; Ronczka, M.; Rochlitz, R.; Müller-Petke, M. Using Drone-Based Electromagnetics for 3D Imaging of Groundwater Salinization. European Association of Geoscientists & Engineers. In Proceedings of the NSG2022 3rd Conference on Airborne, Drone and Robotic Geophysics, Belgrade, Serbia, 18–22 September 2022; Volume 2022, pp. 1–5. [Google Scholar] [CrossRef]
- Smit, J.P.; Stettler, E.H.; Price, A.B.W.; Schaefer, M.O.; Schodlok, M.C.; Zhang, R. Use of drones in acquiring B-feld total-feld electromagnetic data for mineral exploration. Miner. Econ. 2022, 35, 455–465. [Google Scholar] [CrossRef]
- Parshin, A.; Bashkeev, A.; Davidenko, Y.; Persova, M.; Iakovlev, S.; Bukhalov, S.; Grebenkin, N.; Tokareva, M. Lightweight Unmanned Aerial System for Time-Domain Electromagnetic Prospecting—The Next Stage in Ap-plied UAV-Geophysics. Appl. Sci. 2021, 11, 2060. [Google Scholar] [CrossRef]
- Davidenko, Y.; Hallbauer-Zadorozhnaya, V.; Bashkeev, A.; Parshin, A. Semi-Airborne UAV-TEM Sys-tem Data Inversion with S-Plane Method—Case Study over Lake Baikal. Remote Sens. 2023, 15, 5310. [Google Scholar] [CrossRef]
- Wu, J.; Xiao, D.; Du, B.; Liu, Y.; Zhi, Q.; Wang, X.; Deng, X.; Chen, X.; Zhao, Y.; Huang, Y. Exploring Shallow Geological Structures in Landslides Using the Semi-Airborne Transient Electromagnetic Method. Remote Sens. 2024, 16, 3186. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, N.; Li, D.; Liu, S.; Ye, Q. The first semi-airborne transient electromagnetic survey for tunnel investigation in very complex terrain areas. Tunn. Undergr. Space Technol. 2023, 132, 104893, ISSN 0886-7798. [Google Scholar] [CrossRef]
- Tarkhanova, G.A.; Prokhorov, D.A. Genetic features of “Vitim” type uranium ore formation. Razved. I Ohr. Nedr = Prospect Miner. Resour. 2017, 11, 47–59. (In Russian) [Google Scholar]
- Federal Agency for Subsoil, Federal State Unitary Enterprise All-Russian Scientific Research Institute of Mineral Resources. Geological and Industrial Types of Uranium Deposits in the CIS Countries; VIMS: Moscow, Russia, 2008; 72p, ISBN 978-5-901837-43-6. (In Russian) [Google Scholar]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics. Alternating current characteristics. J. Chem. Phys 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Pelton, W.H.; Ward, S.H.; Hallof, P.G.; Sill, W.R.; Nelson, P.H. Mineral discrimination and removal of inductive coupling with multifrequency IP. Geophysics 1978, 43, 588–609. [Google Scholar] [CrossRef]
- Zaharkin, A.K. Compact receiving loop for pulsed electrical prospecting. Ross. Geofiz. Zhurnal Russ. Geophys. J. 1998, 9–10, 95–99. (In Russian) [Google Scholar]
- Hampel, F.R.; Ronchetti, E.M.; Rousseeuw, P.J.; Stahel, W.A. Robust Statistics: The Approach Based on Influence Functions; John Wiley & Sons, Inc.: New York, NY, USA, 1986; 502p. [Google Scholar]
- Pushkarev, P.Y.; Yakovlev, A.G.; Yakovlev, A.D. Program for Solving the Direct and Inverse One-Dimensional Problem of the Frequency Sounding Method; Moskow State University: Moscow, Russia, 1999; 12p, Available online: https://spectra-geo.narod.ru/Publications/msu_fs1d.pdf (accessed on 18 February 2021). (In Russian)
- Ryzhov, A.A. Optimal algorithm for solving the direct VES problem. Fiz. Zemli Izv. Phys-Ics Solid Earth 1983, 3, 68–75. [Google Scholar]
- Gegenfurtner, K.R. PRAXIS: Brent’s algorithm for function minimization. Behavior Research Meth-ods. Instrum. Comput. 1992, 24, 560–564. [Google Scholar] [CrossRef]
- Soloveichik, Y.G.; Persova, M.G.; Domnikov, P.A.; Koshkina, Y.I.; Vagin, D.V. Finite element solution to multidimensional multisource electromagnetic problems in the frequency domain using non-conforming meshes. Geophys. J. Int. 2018, 212, 2159–2193. [Google Scholar] [CrossRef]
- Persova, M.; Soloveichik, Y.; Vagin, D.; Kiselev, D.; Kondratyev, N.; Koshkina, Y.; Trubacheva, O. Application of non-conforming meshes with hexahedral cells for3D modelling of airborne electro-magnetic technologies. Dokl. Akad. Nauk Vyss. Shkoly Ross. Fed. Proceed-Ings Russ. High. Sch. Acad. Sci. 2018, 1, 64–79. (In Russian) [Google Scholar] [CrossRef]
- Ovsyannikova, T.; Grebenkin, N.; Mashnin, D.; Nesmeyanova, A.; Prokhorov, D.; Starodubov, A.; Tuboltsev, I. Cases and practices of implementing isotopic geochemical methods in search for consealed uranium deposites. Razved. I Ohr. Nedr Prospect. Miner. Resour. 2022, 8, 53–63. (In Russian) [Google Scholar] [CrossRef]




| KER-100 Current Switch | |
| Amplitude of stabilized current pulses | 0.1–100 A; |
| Maximum output voltage | 950 V |
| Maximum power output | 54,000 W |
| Duration of current pulses in pulse (+)-pause-pulse (−)-pause mode | 0.01, 0.1, 0.125, 0.25, 0.5, 1, 2, 4, 8 s |
| Pulse repetition error | 1 µs |
| Current amplitude setting error | Not more than 1% |
| Satellite systems | GPS/GLONASS |
| Protection complies with IP 54 | |
| Possibility of synchronization with the measuring system by GNSS time | |
| MARS v2.0 ADC and measuring unit | |
| Number of channels | 2 |
| Compensation for voltage offset of electrode potentials | ±1 V |
| Input impedance not less than | 20 MΩ |
| Gains | 0.25, 0.5, 1, 2, 4, …, 128 |
| Sampling frequency | 100 kHz |
| ADC digit capacity | 18 bits |
| Maximum input signal | ±4.096 V. |
| Battery power | 12 V (range: 10 V to 15 V). |
| Current consumption (approx.) | max. 0.3 A |
| Satellite time synchronization | GPS/GLONASS/Galileo/BeiDou |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bashkeev, A.; Parshin, A.; Trofimov, I.; Bukhalov, S.; Prokhorov, D.; Grebenkin, N. Modern Capabilities of Semi-Airborne UAV-TEM Technology on the Example of Studying the Geological Structure of the Uranium Paleovalley. Minerals 2025, 15, 630. https://doi.org/10.3390/min15060630
Bashkeev A, Parshin A, Trofimov I, Bukhalov S, Prokhorov D, Grebenkin N. Modern Capabilities of Semi-Airborne UAV-TEM Technology on the Example of Studying the Geological Structure of the Uranium Paleovalley. Minerals. 2025; 15(6):630. https://doi.org/10.3390/min15060630
Chicago/Turabian StyleBashkeev, Ayur, Alexander Parshin, Ilya Trofimov, Sergey Bukhalov, Danila Prokhorov, and Nikolay Grebenkin. 2025. "Modern Capabilities of Semi-Airborne UAV-TEM Technology on the Example of Studying the Geological Structure of the Uranium Paleovalley" Minerals 15, no. 6: 630. https://doi.org/10.3390/min15060630
APA StyleBashkeev, A., Parshin, A., Trofimov, I., Bukhalov, S., Prokhorov, D., & Grebenkin, N. (2025). Modern Capabilities of Semi-Airborne UAV-TEM Technology on the Example of Studying the Geological Structure of the Uranium Paleovalley. Minerals, 15(6), 630. https://doi.org/10.3390/min15060630







