Geoscientific Input Feature Selection for CNN-Driven Mineral Prospectivity Mapping
Abstract
1. Introduction
2. Methodology
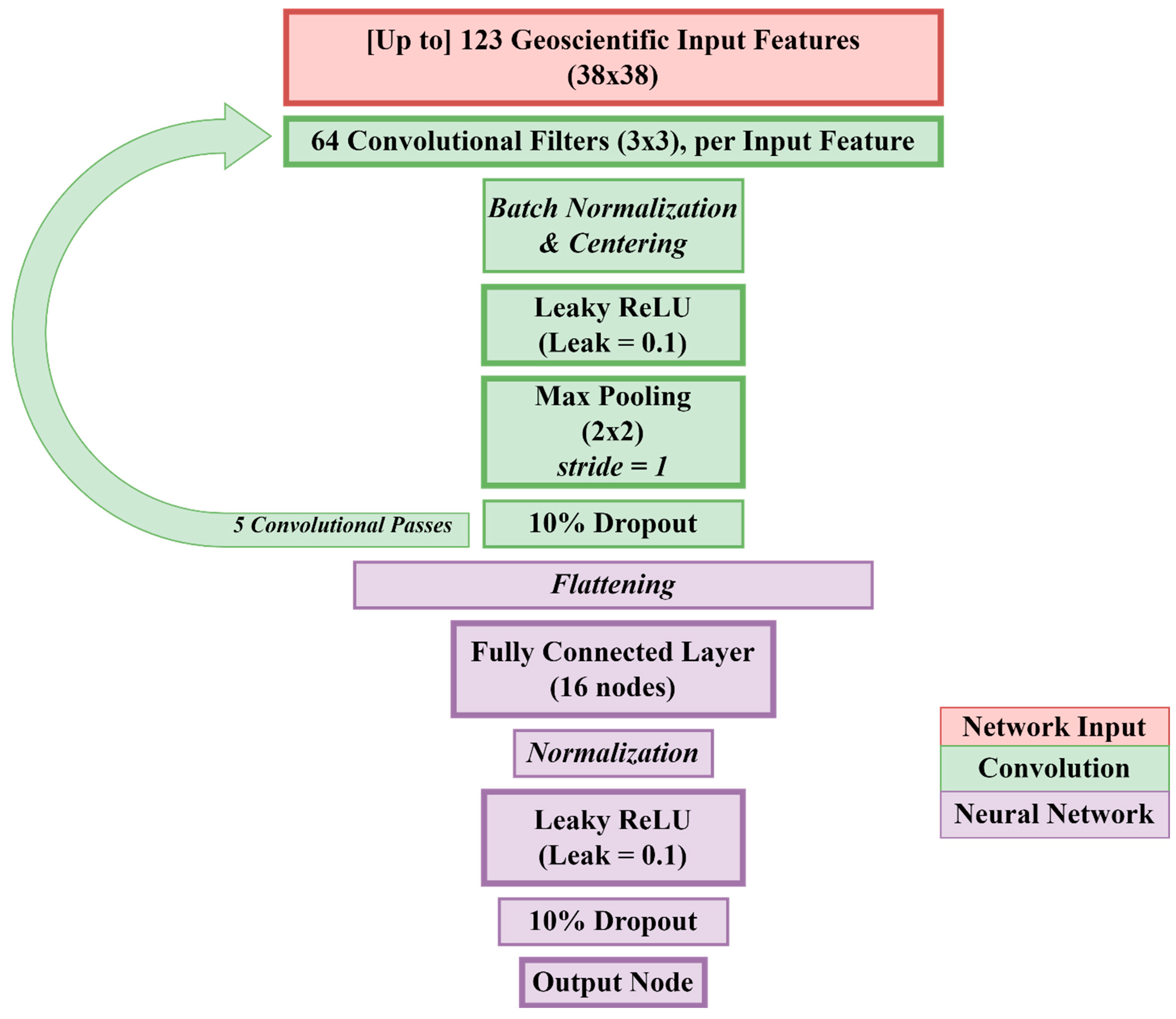
2.1. Data and CNN Model
2.2. Optimal Input Feature Selection
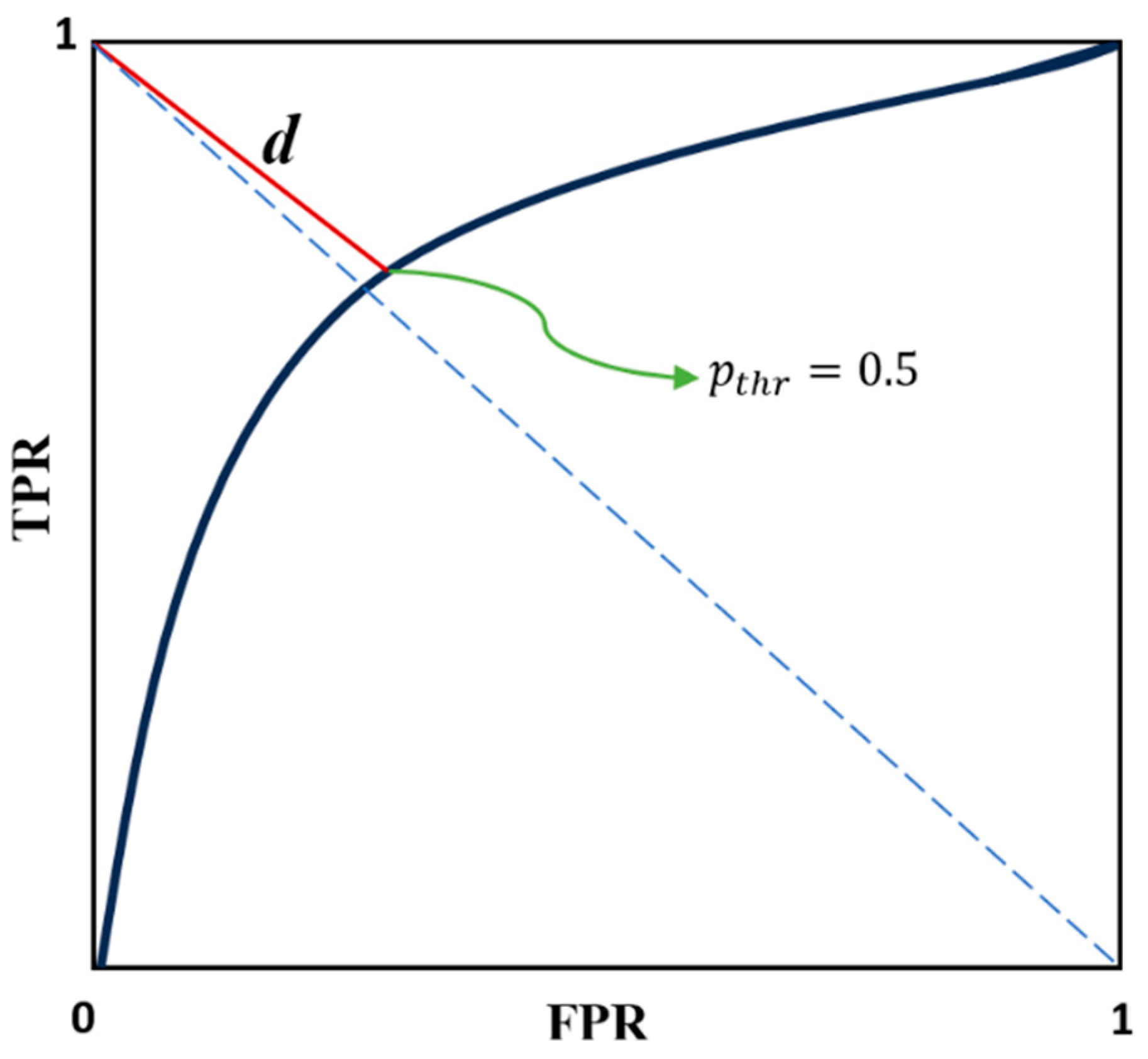
2.2.1. Optimization Metric
2.2.2. Exhaustive Search
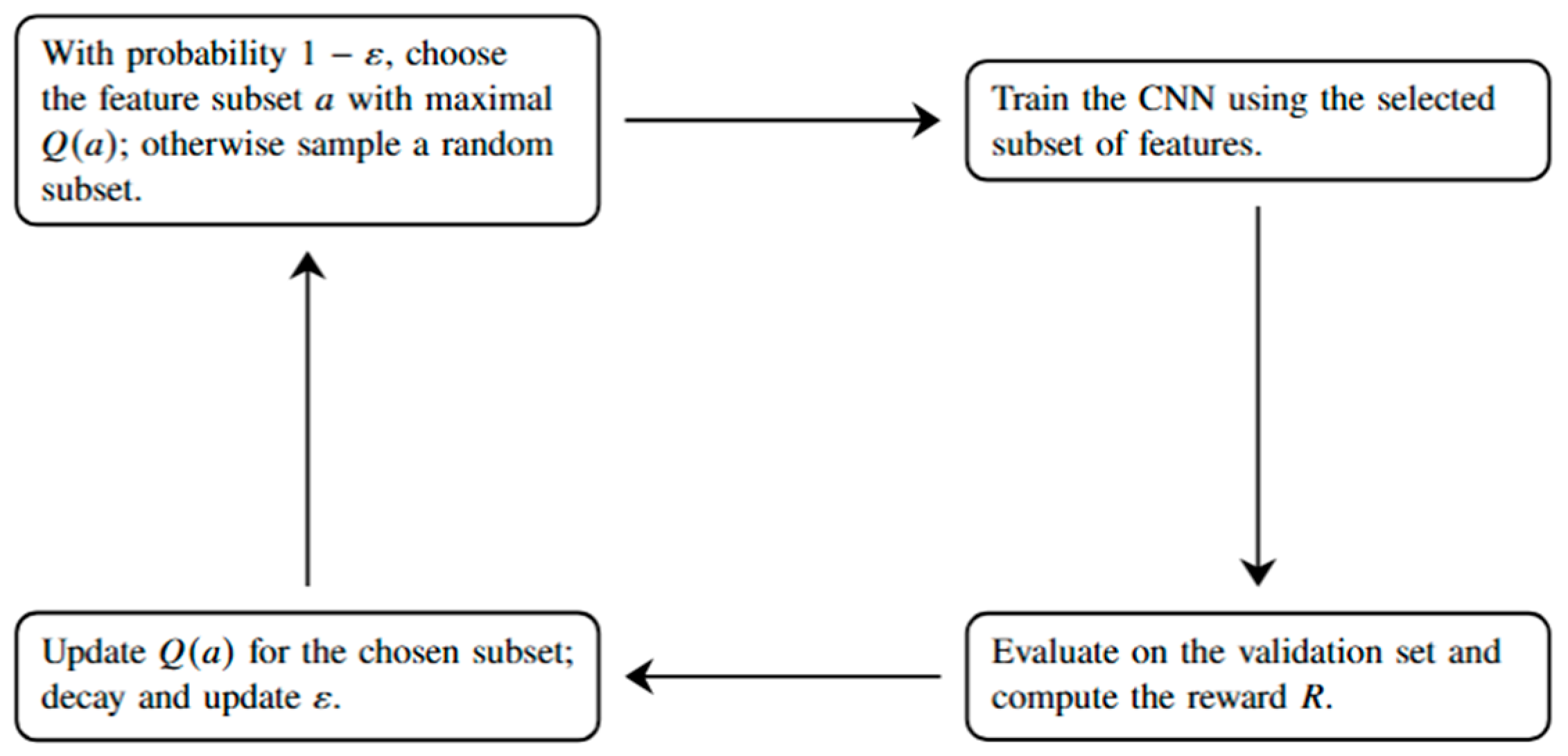
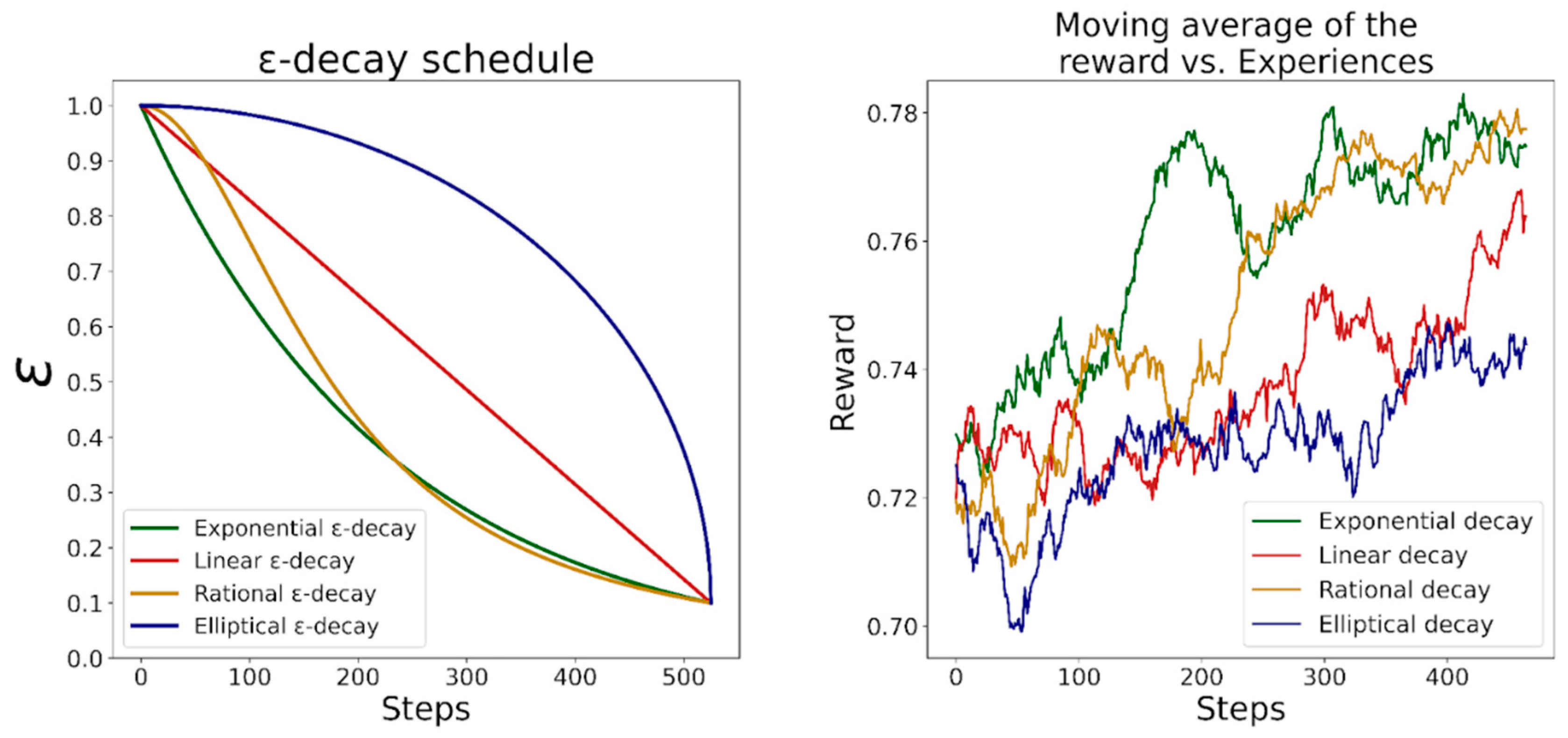
2.2.3. Multi-Armed Bandits
3. Optimized Mineral Prospectivity Results
3.1. Exhaustive Search for Optimal Input
3.2. MAB Search for Optimal Input
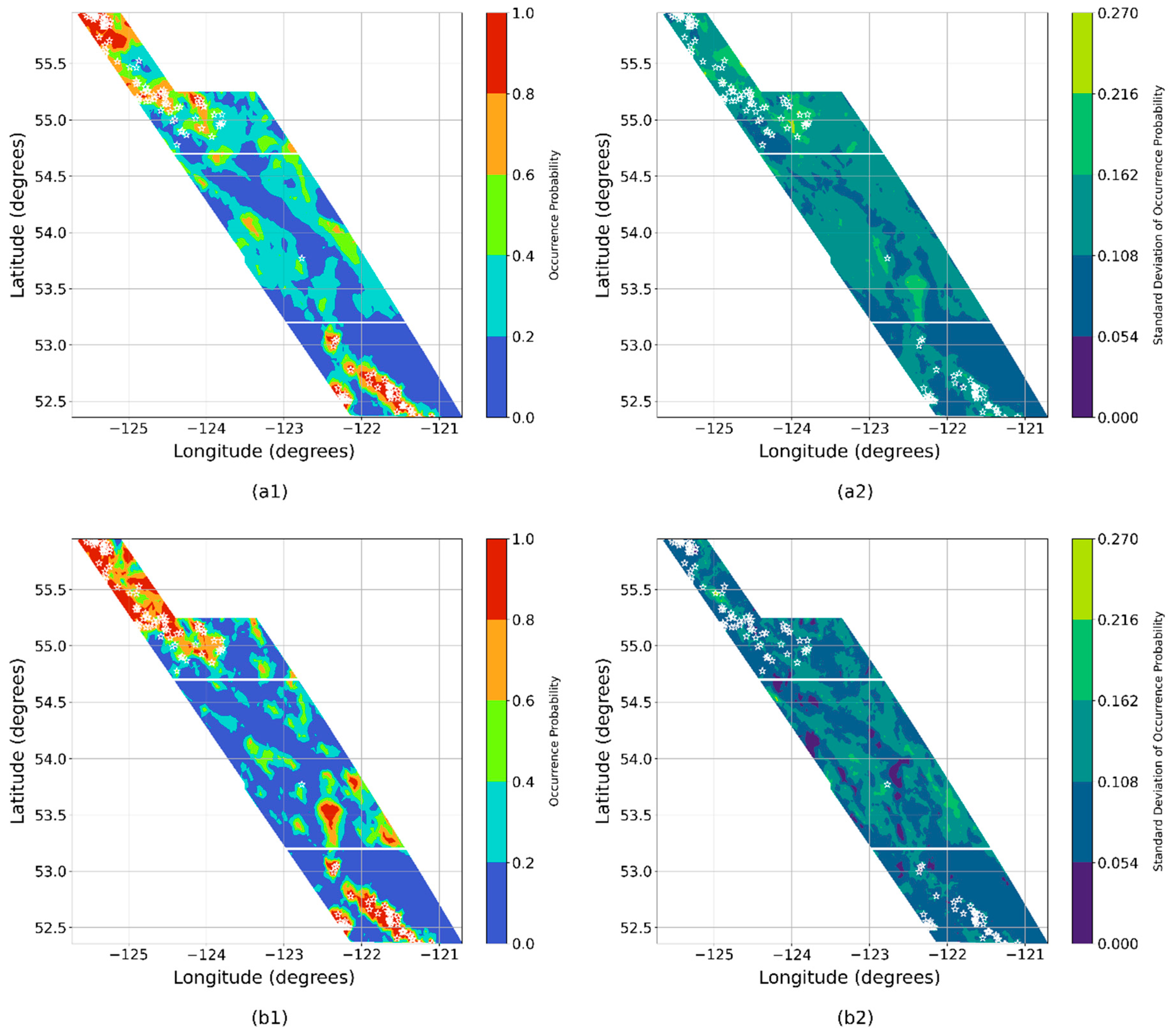
3.3. Copper Porphyry Prospectivity Maps
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. CNN and MAB Parameters
| CNN depth | 5 |
| FC depth | 2 |
| Dense size | 16 |
| Dropout rate | 0.1 |
| Learning rate | 0.0001 |
| Total epochs | 100 |
| Patch size | 0.114° |
| Batch size | 32 |
| αLRELU | 0.1 |
| Fmap size | 64 |
| Kernel size | 3 |
| Stride size | 1 |
| Decay Schedule | |
|---|---|
| Linear | |
| Exponential | |
| Rational | |
| Elliptical |
References
- Knox-Robinson, C.M.; Wyborn, L.A.I. Towards a holistic exploration strategy: Using Geographic Information Systems as a tool to enhance exploration. Aust. J. Earth Sci. 1997, 44, 453–463. [Google Scholar] [CrossRef]
- Reddy, R.K.T.; Bonham-Carter, G.F. A Decision-Tree Approach to Mineral Potential Mapping in Snow Lake Area, Manitoba. Can. J. Remote Sens. 1991, 17, 191–200. [Google Scholar] [CrossRef]
- Lawley, C.J.M.; Tschirhart, V.; Smith, J.W.; Pehrsson, S.J.; Schetselaar, E.M.; Schaeffer, A.J.; Houlé, M.G.; Eglington, B.M. Prospectivity modelling of Canadian magmatic Ni (±Cu±Co±PGE) sulphide mineral systems. Ore Geol. Rev. 2021, 132, 103985. [Google Scholar] [CrossRef]
- Cracknell, M.J.; Reading, A.M. Geological mapping using remote sensing data: A comparison of five machine learning algorithms, their response to variations in the spatial distribution of training data and the use of explicit spatial information. Comput. Geosci. 2014, 63, 22–33. [Google Scholar] [CrossRef]
- McMillan, M.; Haber, E.; Peters, B.; Fohring, J. Mineral prospectivity mapping using a VNet convolutional neural network. Lead. Edge 2021, 40, 99–105. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, Z.; Yang, J.; Hong, Z. Applications of data augmentation in mineral prospectivity prediction based on Convolutional Neural Networks. Comput. Geosci. 2022, 161, 105075. [Google Scholar] [CrossRef]
- Li, Q.; Chen, G.; Luo, L. Mineral prospectivity mapping using attention-based convolutional neural network. Ore Geol. Rev. 2023, 156, 105381. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Cukierski, W. Dogs vs. Cats. Kaggle. 2013. Available online: https://kaggle.com/competitions/dogs-vs-cats (accessed on 15 March 2024).
- Sahu, R.K.; Müller, J.; Park, J.; Varadharajan, C.; Arora, B.; Faybishenko, B.; Agarwal, D. Impact of input feature selection on groundwater level prediction from a multi-layer perceptron neural network. Front. Water 2020, 2, 573034. [Google Scholar] [CrossRef]
- Hall, M.A. Correlation-Based Feature Selection for Machine Learning. Ph.D. Thesis, The University of Waikato, Hamilton, New Zealand, 1999. [Google Scholar]
- Egwu, N.; Mrziglod, T.; Schuppert, A. Neural network input feature selection using structured L2L_2L2-Norm Penalization. Appl. Intell. 2022, 53, 5732–5749. [Google Scholar] [CrossRef]
- Zhang, P. A novel feature selection method based on global sensitivity analysis with application in machine learning-based prediction model. Appl. Soft Comput. 2019, 85, 105859. [Google Scholar] [CrossRef]
- Rodríguez-Galiano, V.F.; Sánchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Behnia, P.; Harris, J.; Sherlock, R.; Naghizadeh, M.; Vayavur, R. Mineral prospectivity mapping for orogenic gold mineralization in the Rainy River Area, Wabigoon Subprovince. Minerals 2023, 13, 1267. [Google Scholar] [CrossRef]
- Lou, Y.; Liu, Y. Mineral prospectivity mapping of tungsten polymetallic deposits using machine learning algorithms and comparison of their performance in the Gannan Region, China. Earth Space Sci. 2023, 10, e2022EA002596. [Google Scholar] [CrossRef]
- Lachaud, A.; Adam, M.; Mišković, I. Comparative study of random forest and support vector machine algorithms in mineral prospectivity mapping with limited training data. Minerals 2023, 13, 1073. [Google Scholar] [CrossRef]
- Kong, W.; Chen, J.; Zhu, P. Machine learning-based uranium prospectivity mapping and model explainability research. Minerals 2024, 14, 128. [Google Scholar] [CrossRef]
- Yang, S.; Yang, W.; Cui, T.; Zhang, M. Prediction and practical application of bauxite mineralization in Wuzhengdao area, Guizhou, China. PLoS ONE 2024, 19, e0305917. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, M.; Dan, S.; Li, M.; Li, Y.; Yang, D.; Wang, Y. Optimization of feature selection in mineral prospectivity using ensemble learning. Minerals 2024, 14, 970. [Google Scholar] [CrossRef]
- Geoscience BC. Quest Project. 2020. Available online: https://www.geosciencebc.com/major-projects/quest/ (accessed on 1 July 2023).
- Mitchinson, D.E.; Fournier, D.; Hart, C.J.R.; Astic, T.; Cowan, D.C.; Lee, R.G. Identification of New Porphyry Potential Under Cover in British Columbia; Geoscience BC Report 2022-07, MDRU Publication 457; Geoscience BC: Vancouver, BC, Canada, 2022. [Google Scholar]
- Montsion, R.M.; Saumur, B.M.; Acosta-Gongora, P.; Gadd, M.G.; Tschirhart, P.; Tschirhart, V. Knowledge-driven mineral prospectivity modeling in areas with glacial overburden: Porphyry Cu exploration in Quesnellia, British Columbia, Canada. Appl. Earth Sci. 2019, 128, 181–196. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Ben-David, S. Stochastic Gradient Descent. In Understanding Machine Learning: From Theory to Algorithms; Cambridge University Press: Cambridge, UK, 2014; pp. 150–166. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A. Multi-armed Bandits. In Reinforcement Learning: An Introduction; The MIT Press: Cambridge, MA, USA, 2020; pp. 25–47. [Google Scholar]
- Dirkx, R.; Dimitrakopoulos, R. Optimizing Infill Drilling Decisions Using Multi-Armed Bandits: Application in a Long-Term, Multi-Element Stockpile. Math. Geosci. 2018, 50, 35–52. [Google Scholar] [CrossRef]
- Silva, N.; Werneck, H.; Silva, T.; Pereira, A.C.; Rocha, L. Multi-armed bandits in recommendation systems: A survey of the state-of-the-art and future directions. Expert Syst. Appl. 2022, 197, 116669. [Google Scholar] [CrossRef]
- Moeini, M. Orthogonal bandit learning for portfolio selection under cardinality constraint. In Computational Science and Its Applications—ICCSA 2019; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; pp. 232–248. [Google Scholar]

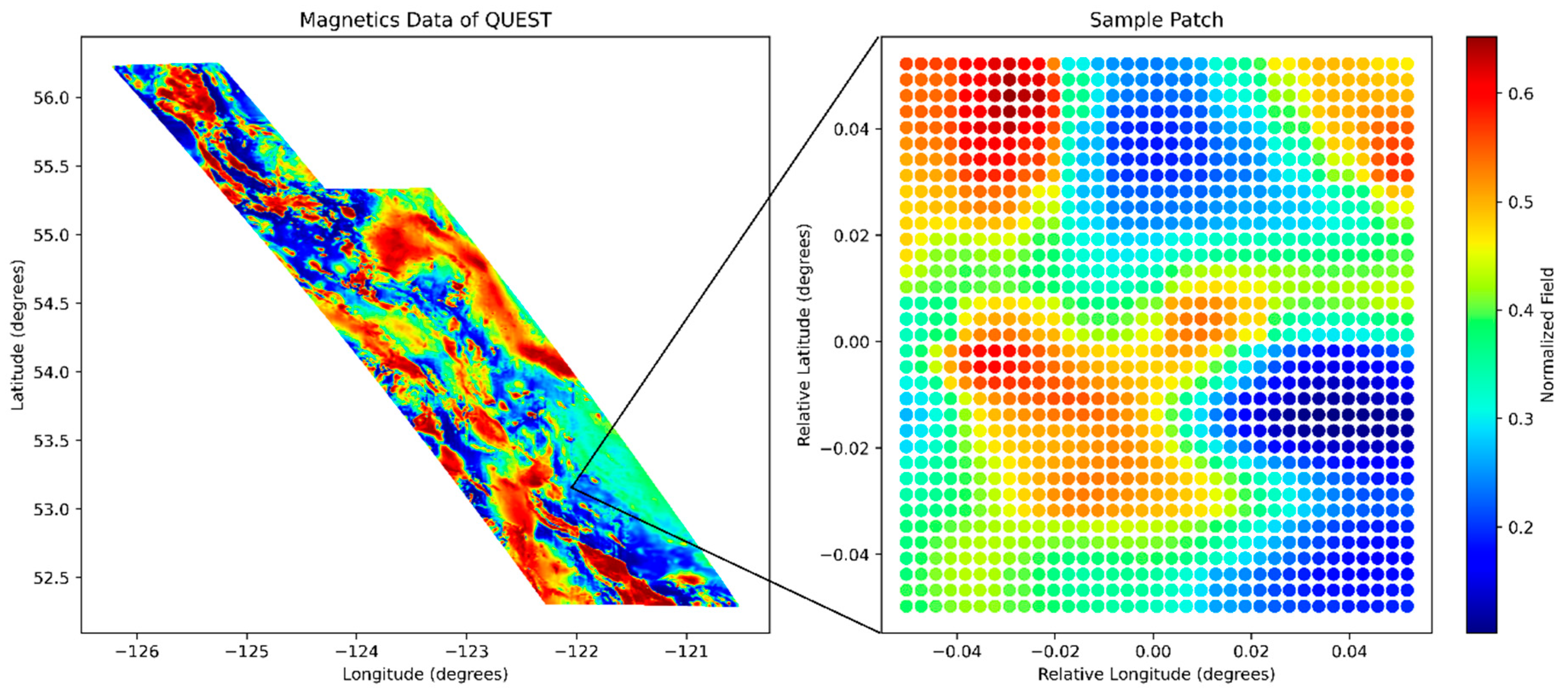
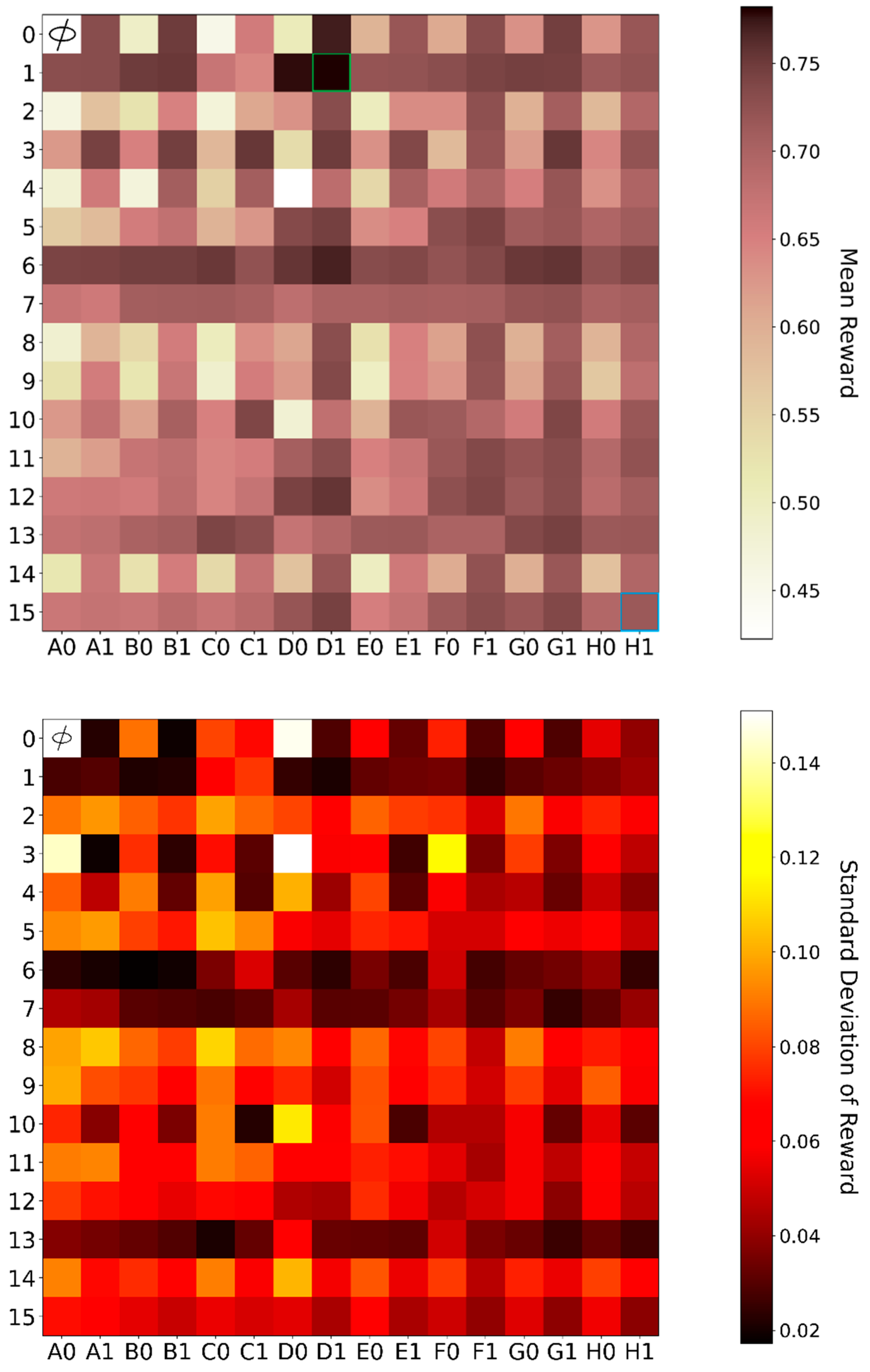
| 0 | No Geological Data | A0 | No Geophysical & No Geochemical Data |
| 1 | Geological Class | A1 | Geochemistry |
| 2 | Geological Subclass | B0 | Gravity |
| 3 | Geological Age | B1 | Gravity & Geochemistry |
| 4 | Distance to Nearest Fault | C0 | Magnetics |
| 5 | Geological Class & Subclass | C1 | Magnetics & Geochemistry |
| 6 | Geological Class & Age | D0 | VTEM |
| 7 | Geological Class & Distance to Nearest Fault | D1 | VTEM & Geochemistry |
| 8 | Geological Subclass & Age | E0 | Gravity & Magnetics |
| 9 | Geological Subclass & Distance to Nearest Fault | E1 | Gravity, Magnetics & Geochemistry |
| 10 | Geological Age & Distance to Nearest Fault | F0 | Gravity & VTEM |
| 11 | Geological Class, Subclass & Age | F1 | Gravity, VTEM & Geochemistry |
| 12 | Geological Class, Subclass & Distance to Nearest Fault | G0 | Magnetics & VTEM |
| 13 | Geological Class, Age & Distance to Nearest Fault | G1 | Magnetics, VTEM & Geochemistry |
| 14 | Geological Subclass, Age & Distance to Nearest Fault | H0 | Gravity, Magnetics & VTEM |
| 15 | Geological Class, Subclass, Age & Distance to Nearest Fault | H1 | Gravity, Magnetics, VTEM & Geochemistry |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kimiaghalam, A.; Noh, K.; Swidinsky, A. Geoscientific Input Feature Selection for CNN-Driven Mineral Prospectivity Mapping. Minerals 2025, 15, 1237. https://doi.org/10.3390/min15121237
Kimiaghalam A, Noh K, Swidinsky A. Geoscientific Input Feature Selection for CNN-Driven Mineral Prospectivity Mapping. Minerals. 2025; 15(12):1237. https://doi.org/10.3390/min15121237
Chicago/Turabian StyleKimiaghalam, Arya, Kyubo Noh, and Andrei Swidinsky. 2025. "Geoscientific Input Feature Selection for CNN-Driven Mineral Prospectivity Mapping" Minerals 15, no. 12: 1237. https://doi.org/10.3390/min15121237
APA StyleKimiaghalam, A., Noh, K., & Swidinsky, A. (2025). Geoscientific Input Feature Selection for CNN-Driven Mineral Prospectivity Mapping. Minerals, 15(12), 1237. https://doi.org/10.3390/min15121237






