Evaluation of Heterogeneous Ensemble Learning Algorithms for Lithological Mapping Using EnMAP Hyperspectral Data: Implications for Mineral Exploration in Mountainous Region
Abstract
1. Introduction
2. Geology of the Study Area
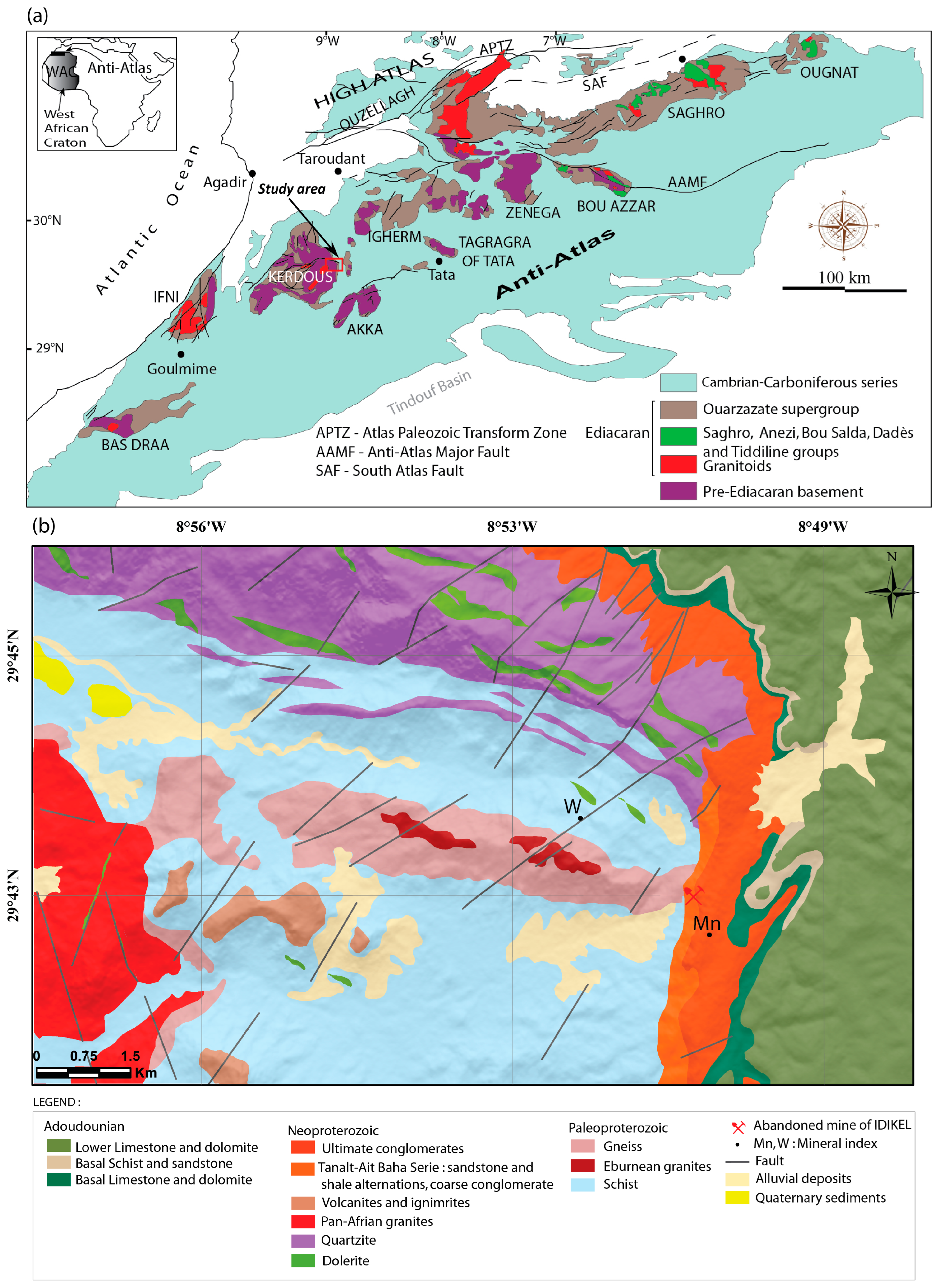
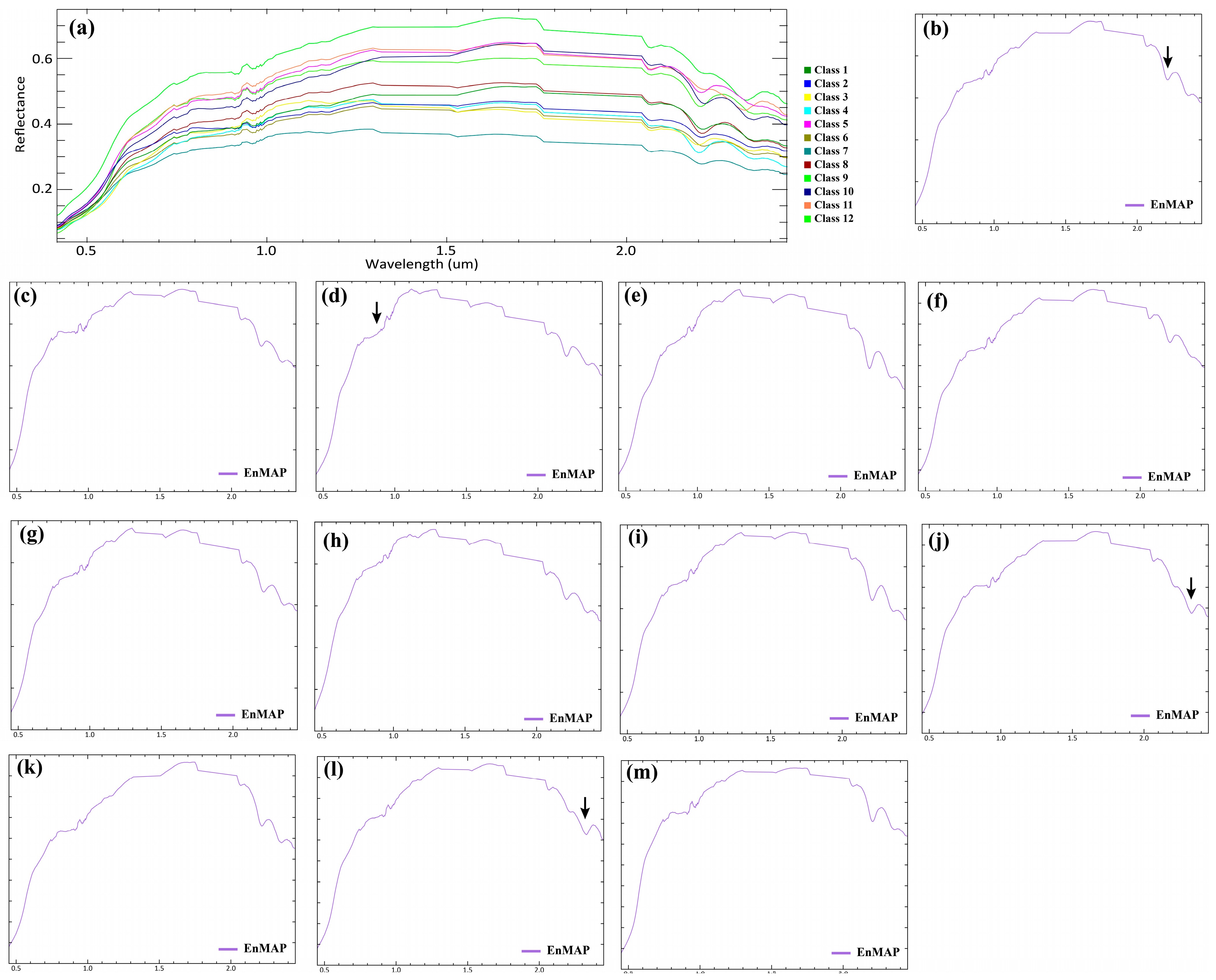
3. Materials and Methods
3.1. EnMAP Hyperspectral Dataset and Ground-Truth Information
3.2. Baseline Classification Algorithms
3.2.1. Support Vector Machines (SVM)
3.2.2. k-Nearest Neighbors (KNNs)
3.2.3. Multi-Layer Perceptron (MLP)
3.2.4. Decision Trees (DTs)
3.3. Homogeneous EL
3.3.1. Bagging
3.3.2. Boosting
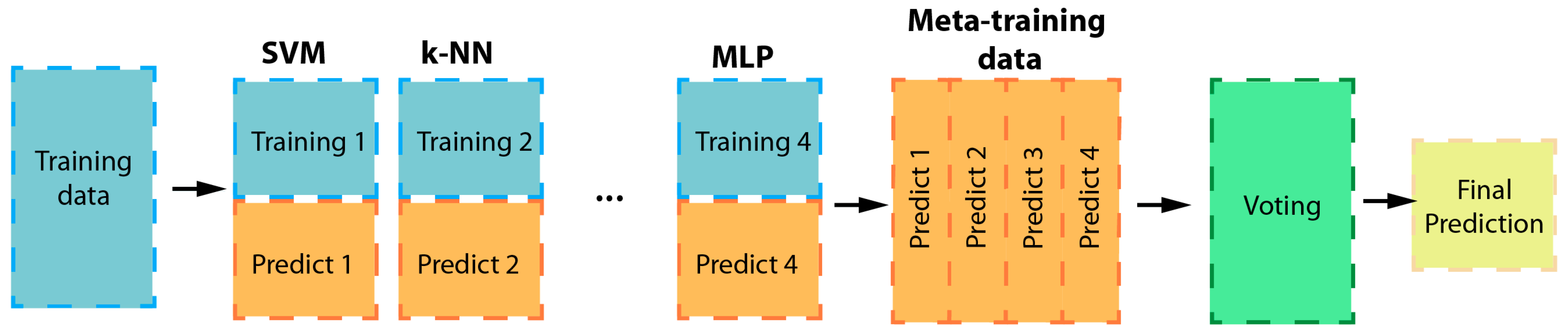
3.4. Heterogeneous EL Methods
3.4.1. Voting
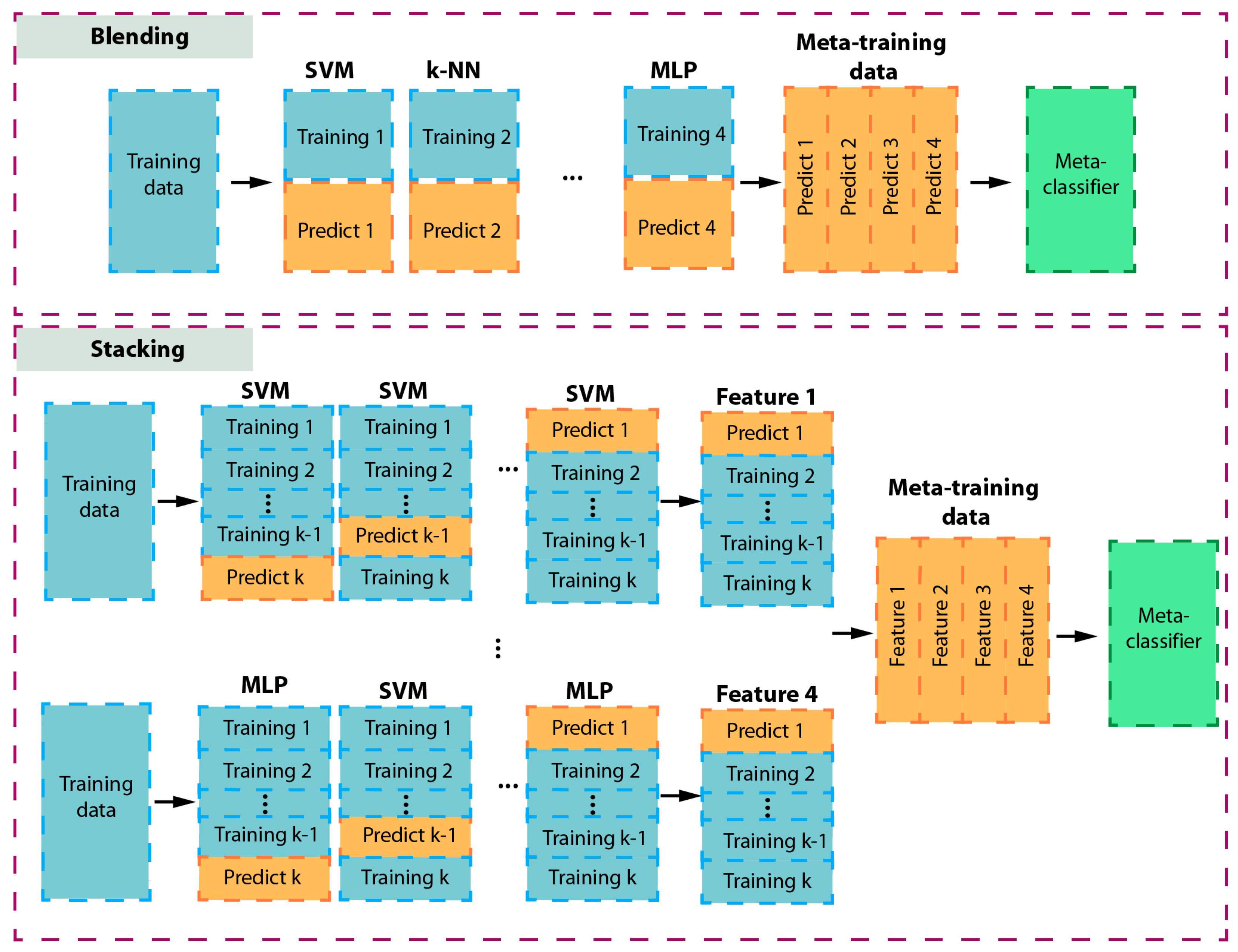
3.4.2. Stacking
3.4.3. Weighting
3.4.4. Blending
3.5. Accuracy Analysis
4. Experimental Results
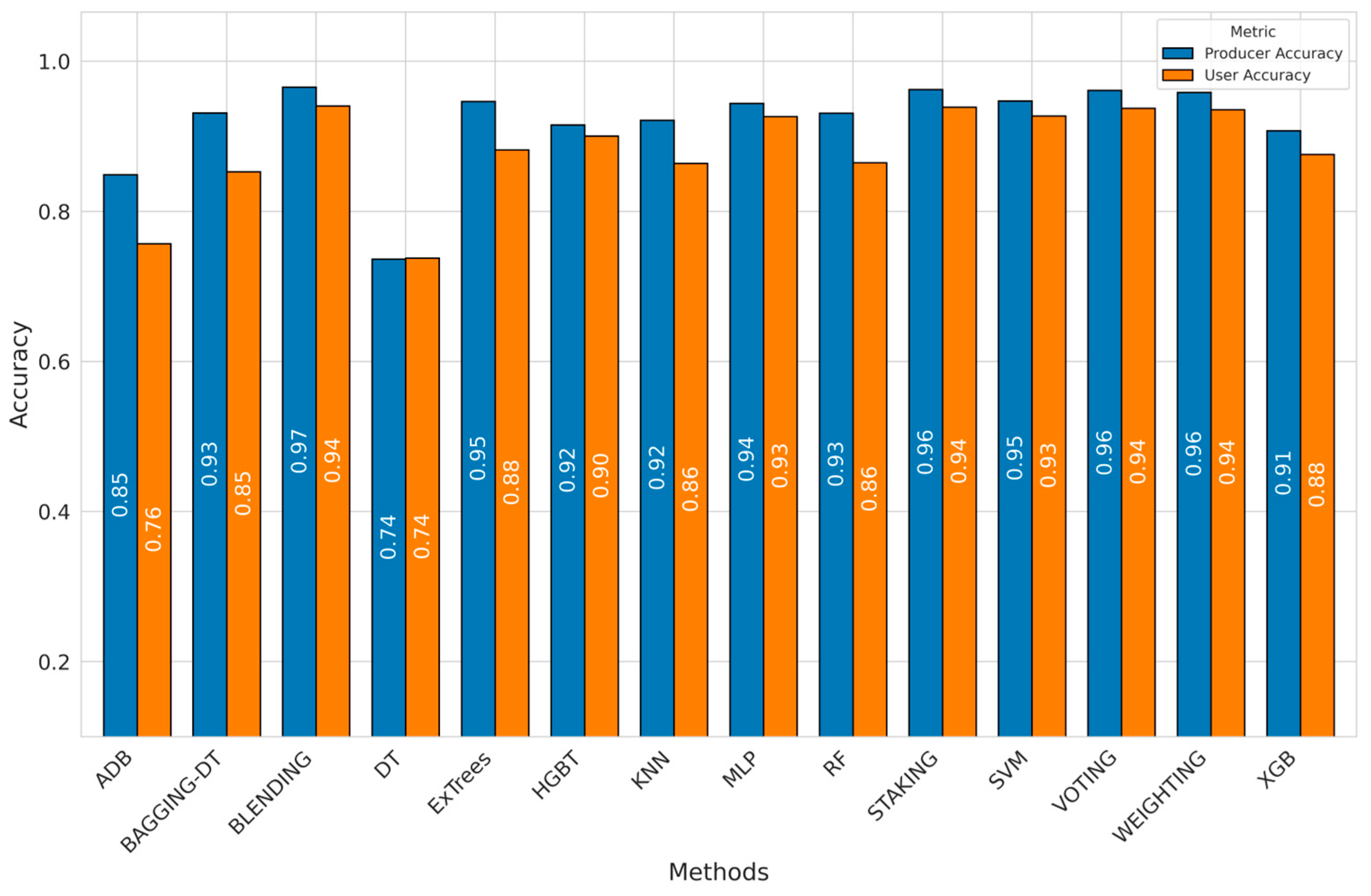
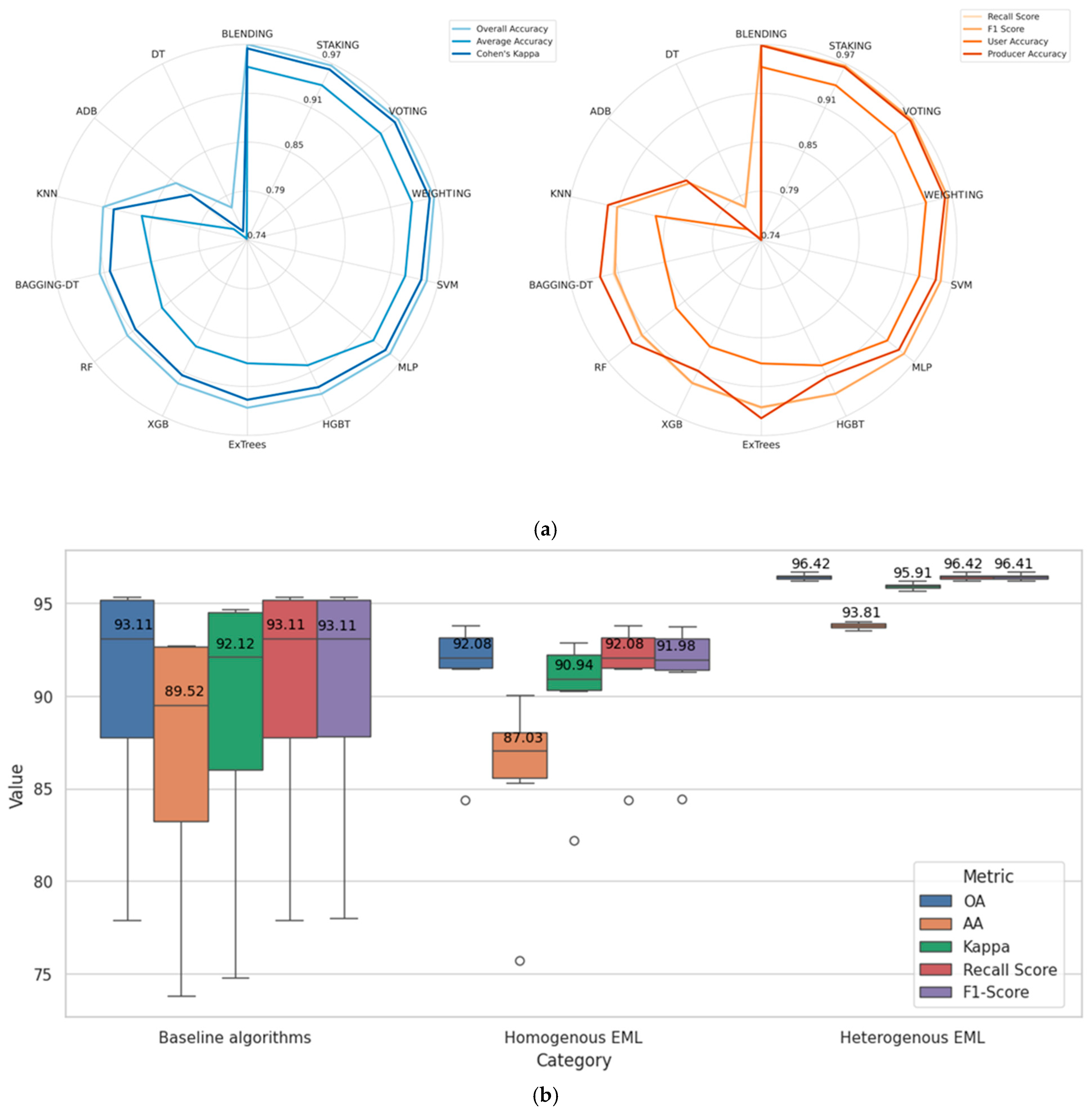
4.1. Performance Metrics over the Used Models


4.2. Training Time
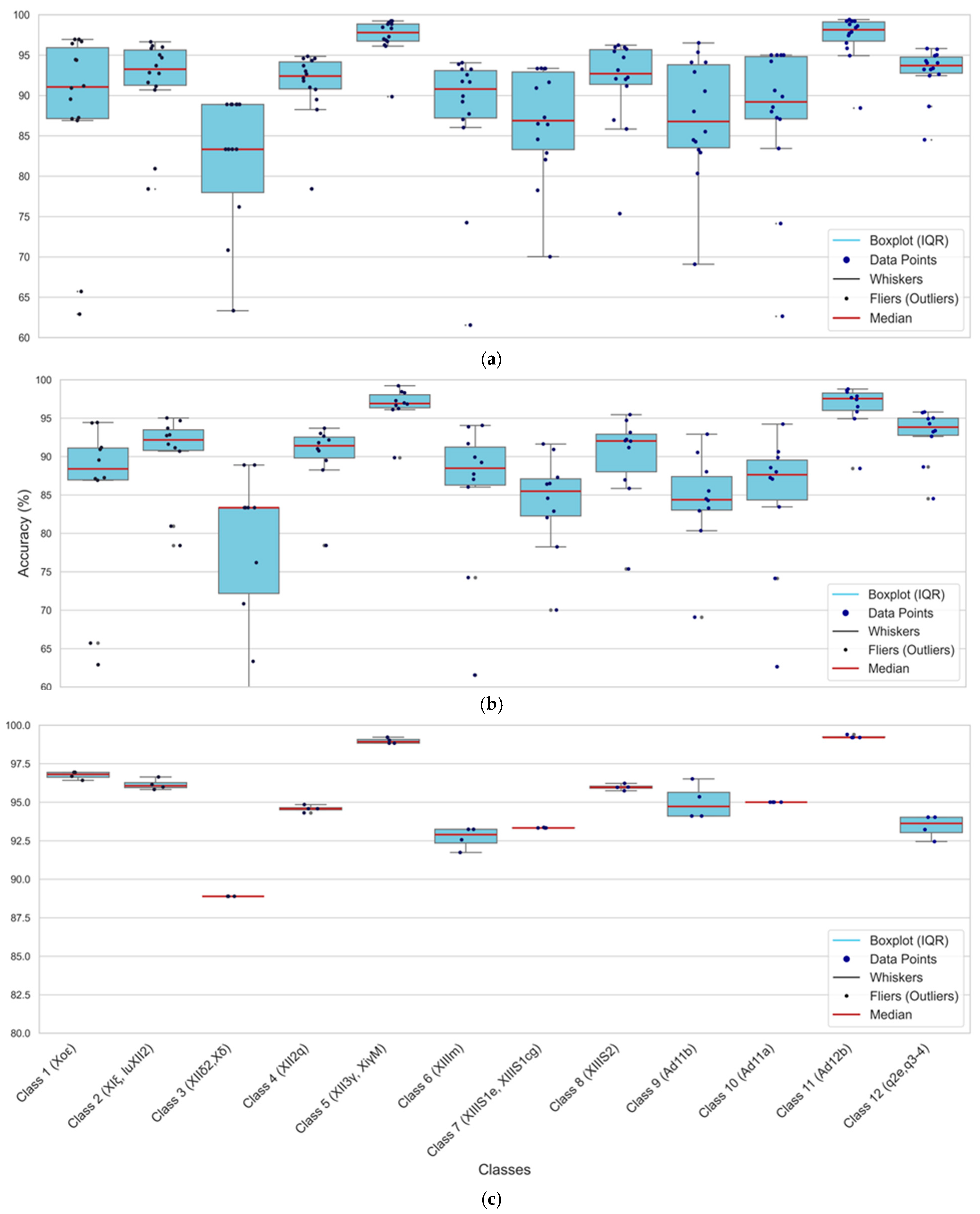
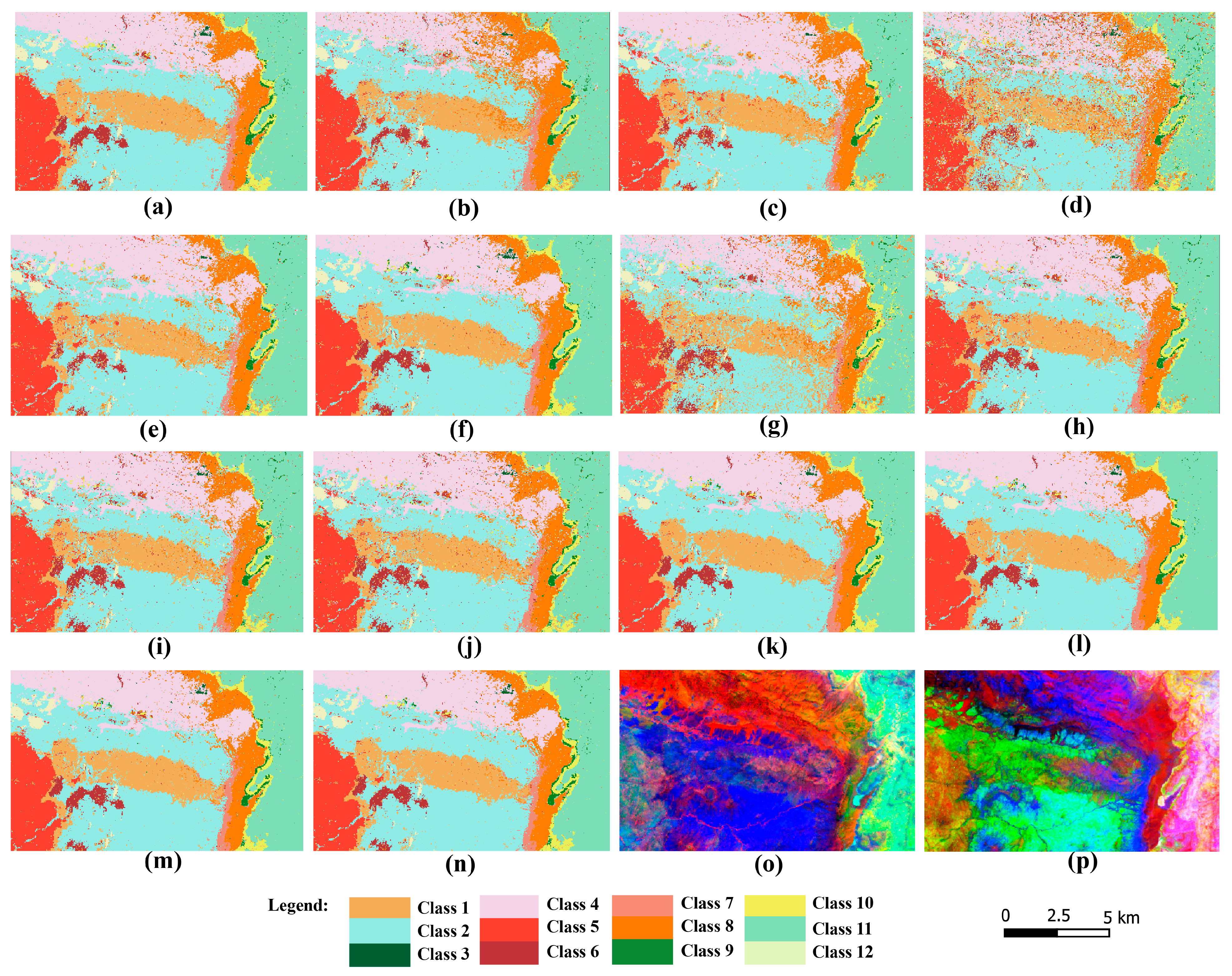
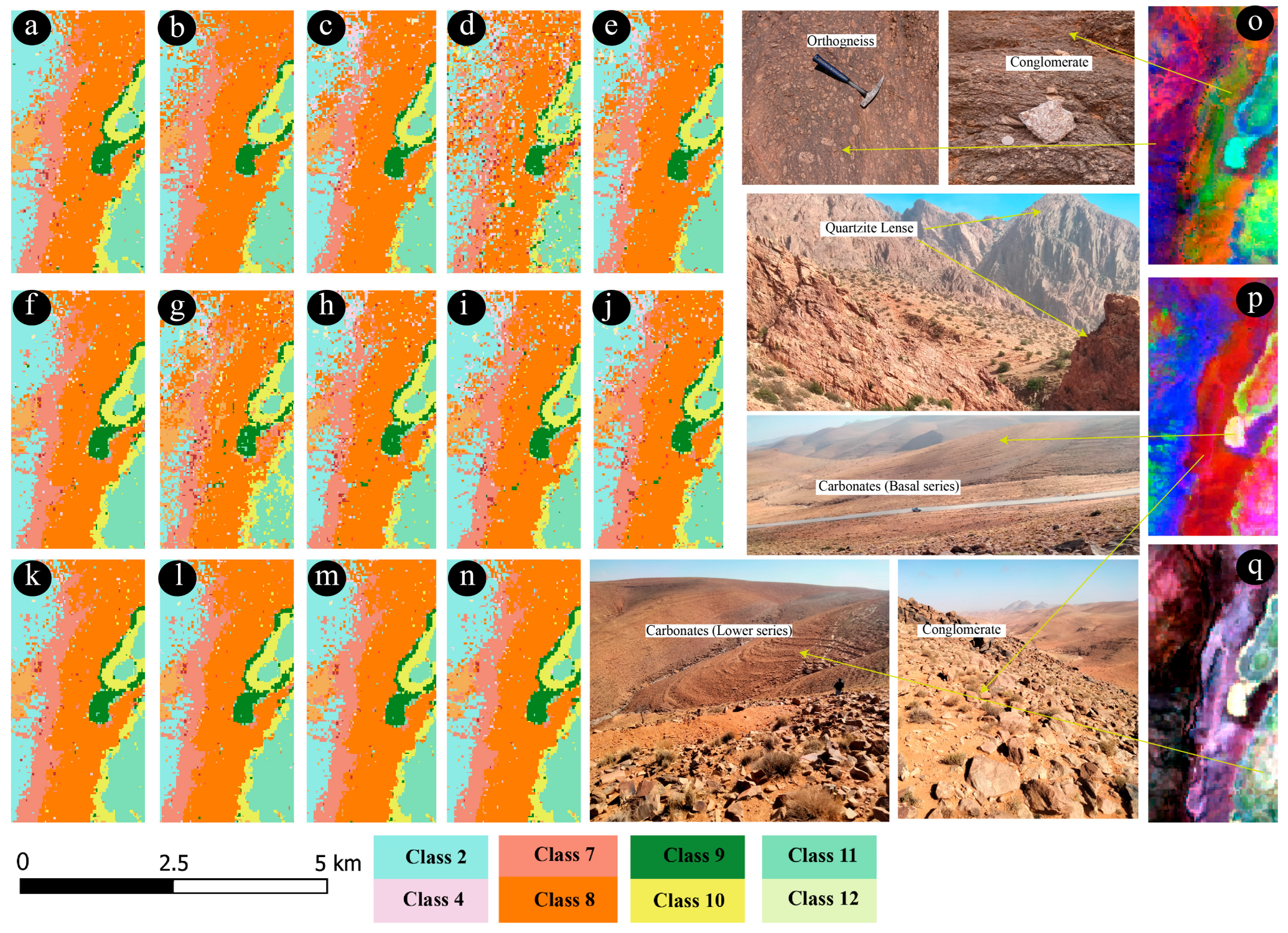
4.3. Accuracy of Lithological Unit Mapping
5. Discussion
5.1. Model Performance Benchmark
5.2. Limitations and Future Directions
6. Conclusions
- This study confirms that hyperspectral data, when paired with ensemble learning techniques, is highly effective for lithological mapping in hydrothermally altered complex terrains. The use of ensemble methods, particularly blending, stacking, voting, and weighting, provided valuable improvements in classification accuracy, demonstrating their suitability for mapping the complex geological features of the Ameln Valley.
- The findings suggest that the proposed EL models play a crucial role in enhancing the accurate and efficient HIS-based identification of lithological units, particularly in geologically similar regions. The benchmarking results demonstrate that the blending EL model achieves an impressive OA of 96.96%. This is further highlighted by the ability of other heterogeneous EL models to deliver consistent high and comparable accuracies while maintaining reasonable computational costs when taking into account the combination of multiple models and their lower computational cost compared to DL models, which are known for their relative complexity and for requiring substantial computational power.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Base Classifier | Hyperparameters | Optimized Parameter |
|---|---|---|
| SVM | C | 10 |
| gamma | 0.01 | |
| kernel | rbf | |
| KNN | n_neighbors | 11 |
| weights | distance | |
| distance | 2 | |
| algorithm | auto | |
| Leaf_size | 10 | |
| RF | n_estimators | 200 |
| max_features | sqrt | |
| max_depth | None | |
| min_samples_split | 2 | |
| min_samples_leaf | 1 | |
| DT | criterion | entropy |
| max_depth | None | |
| min_samples_split | 2 | |
| min_samples_leaf | 1 | |
| max_features | None | |
| Bagging–DT | Estimator | DT |
| n_estimators | 200 | |
| max_samples | 1.0 | |
| max_features | 0.5 | |
| MLP | hidden_layer_sizes | (150, 100, 50) |
| activation | ‘tanh’ | |
| solver | ‘adam’ | |
| alpha | 0.001 | |
| learning_rate | ‘constant’ | |
| max_iter | 100 | |
| AdaBoost | estimator | DT |
| n_estimators | 200 | |
| learning_rate | 1.0 | |
| estimator__max_depth | 3 | |
| XGBoost | n_estimators | 200 |
| max_depth | 6 | |
| learning_rate | 0.1 | |
| subsample | 0.8 | |
| colsample_bytree | 0.8 | |
| gamma | 0 | |
| Histogram-Based GBM | max_iter | 200 |
| learning_rate | 0.1 | |
| max_depth | 15 | |
| min_samples_leaf | 30 | |
| Extra Trees | n_estimators | 200 |
| max_depth | None | |
| min_samples_split | 2 | |
| min_samples_leaf | 1 |
References
- Cocks, T.; Jenssen, R.; Stewart, A.; Wilson, I.; Shields, T. The HyMapTM airborne hyperspectral sensor: The system, calibration and performance. In Proceedings of the 1st EARSeL Workshop on Imaging Spectroscopy, Zurich, Switzerland, 6–8 October 1998. [Google Scholar]
- Bedini, E.; Van Der Meer, F.; Van Ruitenbeek, F. Use of HyMap imaging spectrometer data to map mineralogy in the Rodalquilar caldera, southeast Spain. Int. J. Remote Sens. 2009, 30, 327–348. [Google Scholar] [CrossRef]
- Tripathi, M.K.; Govil, H. Evaluation of AVIRIS-NG hyperspectral images for mineral identification and mapping. Heliyon 2019, 5, e02931. [Google Scholar] [CrossRef]
- Adiri, Z.; El Harti, A.; Jellouli, A.; Maacha, L.; Azmi, M.; Zouhair, M.; Bachaoui, E.M. Mapping copper mineralization using EO-1 Hyperion data fusion with Landsat 8 OLI and Sentinel-2A in Moroccan Anti-Atlas. Geocarto Int. 2020, 35, 781–800. [Google Scholar] [CrossRef]
- Sharma, L.K.; Verma, R.K. AVIRIS-NG hyperspectral data analysis for pre-and post-MNF transformation using per-pixel classification algorithms. Geocarto Int. 2020, 37, 2083–2094. [Google Scholar] [CrossRef]
- Hajaj, S.; El Harti, A.; Pour, A.B.; Khandouch, Y.; Benaouiss, N.; Hashim, M.; Habashi, J.; Almasi, A. Recurrent-spectral convolutional neural networks (RecSpecCNN) architecture for hyperspectral lithological classification optimization. Earth Sci. Inform. 2025, 18, 125. [Google Scholar] [CrossRef]
- Wang, Z.; Zuo, R. An Evaluation of Convolutional Neural Networks for Lithological Mapping Based on Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 6414–6425. [Google Scholar] [CrossRef]
- Yin, J.; Li, N. Ensemble learning models with a Bayesian optimization algorithm for mineral prospectivity mapping. Ore Geol. Rev. 2022, 145, 104916. [Google Scholar] [CrossRef]
- Garini, S.A.; Shiddiqi, A.M.; Utama, W.; Jabar, O.A.; Insani, A.N.F. Enhanced Lithology Classification in Well Log Data Using Ensemble Machine Learning Techniques. In Proceedings of the 2024 IEEE International Conference on Artificial Intelligence and Mechatronics Systems (AIMS), Bandung, Indonesia, 21–23 February 2024; IEEE: New York, NY, USA, 2024. [Google Scholar]
- Li, C.; Li, F.; Liu, C.; Tang, Z.; Fu, S.; Lin, M.; Lv, X.; Liu, S.; Liu, Y. Deep learning-based geological map generation using geological routes. Remote Sens. Environ. 2024, 309, 114214. [Google Scholar] [CrossRef]
- Liu, J.; Guo, H.; He, Y.; Li, H. Vision Transformer-Based Ensemble Learning for Hyperspectral Image Classification. Remote Sens. 2023, 15, 5208. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Tangestani, M.H. Evaluating the VNIR-SWIR datasets of WorldView-3 for lithological mapping of a metamorphic-igneous terrain using support vector machine algorithm; a case study of Central Iran. Adv. Space Res. 2021, 68, 2421–2440. [Google Scholar] [CrossRef]
- Shebl, A.; Hissen, M.; Abdelaziz, M.I.; Csámer, Á. Lithological mapping enhancement by integrating Sentinel 2 and gamma-ray data utilizing support vector machine: A case study from Egypt. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102619. [Google Scholar] [CrossRef]
- Shirmard, H.; Farahbakhsh, E.; Heidari, E.; Pour, A.B.; Pradhan, B.; Müller, D.; Chandra, R. A comparative study of convolutional neural networks and conventional machine learning models for lithological mapping using remote sensing data. Remote Sens. 2022, 14, 819. [Google Scholar] [CrossRef]
- Ge, W.; Cheng, Q.; Tang, Y.; Jing, L.; Gao, C. Lithological classification using sentinel-2A data in the Shibanjing ophiolite complex in inner Mongolia, China. Remote Sens. 2018, 10, 638. [Google Scholar] [CrossRef]
- Jia, X.; Kuo, B.-C.; Crawford, M.M. Feature mining for hyperspectral image classification. Proc. IEEE 2013, 101, 676–697. [Google Scholar] [CrossRef]
- Ustuner, M. Randomized Principal Component Analysis for Hyperspectral Image Classification. In Proceedings of the 2024 IEEE Mediterranean and Middle-East Geoscience and Remote Sensing Symposium (M2GARSS), Oran, Algeria, 15–17 April 2024; IEEE: New York, NY, USA, 2024. [Google Scholar]
- Ganaie, M.A.; Hu, M.; Malik, A.K.; Tanveer, M.; Suganthan, P.N. Ensemble deep learning: A review. Eng. Appl. Artif. Intell. 2022, 115, 105151. [Google Scholar] [CrossRef]
- Majeed, R.; Abdullah, N.A.; Mushtaq, M.F.; Umer, M.; Nappi, M. Intelligent cyber-security system for iot-aided drones using voting classifier. Electronics 2021, 10, 2926. [Google Scholar] [CrossRef]
- Salman, H.A.; Kalakech, A.; Steiti, A. Random forest algorithm overview. Babylon. J. Mach. Learn. 2024, 2024, 69–79. [Google Scholar] [CrossRef]
- Heidari, N.; Khaloozadeh, H. Detection of Fault and Cyber Attack in Cyber-Physical System Based on Ensemble Convolutional Neural Network. In Proceedings of the 2024 10th International Conference on Control, Instrumentation and Automation (ICCIA), Kashan, Iran, 5–7 November 2024; IEEE: New York, NY, USA, 2024. [Google Scholar]
- Wang, H.; Ma, Z.; Qi, W.; Zhang, N.; Zhuang, H. A Research Review of the Stacking Classification Model. In Proceedings of the 2024 6th International Conference on Machine Learning, Big Data and Business Intelligence (MLBDBI), Hangzhou, China, 1–3 November 2024; IEEE: New York, NY, USA, 2024. [Google Scholar]
- Han, W.; Zhang, X.; Wang, Y.; Wang, L.; Huang, X.; Li, J.; Wang, S.; Chen, W.; Li, X.; Feng, R.; et al. A survey of machine learning and deep learning in remote sensing of geological environment: Challenges, advances, and opportunities. ISPRS J. Photogramm. Remote Sens. 2023, 202, 87–113. [Google Scholar] [CrossRef]
- Shebl, A.; Abriha, D.; Fahil, A.S.; El-Dokouny, H.A.; Elrasheed, A.A.; Csámer, Á. PRISMA hyperspectral data for lithological mapping in the Egyptian Eastern Desert: Evaluating the support vector machine, random forest, and XG boost machine learning algorithms. Ore Geol. Rev. 2023, 161, 105652. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, K.; Wang, J.; Zhao, J. Identifying and mapping alteration minerals using HySpex airborne hyperspectral data and random forest algorithm. Front. Earth Sci. 2022, 10, 871529. [Google Scholar] [CrossRef]
- Cardoso-Fernandes, J.; Teodoro, A.C.; Lima, A.; Roda-Robles, E. Evaluating the performance of support vector machines (SVMs) and random forest (RF) in Li-pegmatite mapping: Preliminary results. In Earth Resources and Environmental Remote Sensing/GIS Applications X; SPIE: Bellingham, DC, USA, 2019. [Google Scholar]
- Hajaj, S.; El Harti, A.; Jellouli, A.; Pour, A.B.; Himyari, S.M.; Hamzaoui, A.; Hashim, M. Evaluating the Performance of Machine Learning and Deep Learning Techniques to HyMap Imagery for Lithological Mapping in a Semi-Arid Region: Case Study from Western Anti-Atlas, Morocco. Minerals 2023, 13, 766. [Google Scholar] [CrossRef]
- Lin, N.; Liu, H.; Li, G.; Wu, M.; Li, D.; Jiang, R.; Yang, X. Extraction of mineralized indicator minerals using ensemble learning model optimized by SSA based on hyperspectral image. Open Geosci. 2022, 14, 1444–1465. [Google Scholar] [CrossRef]
- Farhadi, S.; Tatullo, S.; Konari, M.B.; Afzal, P. Evaluating StackingC and ensemble models for enhanced lithological classification in geological mapping. J. Geochem. Explor. 2024, 260, 107441. [Google Scholar] [CrossRef]
- Remidi, S.; Boutaleb, A.; Tachi, S.E.; Hasnaoui, Y.; Szczepanek, R.; Seffari, A. Ensemble machine learning model for exploration and targeting of Pb-Zn deposits in Algeria. Earth Sci. Inform. 2025, 18, 226. [Google Scholar] [CrossRef]
- Faik, F.; Belfoul, M.A.; Bouabdelli, M.; Hassenforder, B. The structures of the Late Neoproterozoic and Early Palæozoic cover of the Tata area, western Anti-Atlas, Morocco: Polyphased deformation or basement/cover interactions during the Variscan orogeny? J. Afr. Earth Sci. 2001, 32, 765–776. [Google Scholar] [CrossRef]
- Gasquet, D.; Levresse, G.; Cheilletz, A.; Azizi-Samir, M.R.; Mouttaqi, A. Contribution to a geodynamic reconstruction of the Anti-Atlas (Morocco) during Pan-African times with the emphasis on inversion tectonics and metallogenic activity at the Precambrian–Cambrian transition. Precambrian Res. 2005, 140, 157–182. [Google Scholar] [CrossRef]
- Hassenforder, B. La Tectonique Panafricaine et Varisque de L’Anti-Atlas Dans le Massif du Kerdous (Maroc); Université Louis Pasteur: Strasbourg, France, 1987; p. 249. [Google Scholar]
- Benssaou, M.; Hamoumi, N. The western Anti-Atlas of Morocco: Sedimentological and palaeogeographical formation studies in the Early Cambrian. J. Afr. Earth Sci. 2001, 32, 351–372. [Google Scholar] [CrossRef]
- Hajaj, S.; El Harti, A.; Jellouli, A.; Pour, A.B.; Himyari, S.M.; Hamzaoui, A.; Bensalah, M.K.; Benaouiss, N.; Hashim, M. HyMap imagery for copper and manganese prospecting in the east of Ameln valley shear zone (Kerdous inlier, western Anti-Atlas, Morocco). J. Spat. Sci. 2023, 69, 81–102. [Google Scholar] [CrossRef]
- Choubert, G.; Faure-Muret, A. The Precambrian Iron and Manganese Deposits of the Anti-Atlas. 1973. Available online: https://unesdoc.unesco.org/ark:/48223/pf0000007174 (accessed on 1 January 2021).
- Gasquet, D.; Ennih, N.; Liégeois, J.-P.; Soulaimani, A. The Pan-African Belt. In Continental Evolution: The Geology of Morocco; Springer: Berlin/Heidelberg, Germany, 2008; pp. 33–64. [Google Scholar]
- Hajaj, S.; El Harti, A.; Jellouli, A.; Pour, A.B.; Himyari, S.M.; Hamzaoui, A.; Bensalah, M.K.; Benaouis, N.; Hashim, M. HyMap airborne imaging spectroscopy for mineral potential mapping of cupriferous mineralization in a semi-arid region based on pixel/sub-pixel hydrothermal alteration minerals mapping–A case study. In Proceedings of the Copernicus Meetings, Vienna, Austria, 24–28 April 2023. [Google Scholar]
- Jellouli, A.; Chakouri, M.; Adiri, Z.; EL Hachimi, J.; Jari, A. Lithological and hydrothermal alteration mapping using Terra ASTER and Landsat-8 OLI multispectral data in the north-eastern border of Kerdous inlier, western Anti-Atlasic belt, Morocco. Artif. Satell. J. Planet. Geod. 2025, 60, 14–36. [Google Scholar] [CrossRef]
- Chabrillat, S.; Segl, K.; Foerster, S.; Brell, M.; Guanter, L.; Schickling, A. EnMAP Pre-Launch and Start Phase: Mission Update. In Proceedings of the IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; IEEE: New York, NY, USA, 2022. [Google Scholar]
- Chabrillat, S.; Guanter, L.; Kaufmann, H.; Foerster, S.; Beamish, A.; Brosinsky, A.; Wulf, H.; Asadzadeh, S.; Bochow, M.; Bohn, N.; et al. EnMAP Science Plan. 2022. Available online: https://www.enmap.org/data/doc/Science_Plan_EnMAP_2022_final.pdf (accessed on 2 February 2023).
- Kaufmann, H.; Segl, K.; Itzerott, S.; Bach, H.; Wagner, A.; Hill, J.; Heim, B.; Oppermann, K.; Heldens, W.; Stein, E.; et al. Hyperspectral Algorithms: Report in the Frame of EnMAP Preparation Activities. 2010. Available online: https://www.researchgate.net/publication/224992289_Hyperspectral_Algorithms_Report_in_the_frame_of_EnMAP_preparation_activities (accessed on 1 January 2021).
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386. [Google Scholar] [CrossRef]
- Apicella, A.; Donnarumma, F.; Isgrò, F.; Prevete, R. A survey on modern trainable activation functions. Neural Netw. 2021, 138, 14–32. [Google Scholar] [CrossRef] [PubMed]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Chern, C.-C.; Chen, Y.-J.; Hsiao, B. Decision tree–based classifier in providing telehealth service. BMC Med. Inform. Decis. Mak. 2019, 19, 104. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests-Random Features; Technical Report 567; Department of Statistics, University of California: Berkeley, CA, USA, 1999; p. 31. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef] [PubMed]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Cui, J.; Hang, H.; Wang, Y.; Lin, Z. GBHT: Gradient boosting histogram transform for density estimation. In Proceedings of the International Conference on Machine Learning, Online, 18–24 July 2021. [Google Scholar]
- Goumghar, L.; Hajaj, S.; Haida, S.; Kili, M.; Mridekh, A.; Khandouch, Y.; Jari, A.; El Harti, A.; El Mansouri, B. Analysis of Baseline and Novel Boosting Models for Flood-Prone Prediction and Explainability: Case from the Upper Drâa Basin (Morocco). Earth 2025, 6, 69. [Google Scholar] [CrossRef]
- Nhat-Duc, H.; Van-Duc, T. Comparison of histogram-based gradient boosting classification machine, random Forest, and deep convolutional neural network for pavement raveling severity classification. Autom. Constr. 2023, 148, 104767. [Google Scholar] [CrossRef]
- Xu, Q.; Yordanov, V.; Amici, L.; Brovelli, M.A. Landslide susceptibility mapping using ensemble machine learning methods: A case study in Lombardy, Northern Italy. Int. J. Digit. Earth 2024, 17, 2346263. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Li, H.; Wang, Y.; Wang, H.; Zhou, B. Multi-window based ensemble learning for classification of imbalanced streaming data. World Wide Web 2017, 20, 1507–1525. [Google Scholar] [CrossRef]
- Töscher, A.; Jahrer, M.; Bell, R.M. The bigchaos solution to the netflix grand prize. Netflix Prize. Doc. 2009, 1–52. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Claesen, M.; De Moor, B. Hyperparameter search in machine learning. arXiv 2015, arXiv:1502.02127. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Story, M.; Congalton, R.G. Accuracy assessment: A user’s perspective. Photogramm. Eng. Remote Sens. 1986, 52, 397–399. [Google Scholar]
- Sulaiman, R.; Azeman, N.H.; Mokhtar, M.H.H.; Mobarak, N.N.; Abu Bakar, M.H.; Bakar, A.A.A. Hybrid ensemble-based machine learning model for predicting phosphorus concentrations in hydroponic solution. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2024, 304, 123327. [Google Scholar] [CrossRef]
- Gupta, R.P. Remote Sensing Geology; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Hajaj, S.; El Harti, A.; Pour, A.B.; Jellouli, A.; Adiri, Z.; Hashim, M. A review on hyperspectral imagery application for lithological mapping and mineral prospecting: Machine learning techniques and future prospects. Remote Sens. Appl. Soc. Environ. 2024, 35, 101218. [Google Scholar] [CrossRef]
- Shirmard, H.; Farahbakhsh, E.; Müller, R.D.; Chandra, R. A review of machine learning in processing remote sensing data for mineral exploration. Remote Sens. Environ. 2022, 268, 112750. [Google Scholar] [CrossRef]
- Sabins, F.F. Remote sensing for mineral exploration. Ore Geol. Rev. 1999, 14, 157–183. [Google Scholar] [CrossRef]
- Peyghambari, S.; Zhang, Y. Hyperspectral remote sensing in lithological mapping, mineral exploration, and environmental geology: An updated review. J. Appl. Remote Sens. 2021, 15, 031501. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Giri, R.N.; Janghel, R.R.; Govil, H.; Mishra, G. A stacked ensemble learning-based framework for mineral mapping using AVIRIS-NG hyperspectral image. J. Earth Syst. Sci. 2024, 133, 107. [Google Scholar] [CrossRef]
- Li, H.; Cui, J.; Zhang, X.; Han, Y.; Cao, L. Dimensionality reduction and classification of hyperspectral remote sensing image feature extraction. Remote Sens. 2022, 14, 4579. [Google Scholar] [CrossRef]
- Hajaj, S.; El Harti, A.; Pour, A.B.; Khandouch, Y.; Üstüner, M.; Amiri, M.M. Balancing Hyperspectral Dimensionality Reduction and Information Preservation for Machine Learning-based Lithological Classification using EnMAP hyperspectral imagery. Remote Sens. Appl. Soc. Environ. 2025, 38, 101618. [Google Scholar] [CrossRef]
- Grewal, R.; Singh Kasana, S.; Kasana, G. Machine learning and deep learning techniques for spectral spatial classification of hyperspectral images: A comprehensive survey. Electronics 2023, 12, 488. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Khatami, R.; Mountrakis, G.; Stehman, S.V. A meta-analysis of remote sensing research on supervised pixel-based land-cover image classification processes: General guidelines for practitioners and future research. Remote Sens. Environ. 2016, 177, 89–100. [Google Scholar] [CrossRef]
- Du, P.; Xia, J.; Zhang, W.; Tan, K.; Liu, Y.; Liu, S. Multiple classifier system for remote sensing image classification: A review. Sensors 2012, 12, 4764–4792. [Google Scholar] [CrossRef] [PubMed]
- Ghoneim, S.M.; Hamimi, Z.; Abdelrahman, K.; Khalifa, M.A.; Shabban, M.; Abdelmaksoud, A.S. Machine learning and remote sensing-based lithological mapping of the Duwi Shear-Belt area, Central Eastern Desert, Egypt. Sci. Rep. 2024, 14, 17010. [Google Scholar] [CrossRef]
- Zhang, T.; Zhao, Z.; Dong, P.; Tang, B.-H.; Zhang, G.; Feng, L.; Zhang, X. Rapid lithological mapping using multi-source remote sensing data fusion and automatic sample generation strategy. Int. J. Digit. Earth 2024, 17, 2420824. [Google Scholar] [CrossRef]
- Njoku, A.O.; Mpinda, B.N.; Awe, O.O. Enhancing Predictive Performance Through Optimized Ensemble Stacking for Imbalanced Classification Problems, in Practical Statistical Learning and Data Science Methods: Case Studies from LISA 2020 Global Network, USA; Springer: Berlin/Heidelberg, Germany, 2024; pp. 575–595. [Google Scholar]
- Portes, L.; Pirot, G.; Nzikou, M.M.; Giraud, J.; Lindsay, M.; Jessell, M.; Cripps, E. Feature fusion-enhanced t-SNE image atlas for geophysical features discovery. Sci. Rep. 2025, 15, 17152. [Google Scholar] [CrossRef]

| SVM | kNN | RF | DT | MLP | ADB | XGB | ExTrees | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Class No (Sign) | UA | PA | UA | PA | UA | PA | UA | PA | UA | PA | UA | PA | UA | PA | UA | PA |
| Cl-1 (Xoε) | 98.28 | 90.48 | 82.76 | 91.72 | 85.06 | 89.16 | 63.79 | 62.01 | 96.55 | 92.31 | 70.11 | 61.31 | 90.8 | 88.27 | 88.51 | 93.33 |
| Cl-2 (XIξ, luXII2) | 92.04 | 97.31 | 92.04 | 91.17 | 89.81 | 92.46 | 78.66 | 78.16 | 93.95 | 96.09 | 79.62 | 82.24 | 90.76 | 94.68 | 92.68 | 92.97 |
| Cl-3 (XIIδ2,Xδ) | 77.78 | 100.0 | 66.67 | 100.0 | 66.67 | 100.0 | 66.67 | 60.0 | 77.78 | 100 | 11.11 | 100 | 66.67 | 85.71 | 66.67 | 100 |
| Cl-4 (XII2q) | 95.98 | 91.39 | 87.44 | 94.57 | 93.97 | 85.00 | 79.40 | 77.45 | 93.47 | 92.54 | 86.43 | 90.05 | 93.97 | 90.34 | 95.98 | 87.61 |
| Cl-5 (XII3γ, XiγM) | 98.83 | 99.61 | 97.28 | 97.28 | 99.22 | 94.44 | 89.49 | 90.20 | 98.44 | 98.44 | 96.5 | 96.88 | 98.44 | 94.05 | 100 | 96.62 |
| Cl-6 (XIIIm) | 90.91 | 84.51 | 83.33 | 88.71 | 83.33 | 96.49 | 57.58 | 65.52 | 92.42 | 95.31 | 74.24 | 74.24 | 86.36 | 87.69 | 83.33 | 100 |
| Cl-7 (XIIIS1e, XIIIS1cg) | 88.52 | 94.74 | 85.25 | 83.87 | 77.05 | 95.92 | 68.85 | 71.19 | 90.16 | 91.67 | 70.49 | 86 | 77.05 | 87.04 | 78.69 | 94.12 |
| Cl-8 (XIIIS2) | 94.97 | 95.94 | 96.48 | 77.42 | 94.97 | 89.15 | 77.39 | 73.33 | 94.47 | 94.95 | 89.95 | 81.74 | 92.46 | 92 | 94.47 | 89.52 |
| Cl- 9 (Ad11b) | 88.37 | 92.68 | 72.09 | 96.88 | 74.42 | 94.12 | 67.44 | 70.73 | 90.7 | 95.12 | 69.77 | 90.91 | 74.42 | 91.43 | 76.74 | 94.29 |
| Cl-10 (Ad11a) | 95.00 | 93.44 | 80.00 | 96.00 | 81.67 | 92.45 | 68.33 | 56.94 | 90 | 87.1 | 83.33 | 64.94 | 85 | 89.47 | 85 | 96.23 |
| Cl-11 (Ad12b) | 98.80 | 98.40 | 96.79 | 94.88 | 98.39 | 94.59 | 84.74 | 92.14 | 98.8 | 98.8 | 93.57 | 96.28 | 98.39 | 96.46 | 99.6 | 96.12 |
| Cl-12 (q2e,q3-4) | 93.22 | 98.21 | 96.61 | 93.44 | 93.22 | 93.22 | 83.05 | 85.96 | 94.92 | 90.32 | 83.05 | 94.23 | 96.61 | 91.94 | 96.61 | 95 |
| OA | 95.33 | 91.07 | 91.72 | 77.87 | 95.15 | 84.38 | 92.43 | 93.43 | ||||||||
| AA | 92.73 | 86.39 | 86.48 | 73.78 | 92.64 | 75.68 | 87.58 | 88.19 | ||||||||
| Kappa | 94.67 | 89.78 | 90.52 | 74.76 | 94.46 | 82.17 | 91.35 | 92.49 | ||||||||
| Recall Score | 95.33 | 91.07 | 91.72 | 77.87 | 95.15 | 84.38 | 92.43 | 93.43 | ||||||||
| F1-Score | 95.33 | 91.06 | 91.61 | 77.98 | 95.15 | 84.41 | 92.35 | 93.34 | ||||||||
| HT Time (s) | 272.317 | 75.5883 | 1241.85 | 58.2372 | 659.843 | 1322.95 | 2563.07 | 158.265 | ||||||||
| Training Time (s) | 1.0219 | 0.0013 | 3.3784 | 0.3655 | 4.6161 | 27.5388 | 5.711 | 1.0347 | ||||||||
| Bagging–DT | Boosting–HGB | Stacking | Voting | Weighting | Blending | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Class No (Sign) | UA | PA | UA | PA | UA | PA | UA | PA | UA | PA | UA | PA |
| Cl-1 (Xoε) | 85.63 | 88.17 | 91.95 | 90.40 | 98.85 | 93.99 | 98.85 | 95.03 | 98.85 | 95.03 | 98.85 | 94.51 |
| Cl-2 (XIξ, luXII2) | 91.40 | 89.97 | 90.45 | 96.93 | 94.90 | 97.39 | 94.90 | 97.07 | 94.59 | 97.06 | 95.86 | 97.41 |
| Cl-3 (XIIδ2,Xδ) | 66.67 | 100.0 | 66.67 | 75.00 | 77.78 | 100.0 | 77.78 | 100.0 | 77.78 | 100.0 | 77.78 | 100.0 |
| Cl-4 (XII2q) | 92.96 | 88.52 | 94.47 | 90.82 | 96.48 | 93.20 | 95.98 | 93.17 | 95.48 | 93.14 | 95.98 | 93.17 |
| Cl-5 (XII3γ, XiγM) | 98.83 | 93.38 | 98.83 | 95.13 | 98.83 | 99.22 | 98.83 | 98.83 | 98.83 | 98.83 | 99.22 | 99.22 |
| Cl-6 (XIIIm) | 80.30 | 98.15 | 95.45 | 92.65 | 93.94 | 91.18 | 93.94 | 92.54 | 92.42 | 91.04 | 93.94 | 92.54 |
| Cl-7 (XIIIS1e, XIIIS1cg) | 72.13 | 93.62 | 81.97 | 92.59 | 91.80 | 94.92 | 90.16 | 96.49 | 90.16 | 96.49 | 90.16 | 96.49 |
| Cl-8 (XIIIS2) | 94.47 | 87.85 | 94.97 | 91.30 | 95.48 | 96.45 | 95.98 | 95.98 | 95.98 | 95.50 | 95.98 | 96.46 |
| Cl- 9 (Ad11b) | 69.77 | 96.77 | 83.72 | 92.31 | 90.70 | 100.0 | 90.70 | 97.50 | 90.70 | 97.50 | 93.02 | 100.0 |
| Cl-10 (Ad11a) | 76.67 | 90.20 | 88.33 | 91.38 | 95.00 | 95.00 | 95.00 | 95.00 | 95.00 | 95.00 | 95.00 | 95.00 |
| Cl-11 (Ad12b) | 99.60 | 95.75 | 98.80 | 98.01 | 99.60 | 98.80 | 99.60 | 98.80 | 99.60 | 98.80 | 99.60 | 99.20 |
| Cl-12 (q2e,q3-4) | 94.92 | 94.92 | 94.92 | 91.80 | 93.22 | 94.83 | 93.22 | 93.22 | 93.22 | 91.67 | 93.22 | 94.83 |
| OA | 91.48 | 93.79 | 96.45 | 96.39 | 96.21 | 96.69 | ||||||
| AA | 85.28 | 90.04 | 93.88 | 93.75 | 93.55 | 94.05 | ||||||
| Kappa | 90.24 | 92.91 | 95.95 | 95.88 | 95.68 | 96.22 | ||||||
| Recall Score | 91.48 | 93.79 | 96.45 | 96.39 | 96.21 | 96.69 | ||||||
| F1-Score | 91.32 | 93.75 | 96.44 | 96.38 | 96.20 | 96.68 | ||||||
| HT Time (s) | 1078.62 | 1665.51 | 2249.6 | 2249.6 | 2249.6 | 2249.6 | ||||||
| Training Time (s) | 9.9043 | 7.0604 | 64.3961 | 13.8811 | 55.4483 | 9.7907 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hajaj, S.; El Harti, A.; Pour, A.B.; Khandouch, Y.; Fels, A.E.A.E.; Elhag, A.B.; Ghazouani, N.; Ustuner, M.; Laamrani, A. Evaluation of Heterogeneous Ensemble Learning Algorithms for Lithological Mapping Using EnMAP Hyperspectral Data: Implications for Mineral Exploration in Mountainous Region. Minerals 2025, 15, 833. https://doi.org/10.3390/min15080833
Hajaj S, El Harti A, Pour AB, Khandouch Y, Fels AEAE, Elhag AB, Ghazouani N, Ustuner M, Laamrani A. Evaluation of Heterogeneous Ensemble Learning Algorithms for Lithological Mapping Using EnMAP Hyperspectral Data: Implications for Mineral Exploration in Mountainous Region. Minerals. 2025; 15(8):833. https://doi.org/10.3390/min15080833
Chicago/Turabian StyleHajaj, Soufiane, Abderrazak El Harti, Amin Beiranvand Pour, Younes Khandouch, Abdelhafid El Alaoui El Fels, Ahmed Babeker Elhag, Nejib Ghazouani, Mustafa Ustuner, and Ahmed Laamrani. 2025. "Evaluation of Heterogeneous Ensemble Learning Algorithms for Lithological Mapping Using EnMAP Hyperspectral Data: Implications for Mineral Exploration in Mountainous Region" Minerals 15, no. 8: 833. https://doi.org/10.3390/min15080833
APA StyleHajaj, S., El Harti, A., Pour, A. B., Khandouch, Y., Fels, A. E. A. E., Elhag, A. B., Ghazouani, N., Ustuner, M., & Laamrani, A. (2025). Evaluation of Heterogeneous Ensemble Learning Algorithms for Lithological Mapping Using EnMAP Hyperspectral Data: Implications for Mineral Exploration in Mountainous Region. Minerals, 15(8), 833. https://doi.org/10.3390/min15080833








