Integrated Bioprocess and Response Surface Methodology-Based Design for Hydraulic Conductivity Reduction Using Sporosarcina pasteurii
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design and Parameters
2.2. Overview of Experimental Design (DoE)
2.3. Explanation of Response Surface Methodology
- Sum of Squares (SS): Measures the total variation in the data, dividing it into contributions from different sources, such as treatments and error.
- Degrees of Freedom (df): Represents the number of independent values available to estimate parameters, indicating the amount of usable information in the analysis.
- Mean Square (MS): Obtained by dividing each sum of squares by its associated degrees of freedom; it reflects the variance for each source. The treatment mean square indicates differences between group means and helps test the significance of model factors.
- F-ratio (F value): The ratio of the treatment mean square to the error mean square. This statistic is used to test hypotheses and is compared against a critical value from the F-distribution based on a chosen significance level (typically α = 0.05).
- p-value: Indicates the probability that the observed results occurred under the null hypothesis. A p-value below 0.05 generally suggests that the observed effects are statistically significant and not due to random variation.
3. Results and Discussion
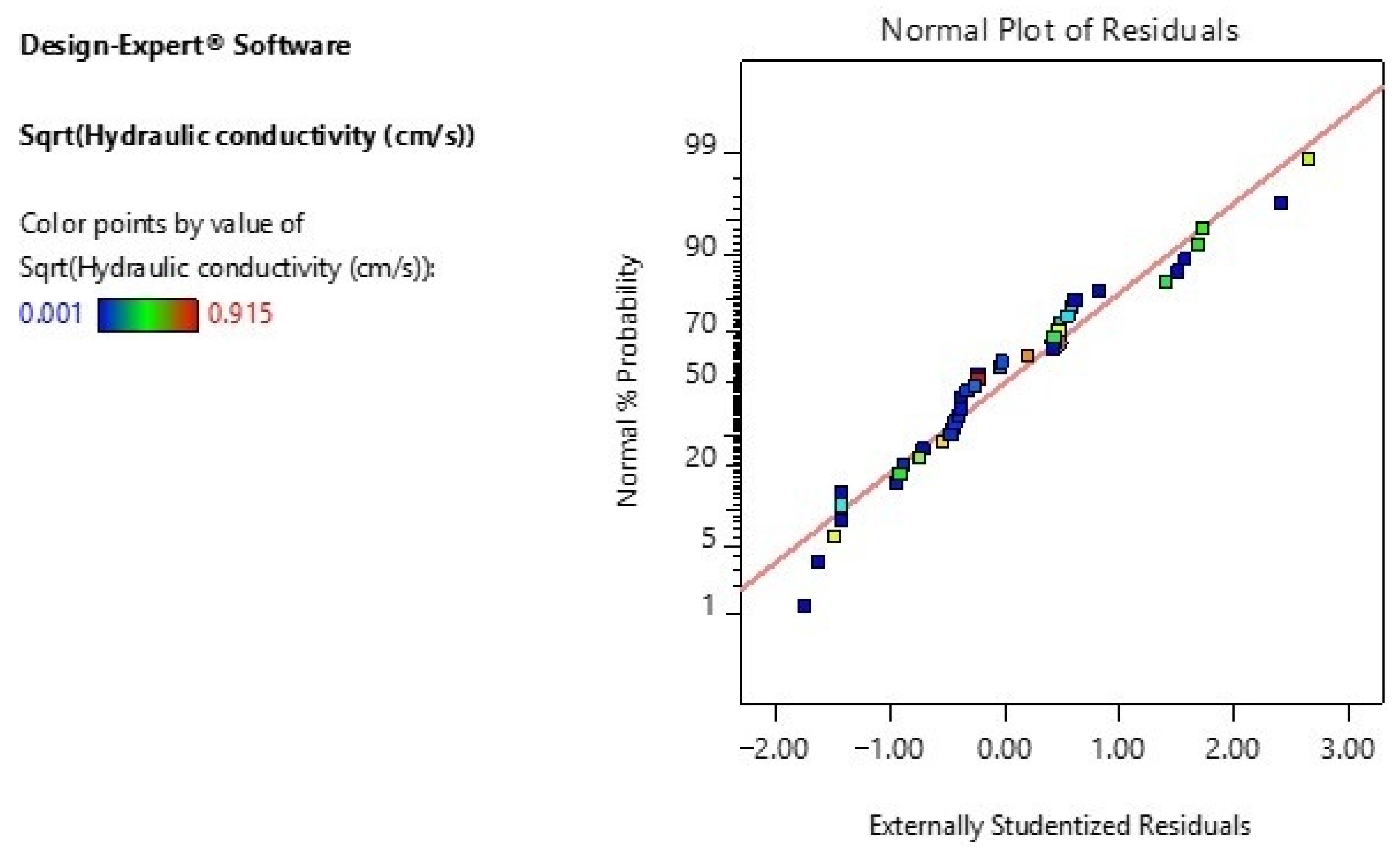
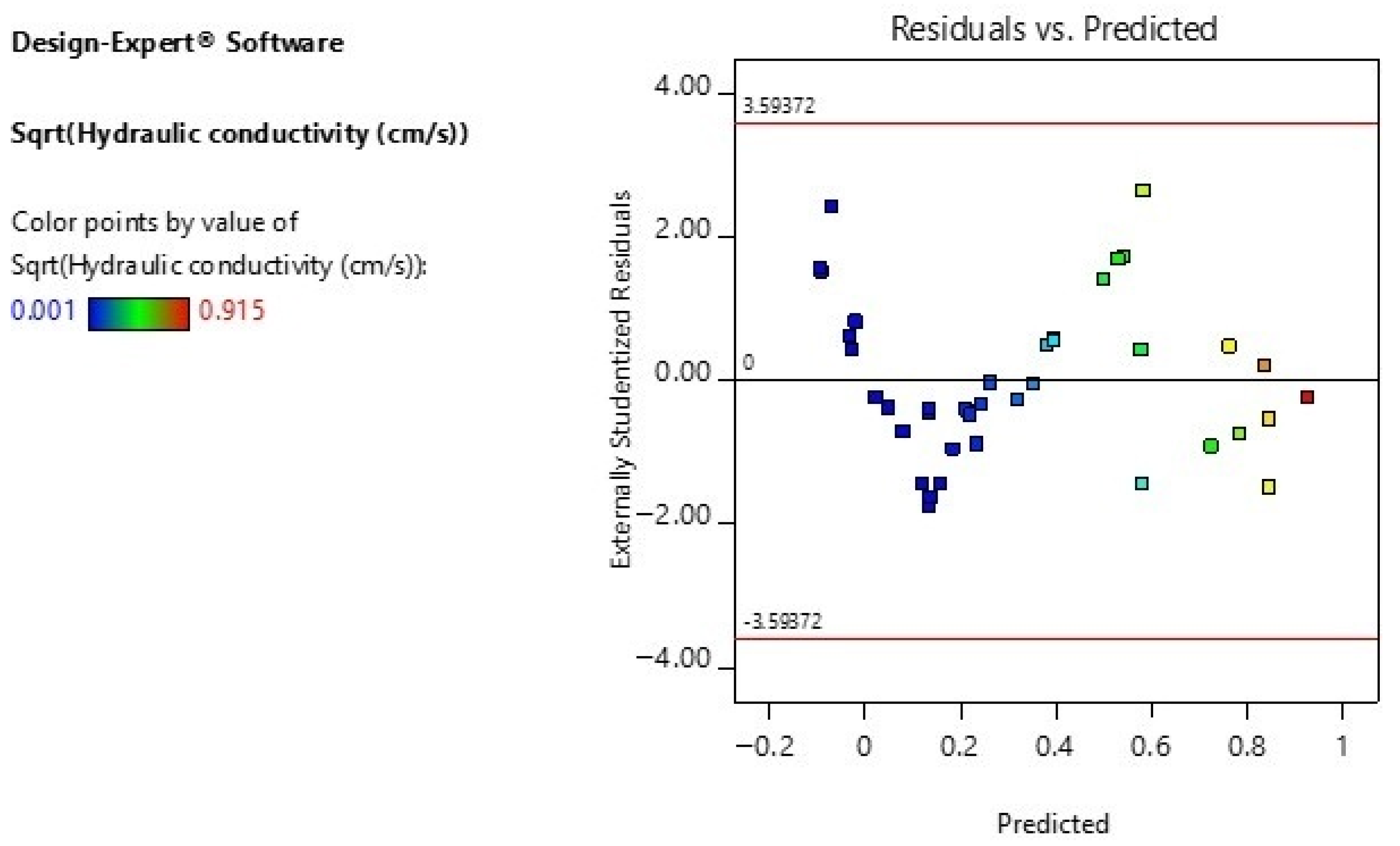
3.1. Normal Probability Plot of Residuals
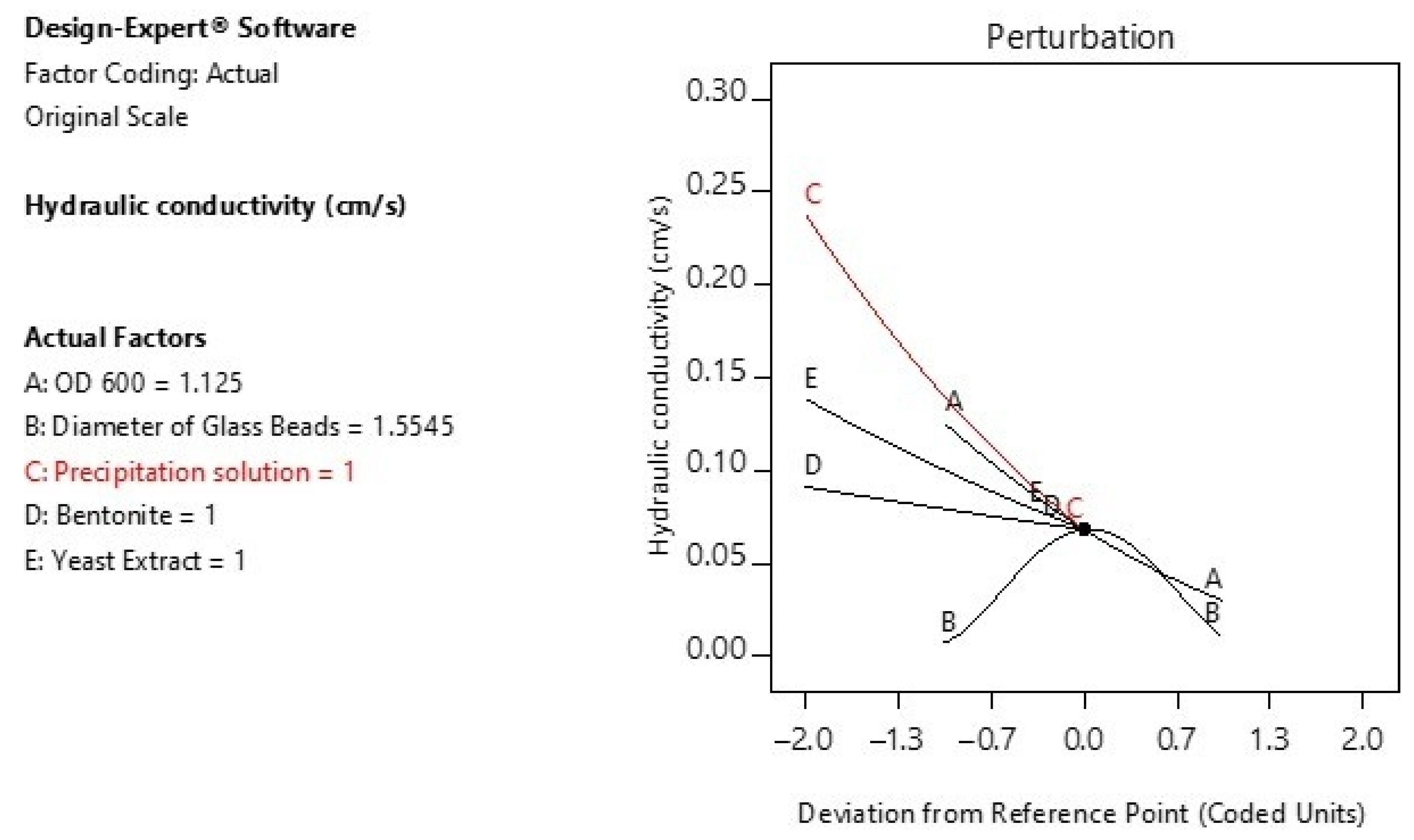
3.2. Perturbation Analysis
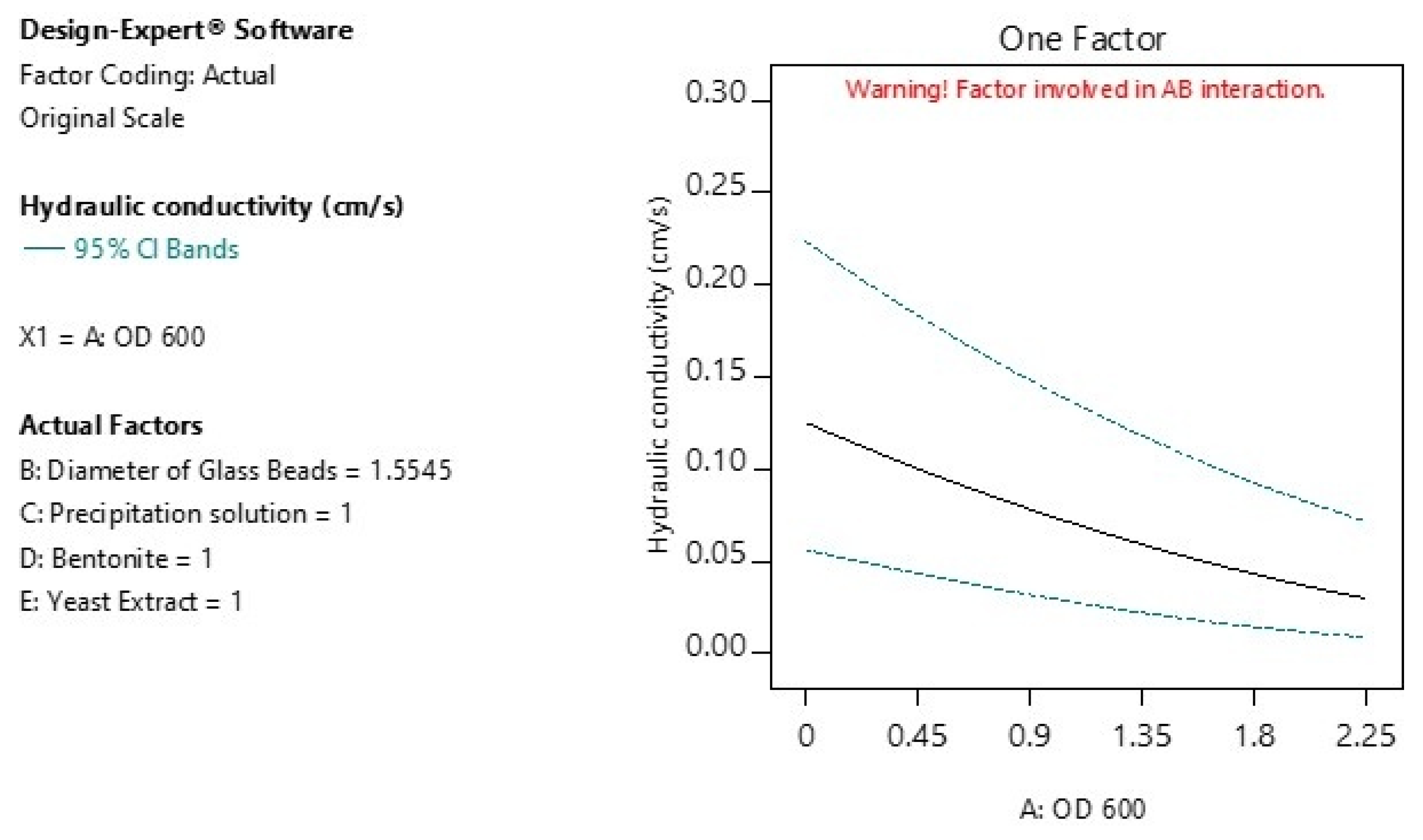
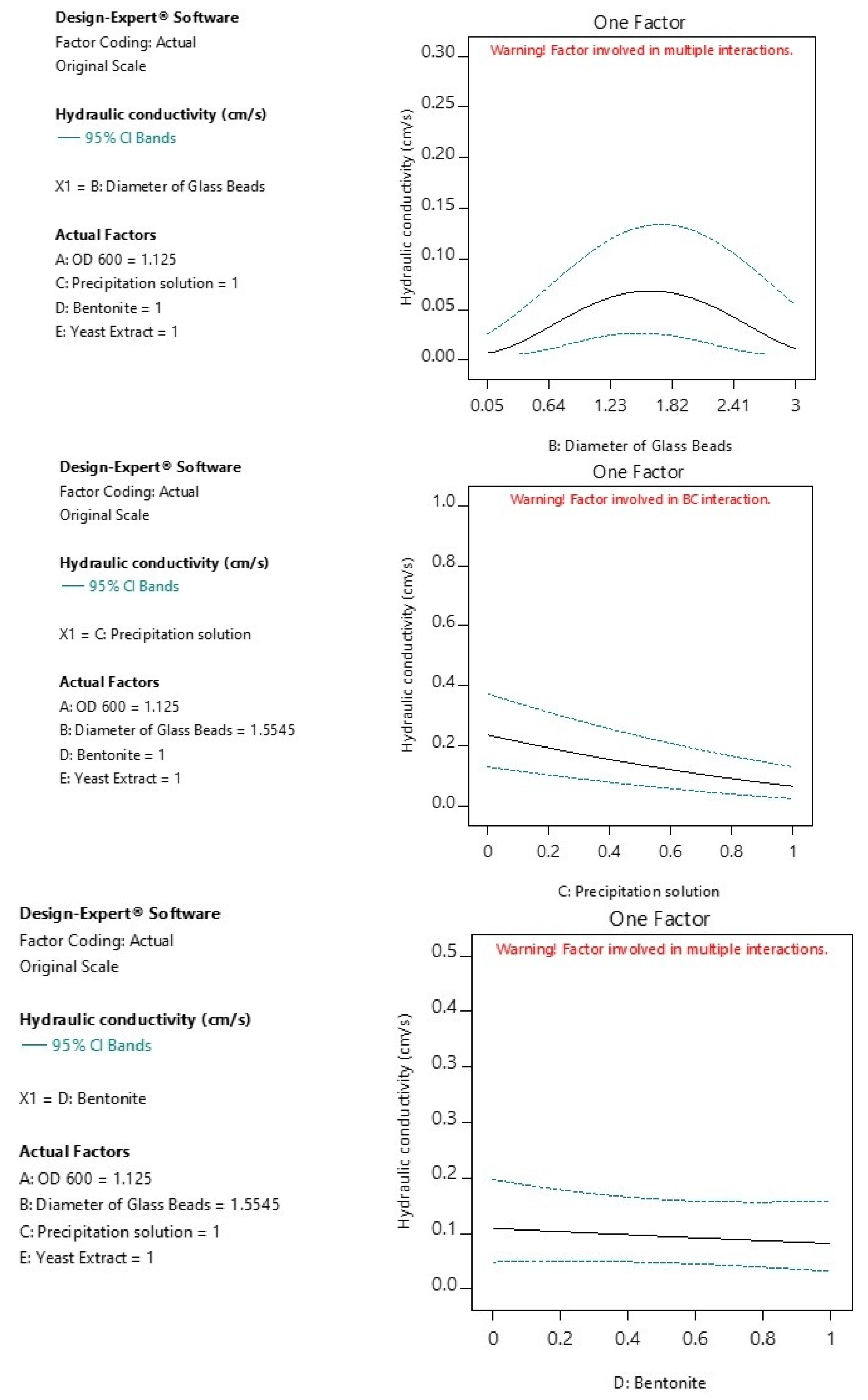
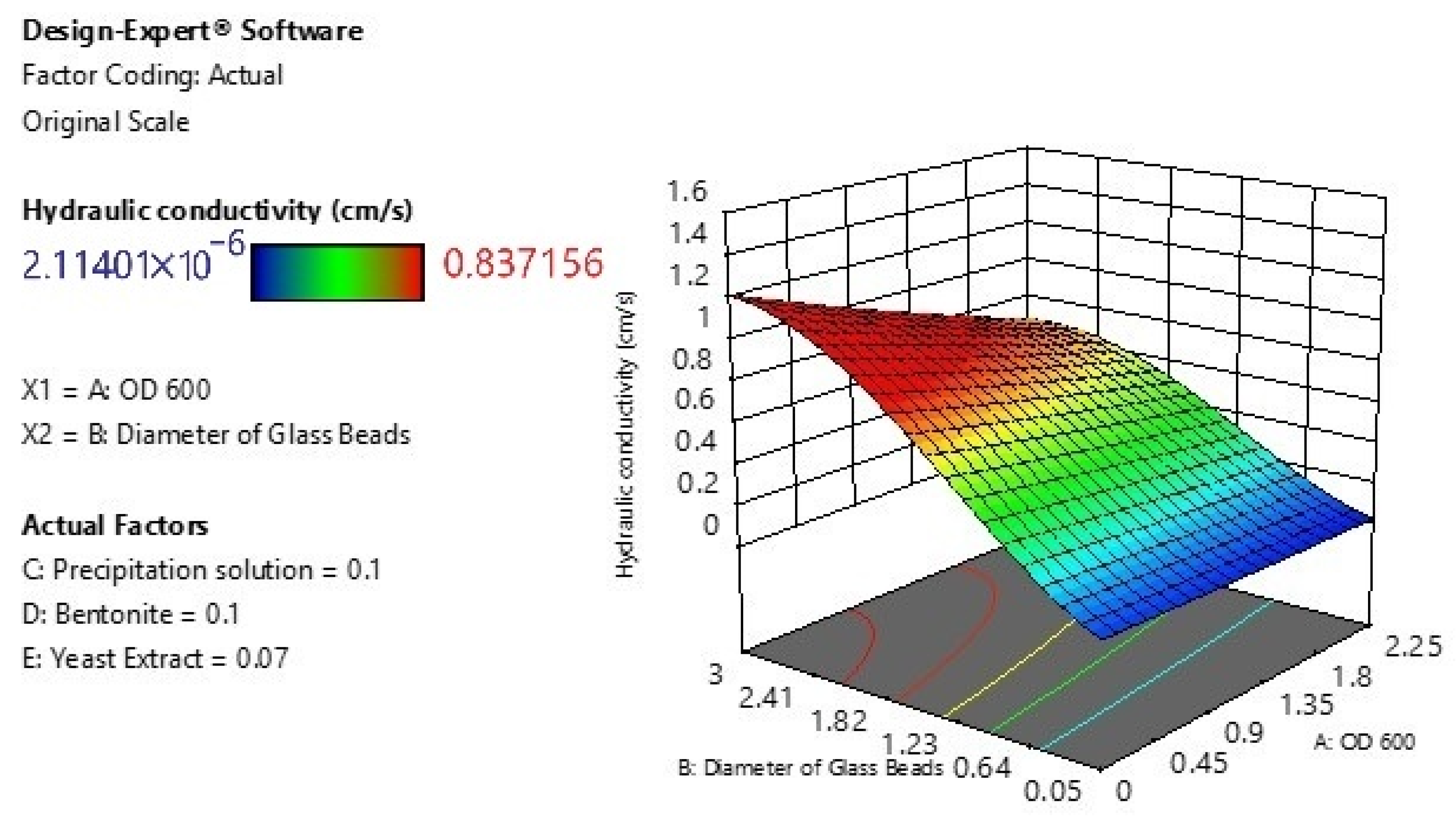
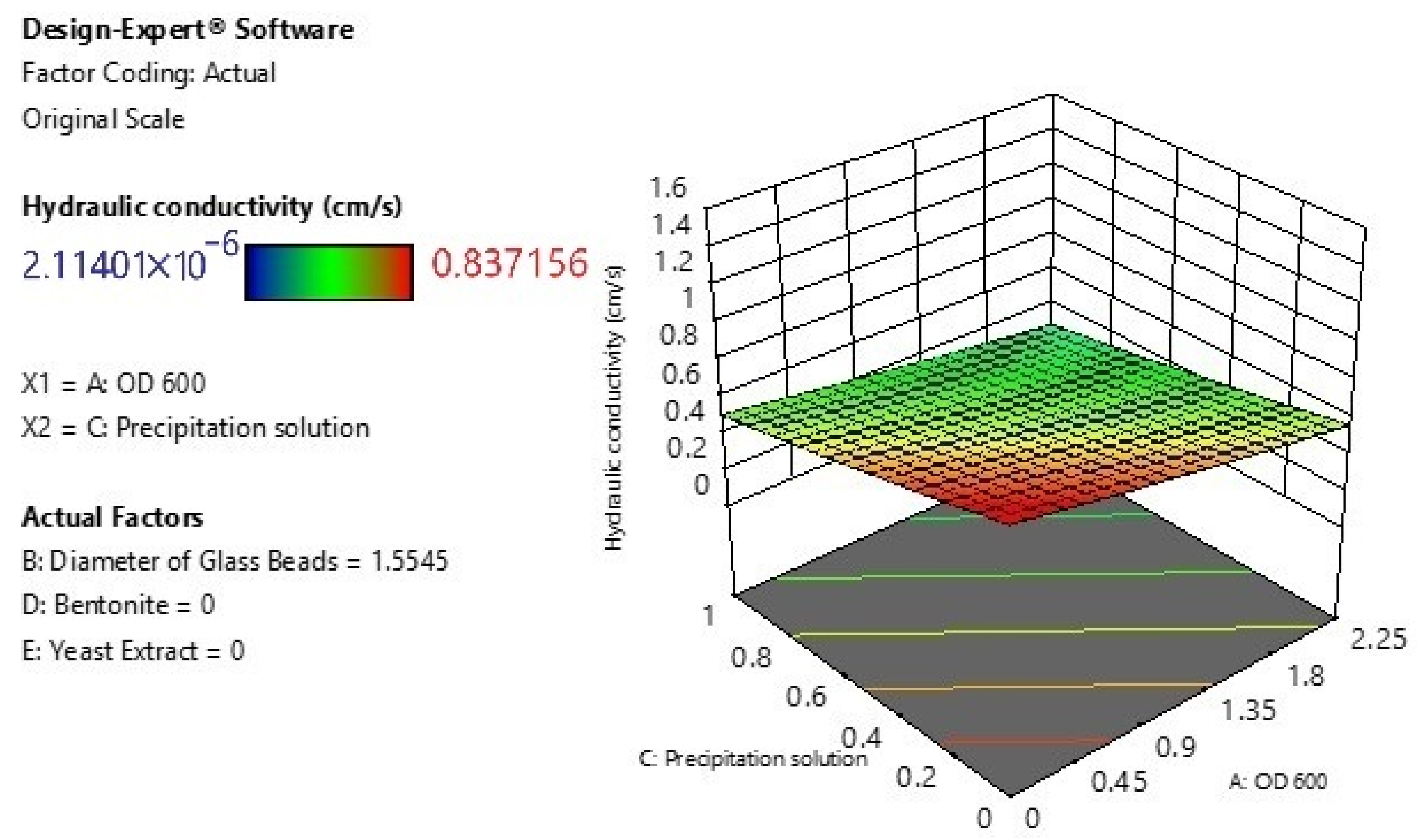
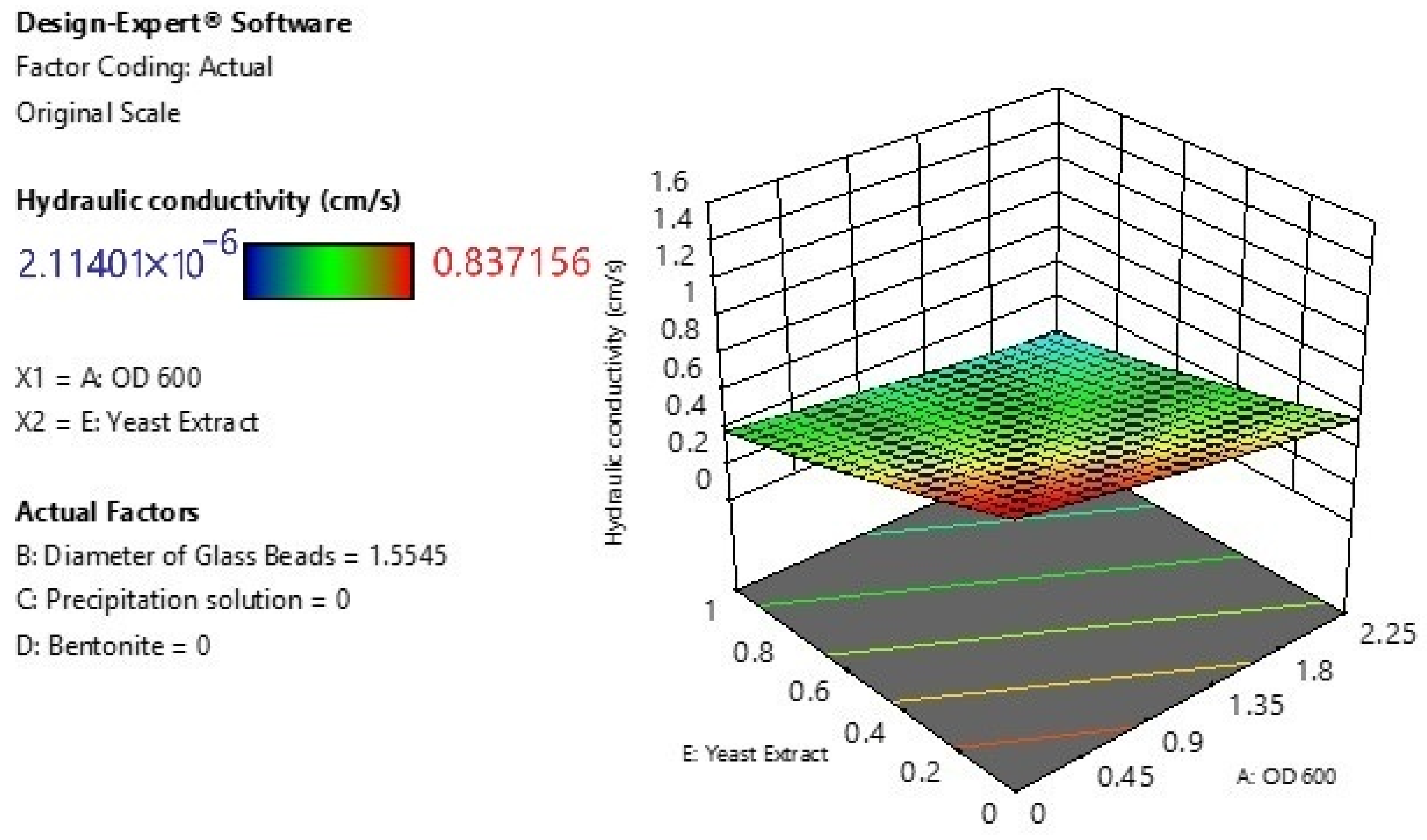
3.3. Main Effects of Individual Factors
- Factor A—OD600: Shows a moderate negative effect on hydraulic conductivity with increasing values, but the impact remains small.
- Factor B—Diameter of Glass Beads: Exhibits minimal influence, with a shallow curvature suggesting a weak interaction with other variables.
- Factor C—Precipitation Solution: Demonstrates the most significant effect, showing a strong inverse relationship with hydraulic conductivity. The broader CI bands reflect some variability.
- Factor D—Bentonite and E—Yeast Extract: Both display negligible effects, with nearly flat slopes and narrow confidence bands. While bentonite and yeast extract exhibited minimal main effects (p < 0.05), their significance emerged through interaction terms.
0.136384 × Bentonite − 0.137911 × Yeast Extract − 0.026521 × OD600 * Diameter of Glass Beads − 0.081325 ×
Diameter of Glass Beads × Precipitation solution − 0.074226 × Diameter of Glass Beads × Bentonite −
0.119793 × Diameter of Glass Beads × Yeast Extract + 0.209455 × Bentonite × Yeast Extract − 0.092460 ×
Diameter of Glass Beads2
0.0547 × B × D − 0.0883 × B × E + 0.0524 × D × E − 0.2012 × B2
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Taharia, M.d.; Dey, D.; Das, K.; Sukul, U.; Chen, J.-S.; Banerjee, P.; Dey, G.; Sharma, R.K.; Lin, P.-Y.; Chen, C.-Y. Microbial Induced Carbonate Precipitation for Remediation of Heavy Metals, Ions and Radioactive Elements: A Comprehensive Exploration of Prospective Applications in Water and Soil Treatment. Ecotoxicol. Environ. Saf. 2024, 271, 115990. [Google Scholar] [CrossRef]
- Spencer, C.A.; Sass, H.; Van Paassen, L. Increased Microbially Induced Calcium Carbonate Precipitation (MICP) Efficiency in Multiple Treatment Sand Biocementation Processes by Augmentation of Cementation Medium with Ammonium Chloride. Geotechnics 2023, 3, 1047–1068. [Google Scholar] [CrossRef]
- Erdmann, N.; Strieth, D. Influencing Factors on Ureolytic Microbiologically Induced Calcium Carbonate Precipitation for Biocementation. World J. Microbiol. Biotechnol. 2023, 39, 61. [Google Scholar] [CrossRef]
- Chittoori, B.C.S.; Rahman, T.; Burbank, M. Microbial-Facilitated Calcium Carbonate Precipitation as a Shallow Stabilization Alternative for Expansive Soil Treatment. Geotechnics 2021, 1, 558–572. [Google Scholar] [CrossRef]
- Song, M.; Ju, T.; Meng, Y.; Han, S.; Lin, L.; Jiang, J. A Review on the Applications of Microbially Induced Calcium Carbonate Precipitation in Solid Waste Treatment and Soil Remediation. Chemosphere 2022, 290, 133229. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Han, S.; Yang, Y.; Zhang, W.; Zou, T.; Cheng, L. Mechanical Behavior and Microstructural Study of Biocemented Sand under Various Treatment Methods. Geofluids 2022, 2022, 6015335. [Google Scholar] [CrossRef]
- Eryürük, K.; Suzuki, D.; Mizuno, S.; Akatsuka, T.; Tsuchiya, T.; Yang, S.; Kitano, H.; Katayama, A. Decrease in Hydraulic Conductivity of a Paddy Field Using Biocalcification in Situ. Geomicrobiol. J. 2016, 33, 690–698. [Google Scholar] [CrossRef]
- Achal, V.; Mukherjee, A.; Kumari, D.; Zhang, Q. Biomineralization for Sustainable Construction–A Review of Processes and Applications. Earth-Sci. Rev. 2015, 148, 1–17. [Google Scholar] [CrossRef]
- Phillips, A.J.; Troyer, E.; Hiebert, R.; Kirkland, C.; Gerlach, R.; Cunningham, A.B.; Spangler, L.; Kirksey, J.; Rowe, W.; Esposito, R. Enhancing Wellbore Cement Integrity with Microbially Induced Calcite Precipitation (MICP): A Field Scale Demonstration. J. Pet. Sci. Eng. 2018, 171, 1141–1148. [Google Scholar] [CrossRef]
- Chen, B.; Sun, W.; Sun, X.; Cui, C.; Lai, J.; Wang, Y.; Feng, J. Crack Sealing Evaluation of Self-Healing Mortar with Sporosarcina Pasteurii: Influence of Bacterial Concentration and Air-Entraining Agent. Process. Biochem. 2021, 107, 100–111. [Google Scholar] [CrossRef]
- Konstantinou, C.; Wang, Y. Statistical and Machine Learning Analysis for the Application of Microbially Induced Carbonate Precipitation as a Physical Barrier to Control Seawater Intrusion. J. Contam. Hydrol. 2024, 263, 104337. [Google Scholar] [CrossRef]
- Alam, M.K.; Motamed, R. Role of MICP Treatment Area in Mitigating Liquefaction-Induced Settlements for Shallow Foundation. Biogeotechnics 2025, 100187. [Google Scholar] [CrossRef]
- Guo, L.; Wang, B.; Guo, J.; Guo, H.; Jiang, Y.; Zhang, M.; Dai, Q. Experimental Study on Improving Hydraulic Characteristics of Sand Via Microbially Induced Calcium Carbonate Precipitation. Geomech. Energy Environ. 2024, 37, 100519. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, X.; Miao, L.; Wang, H.; Wu, L.; Shi, W.; Kawasaki, S. State-of-the-Art Review of Soil Erosion Control by MICP and EICP Techniques: Problems, Applications, and Prospects. Sci. Total Environ. 2024, 912, 169016. [Google Scholar] [CrossRef]
- Li, Y.; Chen, J. Experimental Study on the Permeability of Microbial-Solidified Calcareous Sand Based on MICP. Appl. Sci. 2022, 12, 11447. [Google Scholar] [CrossRef]
- Eryürük, K.; Yang, S.; Suzuki, D.; Sakaguchi, I.; Akatsuka, T.; Tsuchiya, T.; Katayama, A. Reducing Hydraulic Conductivity of Porous Media Using CaCO3 Precipitation Induced by Sporosarcina pasteurii. J. Biosci. Bioeng. 2015, 119, 331–336. [Google Scholar] [CrossRef] [PubMed]
- Rajasekar, A.; Wilkinson, S.; Moy, C.K.S. MICP as a Potential Sustainable Technique to Treat or Entrap Contaminants in the Natural Environment: A Review. Environ. Sci. Ecotechnology 2021, 6, 100096. [Google Scholar] [CrossRef]
- Yang, Y.; Chu, J.; Xiao, Y.; Liu, H.; Cheng, L. Seepage Control in Sand Using Bioslurry. Constr. Build. Mater. 2019, 212, 342–349. [Google Scholar] [CrossRef]
- Eryürük, K.; Yang, S.; Suzuki, D.; Sakaguchi, I.; Katayama, A. Effects of Bentonite and Yeast Extract as Nutrient on Decrease in Hydraulic Conductivity of Porous Media Due to CaCO3 Precipitation Induced by Sporosarcina pasteurii. J. Biosci. Bioeng. 2015, 120, 411–418. [Google Scholar] [CrossRef]
- Shan, Y.; Liufu, Z.; Yuan, J.; Li, Y.; Tong, H.; Cui, J. Liquefaction Resistance of MICP-Treated Calcareous Sand with Different Particle Size and Gradation. Biogeotechnics 2025, 100181. [Google Scholar] [CrossRef]
- Jhuo, Y.-S.; Wong, H.-E.; Tung, H.-H.; Ge, L. Effectiveness of Microbial Induced Carbonate Precipitation Treatment Strategies for Sand. Environ. Technol. Innov. 2025, 38, 104132. [Google Scholar] [CrossRef]
- Eryürük, K. Effect of Cell Density on Decrease in Hydraulic Conductivity by Microbial Calcite Precipitation. AMB Express 2022, 12, 104. [Google Scholar] [CrossRef]
- Erdmann, N.; De Payrebrune, K.M.; Ulber, R.; Strieth, D. Optimizing Compressive Strength of Sand Treated with MICP Using Response Surface Methodology. SN Appl. Sci. 2022, 4, 282. [Google Scholar] [CrossRef]
- Amarakoon, G.G.N.N.; Kawasaki, S. Factors Affecting Sand Solidification Using MICP with Pararhodobacter sp. Mater. Trans. 2018, 59, 72–81. [Google Scholar] [CrossRef]
- Design-Expert; Stat-Ease Inc.: Minneapolis, MN, USA, 2025.
- Tague, N.R. The Quality Toolbox, 2nd ed.; ASQ Quality Press: Milwaukee, WI, USA, 2005; ISBN 978-0-87389-639-9. [Google Scholar]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016; ISBN 978-1-118-91601-8. [Google Scholar]
- Tan, Y.; Xie, X.; Wu, S.; Wu, T. Microbially Induced CaCO3 Precipitation: Hydraulic Response and Micro-Scale Mechanism in Porous Media. ScienceAsia 2017, 43, 1–7. [Google Scholar] [CrossRef]
- Sham, E.; Mantle, M.D.; Mitchell, J.; Tobler, D.J.; Phoenix, V.R.; Johns, M.L. Monitoring Bacterially Induced Calcite Precipitation in Porous Media Using Magnetic Resonance Imaging and Flow Measurements. J. Contam. Hydrol. 2013, 152, 35–43. [Google Scholar] [CrossRef]
- Liu, Z.; Beng, J.; Wu, Y.; Nie, K.; Dang, Y.; Yao, Y.; Li, J.; Fang, M. Microbial Induced Calcite Precipitation for Improving Low-Cohesive Soil: Mechanisms, Methods and Macroscopic Properties. Low-Carbon Mater. Green Constr. 2024, 2, 30. [Google Scholar] [CrossRef]
- Wang, X.; Sun, H. Synergistic Effect of Microbial-Induced Carbonate Precipitation Modified with Hydroxypropyl Methylcellulose on Improving Loess Disintegration and Seepage Resistance. Polymers 2025, 17, 548. [Google Scholar] [CrossRef]
- Pacheco, V.L.; Bragagnolo, L.; Dalla Rosa, F.; Thomé, A. Optimization of Biocementation Responses by Artificial Neural Network and Random Forest in Comparison to Response Surface Methodology. Environ. Sci. Pollut. Res. 2023, 30, 61863–61887. [Google Scholar] [CrossRef]
- Wang, L.; Shao, H.; Yi, C.; Huang, Y.; Feng, D. Optimization of Injection Methods in the Microbially Induced Calcite Precipitation Process by Using a Field Scale Numerical Model. Water 2023, 16, 82. [Google Scholar] [CrossRef]
- Raymond, A.J.; DeJong, J.T.; Gomez, M.G.; Kendall, A.; San Pablo, A.C.M.; Lee, M.; Graddy, C.M.R.; Nelson, D.C. Life Cycle Sustainability Assessment of Microbially Induced Calcium Carbonate Precipitation (MICP) Soil Improvement Techniques. Appl. Sci. 2025, 15, 1059. [Google Scholar] [CrossRef]
- Omoregie, A.I.; Ouahbi, T.; Kan, F.-K.; Sirat, Q.A.; Raheem, H.O.; Rajasekar, A. Advancing Slope Stability and Hydrological Solutions Through Biocementation: A Bibliometric Review. Hydrology 2025, 12, 14. [Google Scholar] [CrossRef]
- Deng, X.; Li, Y.; Liu, H.; Zhao, Y.; Yang, Y.; Xu, X.; Cheng, X.; Wit, B.D. Examining Energy Consumption and Carbon Emissions of Microbial Induced Carbonate Precipitation Using the Life Cycle Assessment Method. Sustainability 2021, 13, 4856. [Google Scholar] [CrossRef]




| L1 | L2 | L3 | L4 | L5 | L6 | |
|---|---|---|---|---|---|---|
| OD600 | 0 | 0.15 | 0.75 | 2.25 | ||
| Coded | −0.7 | −0.56667 | −0.03333 | 1.3 | ||
| Diameter of glass beads | 0.05 | 0.25 | 0.5 | 1 | 2 | 3 |
| Coded | −0.27119 | −0.13559 | 0.0339 | 0.37288 | 1.05085 | 1.72881 |
| Precipitation Solution | 0 | 1 | ||||
| Coded | −1 | 1 | ||||
| Bentonite | 0 | 1 | ||||
| Coded | −1 | 1 | ||||
| Yeast Extract | 0 | 1 | ||||
| Coded | −1 | 1 |
| OD600 | Diameter of Glass Beads (mm) | Precipitation Solution | Bentonite | Yeast Extract | Hydraulic Conductivity (cm/s) |
|---|---|---|---|---|---|
| 2.25 | 0.05 | 1.00 | 0.00 | 0.00 | 0.00041 |
| 2.25 | 0.25 | 1.00 | 0.00 | 0.00 | 0.01008 |
| 2.25 | 0.50 | 1.00 | 0.00 | 0.00 | 0.02709 |
| 2.25 | 1.00 | 1.00 | 0.00 | 0.00 | 0.19334 |
| 2.25 | 2.00 | 1.00 | 0.00 | 0.00 | 0.22401 |
| 2.25 | 3.00 | 1.00 | 0.00 | 0.00 | 0.36925 |
| 0.75 | 0.25 | 1.00 | 0.00 | 0.00 | 0.03255 |
| 0.75 | 0.50 | 1.00 | 0.00 | 0.00 | 0.08915 |
| 0.75 | 1.00 | 1.00 | 0.00 | 0.00 | 0.36856 |
| 0.75 | 2.00 | 1.00 | 0.00 | 0.00 | 0.42898 |
| 0.75 | 3.00 | 1.00 | 0.00 | 0.00 | 0.63324 |
| 0.15 | 0.25 | 1.00 | 0.00 | 0.00 | 0.04755 |
| 0.15 | 0.50 | 1.00 | 0.00 | 0.00 | 0.12277 |
| 0.15 | 1.00 | 1.00 | 0.00 | 0.00 | 0.44610 |
| 0.15 | 2.00 | 1.00 | 0.00 | 0.00 | 0.52876 |
| 0.15 | 3.00 | 1.00 | 0.00 | 0.00 | 0.72205 |
| 2.25 | 0.05 | 1.00 | 0.00 | 0.00 | 0.00041 |
| 0.00 | 0.05 | 0.00 | 1.00 | 0.00 | 0.00095 |
| 2.25 | 0.05 | 1.00 | 1.00 | 0.00 | 0.00003 |
| 2.25 | 0.05 | 1.00 | 0.00 | 1.00 | 0.00000 |
| 2.25 | 0.05 | 1.00 | 1.00 | 1.00 | 0.00000 |
| 2.25 | 0.25 | 1.00 | 0.00 | 0.00 | 0.01110 |
| 0.00 | 0.25 | 0.00 | 1.00 | 0.00 | 0.03525 |
| 2.25 | 0.25 | 1.00 | 1.00 | 0.00 | 0.00135 |
| 2.25 | 0.25 | 1.00 | 0.00 | 1.00 | 0.00008 |
| 2.25 | 0.25 | 1.00 | 1.00 | 1.00 | 0.00004 |
| 2.25 | 1.00 | 1.00 | 0.00 | 0.00 | 0.19152 |
| 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 0.41443 |
| 2.25 | 1.00 | 1.00 | 1.00 | 0.00 | 0.01400 |
| 2.25 | 1.00 | 1.00 | 0.00 | 1.00 | 0.00093 |
| 2.25 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00050 |
| 2.25 | 3.00 | 1.00 | 0.00 | 0.00 | 0.36925 |
| 0.00 | 3.00 | 0.00 | 1.00 | 0.00 | 0.61620 |
| 2.25 | 3.00 | 1.00 | 1.00 | 0.00 | 0.03899 |
| 2.25 | 3.00 | 1.00 | 0.00 | 1.00 | 0.00226 |
| 2.25 | 3.00 | 1.00 | 1.00 | 1.00 | 0.00099 |
| 2.25 | 0.05 | 0.00 | 0.00 | 0.00 | 0.00414 |
| 2.25 | 0.25 | 0.00 | 0.00 | 0.00 | 0.06726 |
| 2.25 | 0.50 | 0.00 | 0.00 | 0.00 | 0.17225 |
| 2.25 | 1.00 | 0.00 | 0.00 | 0.00 | 0.57387 |
| 2.25 | 2.00 | 0.00 | 0.00 | 0.00 | 0.65504 |
| 2.25 | 3.00 | 0.00 | 0.00 | 0.00 | 0.83716 |
| Source | Sum of | df | Mean | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 3.58426 | 11 | 0.325842 | 49.7206 | <0.0001 | significant |
| A-OD 600 | 0.200135 | 1 | 0.200135 | 30.53886 | <0.0001 | |
| B-Diameter of Glass Beads | 0.428351 | 1 | 0.428351 | 65.36267 | <0.0001 | |
| C-Precipitation solution | 0.30892 | 1 | 0.30892 | 47.13851 | <0.0001 | |
| D-Bentonite | 0.110105 | 1 | 0.110105 | 16.80101 | 0.0003 | |
| E-Yeast Extract | 0.192342 | 1 | 0.192342 | 29.34969 | <0.0001 | |
| AB | 0.025458 | 1 | 0.025458 | 3.884734 | 0.0580 | |
| BC | 0.051802 | 1 | 0.051802 | 7.904497 | 0.0086 | |
| BD | 0.054209 | 1 | 0.054209 | 8.271844 | 0.0073 | |
| BE | 0.09376 | 1 | 0.09376 | 14.30692 | 0.0007 | |
| DE | 0.063855 | 1 | 0.063855 | 9.743638 | 0.0040 | |
| B2 | 0.217644 | 1 | 0.217644 | 33.2106 | <0.0001 | |
| Residual | 0.196604 | 30 | 0.006553 | |||
| Lack of Fit | 0.196589 | 26 | 0.007561 | 2105.253 | 4.86 × 10−7 | significant |
| Pure Error | 1.44× 10−5 | 4 | 3.59 × 10−6 | |||
| Cor Total | 3.780863 | 41 |
| Metric | Value | Interpretation |
|---|---|---|
| R2 | 0.948 | Indicates that 94.8% of the variability in hydraulic conductivity is explained by the model. This demonstrates an excellent fit to the experimental data. |
| Adjusted R2 | 0.929 | Adjusts for the number of predictors in the model. The high value suggests that the model is not overfitted and retains strong explanatory power even after penalizing for additional terms. |
| Predicted R2 | 0.868 | Reflects the model’s ability to predict new or unseen data. A predicted R2 above 0.80 indicates very good predictive performance. The reasonable closeness between Adjusted R2 and Predicted R2(< 0.2 difference) supports model reliability and consistency. |
| Adequate Precision | 23.62 | Measures the signal-to-noise ratio. A value > 4 is desirable; here, the value far exceeds this threshold, indicating a strong model signal and that the model can be used to navigate the design space confidently. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eryürük, Ş.; Eryürük, K.; Katayama, A. Integrated Bioprocess and Response Surface Methodology-Based Design for Hydraulic Conductivity Reduction Using Sporosarcina pasteurii. Minerals 2025, 15, 1215. https://doi.org/10.3390/min15111215
Eryürük Ş, Eryürük K, Katayama A. Integrated Bioprocess and Response Surface Methodology-Based Design for Hydraulic Conductivity Reduction Using Sporosarcina pasteurii. Minerals. 2025; 15(11):1215. https://doi.org/10.3390/min15111215
Chicago/Turabian StyleEryürük, Şule, Kağan Eryürük, and Arata Katayama. 2025. "Integrated Bioprocess and Response Surface Methodology-Based Design for Hydraulic Conductivity Reduction Using Sporosarcina pasteurii" Minerals 15, no. 11: 1215. https://doi.org/10.3390/min15111215
APA StyleEryürük, Ş., Eryürük, K., & Katayama, A. (2025). Integrated Bioprocess and Response Surface Methodology-Based Design for Hydraulic Conductivity Reduction Using Sporosarcina pasteurii. Minerals, 15(11), 1215. https://doi.org/10.3390/min15111215







