Simultaneous Adsorption of Copper, Zinc, and Sulfate in a Mixture of Activated Carbon and Barite
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Adsorption Tests
2.3. Data Analysis
3. Results and Discussion
3.1. Characterization of Adsorbent Particles
3.1.1. Size Distribution and Specific Surface Area of the Adsorbent Particle
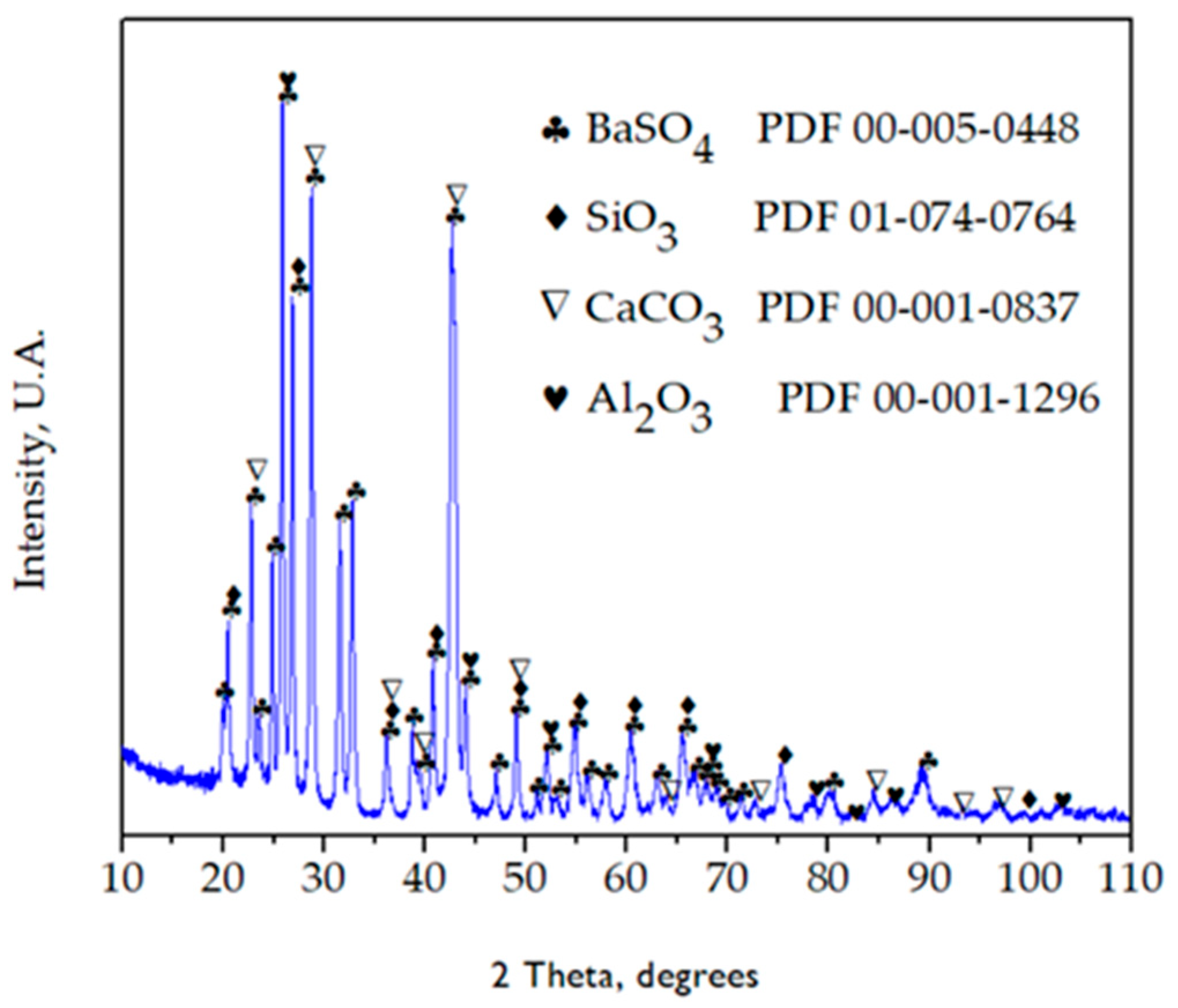
3.1.2. Chemical and Mineralogical Analyses
3.1.3. Zeta Potential
3.2. Adsorption of Ions
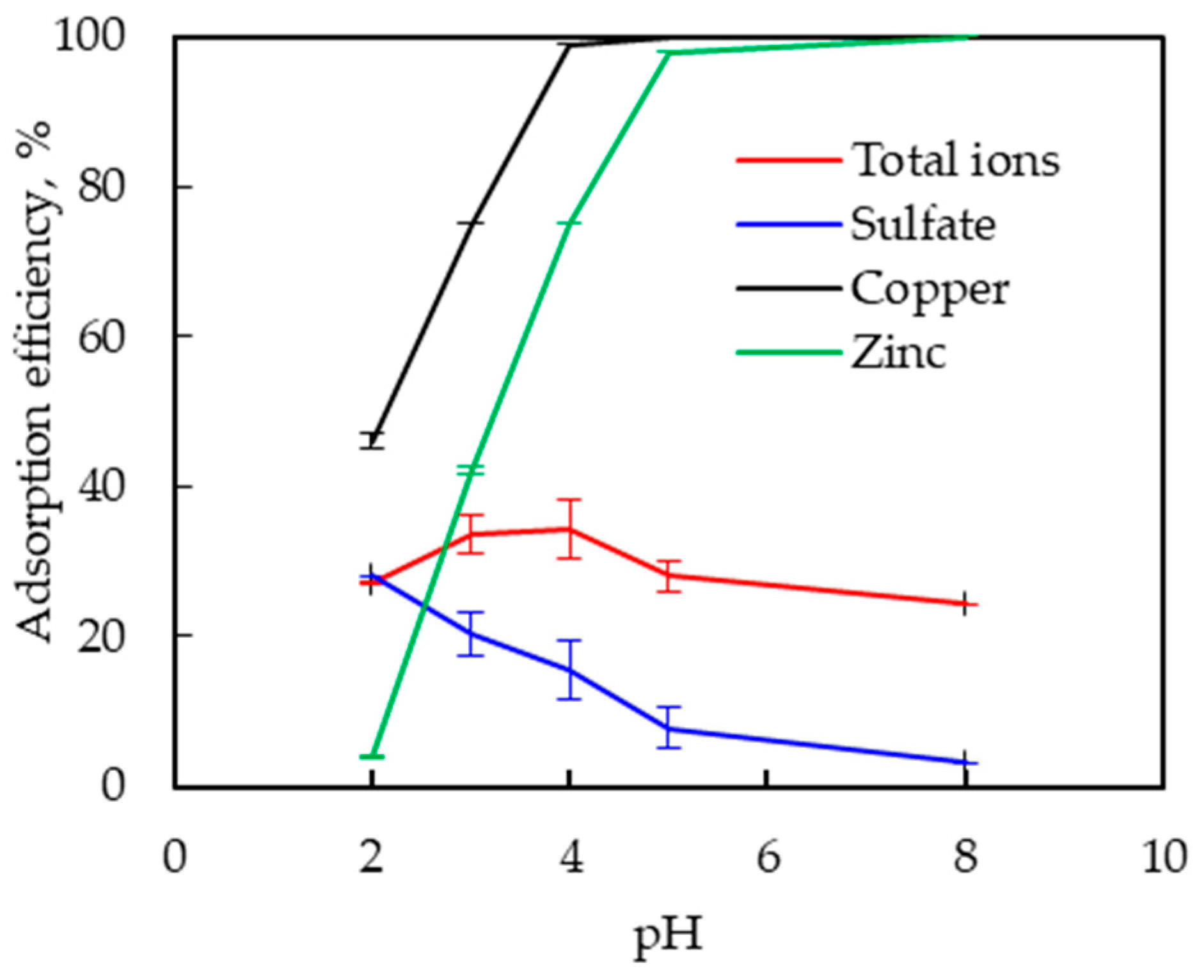
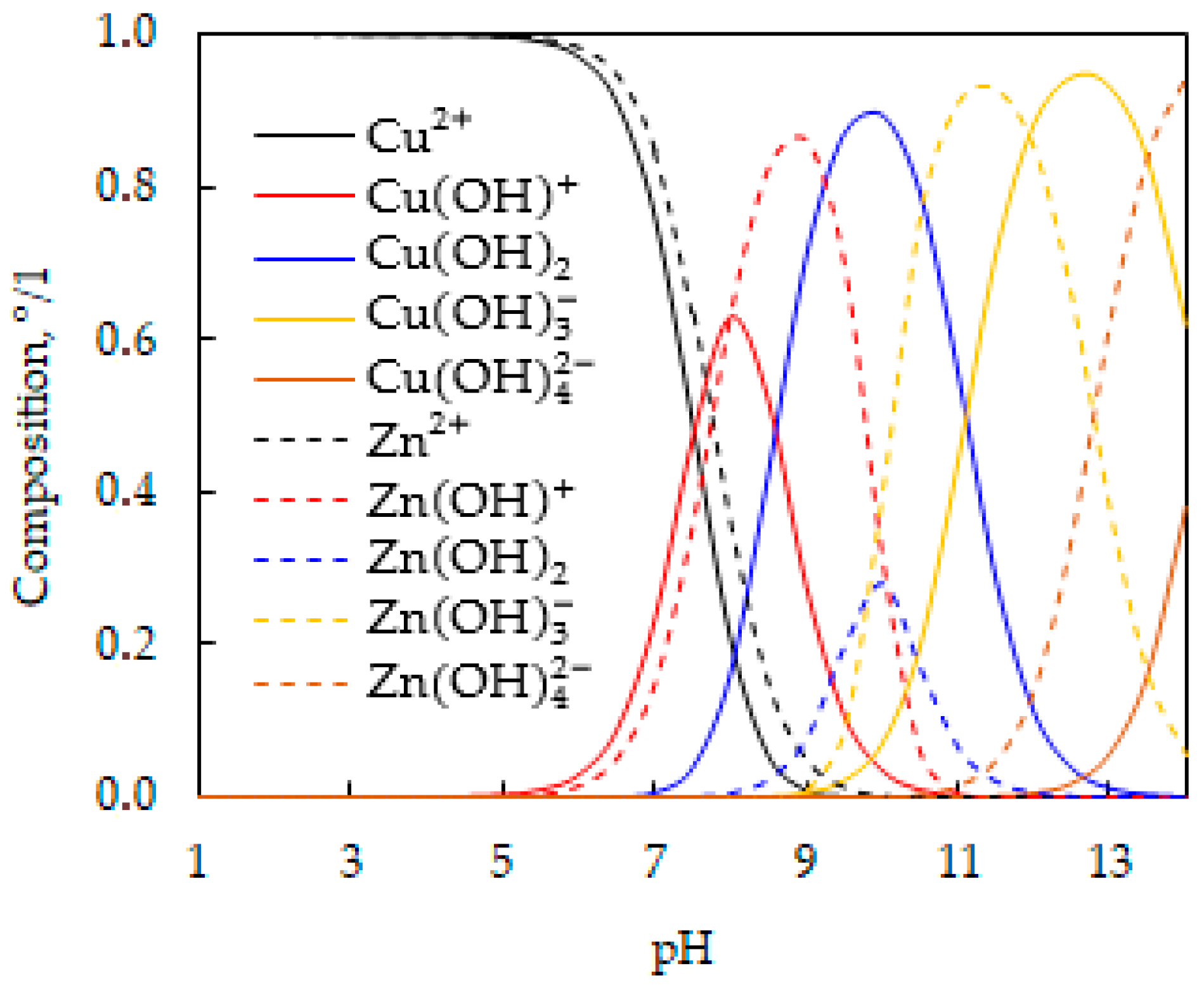
3.2.1. Effect of pH
3.2.2. Effect of Contact Time
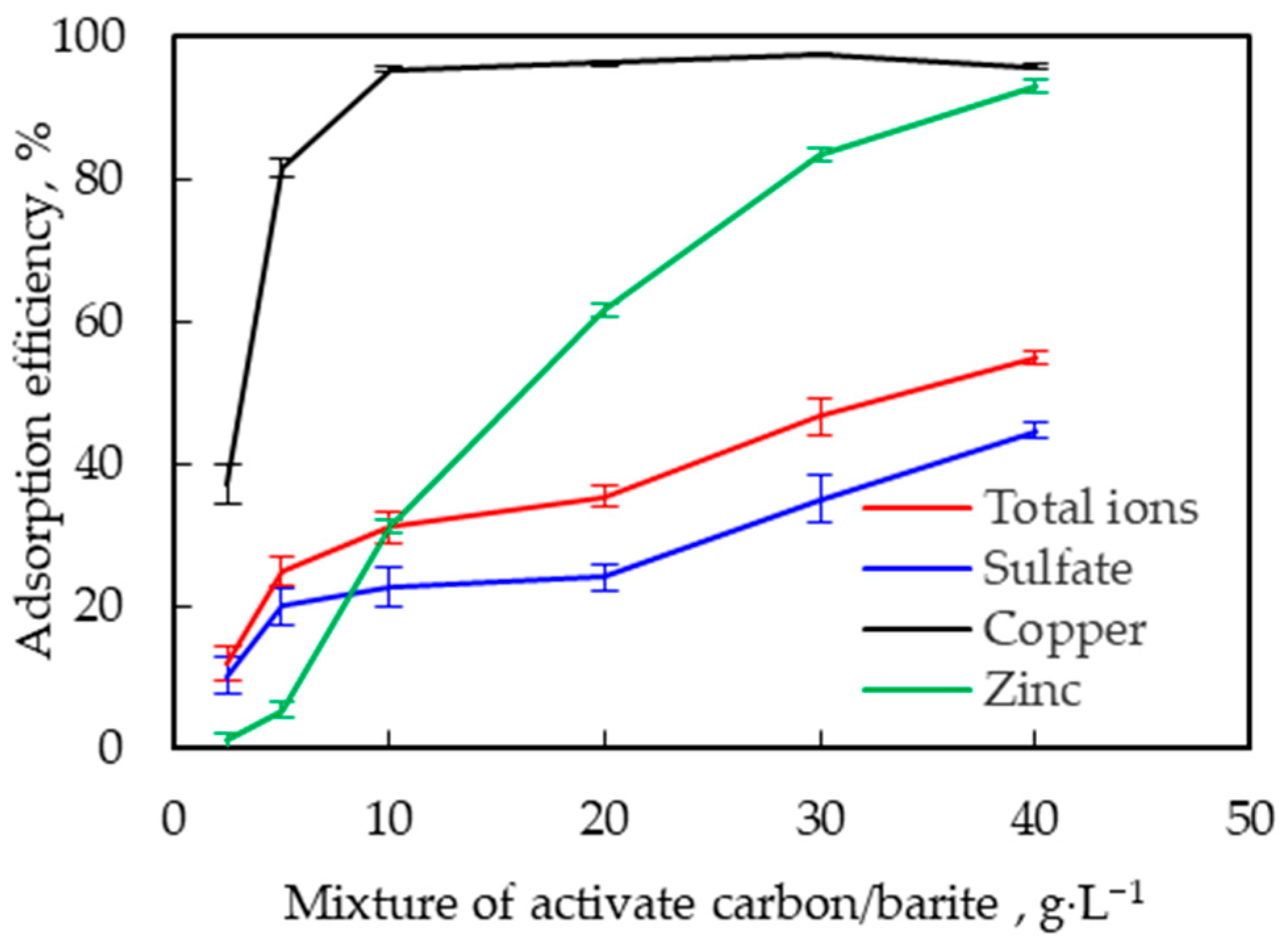
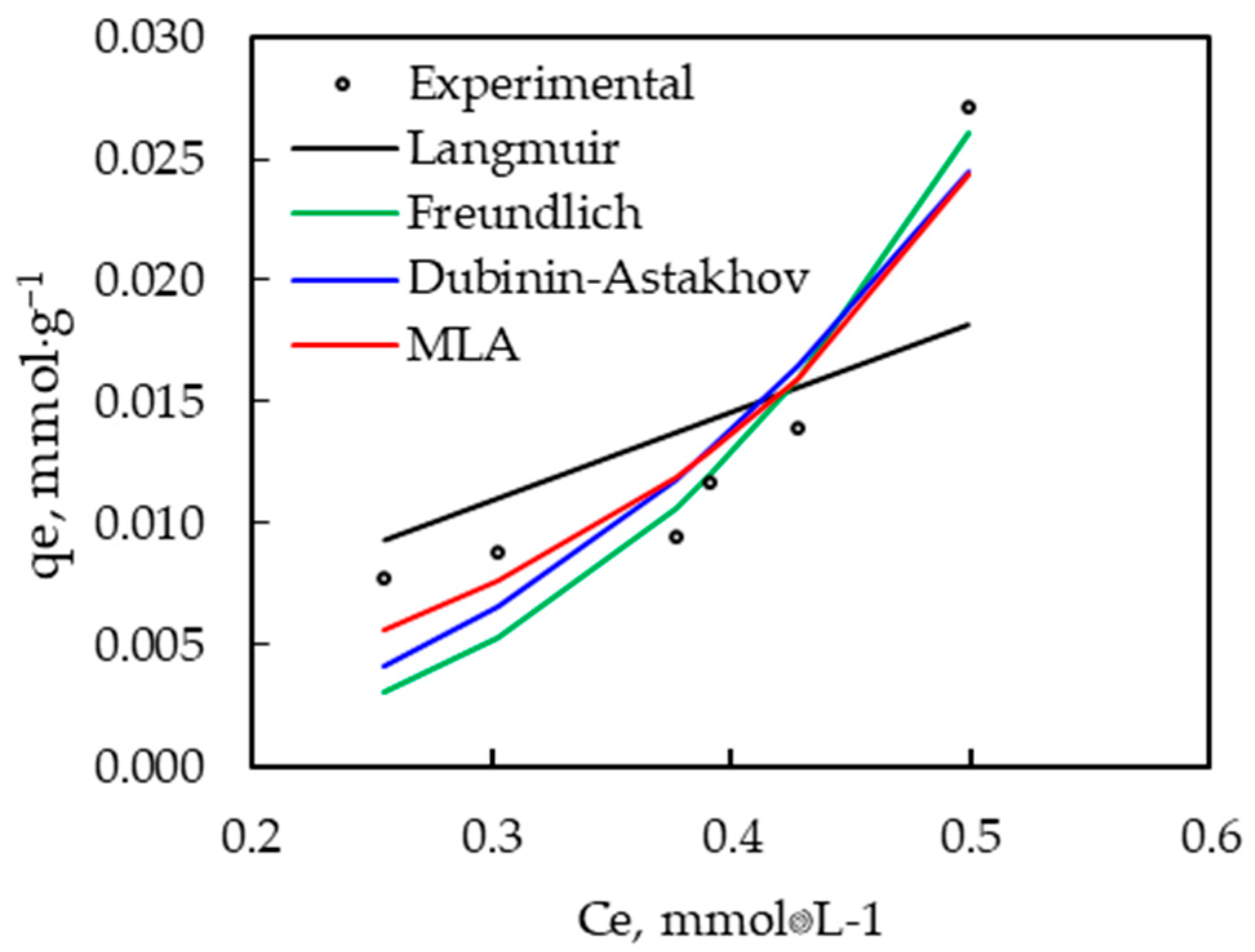
3.2.3. Effect of Concentration
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mashhadikhan, S.; Amooghin, A.; Sanaeepur, H.; Shirazi, M. A critical review on cadmium recovery from wastewater towards environmental sustainability. Desalination 2022, 535, 115815. [Google Scholar] [CrossRef]
- Feng, X.; Long, R.; Wang, L.; Liu, C.; Bai, Z.; Liu, X. A review on heavy metal ions adsorption from water by layered double hydroxide and its composites. Sep. Purif. Technol. 2022, 284, 120099. [Google Scholar] [CrossRef]
- Pooja, G.; Kumar, P.; Indraganti, S. Recent advancements in the removal/recovery of toxic metals from aquatic system using flotation techniques. Chemosphere 2022, 287, 132231. [Google Scholar] [CrossRef] [PubMed]
- McCarthy, T. The impact of acid mine drainage in South Africa. S. Afr. J. Sci. 2011, 107, 1–7. [Google Scholar] [CrossRef]
- Khorasanipour, M.; Moore, F.; Naseh, R. Lime Treatment of Mine Drainage at the Sarcheshmeh Porphyry Copper Mine, Iran. Mine Water Environ. 2011, 30, 216–230. [Google Scholar] [CrossRef]
- Fu, F.; Wang, Q. Removal of heavy metal ions from wastewaters: A review. J. Environ. Manag. 2011, 92, 407–418. [Google Scholar] [CrossRef]
- Özdemir, G.; Yapar, S. Adsorption and desorption behavior of copper ions on Na-montmorillonite: Effect of rhamnolipids and pH. J. Hazard. Mater. 2009, 166, 1307–1313. [Google Scholar] [CrossRef]
- Hu, M.; Wu, W.; Lin, D.; Yang, K. Adsorption of fulvic acid on mesopore-rich activated carbon with high surface area. Sci. Total Environ. 2022, 838, 155918. [Google Scholar] [CrossRef]
- Chen, J.; Hsu, K.; Chang, Y. Surface modification of hydrophobic resin with tricaprylmethylammonium chloride for the removal of trace hexavalent chromium. Ind. Eng. Chem. Res. 2013, 52, 11685–11694. [Google Scholar] [CrossRef]
- Mi, H.; Yi, L.; Wu, Q.; Xia, J.; Zhang, B. Preparation and optimization of a low-cost adsorbent for heavy metal ions from red mud using fraction factorial design and Box-Behnken response methodology. Colloids Surf. A Physicochem. Eng. Asp. 2021, 627, 127198. [Google Scholar] [CrossRef]
- Santander, M.; Valderrama, L. Dissolved Air Flotation of arsenic adsorbent particles. Ing. Investig. 2015, 35, 36–42. [Google Scholar] [CrossRef]
- Chaudhari, V.; Patkar, M. Removal of nickel from aqueous solution by using corncob as adsorbent. Mater. Today Proc. 2022, 61, 307–314. [Google Scholar] [CrossRef]
- Gupta, G.; Khan, J.; Singh, N. Application and efficacy of low-cost adsorbents for metal removal from contaminated water: A review. Mater. Today Proc. 2021, 43, 2958–2964. [Google Scholar] [CrossRef]
- Sadeghalvad, B.; Khorshidi, N.; Azadmehr, A.; Sillanpää, M. Sorption, mechanism, and behavior of sulfate on various adsorbents: A critical review. Chemosphere 2021, 263, 128064. [Google Scholar] [CrossRef]
- Mehta, D.; Mazumdar, S.; Singh, S. Magnetic adsorbents for the treatment of water/wastewate—A review. J. Water Process Eng. 2015, 7, 244–265. [Google Scholar] [CrossRef]
- Melliti, A.; Yılmaz, M.; Sillanpää, M.; Hamrouni, B.; Vurm, R. Low-cost date palm fiber activated carbon for effective and fast heavy metal adsorption from water: Characterization, equilibrium, and kinetics studies. Colloids Surf. A Physicochem. Eng. Asp. 2023, 672, 131775. [Google Scholar] [CrossRef]
- Ma, X.; Yang, S.; Tang, H.; Liu, Y.; Wang, H. Competitive adsorption of heavy metal ions on carbon nanotubes and the desorption in simulated biofluids. J. Colloid Interface Sci. 2015, 448, 347–355. [Google Scholar] [CrossRef]
- Hong, S.; Cannon, F.; Hou, P.; Byrne, T.; Nieto-Delgado, C. Adsorptive removal of sulfate from acid mine drainage by polypyrrole modified activated carbons: Effects of polypyrrole deposition protocols and activated carbon source. Chemosphere 2017, 184, 429–437. [Google Scholar] [CrossRef]
- Yang, X.; Wan, Y.; Zheng, Y.; He, F.; Yu, Z.; Huang, J.; Wang, H.; Ok, Y.S.; Jiang, Y.; Gao, B. Surface functional groups of carbon-based adsorbents and their roles in the removal of heavy metals from aqueous solutions: A critical review. Chem. Eng. J. 2019, 366, 608–621. [Google Scholar] [CrossRef]
- Hong, S.; Cannon, F.; Hou, P.; Byrne, T.; Nieto-Delgado, C. Sulfate removal from acid mine drainage using polypyrrole-grafted granular activated carbon. Carbon 2014, 73, 51–60. [Google Scholar] [CrossRef]
- Aravena, H. Remoción de Iones Cobre, Zinc y Sulfato Mediante Flotación por Partícula Adsorbente Utilizando un Composite de Carbón Activado/Baritina Generado Mediante Molienda. Master’s Thesis, University of Atacama, Copiapó, Chile, 2024. [Google Scholar]
- Ho, Y.; Mckay, G. Kinetics of pollutant sorption by bio sorbents: A Review. Sep. Purif. Methods 2000, 29, 189–232. [Google Scholar] [CrossRef]
- An, B. Cu (II) and As (V) Adsorption Kinetic Characteristic of the Multifunctional Amino Groups in Chitosan. Processes 2020, 8, 1194. [Google Scholar] [CrossRef]
- Foo, K.; Hameed, B. Insights into the modeling of adsorption isotherm systems. Chem. Eng. J. 2010, 156, 2–10. [Google Scholar] [CrossRef]
- Yan, B.; Niu, C.H. Adsorption behavior of norfloxacin and site energy distribution based on the Dubinin-Astakhov isotherm. Sci. Total Environ. 2018, 631, 1525–1533. [Google Scholar] [CrossRef] [PubMed]
- El-Khaiary, M.I. Least-squares regression of adsorption equilibrium data: Comparing the options. J. Hazard. Mater. 2008, 158, 73–87. [Google Scholar] [CrossRef]
- Kavand, M.; Eslami, P.; Razeh, L. The adsorption of cadmium and lead ions from the synthesis wastewater with the activated carbon: Optimization of the single and binary Systems. J. Water Process Eng. 2020, 34, 101151. [Google Scholar] [CrossRef]
- Weng, C.H.; Tsai, C.Z.; Chu, S.H.; Sharma, Y.C. Adsorption characteristics of copper (II) onto spent activated clay. Sep. Purif. Technol. 2007, 54, 187–197. [Google Scholar] [CrossRef]
- Oliva, A.; Martín-Varguez, P.; González-Panzo, I.; González-Chan, I. Papel del diagrama de distribución de especies en el depósito de capas delgadas semiconductoras por baño químico. Rev. Mex. Ing. Quim. 2016, 15, 209–220. [Google Scholar]
- Yuan, J.; Ding, Z.; Bi, Y.; Li, J.; Wen, S.; Bai, S. Resource Utilization of Acid Mine Drainage (AMD): A Review. Water 2022, 14, 2385. [Google Scholar] [CrossRef]
- Wang, J.; Guo, X. Adsorption kinetic models: Physical meanings, applications, and solving methods. J. Hazard. Mater. 2020, 390, 122156. [Google Scholar] [CrossRef]
- Agbovi, H.K.; Wilson, L.D. Adsorption Processes in Biopolymer Systems: Fundamentals to Practical Applications. In Natural Polymers-Based Green Adsorbents for Water Treatment; Elsevier: Amsterdam, The Netherlands, 2021; pp. 1–51. [Google Scholar] [CrossRef]
- Andelescu, A.; Nistor, M.A.; Muntean, S.G.; Rădulescu-Grad, M.E. Adsorption Studies on Copper, Cadmium, and Zinc Ion Removal from Aqueous Solution Using Magnetite/Carbon Nanocomposites. Sep. Sci. Technol. 2018, 53, 2352–2364. [Google Scholar] [CrossRef]
- Nasser, S.M.; Abbas, M.; Trari, M. Understanding the Rate-Limiting Step Adsorption Kinetics onto Biomaterials for Mechanism Adsorption Control. Prog. React. Kinet. Mech. 2024, 49, 6858. [Google Scholar] [CrossRef]
- Hasani, N.; Selimi, T.; Mele, A.; Thaçi, V.; Halili, J.; Berisha, A.; Sadiku, M. Theoretical, Equilibrium, Kinetics and Thermodynamic Investigations of Methylene Blue Adsorption onto Lignite Coal. Molecules 2022, 27, 1856. [Google Scholar] [CrossRef] [PubMed]
- El-Khaiary, M.I.; Malash, G.F.; Ho, Y.S. On the use of linearized pseudo-second-order kinetic equations for modeling adsorption systems. Desalination 2010, 257, 93–101. [Google Scholar] [CrossRef]
- Chen, W.-S.; Chen, Y.-C.; Lee, C.-H. Modified Activated Carbon for Copper Ion Removal from Aqueous Solution. Processes 2022, 10, 150. [Google Scholar] [CrossRef]
- Demiral, H.; Güngör, C. Adsorption of Copper(II) from Aqueous Solutions on Activated Carbon Prepared from Grape Bagasse. J. Clean. Prod. 2016, 124, 103–113. [Google Scholar] [CrossRef]
- Tuomikoski, S.; Tanskanen, J.; Runtti, H.; Kangas, T.; Romar, H.; Lassi, U. Zinc Adsorption by Activated Carbon from Waste Fishing Nets. Appl. Sci. 2019, 9, 4583. [Google Scholar] [CrossRef]
- Leyva-Ramos, R.; Bernal-Jacome, L.A.; Mendoza-Barron, J.; Fuentes-Rubio, L.; Guerrero-Coronado, R.M. Adsorption of Zinc (II) from an Aqueous Solution onto Activated Carbon. J. Hazard. Mater. 2002, 90, 27–38. [Google Scholar] [CrossRef]
- Tejada-Tovar, C.; Villabona-Ortíz, Á.; Gonzalez-Delgado, A.D.; Herrera, A.; Viera De la Voz, A. Efficient Sulfate Adsorption on Modified Adsorbents Prepared from Zea mays Stems. Appl. Sci. 2021, 11, 1596. [Google Scholar] [CrossRef]
- Ao, H.; Cao, W.; Hong, Y.; Wu, J.; Wei, L. Adsorption of Sulfate Ion from Water by Zirconium Oxide-Modified Biochar Derived from Pomelo Peel. Sci. Total Environ. 2020, 708, 135092. [Google Scholar] [CrossRef]
- Rahmati, M.; Yeganeh, G.; Esmaeili, H. Sulfate Ion Removal from Water Using Activated Carbon Powder Prepared by Ziziphus spina-christi Lotus Leaf. Acta Chim. Slov. 2019, 66, 888–898. [Google Scholar] [CrossRef]
- Hsieh, C.-T.; Teng, H. Influence of mesopore volume and adsorbate size on adsorption capacities of activated carbons in aqueous solutions. Carbon 2000, 38, 863–869. [Google Scholar] [CrossRef]



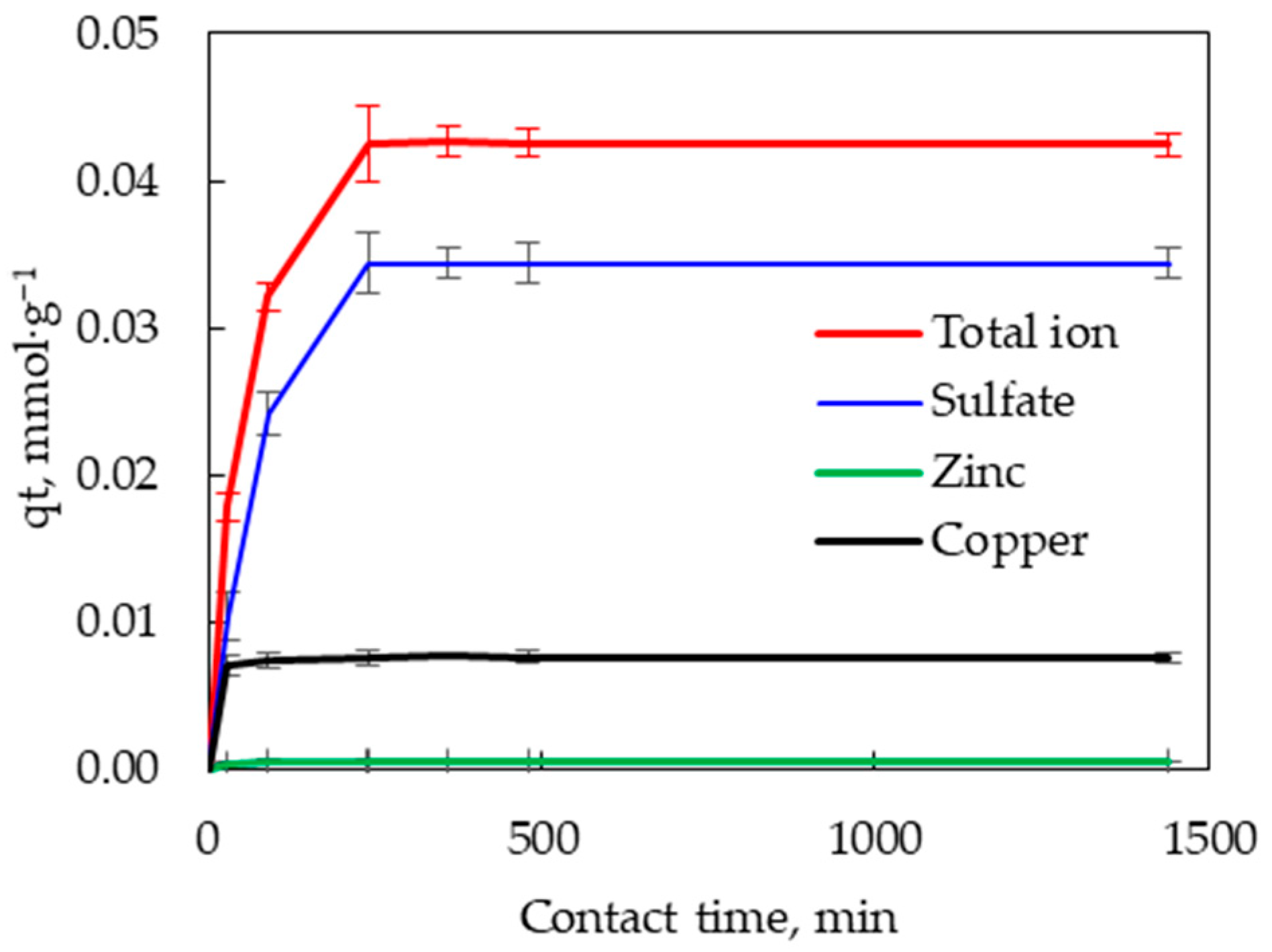


| Pseudo-1st-Order Kinetic Model | ||||
| qe, mmol·g−1 | k1, min−1 | R2 | IC | SEE |
| 0.0426 | 0.017 | 0.995 | 0.002 | 0.037 |
| Pseudo-2nd-order kinetic model | ||||
| qe, mmol·g−1 | k2, g·mmol−1·min−1 | R2 | IC | SEE |
| 0.0463 | 0.579 | 0.959 | 0.005 | 0.002 |
| Intraparticle Diffusion Kinetic Model | ||||
|---|---|---|---|---|
| ki, mmol·g−1·min0.5 | C, mmol·g−1 | R2 | IC | SEE |
| 0.0062 | 0.0254 | 0.483 | 0.018 | 0.007 |
| Langmuir | Value | Freundlich | Value |
| Qmax, mmol·g−1 | 3.262 | KF, mmol·g−1 | 0.237 |
| kL, L·mmol−1 | 0.011 | n, adimensional | 0.315 |
| R2 | 0.556 | R2 | 0.856 |
| SEE | 0.005 | SEE | 0.003 |
| IC | 0.013 | IC | 0.007 |
| Dubinin–Astakhov | Value | Multilayer adsorption | Value |
| q0, mmol·g−1 | 4.541 | Γ, mmol·g−1 | 4.459 |
| ηD, adimensional | 0.792 | k1, L·mmol−1 | 0.003 |
| E, kJ·mol−1 | 0.239 | k2, L·mmol−1 | 1.000 |
| R2 | 0.848 | R2 | 0.842 |
| SEE | 0.003 | SEE | 0.003 |
| IC | 0.011 | IC | 0.007 |
| Adsorbent | BET Specific Surface Area, m2·g−1 | Pore Volume, cm3·g−1 | Ions | KF, mmol·g−1 | n | Reference |
|---|---|---|---|---|---|---|
| Activated carbon (waste wood-based) | 1464.0 | 1.173 | Cu2+ | 0.1633 | 4.76 | [37] |
| Activated carbon (grape bagasse) | 1465.0 | 0.660 | Cu2+ | 0.0892 | 2.03 | [38] |
| Activated carbon (biomass-based) | 860.0 | 0.610 | Zn2+ | 0.1300 | 5.88 | [39] |
| Activated carbon (commercial) | 768.0 | NR | Zn2+ | 0.0309 | 5.47 | [40] |
| Biochar (modified H2SO4) | NR | NR | 0.0023 | 0.96 | [41] | |
| Biochar (modified ZrO2) | 21.8 | NR | 0.0884 | 0.28 | [42] | |
| Activated carbon (Leaves of Ziziphus spina-christi) | 51.0 | NR | 0.0208 | 0.61 | [43] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santander, M.; Aravena, H.; Guzmán, D.; Valderrama, L.; Cárdenas, E. Simultaneous Adsorption of Copper, Zinc, and Sulfate in a Mixture of Activated Carbon and Barite. Minerals 2025, 15, 1214. https://doi.org/10.3390/min15111214
Santander M, Aravena H, Guzmán D, Valderrama L, Cárdenas E. Simultaneous Adsorption of Copper, Zinc, and Sulfate in a Mixture of Activated Carbon and Barite. Minerals. 2025; 15(11):1214. https://doi.org/10.3390/min15111214
Chicago/Turabian StyleSantander, Mario, Hugo Aravena, Danny Guzmán, Luis Valderrama, and Evelyn Cárdenas. 2025. "Simultaneous Adsorption of Copper, Zinc, and Sulfate in a Mixture of Activated Carbon and Barite" Minerals 15, no. 11: 1214. https://doi.org/10.3390/min15111214
APA StyleSantander, M., Aravena, H., Guzmán, D., Valderrama, L., & Cárdenas, E. (2025). Simultaneous Adsorption of Copper, Zinc, and Sulfate in a Mixture of Activated Carbon and Barite. Minerals, 15(11), 1214. https://doi.org/10.3390/min15111214





