Geostatistically Enhanced Learning for Supervised Classification of Wall-Rock Alteration Using Assay Grades of Trace Elements and Sulfides
Abstract
1. Introduction
1.1. Wall-Rock Alteration
1.2. Conceptual Basis of the Research Problem
1.3. Novel Contributions
- 1.
- Is it possible to accurately classify wall-rock alteration types across any location within an ore deposit using concentrations of just four metals (Cu, Au, Mo, and As) and three metal sulfides (chalcopyrite, pyrite, and total sulfides), as input features derived from sampled data points? We posit that a classifier capable of discerning robust numerical patterns linked to distinct alteration types may achieve comparable or superior performance. The features employed are derived from a drill hole data set acquired under industry quality assurance and quality control standards. We will assess the accuracy of predictions by an evaluation with standard model performance metrics for classification.
- 2.
- Does the implemented methodology provide an advantage with regards to its robustness under data constraints? Specifically, two distinct scenarios are evaluated to assess model performance under data constraining conditions: (i) substantial missing values among feature variables, and (ii) sparse spatial sampling. In the first scenario, missing feature values are imputed using the median value computed per alteration type for each corresponding input feature variable. In the second scenario, records with incomplete feature sets are excluded, and only isotopically sampled data points are retained to ensure reliability in spatial representation. The predictive performance for each scenario is evaluated using standard metrics, including accuracy, precision, recall, and F1-score. Comparative analysis of these results will inform the methodology’s resilience and applicability in real-world geochemical classification tasks.
- 3.
- In the presence of unbalanced data—where certain wall-rock alteration types are overrepresented while others are sparsely sampled—does a cost-sensitive classification strategy yield superior predictive accuracy? Two methodological approaches are evaluated: (i) classification of the proxy data set with integration of XGBoost with a cost-matrix informed by thermodynamic and mineral exploration criteria to minimize expected misclassification cost, and (ii) classification of the proxy data set without integration of XGBoost with a cost-matrix. Model performance is assessed using standard metrics (accuracy, precision, recall, and F1-score), thereby providing a robust basis for evaluating the effectiveness of cost-sensitive learning under class imbalance.
2. Related Work & Limitations
- 1.
- Elemental and mineralogical concentrations (grades) are regionalized variables that exhibit spatial auto- and cross-correlations. In other words, the concentrations measured at a drill core bring information on the concentrations at surrounding locations, therefore, indirectly on the alteration class at these locations. Ignoring the information of neighboring drill cores, therefore, implies a loss in efficiency of ML classifiers.
- 2.
- The dependence relationships between alteration classes and elemental and mineralogical concentrations furthermore depend on the spatial scale. While geochemical assays often exhibit short-scale variability and isolated occurrences of outlying values, the same does not happen with the prevailing alteration classes, the variations in which are more regular in space. Accordingly, ML classifiers would perform better if they were able to “extract” from the elemental and mineralogical concentrations the information that relates to the same spatial scale as the alteration classes, i.e., without short-scale variability.
- 3.
- Measurement errors affect the quality of drill core data. It is well-known [22] that geochemical analyses are subject to errors arising from the sampling, preparation, and assaying of drill cores. In the geostatistical modeling of drill core data, these errors are one source of the well-known nugget effect in covariance functions and variograms [23], while in ML classification, they entail a loss in efficiency compared to what would be obtained by training the classifier on error-free data.
- 4.
- Grade data sets are often heterotopic; that is, not all the grade variables are sampled at all the drill cores, which translates into missing values of different elemental and mineralogical grades. The traditional method for handling missing values in a data set is to impute with realistic values. Then arises the question: which value is realistic and which is not?
3. Theoretical Background
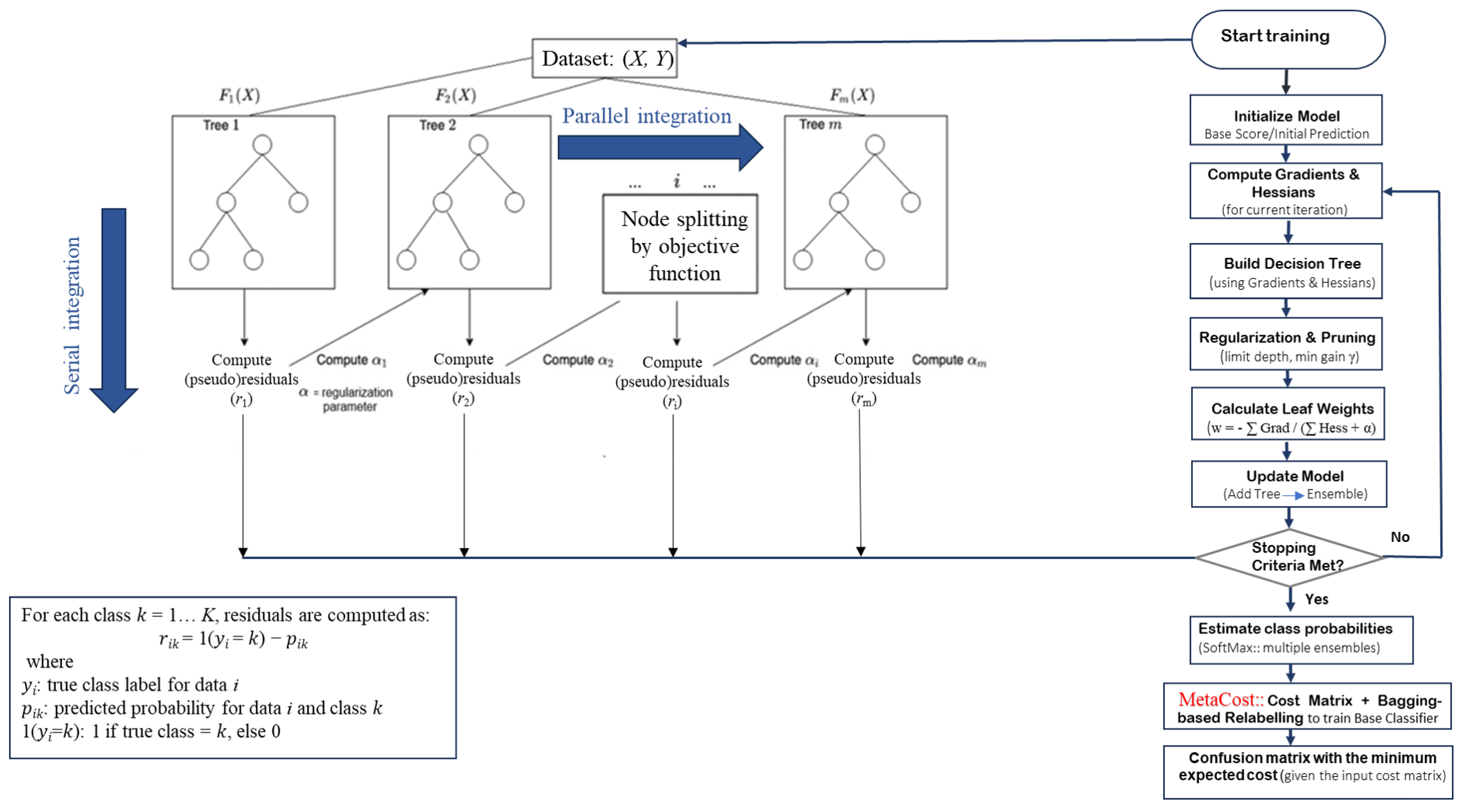
3.1. Basics on XGBoost Classification
- 1.
- Start with a base learner: The first model decision tree is trained on the data.
- 2.
- Calculate the errors: After training, the first tree the errors between the predicted and actual values are calculated.
- 3.
- Train the next tree: The next tree is trained on the errors of the previous tree. This step attempts to correct the errors made by the first tree.
- 4.
- Repeat the process: This process continues with each new tree trying to correct the errors of the previous trees until a stopping criterion is met.
- 5.
- Combine the predictions: The final prediction is a combination of the predictions from all the trees.
3.1.1. Step 1: Data Input and Preprocessing
- 1.
- Input Data: Provide the feature matrix and corresponding target labels.
- 2.
- Preprocessing:
- Encode categorical variables (for example, one-hot encoding).
- Normalize or standardize features if necessary.
- Split the data set into training and test sets.
3.1.2. Step 2: Model Initialization
- 1.
- Initial Prediction: Set an initial prediction for all instances. For classification, this is often the log odds of the positive class.
- 2.
- Parameter Setup: Define hyperparameters such as learning rate, maximum tree depth, and regularization terms. A Bayesian optimization scheme (Optuna) is implemented for hyperparameter tuning.
3.1.3. Step 3: Iterative Boosting Process
- 1.
- Compute Gradients and Hessians: Calculate the gradient (first derivative) and Hessian (second derivative) of the loss function with respect to the current predictions.
- 2.
- Construct a Decision Tree:
- Use the computed gradients and Hessians to build a decision tree that predicts the residuals.
- Determine the best splits by maximizing the gain, which measures the improvement in the loss function.
- Update the model’s predictions by incorporating the scaled output of the newly constructed tree.
3.1.4. Step 4: Objective Function Optimization
- 1.
- Loss Function: XGBoost minimizes a regularized loss function (Equation (1)) that combines the training loss (for example, logistic loss) and a regularization term to penalize model complexity.
- 2.
- Regularization: Helps prevent overfitting by controlling the complexity of the model.
3.1.5. Step 5: Output Aggregation and Prediction
- 1.
- Aggregate Outputs: Sum the outputs from all trees to obtain the final prediction scores.
- 2.
- Apply Softmax Function: Convert the aggregated scores into probabilities for each class using the softmax function.
- 3.
- Final Prediction: Assign the class label with the highest probability as the predicted class.
3.1.6. Step 6: Model Evaluation
- 1.
- Performance Metrics: Evaluate the model using appropriate metrics such as accuracy, precision, recall, F1-score, and confusion matrix.
- 2.
- Cross-Validation: Optionally, perform cross-validation to assess the model’s generalization ability.
3.2. Basics on MetaCost
- 1.
- Training Multiple Classifiers: MetaCost works by training multiple base classifiers on various bootstrap samples (random samples with replacement) of the original training data set.
- 2.
- Estimating Class Probabilities: For each instance in the training set, MetaCost uses the trained classifiers to estimate the probabilities of it belonging to each possible class.
- 3.
- Cost-Sensitive Reclassification: MetaCost then reclassifies each instance based on these estimated probabilities and a given cost matrix. The cost matrix defines the cost associated with each type of misclassification (for example, the cost of predicting Class A when the true class is Class B).
- 4.
- Final Classifier: Finally, MetaCost trains a single classifier on the reclassified data, producing a cost-sensitive classifier that minimizes the expected misclassification cost.
- Bootstrap Sampling: This technique creates multiple random samples from the original training set to improve the robustness of the classifier.
- Cost Matrix: The cost matrix is crucial as it defines the costs associated with different types of misclassifications, guiding the reclassification process.
- Meta-Learning: MetaCost is considered a meta-learning algorithm because it builds upon other classifiers, transforming their predictions into cost-sensitive ones. MetaCost is effective in scenarios where misclassification costs vary significantly. It helps make more informed decisions by taking the costs into account rather than just aiming for the highest accuracy.
3.3. Tuning the XGBoost Classifier
3.4. Uncertainty Analysis
3.5. Basics on Geostatistical Simulation
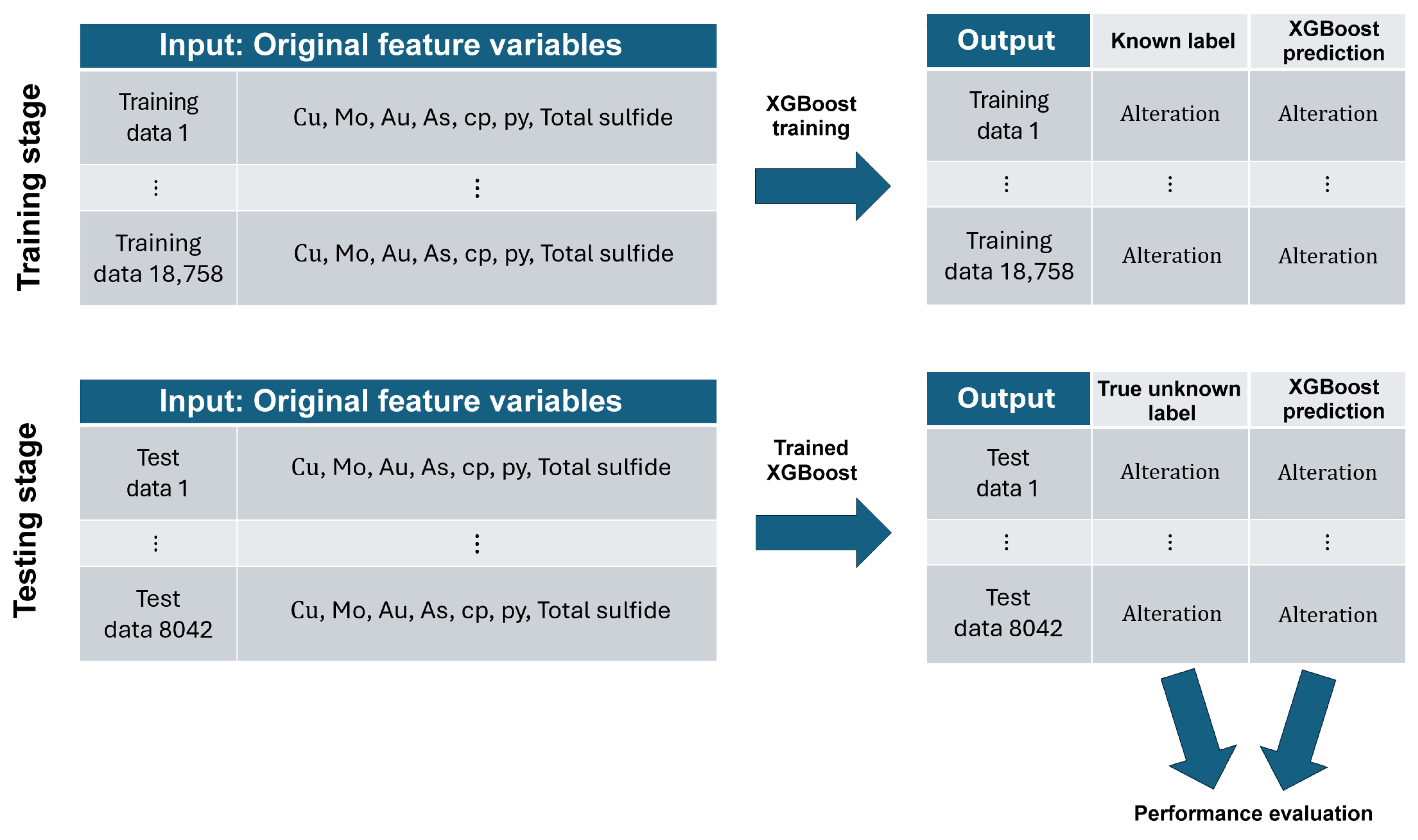
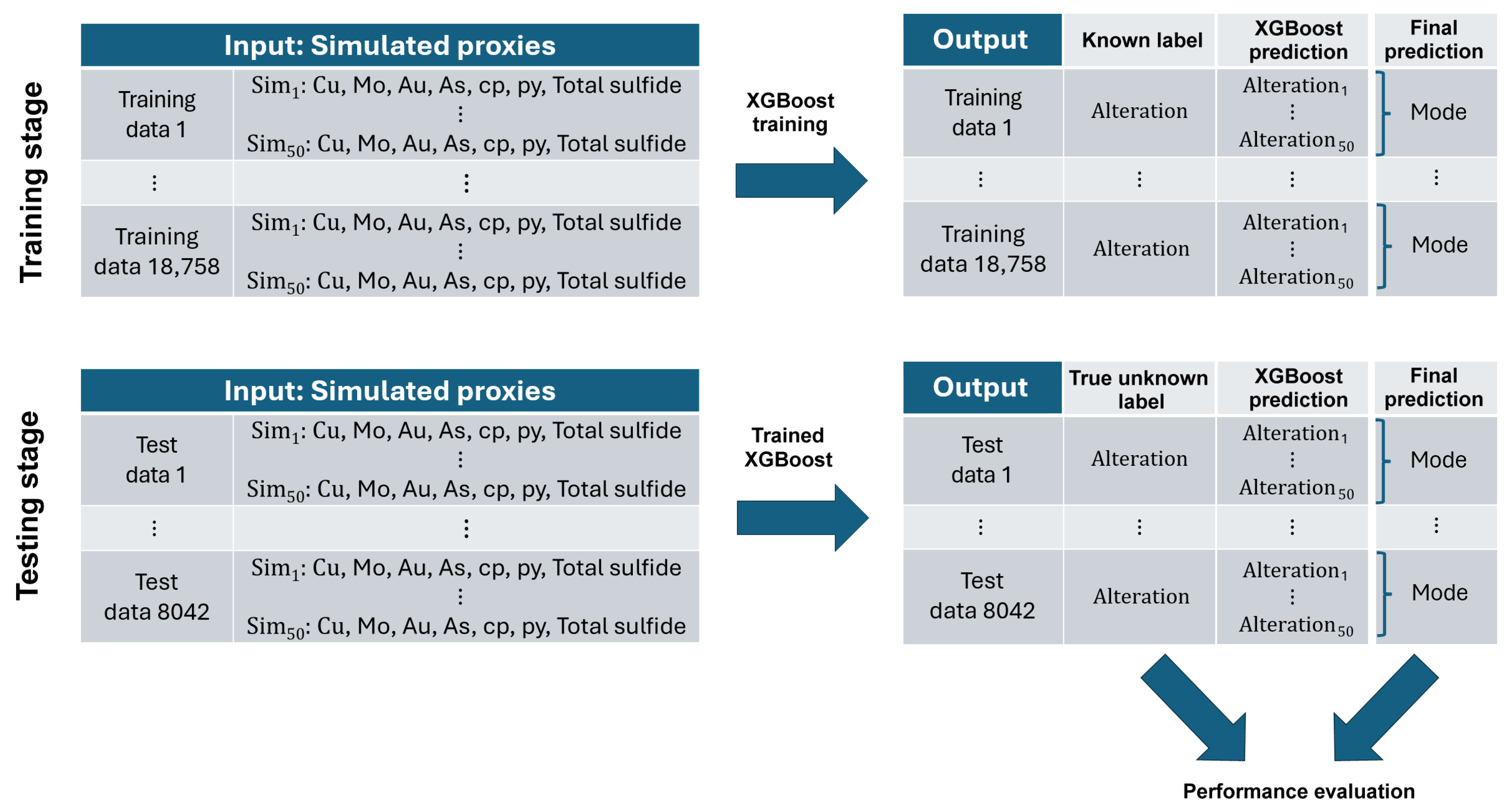
4. Geostatistically Enhanced Learning for Supervised Classification
- 1.
- Supervised classification: In supervised learning, the ML algorithm “learns” to recognize a pattern or make general predictions using known examples. Supervised learning algorithms create a map, or model, that relates a data (or feature) vector to a corresponding label or target vector : using labeled training data—data for which both the input and corresponding label () are known and available to the algorithm—to optimize the model. A well-trained model should be able to generalize and make accurate predictions for previously unseen inputs.
- 2.
- Extreme Gradient Boosting (XGBoost): It emerges as a top-choice classifier for its robustness against overfitting, minimal feature engineering, and ability to manage high-dimensional feature sets and sparse inputs [45]. Recent research shows that in terms of predictive accuracy, XGBoost generally has an advantage over single decision trees, often outperforms Random Forests by a margin in many cases, and is competitive with or better than Support Vector Machines and Neural Networks for tabular data sets [51,52].
- 3.
- MetaCost: This algorithm is designed for cost-sensitive classification and minimizes the expected cost of misclassifications, rather than their number [47].
- 4.
- Variogram analysis: It is the process of calculating experimental covariances or variograms that capture auto- and cross-correlations of spatial data and of fitting them with valid functions that are then inputted in geostatistical simulation [23].
- 5.
- Conditional simulation: It generates multiple scenarios that reproduce the statistical and spatial behavior of one or more regionalized variables, and the observed values of these variables [23].
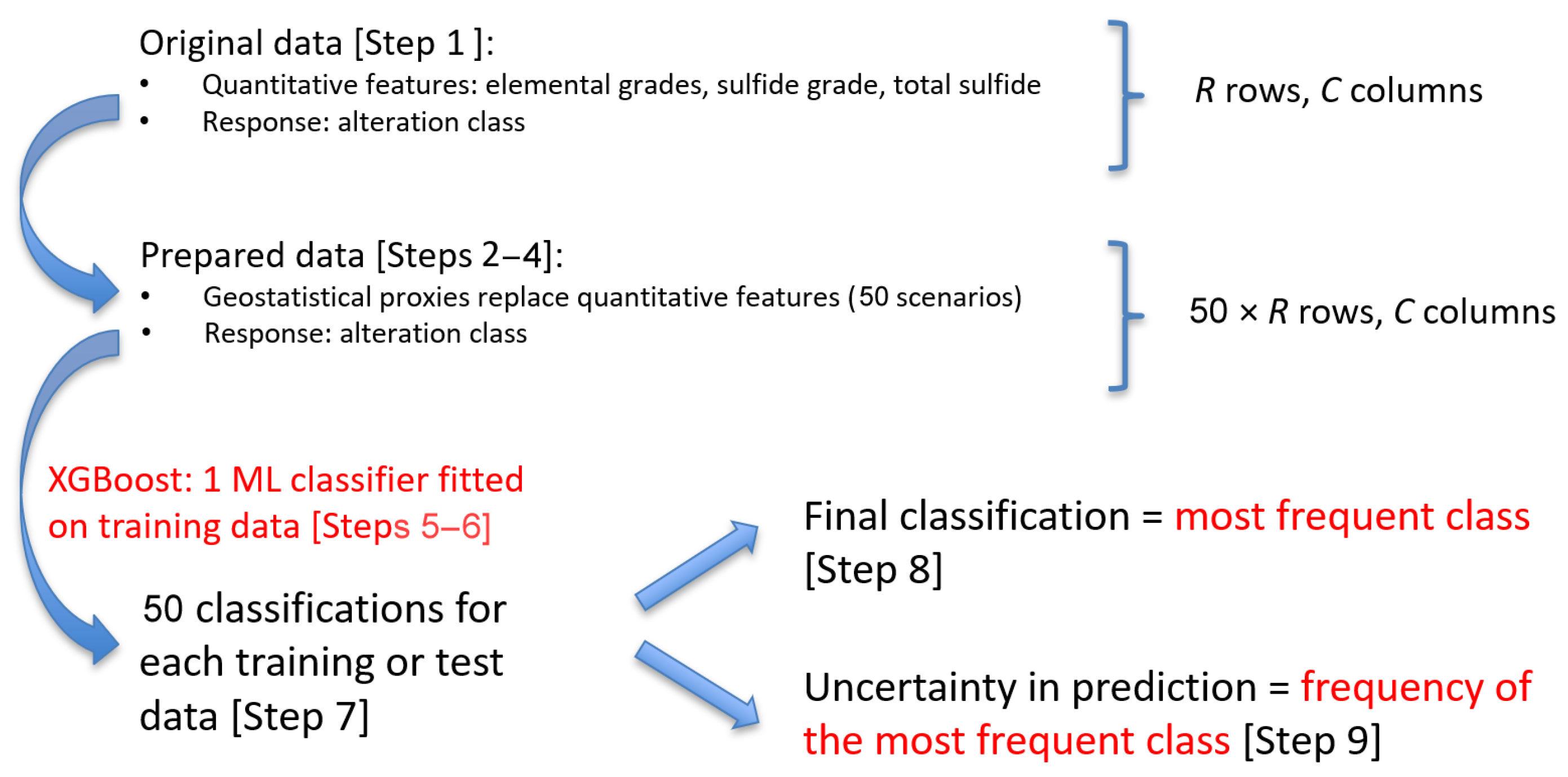
- 6.
- Step 1: Data cleaning.
- Step 2: Transforming each feature variable to a normal scale.
- Step 3: Variogram analysis of the normal score transforms.
- Step 4: Geostatistical simulation with nugget effect filtering to replace the value of each original feature variable at each data location with 50 simulated proxies that are normally distributed.
- Step 5: Random splitting of the data set into training (70%) and test (30%) subsets.
- Step 6: Training XGBoost with MetaCost on the training data with the simulated proxies.
- Step 7: Applying XGBoost to obtain 50 classifications for each training or test data.
- Step 8: Selecting the most frequent classification at each data location.
- Step 9: Assessing the classification confidence at each data location by calculating the frequency of the most frequent class.
4.1. Geostatistical Simulation with Filtering to Create Proxy Variables (Step 4)
- 1.
- The classifier needs to be trained only once.
- 2.
- All the simulated scenarios are equally important in the classification process.
- 3.
- This classifier can be applied to any set of simulated scenarios, even if they are not the same as the scenarios used to train the classifier. In other words, the simulated scenarios that have been used to train the classifier do not need to be extended to new locations where drill hole data become available, and the classifier does not need to be retrained.
4.2. Uncertainty Analysis Based on Simulated Proxies (Step 9)
5. Application Case Study
5.1. Deposit Geology
5.2. Data Description
5.3. Geostatistical Modeling and Simulation of Proxies
- 1.
- Normal score transformation: The values of each of the 7 feature variables were converted into Gaussian values based on a quantile-quantile transformation of their experimental distribution into a standard Gaussian distribution. As a result, we obtained 7 Gaussian variables, which were used in the subsequent steps in place of the original feature variables.
- 2.
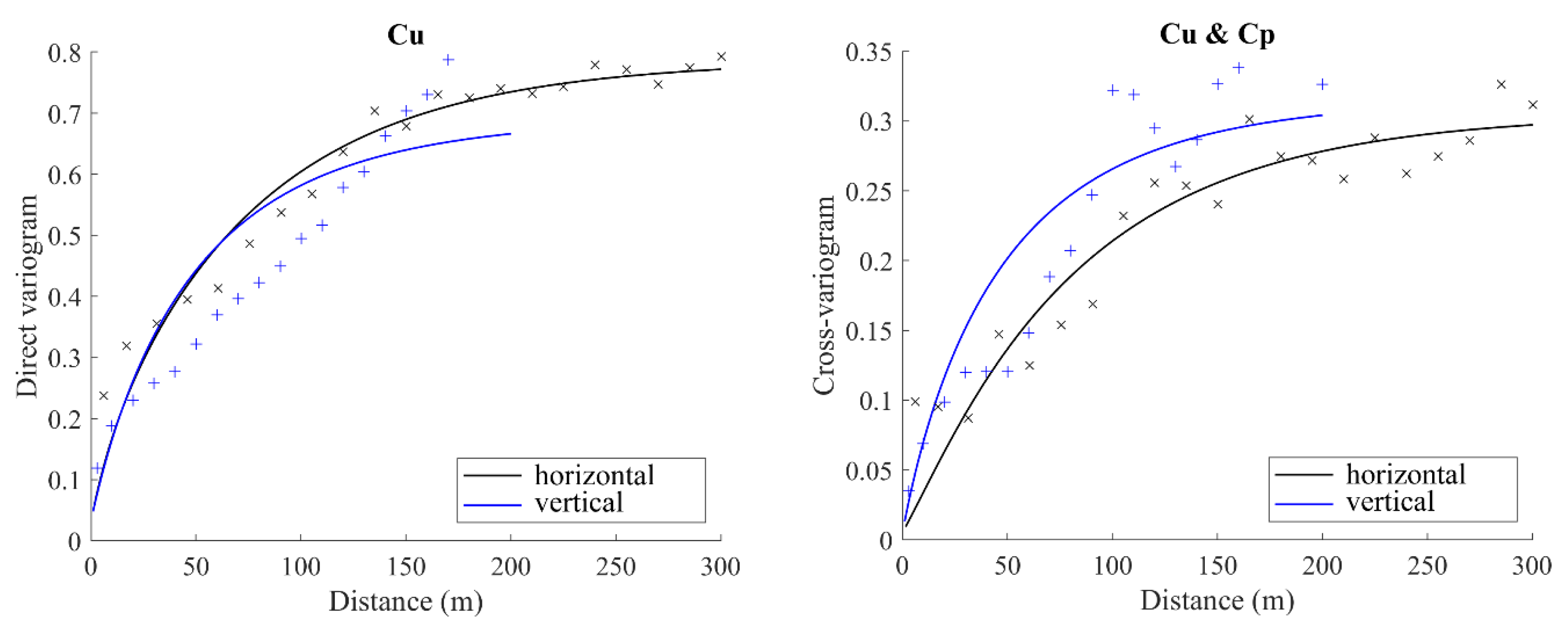
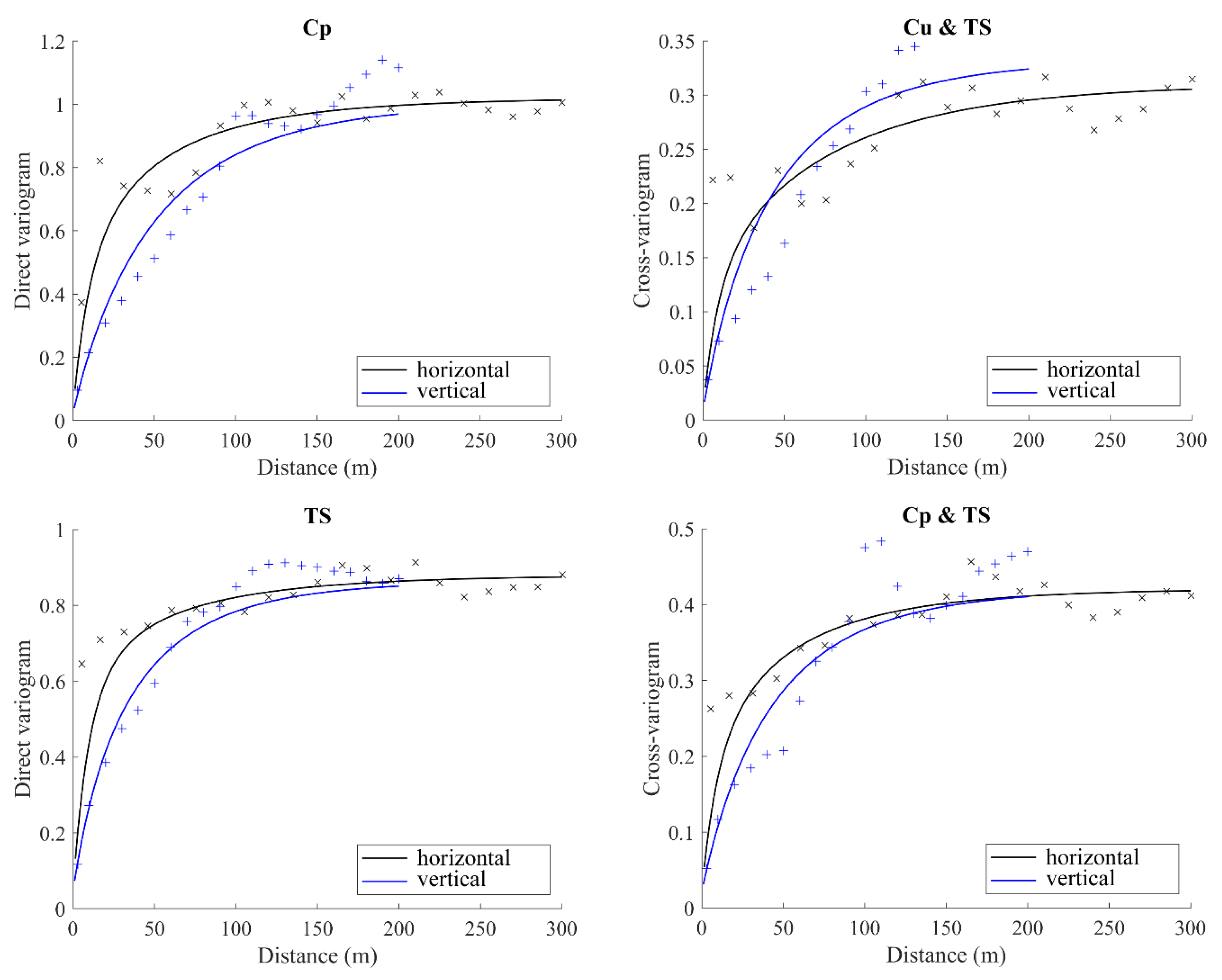
- Variogram analysis: The experimental direct and cross-variograms of the normal score data were calculated along the horizontal and vertical directions, recognized as the main anisotropy directions, and fitted with a linear model of coregionalization [49] consisting of a nugget effect and nested exponential variograms with practical ranges between 25 m and 250 m (Figure 5). The fitting was performed with a semi-automated algorithm [60] that ensures the positive semidefiniteness of each coregionalization matrix of size .
- 3.
- Simulation of the proxies at the data locations: A spectral algorithm was used to jointly simulate the 7 Gaussian variables at the data locations without the nugget effect component [53,55], and to condition the simulation to the normal score values observed at the 30 nearest data locations (including the target data location). This resulted in 50 sets of normally distributed proxies at the data locations. The proxies simulated at the training data locations were used for training the XGBoost classifier, while the proxies simulated at the test data were used for assessing the performance of the fitted XGBoost classifier and for uncertainty quantification.
5.4. Cost Matrix Definition
5.5. Experimental Setup
- 1.
- Experiment 1: This experiment was performed to answer the following question: does our implemented methodology provide an advantage with regards to its robustness under data constraints?For case 1 (classification based on original feature variables), two distinct scenarios were evaluated to assess model performance under data constraining conditions: (A) substantial missing values among feature variables, and (B) sparse spatial sampling. In scenario A (Figure 7), missing feature values were imputed using the median value computed per alteration type, for each corresponding input feature variable. In scenario B, the training data with missing values were excluded, and only isotopically sampled data points were retained.For case 2 (classification based on simulated proxies), data imputation or data remotion was not needed, insofar as conditional geostatistical simulation could be performed with heterotopic data (Figure 8).
- 2.
- Experiment 2: This experiment was performed to answer the following question: in the presence of unbalanced data, does a cost-sensitive classification strategy yield superior predictive scores?For case 2, two methodological scenarios were evaluated to answer the question: (A) classification of the proxy data set with integration of XGBoost with a cost-matrix informed by thermodynamic and mineral exploration criteria to minimize expected misclassification cost (same as case 2 of Experiment 1), and (B) classification of the proxy data set without integration of XGBoost with any cost-matrix.
5.6. Prediction Results
5.6.1. Experiment 1
- (A)
- (B)
5.6.2. Experiment 2
5.6.3. Analysis
- 1.
- In the traditional workflow, data imputation deteriorates all the scores ( to in accuracy, precision, recall, and F1-score) with respect to the case when the missing data are simply removed (Table 7 and Table 8). This is a warning against “blind” imputation procedures that ignore the spatial correlation structure of the data.
- 2.
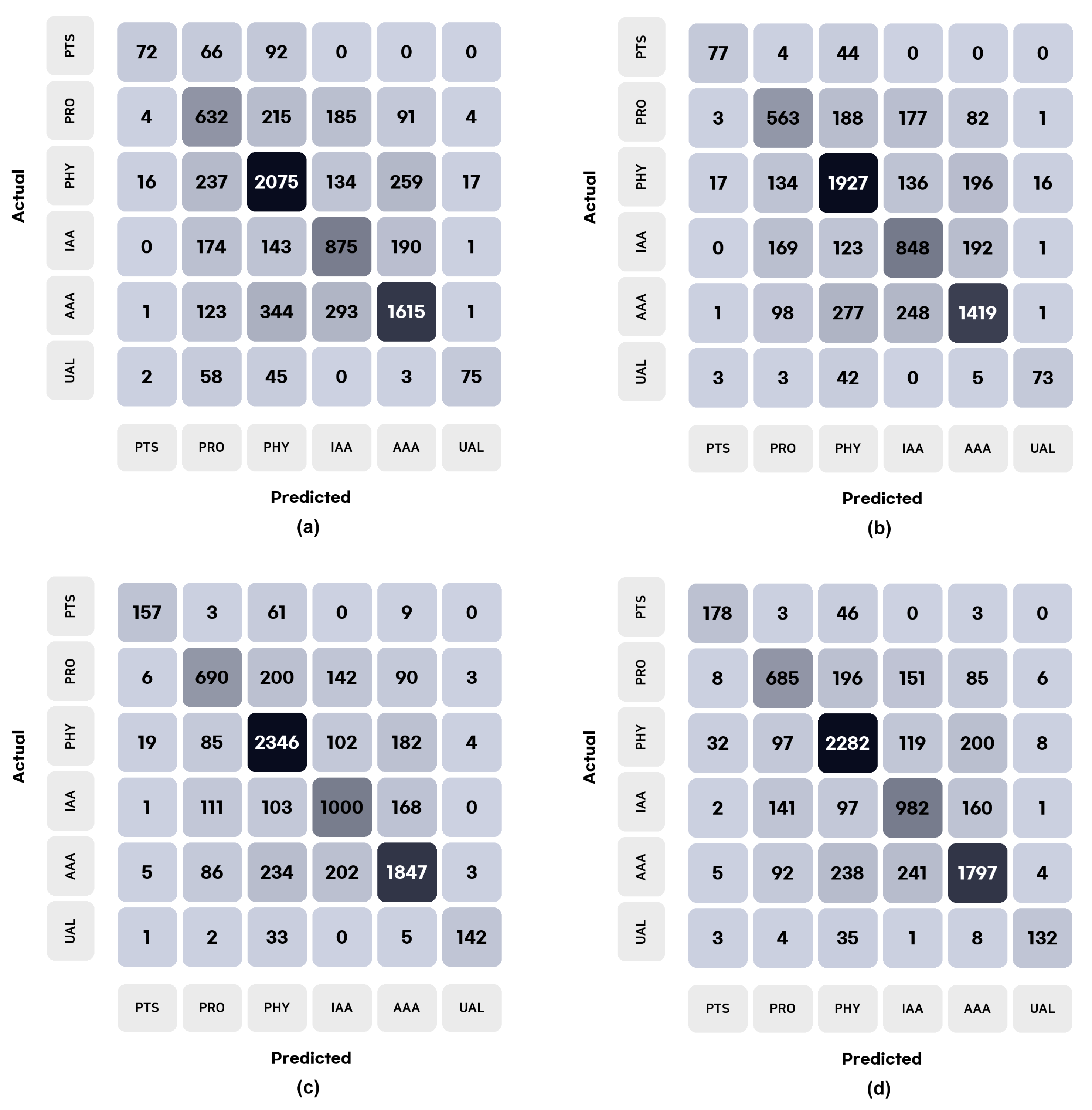
- In all cases, the classification based on geostatistically enhanced learning outperforms the traditional workflow, with a significant improvement of all the scores ( to in accuracy, precision, recall, and F1-score, when comparing cases 1 and 2 of Experiment 1; to when comparing case 1 of Experiment 1 and scenario B of Experiment 2). This indicates that geostatistically enhanced learning substantially reduces misclassifications, both false positives and false negatives, as corroborated by the confusion matrices in Figure 9.
- 3.
- Although it is designed to minimize the expected cost of misclassifications rather than their number, MetaCost slightly improves the accuracy, precision, recall, and F1-score ( when used in combination with the geostatistical proxies. This may be explained because the costs defined in Table 4 depend on regionalized properties of the alteration classes (thermodynamic and geology), therefore enhancing the classification with respect to costs that are blind to the spatial setting.
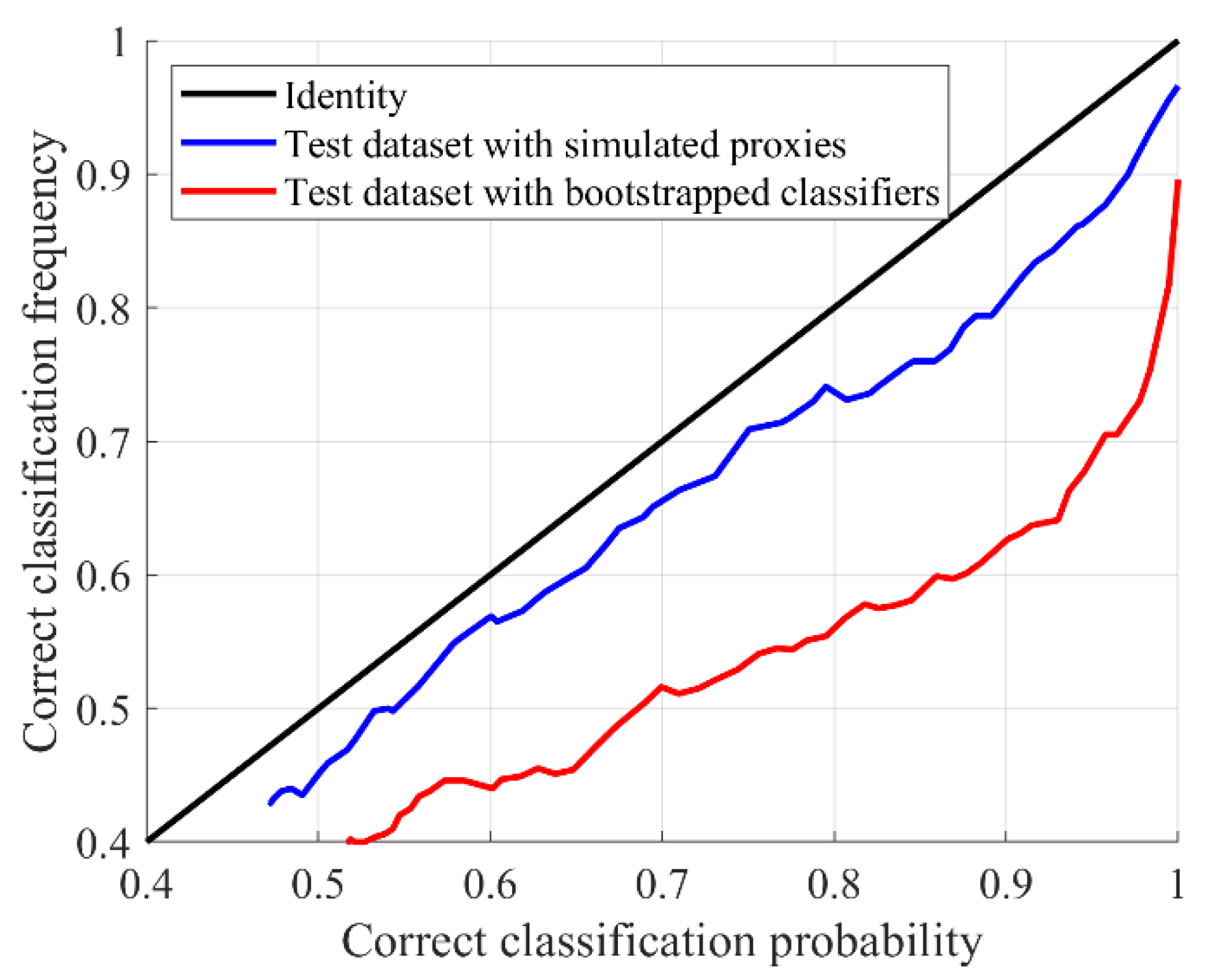
5.7. Prediction Uncertainty Quantification
6. Discussion: Significance and Outlook
6.1. Advantages of Using Simulated Proxies
- 1.
- Spatial context encoding: Geostatistical simulation injects knowledge of spatial continuity and geological trends into the data set. The proxies are not unconditionally simulated values—they honor the spatial locations, sample distributions, and variograms. Thus, when XGBoost trains on these features, it is indirectly learning from the spatial patterns of geochemistry and mineralogy, not just point values. This is a form of data augmentation that encodes the 3D spatial context, and constitutes a big advantage over using raw, point-sampled data where the spatial relationships would be invisible to the algorithm.
- 2.
- Holistic use of data: Our method avoids discarding drill intervals that lack a particular measurement by filling in a geostatistically plausible value. Traditional ML models would either drop those samples or impute that feature value, losing information. Here, no part of the drill core data goes unused—every location has a full complement of features, albeit they are simulated. This means the ML classifier is not biased by only the complete-case data; it benefits from mineralogical indicators even where originally absent, because those gaps were filled in a geologically informed manner. The result is a classifier that exploits the full richness of the data set—something that is particularly advantageous in 3D exploration settings where data are inherently sparse and clustered in drill holes—and is more robust since it relies on a much larger effective training set.
- 3.
- Noise filtering: The feature variables exhibit short-scale variations that complicate the classification task, whereas alterations classes often show highly continuous variations in space and not isolated occurrences. The noise-free simulated features only retain the large-scale variations and allow to better correlate the output with the input, enhancing the classification accuracy. Note that, if no nugget effect filtering were applied, the proxies simulated at the data locations would exactly match the normal score transforms of the feature variables. That is, without nugget effect filtering, the classification of case 2 would be the same as a classification based on the original feature variables (case 1).
- 4.
- Spatial interpolation: The proxies can be simulated at any location in space, even a completely unobserved one, which means that one can make the alteration “response” densely predictable by simulating the correlated predictors everywhere.
- 5.
- Uncertainty quantification: The multiple scenarios of simulated proxies not only provide a prediction at each target location, but also a measurement of how reliable this prediction is, whereas ML fails at measuring the uncertainty in the classification results.
6.2. Application to Geological and Alteration Mapping with Remote Sensing Big Data
- Field data, such as geochemical and mineralogical concentrations of ground samples;
- Two-dimensional remote sensing data from airborne or spaceborne multispectral (e.g., ASTER, Landsat, Sentinel) or hyperspectral (e.g., AVIRIS, PRISMA, EMIT, Hyperion) sensors.
6.3. Practical Utility and Implications for Mining Workflows
- 1.
- Data augmentation for mineral prospectivity mapping and AI-driven targeting: In mineral deposit targeting, training data are often sparse and incomplete (read: affected by heterotopic sampling designs). Geostatistical simulation creates spatially exhaustive and complete realizations of geological variables, effectively augmenting the dataset for machine learning and, more generally, artificial intelligence (AI) models, along the lines of the digital-twin solution in [69].
- 2.
- Risk-aware exploration decisions: By assessing the uncertainty in alteration predictions at each location, one can produce probability volumes for ore-bearing alteration type (read: probabilistic prospectivity maps). The implication is a better grasp of risk: areas with consistent predictions across scenarios are robust and could be trusted for decision-making, whereas areas with a high potential of ore-bearing alteration but uncertain predictions might need additional drilling for data acquisition to improve model reliability and reduce exploration risks. Confidence levels above are generally considered acceptable for geological classification tasks, while confidence levels below this threshold may indicate excessive uncertainty; more conservative thresholds may be justified for class assignment especially when economic consequences are high. Uncertainty-aware models can furthermore guide how to prioritize exploration targets according to the exploration program and risk preferences of the project developers (e.g., junior or major mining company) [70]. For instance, in advanced exploration stages, drilling programs may focus on those critical areas where the scenarios flip between ore-bearing and non-mineralized alteration classes, whereas other areas may be deprioritized as the additional data would not substantially impact project valuation. This approach contrasts with traditional geometry-based drilling plans, facilitating more cost-effective and risk-aligned programs, and ultimately reducing drilling requirements by focusing on uncertainty-informed target areas.
- 3.
- Geological modeling: In ore geology research, geological models of alteration, lithology, and mineralization provide a quantitative basis to discuss the geometry of hydrothermal systems and can be used to test genetic hypotheses, for example, checking if the spatial distribution of predicted alteration aligns with expected fluid flow patterns or metal zoning. Our approach can generate multiple geological models, which AI can then analyze for spatial patterns consistent with mineral system theory. Mineral system modeling platforms (e.g., those that simulate fluid flow, heat transport, or geochemical dispersion) can incorporate the simulation outputs as stochastic priors for permeability, lithology, or structural features. This is complementary to current practices in mineral resource estimation where geostatistical simulation is used to quantify ore grade uncertainty—here we would quantify geological interpretation uncertainty.
- 4.
- Mineral resource estimation: Assessing the uncertainty in the classification of alteration, lithology, or mineralization also supports probabilistic resource quantification, improves the efficiency of resource delineation, and enables scenario-based planning and more defensible reporting of mineral resources.
- 5.
- Geometallurgical planning: Different alterations imply different ore hardness and processing characteristics. A 3D alteration model can outline geometallurgical domains (hard vs. soft ore, acid-consuming gangue, metallurgical recovery, sedimentation velocity, etc.), bridging geology and metallurgy.
7. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Data Sources and Experimental Setup
- Original Data set Workflow: For the original data set, the script XGBMetaCostTrad.py was used to apply the MetaCost framework on a fixed training and test data set split (specified within the script). Output includes both prediction files and printed evaluation metrics.
- Bootstrapping for Confidence Estimation: To estimate the robustness of predictions, we applied a bootstrapping approach using the Bootstrapping.py script. For each test sample, the most frequent predicted class and an associated confidence score were computed based on repeated sampling from the training data. This method provides a nonparametric measure of predictive certainty.
- Simulated Proxies Workflow: The simulated data set workflow comprises five main stages:
- 1.
- Generation of Simulated Proxies under Matlab: The script instructions.m generates the geostatistical proxies at the training and test data locations. This includes normal scores transformation of feature variables, variogram calculation and fitting, and spectral simulation with nugget effect filtering. The script reads from the entire data set (alldata.csv) and outputs the simulated proxies results to a file named proxies_alldata.csv. These proxies are conditioned to the feature data observed at both the training and test data locations. Intermediate outputs are the normal score transforms of the feature variables and the experimental and fitted direct and cross-variograms needed for simulation (as ASCII files and as png images).
- 2.
- Prediction Generation: Using the script XGBMetaCostSim.py, a MetaCost-augmented XGBoost classifier was trained on the simulated proxies at the training data locations. The script outputs prediction results to a file named MetaCostPredictions.csv.
- 3.
- Mode-Based Aggregation: To simulate repeated measurements and model stability under variability, we computed the modal prediction across 50 replicates per data point using the script SimMode.py. This script reads from MetaCostPredictions.csv and writes to MetaCost_PredictionsMode.csv, adding a ModePred column.
- 4.
- Performance Evaluation: Evaluation metrics were calculated based on the modal predictions using SimModeMetrics.py. The results, including standard classification metrics (accuracy, precision, recall, and F1-score), were reported via console output.
- 5.
- Frequency–Accuracy Analysis: To investigate the relationship between prediction frequency and model confidence, we conducted an accuracy–frequency analysis using the AccuracyFrequency.py script. This script computes the average accuracy within each frequency class, leveraging the modal predictions from the simulated workflow.
- Implementation notes: All the scripts contain hardcoded paths to training and test data sets, and no additional command-line arguments are required. Proper data set placement and environment setup are assumed for successful execution.
Appendix B. Parameter Fitting for XGBoost
Appendix B.1. Case 1 (Classification Based on Original Features Cu, Au, Mo, As, Cp, Py, and TS)
- max_depth: 8learning_rate: 0.07
- n_estimators: 800
- subsample: 1.0
- colsample_bytree: 0.8
- gamma: 0.1
- min_child_weight: 2
- reg_alpha: 0.01
- reg_lambda: 0.3
- tree_method: hist
- eval_metric: mlogloss
- random_state: 42.
Appendix B.2. Case 2 (Classification Based on Simulated Proxies)
- max_depth: 10
- learning_rate: 0.07
- n_estimators: 1500
- subsample: 0.9
- colsample_bytree: 0.8
- gamma: 0.2
- min_child_weight: 3
- reg_alpha: 0.1
- reg_lambda: 0.5
- tree_method: hist
- eval_metric: mlogloss
- random_state: 42.
References
- Deb, M.; Sarkar, S. Minerals and Allied Natural Resources and Their Sustainable Development; Springer: Singapore, 2017. [Google Scholar]
- Robb, L. Introduction to Ore-Forming Processes; Blackwell Publishing: Oxford, UK, 2005. [Google Scholar]
- Guilbert, J.; Park, C. The Geology of Ore Deposits; W.H. Freeman and Company: New York, NY, USA, 1986. [Google Scholar]
- Barnes, H. Geochemistry of Hydrothermal Ore Deposits; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Lowell, J.; Guilbert, J. Lateral and vertical alteration mineralization zoning in porphyry ore deposits. Econ. Geol. 1970, 65, 373–408. [Google Scholar] [CrossRef]
- Mathieu, L. Quantifying hydrothermal alteration: A review of methods. Geosciences 2018, 8, 245. [Google Scholar] [CrossRef]
- Dutta, P.; Emery, X. Classifying rock types by geostatistics and random forests in tandem. Mach. Learn. Sci. Technol. 2024, 5, 025013. [Google Scholar] [CrossRef]
- Smirnoff, A.; Boisvert, E.; Paradis, S.J. Support vector machine for 3D modelling from sparse geological information of various origins. Comput. Geosci. 2008, 34, 127–143. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Hezarkhani, A.; Soltani-Mohammadi, S. Classification of alteration zones based on whole-rock geochemical data using support vector machine. J. Geol. Soc. India 2015, 85, 500–508. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Caté, A.; Schetselaar, E.; Mercier-Langevin, P.; Ross, P. Classification of lithostratigraphic and alteration units from drillhole lithogeochemical data using machine learning: A case study from the Lalor volcanogenic massive sulphide deposit, Snow Lake, Manitoba, Canada. J. Geochem. Explor. 2018, 188, 216–228. [Google Scholar] [CrossRef]
- Xiang, J.; Xiao, K.; Carranza, E.J.M.; Chen, J.; Li, S. 3D mineral prospectivity mapping with random forests: A case study of Tongling, Anhui, China. Nat. Resour. Res. 2019, 29, 395–414. [Google Scholar] [CrossRef]
- Chen, J.; Mao, X.; Deng, H.; Liu, Z.; Wang, Q. Three-dimensional modelling of alteration zones based on geochemical exploration data: An interpretable machine-learning approach via generalized additive models. Appl. Geochem. 2020, 123, 104781. [Google Scholar] [CrossRef]
- Dumakor-Dupey, N.K.; Arya, S. Machine learning—A review of applications in mineral resource estimation. Energies 2021, 14, 4079. [Google Scholar] [CrossRef]
- Jooshaki, M.; Nad, A.; Michaux, S. A systematic review on the application of machine learning in exploiting mineralogical data in mining and mineral industry. Minerals 2021, 11, 816. [Google Scholar] [CrossRef]
- Jung, D.; Choi, Y. Systematic review of machine learning applications in mining: Exploration, exploitation, and reclamation. Minerals 2021, 11, 148. [Google Scholar] [CrossRef]
- Jia, R.J.; Lv, Y.; Wang, G.; Carranza, E.J.M.; Chen, Y.; Wei, C.; Zhang, Z. A stacking methodology of machine learning for 3D geological modeling with geological-geophysical datasets, Laochang Sn camp, Gejiu (China). Comput. Geosci. 2021, 151, 104754. [Google Scholar] [CrossRef]
- Pour, A.B.; Harris, J.; Zuo, R. Machine learning for analysis of geo-exploration data. In Geospatial Analysis Applied to Mineral Exploration; Pour, A.B., Parsa, M., Eldosouky, A.M., Eds.; Elsevier: Amsterdam, The Netherlands, 2023; pp. 279–294. [Google Scholar]
- Shi, Z.; Zuo, R.; Zhou, B. Deep reinforcement learning for mineral prospectivity mapping. Math. Geosci. 2023, 55, 773–797. [Google Scholar] [CrossRef]
- Farhadi, S.; Tatullo, S.; Konari, M.B.; Afzal, P. Evaluating StackingC and ensemble models for enhanced lithological classification in geological mapping. J. Geochem. Explor. 2024, 260, 107441. [Google Scholar] [CrossRef]
- Sun, K.; Chen, Y.; Geng, G.; Lu, Z.; Zhang, W.; Song, Z.; Guan, J.; Zhao, Y.; Zhang, Z. A review of mineral prospectivity mapping using deep learning. Minerals 2024, 14, 1021. [Google Scholar] [CrossRef]
- Gy, P. Sampling of Particulate Materials: Theory and Practice; Elsevier: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Chilès, J.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Banerjee, S.; Carlin, B.; Gelfand, A. Hierarchical Modeling and Analysis for Spatial Data; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Zhang, C.; Zuo, R.; Xiong, Y. Detection of the multivariate geochemical anomalies associated with mineralization using a deep convolutional neural network and a pixel-pair feature method. Appl. Geochem. 2021, 130, 104994. [Google Scholar] [CrossRef]
- Zhang, S.; Carranza, E.J.M.; Wei, H.; Xiao, K.; Yang, F.; Xiang, J.; Xu, Y. Data-driven mineral prospectivity mapping by joint application of unsupervised convolutional auto-encoder network and supervised convolutional neural network. Nat. Resour. Res. 2021, 30, 1011–1031. [Google Scholar] [CrossRef]
- Behrens, T.; Schmidt, K.; Rossel, R.A.V.; Gries, P.; Scholten, T.; MacMillan, R.A. Spatial modelling with Euclidean distance fields and machine learning. Eur. J. Soil Sci. 2018, 69, 757–770. [Google Scholar] [CrossRef]
- Balk, B.; Elder, K. Combining binary decision tree and geostatistical methods to estimate snow distribution in a mountain watershed. Water Resour. Res. 2000, 36, 13–26. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D.; Potter, A.; Daniell, J.J. Application of machine learning methods to spatial interpolation of environmental variables. Environ. Model. Softw. 2011, 26, 1647–1659. [Google Scholar] [CrossRef]
- Fayad, I.; Baghdadi, N.; Bailly, J.; Barbier, N.; Gond, V.; Hérault, B.; El Hajj, M.; Fabre, F.; Perrin, J. Regional scale rain-forest height mapping using regression-kriging of spaceborne and airborne LiDAR data: Application on French Guiana. Remote Sens. 2016, 8, 240. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, G.; Zhao, N.; Mulligan, K.; Ye, X. Improve ground-level PM2.5 concentration mapping using a random forests-based geostatistical approach. Environ. Pollut. 2018, 235, 272–282. [Google Scholar] [CrossRef]
- Fox, E.; Ver Hoef, J.; Olsen, A.R. Comparing spatial regression to random forests for large environmental data sets. PLoS ONE 2020, 15, e0229509. [Google Scholar] [CrossRef]
- Schmidinger, J.; Barkov, V.; Vogel, S.; Atzmueller, M.; Heuvelink, G.B.M. Kriging prior regression: A case for kriging-based spatial features with TabPFN in soil mapping. arXiv 2025, arXiv:2509.09408v2. [Google Scholar]
- Saha, A.; Basu, S.; Datta, A. Random forests for spatially dependent data. J. Am. Stat. Assoc. 2023, 118, 665–683. [Google Scholar] [CrossRef]
- Hengl, T.; Nussbaum, M.; Wright, M.; Heuvelink, G.; Gräler, B. Random forest as a generic framework for predictive modeling of spatial and spatio-temporal variables. PeerJ 2018, 6, e5518. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Niang Gadiaga, A.; Linard, C.; Lennert, M.; Vanhuysse, S.; Mboga, N.; Wolff, E.; Kalogirou, S. Geographical random forests: A spatial extension of the random forest algorithm to address spatial heterogeneity in remote sensing and population modelling. Geocarto Int. 2021, 36, 121–136. [Google Scholar] [CrossRef]
- Qin, Z.; Peng, Q.; Jin, C.; Xu, J.; Xing, S.; Zhu, P.; Yang, G. Geographically weighted random forest fusing multi-source environmental covariates for spatial prediction of soil heavy metals. Environ. Pollut. 2025, 385, 127135. [Google Scholar] [CrossRef] [PubMed]
- Sekulić, A.; Kilibarda, M.; Heuvelink, G.B.M.; Nikolić, M.; Bajat, B. Random forest spatial interpolation. Remote Sens. 2020, 12, 1687. [Google Scholar] [CrossRef]
- Talebi, H.; Peeters, L.J.M.; Otto, A.; Tolosana-Delgado, R. A truly spatial random forests algorithm for geoscience data analysis and modelling. Math. Geosci. 2022, 54, 1–22. [Google Scholar] [CrossRef]
- Nwaila, G.T.; Zhang, S.E.; Frimmel, H.E.; Manzi, M.S.D.; Dohm, C.; Durrheim, R.J.; Burnett, M.; Tolmay, L. Local and target exploration of conglomerate-hosted gold deposits using machine learning algorithms: A case study of the Witwatersrand gold ores, South Africa. Nat. Resour. Res. 2020, 29, 135–159. [Google Scholar] [CrossRef]
- Erten, G.E.; Yavuz, M.; Deutsch, C.V. Combination of machine learning and kriging for spatial estimation of geological attributes. Nat. Resour. Res. 2022, 31, 191–213. [Google Scholar] [CrossRef]
- Adeli, A.; Emery, X.; Dowd, P. Geological modelling and validation of geological interpretations via simulation and classification of quantitative covariates. Minerals 2018, 8, 7. [Google Scholar] [CrossRef]
- Talebi, H.; Mueller, U.; Tolosana-Delgado, R.; Grunsky, E.; McKinley, J.; de Caritat, P. Surficial and deep earth material prediction from geochemical compositions. Nat. Resour. Res. 2019, 28, 869–891. [Google Scholar] [CrossRef]
- Bai, T.; Tahmasebi, P. Hybrid geological modeling: Combining machine learning and multiple-point statistics. Comput. Geosci. 2020, 142, 104519. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the KDD ’16: The 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Krishnapuram, B., Shah, M., Eds.; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Domingos, P. MetaCost: A general method for making classifiers cost-sensitive. In Proceedings of the KDD ’99: The Fifth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 15–18 August 1999; Fayyad, U., Chaudhuri, S., Madigan, D., Eds.; Association for Computing Machinery: New York, NY, USA, 1999; pp. 155–164. [Google Scholar]
- Efron, B. Bootstrap methods: Another look at the jackknife. Ann. Stat. 1979, 7, 101–118. [Google Scholar] [CrossRef]
- Wackernagel, H. Multivariate Geostatistics: An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Lantuéjoul, C. Geostatistical Simulation: Models and Algorithms; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Shwartz-Ziv, R.; Armon, A. Tabular data: Deep learning is not all you need. Inf. Fusion 2022, 81, 84–90. [Google Scholar] [CrossRef]
- Li, H.; Gao, M.; Ji, X.; Zhang, Z.; Cheng, Z.; Santosh, M. Machine learning-based tectonic discrimination using basalt element geochemical data: Insights into the Carboniferous-Permian tectonic regime of western Tianshan orogen. Minerals 2025, 15, 122. [Google Scholar] [CrossRef]
- Adeli, A.; Emery, X. Geostatistical simulation of rock physical and geochemical properties with spatial filtering and its application to predictive geological mapping. J. Geochem. Explor. 2021, 220, 106661. [Google Scholar] [CrossRef]
- Guartán, J.A.; Emery, X. Regionalized classification of geochemical data with filtering of measurement noises for predictive lithological mapping. Nat. Resour. Res. 2021, 30, 1033–1052. [Google Scholar] [CrossRef]
- Emery, X.; Arroyo, D.; Porcu, E. An improved spectral turning-bands algorithm for simulating stationary vector Gaussian random fields. Stoch. Environ. Res. Risk Assess. 2016, 30, 1863–1873. [Google Scholar] [CrossRef]
- Yakubchuk, A.; Cole, A.; Seltmann, R.; Vitalievich, S.V. Tectonic setting, characteristics, and regional exploration criteria for gold mineralization in the Altaid orogenic collage: The Tien Shan Province as a key example. In Integrated Methods for Discovery: Global Exploration in Twenty-First Century; Goldfarb, R.J., Nielsen, R.L., Eds.; Society of Economic Geologists: Littleton, CO, USA, 2002; pp. 177–201. [Google Scholar]
- Seedorff, E.; Dilles, J.H.; Proffett, J.M.; Einaudi, M.T.; Zurcher, L.; Stavast, W.J.A.; Johnson, D.A.; Barton, M.D. Porphyry deposits: Characteristics and origin of hypogene features. In Economic Geology One Hundredth Anniversary Volume; Hedenquist, J.W., Thompson, J.F.H., Goldfarb, R.J., Richards, J.P., Eds.; Society of Economic Geologists: Littleton, CO, USA, 2005; pp. 251–298. [Google Scholar]
- Sillitoe, R.H. Porphyry copper systems. Econ. Geol. 2010, 105, 3–41. [Google Scholar] [CrossRef]
- Porter, T. The geology, structure and mineralisation of the Oyu Tolgoi porphyry copper-gold-molybdenum deposits, Mongolia: A review. Geosci. Front. 2016, 7, 375–407. [Google Scholar] [CrossRef]
- Emery, X. Iterative algorithms for fitting a linear model of coregionalization. Comput. Geosci. 2010, 36, 1150–1160. [Google Scholar] [CrossRef]
- Zhang, S.; Nwaila, G.; Bourdeau, J.; Ghorbani, Y.; Carranza, E. Machine learning-based delineation of geodomain boundaries: A proof-of-concept study using data from the Witwatersrand goldfields. Nat. Resour. Res. 2023, 32, 879–900. [Google Scholar] [CrossRef]
- Chen, X.; Warner, T.A.; Campagna, D.J. Integrating visible, near-infrared and short-wave infrared hyperspectral and multispectral thermal imagery for geological mapping at Cuprite, Nevada: A rule-based system. Int. J. Remote Sens. 2010, 31, 1733–1752. [Google Scholar] [CrossRef]
- Bishop, C.A.; Liu, J.G.; Mason, P.J. Hyperspectral remote sensing for mineral exploration in Pulang, Yunnan Province, China. Int. J. Remote Sens. 2011, 32, 2409–2426. [Google Scholar] [CrossRef]
- Pour, A.B.; Hashim, M. ASTER, ALI and Hyperion sensors data for lithological mapping and ore minerals exploration. SpringerPlus 2014, 3, 130. [Google Scholar] [CrossRef]
- Alimohammadi, M.; Alirezaei, S.; Kontak, D.J. Application of ASTER data for exploration of porphyry copper deposits: A case study of Daraloo–Sarmeshk area, southern part of the Kerman copper belt, Iran. Ore Geol. Rev. 2015, 33, 183–199. [Google Scholar] [CrossRef]
- Canbaz, O.; Gürsoy, O.; Karaman, M.; Çalışkan, A.B.; Gökce, A. Hydrothermal alteration mapping using EO-1 Hyperion hyperspectral data in Kosedag, Central Eastern Anatolia (Sivas-Turkey). Arab. J. Geosci. 2021, 14, 2245. [Google Scholar] [CrossRef]
- Madani, N.; Emery, X. A comparison of search strategies to design the cokriging neighborhood for predicting coregionalized variables. Stoch. Environ. Res. Risk Assess. 2019, 33, 183–199. [Google Scholar] [CrossRef]
- Babak, O.; Deutsch, C.V. Collocated cokriging based on merged secondary attributes. Math. Geosci. 2009, 41, 921–926. [Google Scholar] [CrossRef]
- Liang, M.; Putzmann, C.; Gokaydin, D. Enhancing Geoscience Model Confidence via Digital Twins—Integrated Modelling, Simulation, and Machine Learning Technologies; The Australasian Institute of Mining and Metallurgy: Carlton, VIC, Australia, 2024. [Google Scholar]
- Cáceres, A.; Emery, X.; Ibarra, F.; Pérez, J.; Seguel, S.; Fuster, G.; Pérez, A.; Riquelme, R. A stochastic framework for mineral resource uncertainty quantification and management at Compañía Minera Doña Inés de Collahuasi. Minerals 2025, 15, 855. [Google Scholar] [CrossRef]

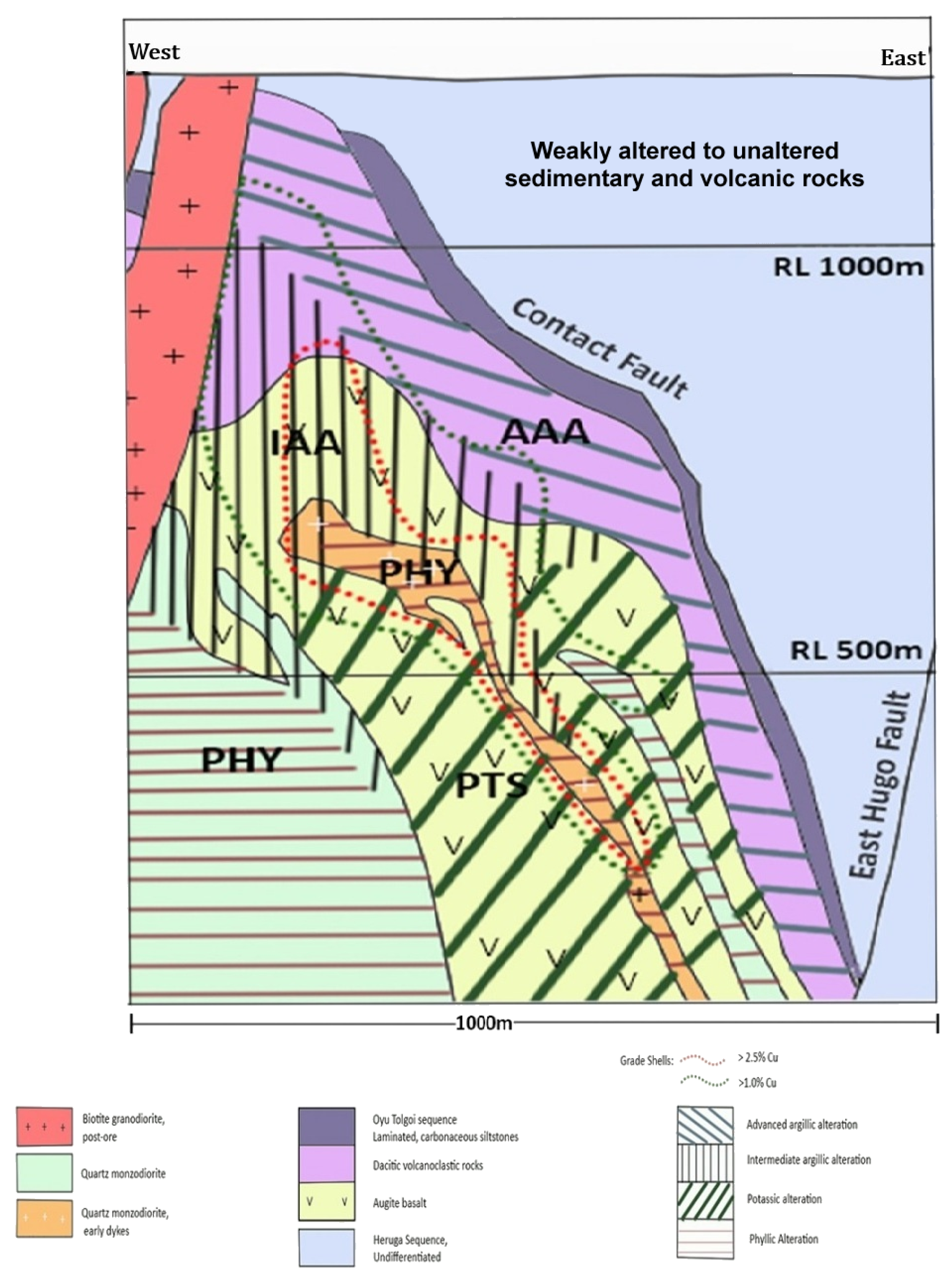
| Serial Number | Rock Type | Age |
|---|---|---|
| 1 | Quaternary cover | Quaternary |
| 2 | Cretaceous clay | Cretaceous |
| 3 | Carboniferous andesite dykes | Carboniferous |
| 4 | Basalt dykes | Carboniferous |
| 5 | Carboniferous intrusive | Carboniferous |
| 6 | Carboniferous rhyolite dykes | Carboniferous |
| 7 | Faulted rocks | Late Devonian and older |
| 8 | Biotite granodiorite dykes | Late Devonian and older |
| 9 | Hydrothermal breccia | Late Devonian and older |
| 10 | Quartz monzodiorite | Late Devonian and older |
| 11 | Ignimbrite | Late Devonian and older |
| 12 | Augite basalt | Late Devonian and older |
| 13 | Hanging wall sequence | Late Devonian and older |
| Alteration Class | Alteration Code | Number of Records in Training Set | Number of Records in Test Set | |
|---|---|---|---|---|
| Entire drill hole data base | Advanced argillic | AAA | 5348 | 2377 |
| Intermediate argillic | IAA | 2979 | 1383 | |
| Phyllic | PHY | 6478 | 2738 | |
| Propylitic | PRO | 2882 | 1131 | |
| Potassic | PTS | 475 | 230 | |
| Unaltered | UAL | 596 | 183 | |
| All classes | 18,758 | 8042 | ||
| Drill hole composites without missing data | Advanced argillic | AAA | 4427 | 2044 |
| Intermediate argillic | IAA | 2883 | 1333 | |
| Phyllic | PHY | 5785 | 2426 | |
| Propylitic | PRO | 2650 | 1014 | |
| Potassic | PTS | 239 | 125 | |
| Unaltered | UAL | 463 | 126 | |
| All classes | 16,447 | 7068 |
| Feature | Number of Records in Training Set | Number of Records in Test Set | Min. | Max. | Mean | St. Dev. |
|---|---|---|---|---|---|---|
| Cu (%) | 16,811 | 7246 | 0.0 | 21.5 | 0.807 | 0.845 |
| Au (ppm) | 16,810 | 7246 | 0.0 | 26.8 | 0.097 | 0.285 |
| Mo (ppm) | 16,751 | 7218 | 0.06 | 3730 | 58.06 | 82.43 |
| As (ppm) | 16,448 | 7068 | 0.5 | 13,400 | 167.56 | 392.64 |
| chalcopyrite (%) | 18,758 | 8042 | 0.0 | 11.2 | 1.102 | 1.051 |
| pyrite (%) | 18,758 | 8042 | 0.0 | 38.0 | 2.011 | 1.970 |
| TS (%) | 18,758 | 8042 | 0.0 | 60.0 | 3.457 | 2.160 |
| Predicted Class | |||||||
|---|---|---|---|---|---|---|---|
| PTS | PRO | PHY | IAA | AAA | UAL | ||
| True Class | PTS | 0 | 5 | 7 | 9 | 8 | 12 |
| PRO | 5 | 0 | 10 | 12 | 9 | 10 | |
| PHY | 7 | 10 | 0 | 4 | 7 | 16 | |
| IAA | 9 | 12 | 4 | 0 | 5 | 16 | |
| AAA | 8 | 9 | 7 | 5 | 0 | 12 | |
| UAL | 12 | 10 | 16 | 16 | 12 | 0 | |
| Predicted Class | |||||||
|---|---|---|---|---|---|---|---|
| PTS | PRO | PHY | IAA | AAA | UAL | ||
| True Class | PTS | 0 | 1 | 3 | 5 | 6 | 8 |
| PRO | 1 | 0 | 2 | 4 | 5 | 8 | |
| PHY | 3 | 2 | 0 | 2 | 3 | 8 | |
| IAA | 5 | 4 | 2 | 0 | 1 | 8 | |
| AAA | 6 | 5 | 3 | 1 | 0 | 8 | |
| UAL | 8 | 8 | 8 | 8 | 8 | 0 | |
| Predicted Class | |||||||
|---|---|---|---|---|---|---|---|
| PTS | PRO | PHY | IAA | AAA | UAL | ||
| True Class | PTS | 0 | 4 | 4 | 4 | 2 | 4 |
| PRO | 4 | 0 | 8 | 8 | 4 | 2 | |
| PHY | 4 | 8 | 0 | 2 | 4 | 8 | |
| IAA | 4 | 8 | 2 | 0 | 4 | 8 | |
| AAA | 2 | 4 | 4 | 4 | 0 | 4 | |
| UAL | 4 | 2 | 8 | 8 | 4 | 0 | |
| Metric | Classification from Original Feature Variables (8042 Test Data) | Classification from Geostatistical Proxies (8042 Test Data) |
|---|---|---|
| Accuracy | 0.66 | 0.77 |
| Cohen’s Kappa | 0.55 | 0.69 |
| Precision | 0.67 | 0.77 |
| Recall | 0.66 | 0.77 |
| F1-score | 0.66 | 0.77 |
| Specificity | 0.92 | 0.95 |
| Sensitivity | 0.55 | 0.74 |
| Metric | Classification from Original Feature Variables (7068 Test Data) | Classification from Geostatistical Proxies (8042 Test Data) |
|---|---|---|
| Accuracy | 0.69 | 0.77 |
| Cohen’s Kappa | 0.58 | 0.69 |
| Precision | 0.69 | 0.77 |
| Recall | 0.69 | 0.77 |
| F1-score | 0.69 | 0.77 |
| Specificity | 0.93 | 0.95 |
| Sensitivity | 0.68 | 0.74 |
| Metric | (A) Classification from Geostatistical Proxies with MetaCost (8042 Test Data) | (B) Classification from Geostatistical Proxies Without MetaCost (8042 Test Data) |
|---|---|---|
| Accuracy | 0.77 | 0.75 |
| Cohen’s Kappa | 0.69 | 0.67 |
| Precision | 0.77 | 0.75 |
| Recall | 0.77 | 0.75 |
| F1-score | 0.77 | 0.75 |
| Specificity | 0.95 | 0.94 |
| Sensitivity | 0.74 | 0.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borah, A.; Dutta, P.J.; Emery, X. Geostatistically Enhanced Learning for Supervised Classification of Wall-Rock Alteration Using Assay Grades of Trace Elements and Sulfides. Minerals 2025, 15, 1128. https://doi.org/10.3390/min15111128
Borah A, Dutta PJ, Emery X. Geostatistically Enhanced Learning for Supervised Classification of Wall-Rock Alteration Using Assay Grades of Trace Elements and Sulfides. Minerals. 2025; 15(11):1128. https://doi.org/10.3390/min15111128
Chicago/Turabian StyleBorah, Abhishek, Parag Jyoti Dutta, and Xavier Emery. 2025. "Geostatistically Enhanced Learning for Supervised Classification of Wall-Rock Alteration Using Assay Grades of Trace Elements and Sulfides" Minerals 15, no. 11: 1128. https://doi.org/10.3390/min15111128
APA StyleBorah, A., Dutta, P. J., & Emery, X. (2025). Geostatistically Enhanced Learning for Supervised Classification of Wall-Rock Alteration Using Assay Grades of Trace Elements and Sulfides. Minerals, 15(11), 1128. https://doi.org/10.3390/min15111128







