Comparative Evaluation of Flow Rate Distribution Methods for Uranium In-Situ Leaching via Reactive Transport Modeling
Abstract
1. Introduction
- 1
- Exploration—the identification, delineation, and localization of ore-bearing zones through exploratory drilling and well-logging [4]. At this stage, well log data are also interpreted, and borehole information is interpolated to evaluate the filtration capacity properties and the distribution of mineralization in the inter-well space.
- 2
- Zoning—the division of a deposit into geological and technological blocks. A technological block is understood as an area, typically characterized by relatively homogeneous filtration properties, with a separate budget and developed under an independent project.
- 3
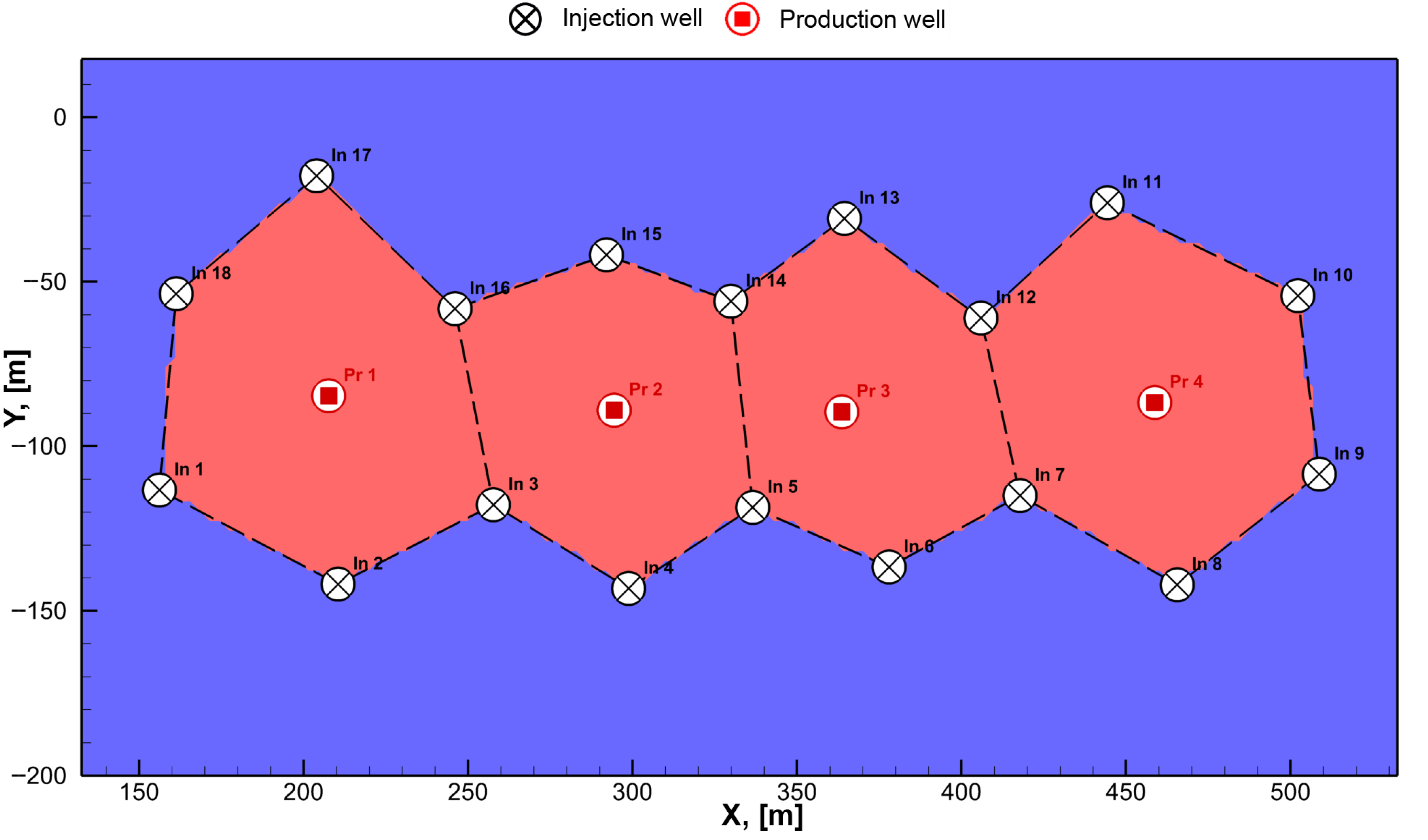
- Design of the technological block—involves determining the number and placement of wells, selecting a deposit extraction pattern (e.g., hexagonal, linear, or other configurations of well locations) [5,6], and performing preliminary predictive calculations of production curves under anticipated operating conditions. These calculations account for parameters such as well flow rates, the composition and acidity of the leaching solution, the vertical distribution of well screens, and other factors.
- 4
- Commissioning, exploitation, and decommissioning of a technological block—encompasses the actual extraction process, accompanied by continuous monitoring using data from production and observation wells.
2. Materials and Methods
- Thickness averaged throughout the deposit— [m];
- Average uranium mass fraction— [kg/kg];
- Uranium content in meter-percent— [m%];
- Hydraulic conductivity of the ore-bearing layer— [m/day];
- Average density of the uranium-containing formation— [kg/m3];
- Average porosity of the layer— [m3/m3].
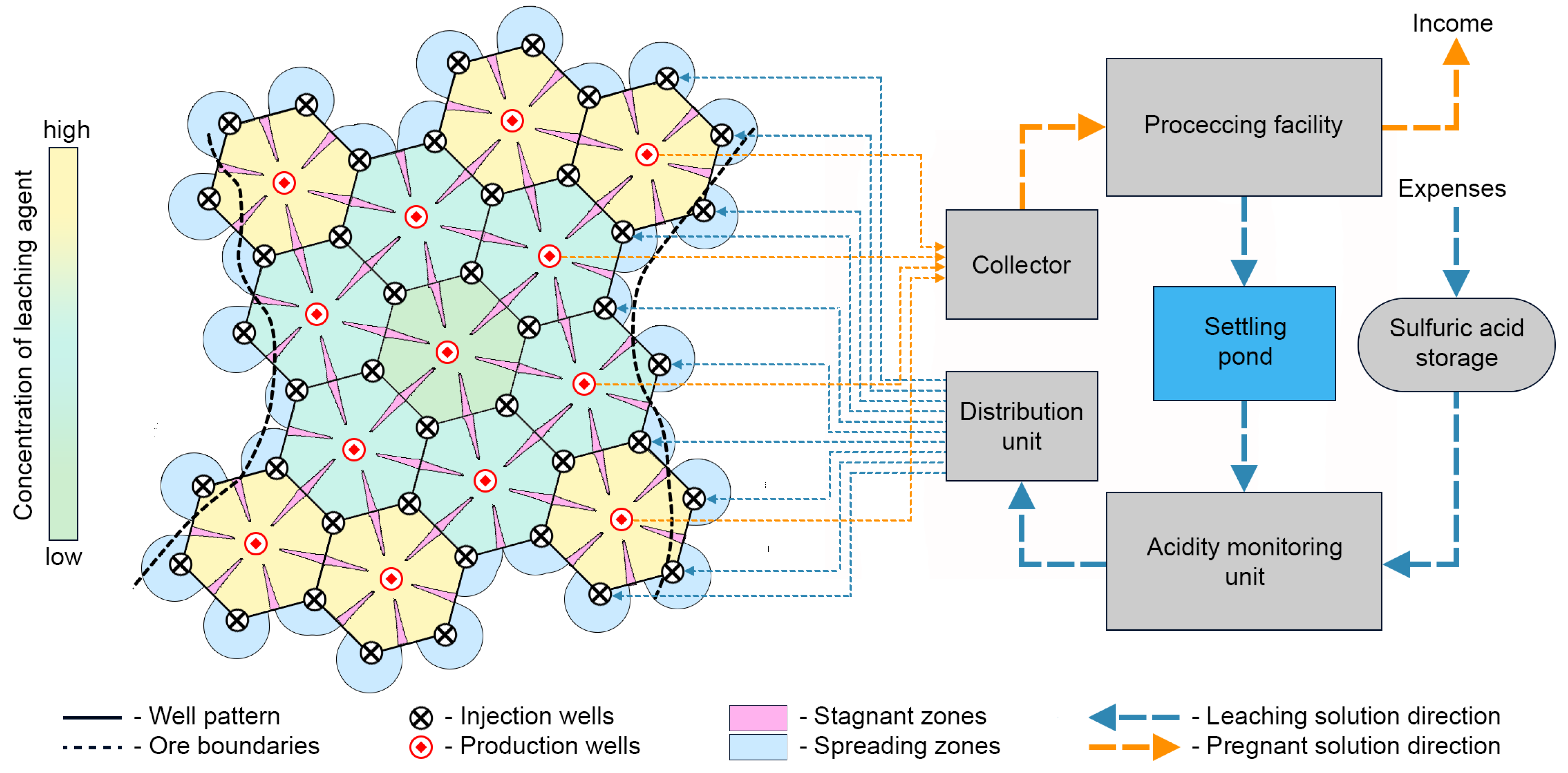
2.1. Reactive Transport Modeling
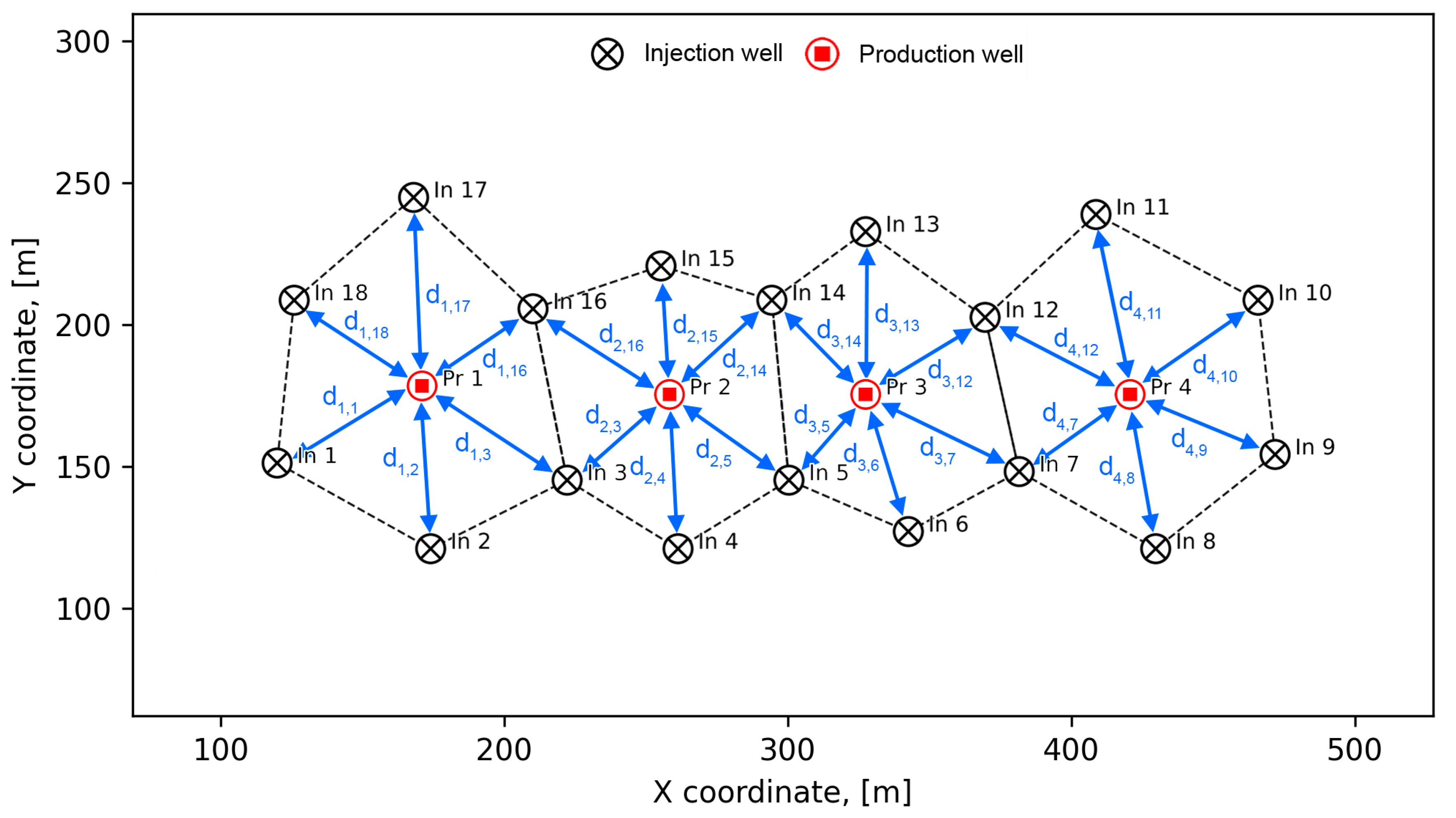
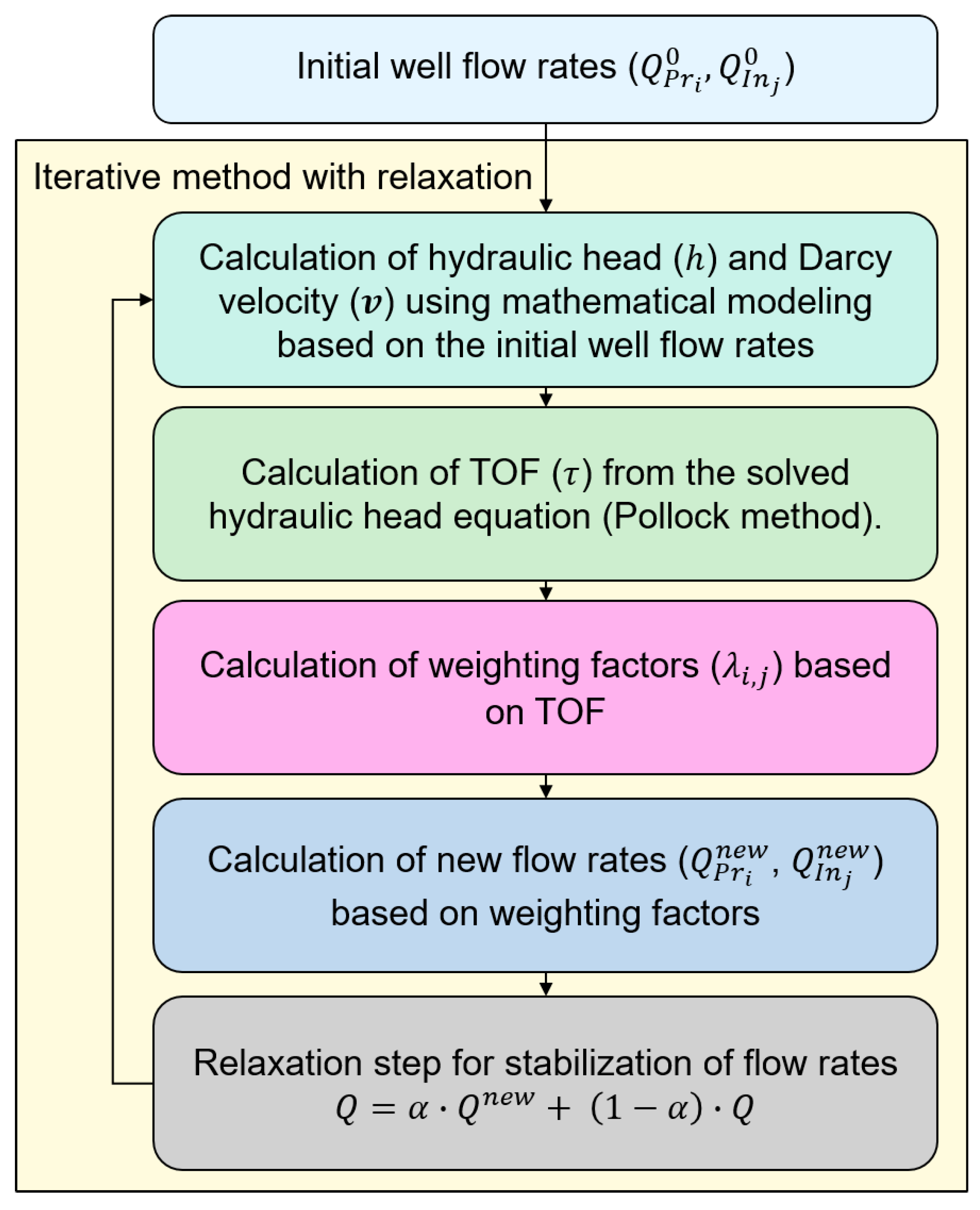
2.2. Methods for Flow Rate Optimization
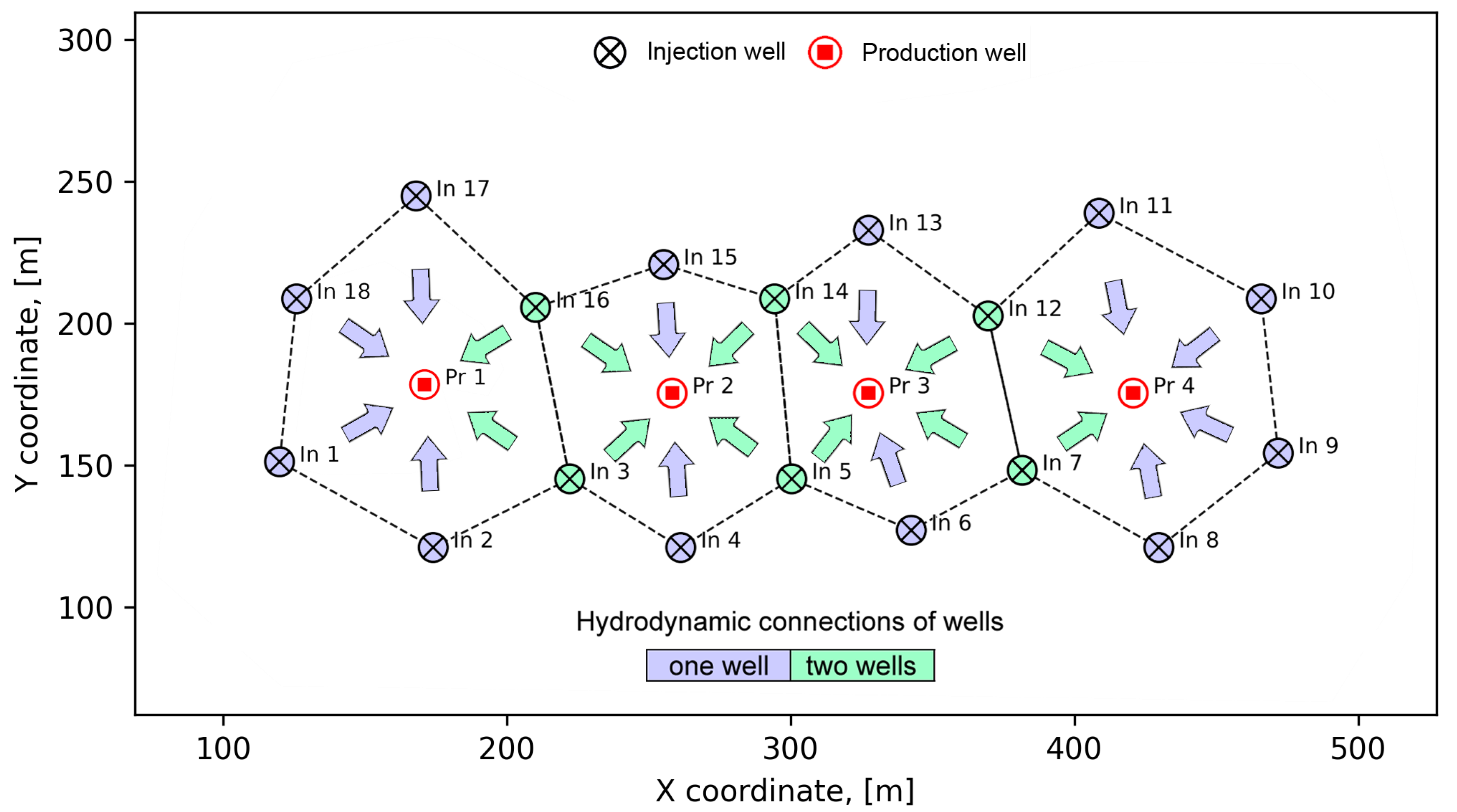
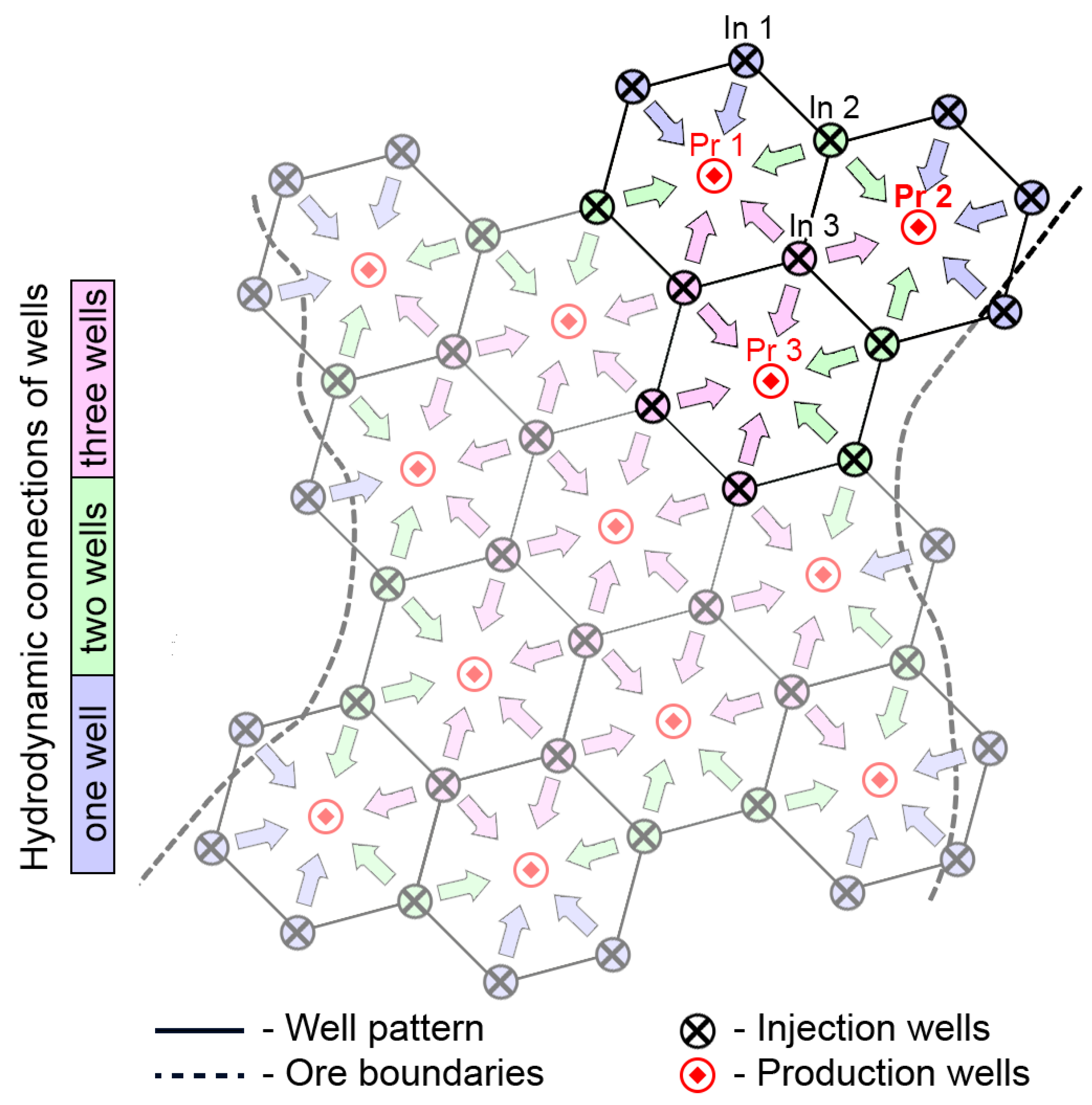
- For production wells—;
- For injection wells connected to one production well—;
- For injection wells connected to two production wells—.
- 1
- Linear distance between wells (LD)—accounts for the direct distance between a pair of injection and production wells;
- 2
- Squared distance (SD)—assumes that the influence of distance on well interactions increases quadratically, which may reflect nonlinear filtration losses;
- 3
- Area of the quadrilateral formed between injection and production wells (AQ)—allows the spatial configuration of the well grid to be considered;
- 4
- Minimum time of flight along the streamline (TOFmin)—determined on the basis of the hydrodynamic model and reflects the shortest time for fluid movement between the wells;
- 5
- Average time of flight along all streamlines between a pair of wells (TOFavg)—also calculated on the basis of the hydrodynamic model and characterizes the average time of solution transport between injection and production wells.
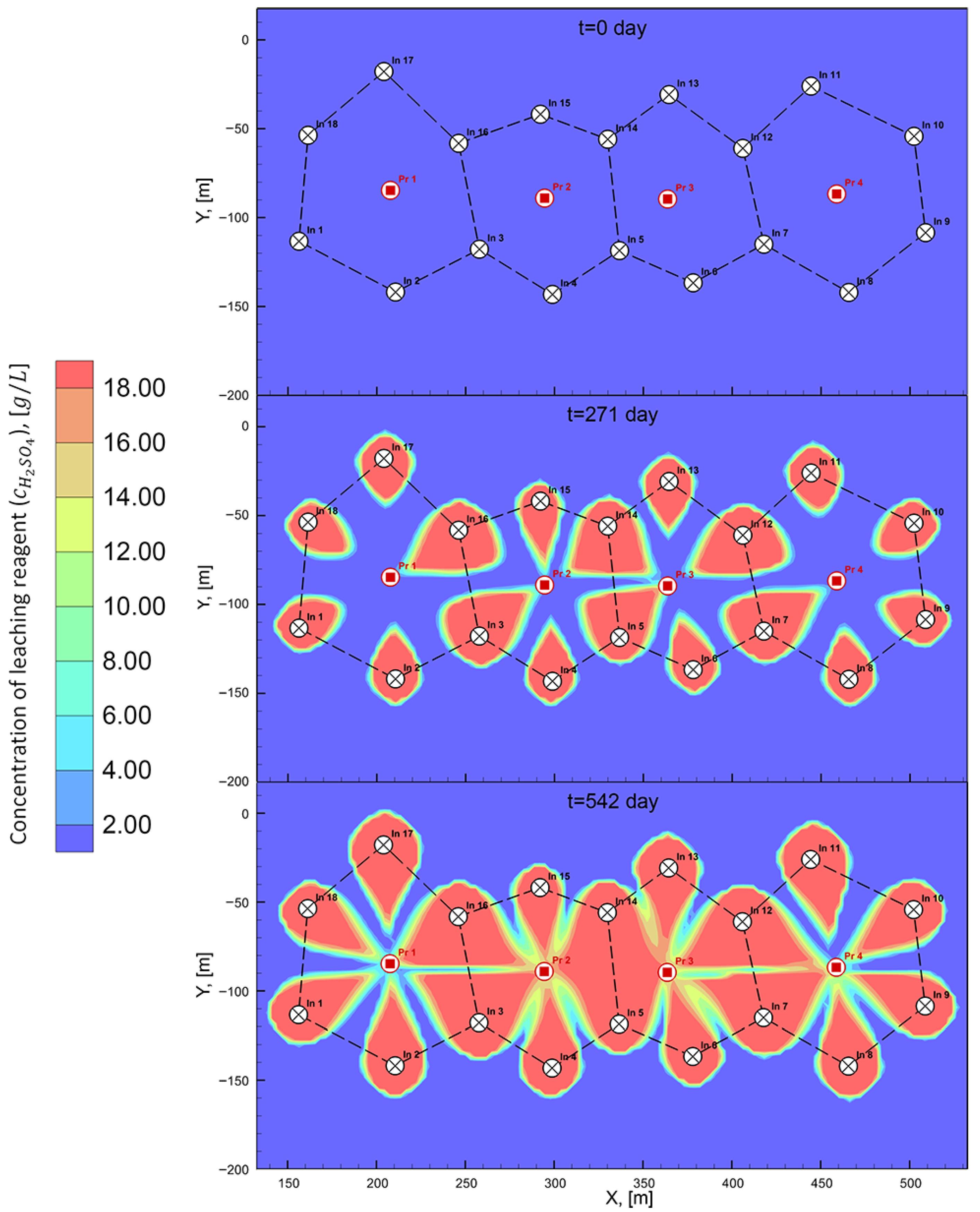
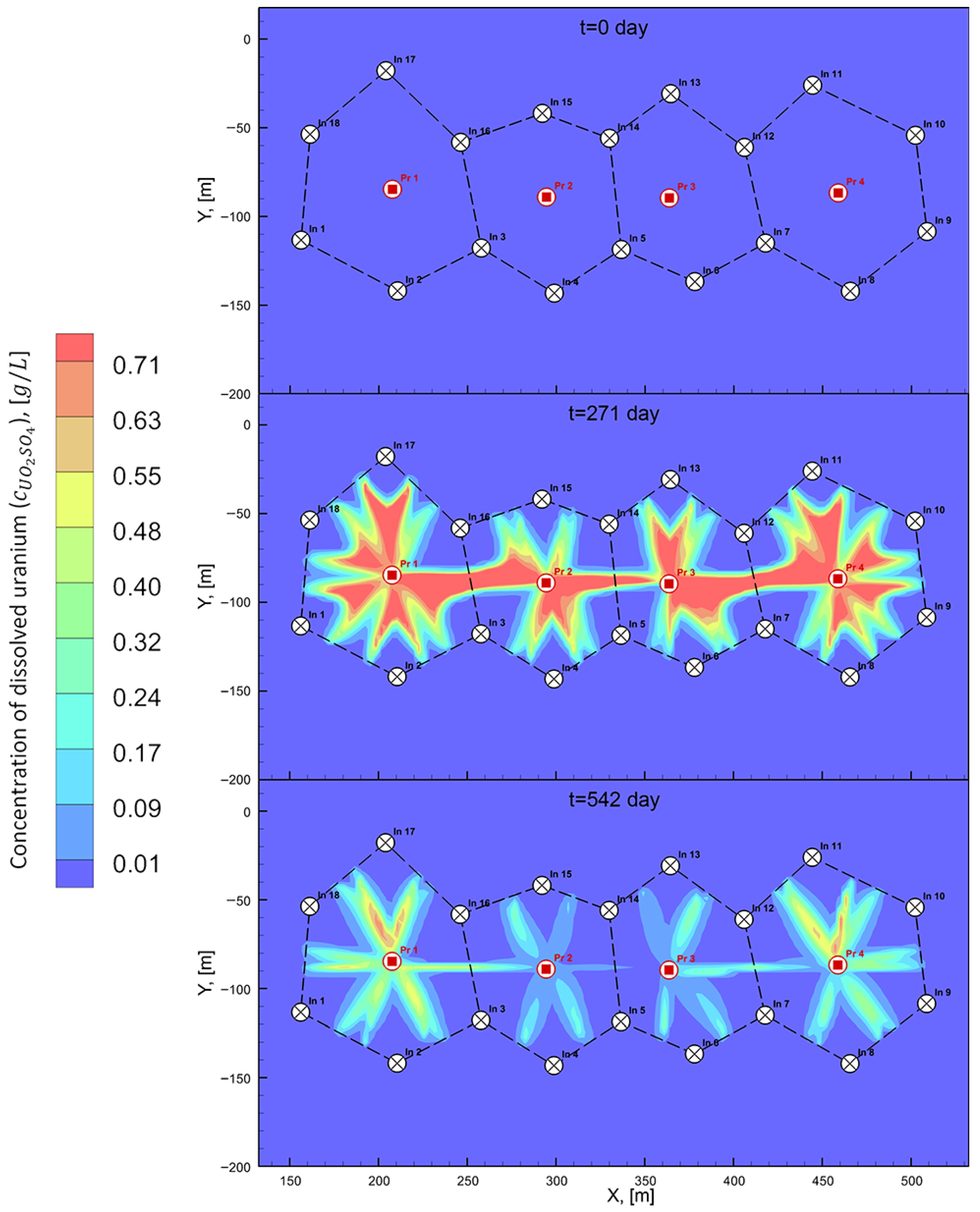
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, G.; Yao, J. A Review of In Situ Leaching (ISL) for Uranium Mining. Mining 2024, 4, 120–148. [Google Scholar] [CrossRef]
- Sinclair, L.; Thompson, J. In Situ Leaching of Copper: Challenges and Future Prospects. Hydrometallurgy 2015, 157, 306–324. [Google Scholar] [CrossRef]
- Gui, Y.; Li, N.; Luo, S.; Wang, G. The Steady Seepage Line Equation of Ionic Rare Earth Ore (IREO) In Situ Leached with Long Strip Bare Feet and Its Application. Sustainability 2023, 15, 2223. [Google Scholar] [CrossRef]
- Müller, D.; Groves, D.I.; Santosh, M.; Yang, C.-X. Critical Metals: Their Mineral Systems and Exploration. Geosyst. Geoenviron. 2024, 4, 100323. [Google Scholar] [CrossRef]
- Jia, M.; Luo, B.; Lu, F.; Yang, Y.; Chen, M.; Zhang, C.; Xu, Q. Improved FMM for well locations optimization in in-situ leaching areas of sandstone uranium mines. Nucl. Eng. Technol. 2024, 56, 3750–3757. [Google Scholar] [CrossRef]
- Shayakhmetov, N.M.; Aizhulov, D.Y.; Alibayeva, K.A.; Serovajsky, S.; Panfilov, I. Application of hydrochemical simulation model to determination of optimal well pattern for mineral production with In-Situ Leaching. Procedia Comput. Sci. 2020, 178, 84–93. [Google Scholar] [CrossRef]
- Aizhulov, D.Y.; Shayakhmetov, N.M.; Kaltayev, A. Quantitative Model of the Formation Mechanism of the Roll-Front Uranium Deposits. Eurasian Chem.-Technol. J. 2018, 20, 213–221. [Google Scholar] [CrossRef]
- Doucmak, R.; Seigneur, N.; Escario, S.; Chanvry, E.; Lagneau, V.; Khaibulin, R.; Yegorov, R.; Kairambayev, S.; Descostes, M. The first modeling, measurement, and confirmation of natural attenuation over a 30-year period in a uranium in-situ recovery context: Approaches and perspectives. J. Contam. Hydrol. 2025, 273, 104607. [Google Scholar] [CrossRef]
- Wang, B.; Luo, Y.; Liu, J.-H.; Li, X.; Zheng, Z.-H.; Chen, Q.-Q.; Li, L.-Y.; Wu, H.; Fan, Q.-R. Ion migration in in-situ leaching (ISL) of uranium: Field trial and reactive transport modelling. J. Hydrol. 2022, 615, 128634. [Google Scholar] [CrossRef]
- Seigneur, N.; Grozeva, N.; Purevsan, B.; Descostes, M. Reactive transport modelling as a toolbox to compare remediation strategies for aquifers impacted by uranium in situ recovery. J. Contam. Hydrol. 2024, 265, 104392. [Google Scholar] [CrossRef]
- Mwetulundila, A.L.; Atangana, A. Modeling Borehole Interactions and In-situ Leach Uranium Mining Impacts on Groundwater in the Stampriet Aquifer. Earth Syst. Environ. 2025, 7, 102. [Google Scholar] [CrossRef]
- Tungatarova, M.; Kurmanseiit, M.B.; Shayakhmetov, N. GPU Accelerated Modeling of In-Situ Leaching Process and Streamline Based Reactive Transport Simulation. Procedia Comput. Sci. 2020, 178, 145–152. [Google Scholar] [CrossRef]
- Ji, W.; Zhang, H.; Zhang, L.; Xu, X.; Li, X.; Wang, X.; Chen, X. Integrated surrogate framework for reactive transport modeling of uranium in groundwater using deep learning. J. Hydrol. 2024, 630, 130737. [Google Scholar] [CrossRef]
- Kurmanseiit, M.B.; Tungatarova, M.S.; Abdullayeva, B.Z.; Aizhulov, D.Y.; Shayakhmetov, N.M. Acceleration of Numerical Modeling of Uranium In Situ Leaching: Application of IDW Interpolation and Neural Networks for Solving the Hydraulic Head Equation. Minerals 2024, 14, 1043. [Google Scholar] [CrossRef]
- Aizhulov, D.; Tungatarova, M.; Kurmanseiit, M.; Shayakhmetov, N. Artificial Neural Networks for Mineral Production Forecasting in the In Situ Leaching Process: Uranium Case Study. Processes 2024, 12, 2285. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Tang, Z.; Li, C.; Liu, Z.; Tan, K.; Liu, L. Hydrodynamics control for the well field of in-situ leaching of uranium. Nucl. Eng. Technol. 2024, 56, 4176–4183. [Google Scholar] [CrossRef]
- Li, H.; Tang, Z.; Xiang, D. Study on Numerical Simulation of Reactive-Transport of Groundwater Pollutants Caused by Acid Leaching of Uranium: A Case Study in Bayan-Uul Area, Northern China. Water 2024, 16, 500. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, W.; Liu, K.; Cheng, L.; Wang, X.; Cai, X. A HLLC method based on the local multi-layer SWEs to simulate partial obstructed flow in 2D model. J. Hydrol. 2023, 628, 130234. [Google Scholar] [CrossRef]
- Qiu, W.; Yang, Y.; Song, J.; Que, W.; Zhang, X.; Liu, Y.; Li, Z.; Zhang, J.; Zhang, L. A deep-learning-based multiobjective optimization for the design of in-situ uranium leaching system under multiple uncertainties. J. Hydrol. 2025, 651, 132576. [Google Scholar] [CrossRef]
- Luo, J.; Cui, G.; Yang, D.; Huo, C.; Zhang, X.; Liu, Y.; Li, Z.; Zhang, J.; Zhang, L. Impact of the existence of carbonate minerals on the performance of CO2 + O2 during in situ leaching in uranium deposits. Nucl. Eng. Technol. 2025, 57, 103821. [Google Scholar] [CrossRef]
- Shayakhmetov, N.M.; Aizhulov, D.Y.; Alibayeva, K.A.; Serovajsky, S.; Panfilov, I. Enhancing uranium in-situ leaching efficiency through the well reverse technique: A study of the effects of reversal time on production efficiency and cost. Hydrometallurgy 2023, 219, 106086. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Niu, Y.; Tan, K.; Xie, T.; Yao, Y.; Li, C.; Liu, Z. Quantitative determination of the leaching range of in-situ leaching mining area by stagnation point. Nucl. Eng. Technol. 2025, 57, 103204. [Google Scholar] [CrossRef]
- Lanzhi, Y.; Pingchao, K.; Lingling, X.; Guangrong, L.; Kai, Z.; Feifan, Y.; Yipeng, Z. The role of P(V) salts in inhibiting CaCO3 precipitation in the uranium in-situ leaching process using CO2 and O2. Hydrometallurgy 2025, 234, 106462. [Google Scholar] [CrossRef]
- Yussupov, K.; Abdissattar, G.; Aben, E.; Myrzakhmetov, S.; Akhmetkanov, D.; Yelzhanov, E. A Novel Process for Decolmatation of Wells During In Situ Leach Mining of Uranium. Civ. Eng. J. 2025, 11, 1447–1457. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, C. Advancements in regional geological surveys: Insights from the 2024 China National Regional Geological Survey Conference and a six-year uranium exploration case study in Shaoguan, Guangdong. Phys. Chem. Earth Parts A/B/C 2025, 139, 103953. [Google Scholar] [CrossRef]
- Poezhaev, I.P.; Polynovsky, K.D.; Gorbatenko, O.A.; Panova, E.N.; Bulenova, K.Z.; Karmanov, E.M.; Blynsky, P.A.; Bitovt, O.A. Geotechnology of Uranium [Geotehnologiya Urana]; Kazakh Universitety: Almaty, Kazakhstan, 2017; p. 319. (In Russian) [Google Scholar]
- Kurmanseiit, M.; Shayakhmetov, N.; Aizhulov, D.; Abdullayeva, B.; Tungatarova, M. Computational Approaches to Assess Flow Rate Efficiency During In Situ Recovery of Uranium: From Reactive Transport to Streamline- and Trajectory-Based Methods. Minerals 2025, 15, 835. [Google Scholar] [CrossRef]
- Kurmanseiit, M.B.; Tungatarova, M.S.; Kaltayev, A.; Royer, J.-J. Reactive Transport Modeling during Uranium In Situ Leaching (ISL): The Effects of Ore Composition on Mining Recovery. Minerals 2022, 12, 1340. [Google Scholar] [CrossRef]
- Patrin, A.P.; Zabaznov, V.L.; Chistilin, P.E. The main results of a full-scale field experiment on the ISL of Uranium at site №2 of the Budenovskoye deposit. In Proceedings of the Vth International Conference, “Actual Problems of the Uranium Industry”, Almaty, Kazakhstan, 19–20 September 2008; pp. 198–204. [Google Scholar]
- Podrezov, D.R. Development and Identification of Models for the Reserves Estimating of the URANIUM In-Situ Leaching Mine. Master’s Thesis, National Research Technological University “MISIS”, Moscow, Russia, 2021. [Google Scholar]
- DePonty Jersy, D.; Shane, R.G.; DePinto, P.; Grant Kornrumph, S.; Marvin, F.; Glotfelty, R.G. Plumbness and Alignment Standards—Analysis and Recommendations for Operational Applicability. pp. 1–7. Available online: https://inspectapedia.com/water/Water-well-plumbness-alignment-standards-DePonty.pdf (accessed on 20 August 2025).
- Pollock, D.W. Semi-analytical Computation of Path Line for Finite Difference Models. Ground Water 1988, 6, 743–750. [Google Scholar] [CrossRef]
- JSC “NAC Kazatomprom”. Consolidated Financial Statements for the Year Ended 31 December 2024 and Independent Auditor’s Report; JSC “NAC Kazatomprom”: Astana, Kazakhstan, 2024; p. 77. Available online: https://www.kazatomprom.kz/storage/cb/konsolidirovannaya_finansovaya_otchetnost_ao_nak_kazatomprom_za_god_zakonchivshiisya_31_dekabrya_2024_g_na_angliiskom_yazikevy4nnjlepyasihvj4esdh.pdf (accessed on 20 August 2025).
- JSC “NAC Kazatomprom”. Operating and Financial Review for 2024; JSC “NAC Kazatomprom”: Astana, Kazakhstan, 2024; pp. 19–20. Available online: https://www.kazatomprom.kz/storage/66/ofr_eng_12m_2024hu7sk2kzthic5kjkpyx5j.pdf (accessed on 20 August 2025).
- National Bank of the Republic of Kazakhstan. Daily Official (Market) Foreign Exchange Rates. Available online: https://nationalbank.kz/en/exchangerates/ezhednevnye-oficialnye-rynochnye-kursy-valyut (accessed on 20 August 2025).




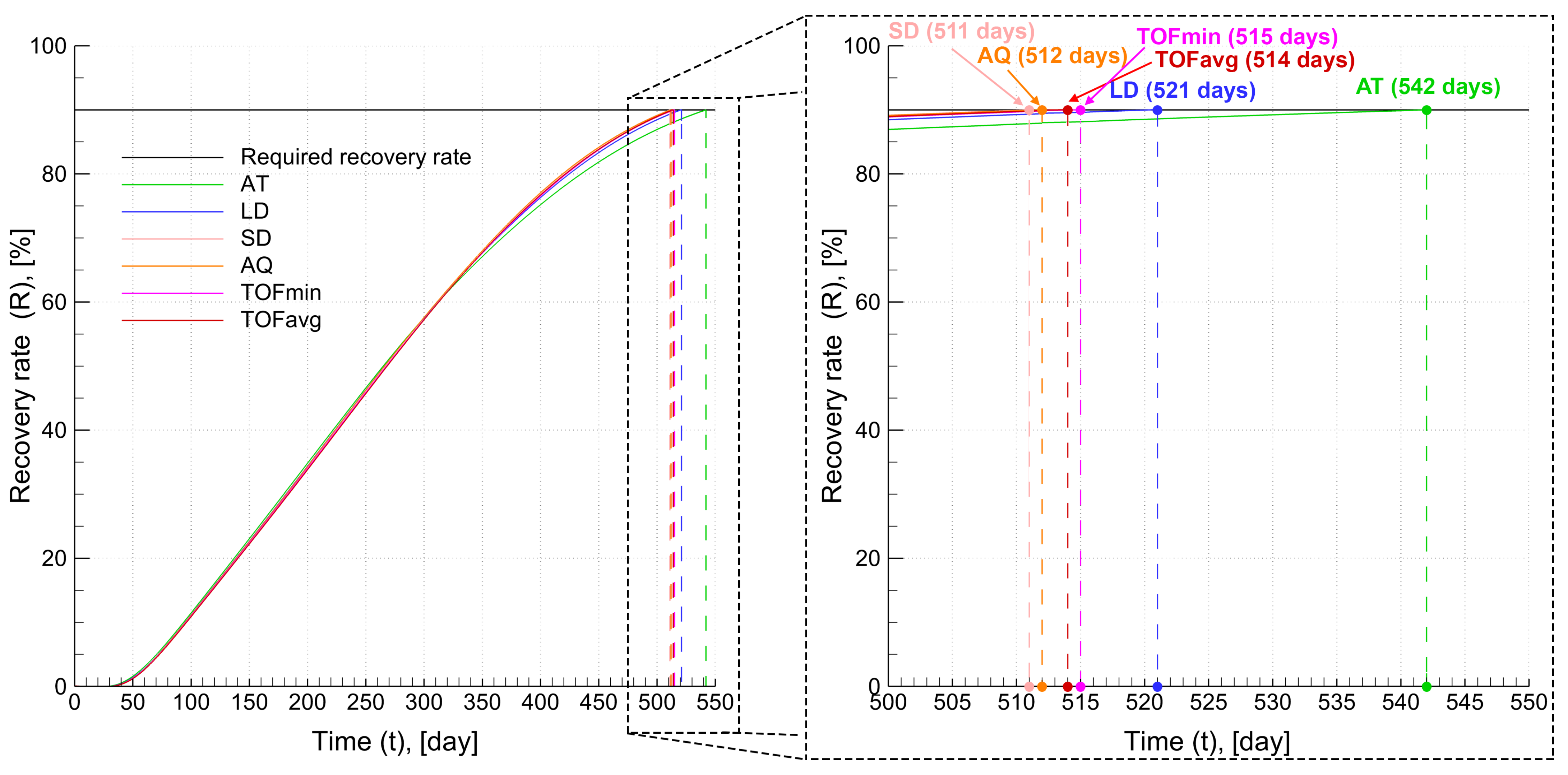
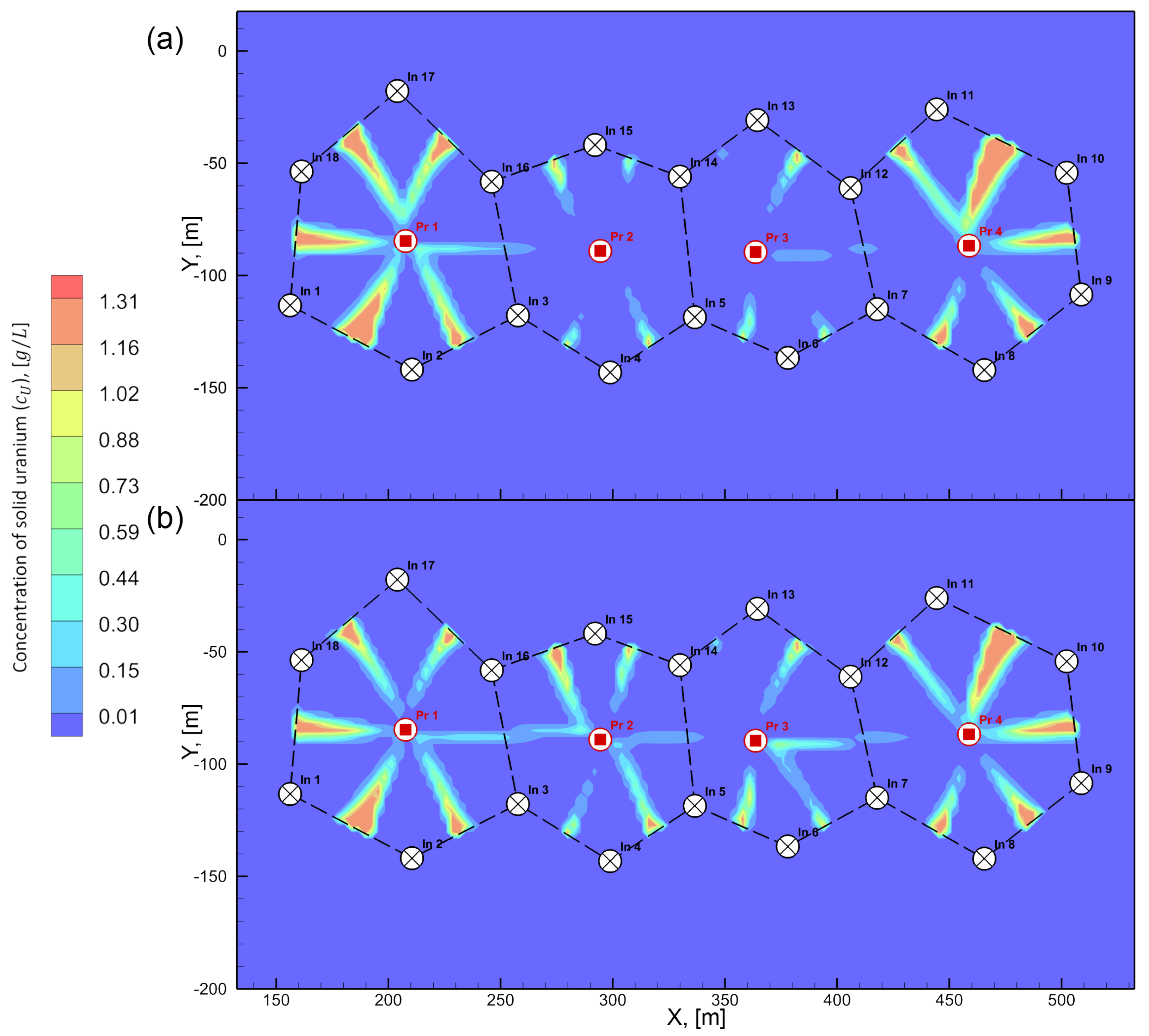
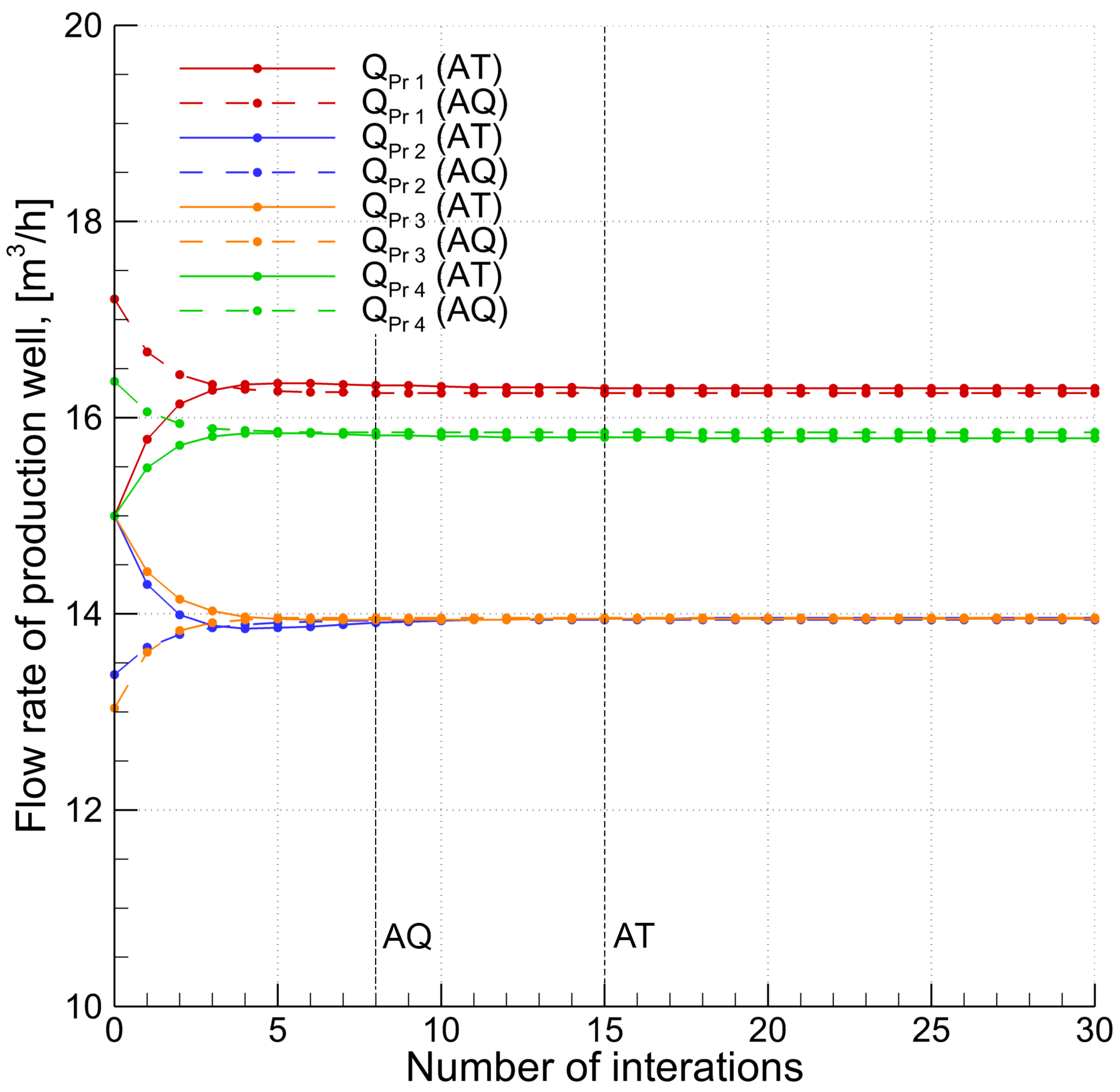
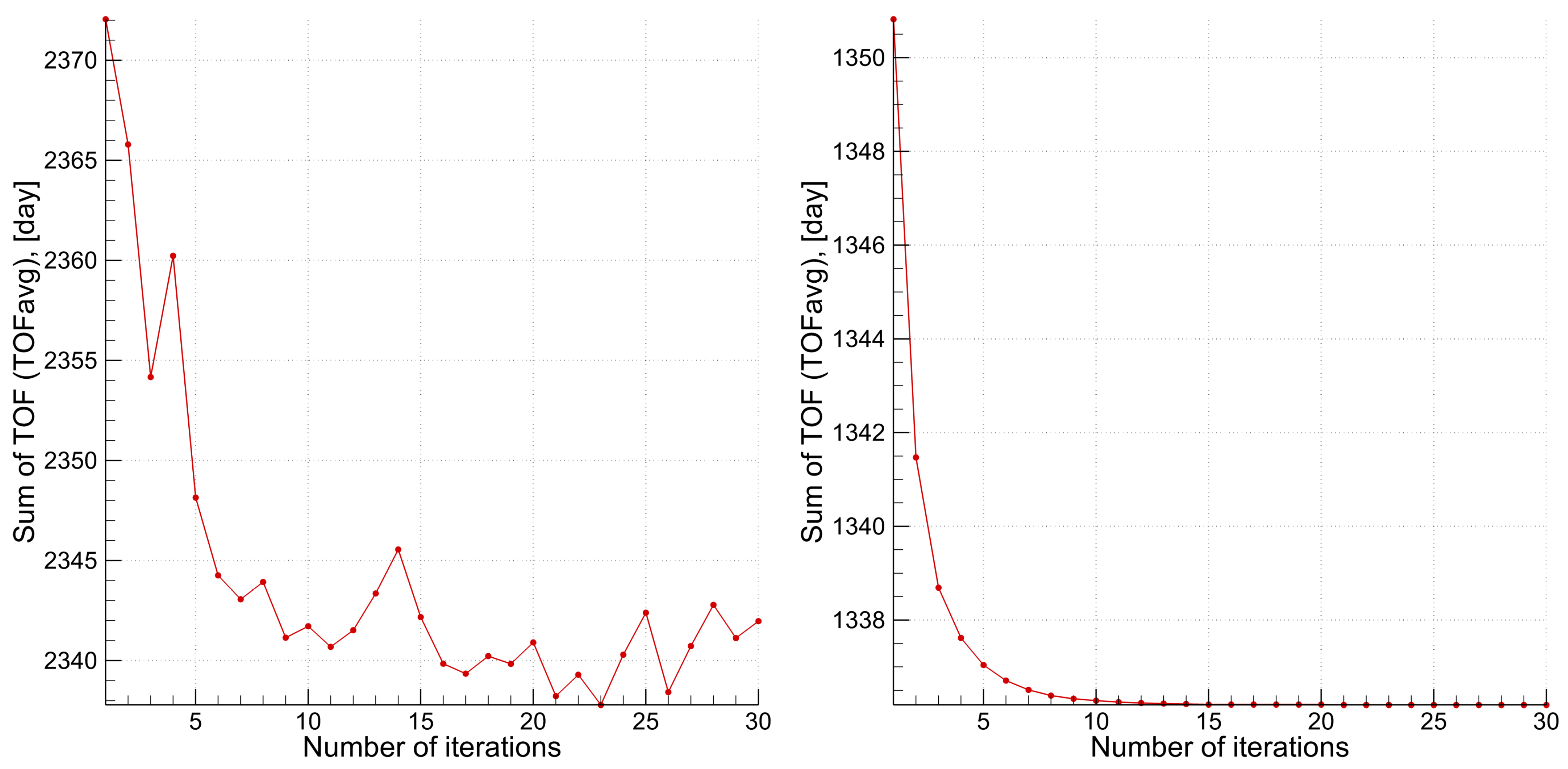
| Cell | AT | LD | SD | AQ | TOFmin | TOFavg |
|---|---|---|---|---|---|---|
| [g/L] | [g/L] | [g/L] | [g/L] | [g/L] | [g/L] | |
| Cell with | 0.191 | 0.167 | 0.140 | 0.145 | 0.165 | 0.161 |
| Cell with | 0.023 | 0.041 | 0.072 | 0.057 | 0.056 | 0.059 |
| Cell with | 0.021 | 0.033 | 0.046 | 0.063 | 0.039 | 0.045 |
| Cell with | 0.166 | 0.160 | 0.151 | 0.143 | 0.144 | 0.139 |
| Average by all 4 cells | 0.100 | 0.100 | 0.102 | 0.102 | 0.101 | 0.101 |
| Deviation from average in | 0.091 | 0.067 | 0.038 | 0.043 | 0.064 | 0.060 |
| Deviation from average in | 0.077 | 0.059 | 0.030 | 0.045 | 0.045 | 0.042 |
| Deviation from average in | 0.079 | 0.068 | 0.056 | 0.039 | 0.062 | 0.056 |
| Deviation from average in | 0.065 | 0.060 | 0.049 | 0.041 | 0.044 | 0.038 |
| Sum of average deviation | 0.313 | 0.254 | 0.173 | 0.168 | 0.215 | 0.196 |
| AT | LD | SD | AQ | TOFmin | TOFavg | |
|---|---|---|---|---|---|---|
| Operation time to reach 90% recovery (), [day] | 542 | 521 | 511 | 512 | 515 | 514 |
| Acid consumption, [ton] | 15,609.6 | 15,004.8 | 14,716.8 | 14,745.6 | 14,832.0 | 14,803.2 |
| Acid expenses (), [thousand USD] | 1639.0 | 1575.5 | 1545.3 | 1548.3 | 1557.4 | 1554.3 |
| Efficiency (% decrease in operational costs) | 0 | 3.9 | 5.7 | 5.5 | 5.0 | 5.2 |
| AT | LD | SD | AQ | TOFmin | TOFavg | |
|---|---|---|---|---|---|---|
| AT | 0.0 | −3.9 | −5.7 | −5.5 | −5.0 | −5.2 |
| LD | 3.9 | 0.0 | −1.8 | −1.7 | −1.1 | −1.3 |
| SD | 5.7 | 1.8 | 0.0 | 0.2 | 0.7 | 0.5 |
| AQ | 5.5 | 1.7 | −0.2 | 0.0 | 0.6 | 0.4 |
| TOFmin | 5.0 | 1.1 | −0.7 | −0.6 | 0.0 | −0.2 |
| TOFavg | 5.2 | 1.3 | −0.5 | −0.4 | 0.2 | 0.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurmanseiit, M.; Shayakhmetov, N.; Aizhulov, D.; Tleuberdy, A.; Abdullayeva, B.; Tungatarova, M. Comparative Evaluation of Flow Rate Distribution Methods for Uranium In-Situ Leaching via Reactive Transport Modeling. Minerals 2025, 15, 1066. https://doi.org/10.3390/min15101066
Kurmanseiit M, Shayakhmetov N, Aizhulov D, Tleuberdy A, Abdullayeva B, Tungatarova M. Comparative Evaluation of Flow Rate Distribution Methods for Uranium In-Situ Leaching via Reactive Transport Modeling. Minerals. 2025; 15(10):1066. https://doi.org/10.3390/min15101066
Chicago/Turabian StyleKurmanseiit, Maksat, Nurlan Shayakhmetov, Daniar Aizhulov, Aray Tleuberdy, Banu Abdullayeva, and Madina Tungatarova. 2025. "Comparative Evaluation of Flow Rate Distribution Methods for Uranium In-Situ Leaching via Reactive Transport Modeling" Minerals 15, no. 10: 1066. https://doi.org/10.3390/min15101066
APA StyleKurmanseiit, M., Shayakhmetov, N., Aizhulov, D., Tleuberdy, A., Abdullayeva, B., & Tungatarova, M. (2025). Comparative Evaluation of Flow Rate Distribution Methods for Uranium In-Situ Leaching via Reactive Transport Modeling. Minerals, 15(10), 1066. https://doi.org/10.3390/min15101066






