Numerical Simulation of Air–Water–Flake Graphite Triple-Phase Flow Field in a Homemade Double-Nozzle Jet Micro-Bubble Generator
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulation Parameters
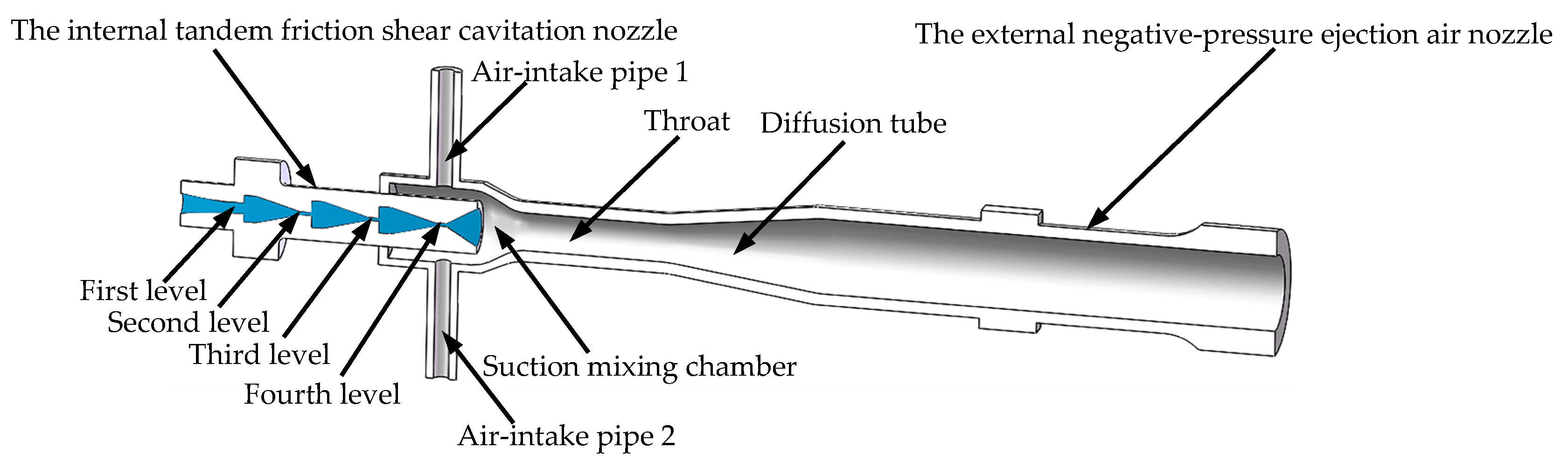
2.2. Double-Nozzle Jet Micro-Bubble Generator
2.2.1. Overall Structure
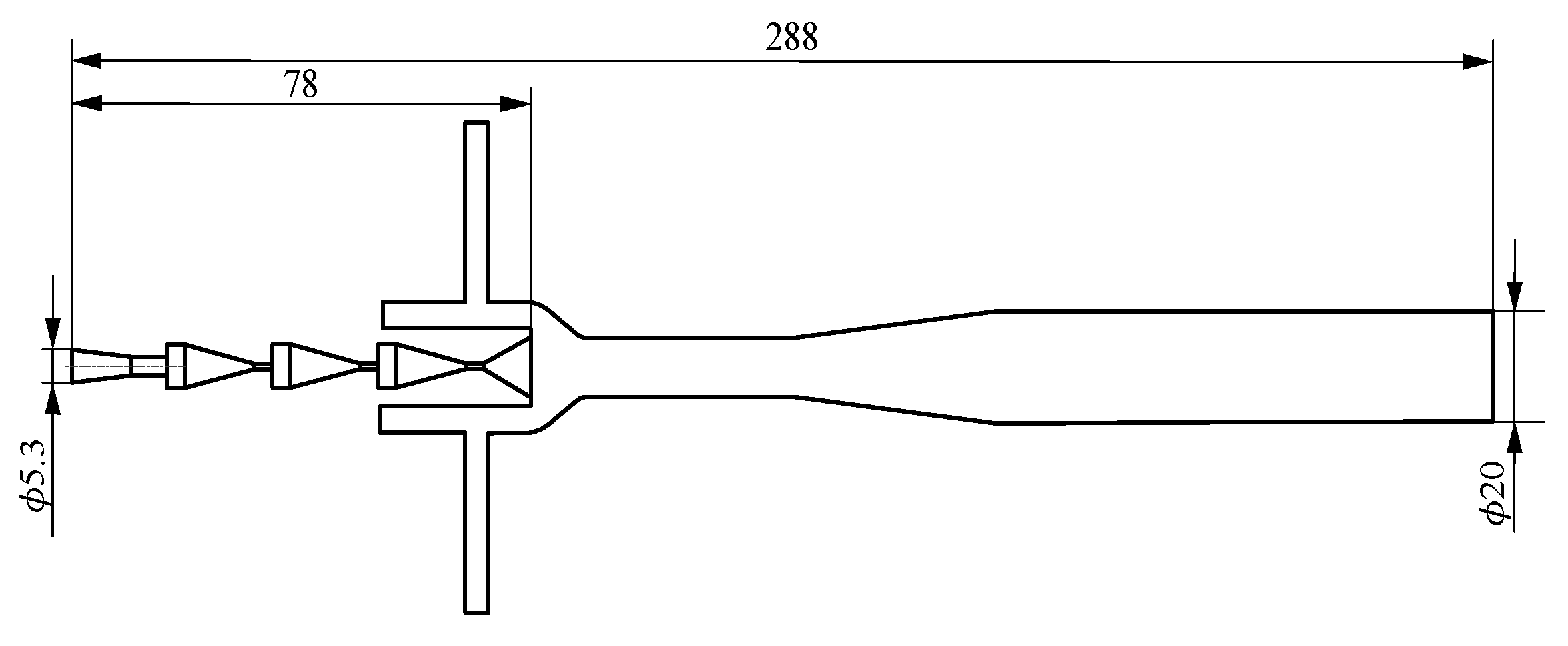
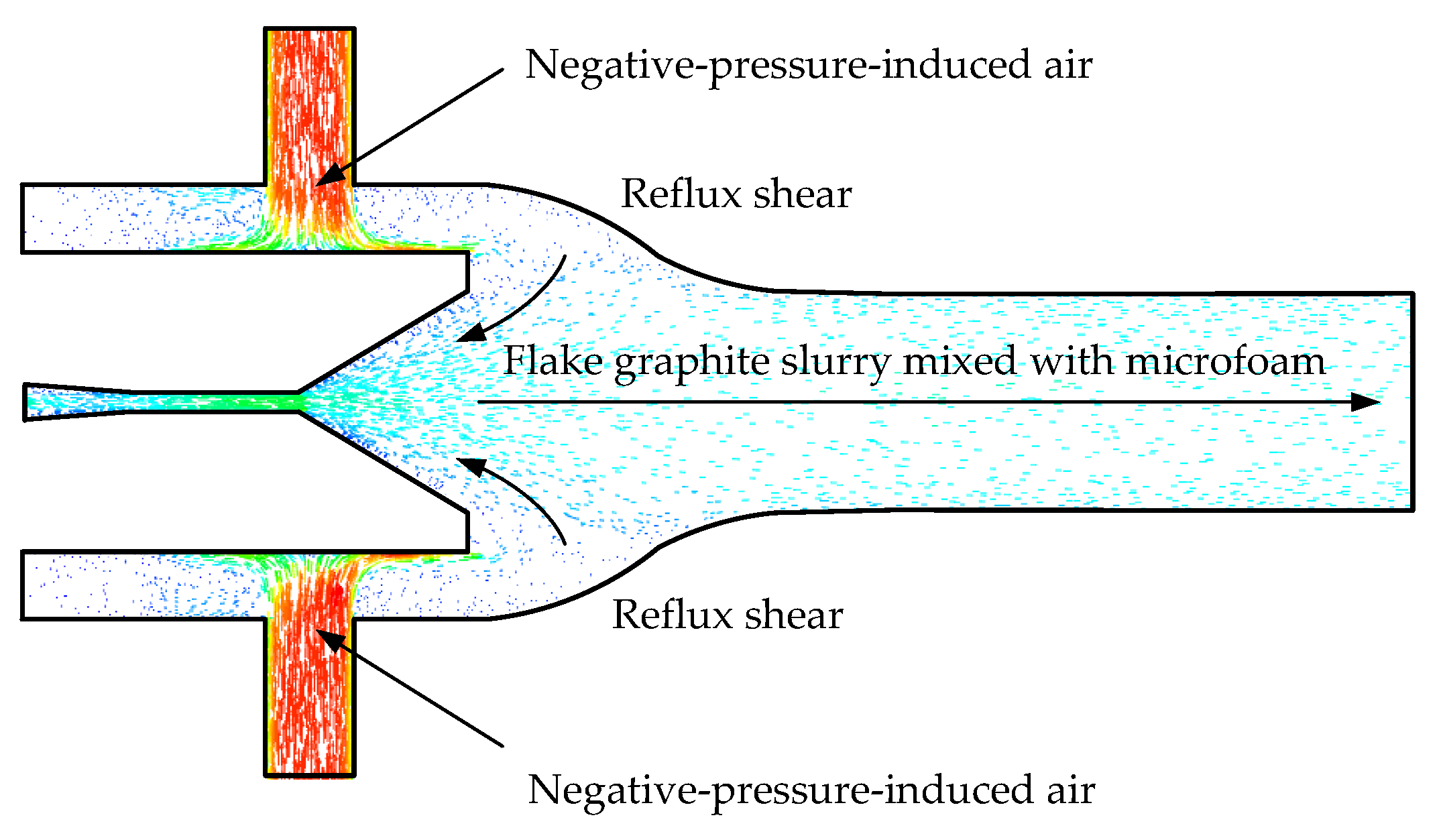
2.2.2. Internal Tandem Friction Shear Cavitation Nozzle Design
2.2.3. External Negative-Pressure-Induced Air Nozzle Design
2.3. Calculation Method and Boundary Condition Setting
3. Mathematical Mode
3.1. Control Equations for the Three-Phase Flow of Air–Water–Flake Graphite
- (1)
- The equations for the conservation of mass for air, water, and flake graphite are as follows [42]:
- (2)
- The equations for the conservation of momentum for air, water, and flake graphite are as follows [42]:
- (3)
- Interphase forces of air, water, and flake graphite
- ①
- Interphase forces in the air phase–water phase
- ②
- Interphase forces in the water phase–flake graphite phase
- ③
- Interphase forces in the air phase–flake graphite phase
3.2. Turbulence Model
4. Simulation Results and Discussion
4.1. Finite Element Model
4.2. Mesh-Independence Test
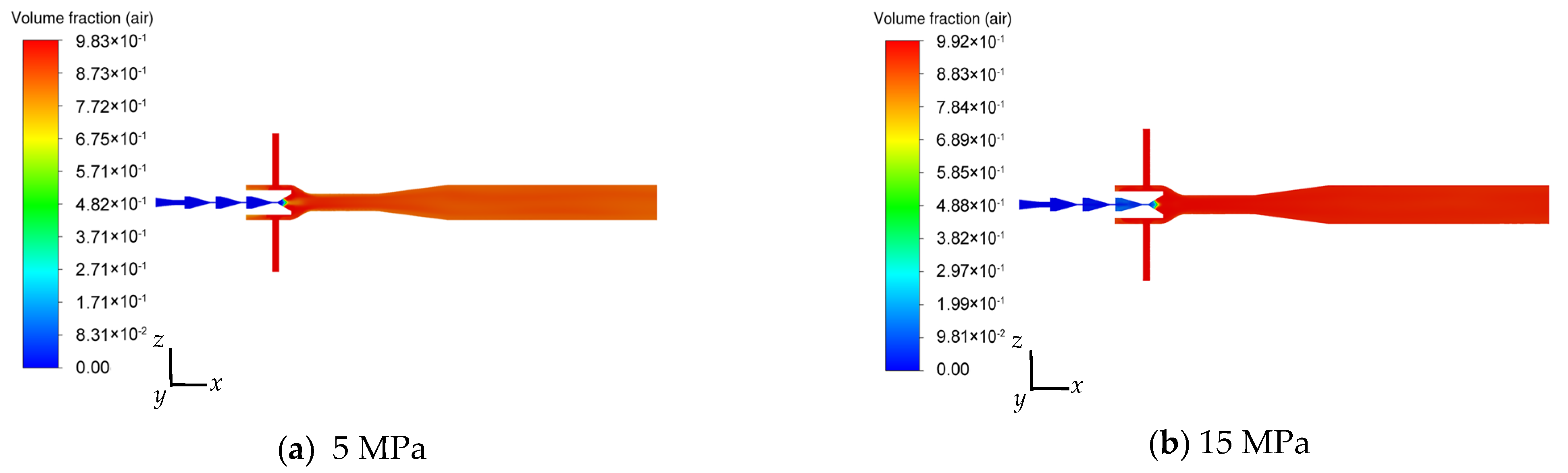
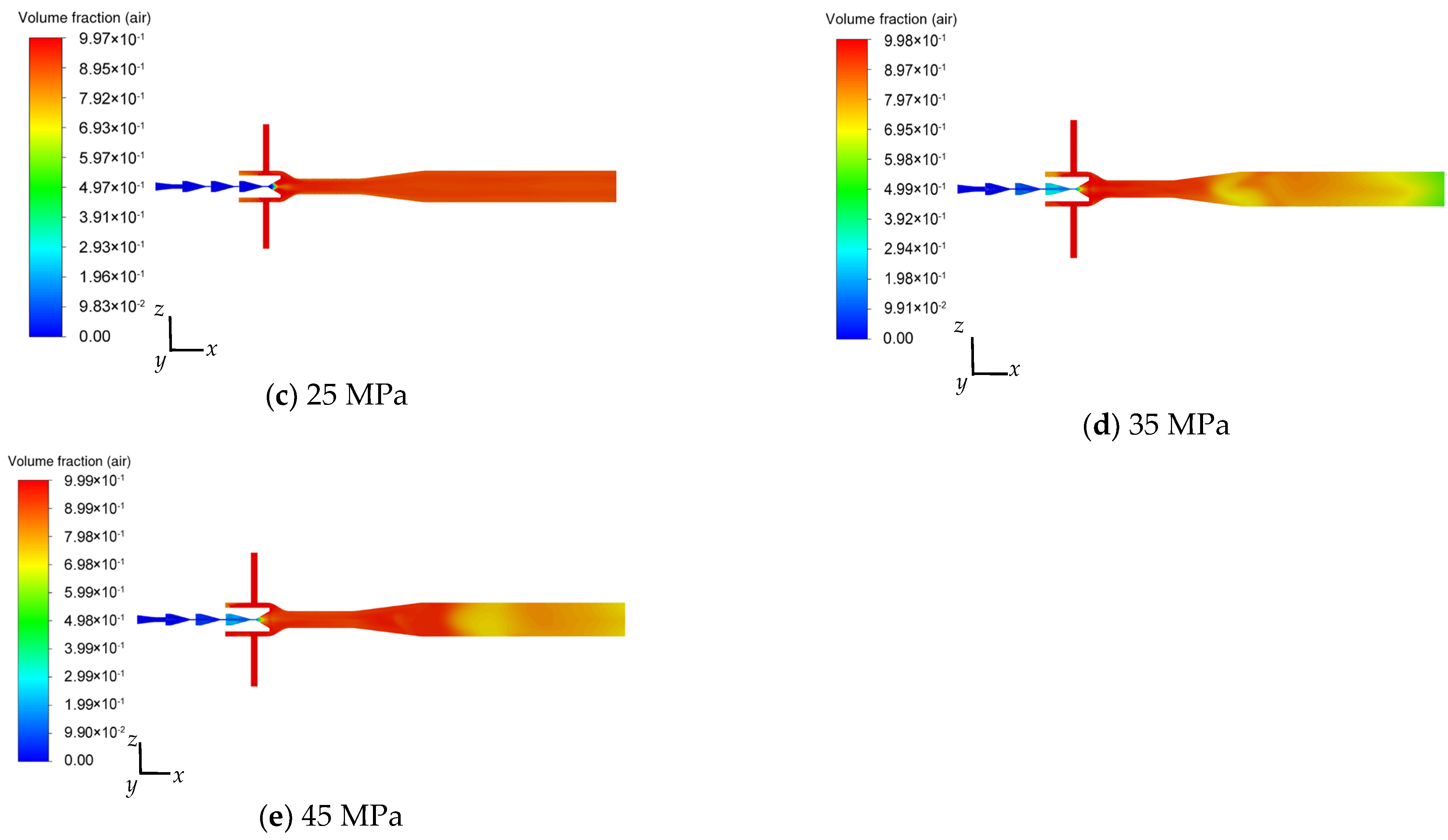
4.3. Effect of Inlet Pressure on the Air Flow Field
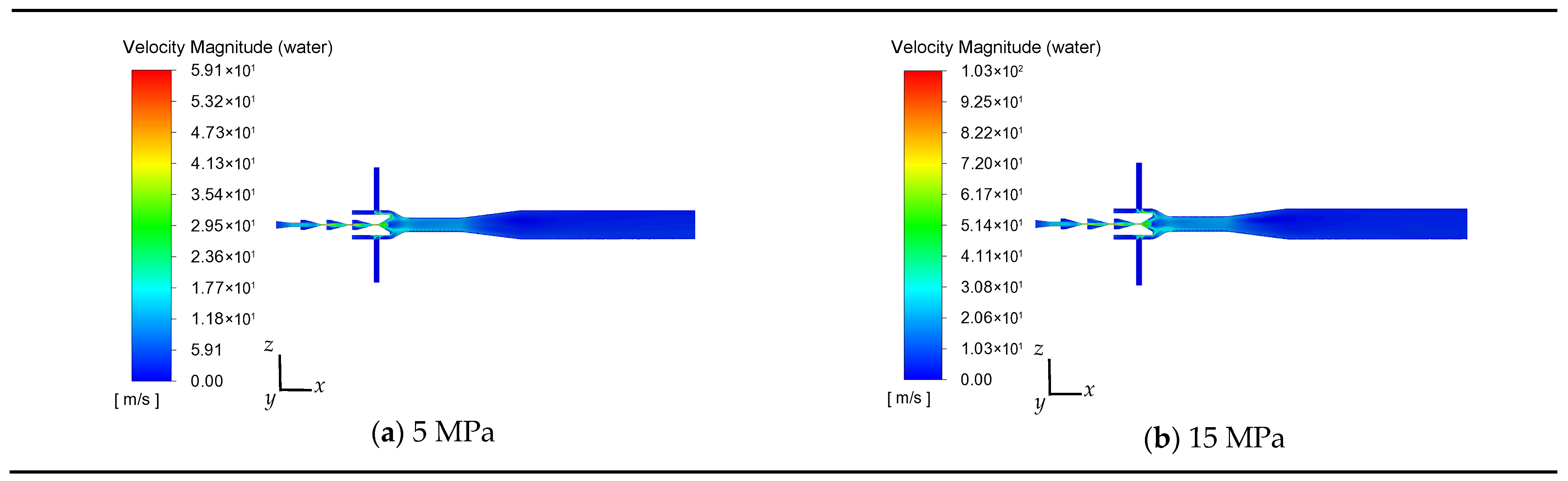
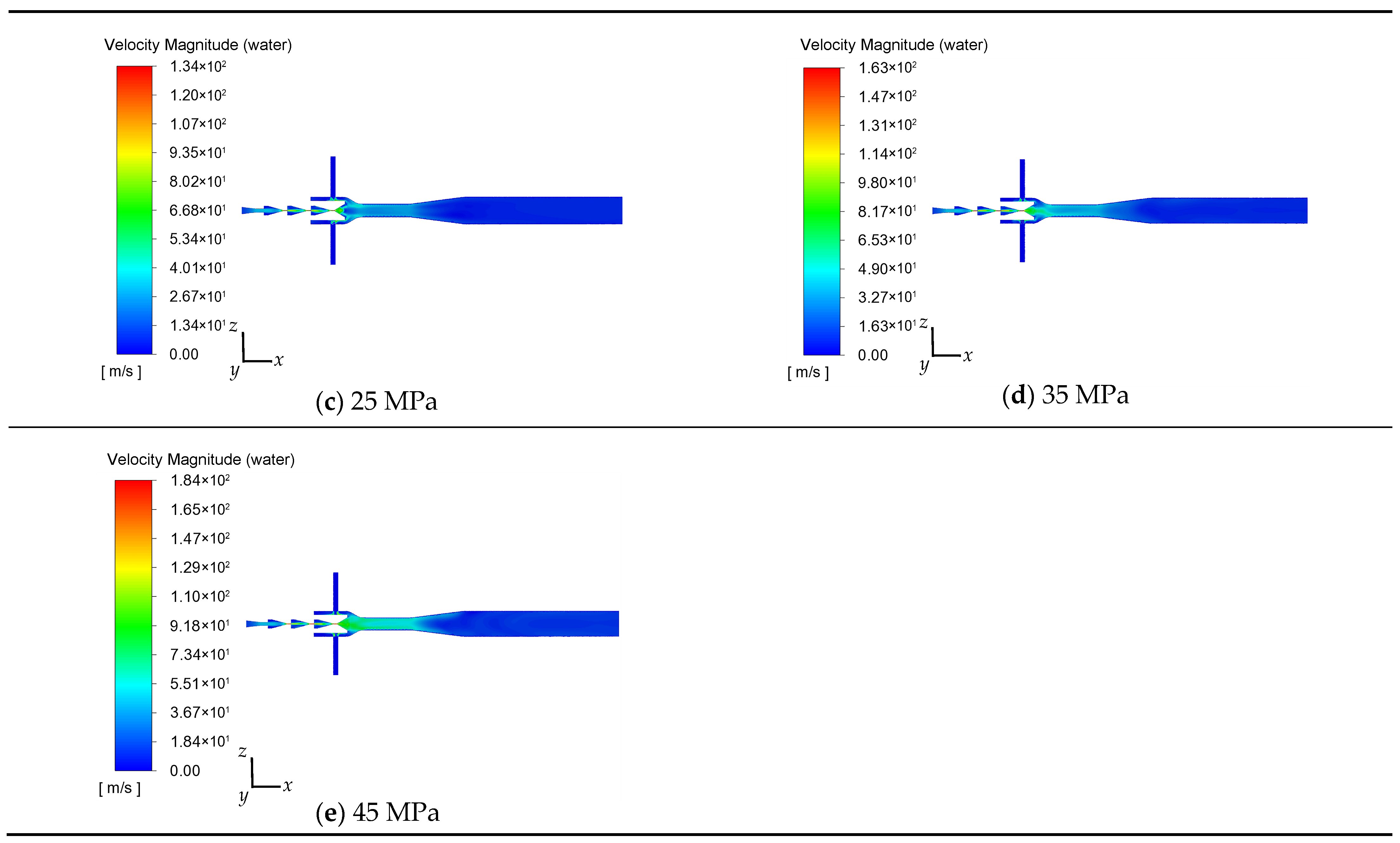
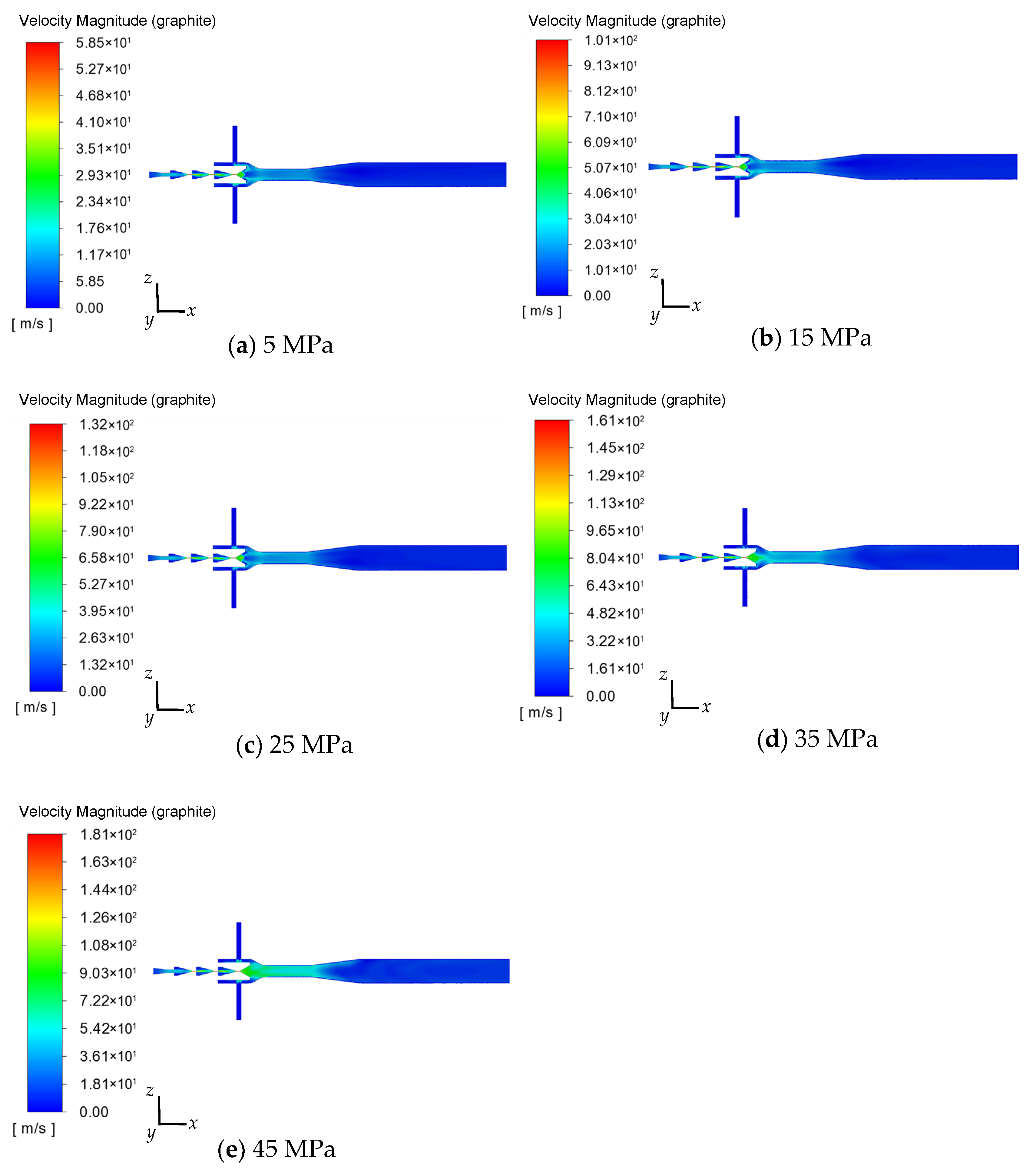
4.4. Effect of Inlet Pressure on the Flow Field of Water and the Flow Field of Flake Graphite
4.5. Experimental Validation
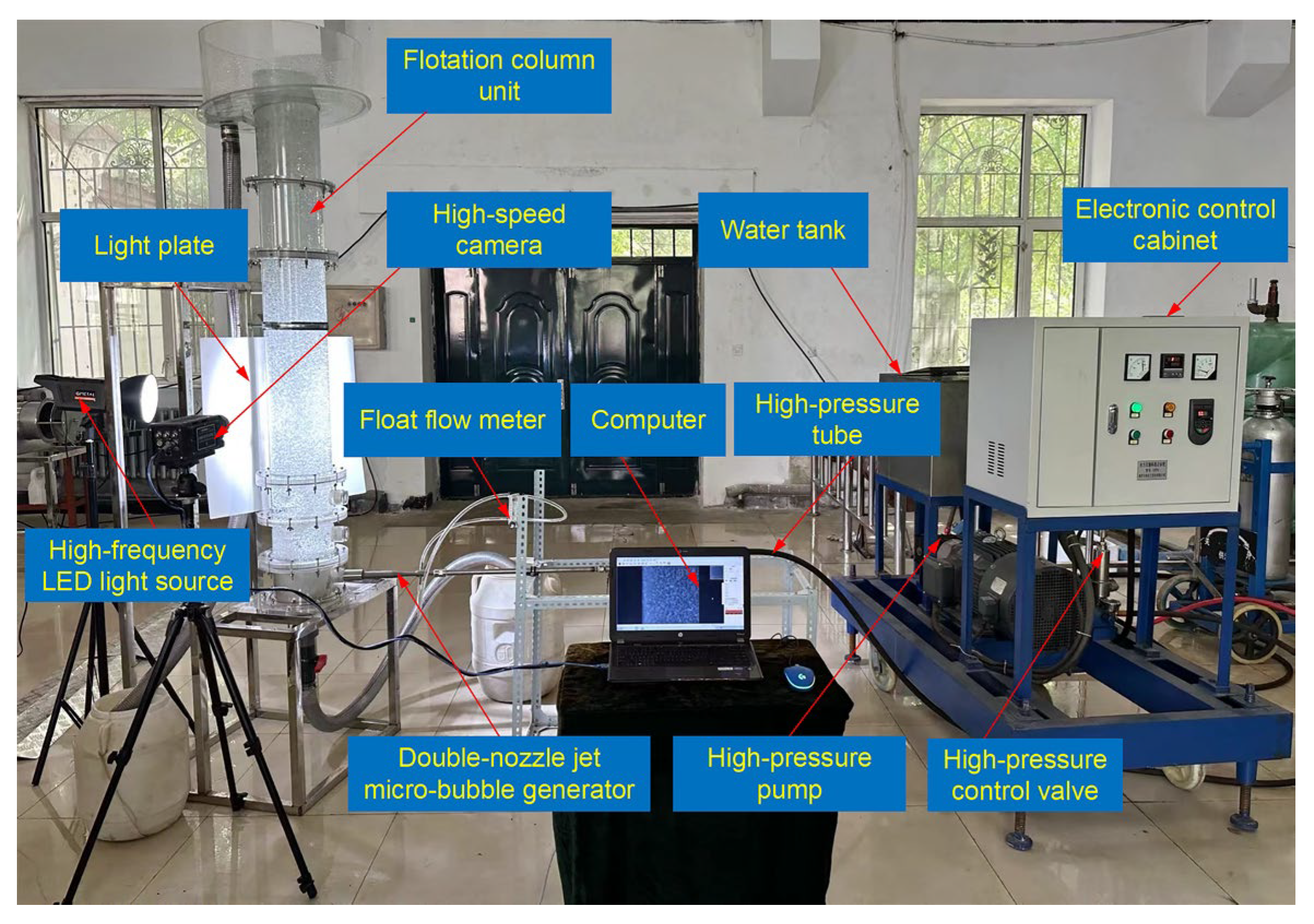
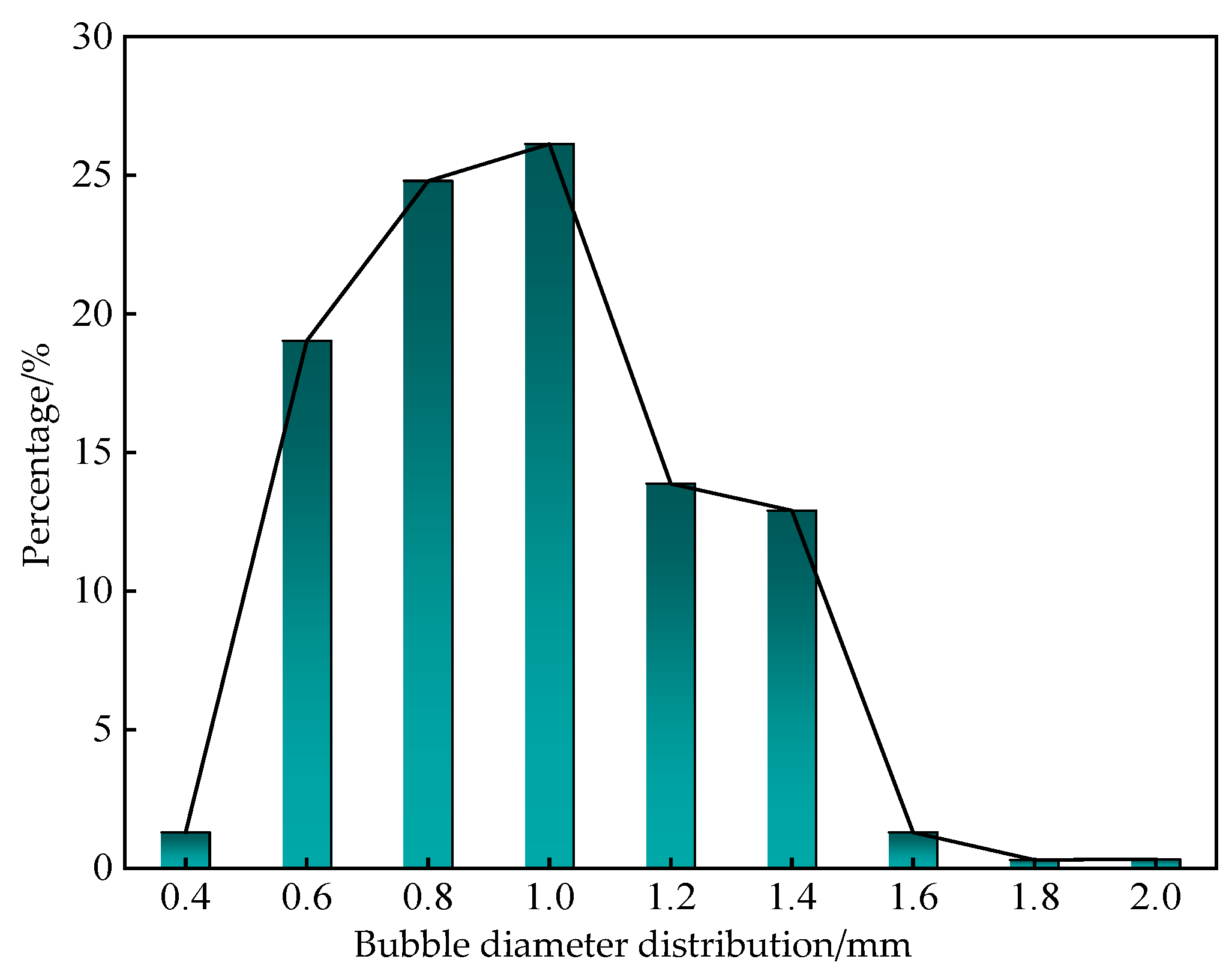
4.5.1. Bubble Cluster Visualization Test
4.5.2. Integration Test of Flake Graphite Grinding and Floating
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bernard, A.; Khalil, N.; Ahmed, I.; McCalden, D.; Haelssig, J.; Macchi, A.; Duchesne, M. Gas fluidization of natural graphite flakes. Powder Technol. 2024, 431, 119097. [Google Scholar] [CrossRef]
- Sun, K.K.; Qiu, Y.S.; Zhang, L.Y. Preserving Flake Size in an African Flake Graphite Ore Beneficiation Using a Modified Grinding and Pre-Screening Process. Minerals 2017, 7, 115. [Google Scholar] [CrossRef]
- Al-Ani, T.; Leinonen, S.; Ahtola, T.; Salvador, D. High-Grade Flake Graphite Deposits in Metamorphic Schist Belt, Central Finland-Mineralogy and Beneficiation of Graphite for Lithium-Ion Battery Applications. Minerals 2020, 10, 680. [Google Scholar] [CrossRef]
- Vasumathi, N.; Sarjekar, A.; Chandrayan, H.; Chennakesavulu, K.; Reddy, G.R.; Kumar, T.V.V.; El-Gendy, N.S.; Gopalkrishna, S.J. A Mini Review on Flotation Techniques and Reagents Used in Graphite Beneficiation. Int. J. Chem. Eng. 2023, 2023, 1007689. [Google Scholar] [CrossRef]
- Srikant, S.S.; Rao, R.B. Preparation of High Purity Graphite using Comminution, Pressure Leaching and Flotation. J. Min. Environ. 2023, 14, 2461. [Google Scholar] [CrossRef]
- Peng, Z.M.; Li, D.S.; Fang, W.J.; Zhang, J.; Zhang, R.Y.; Qiu, Y.S.; Sun, K.K. Improved Flotation of Fine Flake Graphite Using a Modified Thickening Process. Separations 2023, 10, 275. [Google Scholar] [CrossRef]
- Ghosh, A.K. Literature quest and survey on graphite beneficiation through flotation. Renew. Sustain. Energy Rev. 2024, 189, 113980. [Google Scholar] [CrossRef]
- Gao, J.X.; Bu, X.N.; Dong, L.S.; Qiu, Y.S.; Xie, G.Y.; Chelgani, S.C. Natural Graphite Froth Flotation—An Overview. Miner. Process. Extr. Metall. Rev. 2024, 1–18. [Google Scholar] [CrossRef]
- Yoon, R.H. Microbubble flotation. Miner. Eng. 1993, 6, 619–630. [Google Scholar] [CrossRef]
- Lee, J.E.; Choi, W.S.; Lee, J.K. A study of the bubble properties in the column flotation system. Korean J. Chem. Eng. 2003, 20, 942–949. [Google Scholar] [CrossRef]
- Gui, X.H.; Liu, J.T.; Cao, Y.J.; Ding, Q.P. Research and Progress on the Structural Properties of Bubble Generators. Coal Prep. Technol. 2009, 2, 66–70+81. [Google Scholar] [CrossRef]
- Matiolo, E.; Couto, H.J.B.; Lima, N.; Silva, K.; de Freitas, A.S. Improving recovery of iron using column flotation of iron ore slimes. Miner. Eng. 2020, 158, 106608. [Google Scholar] [CrossRef]
- Tortorelli, J.P.; Craven, J.W.; Toguri, J.M.; Dobby, G.S.; Agar, G.E. The effect of external gas/slurry contact on the flotation of fine particles. Miner. Eng. 1997, 10, 1127–1138. [Google Scholar] [CrossRef]
- Shuai, Y.; Wang, X.Y.; Huang, Z.L.; Yang, Y.; Sun, J.Y.; Wang, J.D.; Yang, Y.R. Structural Design and Performance of a Jet-Impinging TypeMicrobubble Generator. Ind. Eng. Chem. Res. 2022, 61, 4445–4459. [Google Scholar] [CrossRef]
- Chen, W.Y.; Wang, J.B.; Jiang, N.; Zhao, B.; Wang, Z.D. Numerical simulation of gas-liquid two-phase jet flow in air-bubble generator. J. Cent. South Univ. Technol. 2008, 15, 140–144. [Google Scholar] [CrossRef]
- Wu, M.; Yuan, S.Y.; Song, H.Y.; Li, X.B. Micro-nano bubbles production using a swirling-type venturi bubble generator. Chem. Eng. Process.-Process Intensif. 2022, 170, 108697. [Google Scholar] [CrossRef]
- Sadatomi, M.; Kawahara, A.; Kano, K.; Ohtomo, A. Performance of a new micro-bubble generator with a spherical body in a flowing water tube. Exp. Therm. Fluid Sci. 2005, 29, 615–623. [Google Scholar] [CrossRef]
- Gordiychuk, A.; Svanera, M.; Benini, S.; Poesio, P. Size distribution and Sauter mean diameter of micro bubbles for a Venturi type bubble generator. Exp. Therm. Fluid Sci. 2016, 70, 51–60. [Google Scholar] [CrossRef]
- Deng, X.W.; Lv, B.; Cheng, G.; Lu, Y. Mechanism of micro/nano-bubble formation and cavitation effect on bubbles size distribution in flotation. Physicochem. Probl. Miner. Process. 2020, 56, 504–512. [Google Scholar] [CrossRef]
- Fujiwara, A.; Okamoto, K.; Hashiguchi, K.; Peixinho, J.; Takagi, S.; Matsumoto, Y.; ASME. Bubble breakup phenomena in a venturi tube. In Proceedings of the 5th Joint ASME/JSME Fluids Engineering Summer Conference, San Diego, CA, USA, 30 July–2 August 2007. [Google Scholar]
- Tsave, P.K.; Kostoglou, M.; Karapantsios, T.D.; Lazaridis, N.K. A Hybrid Device for Enhancing Flotation of Fine Particles by Combining Micro-Bubbles with Conventional Bubbles. Minerals 2021, 11, 561. [Google Scholar] [CrossRef]
- Fu, X.Z.; Niu, Z.; Lin, M.; Gao, Y.; Sun, W.; Yue, T. Strengthened Oxygen Oxidation of Ferrous Ions by A Homemade Venturi Jet Microbubble Generator towards Iron Removal in Hydrometallurgy. Minerals 2021, 11, 1342. [Google Scholar] [CrossRef]
- Li, Q.; Guo, X.; Zhang, J.; Lei, M.; Liu, J.L.; Ming, D.Z.; Fang, L. Mechanism of Microbubbles and Cavitation Effect on Bubble Breakage in a Venturi Bubble Generator. J. Appl. Fluid Mech. 2023, 16, 778–793. [Google Scholar] [CrossRef]
- Xu, W.G.; Li, W.J.; Wang, J.W.; Song, Y.S.; Wu, B.A.; Wen, J.K.; Li, K.G.; Li, B. Numerical Simulation of Gas-Liquid Two-Phase Flow CFD-PBM Model in a Micro-Nanobubble Generator. Minerals 2022, 12, 1270. [Google Scholar] [CrossRef]
- Li, X.H.; Su, W.B.; Liu, Y.; Yan, X.K.; Wang, L.J.; Zhang, H.J. Comparison of bubble velocity, size, and holdup distribution between single- and double-air inlet in jet microbubble generator. Asia-Pac. J. Chem. Eng. 2021, 16, e2611. [Google Scholar] [CrossRef]
- Basso, A.; Hamad, F.; Ganesan, P. Effects of the geometrical configuration of air-water mixer on the size and distribution of microbubbles in aeration systems. Asia-Pac. J. Chem. Eng. 2018, 13, e2259. [Google Scholar] [CrossRef]
- Wang, L.J.; Wang, Y.H.; Yan, X.K.; Wang, A.; Cao, Y.J. A numerical study on efficient recovery of fine-grained minerals with vortex generators in pipe flow unit of a cyclonic-static micro bubble flotation column. Chem. Eng. Sci. 2017, 158, 304–313. [Google Scholar] [CrossRef]
- Alam, H.S.; Sutikno, P.; Soelaiman, T.A.F.; Sugiarto, A.T. CFD-PBM Coupled modeling of bubble size distribution in a swirling-flow nanobubble generator. Eng. Appl. Comput. Fluid Mech. 2022, 16, 677–693. [Google Scholar] [CrossRef]
- Al-Azzawi, A.; Al-Shimmery, A.; Alshara, A.; Mohammed, M.R. Computational Fluid Dynamics Simulation Assessment of Inlet Configuration Influence on Enhancing Swirl Flow Microbubble Generator Performance. J. Eng. 2023, 2023, 1457986. [Google Scholar] [CrossRef]
- Palazuelos, L.P.A.; Guerrero, M.U.F.; Labra, M.P.; Domínguez, I.A.R.; García, R.E.; Cardona, F.P.; Hernández, F.R.B.; Tapia, J.C.J.; Pérez, M.R. Silver(I) Recovery by Ion Flotation Process from Aqueous Solutions in Cells with Spargers. Minerals 2023, 13, 572. [Google Scholar] [CrossRef]
- Taghavi, F.; Noaparast, M.; Pourkarimi, Z.; Nakhaei, F. Comparison of mechanical and column flotation performances on recovery of phosphate slimes in presence of nano-microbubbles. J. Cent. South Univ. 2022, 29, 102–115. [Google Scholar] [CrossRef]
- Parga, J.R.; Valenzuela, J.L.; Aguayo, S. Bacis flotation cell for gold- and silver-beard pyrite recovery. Miner. Metall. Process. 2009, 26, 25–29. [Google Scholar] [CrossRef]
- Ni, C.; Jin, M.G.; Chen, Y.R.; Xie, G.Y.; Peng, Y.L.; Xia, W.C. Improving the Recovery of Coarse-Coal Particles by Adding Premineralization Prior to Column Flotation. Int. J. Coal Prep. Util. 2017, 37, 87–99. [Google Scholar] [CrossRef]
- Ma, F.Y.; Tao, D.P. A Study of Mechanisms of Nanobubble-Enhanced Flotation of Graphite. Nanomaterials 2022, 12, 3361. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.F.; Han, H.; Liu, R.H.; Gao, R.Z.; Wu, G.G. Effect of outlet diameter on atomization characteristics and dust reduction performance of X-swirl pressure nozzle. Process Saf. Environ. Prot. 2020, 137, 340–351. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Zou, D.H.; Yang, X.L.; Mou, J.G.; Zhou, Q.W.; Xu, M.S. Liquid-Gas Jet Pump: A Review. Energies 2022, 15, 6978. [Google Scholar] [CrossRef]
- Lu, H.Q. Theory and Application of Jet Pump Technology; Water Resources and Electric Power Press: Beijing, China, 1989; p. 316. [Google Scholar]
- Liu, J.Z. Research on performance of liquid-air jet pump. J. Wuhan Inst. Water Conserv. Electr. Power. 1982, 3, 105–114. [Google Scholar]
- Wu, Y.X.; Chen, H.; Song, X.F. An investigation on the effect of open hole number and scheme on single-phase flow of a swirl flow bubble generator. Korean J. Chem. Eng. 2023, 40, 754–769. [Google Scholar] [CrossRef]
- Cheng, J.C.; Li, Q.; Yang, C.; Zhang, Y.Q.; Mao, Z.S. CFD-PBE simulation of a bubble column in OpenFOAM. Chin. J. Chem. Eng. 2018, 26, 1773–1784. [Google Scholar] [CrossRef]
- Mutharasu, L.C.; Kalaga, D.V.; Sathe, M.; Turney, D.E.; Griffin, D.; Li, X.L.; Kawaji, M.; Nandakumar, K.; Joshi, J.B. Experimental study and CFD simulation of the multiphase flow conditions encountered in a Novel Down-flow bubble column. Chem. Eng. J. 2018, 350, 507–522. [Google Scholar] [CrossRef]
- Muthiah, P.; Ponnusamy, K.; Radhakrishnan, T.K. CFD Modeling of Flow Pattern and Phase Holdup of Three Phase Fluidized Bed Contactor. Chem. Prod. Process Model. 2009, 4, 1366. [Google Scholar] [CrossRef]
- Fluent, A. Ansys Fluent Theory Guide; Ansys Inc.: Canonsburg, PA, USA, 2020; pp. 724–746. [Google Scholar]
- Mwandawande, I.; Akdogan, G.; Bradshaw, S.M.; Karimi, M.; Snyders, N. Prediction of gas holdup in a column flotation cell using computational fluid dynamics (CFD). J. S. Afr. Inst. Min. Metall. 2019, 119, 81–95. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, T.; Cong, T.L.; Peng, M.J. Effects of interaction models on upward subcooled boiling flow in annulus. Prog. Nucl. Energy 2018, 105, 61–75. [Google Scholar] [CrossRef]
- Du, W.; Bao, X.J.; Xu, J.; Wei, W.S. Computational fluid dynamics (CFD) modeling of spouted bed: Assessment of drag coefficient correlations. Chem. Eng. Sci. 2006, 61, 1401–1420. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Qin, B.; Li, S.H.; Liu, Y.G.; Li, X.; Cui, P.Z.; Wang, Y.L.; Gao, J. Multi-dimensional analysis of turbulence models for immiscible liquid-liquid mixing in stirred tank based on numerical simulation. Sep. Sci. Technol. 2021, 56, 411–424. [Google Scholar] [CrossRef]
- Lee, M.; Park, G.; Park, C.; Kim, C. Improvement of Grid Independence Test for Computational Fluid Dynamics Model of Building Based on Grid Resolution. Adv. Civ. Eng. 2020, 2020, 8827936. [Google Scholar] [CrossRef]
- Zulkifli, Z.; Halim, N.H.A.; Solihin, Z.H.; Saedon, J.; Ahmad, A.A.; Abdullah, A.H.; Raof, N.A.; Hadi, M.A. The analysis of grid independence study in continuous disperse of MQL delivery system. J. Mech. Eng. Sci. 2023, 17, 9586–9596. [Google Scholar] [CrossRef]
- Maeda, Y.; Hosokawa, S.; Baba, Y.; Tomiyama, A.; Ito, Y. Generation mechanism of micro-bubbles in a pressurized dissolution method. Exp. Therm. Fluid Sci. 2015, 60, 201–207. [Google Scholar] [CrossRef]
- Huang, J.; Sun, L.C.; Du, M.; Liang, Z.; Mo, Z.Y. An investigation on the performance of a micro-scale Venturi bubble generator. Chem. Eng. J. 2020, 386, 120980. [Google Scholar] [CrossRef]


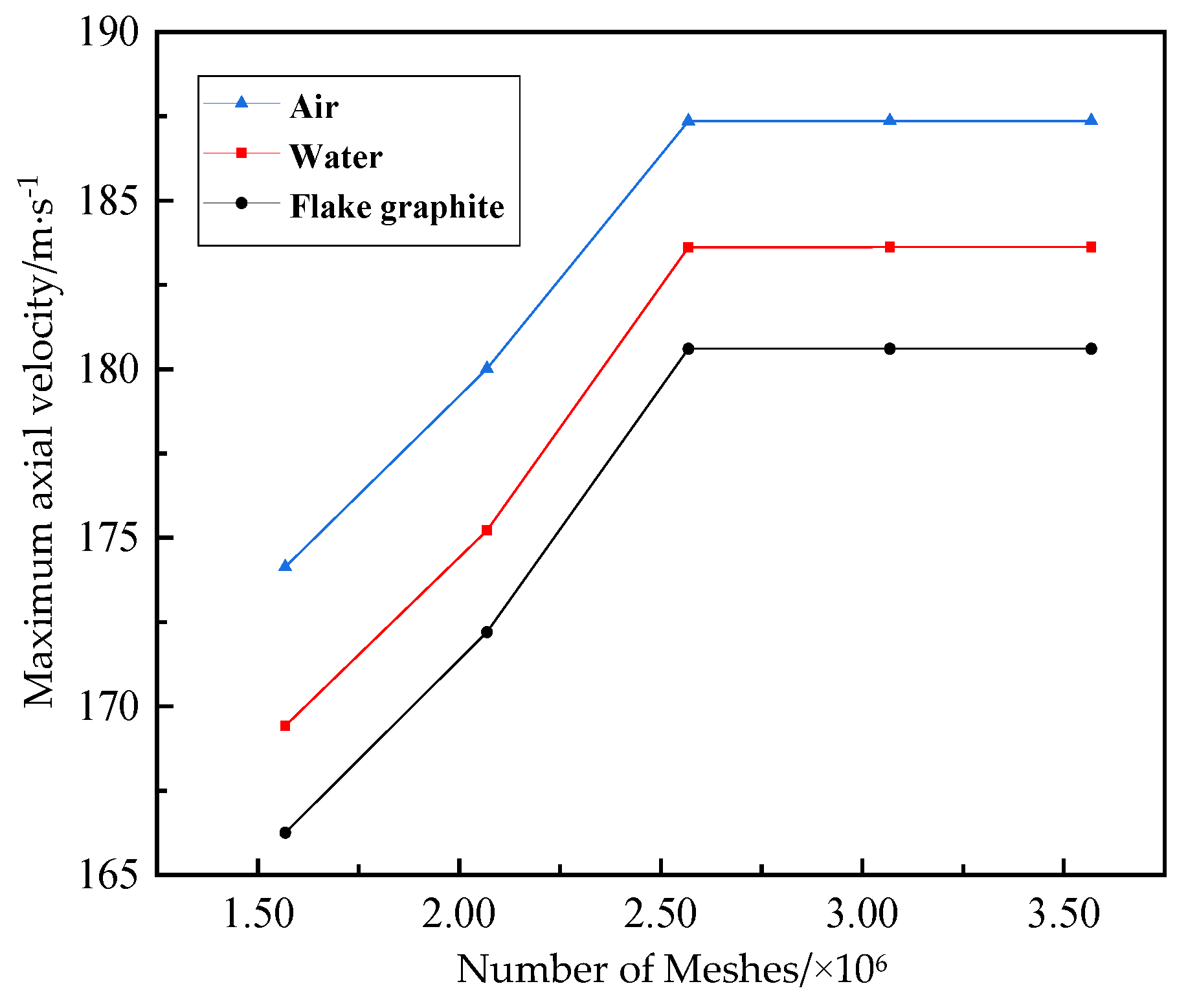



| Maximum Axial Velocity (m·s−1) | Number of Meshes | ||||
|---|---|---|---|---|---|
| 1,568,291 | 2,068,291 | 2,568,291 | 3,068,291 | 3,568,291 | |
| Air-phase flow field | 174.135 | 180.011 | 187.355 | 187.358 | 187.359 |
| Water-phase flow field | 169.418 | 175.213 | 183.615 | 183.619 | 183.620 |
| Flake-graphite-phase flow field | 166.254 | 172.201 | 180.606 | 180.607 | 180.609 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, X.; Guo, C.; Peng, D.; Jiang, Y. Numerical Simulation of Air–Water–Flake Graphite Triple-Phase Flow Field in a Homemade Double-Nozzle Jet Micro-Bubble Generator. Minerals 2024, 14, 533. https://doi.org/10.3390/min14060533
Dong X, Guo C, Peng D, Jiang Y. Numerical Simulation of Air–Water–Flake Graphite Triple-Phase Flow Field in a Homemade Double-Nozzle Jet Micro-Bubble Generator. Minerals. 2024; 14(6):533. https://doi.org/10.3390/min14060533
Chicago/Turabian StyleDong, Xing, Chenhao Guo, Deqiang Peng, and Yun Jiang. 2024. "Numerical Simulation of Air–Water–Flake Graphite Triple-Phase Flow Field in a Homemade Double-Nozzle Jet Micro-Bubble Generator" Minerals 14, no. 6: 533. https://doi.org/10.3390/min14060533
APA StyleDong, X., Guo, C., Peng, D., & Jiang, Y. (2024). Numerical Simulation of Air–Water–Flake Graphite Triple-Phase Flow Field in a Homemade Double-Nozzle Jet Micro-Bubble Generator. Minerals, 14(6), 533. https://doi.org/10.3390/min14060533









