Modeling and Hybrid Inversion of Mineral Deposits Using the Dipping Dike Model with Finite Depth Extent
Abstract
1. Introduction
2. Method
2.1. Forward Modeling
2.2. Inversion Algorithm
3. Results and Discussion
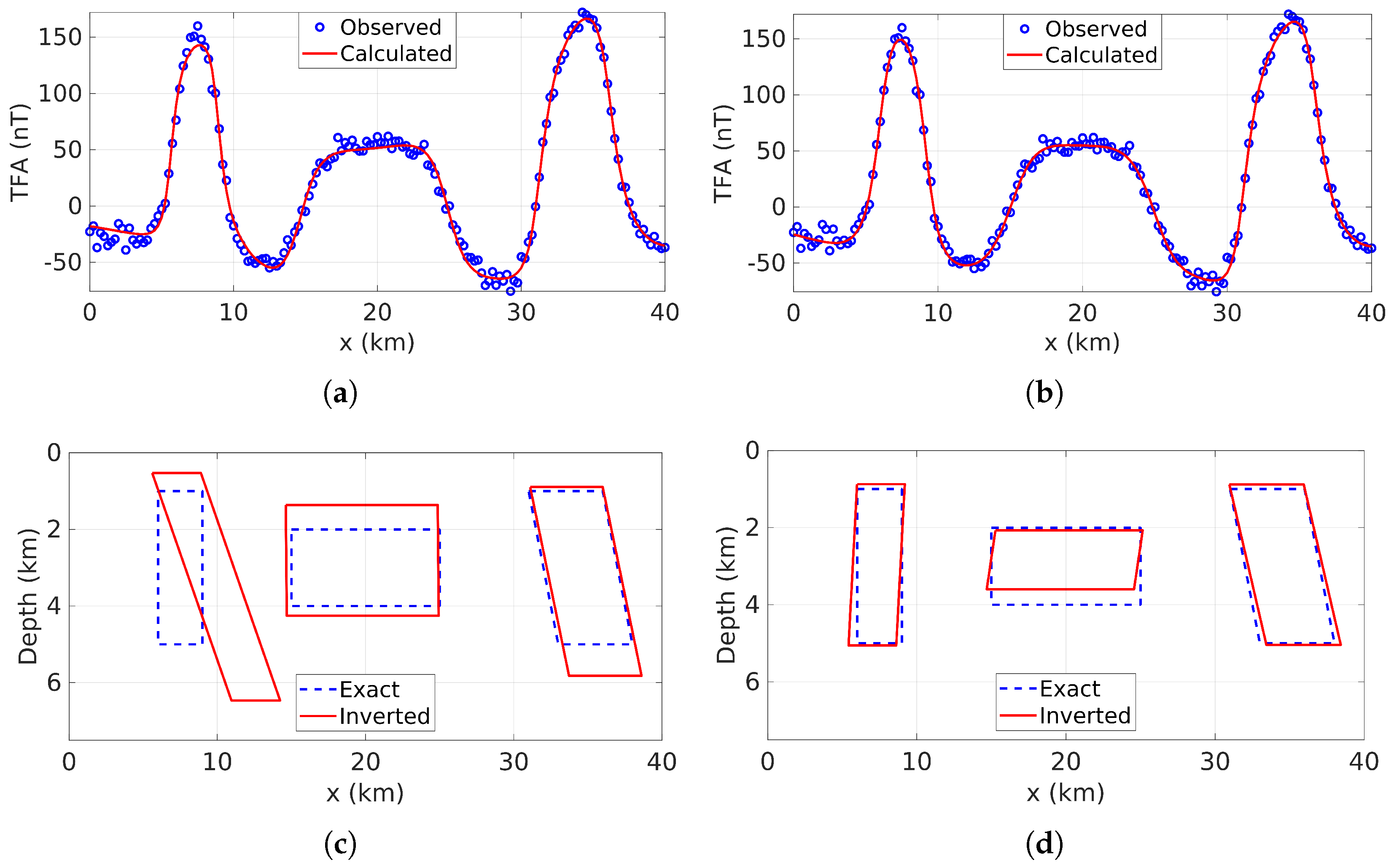
3.1. Synthetic Data
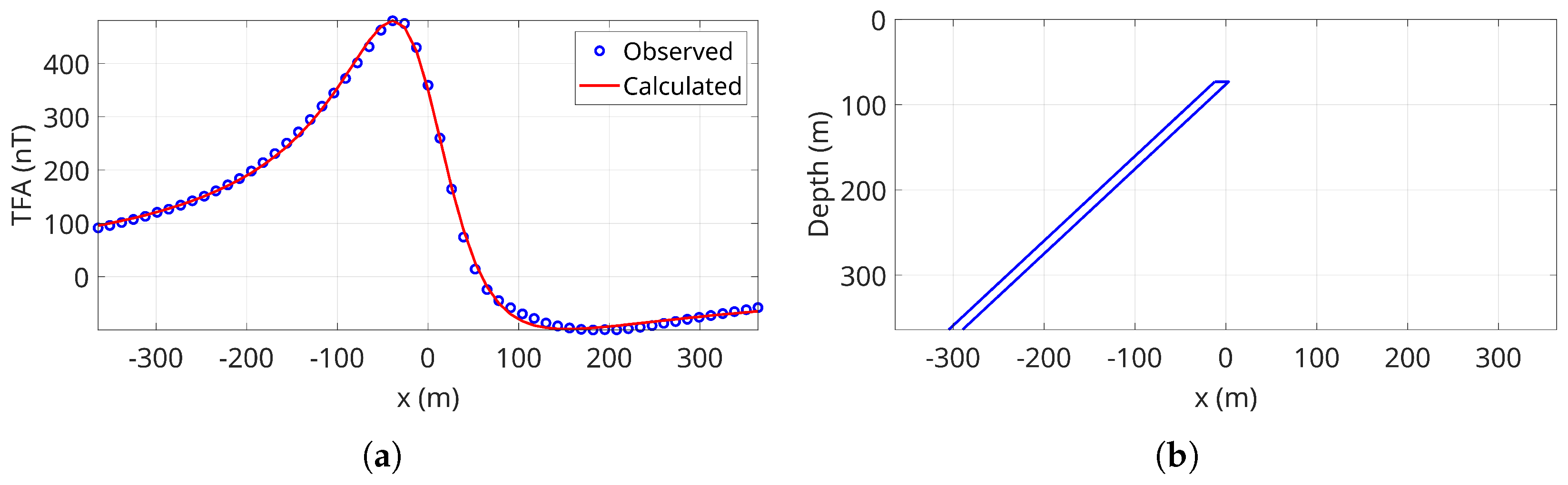
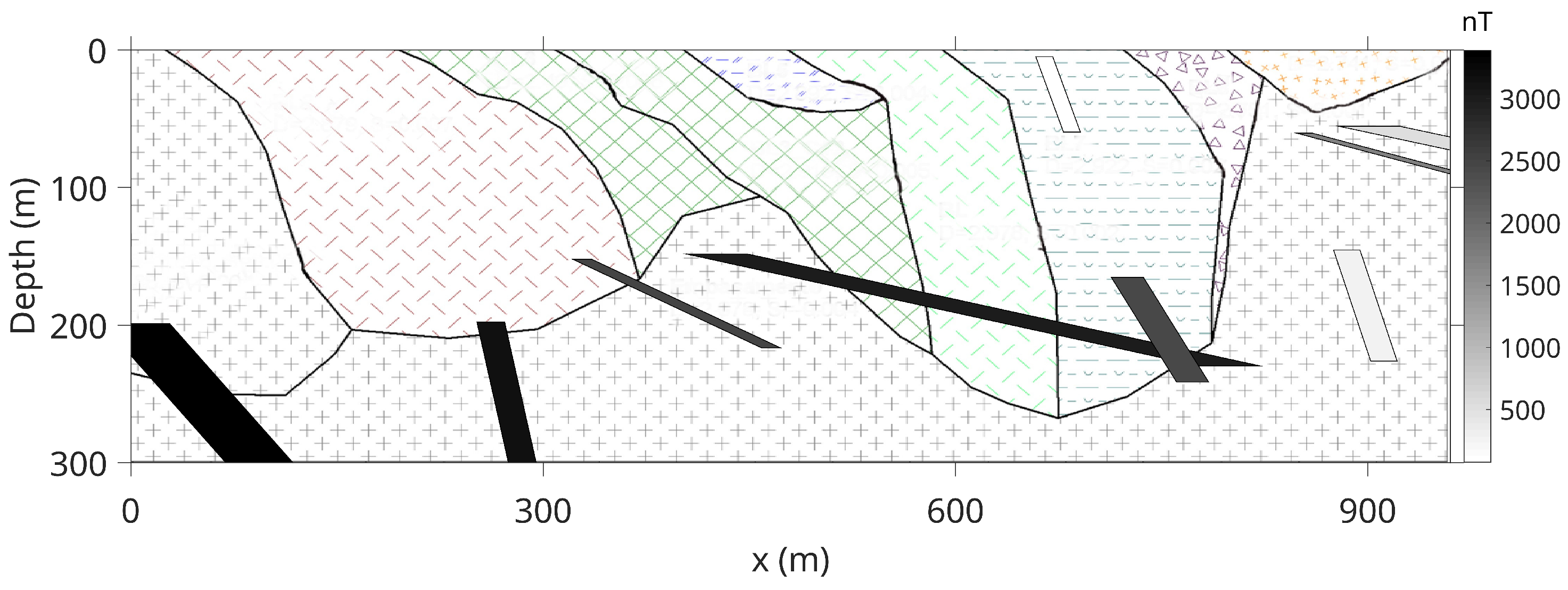
3.2. Pima Copper Mine
- Depth: m;
- Dip: ;
- Half-width: m (or m perpendicular to the dip).
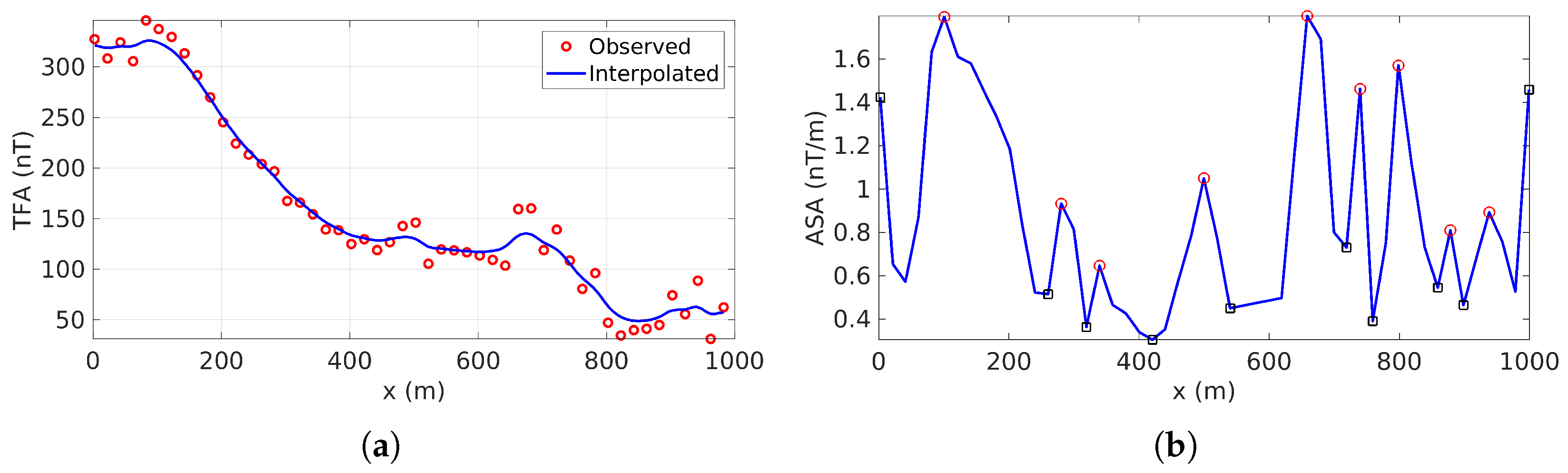
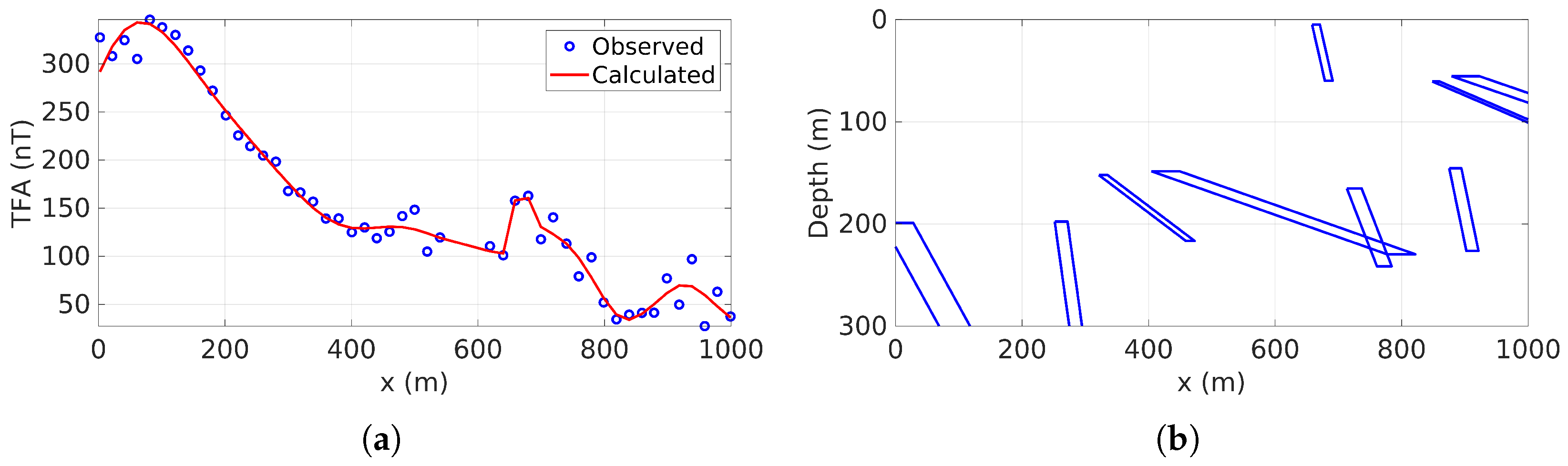
3.3. Laje Iron Ore Deposit
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Jacobian Matrix
References
- Hood, P. The Königsberger ratio and the dipping-dyke equation. Geophys. Prospect. 1964, 12, 440–456. [Google Scholar] [CrossRef]
- Barongo, J.O. Method for depth estimation on aeromagnetic vertical gradient anomalies. Geophysics 1985, 50, 963–968. [Google Scholar] [CrossRef]
- Gobashy, M.; Abdelazeem, M.; Abdrabou, M. Minerals and ore deposits exploration using meta-heuristic based optimization on magnetic data. Contrib. Geophys. Geod. 2020, 50, 161–199. [Google Scholar] [CrossRef]
- Balkaya, Ç.; Kaftan, I. Inverse modelling via differential search algorithm for interpreting magnetic anomalies caused by 2D dyke-shaped bodies. J. Earth Syst. Sci. 2021, 130, 135. [Google Scholar] [CrossRef]
- Biswas, A.; Rao, K.; Mondal, T.S. Inverse modeling and uncertainty assessment of magnetic data from 2D thick dipping dyke and application for mineral exploration. J. Appl. Geophys. 2022, 207, 104848. [Google Scholar] [CrossRef]
- Ai, H.; Ekinci, Y.L.; Balkaya, Ç.; Essa, K.S. Inversion of geomagnetic anomalies caused by ore masses using Hunger Games Search algorithm. Earth Space Sci. 2023, 10, e2023EA003002. [Google Scholar] [CrossRef]
- Rao, B.S.R.; Murthy, I.V.R.; Rao, C.V. Two methods for computer interpretation of magnetic anomalies of dikes. Geophysics 1973, 38, 710–718. [Google Scholar] [CrossRef]
- Won, I.J. Application of Gauss’s method to magnetic anomalies of dipping dikes. Geophysics 1981, 46, 211–215. [Google Scholar] [CrossRef]
- Johnson, W.W. A least-squares method of interpreting magnetic anomalies caused by two-dimensional structures. Geophysics 1969, 34, 65–74. [Google Scholar] [CrossRef]
- Ku, C.C.; Sharp, J.A. Werner deconvolution for automated magnetic interpretation and its refinement using Marquardt’s inverse modeling. Geophysics 1983, 48, 754–774. [Google Scholar] [CrossRef]
- Marobhe, I.M. A versatile Turbo-Pascal program for optimization of magnetic anomalies caused by two-dimensional dike, prism, or slope models. Comput. Geosci. 1990, 16, 341–365. [Google Scholar] [CrossRef]
- Biswas, A.; Parija, M.P.; Kumar, S. Global nonlinear optimization for the interpretation of source parameters from total gradient of gravity and magnetic anomalies caused by thin dyke. Ann. Geophys. 2017, 60, 0218. [Google Scholar] [CrossRef]
- Kaftan, İ. Interpretation of magnetic anomalies using a genetic algorithm. Acta Geophys. 2017, 65, 627–634. [Google Scholar] [CrossRef]
- Essa, K.S.; Elhussein, M. PSO (Particle Swarm Optimization) for interpretation of magnetic anomalies caused by simple geometrical structures. Pure Appl. Geophys. 2018, 175, 3539–3553. [Google Scholar] [CrossRef]
- Ekwok, S.E.; Eldosouky, A.M.; Essa, K.S.; George, A.M.; Abdelrahman, K.; Fnais, M.S.; Andráš, P.; Akaerue, E.I.; Akpan, A.E. Particle swarm optimization (PSO) of high-quality magnetic data of the Obudu Basement Complex, Nigeria. Minerals 2023, 13, 1209. [Google Scholar] [CrossRef]
- Ekinci, Y.L.; Balkaya, Ç.; Göktürkler, G.; Turan, S. Model parameter estimations from residual gravity anomalies due to simple-shaped sources using differential evolution algorithm. J. Appl. Geophys. 2016, 129, 133–147. [Google Scholar] [CrossRef]
- Ai, H.; Ekinci, Y.L.; Balkaya, Ç.; Alvandi, A.; Ekinci, R.; Roy, A.; Su, K.; Pham, L.T. Modified Barnacles mating optimizing algorithm for the inversion of self-potential anomalies due to ore deposits. Nat. Resour. Res. 2024, 33, 1073–1102. [Google Scholar] [CrossRef]
- Su, K.; Ai, H.; Alvandi, A.; Lyu, C.; Wei, X.; Qin, Z.; Tu, Y.; Yan, Y.; Nie, T. Hunger Games Search for the elucidation of gravity anomalies with application to geothermal energy investigations and volcanic activity studies. Open Geosci. 2024, 16, 20220641. [Google Scholar] [CrossRef]
- Wigh, M.D.; Hansen, T.M.; Døssing, A. Inference of unexploded ordnance (UXO) by probabilistic inversion of magnetic data. Geophys. J. Int. 2020, 220, 37–58. [Google Scholar] [CrossRef]
- Titus, W.J.; Titus, S.J.; Davis, J.R. A Bayesian approach to modeling 2D gravity data using polygons. Geophysics 2017, 82, G1–G21. [Google Scholar] [CrossRef]
- Zunino, A.; Ghirotto, A.; Armadillo, E.; Fichtner, A. Hamiltonian Monte Carlo Probabilistic Joint Inversion of 2D (2.75 D) Gravity and Magnetic Data. Geophys. Res. Lett. 2022, 49, e2022GL099789. [Google Scholar] [CrossRef]
- Mosegaard, K.; Sambridge, M. Monte Carlo analysis of inverse problems. Inverse Probl. 2002, 18, R29. [Google Scholar] [CrossRef]
- Ben, U.C.; Akpan, A.E.; Mbonu, C.C.; Ebong, E.D. Novel methodology for interpretation of magnetic anomalies due to two-dimensional dipping dikes using the Manta Ray Foraging Optimization. J. Appl. Geophys. 2021, 192, 104405. [Google Scholar] [CrossRef]
- Sen, M.K.; Stoffa, P.L. Global Optimization Methods in Geophysical Inversion, 2nd ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Di Maio, R.; Milano, L.; Piegari, E. Modeling of magnetic anomalies generated by simple geological structures through Genetic-Price inversion algorithm. Phys. Earth Planet. Inter. 2020, 305, 106520. [Google Scholar] [CrossRef]
- Talwani, M.; Heirtzler, J. Computation of magnetic anomalies caused by two-dimensional bodies of arbitrary shape. In Computers in the Mineral Industries; Part 1; Parks, G.A., Ed.; Stanford University Publications: Redwood City, CA, USA, 1964; pp. 464–480. [Google Scholar]
- Al-Mamun, A.; Barber, J.; Ginting, V.; Pereira, F.; Rahunanthan, A. Contaminant transport forecasting in the subsurface using a Bayesian framework. Appl. Math. Comput. 2020, 387, 124980. [Google Scholar] [CrossRef]
- Gay, S.P. Standard curves for interpretation of magnetic anomalies over long tabular bodies. Geophysics 1963, 28, 161–200. [Google Scholar] [CrossRef]
- Sampaio, E.E.S.; Batista, J.C.; Santos, E.S.M. Interpretation of geophysical data for iron ore detailed survey in Laje, Bahia, Brazil. An. Acad. Bras. CiêNcias 2021, 93, e20200178. [Google Scholar] [CrossRef]
- McGrath, P.H.; Hood, P.J. The dipping dike case: A computer curve-matching method of magnetic interpretation. Geophysics 1970, 35, 831–848. [Google Scholar] [CrossRef]
- Mosegaard, K.; Tarantola, A. Monte Carlo sampling of solutions to inverse problems. J. Geophys. Res. Solid Earth 1995, 100, 12431–12447. [Google Scholar] [CrossRef]
- Darroch, J.N. On the Distribution of the Number of Successes in Independent Trials. Ann. Math. Stat. 1964, 35, 1317–1321. [Google Scholar] [CrossRef]
- Borges, M.R.; Pereira, F. A novel approach for subsurface characterization of coupled fluid flow and geomechanical deformation: The case of slightly compressible flows. Comput. Geosci. 2020, 24, 1693–1706. [Google Scholar] [CrossRef]
- Gamerman, D.; Lopes, H.F. Markov Chain Monte Carlo: Stochastic Simulation for Bayesian Inference; Chapman & Hall/CRC Texts in Statistical Science; Taylor & Francis: Abingdon, UK, 2006. [Google Scholar] [CrossRef]
- Yamashita, N.; Fukushima, M. On the rate of convergence of the Levenberg-Marquardt method. In Topics in Numerical Analysis: With Special Emphasis on Nonlinear Problems; Springer: Berlin/Heidelberg, Germany, 2001; pp. 239–249. [Google Scholar] [CrossRef]
- Boos, E.; Gonçalves, D.S.; Bazán, F.S. Levenberg-Marquardt method with singular scaling and applications. Appl. Math. Comput. 2024, 474, 128688. [Google Scholar] [CrossRef]
- Fernandes, J.A.; Azevedo, J.S.; Oliveira, S.P. A combined Markov Chain Monte Carlo and Levenberg-Marquardt inversion method for heterogeneous subsurface reservoir modeling. Discov. Appl. Sci. 2024, 6, 514. [Google Scholar] [CrossRef]
- Raju, D.C.V. LIMAT: A computer program for least-squares inversion of magnetic anomalies over long tabular bodies. Comput. Geosci. 2003, 29, 91–98. [Google Scholar] [CrossRef]
- Essa, K.S. A particle swarm optimization method for interpreting self-potential anomalies. J. Geophys. Eng. 2019, 16, 463–477. [Google Scholar] [CrossRef]
- Pham, L.T.; Oksum, E.; Le, D.V.; Ferreira, F.J.F.; Le, S.T. Edge detection of potential field sources using the softsign function. Geocarto Int. 2022, 37, 4255–4268. [Google Scholar] [CrossRef]
- Abdelrahman, E.M.; Sharafeldin, S.M. An iterative least-squares approach to depth determination from residual magnetic anomalies due to thin dikes. J. Appl. Geophys. 1996, 34, 213–220. [Google Scholar] [CrossRef]
- Asfahani, J.; Tlas, M. A robust nonlinear inversion for the interpretation of magnetic anomalies caused by faults, thin dikes and spheres like structure using stochastic algorithms. Pure Appl. Geophys. 2007, 164, 2023–2042. [Google Scholar] [CrossRef]
- Ekinci, Y.L. MATLAB-based algorithm to estimate depths of isolated thin dike-line sources using higher-order horizontal derivatives of magnetic anomalies. SpringerPlus 2016, 5, 1384. [Google Scholar] [CrossRef]
- Dannemiller, N.; Li, Y. A new method for determination of magnetization direction. Geophysics 2006, 71, L69–L73. [Google Scholar] [CrossRef]
- Barbosa, J.S.F.; Sabaté, P. Archean and Paleoproterozoic crust of the São Francisco craton, Bahia, Brazil: Geodynamic features. Precambrian Res. 2004, 133, 1–27. [Google Scholar] [CrossRef]
- Smithies, R.H.; Bagas, L. High pressure amphibolite-granulite facies metamorphism in the Paleoproterozoic Rudall Complex, central Western Australia. Precambrian Res. 1997, 83, 243–265. [Google Scholar] [CrossRef]
- Beukes, N.J.; Mukhopadhyay, J.; Gutzmer, J. Genesis of high-grade iron ores of the Archean Iron Ore Group around Noamundi, India. Econ. Geol. 2008, 103, 365–386. [Google Scholar] [CrossRef]
- Inoue, H. A least-squares smooth fitting for irregularly spaced data: Finite-element approach using the cubic B-spline basis. Geophysics 1986, 51, 2051–2066. [Google Scholar] [CrossRef]
- de Souza, J.; Oliveira, S.P.; Ferreira, F.J.F. Using parity decomposition for interpreting magnetic anomalies from dikes having arbitrary dip angles, induced and remanent magnetization. Geophysics 2020, 85, J51–J58. [Google Scholar] [CrossRef]




| h (km) | t (km) | K (nT) | (km) | d (km) | |||
|---|---|---|---|---|---|---|---|
| Prism 1 | 180 | 90 | 1 | 4 | 126 | 7.5 | 1.5 |
| Prism 2 | 180 | 90 | 2 | 2 | 126 | 20 | 5 |
| Prism 3 | 180 | 63.4 | 1 | 4 | 126 | 33.5 | 2.5 |
| Noise-Free | Noisy | |||||||
|---|---|---|---|---|---|---|---|---|
| RMS (nT) | (%) | RMS (nT) | (%) | |||||
| 0 | 118 | 285,563 | 2.942 | 16.801 | 80 | 283,684 | 6.422 | 17.062 |
| 1 | 80 | 258,966 | 1.984 | 11.055 | 114 | 244,822 | 5.407 | 15.164 |
| 2 | 72 | 243,736 | 1.366 | 9.511 | 64 | 237,269 | 6.142 | 16.610 |
| 4 | 80 | 246,701 | 1.081 | 8.483 | 50 | 265,891 | 4.979 | 10.879 |
| 8 | 53 | 244,945 | 0.299 | 5.513 | 13 | 260,869 | 4.923 | 7.434 |
| RMS (nT) | (%) | (%) | (%) | |||
|---|---|---|---|---|---|---|
| 0 | 122 | 212,803 | 6.179 | 0.710 | 8.636 | 14.824 |
| 1 | 94 | 203,951 | 6.165 | 1.196 | 8.692 | 11.203 |
| 2 | 95 | 213,370 | 6.175 | 2.345 | 8.844 | 8.046 |
| 4 | 75 | 262,875 | 6.178 | 0.099 | 8.605 | 6.598 |
| 8 | 67 | 207,527 | 6.169 | 0.134 | 8.556 | 1.249 |
| h (m) | t (m) | K (nT) | (m) | d (m) | |||
|---|---|---|---|---|---|---|---|
| Interval | −180 to 180 | 0 to 180 | 0 to 100 | 100 to 1000 | 0 to 4000 | −15 to 10 | 0 to 50 |
| MH-LM | 85.81 | 135.18 | 73.06 | 984.56 | 3956.87 | −4.62 | 7.63 |
| Ref. [4] | - | 107.03 | 66.54 | - | 3842.61 | −5.38 | 8.50 |
| Ref. [5] | - | 48.60 | 66.40 | - | 1330.00 | −4.7 | 15.80 |
| Ref. [6] | - | 109.86 | 68.02 | - | 634.08 | −4.25 | - |
| Ref. [25] | - | 109.87 | 77.84 | - | 546.57 | 5.24 | - |
| RMS (nT) | |||
|---|---|---|---|
| 0 | 21 | 154,716 | 13.415 |
| 1 | 12 | 109,833 | 12.250 |
| 2 | 10 | 158,796 | 13.772 |
| 4 | 13 | 250,195 | 13.223 |
| 8 | 1 | 429,516 | 13.664 |
| h (m) | t (m) | K (nT) | (m) | d (m) | |||
|---|---|---|---|---|---|---|---|
| Interval | −180 to 180 | 0 to 90 | 0 to 200 | 50 to 200 | 0 to 4000 | see caption | 5 to 25 |
| Prism 1 | −179.402 | 48.414 | 199.058 | 197.119 | 3387.864 | 3.761 | 24.430 |
| Prism 2 | −178.783 | 77.361 | 197.720 | 196.879 | 3164.380 | 261.752 | 10.103 |
| Prism 3 | −164.691 | 25.117 | 152.085 | 64.518 | 2488.640 | 328.117 | 6.874 |
| Prism 4 | −164.402 | 12.306 | 148.394 | 81.313 | 3023.467 | 426.551 | 22.283 |
| Prism 5 | −172.033 | 69.814 | 4.903 | 54.907 | 79.134 | 664.527 | 6.161 |
| Prism 6 | −175.235 | 58.055 | 165.336 | 76.151 | 2406.299 | 725.036 | 11.667 |
| Prism 7 | 171.985 | 14.870 | 60.530 | 79.416 | 1695.706 | 854.040 | 5.685 |
| Prism 8 | −42.077 | 71.502 | 145.492 | 80.779 | 275.657 | 884.711 | 9.601 |
| Prism 9 | −173.293 | 12.044 | 55.391 | 56.675 | 504.832 | 900.702 | 22.145 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, S.P.; Azevedo, J.d.S.; Batista, J.d.C.; Novais, D.M. Modeling and Hybrid Inversion of Mineral Deposits Using the Dipping Dike Model with Finite Depth Extent. Minerals 2024, 14, 1054. https://doi.org/10.3390/min14101054
Oliveira SP, Azevedo JdS, Batista JdC, Novais DM. Modeling and Hybrid Inversion of Mineral Deposits Using the Dipping Dike Model with Finite Depth Extent. Minerals. 2024; 14(10):1054. https://doi.org/10.3390/min14101054
Chicago/Turabian StyleOliveira, Saulo Pomponet, Juarez dos Santos Azevedo, Joelson da Conceição Batista, and Diego Menezes Novais. 2024. "Modeling and Hybrid Inversion of Mineral Deposits Using the Dipping Dike Model with Finite Depth Extent" Minerals 14, no. 10: 1054. https://doi.org/10.3390/min14101054
APA StyleOliveira, S. P., Azevedo, J. d. S., Batista, J. d. C., & Novais, D. M. (2024). Modeling and Hybrid Inversion of Mineral Deposits Using the Dipping Dike Model with Finite Depth Extent. Minerals, 14(10), 1054. https://doi.org/10.3390/min14101054






