Conversion of Induced Polarization Data and Their Uncertainty from Time Domain to Frequency Domain Using Debye Decomposition
Abstract
1. Introduction
2. Time-Domain to Frequency-Domain Conversion of Induced Polarization Data
2.1. Induced Polarization in the Time Domain
2.2. Debye Decomposition
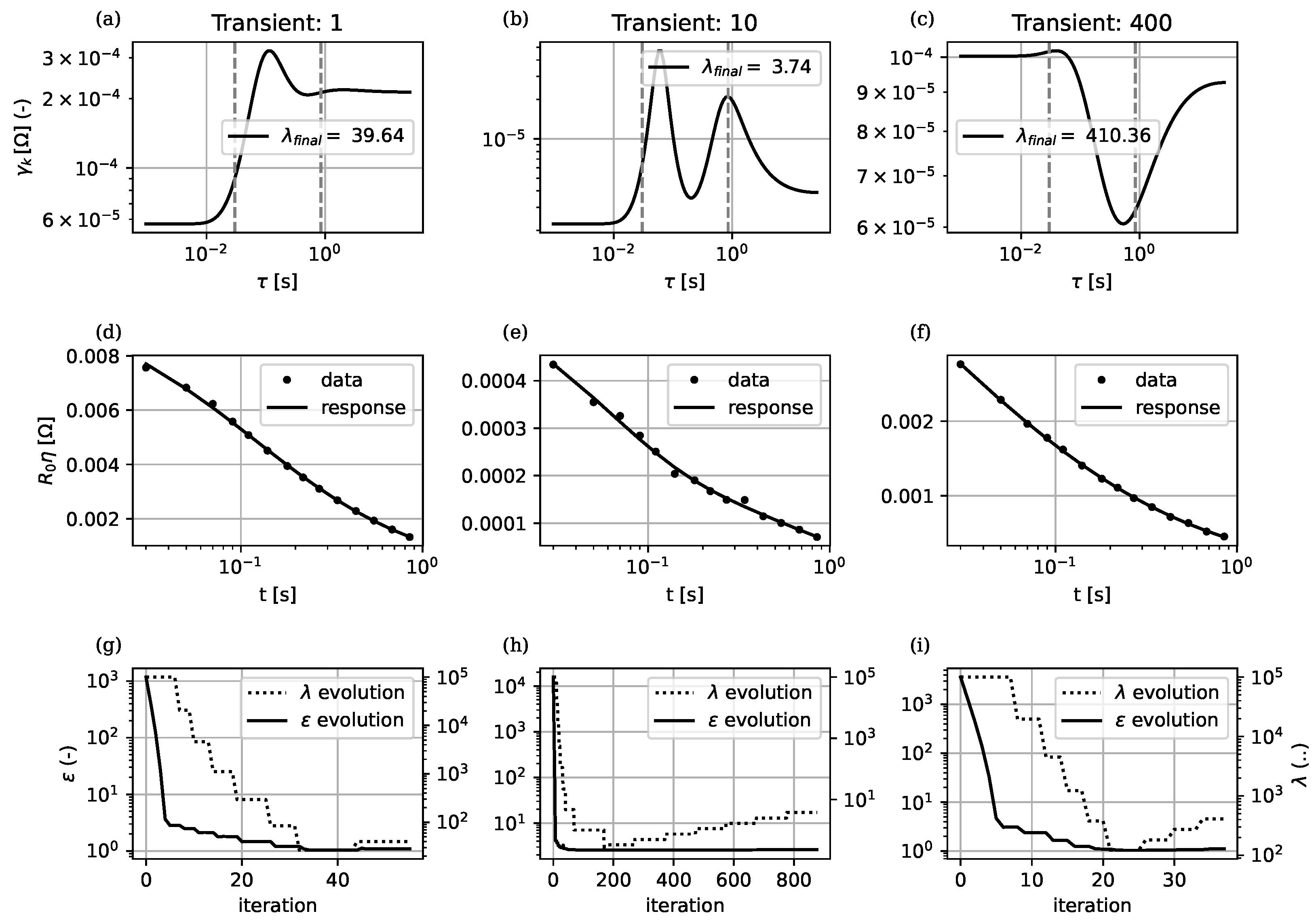
2.3. Formulation of the Inverse Problem
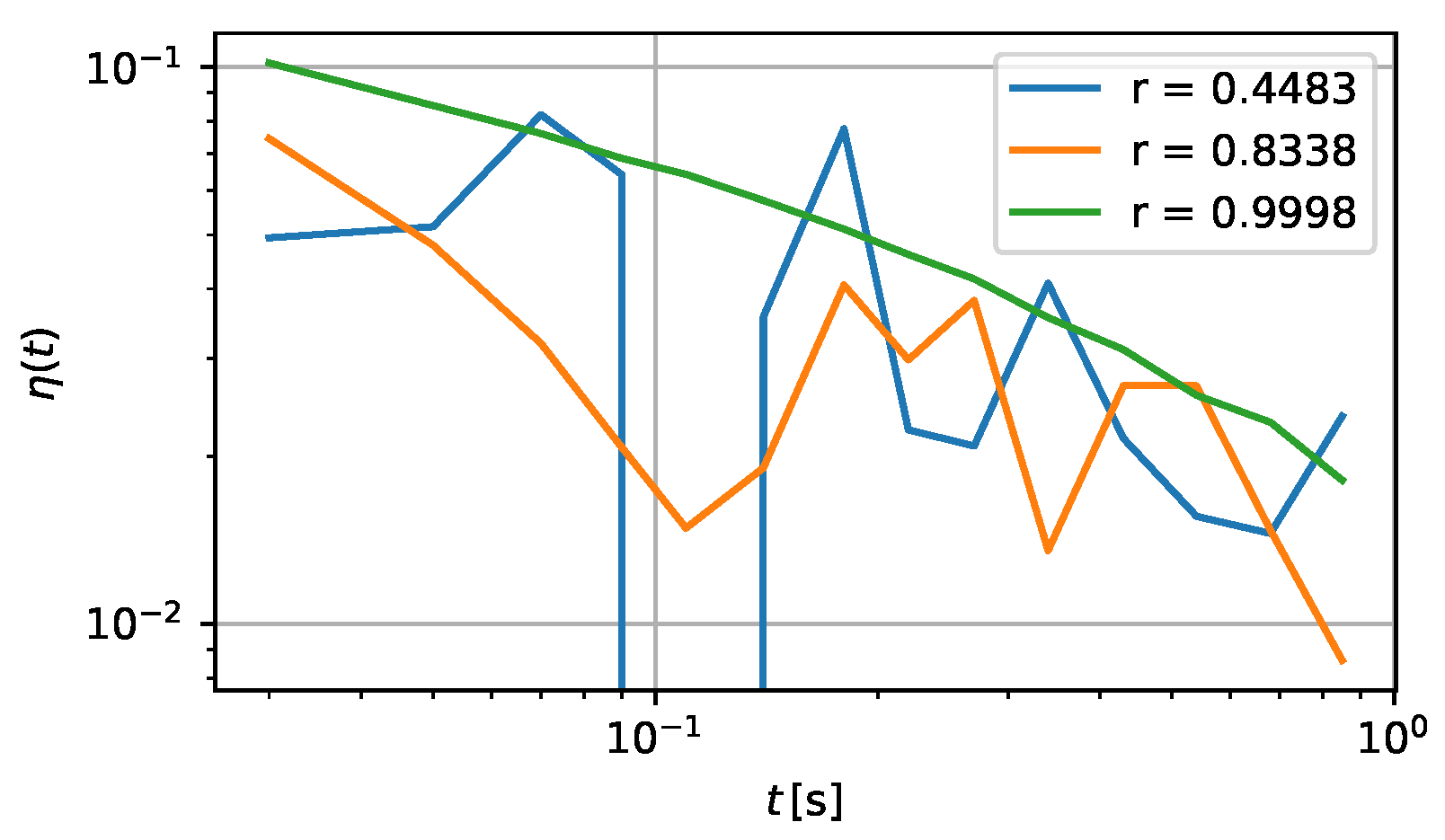
2.4. Adaptation to Common Data-Acquisition Strategies
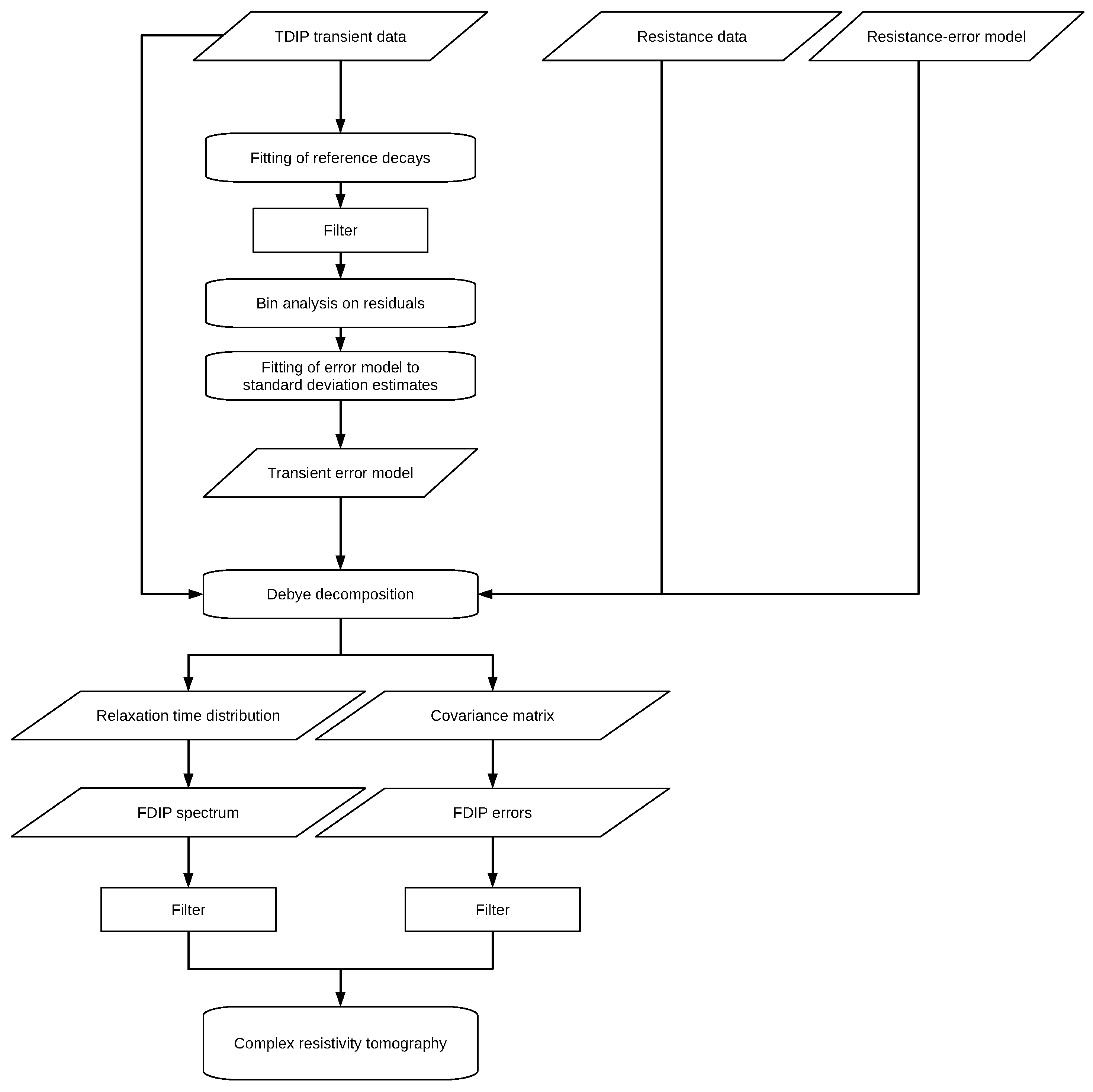
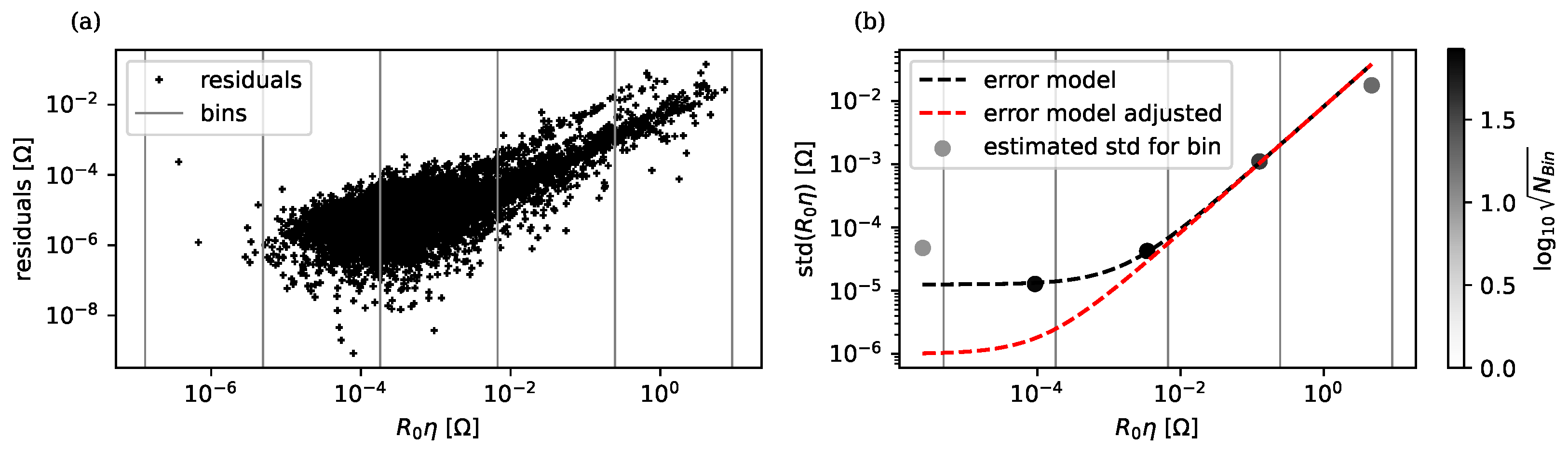
3. Uncertainty Approximation and Propagation
4. Synthetic Validation Study
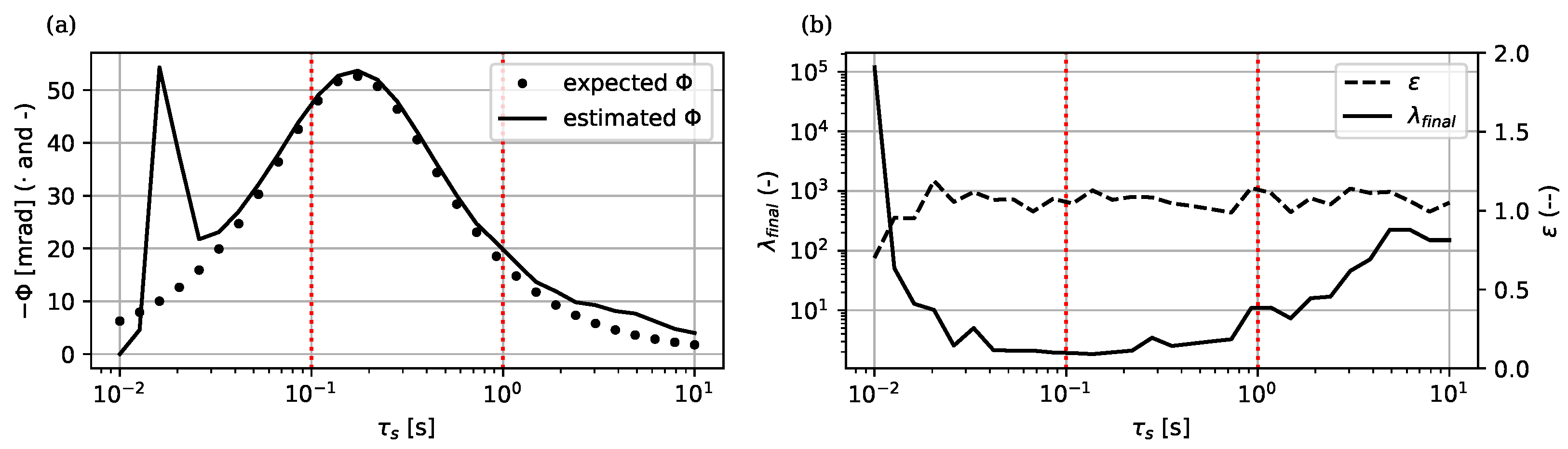
4.1. Accuracy of the TD to FD Conversion
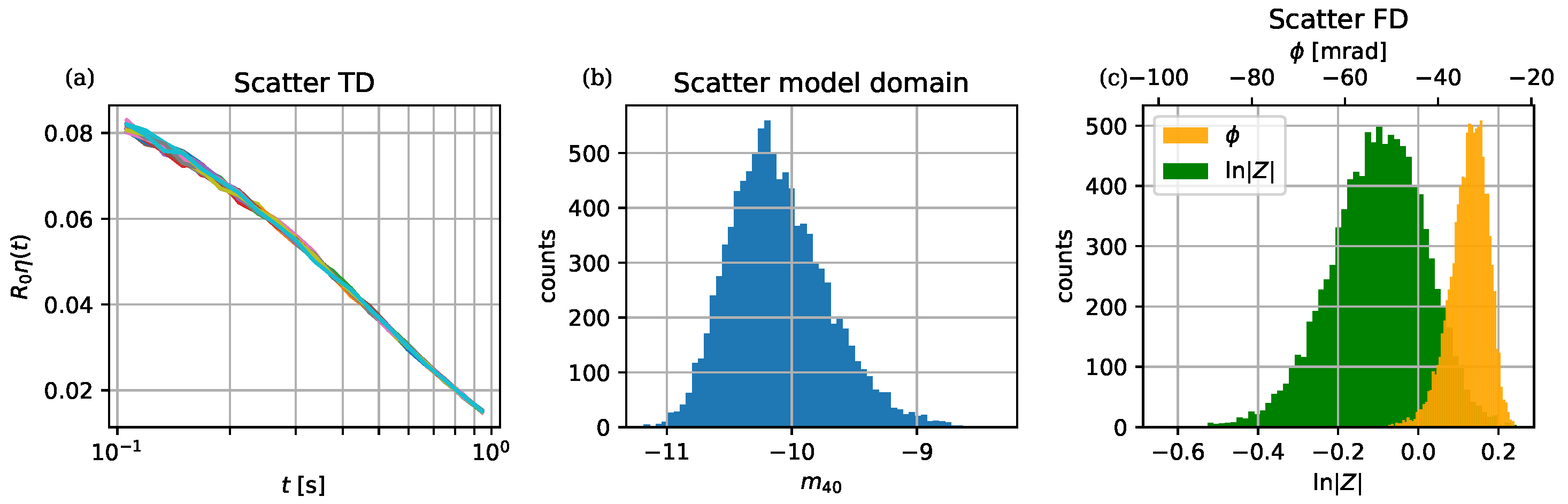
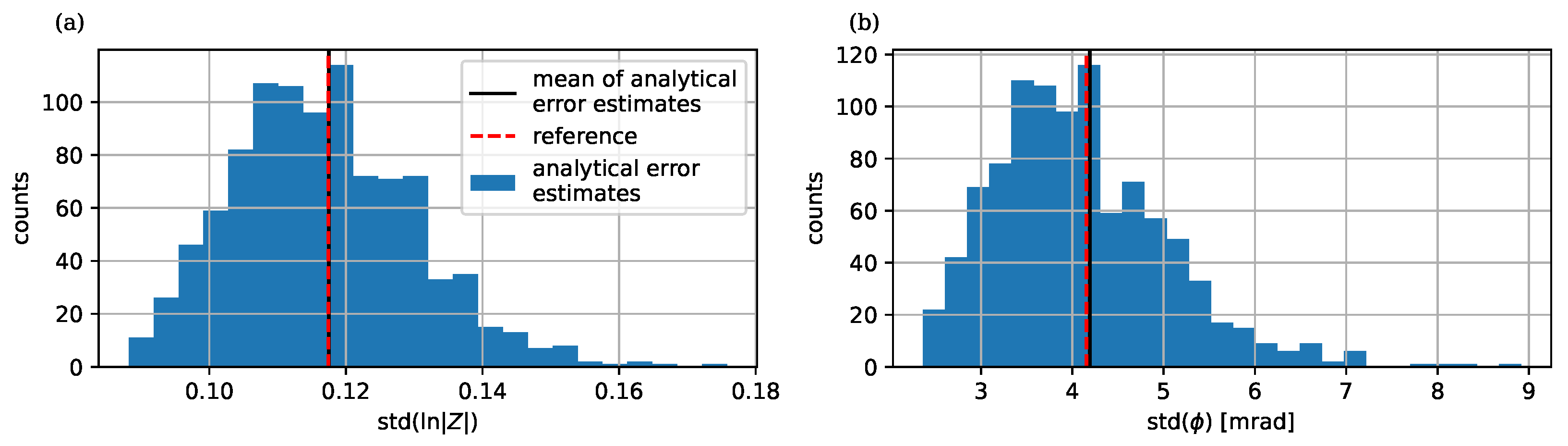
4.2. Validation of Error Propagation
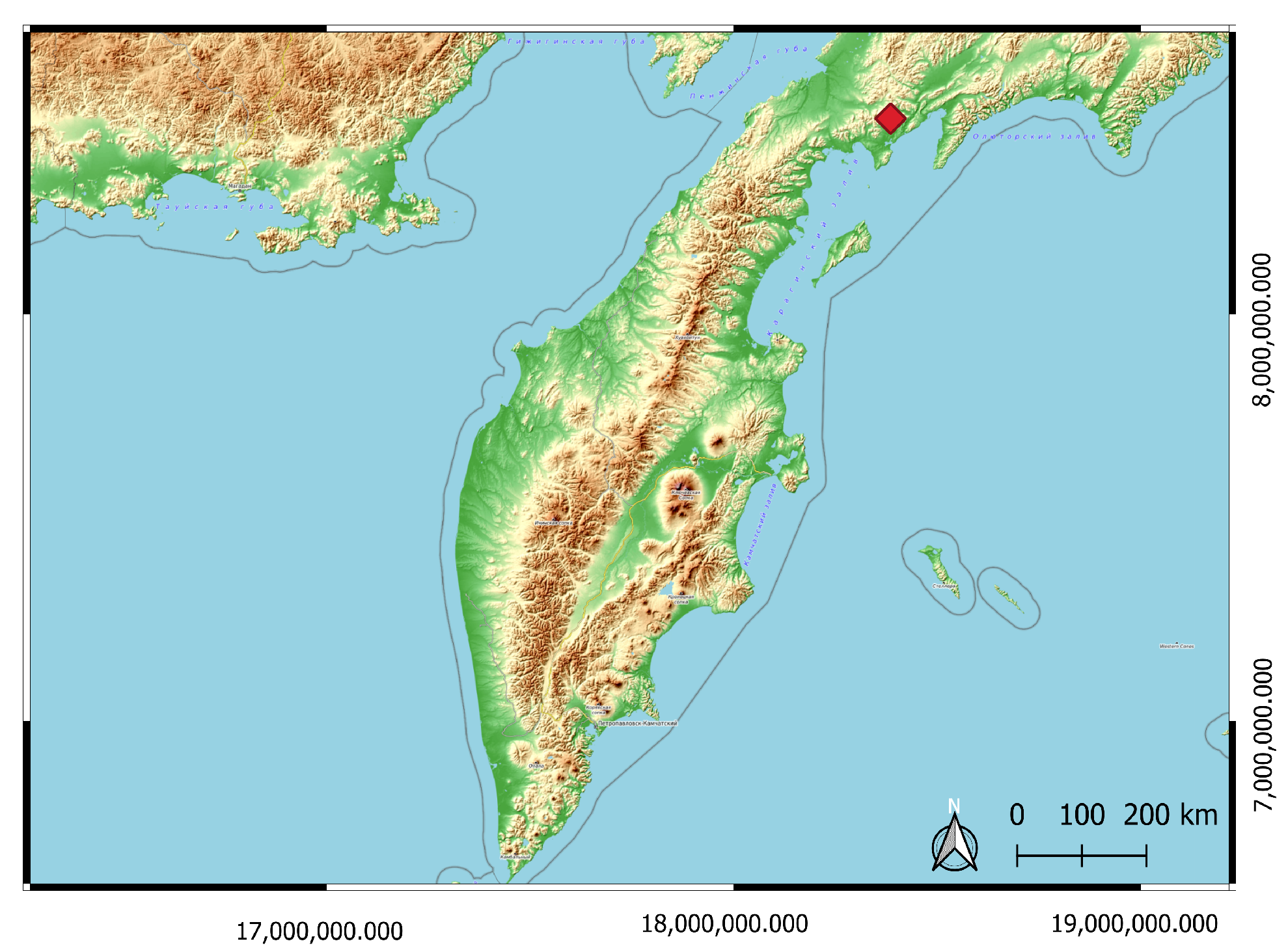
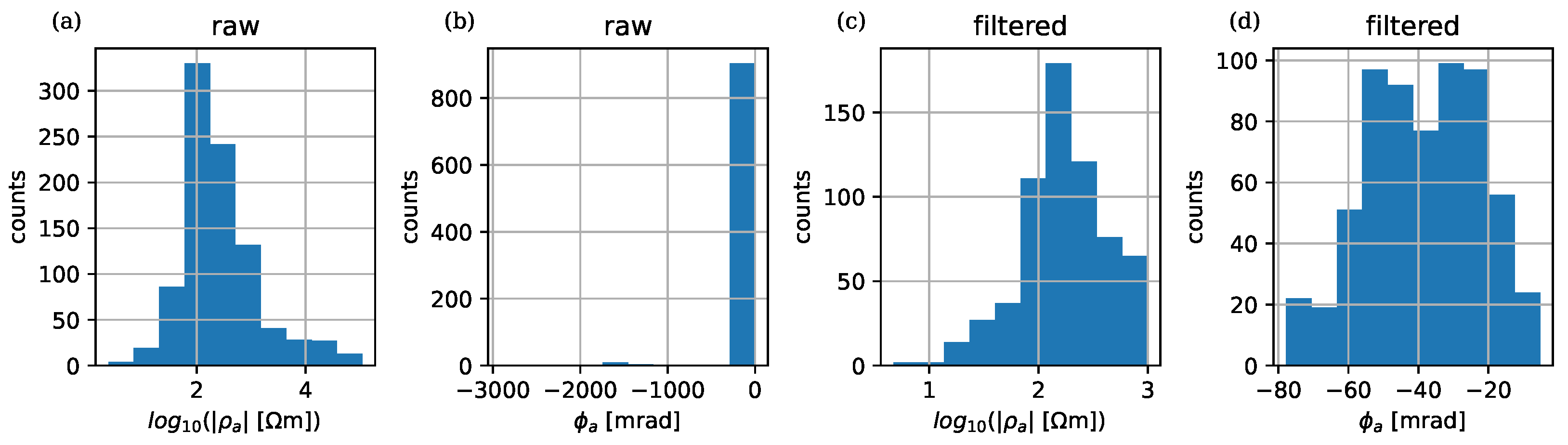
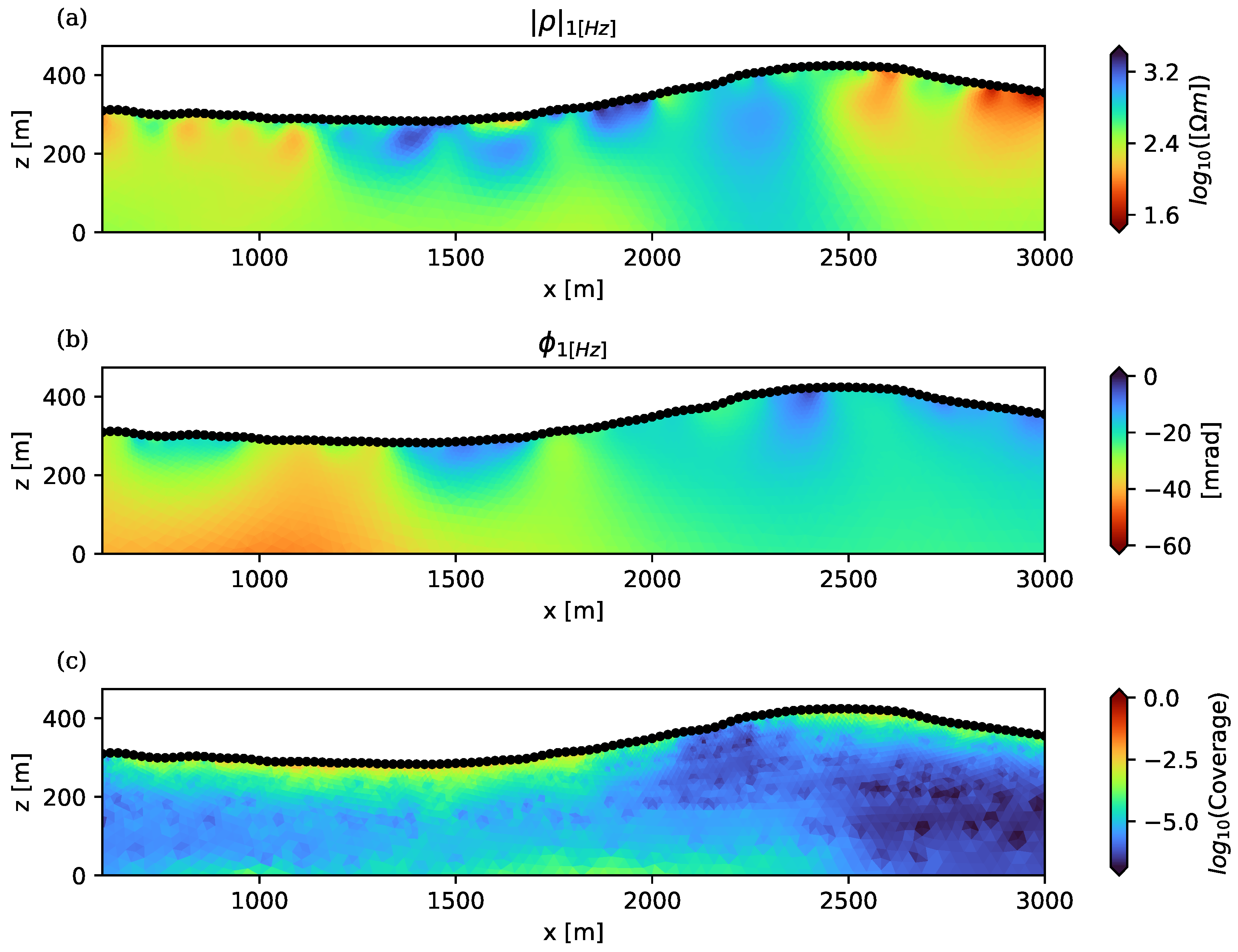
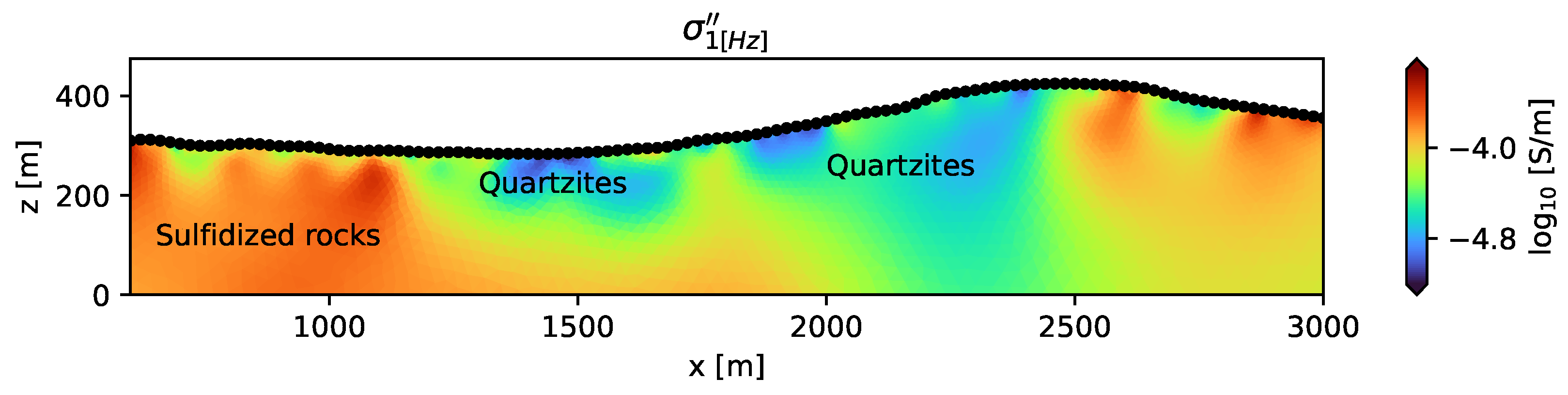
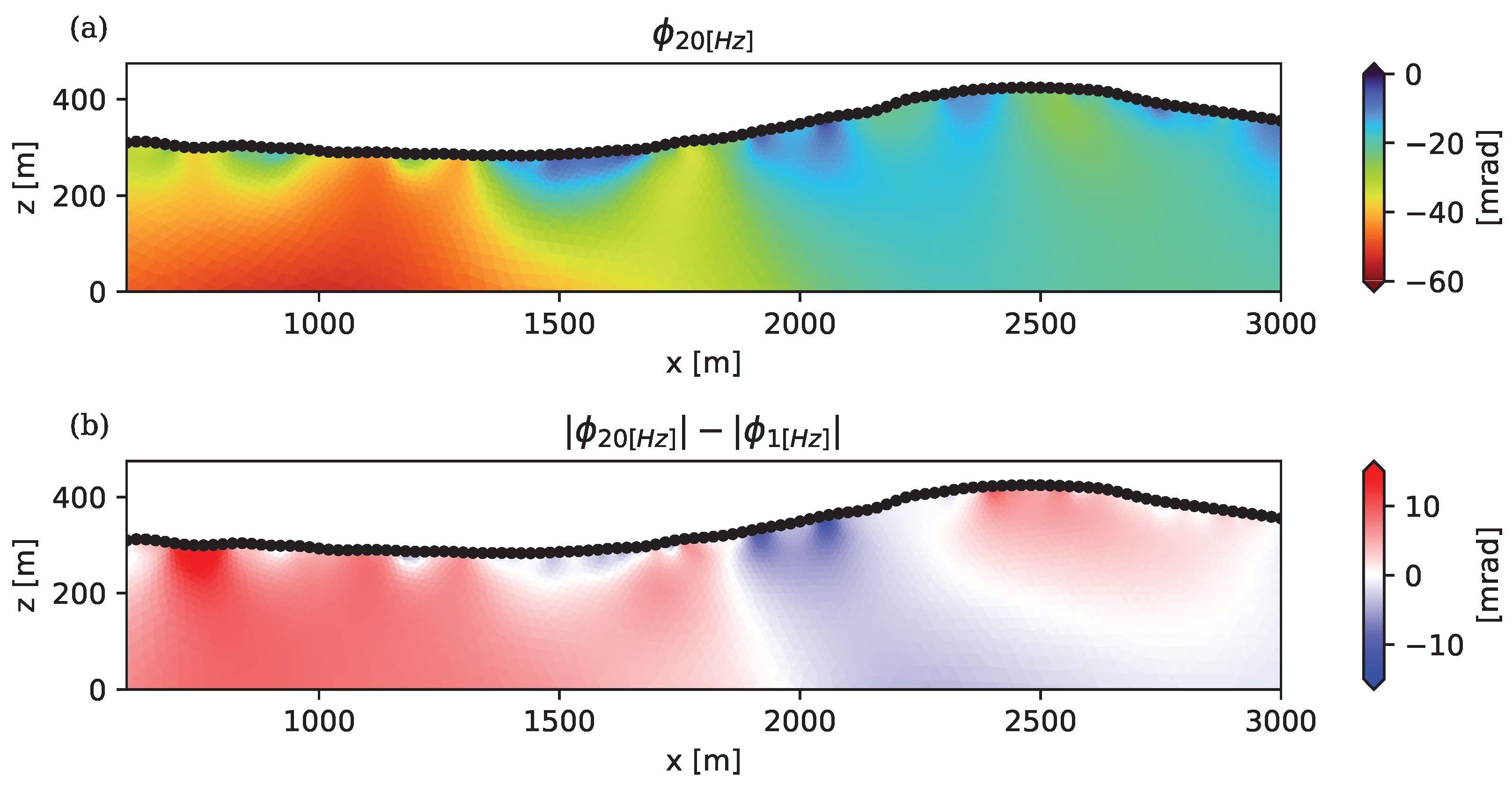
5. Demonstration of the Application to Tomographic Field Measurements
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CPA | constant phase angle |
| DC | direct current |
| DD | Debye decomposition |
| FD | frequency domain |
| HS | high sulfidation |
| IP | induced polarization |
| MAP | maximum a posteriori |
| MOF | Maletoyvaemskoie ore field |
| RMSE | root-mean-square error |
| RTD | relaxation-time distribution |
| TD | time domain |
Appendix A
References
- Bleil, D.F. Induced polarization: A method of geophysical prospecting. Geophysics 1953, 18, 636–661. [Google Scholar] [CrossRef]
- Seigel, H.O. Mathematical formulation and type curves for induced polarization. Geophysics 1959, 24, 547–565. [Google Scholar] [CrossRef]
- Van Voorhis, G.; Nelson, P.; Drake, T. Complex resistivity spectra of porphyry copper mineralization. Geophysics 1973, 38, 49–60. [Google Scholar] [CrossRef]
- Nabighian, M.N.; Elliot, C.L. Negative induced-polarization effects from layered media. Geophysics 1976, 41, 1236–1255. [Google Scholar] [CrossRef]
- Pelton, W.H.; Ward, S.; Hallof, P.; Sill, W.; Nelson, P.H. Mineral discrimination and removal of inductive coupling with multifrequency IP. Geophysics 1978, 43, 588–609. [Google Scholar] [CrossRef]
- Yuval, D.; Oldenburg, W. DC resistivity and IP methods in acid mine drainage problems: Results from the Copper Cliff mine tailings impoundments. J. Appl. Geophys. 1996, 34, 187–198. [Google Scholar] [CrossRef]
- Seigel, H.; Nabighian, M.; Parasnis, D.S.; Vozoff, K. The early history of the induced polarization method. Lead. Edge 2007, 26, 312–321. [Google Scholar] [CrossRef]
- Vanhala, H. Mapping oil-contaminated sand and till with the spectral induced polarization (SIP) method. Geophys. Prospect. 1997, 45, 303–326. [Google Scholar] [CrossRef]
- Binley, A.; Slater, L.D.; Fukes, M.; Cassiani, G. Relationship between spectral induced polarization and hydraulic properties of saturated and unsaturated sandstone. Water Resour. Res. 2005, 41, 1–13. [Google Scholar] [CrossRef]
- Slater, L.; Ntarlagiannis, D.; Wishart, D. On the relationship between induced polarization and surface area in metal-sand and clay-sand mixtures. Geophysics 2006, 71, A1–A5. [Google Scholar] [CrossRef]
- Placencia-Gómez, E.; Slater, L.; Ntarlagiannis, D.; Binley, A. Laboratory SIP signatures associated with oxidation of disseminated metal sulfides. J. Contam. Hydrol. 2013, 148, 25–38. [Google Scholar] [CrossRef]
- Gurin, G.; Tarasov, A.; Ilyin, Y.; Titov, K. Time domain spectral induced polarization of disseminated electronic conductors: Laboratory data analysis through the Debye decomposition approach. J. Appl. Geophys. 2013, 98, 44–53. [Google Scholar] [CrossRef]
- Revil, A.; Florsch, N.; Mao, D. Induced polarization response of porous media with metallic particles—Part 1: A theory for disseminated semiconductors. Geophysics 2015, 80, D525–D538. [Google Scholar] [CrossRef]
- Martin, T.; Weller, A.; Behling, L. Desaturation effects of pyrite–sand mixtures on induced polarization signals. Geophys. J. Int. 2022, 228, 275–290. [Google Scholar] [CrossRef]
- Vinegar, H.; Waxman, M. Induced polarization of shaly sands. Geophysics 1984, 49, 1267–1287. [Google Scholar] [CrossRef]
- Kemna, A.; Binley, A.; Slater, L. Crosshole IP imaging for engineering and environmental applications. Geophysics 2004, 69, 97–107. [Google Scholar] [CrossRef]
- Weller, A.; Slater, L.; Nordsiek, S.; Ntarlagiannis, D. On the estimation of specific surface per unit pore volume from induced polarization: A robust empirical relation fits multiple data sets. Geophysics 2010, 75, WA105–WA112. [Google Scholar] [CrossRef]
- Weller, A.; Slater, L.; Nordsiek, S. On the relationship between induced polarization and surface conductivity: Implications for petrophysical interpretation of electrical measurements. Geophysics 2013, 78, D315. [Google Scholar] [CrossRef]
- Weller, A.; Slater, L.; Huisman, J.A.; Esser, O.; Haegel, F.H. On the specific polarizability of sands and sand-clay mixtures. Geophysics 2015, 80, A57–A61. [Google Scholar] [CrossRef]
- LaBrecque, D.J.; Miletto, M.; Daily, W.; Ramirez, A.; Owen, E. The effects of noise on Occam’s inversion of resistivity tomography data. Geophysics 1996, 61, 538–548. [Google Scholar] [CrossRef]
- Kemna, A.; Binley, A.; Ramirez, A.; Daily, W. Complex resistivity tomography for environmental applications. Chem. Eng. J. 2000, 77, 11–18. [Google Scholar] [CrossRef]
- Kemna, A.; Räkers, E.; Binley, A. Application of complex resistivity tomography to field data from a kerosene-contaminated site. In Proceedings of the 3rd EEGS Meeting, Aarhus, Denmark, 9–11 August 1997; EAGE Publications BV: Houten, The Netherlands, 1997; pp. 151–154. [Google Scholar]
- Binley, A.; Keery, J.; Slater, L.; Barrash, W.; Cardiff, M. The hydrogeologic information in cross-borehole complex conductivity data from an unconsolidated conglomeratic sedimentary aquifer. Geophysics 2016, 81, E409–E421. [Google Scholar] [CrossRef]
- Hönig, M.; Tezkan, B. 1D and 2D Cole-Cole-inversion of time-domain induced-polarization data. Geophys. Prospect. 2007, 55, 117–133. [Google Scholar] [CrossRef]
- Fiandaca, G.; Auken, E.; Christiansen, A.V.; Gazoty, A. Time-domain-induced polarization: Full-decay forward modeling and 1D laterally constrained inversion of Cole-Cole parameters. Geophysics 2012, 77, E213–E225. [Google Scholar] [CrossRef]
- Fiandaca, G.; Ramm, J.; Binley, A.; Gazoty, A.; Christiansen, A.V.; Auken, E. Resolving spectral information from time domain induced polarization data through 2-D inversion. Geophys. J. Int. 2013, 192, 631–646. [Google Scholar] [CrossRef]
- Tezkan, B. 2D Cole Cole Inversion of Time Domain Induced Polarization Data-Model Studies and Field Measurements. In Proceedings of the Near Surface Geoscience 2014-20th European Meeting of Environmental and Engineering Geophysics, Athens, Greece, 14–18 September 2014; EAGE Publications BV: Houten, The Netherlands, 2014; Volume 2014, pp. 1–5. [Google Scholar]
- Revil, A.; Koch, K.; Holliger, K. Is it the grain size or the characteristic pore size that controls the induced polarization relaxation time of clean sands and sandstones? Water Resour. Res. 2012, 48, 1–7. [Google Scholar] [CrossRef]
- Morgan, F.D.; Lesmes, D.P. Inversion for dielectric relaxation spectra. J. Chem. Phys. 1994, 100, 671–681. [Google Scholar] [CrossRef]
- Tong, M.; Li, L.; Wang, W.; Jiang, Y. A time-domain induced-polarization method for estimating permeability in a shaly sand reservoir. Geophys. Prospect. 2006, 54, 623–631. [Google Scholar] [CrossRef]
- Nordsiek, S.; Weller, A. A new approach to fitting induced-polarization spectra. Geophysics 2008, 73, F235–F245. [Google Scholar] [CrossRef]
- Martin, T.; Titov, K.; Tarasov, A.; Weller, A. Spectral induced polarization: Frequency domain versus time domain laboratory data. Geophys. J. Int. 2021, 225, 1982–2000. [Google Scholar] [CrossRef]
- Tong, M.; Li, L.; Wang, W.; Jiang, Y. Determining capillary-pressure curve, pore-size distribution, and permeability from induced polarization of shaley sand. Geophysics 2006, 71, N33–N40. [Google Scholar] [CrossRef]
- Tarasov, A.; Titov, K. Relaxation time distribution from time domain induced polarization measurements. Geophys. J. Int. 2007, 170, 31–43. [Google Scholar] [CrossRef]
- Weigand, M.; Kemna, A. Debye decomposition of time-lapse spectral induced polarisation data. Comput. Geosci. 2016, 86, 34–45. [Google Scholar] [CrossRef]
- Kumar, I.; Kumar, B.V.; Babu, R.V.; Dash, J.K.; Chaturvedi, A.K. Relaxation time distribution approach of mineral discrimination from time domain-induced polarisation data. Explor. Geophys. 2019, 50, 337–350. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; SIAM: Philadelphia, PA, USA, 2005; Volume 89. [Google Scholar]
- Kemna, A. Tomographic Inversion of Complex Resistivity: Theory and Application. Ph.D. Thesis, Ruhr Universität Bochum, Bochum, Germany, 2000. [Google Scholar]
- deGroot Hedlin, C.; Constable, S. Occam’s inversion to generate smooth, two-dimensional models from magnetotelluric data. Geophysics 1990, 55, 1613–1624. [Google Scholar] [CrossRef]
- Gubbins, D. Time Series Analysis and Inverse Theory for Geophysicists; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Volchkov, A.; Zvezdov, V. The nature of Cu-As mineralization occurrences in the Maletoyvayamsky stratovolcano. RUDY I METALLY 1997, 44–51. [Google Scholar]
- Tolstykh, N.; Vymazalová, A.; Tuhỳ, M.; Shapovalova, M. Conditions of formation of Au–Se–Te mineralization in the Gaching ore occurrence (Maletoyvayam ore field), Kamchatka, Russia. Mineral. Mag. 2018, 82, 649–674. [Google Scholar] [CrossRef]
- Gurin, G. Geophysical prospecting for epithermal gold deposits (a case study from the Maletoivayam gold ore field, Kamchatka Peninsula). Lithosphere 2021, 21, 116–132. [Google Scholar] [CrossRef]
- Gurin, G.; Tarasov, A.; Titov, K. Analysis of Transient Characteristics of Induced Polarization in Innovative Mineral Exploration Solutions (from Case Studies of Gold Deposits). Russ. Geol. Geophys. 2023, 64, 348–356. [Google Scholar] [CrossRef]
- OpenStreetMap Contributors. Planet Dump. 2017. Available online: https://www.openstreetmap.org (accessed on 13 July 2023).
- Flores Orozco, A.; Gallistl, J.; Bücker, M.; Williams, K.H. Decay curve analysis for data error quantification in time-domain induced polarization imaging. Geophysics 2018, 83, E75–E86. [Google Scholar] [CrossRef]
- Koestel, J.; Kemna, A.; Javaux, M.; Binley, A.; Vereecken, H. Quantitative imaging of solute transport in an unsaturated and undisturbed soil monolith with 3-D ERT and TDR. Water Resour. Res. 2008, 44, 1–17. [Google Scholar] [CrossRef]
- Flores Orozco, A.; Kemna, A.; Zimmermann, E. Data error quantification in spectral induced polarization imaging. Geophysics 2012, 77, E227–E237. [Google Scholar] [CrossRef]
- Marshall, D.J.; Madden, T.R. Induced polarization, a study of its causes. Geophysics 1959, 24, 790–816. [Google Scholar] [CrossRef]
- Hallof, P.G. A comparison of the various parameters employed in the variable-frequency induced-polarization method. Geophysics 1964, 29, 425–433. [Google Scholar] [CrossRef]
- Wong, J. An electrochemical model of the induced-polarization phenomenon in disseminated sulfide ores. Geophysics 1979, 44, 1245–1265. [Google Scholar] [CrossRef]
- Revil, A.; Vaudelet, P.; Su, Z.; Chen, R. Induced polarization as a tool to assess mineral deposits: A review. Minerals 2022, 12, 571. [Google Scholar] [CrossRef]
- Dahlin, T.; Loke, M.H. Negative apparent chargeability in time-domain induced polarisation data. J. Appl. Geophys. 2015, 123, 322–332. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hase, J.; Gurin, G.; Titov, K.; Kemna, A. Conversion of Induced Polarization Data and Their Uncertainty from Time Domain to Frequency Domain Using Debye Decomposition. Minerals 2023, 13, 955. https://doi.org/10.3390/min13070955
Hase J, Gurin G, Titov K, Kemna A. Conversion of Induced Polarization Data and Their Uncertainty from Time Domain to Frequency Domain Using Debye Decomposition. Minerals. 2023; 13(7):955. https://doi.org/10.3390/min13070955
Chicago/Turabian StyleHase, Joost, Grigory Gurin, Konstantin Titov, and Andreas Kemna. 2023. "Conversion of Induced Polarization Data and Their Uncertainty from Time Domain to Frequency Domain Using Debye Decomposition" Minerals 13, no. 7: 955. https://doi.org/10.3390/min13070955
APA StyleHase, J., Gurin, G., Titov, K., & Kemna, A. (2023). Conversion of Induced Polarization Data and Their Uncertainty from Time Domain to Frequency Domain Using Debye Decomposition. Minerals, 13(7), 955. https://doi.org/10.3390/min13070955








