Three-Dimensional Inversion of Long-Offset Transient Electromagnetic Method over Topography
Abstract
1. Introduction
2. Methods
2.1. Forward Modeling
2.2. Inverse Problem
3. Synthetic Examples
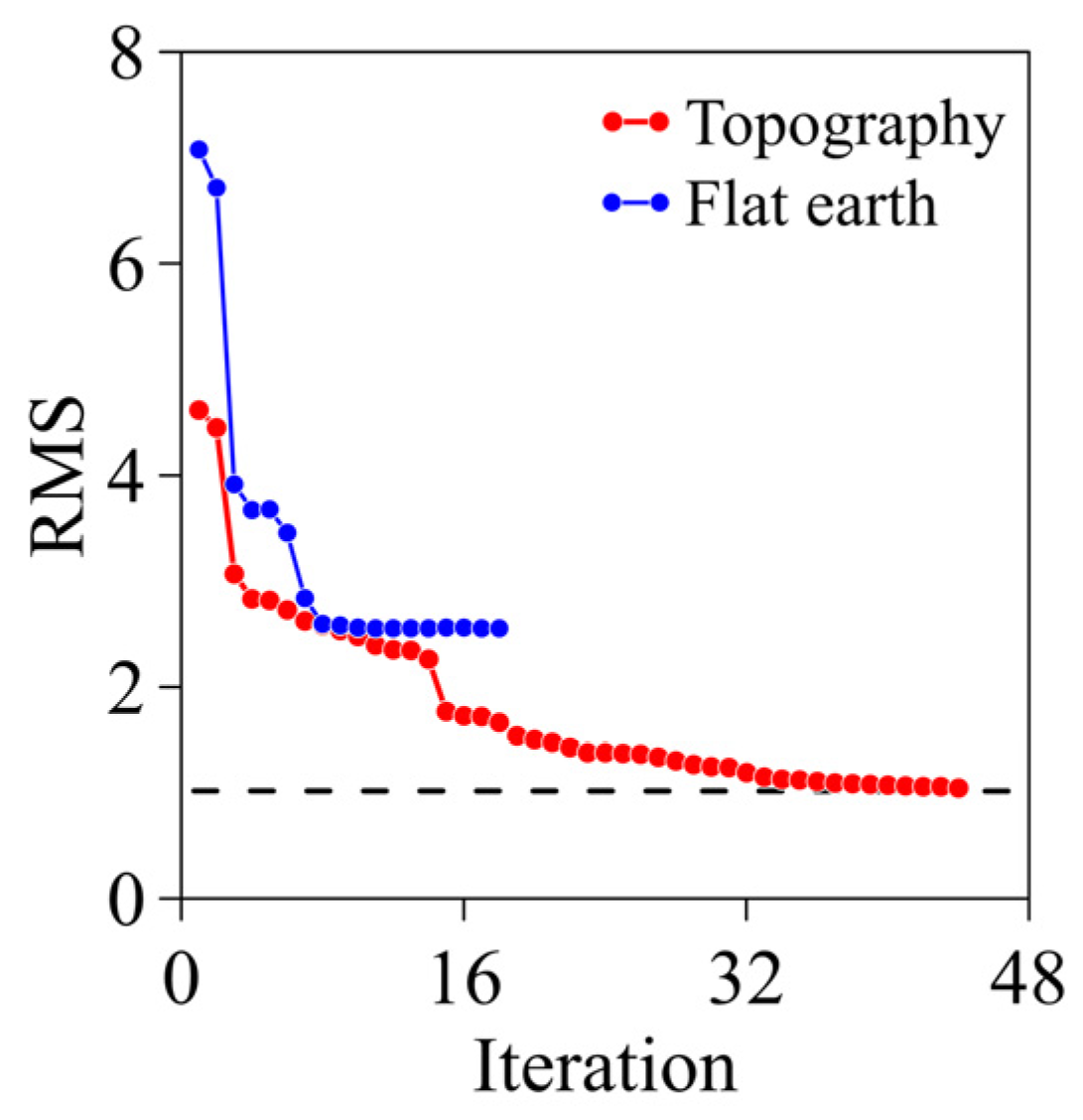
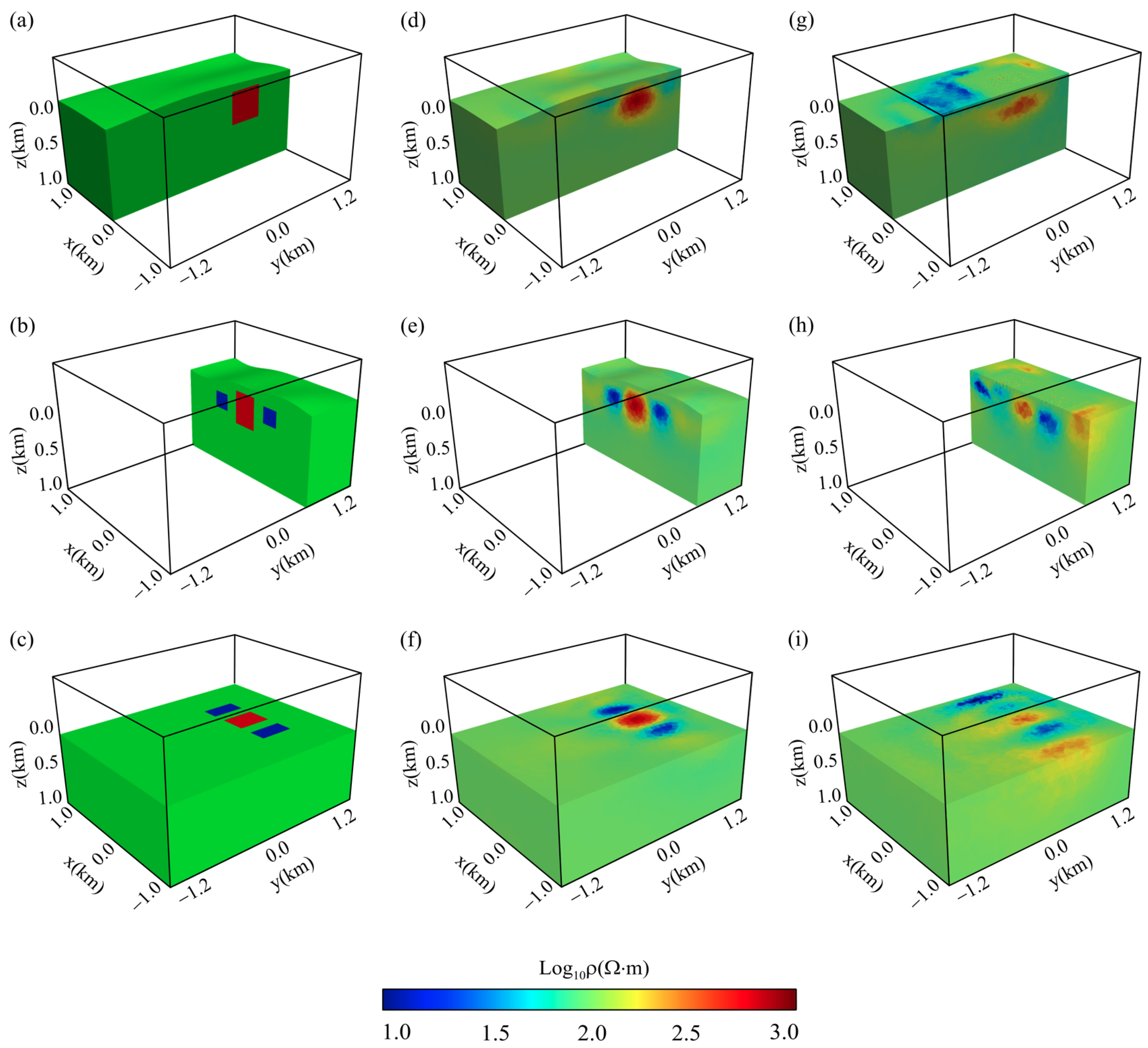
3.1. Flat Earth Model
3.2. Synthetic Model with Topography
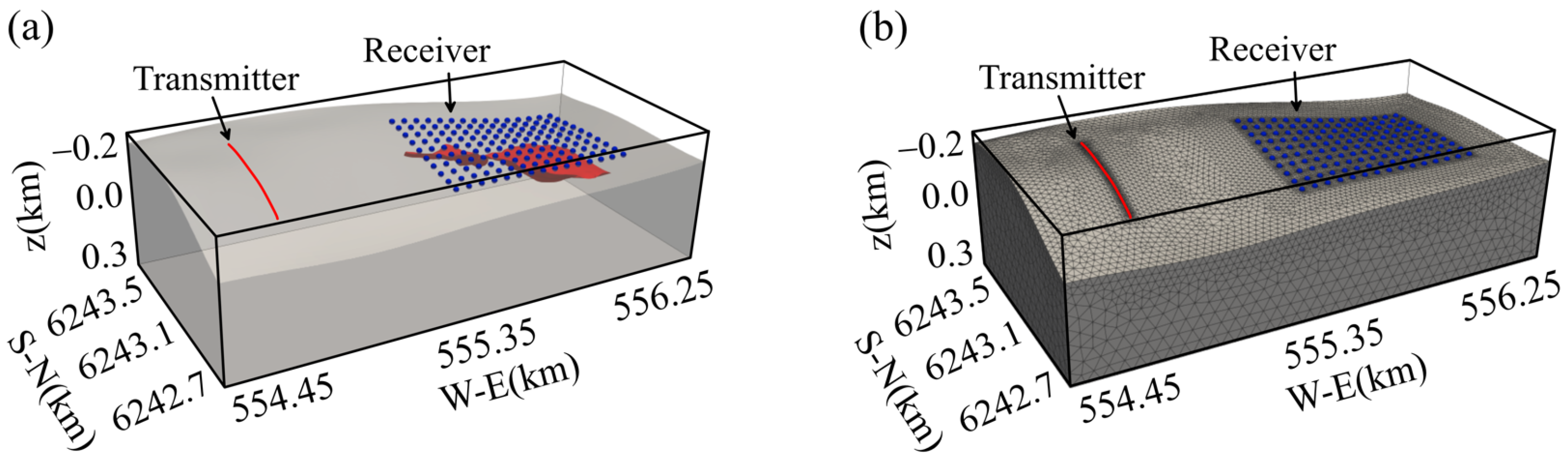
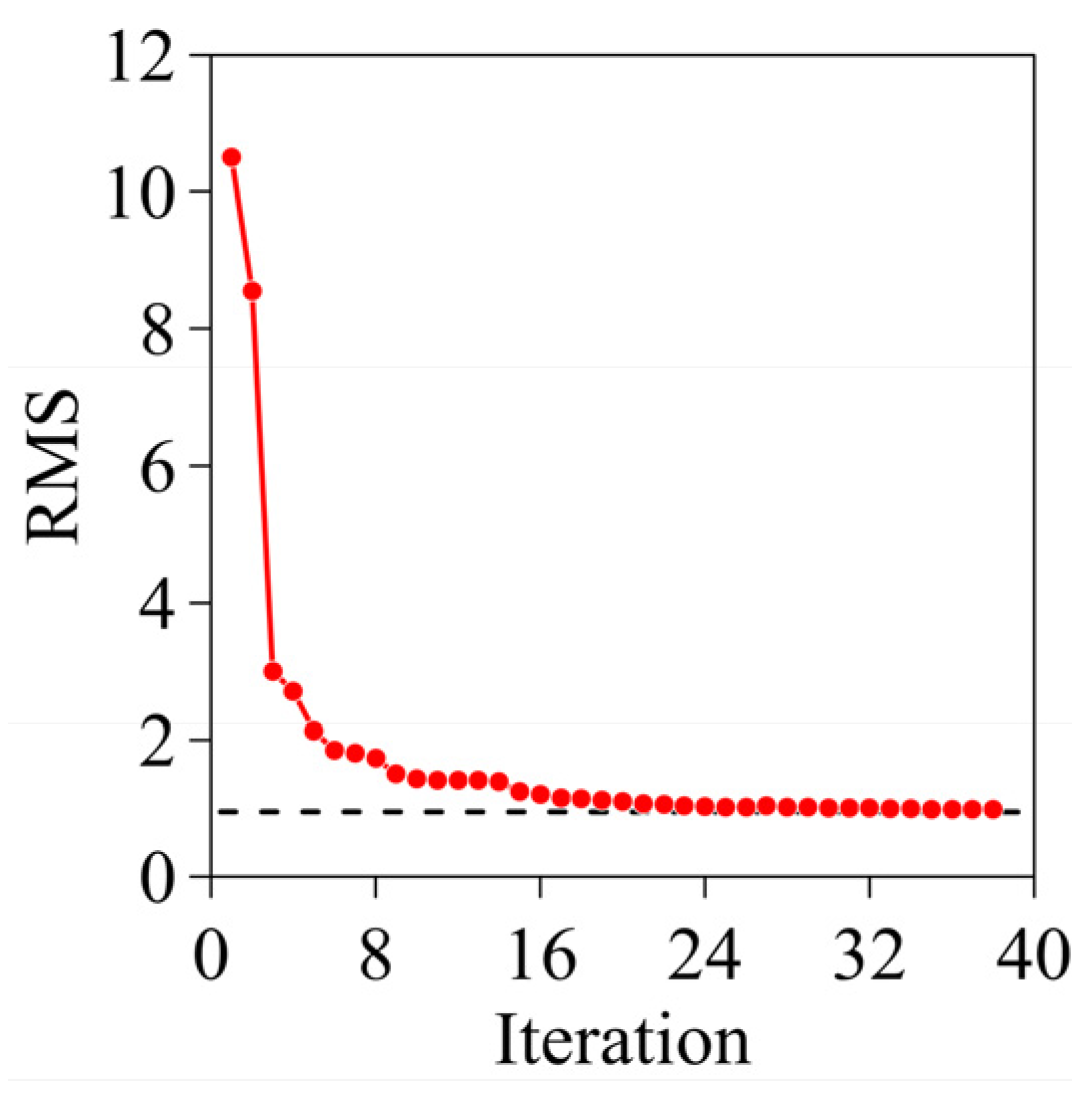
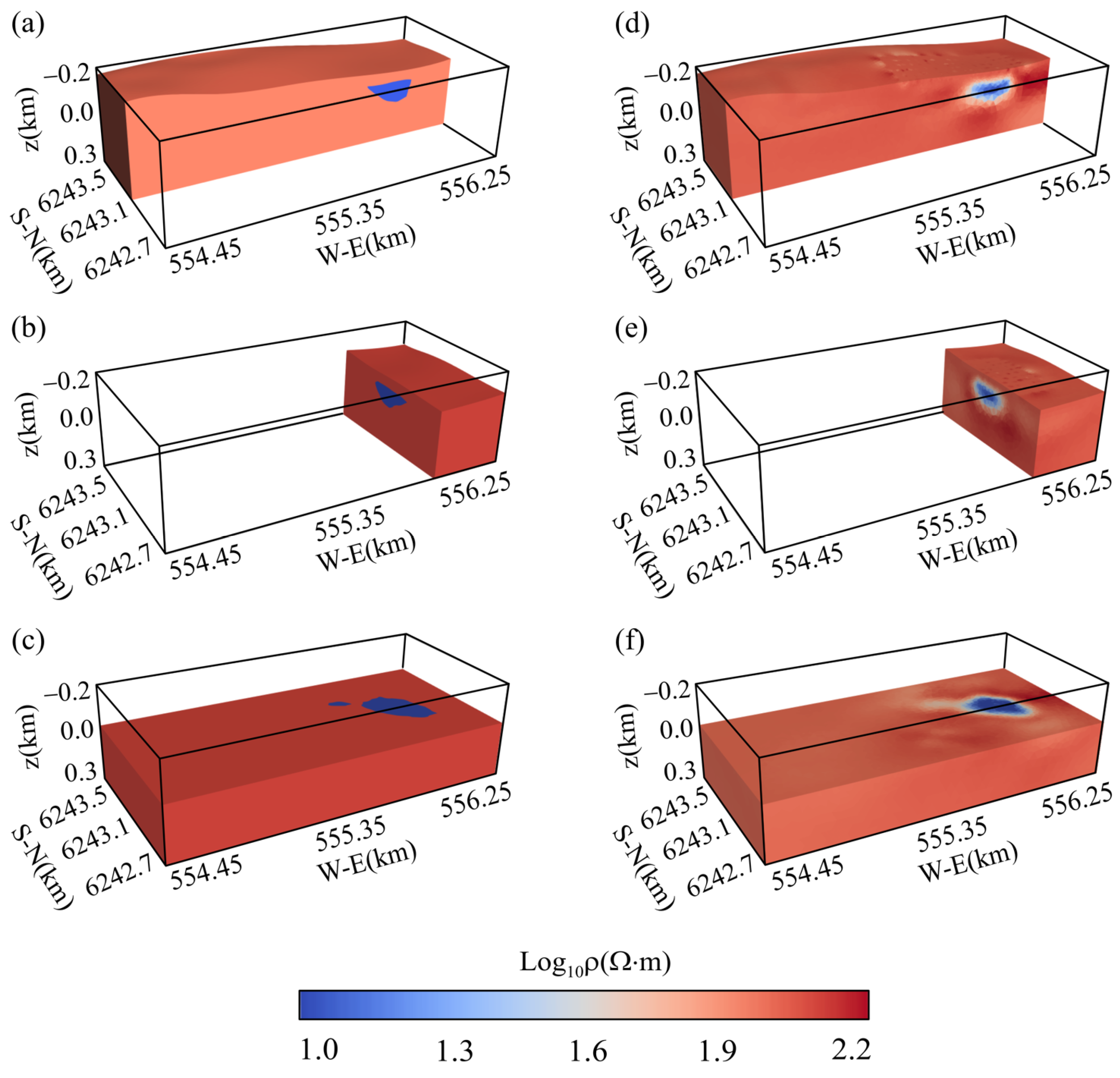
4. Application to a Realistic Mineral Deposit Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Strack, K.M. Exploration with Deep Transient Electromagnetics; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Commer, M.; Helwig, S.L.; Hördt, A.; Scholl, C.; Tezkan, B. New results on the resistivity structure of Merapi Volcano (Indonesia), derived from three-dimensional restricted inversion of long-offset transient electromagnetic data. Geophys. J. Int. 2006, 167, 1172–1187. [Google Scholar] [CrossRef]
- Vozoff, K.; Moss, D.; LeBrocq, K.; McAllister, K. LOTEM electric field measurements for mapping resistive horizons in petroleum exploration. Explor. Geophys. 1985, 16, 309–312. [Google Scholar] [CrossRef]
- Xie, X.; Lei, Z.; Yan, L.; Hu, W. Remaining oil detection with time-lapse long offset & window transient electromagnetic sounding. Oil Geophys. Prospect. 2016, 51, 605–612. [Google Scholar]
- Yan, L.J.; Chen, X.X.; Tang, H.; Xie, X.B.; Zhou, L.; Hu, W.B.; Wang, Z.X. Continuous TDEM for monitoring shale hydraulic fracturing. Appl. Geophys. 2018, 15, 26–34. [Google Scholar] [CrossRef]
- Keller, G.V.; Pritchard, J.I.; Jacobson, J.J.; Harthill, N. Megasource time-domain electromagnetic sounding methods. Geophysics 1984, 49, 993–1009. [Google Scholar] [CrossRef]
- Stephan, A.; Schniggenfittig, H.; Strack, K.M. Long-offset transient em sounding north of the rhine-ruhr coal district, germany1. Geophys. Prospect. 1991, 39, 505–525. [Google Scholar] [CrossRef]
- Müller, M.; Hördt, A.; Neubauer, F. Internal structure of Mount Merapi, Indonesia, derived from long-offset transient electromagnetic data. J. Geophys. Res. Solid Earth 2002, 107, ECV 2-1–ECV 2-14. [Google Scholar] [CrossRef]
- Haroon, A.; Adrian, J.; Bergers, R.; Gurk, M.; Tezkan, B.; Mammadov, A.; Novruzov, A. Joint inversion of long-offset and central-loop transient electromagnetic data: Application to a mud volcano exploration in Perekishkul, Azerbaijan. Geophys. Prospect. 2015, 63, 478–494. [Google Scholar] [CrossRef]
- Zhou, N.N.; Xue, G.Q.; Li, H.; Lei, K.X.; Chen, W.Y. Comparison of transient electromagnetic fields excited by single-and double-line grounded-wire sources on land. Geophys. J. Int. 2022, 229, 1856–1869. [Google Scholar] [CrossRef]
- Zhou, N.N.; Xue, G.Q.; Li, H.; Chen, W.Y.; Lei, K.X. Electromagnetic characteristics of the magmatic Ni-Cu sulfide deposits in the orogenic belt: A case study from Kalatongke deposits in the Central Asian orogenic belt. Econ. Geol. 2022, 117, 1779–1789. [Google Scholar] [CrossRef]
- Strack, K.; Lüschen, E.; Kötz, A. Long-offset transient electromagnetic (LOTEM) depth soundings applied to crustal studies in the Black Forest and Swabian Alb, Federal Republic of Germany. Geophysics 1990, 55, 834–842. [Google Scholar] [CrossRef]
- Hördt, A.; Druskin, V.L.; Knizhnerman, L.A.; Strack, K.M. Interpretation of 3-D effects in long-offset transient electromagnetic (LOTEM) soundings in the Münsterland area/Germany. Geophysics 1992, 57, 1127–1137. [Google Scholar] [CrossRef]
- Hördt, A.; Jödicke, H.; Strack, K.M.; Vozoff, K.; Wolfgram, P. Inversion of long-offset TEM soundings near the borehole Münsterland 1, Germany, and comparison with MT measurements. Geophys. J. Int. 1992, 108, 930–940. [Google Scholar] [CrossRef]
- Di, Q.Y.; Fang, G.Y.; Zhang, Y.M. Research of the surface electromagnetic prospecting (SEP) system. Chin. J. Geophys. 2013, 56, 3629–3639. [Google Scholar]
- Lü, Q.; Zhang, X.; Tang, J.; Jin, S.; Liang, L.; Niu, J.; Wang, X.; Lin, P.; Yao, C.; Gao, W. Review on advancement in technology and equipment of geophysical exploration for metallic deposits in China. Chin. J. Geophys. 2019, 62, 3629–3664. [Google Scholar]
- Stolz, R.; Schiffler, M.; Becken, M.; Thiede, A.; Schneider, M.; Chubak, G.; Marsden, P.; Bergshjorth, A.B.; Schaefer, M.; Terblanche, O. SQUIDs for magnetic and electromagnetic methods in mineral exploration. Miner. Econ. 2022, 35, 467–494. [Google Scholar] [CrossRef]
- Hördt, A.; Müller, M. Understanding LOTEM data from mountainous terrain. Geophysics 2000, 65, 1113–1123. [Google Scholar] [CrossRef]
- Wang, T.; Hohmann, G.W. A finite-difference, time-domain solution for three-dimensional electromagnetic modeling. Geophysics 1993, 58, 797–809. [Google Scholar] [CrossRef]
- Haber, E.; Oldenburg, D.W.; Shekhtman, R. Inversion of time domain three-dimensional electromagnetic data. Geophys. J. Int. 2007, 171, 550–564. [Google Scholar] [CrossRef]
- Oldenburg, D.W.; Haber, E.; Shekhtman, R. Three dimensional inversion of multisource time domain electromagnetic data. Geophysics 2013, 78, E47–E57. [Google Scholar] [CrossRef]
- Yang, D.; Oldenburg, D.W.; Haber, E. 3-D inversion of airborne electromagnetic data parallelized and accelerated by local mesh and adaptive soundings. Geophys. J. Int. 2014, 196, 1492–1507. [Google Scholar] [CrossRef]
- Cai, H.; Liu, M.; Zhou, J.; Li, J.; Hu, X. Effective 3D-transient electromagnetic inversion using finite-element method with a parallel direct solver. Geophysics 2022, 87, E377–E392. [Google Scholar] [CrossRef]
- Commer, M.; Newman, G. A parallel finite-difference approach for 3D transient electromagnetic modeling with galvanic sources. Geophysics 2004, 69, 1192–1202. [Google Scholar] [CrossRef]
- Tang, X.G.; Hu, W.B.; Yan, L.J. Topographic effects on long offset transient electromagnetic response. Appl. Geophys. 2011, 8, 277–284. [Google Scholar] [CrossRef]
- Liu, Y.; Yogeshwar, P.; Hu, X.; Peng, R.; Tezkan, B.; Mörbe, W.; Li, J. Effects of electrical anisotropy on long-offset transient electromagnetic data. Geophys. J. Int. 2020, 222, 1074–1089. [Google Scholar] [CrossRef]
- Li, J.; Hu, X.; Cai, H.; Liu, Y. A finite-element time-domain forward-modelling algorithm for transient electromagnetics excited by grounded-wire sources. Geophys. Prospect. 2020, 68, 1379–1398. [Google Scholar] [CrossRef]
- Khan, M.Y.; Xue, G.Q.; Chen, W.Y.; Zhong, H.S. Analysis of long-offset transient electromagnetic (LOTEM) data in time, frequency, and pseudo-seismic domain. J. Environ. Eng. Geophys. 2018, 23, 15–32. [Google Scholar] [CrossRef]
- Carter, S.; Xie, X.; Zhou, L.; Yan, L. Hybrid Monte Carlo 1-D joint inversion of LOTEM and MT. J. Appl. Geophys. 2021, 194, 104424. [Google Scholar] [CrossRef]
- Scholl, C. The Influence of Multidimensional Structures on the Interpretation of Lotem Data with One-Dimensional Models and the Application to Data from Israel. Ph.D. Thesis, Universität Zu Köln, Cologne, Germany, 2005. [Google Scholar]
- Sudha, K.; Tezkan, B.; Israil, M.; Rai, J. Combined electrical and electromagnetic imaging of hot fluids within fractured rock in rugged Himalayan terrain. J. Appl. Geophys. 2011, 74, 205–214. [Google Scholar] [CrossRef]
- Cai, J.; Yogeshwar, P.; Mörbe, W.; Smirnova, M.; Haroon, A.; Becken, M.; Tezkan, B. 2-D joint inversion of semi-airborne CSEM and LOTEM data in eastern Thuringia, Germany. Geophys. J. Int. 2022, 229, 1475–1489. [Google Scholar] [CrossRef]
- Mitsuhata, Y.; Uchida, T.; Amano, H. 2.5-D inversion of frequency-domain electromagnetic data generated by a grounded-wire source. Geophysics 2002, 67, 1753–1768. [Google Scholar] [CrossRef]
- Sasaki, Y.; Yi, M.J.; Choi, J.; Son, J.S. Frequency and time domain three-dimensional inversion of electromagnetic data for a grounded-wire source. J. Appl. Geophys. 2015, 112, 106–114. [Google Scholar] [CrossRef]
- Revil, A.; Woodruff, W.; Torres-Verdín, C.; Prasad, M. Complex conductivity tensor of anisotropic hydrocarbon-bearing shales and mudrocks. Geophysics 2013, 78, D403–D418. [Google Scholar] [CrossRef]
- Woodruff, W.F.; Revil, A.; Torres-Verdín, C. Laboratory determination of the complex conductivity tensor of unconventional anisotropic shales. Geophysics 2014, 79, E183–E200. [Google Scholar] [CrossRef]
- Cai, H.; Hu, X.; Xiong, B.; Zhdanov, M.S. Finite-element time-domain modeling of electromagnetic data in general dispersive medium using adaptive Padé series. Comput. Geosci. 2017, 109, 194–205. [Google Scholar] [CrossRef]
- Jahandari, H.; Farquharson, C.G. A finite-volume solution to the geophysical electromagnetic forward problem using unstructured grids. Geophysics 2014, 79, E287–E302. [Google Scholar] [CrossRef]
- Um, E.S.; Harris, J.M.; Alumbaugh, D.L. 3D time-domain simulation of electromagnetic diffusion phenomena: A finite-element electric-field approach. Geophysics 2010, 75, F115–F126. [Google Scholar] [CrossRef]
- Jin, J.M. The Finite Element Method in Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Liu, Y.; Yin, C.; Qiu, C.; Hui, Z.; Zhang, B.; Ren, X.; Weng, A. 3-D inversion of transient EM data with topography using unstructured tetrahedral grids. Geophys. J. Int. 2019, 217, 301–318. [Google Scholar] [CrossRef]
- Bollhöfer, M.; Eftekhari, A.; Scheidegger, S.; Schenk, O. Large-scale sparse inverse covariance matrix estimation. SIAM J. Sci. Comput. 2019, 41, A380–A401. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Arsenin, V.Y. Soulutions of Ill-Posed Problems. SIAM Rev. 1977, 21, 266. [Google Scholar]
- Cao, X.Y.; Yin, C.C.; Zhang, B.; Huang, X.; Liu, Y.H.; Cai, J. 3D magnetotelluric inversions with unstructured finite-element and limited-memory quasi-Newton methods. Appl. Geophys. 2018, 15, 556–565. [Google Scholar] [CrossRef]
- Key, K. MARE2DEM: A 2-D inversion code for controlled-source electromagnetic and magnetotelluric data. Geophys. J. Int. 2016, 207, 571–588. [Google Scholar] [CrossRef]
- Commer, M.; Newman, G.A. New advances in three-dimensional controlled-source electromagnetic inversion. Geophys. J. Int. 2008, 172, 513–535. [Google Scholar] [CrossRef]
- Balch, S.; Crebs, T.; King, A.; Verbiski, M. Geophysics of the Voisey’s Bay Ni-Cu-Co deposits. In SEG Technical Program Expanded Abstracts 1998; Society of Exploration Geophysicists: Houston, TX, USA, 1998; pp. 784–787. [Google Scholar]
- Li, J.; Lu, X.; Farquharson, C.G.; Hu, X. A finite-element time-domain forward solver for electromagnetic methods with complex-shaped loop sources. Geophysics 2018, 83, E117–E132. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Cai, H.; Liu, L.; Revil, A.; Hu, X. Three-Dimensional Inversion of Long-Offset Transient Electromagnetic Method over Topography. Minerals 2023, 13, 908. https://doi.org/10.3390/min13070908
Wang X, Cai H, Liu L, Revil A, Hu X. Three-Dimensional Inversion of Long-Offset Transient Electromagnetic Method over Topography. Minerals. 2023; 13(7):908. https://doi.org/10.3390/min13070908
Chicago/Turabian StyleWang, Xinyu, Hongzhu Cai, Lichao Liu, André Revil, and Xiangyun Hu. 2023. "Three-Dimensional Inversion of Long-Offset Transient Electromagnetic Method over Topography" Minerals 13, no. 7: 908. https://doi.org/10.3390/min13070908
APA StyleWang, X., Cai, H., Liu, L., Revil, A., & Hu, X. (2023). Three-Dimensional Inversion of Long-Offset Transient Electromagnetic Method over Topography. Minerals, 13(7), 908. https://doi.org/10.3390/min13070908






