A Model of Froth Flotation with Drainage: Simulations and Comparison with Experiments
Abstract
1. Introduction
2. Materials and Methods
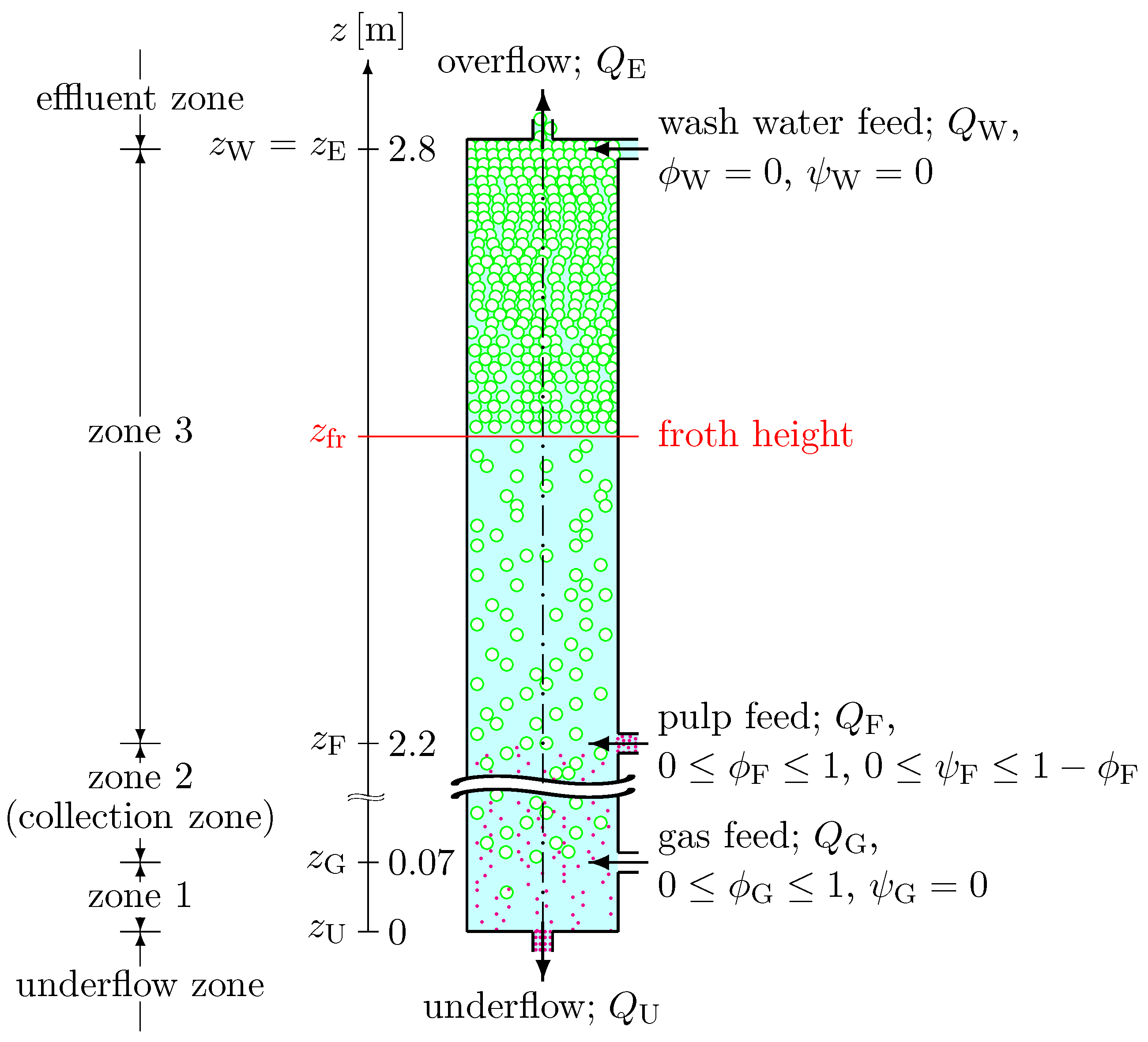
2.1. Pilot Flotation Column and Experimental Setup
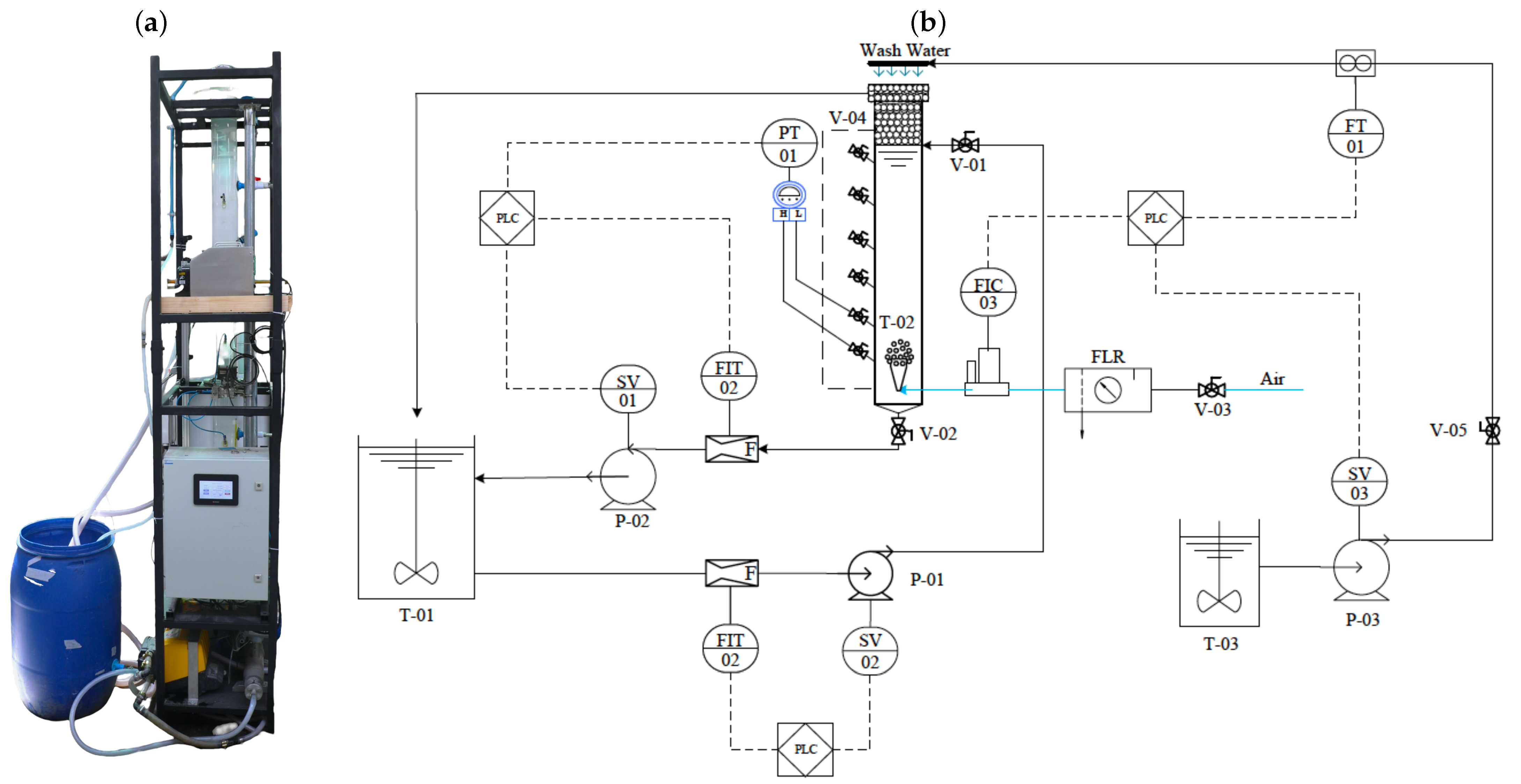
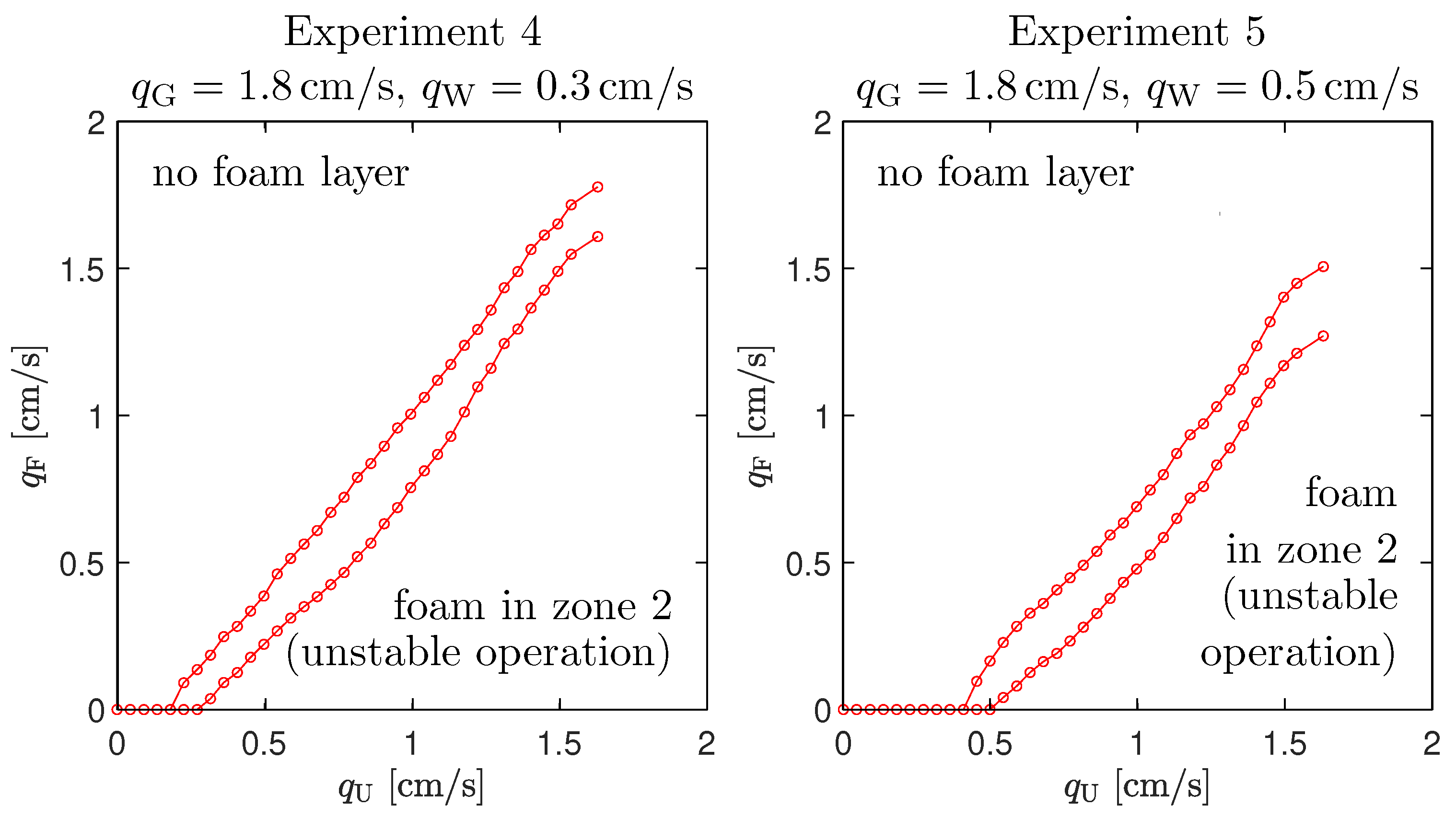
2.2. Experimental Determination of Stability Regions
3. Theory
3.1. Mathematical Model
3.2. Reduced Model for Two-Phase Flow of Bubbles in Liquid
3.3. Numerical Method
3.4. Desired Steady States for the Two-Phase System
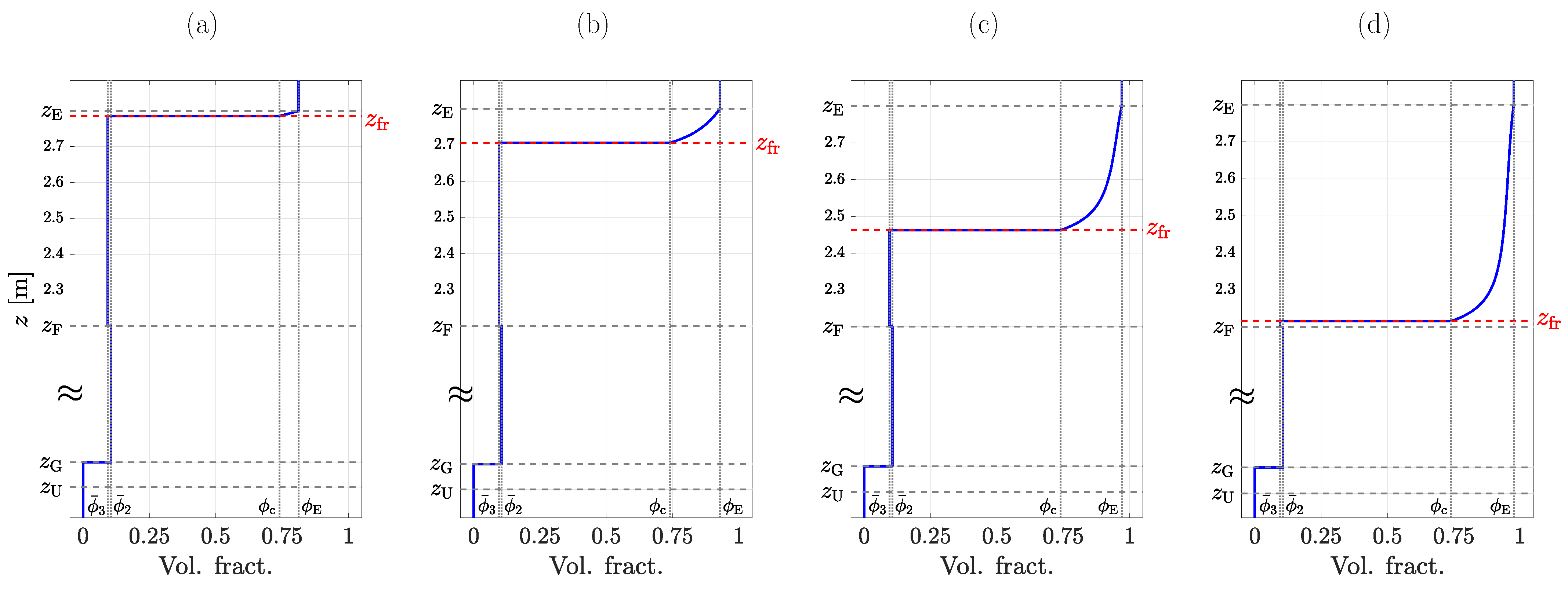
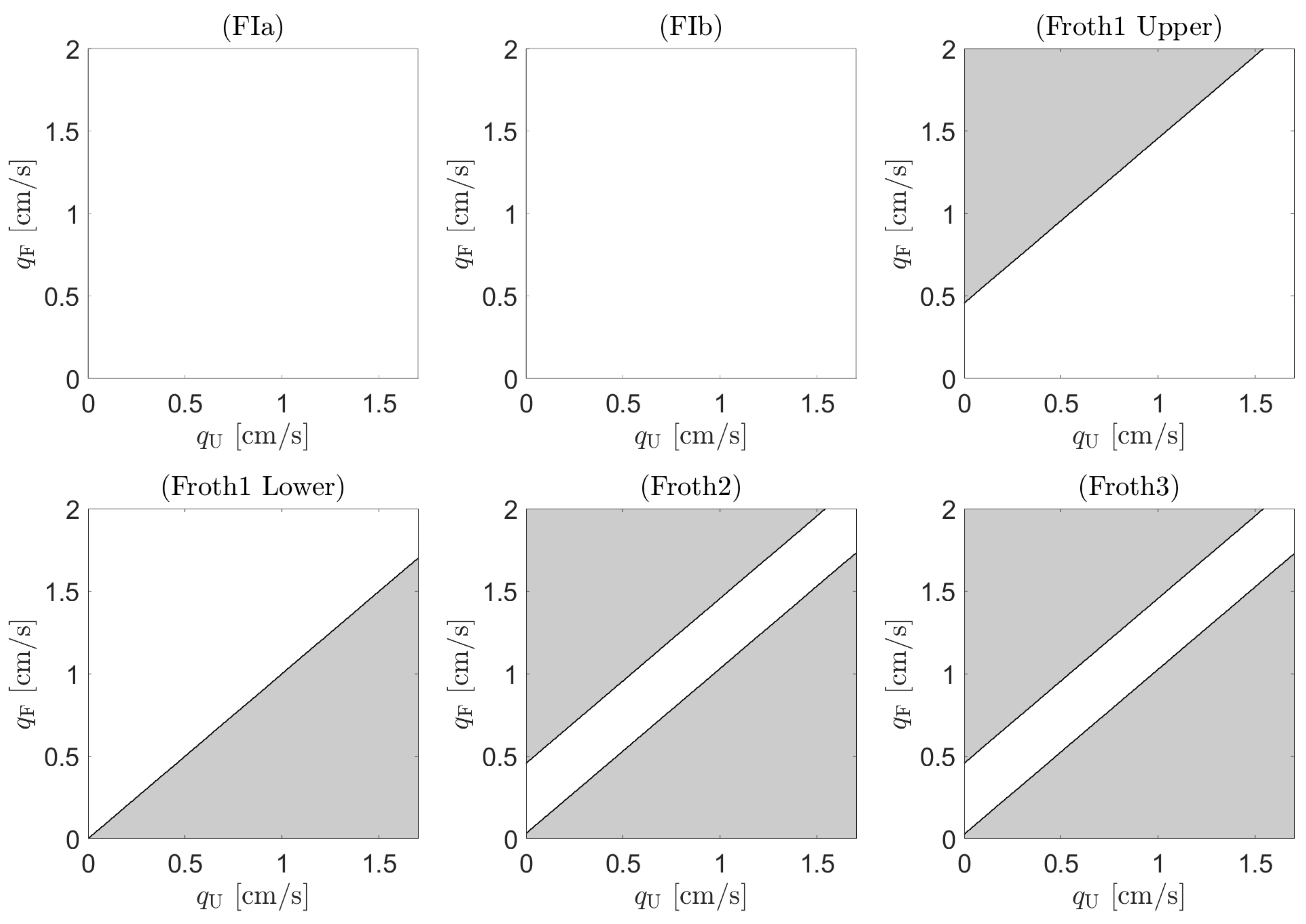
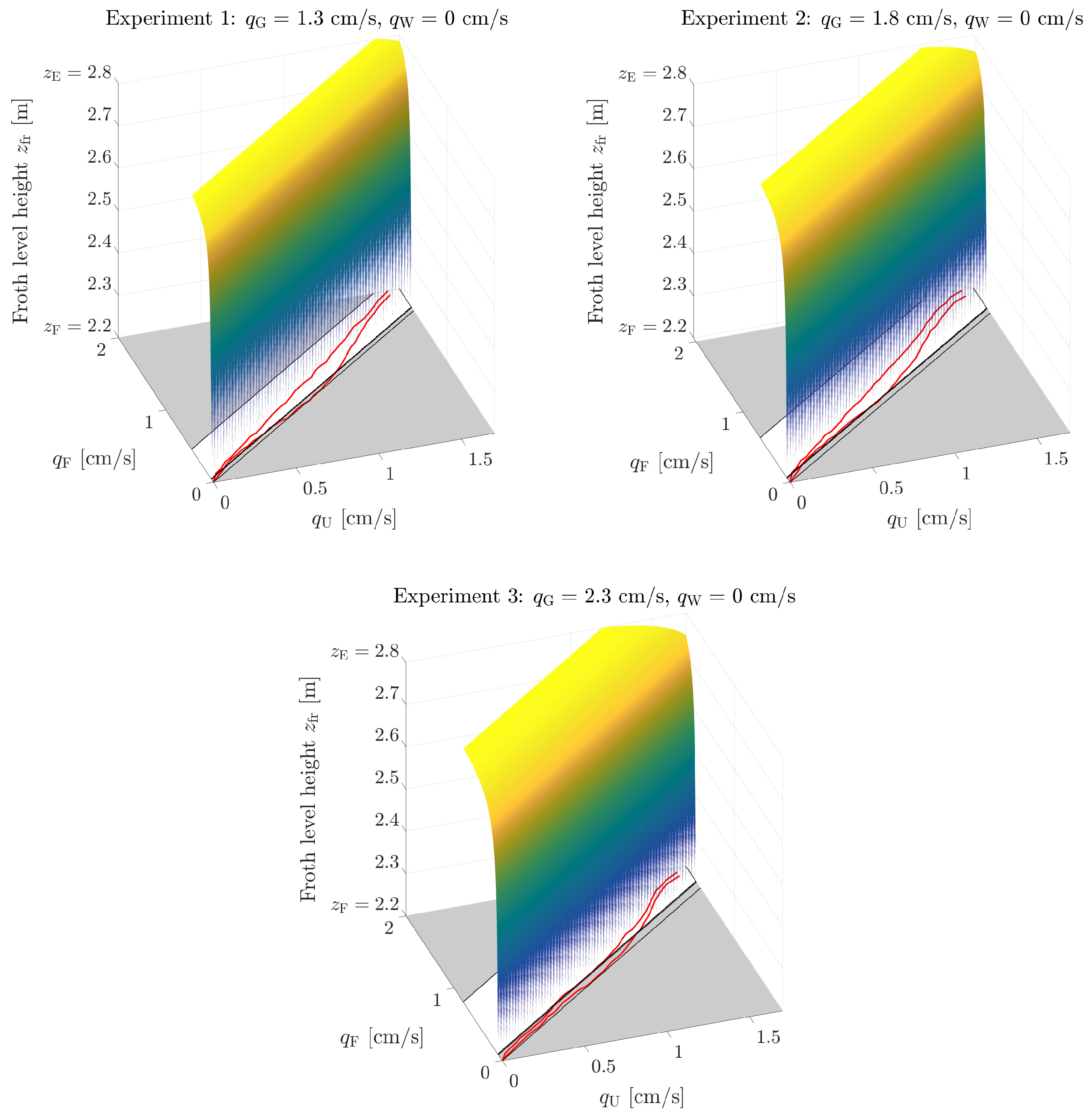
4. Results
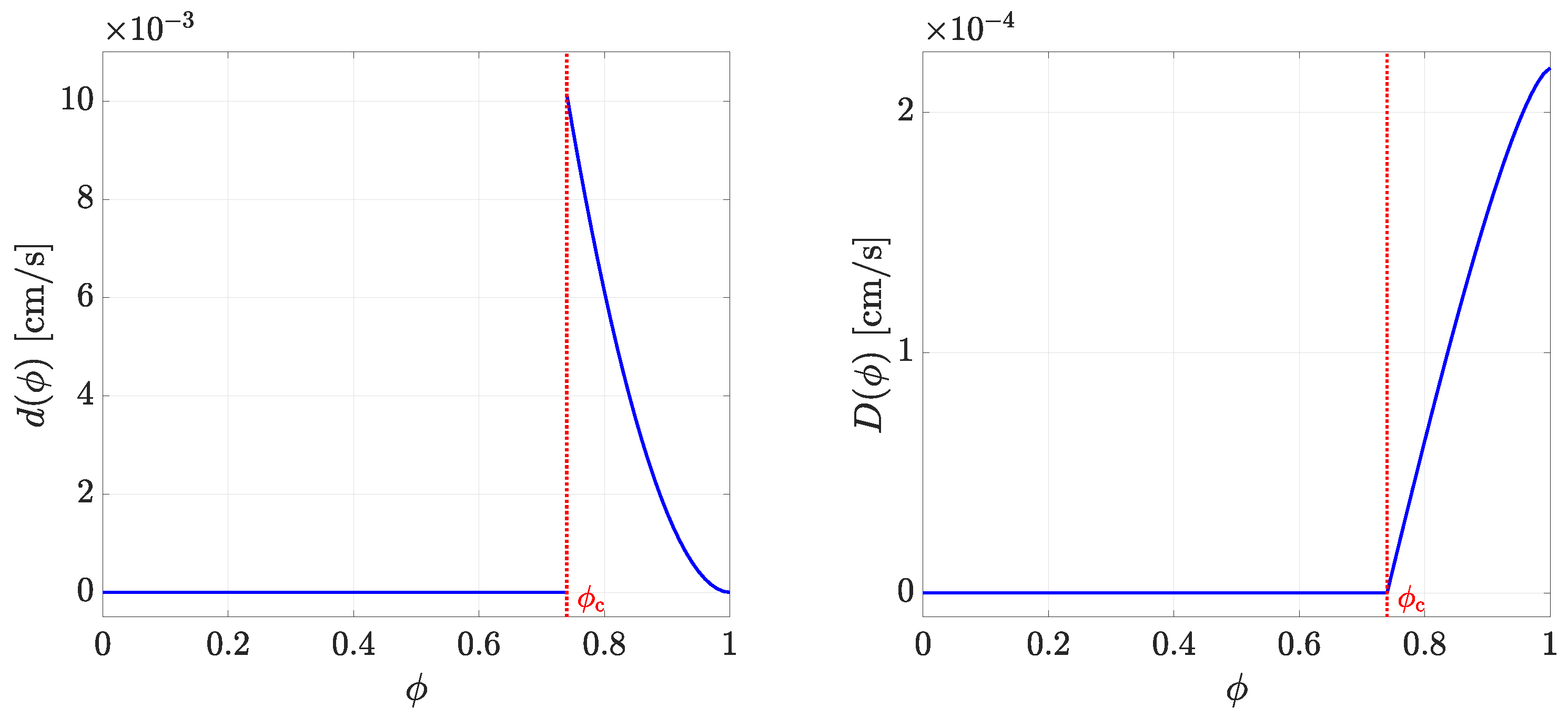
4.1. Choice of Parameters
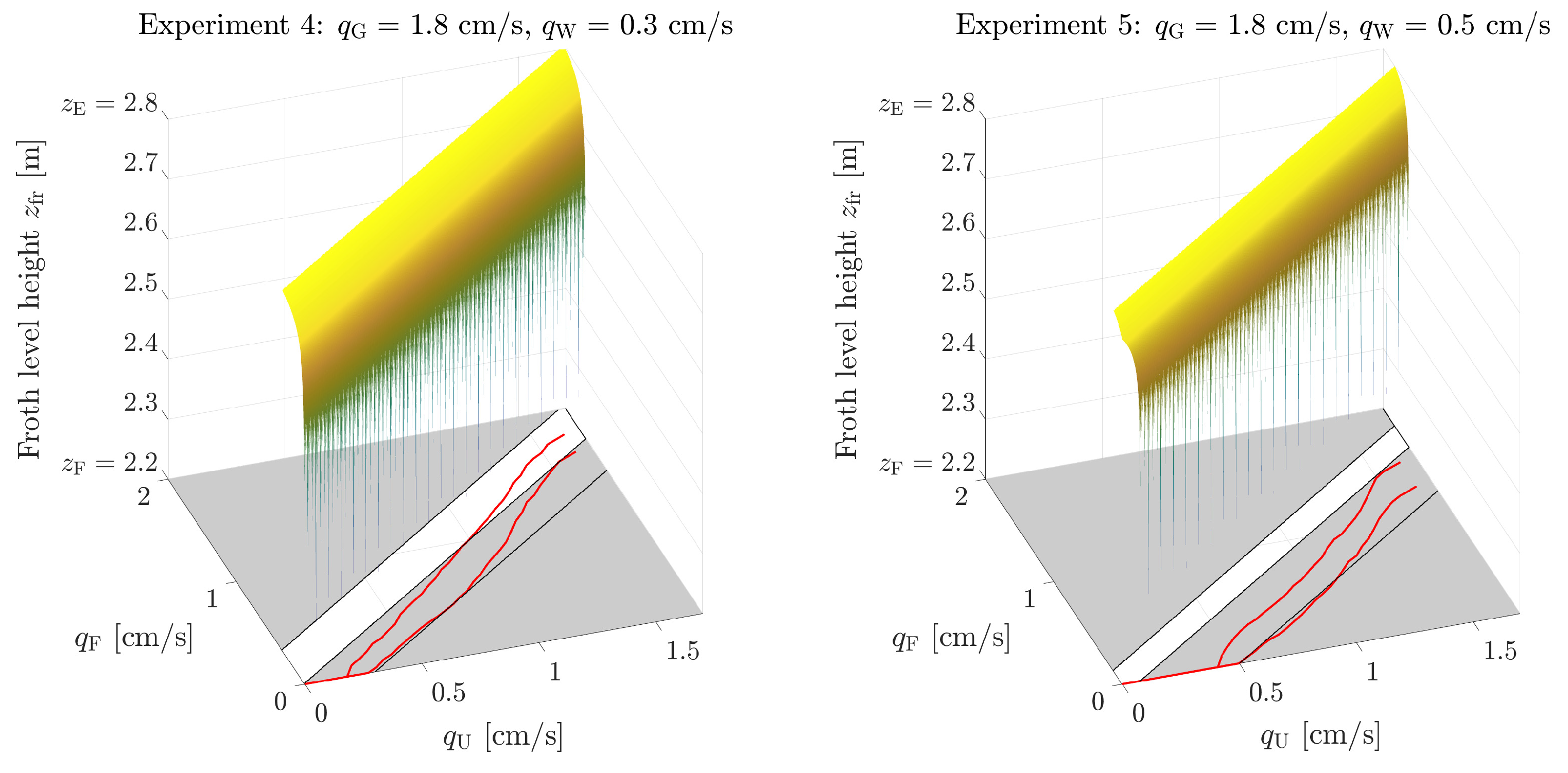
4.2. Comparison between the Model and Experimental Stationary Data
4.3. Simulation of Dynamic Behaviour and a Case with a Solids Feed
4.3.1. A Dynamic Simulation of Two-Phase Bubble–Liquid Flow
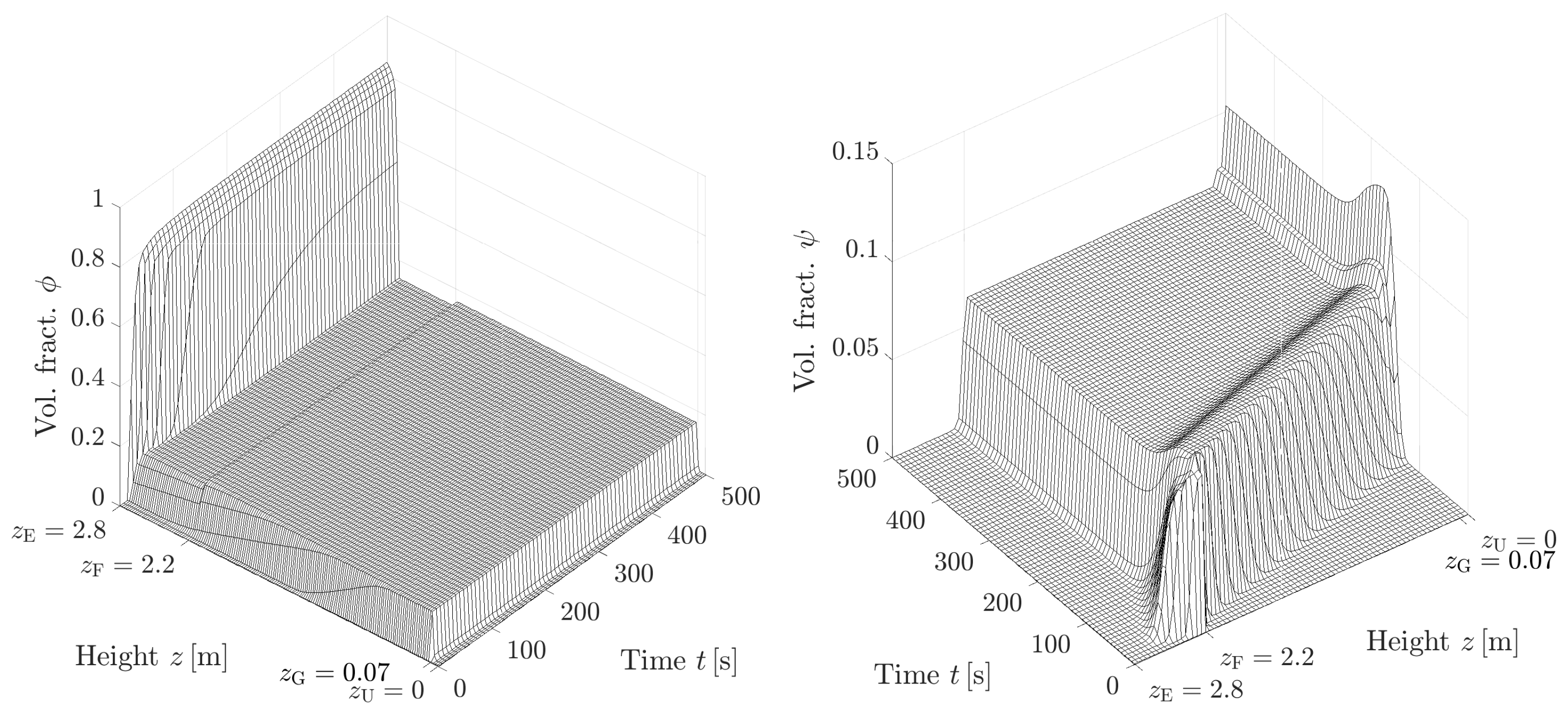
4.3.2. A Dynamic Simulation of Three-Phase Bubble–Solids–Liquid Flow
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Glossary
| List of Symbols | |
| The following symbols are used in this manuscript: | |
| Symbol | Significance and Unit |
| A | interior cross-sectional area of column |
| integrated capillarity function | |
| convective flux function of bubbles | |
| convective flux function of solids | |
| convective flux function of solids | |
| Heaviside step function | |
| N | no. of numerical subintervals for numerical method |
| Q | volumetric flow |
| function giving height of pulp–froth interface | |
| capillarity function | |
| capillarity constant | |
| bubble batch flux function | |
| solids batch sedimentation flux function | |
| constant exponent in bubble batch flux | |
| constant exponent related to Plateau borders in foam | |
| Richardson–Zaki exponent | |
| q | bulk velocity, flow rate |
| t | time |
| drift–flux velocity function | |
| hindered–settling velocity function | |
| terminal velocity of single bubble | |
| terminal velocity of single particle | |
| z | height |
| height of pulp–froth interface | |
| Dirac delta distribution | |
| temporal step size of numerical method | |
| spatial step size of numerical method | |
| characteristic function; inside column; outside | |
| volume fraction of bubbles (aggregates) | |
| steady-state solution | |
| critical volume fraction | |
| volume fraction of fluid | |
| volume fraction of bubbles of numerical method | |
| volume fraction of solids in suspension outside bubbles | |
| volume fraction of solids | |
| Subscripts and Superscript | |
| The following sub- and superscripts are used in this manuscript: | |
| Sub-/Superscript | Significance |
| , , | zone 1, zone 2, zone 3 |
| effluent | |
| feed | |
| gas | |
| (local) minimum point | |
| steady state | |
| underflow | |
| wash water | |
| zero (of a function) | |
| critical | |
| batch | |
| fluid | |
| froth | |
| parabolic | |
| (local) maximum point | |
| Abbreviations | |
| The following abbreviations are used in this manuscript: | |
| CFD | computational fluid dynamics |
| CFL | Courant–Friedrichs–Lewy (condition) |
| MIBC | methyl isobutyl carbinol |
| ODE | ordinary differential equation |
| PDE | partial differential equation |
References
- Finch, J.A.; Dobby, G.S. Column Flotation; Pergamon Press: London, UK, 1990. [Google Scholar]
- Wills, B.A.; Napier-Munn, T.J. Wills’ Mineral Processing Technology, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2006. [Google Scholar]
- Dunne, R.C.; Kawatra, S.K.; Young, C.A. (Eds.) SME Mineral Processing & Extractive Metallurgy Handbook; Society for Mining, Metallurgy, and Exploration: Englewood, CO, USA, 2019. [Google Scholar]
- Pal, R.; Masliyah, J.H. Flow characterization of a flotation column. Can. J. Chem. Eng. 1989, 67, 916–923. [Google Scholar] [CrossRef]
- Vandenberghe, J.; Chung, J.; Xu, Z.; Masliyah, J. Drift flux modelling for a two-phase system in a flotation column. Can. J. Chem. Eng. 2005, 83, 169–176. [Google Scholar] [CrossRef]
- Cruz, E.B. A Comprehensive Dynamic Model of the Column Flotation Unit Operation. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 1997. [Google Scholar]
- Maldonado, M.; Desbiens, A.; del Villar, R. Potential use of model predictive control for optimizing the column flotation process. Int. J. Miner. Process. 2009, 93, 26–33. [Google Scholar] [CrossRef]
- Bergh, L.G.; Yianatos, J.B. The long way to multivariate predictive control of flotation processes. J. Process Control 2022, 21, 226–234. [Google Scholar] [CrossRef]
- Tian, Y.; Azhin, M.; Luan, X.; Liu, F.; Dubljevic, S. Three-phases dynamic modelling of column flotation process. IFAC-PapersOnLine 2018, 51, 99–104. [Google Scholar] [CrossRef]
- Tian, Y.; Luan, X.; Liu, F.; Dubljevic, S. Model predictive control of mineral column flotation process. Mathematics 2018, 6, 100. [Google Scholar] [CrossRef]
- Azhin, M.; Popli, K.; Afacan, A.; Liu, Q.; Prasad, V. A dynamic framework for a three phase hybrid flotation column. Miner. Eng. 2021, 170, 107028. [Google Scholar] [CrossRef]
- Azhin, M.; Popli, K.; Prasad, V. Modelling and boundary optimal control design of hybrid column flotation. Can. J. Chem. Eng. 2021, 99 (Suppl. 1), S369–S388. [Google Scholar] [CrossRef]
- Quintanilla, P.; Neethling, S.J.; Brito-Parada, P.R. Modelling for froth flotation control: A review. Miner. Eng. 2021, 162, 106718. [Google Scholar] [CrossRef]
- Quintanilla, P.; Neethling, S.J.; Navia, D.; Brito-Parada, P.R. A dynamic flotation model for predictive control incorporating froth physics. Part I: Model development. Miner. Eng. 2021, 173, 107192. [Google Scholar] [CrossRef]
- Quintanilla, P.; Neethling, S.J.; Mesa, D.; Navia, D.; Brito-Parada, P.R. A dynamic flotation model for predictive control incorporating froth physics. Part II: Model calibration and validation. Miner. Eng. 2021, 173, 107190. [Google Scholar] [CrossRef]
- Wang, G.; Ge, L.; Mitra, S.; Evans, G.M.; Joshi, J.B.; Chen, S. A review of CFD modelling studies on the flotation process. Miner. Eng. 2018, 127, 153–177. [Google Scholar] [CrossRef]
- Wallis, G.B. One-Dimensional Two-Phase Flow; McGraw-Hill: New York, NY, USA, 1969. [Google Scholar]
- Narsimhan, G. Analysis of creaming and formation of foam layer in aerated liquid. J. Colloid Interface Sci. 2010, 345, 566–572. [Google Scholar] [CrossRef]
- Bürger, R.; Diehl, S.; Martí, M.C.; Vásquez, Y. A degenerating convection-diffusion system modelling froth flotation with drainage. IMA J. Appl. Math. 2022, 87, 1151–1190. [Google Scholar] [CrossRef]
- Vásquez, Y. Conservation Laws with Discontinuous Flux Modeling Flotation Columns. Doctoral Thesis, Universidad de Concepción, Concepción, Chile, 2022. [Google Scholar]
- Bürger, R.; Wendland, W.L.; Concha, F. Model equations for gravitational sedimentation-consolidation processes. Z. Angew. Math. Mech. 2000, 80, 79–92. [Google Scholar] [CrossRef]
- Bascur, O.A. A unified solid/liquid separation framework. Fluid/Part. Sep. J. 1991, 4, 117–122. [Google Scholar]
- Stevenson, P.; Fennell, P.S.; Galvin, K.P. On the drift-flux analysis of flotation and foam fractionation processes. Can. J. Chem. Eng. 2008, 86, 635–642. [Google Scholar] [CrossRef]
- Dickinson, J.E.; Galvin, K.P. Fluidized bed desliming in fine particle flotation, Part I. Chem. Eng. Sci. 2014, 108, 283–298. [Google Scholar] [CrossRef]
- Galvin, K.P.; Dickinson, J.E. Fluidized bed desliming in fine particle flotation Part II: Flotation of a model feed. Chem. Eng. Sci. 2014, 108, 299–309. [Google Scholar] [CrossRef]
- Galvin, K.P.; Harvey, N.G.; Dickinson, J.E. Fluidized bed desliming in fine particle flotation – Part III flotation of difficult to clean coal. Miner. Eng. 2014, 66–68, 94–101. [Google Scholar] [CrossRef]
- Bürger, R.; Diehl, S.; Martí, M.C. A conservation law with multiply discontinuous flux modelling a flotation column. Netw. Heterog. Media 2018, 13, 339–371. [Google Scholar] [CrossRef]
- Bürger, R.; Diehl, S.; Martí, M.C. A system of conservation laws with discontinuous flux modelling flotation with sedimentation. IMA J. Appl. Math. 2019, 84, 930–973. [Google Scholar] [CrossRef]
- Bürger, R.; Diehl, S.; Martí, M.C.; Vásquez, Y. Flotation with sedimentation: Steady states and numerical simulation of transient operation. Miner. Eng. 2020, 157, 106419. [Google Scholar] [CrossRef]
- Bürger, R.; Diehl, S.; Martí, M.C.; Vásquez, Y. Simulation and control of dissolved air flotation and column froth flotation with simultaneous sedimentation. Water Sci. Technol. 2020, 81, 1723–1732. [Google Scholar] [CrossRef] [PubMed]
- Kynch, G.J. A theory of sedimentation. Trans. Faraday Soc. 1952, 48, 166–176. [Google Scholar] [CrossRef]
- Diehl, S. Operating charts for continuous sedimentation I: Control of steady states. J. Eng. Math. 2001, 41, 117–144. [Google Scholar] [CrossRef]
- Diehl, S. The solids-flux theory—Confirmation and extension by using partial differential equations. Water Res. 2008, 42, 4976–4988. [Google Scholar] [CrossRef]
- Bürger, R.; Karlsen, K.H.; Risebro, N.H.; Towers, J.D. Well-posedness in BVt and convergence of a difference scheme for continuous sedimentation in ideal clarifier-thickener units. Numer. Math. 2004, 97, 25–65. [Google Scholar] [CrossRef]
- Bürger, R.; Karlsen, K.H.; Towers, J.D. A model of continuous sedimentation of flocculated suspensions in clarifier-thickener units. SIAM J. Appl. Math. 2005, 65, 882–940. [Google Scholar] [CrossRef]
- Diehl, S. On scalar conservation laws with point source and discontinuous flux function. SIAM J. Math. Anal. 1995, 26, 1425–1451. [Google Scholar] [CrossRef]
- Diehl, S. A conservation law with point source and discontinuous flux function modelling continuous sedimentation. SIAM J. Appl. Math. 1996, 56, 388–419. [Google Scholar] [CrossRef]
- Neethling, S.J.; Lee, H.T.; Cilliers, J.J. A foam drainage equation generalized for all liquid contents. J. Phys. Condens. Matter 2002, 14, 331–342. [Google Scholar] [CrossRef]
- Neethling, S.J.; Cilliers, J.J. Modelling flotation froths. Int. J. Miner. Process. 2003, 72, 267–287. [Google Scholar] [CrossRef]
- Neethling, S.J.; Brito-Parada, P.R. Predicting flotation behaviour – The interaction between froth stability and performance. Miner. Eng. 2018, 120, 60–65. [Google Scholar] [CrossRef]
- Neethling, S.J.; Cilliers, J.J. Solids motion in flowing froths. Chem. Eng. Sci. 2002, 57, 607–615. [Google Scholar] [CrossRef]
- Richardson, J.F.; Zaki, W.N. Sedimentation and fluidisation: Part I. Trans. Inst. Chem. Eng. 1954, 32, 35–53. [Google Scholar] [CrossRef]
- Xu, M.; Finch, J.A.; Uribe-Salas, A. Maximum gas and bubble surface rates in flotation columns. Int. J. Miner. Process. 1991, 32, 233–250. [Google Scholar] [CrossRef]
- Bergh, L.G.; Yianatos, J.B. Experimental studies on flotation column dynamics. Miner. Eng. 1994, 7, 345–355. [Google Scholar] [CrossRef]
- Bergh, L.G.; Yianatos, J.B. Flotation column automation: State of the art. Control Eng. Pract. 2003, 11, 67–72. [Google Scholar] [CrossRef]
- Yianatos, J.B.; Bucarey, R.; Larenas, J.; Henríquez, F.; Torres, L. Collection zone kinetic model for industrial flotation columns. Miner. Eng. 2005, 18, 1373–1377. [Google Scholar] [CrossRef]
- Yianatos, J.B.; Henríquez, F.H.; Oroz, A.G. Characterization of large size flotation cells. Miner. Eng. 2006, 19, 531–538. [Google Scholar] [CrossRef]
- Bürger, R.; Diehl, S.; Martí, M.C.; Vásquez, Y. A difference scheme for a triangular system of conservation laws with discontinuous flux modeling three-phase flows. Netw. Heterog. Media 2023, 18, 140–190. [Google Scholar] [CrossRef]
- Diehl, S. A uniqueness condition for nonlinear convection-diffusion equations with discontinuous coefficients. J. Hyperbolic Differ. Equations 2009, 18, 127–159. [Google Scholar] [CrossRef]
- Wallis, G.B. The terminal speed of single drops or bubbles in an infinite medium. Int. J. Multiph. Flow 1974, 1, 491–511. [Google Scholar] [CrossRef]
- Diehl, S. Operating charts for continuous sedimentation III: Control of step inputs. J. Eng. Math. 2006, 54, 225–259. [Google Scholar] [CrossRef]
- Diehl, S. Operating charts for continuous sedimentation IV: Limitations for control of dynamic behaviour. J. Eng. Math. 2008, 60, 249–264. [Google Scholar] [CrossRef]
- Diehl, S. A regulator for continuous sedimentation in ideal clarifier-thickener units. J. Eng. Math. 2008, 60, 265–291. [Google Scholar] [CrossRef]
- Diehl, S.; Farås, S. Control of an ideal activated sludge process in wastewater treatment via an ODE-PDE model. J. Process Control 2013, 23, 359–381. [Google Scholar] [CrossRef]
- Betancourt, F.; Bürger, R.; Diehl, S.; Farås, S. Modelling and controlling clarifier-thickeners fed by suspensions with time-dependent properties. Miner. Eng. 2014, 62, 91–101. [Google Scholar] [CrossRef]
- Torfs, E.; Maere, T.; Bürger, R.; Diehl, S.; Nopens, I. Impact on sludge inventory and control strategies using the benchmark simulation model no. 1 with the Bürger-Diehl settler model. Water Sci. Technol. 2015, 71, 1524–1535. [Google Scholar] [CrossRef]

| Symbol | Significance | Value |
|---|---|---|
| underflow level | ||
| gas feed level | ||
| pulp feed level | ||
| wash water feed level | ||
| overflow level | ||
| A | interior cross-sectional area |
| Instrument | Tag | Quantity Measured | Connected to PLC? |
|---|---|---|---|
| Mass flowmeter transmitter | FIT-01/02 | feed/discharge flowrate | yes |
| Mass flowmeter controller | FIC-03 | air flowrate | yes |
| Magnetic flowmeter | FT-01 | wash water flowrate | yes |
| Variable frequency drive | SV-01/02/03 | pump velocity | yes |
| Differential pressure transmitter | PT-01 | holdup | yes |
| Feed manual valve | V-01 | —— | no |
| Discharge manual valve | V-02 | —— | no |
| Air manual valve | V-03 | —— | no |
| Pressure taps valve | V-04 | —— | no |
| Wash water manual valve | V-05 | —— | no |
| Equipment | Tag | Type | Range/Dimensions and Unit |
| Feed pump | P-01 | centrifuge | 20–110 L/min |
| Discharge pump | P-02 | peristaltic | 0–18 L/min |
| Wash water pump | P-03 | peristaltic | 0–12 L/min |
| Regulator filter with water decanter | FLR | manual | 0–16 |
| Pulp tank | T-01 | plastic cylinder | 200 L |
| Flotation column | T-02 | acrylic tube | 55 L |
| Wash water tank | T-03 | plastic cylinder | 200 L |
| Experiment No. | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| [−] | 1 | 1 | 1 | 1 | 1 |
| [−] | 0 | 0 | 0 | 0 | 0 |
| [cm/s] | 1.3 | 1.8 | 2.3 | 1.8 | 1.8 |
| [cm/s] | 0 | 0 | 0 | 0.3 | 0.5 |
| [cm/s] | |||||
| [cm/s] | see Figure 3 | see Figure 3 | see Figure 3 | see Figure 4 | see Figure 4 |
| Parameter | Symbol | Working Range (Literature) | Range in Present Work |
|---|---|---|---|
| Froth height | 0.5–2.0 | 0.5–1.5 | |
| Bubble diameter | 0.5–2.0 | 0.5–1.3 | |
| Hold-up in zone 2 | 0.05–0.30 | 0.09–0.20 | |
| Gas feed rate | 0.5–3.0 | 1.3–2.3 | |
| Pulp feed rate | 0.2–2.0 | 0.8–1.5 | |
| Discharge rate | 0.2–2.0 | 1.0–1.4 | |
| Wash water rate | 0.2–1.0 | 0.3–0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Betancourt, F.; Bürger, R.; Diehl, S.; Gutiérrez, L.; Martí, M.C.; Vásquez, Y. A Model of Froth Flotation with Drainage: Simulations and Comparison with Experiments. Minerals 2023, 13, 344. https://doi.org/10.3390/min13030344
Betancourt F, Bürger R, Diehl S, Gutiérrez L, Martí MC, Vásquez Y. A Model of Froth Flotation with Drainage: Simulations and Comparison with Experiments. Minerals. 2023; 13(3):344. https://doi.org/10.3390/min13030344
Chicago/Turabian StyleBetancourt, Fernando, Raimund Bürger, Stefan Diehl, Leopoldo Gutiérrez, M. Carmen Martí, and Yolanda Vásquez. 2023. "A Model of Froth Flotation with Drainage: Simulations and Comparison with Experiments" Minerals 13, no. 3: 344. https://doi.org/10.3390/min13030344
APA StyleBetancourt, F., Bürger, R., Diehl, S., Gutiérrez, L., Martí, M. C., & Vásquez, Y. (2023). A Model of Froth Flotation with Drainage: Simulations and Comparison with Experiments. Minerals, 13(3), 344. https://doi.org/10.3390/min13030344







