Abstract
CO2 is a widespread fluid naturally occurring within the Earth crust or injected in deep strata for technological issues such as Carbon Capture and Storage (CCS). At STP conditions, CO2 is a gas, with a net zero dipole moment. Growing pressures produce an increase in its density. The reduced intermolecular distance causes a variation in the molecular structure, due to the intensification of mutual interactions. Some published spot data reveal the departure from the planarity of the bond angle while others provide few values of the CO2 dipole moment. Based on a small amount of literature-measured angle values, it was possible first to extrapolate a correlation between bond angle and density (R2 = 0.879). By fixing the partial charges distribution, we present a simple model that allows the calculation of the CO2 dipole moment directly from the geometry of the molecule, in the range of 179–162 degrees, 1-degree step. Results give values up to about 1 D. Being aware that this model is qualitative, it gives, however, an explanation of the experimental reactivity, and it also provides a valid tool in identifying zones in the crust where these reactions are likely to occur efficiently. Finally, we hypothesise the role of dry CO2 in the carbonate formation through the interactions with the basalts.
1. Introduction
At standard conditions, CO2 is gaseous; at standard temperature and at pressures above 3.5 MPa, CO2 changes to liquid, while at over 304.13 K and 7.4 MPa it reaches supercritical conditions (Figure 1). The Carbon dioxide molecule is generally assumed as a non-polar or at least as a non-dipolar molecule.
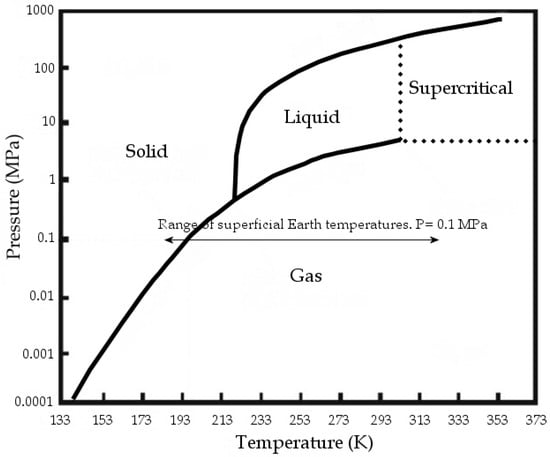
Figure 1.
CO2 phase diagram, modified from [1].
The geometry is linear: the Carbon is the central atom, and the two Oxygens are on the sides, both linked with the Carbon by double covalent bonds. Due to the electronegativity difference between the Carbon and the Oxygens, the molecule has a high charge separation between the central Carbon atom and the two side Oxygen atoms. This configuration produces two C-O couples, each with a dipole moment, identical in value, but pointing in opposite directions. The resulting molecule dipole moment is null; however, the molecule has a quadrupole moment. This allows the CO2 to act as a Lewis acid and/or base [2,3]. Therefore, it is able to link to other molecules with hydrogen bonds [4]. Effectively, supercritical CO2 (scCO2) is widely used as a green solvent in many industrial processes such as in the lipid [5], food oil [6], caffeine [7] and pharmaceutical [8] industries, and in hydrogenation catalytic processes [9]. On the other hand, if subjected to conditions of temperature and pressure higher than the standard ones, dry CO2 demonstrates its capability to bind and to coordinate ionic molecules. On the one hand, the relationship between CO2 and ionic liquids has been sufficiently studied, also in different aggregation phases, such as, for example, in ionic liquids [10], scCO2 in liquid water [11] and water in scCO2 [12]; on the other hand, studies of its behaviour with ionic solutes has given quite surprisingly different results.
As a matter of fact, some researchers point out the experimental affinity of liquid and supercritical CO2 for some ions, and for some ionic solutes as well. Regnault et al. [13,14] demonstrated the solvent capability of dry scCO2 with portlandite that lead to the formation of carbonates after the attack. Criscenti and Cygan [15] investigated the partition of alkaline and earth alkaline elements between water and liquid CO2. In addition to the well-recognised effectiveness of water in ion solvation, the variable, albeit minor, ability of CO2 to bind alkaline ions and, more effectively, earth alkaline elements, stands out. Furthermore, the less the density charge of ions (i.e., with increasing ionic radius and fixed charge), the less the solvation energy gap between water and liquid CO2, which even reduces close to zero, as in the case of Cs+. In other words, liquid CO2 and H2O have quite the same capability to bind (solvation?) Cs+. Furthermore, in CCS lab experiments, Rempel et al. [16] estimated partition coefficients between a brine and supercritical CO2, showing that final concentrations of Na, Fe, Cu and Zn ions in the scCO2 phase were in the range of mg/kg, which is much higher than what was originally expected. High uncertainties in the concentration measurements, however, did not allow drawing a correlation between metal concentrations and scCO2 density. It has also been observed that CO2 has the capability to bind cations and transition elements (see Section 4).
All these observations point out the possibility that, in specific conditions, CO2 could behave as a fluid with some ionic characteristics.
Di Noto et al. [17] detected variations in electrochemical values as soon as pressure is applied on the gas: namely, the onset of a dipole moment of CO2—above 0.20 D—and the increase in the dielectric constant well above 1. The explanation they give resides in the fact that the geometry of single molecules changes due to the increase in mutual intermolecular interactions.
At the same time, a series of direct measurements of the geometrical structure in liquid and supercritical conditions have been accomplished in recent years (see Section 2, Table 1), showing the departure of OCO angle well below 180° degrees in conditions of pressure and, to a minor extent, temperature, above standard values. This geometry has also been modelled with computational chemistry methods (see Section 2).
According to the principle that “like dissolves like”, it follows that non-polar solvents react only with non-polar solutes, while polar solvents react and dissolves ionic compounds. In fact, it has been noted that CO2, is a solvent for some compounds, not strictly belonging to the quadrupolar class and/or not for molecular systems containing hydrocarbon chains.
In short, experimental facts support the hypothesis that dry CO2 has also ionic solvent capability; therefore, it is able to behave as a polar solvent within specific P/T ranges. This issue is fundamental in many Earth Sciences disciplines, because CO2 is a common fluid in crustal environments. CO2 originates naturally from the mantle [18], and minerals decarbonation reactions [19]; it is also artificially injected into deep strata for CCS [20] and for hydrocarbon reservoir re-pressurisation [21]. Injection of CO2 is even suggested for geothermal heat extraction [22,23] and fault imaging [24].
In this paper, we first review the molecular structure of CO2 and its geometry. Subsequently, we analyse the published data, focusing on the modifications induced by neighbouring molecules in conditions of temperature and, above all, pressure above the standard values, inducing the onset of a dipole moment. Finally, having observed a statistical correlation between the OCO angle and the CO2 density, we present a simple model to evaluate the dipole moment, based on the OCO angle measured during laboratory experiments. The bond angle values found in the literature determine the upper and lower limits of the field of existence of our model. With our model, we produce a simple way to estimate the dipole moment, according to the estimated density values compatible with a static profile of the earth crust. Here, the principal aim is to indicate the depths where its polar behaviour is likely to occur, speculating on its role in both the liquid and the supercritical phases and in solvating and coordinate metal ions, and therefore in mineral dissolution/deposition processes. As a final point, the role of dry CO2 in carbonate formation is investigated.
2. CO2 Molecular Structure Generalities and Geometry Variations
In the CO2 molecule, the two C=O bonds have a length of 116.21 pm (NIST data), resulting in a significant opposite charge separation and a consequent dipole moment within each bond. Due to the fact that the molecule has a linear geometry, the entire molecule CO2 has a zero total dipole moment, and the two opposite partial-moment vectors nullify each other (Figure 2). However, at a molecular scale, the two dipole moments give the molecule a quadrupole moment that causes a noticeable solvation capability by means of quadrupole–dipole and quadrupole-induced dipole interactions [3].
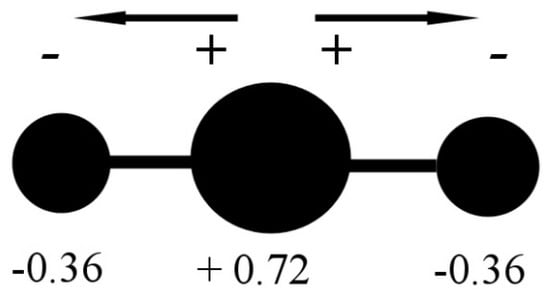
Figure 2.
CO2 molecule charge separation with negative partial charge (−0.36 electron unit) on the Oxygen atoms and positive partial charge (+0.72 electron unit) on the Carbon atom. Data from [3].
Carbon dioxide behaves, in general, as a Lewis acid/base by binding the nucleophiles to the Carbon atom and the electrophiles to the two Oxygen atoms [25]. In self coordination, the acid/base Lewis mechanism should result in the interaction between a lone pair of O of one CO2 molecule to the electron deficiency of C of the second CO2 molecule (Figure 3). In water coordination, the CO2 Lewis acid/base behaviour results in an interaction between a lone pair of the O atom of a H2O molecule and the lacking lone pair of the C atom of a CO2 molecule. Computational chemistry methods could give a useful framework on intermolecular interactions and resulting geometry, both in CO2 coordination chemistry, as in the case of CO2-H2O and in self-aggregation of the pure phase.
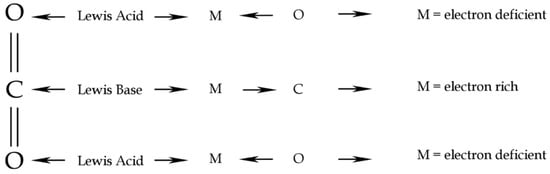
Figure 3.
CO2 Lewis acid/base behaviour. Redrawn from [25].
Starting from the consideration that CO2 is more soluble in water in comparison to CO, Sato et al. [26] stress the apparent incongruence between experimental data and the classic narrative that the solvation process is directly proportional to the dipole moment.
Some hypotheses indicate the possibility of CO2 to establish hydrogen bonds. Xantheas [27] observed that the hydrogen bonds could play an essential role in solvating highly-polar molecules and ions in aqueous solutions. Therefore, the high carbon dioxide solubility in water could be a consequence of the existence of hydrogen bonds between one of the oxygens of the carbon dioxide molecule and the hydrogens of neighbouring water molecules (cf. [26,28]). Hydrogen bonding is so effective in binding two different elements that the CO2 molecule should also establish hydrogen bonds with organic molecules by binding one of its two oxygen atoms with a hydrogen atom bonded to their carbonyl carbon [3].
A reliable hypothesis foresees the acquisition of a dipole moment due to the OCO angle variation, caused by the influence of water molecule. Jena and Mishra [28] analysed the CO2 geometry in the case of interaction with H2O. They conducted an ab initio simulation focusing on CO2 molecular structure variation in the case of a mutual relationship in the [CO2-(H2O)n] coordination group, with 1 ≤ n ≤ 8. Their simulation focused attention on the distortion of both CO2 and H2O bond angles as soon as the two molecules establish an interaction. With n = 1, the coordination has two, simulated, possibilities; the first one is a unique bond between the central Carbon of CO2 and the central Oxygen of H2O (angle of 178.1°), and the second one similar to the first one with a hydrogen bond between one hydrogen and the peripheral oxygen of CO2 (angle of 178.5°). In this second case, the CO2 angle is closer to linearity compared to the first one. H2O is rotated in respect of the first one, and a link is established when a hydrogen reaches a distance of around 2.78 Å with the CO2 oxygen. As a consequence, the second oxygen of the CO2 becomes closer to the central H2O oxygen. The result is that the OCO angle is forced back to the slightly wider values.
With growing coordination numbers, the variation of OCO angle is often higher. Results seem to indicate that one of the most reliable mechanisms responsible for the CO2 bond angle variation is its response to the proximity of an external force, due to other polarised CO2 or H2O molecules.
The analysis of the self-aggregation structure, again by means of computing chemistry methods, shows a modelled framework with some common points. The dimeric structures are the most common forms of CO2 molecule binding in self-aggregation. Two of them are the principal dimeric forms: slipped-parallel, and T-shaped (Figure 4).
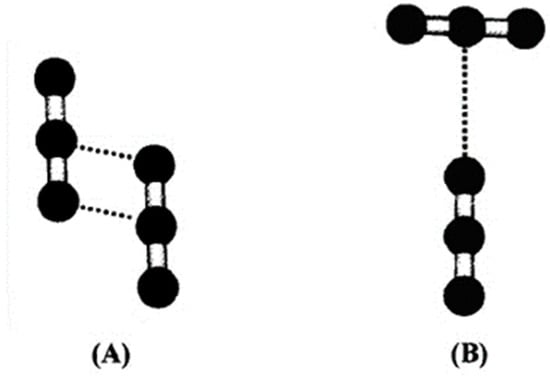
Figure 4.
CO2 dimers after [29]: (A) slipped-parallel and (B) T-Shaped.
In a slipped-parallel structure, a hydrogen bond is established between the central Carbon atom of one molecule and one Oxygen of the coordinated molecule, while the Carbon of the second molecule binds the second Oxygen of the first molecule (Figure 4A). This configuration prevails mostly in the gas phase [17]; its prevalence decreases with growing pressure, becoming minor in the liquid and supercritical phases [30], where the T-shape configuration prevails (Figure 4B). In this configuration, the axis of the two binding molecules forms a 90° angle, lying on the same plane, and the oxygen of one molecule binds the central carbon of the other molecule.
A third structure in self coordination has been theorised, which is crossed geometry [30] or distorted T-shape [31]; it is similar to the T-shaped structure, but the molecules of the dimer lie on different planes, forming an angle. Nonetheless, in a recent work, Mi et al. [32] calculated the angular distribution function of the CO2 molecules of the first solvation shell at T = 304.2 °C and a pressure of 7.4 MPa and found that the angle between the two planes was close to zero.
Anisotropy is present in low-density states, due to localised clusters of molecules [29,30]. With growing density, the anisotropy tends to disappear; in its place, the structure assumes a more ordered geometry. Saharay and Balasubramanian [33] have explained in detail the reasons, presenting the results of an ab initio molecular dynamics simulation on the scCO2 coordination along the 318.15 K isotherm and pressure ranging from 19 to 502 MPa. The first coordination shell is located in the equatorial plane; it is constituted by about six CO2 molecules around a central one, generally linked with distorted T-shape geometry, through lone pairs of one equatorial oxygen to the central carbon [31]. At a density around 1400 kg/m3, the equatorial CO2 molecules of the first shell change orientation: they assume a configuration that tends to return to slipped-parallel geometry. On both poles, a total of six more CO2 molecules complete the scCO2 structure with a configuration similar to CO2 crystals (density = 1740 kg/m3); here, the polarisation of the central CO2 should disappear. In this framework, they argue that the interaction with near neighbours induces a dipole moment, and that density has, not a quantifiable, but a systematic effect on the intramolecular structure (i.e., on the OCO bond angle). Even if based on little data, Anderson et al. [34] suggested that the bond angle varies mostly as a function of temperature. At present, it is reasonable to accept that a series of factors can influence the geometry of the CO2 molecule; among these, there are the density and the thermodynamic conditions.
In order to detect the potential factors affecting the variations of CO2 bond angle in response to variations in the environmental conditions, we analyse the bond angle values, as indicated in Table 1. These values are exclusively from experimental measurements. The correlation matrix in Table 2 shows the matches among variables. Bond angle has a high correlation with density.

Table 2.
Correlation matrix. Highlighted values are >|0.7|. The correlation matrix, carried out on the data of Table 1, highlights that the variation of the geometry of the molecule, the angle, is mainly due to the density.

Table 1.
Bond-angle values at different temperature, pressure and density conditions. Specific Enthalpy, Internal Energy, Cv and Cp have been calculated using NIST facility after [27,32,34,35,36].
Table 1.
Bond-angle values at different temperature, pressure and density conditions. Specific Enthalpy, Internal Energy, Cv and Cp have been calculated using NIST facility after [27,32,34,35,36].
| Temp (K) | Press (MPa) | Density (kg/m3) | Bond Angle | Specific Enthalpy (kJ/mol) | Aggr. State According NIST | Internal Energy (kJ/mol) | Cv (J/mol·K) | Cp (J/mol·K) | Ref |
|---|---|---|---|---|---|---|---|---|---|
| 273.15 | 0.1 | 1.78 | 180 | 21.34 | 19.08 | 27.81 | 36.38 | ||
| 298 | 0.1 | 1.78 | 178.3 | 22.257 | 19.792 | 28.928 | 37.435 | [27] | |
| 220 | 0.85 | 1167 | 166.27 | 3.8198 | liq | 3.7877 | 42.696 | 86.257 | [35] |
| 320 | 10.2 | 477.4 | 169.4 | 15.659 | sc | 14.719 | 46.314 | 328.55 | [32] |
| 222 | 0.65 | 1158 | 163 | 19.027 | liq | 17.354 | 28.374 | 41.522 | [34] |
| 310 | 10.1 | 690.36 | 169 | 13.046 | sc | 12.402 | 43.801 | 190.11 | [36] |
| 320 | 9.7 | 403 | 165.01 | 16.486 | sc | 15.427 | 46.475 | 315.33 | [36] |
| 320 | 9.2 | 335.8 | 165.01 | 17.327 | sc | 16.121 | 45.272 | 240.56 | [36] |
The factor analysis in Table 3 provides a model that accounts for 87% of the dataset total variance, with two factors. The first factor indicates a clear association of four original variables: the bond angle, the density, the specific enthalpy and the related internal energy. It accounts for 48% of the total variability of the model. The uniqueness of the density, the enthalpy and the internal energy is high; these variables correlate only here and are highly representative of this first factor. The uniqueness of the bond angle is sufficiently high, being weakly represented in the second factor.

Table 3.
Factor analysis and varimax rotation. Highlighted values are >|0.7|.
The correlation between bond angle and density is presented in Figure 5 and may be described by the following equation:
where α is the bond angle and ρCO2 is the CO2 density. In Equation (1), the correlation coefficient, R2, is equal to 0.879; however, we realise that this value represents a limited number of experimental data.
α = 180.24 – 2.159 × ln(ρCO2)
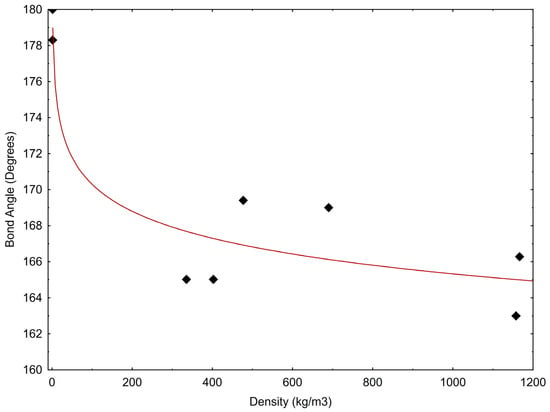
Figure 5.
CO2 bond angle versus density. Data are from Table 1.
These first observations suggest that the decrease in the OCO angle seems to be directly correlated to the decreasing internal energy and inversely correlated to the increasing density. The reduction of intermolecular distances probably produces the deviation from linearity that in turn could be responsible for the onset of the molecular dipole moment.
In fact, Di Noto et al. [17], showing the correlation between the pressure and the temperature of the gaseous/liquid CO2 and the dipole moment, indicated how even in the gaseous phase a closer intermolecular distance is able to yield distortion in the CO2 molecules. Sharp changes in the trends apparently indicate a transition from the slipped−parallel to the T-shaped CO2 molecules configurations. The slipped-parallel configuration contributes only to about 0.04 D of the static dipole moment, while the base contribution of a T-Shaped configuration reaches about 0.3 D.
Furthermore, Jena and Mishra [28] found that, at standard conditions, the OCO bond angle in complexes deviates from linearity up to 2.3°, just like the H-O-H angle, which varies by about 1°. The dipole property appears (in the case of CO2) and varies (in the case of H2O) so that, in a CO2-H2O solution, the group [CO2 (H2O)n] also obtains a dipole moment. The authors reported a value of 4.19 D with n = 5 and 4.42 D with n = 7, the lowest value being at n = 3 with 0.84 D (Table 4).

Table 4.
Coordination number of water molecules with carbon dioxide and complex dipole moment. Data from [27].
The intramolecular OCO bond angle of the central molecule of each group is 178.23°, with a slight deviation of the O-O intramolecular distance of about 0.01 Å.
Summarising, the deviation from the planarity of OCO angle and the relative appearance of the dipole moment of CO2 seems to be correlated with the proximity of polar substances (H2O) and to the reduced intermolecular distances in self aggregation driven by density increase. By analysing this last case, we present a simple geometric model to obtain practical values of the CO2 dipole moment.
3. A Simple Model to Evaluate the Single Molecule CO2 Dipole Moment
We present a simple geometric model to obtain practical values of the microscopic dipole moment for the single carbon dioxide molecule, based exclusively on variations of its molecular geometry, namely the bond angle and the bond length. This model does not want to substitute the more accurate molecular-dynamic-based models that calculate the distortion of the OCO bond angle from the first principles. It gives, though, a handy way to obtain a “back-of-the-envelope” value for this bond angle.
First, we make the hypothesis that CO2 can be considered to be composed of two C=O couples. The dipole moment of the molecule is the vector sum of each C=O couple vector dipole moments, which we assume to have directions towards the respective electronegative Oxygen atom and is given by:
where µ is the dipole moment, Q is the total charge and L is the distance between the central carbon and the bonded oxygen. The total charge is due to the electronegativity difference between the two atoms. In the calculations, lone pairs and non-bonding electrons have been taken into account, because they influence the charge separation. The model calculates (a) the partial charge of the carbon and oxygen atoms, (b) the total charge of the C=O couple, (c) the dipole moment of the C=O couple and (d) the dipole moment of the entire CO2 molecule.
µ = Q × L
3.1. Partial Charge of Carbon and Oxygen Atoms
The following parameters take part in the partial charge calculation:
The valence electrons (V): Every electron on the last energy level. C has 4 valence electrons, whereas O has 6 valence electrons.
The non-bonding electrons (ENL): The number of electrons of an element not involved in any bond. The CO2 molecule is considered to be made of two identical C=O couples, so the oxygen atom has two unshared electron pairs (4 electrons), and the carbon atom has only one unshared electron pair (2 electrons), as in Figure 6.
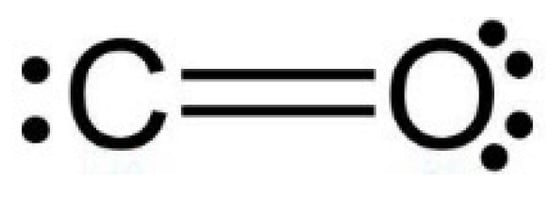
Figure 6.
C=O couple structure.
The bonding electrons (EL): The number of electrons taking part in a bond. C=O bond is covalent, and Carbon and Oxygen share two electrons each. So, C and O have 4 bonding electrons.
EN stands for electronegativity.
Following the general formula [37,38]
and considering a single C=O pair of the CO2 molecule:
we may write,
δ(a) = V(a) − [ENL(a) + EL(a) × (EN(a)/(EN(a) + EN(b)))]
V(c) = 4; V(o) = 6
ENL(c) = 2; ENL(o) = 4;
EL(c) = 4; EL(o) = 4;
EN(c) = 2.55; EN(o) = 3.44.
δ (c) = V(c) − [ENL(c) + EL(c) × (EN(c)/(EN(c) + EN(o)))]
= 4 − [2 + 4 × (2.55/(2.55 + 3.44))] = +0.29 e;
= 4 − [2 + 4 × (2.55/(2.55 + 3.44))] = +0.29 e;
δ(o) = V(o) − [ENL(o) + EL(o) × (EN(o)/(EN(o) + EN(c)))]
= 6 − [4 + 4 × (3.44/(3.44 + 2.55))] = −0.29 e.
= 6 − [4 + 4 × (3.44/(3.44 + 2.55))] = −0.29 e.
Because
e = electron charge = 1.609 × 10−19 Coulomb (C);
then,
δ(c) = +4.65 × 10−20 C;
δ(o) = −4.65 × 10−20 C.
3.2. Partial Charge of the C=O Couple
Once the partial atom charge is obtained, we calculate the charge of the C=O couple within the CO2 molecule. Each oxygen atom has a partial charge of −0.29 e. However, the C atom must be considered twice, because each C takes part in both CO couples. Thus, the partial charge of the carbon atom of the carbon dioxide molecule is +0.58 e. The CO charge is calculated by adding two vectors, applied to the same point with opposite directions.
Q = a|q+| − b|q−|;
Q = 2|q+| − |q−| = 0.58 – 0.29 = +0.29 e.
3.3. The Dipole Moment of the C=O Couple
The dipole moment of a couple is the product between its net charge and the bond length. The bond length (L) between the Carbon and the Oxygen is between 112 pm and 122 pm, with an average value (arithmetic mean) of 117 pm. Therefore, the single C=O bond dipole moment, by applying Equation (2), is:
μ = Q × L = +4.65 × 10−20 C × 1.179 × 10−10 m = 5.482 × 10−30 C m = 1.64 D
3.4. The Dipole Moment of the Entire CO2 Molecule
In order to obtain the dipole moment, we now need to vector sum the dipolar couple of the molecule, following the general formula:
We define La and Lb as the bond lengths of the two C=O couples, μa and μb are the two dipole moment vectors and θ is the bond angle (i.e., the angle formed by μa and μb vectors).
A different isotopic composition, coordination with other molecules such as water or pressure increases, can also determine a change in the bond length, so that the two couples, C=O, no longer have the same bond length.
then,
La ≠ Lb,
a: μa = q × La | b: μb = q × Lb,
μ = (μa2 + μb2 + 2 μaμb × cosθ)1/2,
if: μa ≠ μb and θ = 180°,
μ = (μa2 + μb2 − 2μa μb)1/2 ≠ 0.
From the data reported in [27], the bond length ranges from 112 pm to 122 pm. Accordingly, in this model, the absolute difference between the two C-O bond lengths (ΔL) ranges from 0 to 10 pm.
0 ≤ ΔL ≤ 10.
Here we anticipate results showing that the contribution of the bond variation has, in this model and in the case of asymmetry in the bond length variation, an influence equal to 0.07 D; so, as will be presented below, the bond length variation has an influence that could be considered negligible.
The dipole moment due to the bond angle variation is calculated as follows. Given that
then,
La = Lb;
μ = (μa2 + μb2 + 2 μa ·μb × cosθ)1/2.
If:
μa = μb and θ = 180°
μ = (2μa2 − 2μa2)1/2 = 0
As expected, a linear and symmetric molecule has a dipole moment equal to zero.
Instead, if:
and if:
μ = (μa2 + μb2 + 2 μa × μb × cosθ)1/2,
μa = μb and θ ≠ 180°,
μ = (2μa2 + 2μa2 × cosθ)1/2 ≠ 0.
Once the dipole moment for a single molecule is calculated, we can calculate the dipole moment for a T-Shaped dimer. For the dimer calculation, we assume that this configuration lies in the same plane and the angle between the two resulting vectors is 90° (Figure 7).
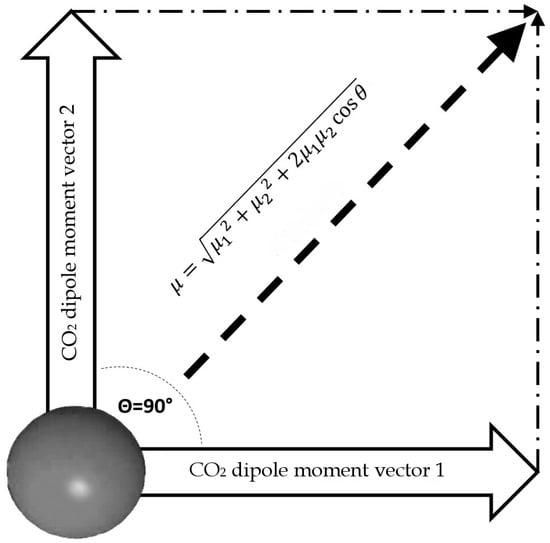
Figure 7.
Outline of total dipole moment of dimer configuration, assuming that vectors of each CO2 molecule are coplanar.
The results are plotted in Figure 8. According to the data reported in Tab. 1, the bond angles used for calculations range from 180° to 160°. The data are based on the partial charge calculations from Section 3.1, and as comparison, based on partial charge value according to [3]. They calculate a charge separation with a negative partial charge of −0.36 e on the Oxygen atoms, a positive partial charge of +0.72 e on the Carbon atom (Figure 2) and a C=O partial charge separation of 0.36 e. These results are based on the CHELPG scheme (CHarges from ELectrostatic Potentials using a Grid based method, described in [39]); the atomic charges are fitted to reproduce the molecular electrostatic potential (MEP) at a number of points around the molecule.
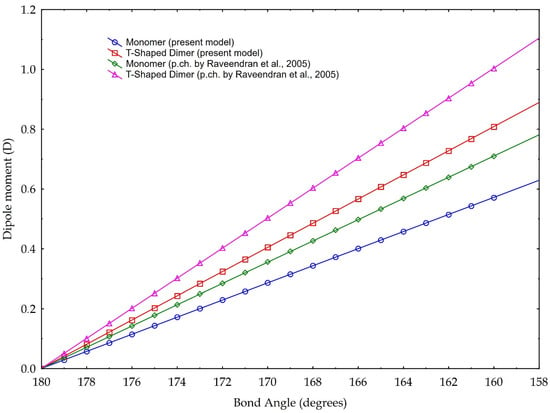
Figure 8.
Dipole moment versus molecule CO2 bond angle. Blue and red graphics are based on the partial charge values calculated in our model, according to Pauling electronegativity. Green and purple graphics are the values calculated according to the partial charge calculated in [3]. Two cases are presented: blue and green are values referring to monomer, red and purple refer to a T-shaped dimer (see text for explanation).
The values of our model, instead, are based on the charge separation computed using the valence electrons, the bonding and the non-bonding electrons, and Pauling electronegativity, which give a partial charge of −0.29 e for the Oxygen and +0.58 e for the Carbon, and, in turn, calculates a C=O partial charge separation of 0.29 e.
Differences in resulting values arise compared with the original parameter choice, namely in the partial charge calculation method.
4. Discussion
The results illustrated in Figure 8 highlight both the considerable dipole moment values, achievable with the molecule bending. Even if the different slopes of different lines are linked to the choice of the partial charge separation value, computed with different methodologies, we present our model calculated with the two distinct values of partial charges, considering them both valid. Indeed, whatever the choice of partial charge value, we link the increase in the dipole moment to the decrease in the angle of the molecule, within the angle value limits found in the literature. In other words, besides the noticeable absolute values, especially those referring to the T-Shaped configuration, trends are for us more important: they indicate a rising capability of carbon dioxide to act as a polar solvent with decreasing bending values, i.e., with rising density.
In detail, for a bond angle of 160°, our model calculates a dipole moment ranging from 0.57 D (for the monomer configuration) to 0.80 D (for the dimer configuration). If we apply, instead, the partial charge separation calculated by Raveendran et al. [3], our model calculates the dipole moments of 0.7 D (monomer configuration) and 1.0 D (dimer configuration). As a comparison, Saharay and Balasubramanian [31] calculated, with the quantum chemistry method, a dipole moment of 0.85 D at a density of 703 kg/m3. Given this density and using Equation (1), we obtain a bond angle of 165.8°, which leads to a dipole moment of 0.71 D (0.78 D if we would consider the eventual case of maximum asymmetry in the bond length) for the T-Shaped configuration (cf. Figure 8), according to the partial charge separation of [3].
The existence of a dipole moment at specific thermodynamic conditions qualifies the CO2 as a polar solvent, whose solvent ability is currently not quantified. We believe that the role of the CO2 in crustal environments should be reassessed because it is generally considered non-reactive in dry conditions. Indeed, it could effectively interact with ionic minerals, and our model may provide a qualitative estimate of CO2 reactivity in the Earth crust.
Using density as a proxy for the dipole moment, we know that
where P is the pressure, g is the gravity acceleration and h is the depth. In the hydrostatic pressure case, ρaq = 1000 kg/m3, while in the lithostatic pressure case, ρ = 2700 kg/m3 as an average rock-grain density. Based on these values, the relation between pressure and temperature is shown in Figure 9, assuming an average geothermal gradient of 0.025 K/m. Given the increase in CO2 reactivity with the density, the figures show that, at constant temperature, the supercritical state should always be more reactive than the vapour phase, and at constant pressure the liquid phase should always result more reactive than the supercritical state. In other words, lower geothermal gradients should favour the CO2 reactivity.
P = ρgh
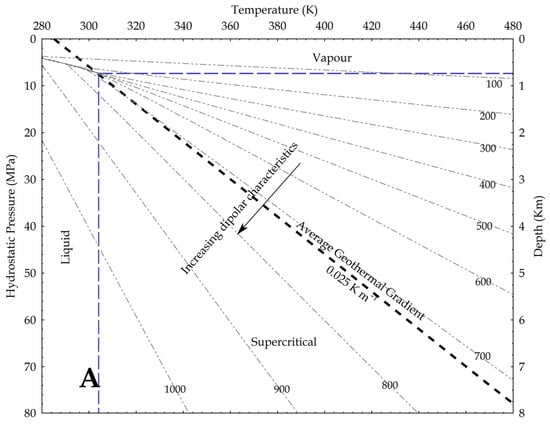
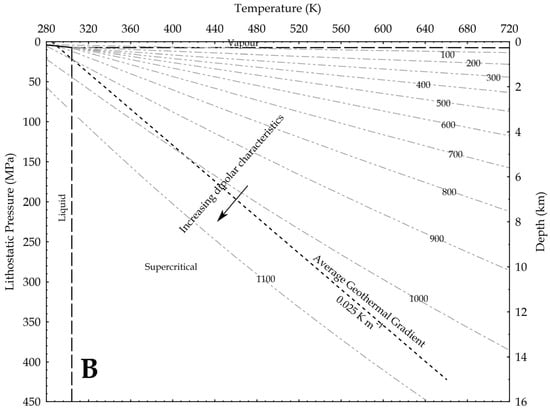
Figure 9.
Density of CO2 in upper crust in a pressure versus temperature diagram that includes the CO2 phase diagram. In the graph, density values are in kg/m3; average geothermal gradient is 0.025 K/m; arrows point toward conditions in the Earth crust where CO2 is supposed to be more reactive due to a higher dipole moment. (A) depths are based on the H2O hydrostatic pressure; (B) depths are based on a lithostatic pressure.
Given the relation between the density, the OCO angle and the dipole moment, Saharay and Balasubramanian [33] indirectly fixed the highest density limit for the dipole moment to occur. In an ab initio MD study, they found that, close to the 1400 kg/m3 density value (not shown in the upper figures), the polarisation starts to nullify because of the structure of the first shell solvation. A total of 12 CO2 molecules spherically surrounded a central one and disposed again in a slipped-parallel configuration. So, at this extreme density value, no dipole moment exists, because every molecule has a planar configuration.
Capability of CO2 to Bind and Solubilise Elements
Criscenti and Cygan [12] discussed the solvation capability of dry liquid and supercritical CO2 in comparison with water. They showed the formation of a first solvation shell around alkali and alkaline-earth elements in liquid (770 kg/m3, 8 MPa and 300 K) and suggested that a comparable structure can be found with scCO2 (620 kg/m3, 20 MPa and 350 K). In particular, based on the calculated solvation energy, they found that the liquid CO2 solvates better the alkaline-earth than the alkali metals. The solvation energies of the liquid CO2 are, for the alkali metals, only slightly higher than those of the liquid water, while for the alkaline-earth elements, they are much higher than for the liquid water.
Schaef et al. [40] studied the interaction of dry supercritical CO2 (P = 9 MPa, T = 312 K, ρ = 200 kg/m3) with montmorillonite rich in Na+, NH4+ and Cs+. They calculated the free solvation energy of the cations with CO2 in relation to the ionic radius (charge density), obtaining values that were less negative than those of Criscenti and Cygan [12]. Nevertheless, they reiterated a sufficient affinity for the alkaline elements, noticing that NH4+ and Cs+ bind anhydrous scCO2 in the montmorillonite interlayers, while Na+ does not. They conclude that this behaviour could be linked to the layer charge rather than to a weak polar solvent character. Instead, in a cation partition experiment between brine and supercritical CO2, Rempel et al. [16] demonstrated that the partition of Na+ towards scCO2 is substantial, and it is a direct function of the density at constant temperature.
A comparative extraction and dissolution experiment carried out by Propp et al. [41] from the solid sulphide used CO2 and water at similar temperatures, comparable densities and at an estimated pressure of about 27 MPa; the water was in liquid state, while the CO2 was supercritical (Table 5). The results showed that some metals and metalloid elements become more concentrated in the scCO2 rather than in the liquid water.

Table 5.
Comparison of extraction in two cases: pure CO2 and pure water. Bold characters indicate the higher solubility between the two solvents. From [39].
The dipolar character of CO2 has been indicated in the experiments of Sanguinito et al. [42], which show how Illite-smectite minerals of the Utica Shale absorb more scCO2 at increasing pressure, while the kerogen absorbance, because of its “organic character”, has the opposite behaviour. Moreover, the FT-IR spectra show carbonate formation as a function of increasing CO2 pressure.
Accordingly detailed experiments by Regnault et al. [10,11] showed that the dry scCO2 reacts with some minerals, forming calcite and “secondary clays”. In particular, they focused on the scCO2 reaction with Portlandite and Anorthite, and secondarily with Forsterite. The suggested reactions should be:
at 200 °C, 10.5 MPa, and ρCO2 = 128.73 kg/m3
and at 200 °C, 16 MPa, ρCO2 = 203.46 kg/m3 for the following two reactions
Ca(OH)2 + CO2 = CaCO3 + H2O
CaAl2Si2O8 + CO2 = CaCO3 + Al2Si2O7
Mg2SiO4 + 2CO2 = 2MgCO3 + SiO2
Equation (29) produces Calcite (carbonation reactions) and water; it is completed in 45 days. Equation (30) produces Calcite and a “generic clay mineral”. Equation (31) is the weakest, described, however, as significant; the authors do not indicate final products. Kwak et al. [43] demonstrated that Equation (31) occurs at even lower scCO2 densities (T = 353.15 K, P = 7.7 MPa, ρCO2 = 149.52 kg/m3), with a weak reaction forming amorphous products. Rahmani et al. [44] point out that Equation (31) is thermodynamically favoured, even if extremely slow; the addition of water, as well as acid and/or heat, increases the kinetics of this reaction. We suggest that the slow kinetics of the reaction may be due to the low density of the scCO2.
Finally, Sugama et al. [45] showed that scCO2 at 523 K and 17.23 MPa, and 187.83 kg/m3, reacts with a wet powder of granite and diorite, forming carbonates and other mineral phases. Potentially, Dolomite and Siderite may also result from these reactions [46,47].
Liquid CO2 of magmatic origin has been found in terrestrial environments at the Eifucu Volcano at 1600 m bsl (Champagne vent [48]) and in a 2500 m deep borehole on Mount Gambier (Australia [49]). Hence, we may speculate that the Dolomite found in the lower 10 m of sediments of the ODP site 650, at a hydrostatic pressure of about 40 MPa (Marsili Volcano, Tyrrhenian Sea [50]), could perhaps have been formed by the reaction of a H2O-saturated scCO2 phase, originating from the volcanic hydrothermal circulation and the Ca-Mg-rich silicates.
Following the ideas developed for the Earth crust, we suggest in Figure 10 potential applications for Mars, where the dominant fluid is CO2, with water existing as liquid probably only deep into the crust [51]. In fact, the Urey-type carbonation reaction may justify the dry formation of carbonates wherever the existence of carbonates has been detected on Mars [52,53,54].
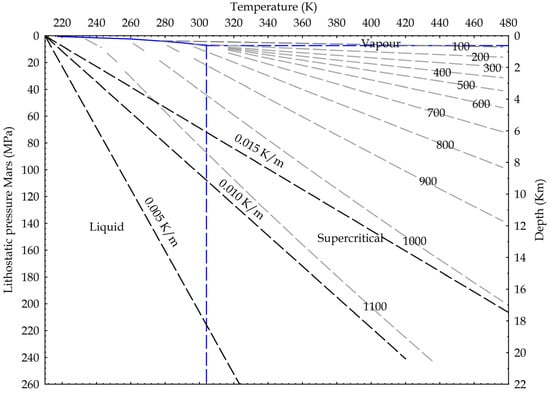
Figure 10.
Martian crustal profile and CO2 state diagram. Three possible thermal gradients from 0.005 K/m to 0.015 K/m; lithostatic pressure calculated on basalts (3100 kg/m3) and Martian gravity acceleration (3.711 m/s2). Density isolines are indicated, calculated from NIST data.
Again, because the CO2 reactivity seems to be a direct function of the density and, in turn, of the pressure, these findings may indicate that CO2 will become more reactive deeper in the Earth and even in Martian crust. In this respect, the dry carbonate formation reaction proposed by Urey is as follows [55]:
where M is a divalent cation, such as Ca2+, Mg2+ or Fe2+, and may well occur at some depth, where denser liquid or supercritical CO2 may be present without the need of the water. Reactions may involve many silicate minerals such as olivine, pyroxenes, wollastonite, amphiboles, serpentine or Ca-plagioclase, as desired for, as an example, in CCS technology [56].
MSiO3 + CO2 = MCO3 + SiO2
5. Conclusions
In the Earth’s crust, CO2 aggregates in several ways according to the thermodynamic values of the environment. Starting from the surface, where it is mainly found in gaseous form, downward we may find liquid or supercritical phases. In particular, we point out that these last two forms of aggregation have ionic properties that allow CO2 to react with the host rocks. The ionic polar solvent and reactive capacity of high-density CO2 seems to be more effective for earth-alkali rather than for alkali metals.
Our model computes the dipole CO2 moment using a standard algebraic method to calculate it from the OCO bond angle, and it produces high dipole moments for relatively small angles. In turn, high dipole moments result in substantial molecular reactivity. Our model supports the experimental finding that correlate scCO2 densities to ion concentrations of Na, Fe, Cu and Zn. Moreover, the dry carbonate formations proposed here could find an exhaustive explanation, especially with divalent cations, here agreeing in what has been observed by authors in computing liquid CO2 reactivity through the solvation energies.
One of the key points of CCS technology is the definitive capture of CO2 through the production of carbonates. Understanding the process of carbonate formation, even without the action of water, becomes of fundamental importance in dry, and then in CO2-rich fluids, so as to have a wider view of the eventual processes and reaction possibilities in the different zones of CO2 injection.
Author Contributions
Conceptualization, M.C. (Massimo Calcara) and M.C. (Matteo Caricaterra); Methodology, M.C. (Matteo Caricaterra); Investigation, M.C. (Massimo Calcara); Data curation, M.C. (Matteo Caricaterra); Writing—original draft, M.C. (Massimo Calcara); Supervision, M.C. (Massimo Calcara). All authors have read and agreed to the published version of the manuscript.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial or not-for-profit sectors.
Data Availability Statement
Data are obtained from published papers, cited in the manuscript, and in some cases (explicitly declared) by means of the facilities supplied on the National Institute of Standards and Technology web site. Results have been generated during present study.
Acknowledgments
We thank Giovanni Grieco, Dmitri Rouwet and, in a special way, Andrea Borgia for the corrections and suggestions provided in an early version of this manuscript. We are thankful to Luciane Duarte Calcara for some “British” suggestions. Finally, we would like to thank the two anonymous reviewers for precious corrections and suggestions.
Conflicts of Interest
We affirm furthermore that no competing interests exist, nor conflict of interest of any kind.
References
- Witowski, A.; Majkut, M.; Rulik, S. Analysis of pipeline transportation systems for carbon dioxide sequestration. Arch. Thermodyn. 2014, 35, 117–140. [Google Scholar] [CrossRef]
- Buckingham, A.D.; Disch, R.L. The Quadrupole Moment of the Carbon Dioxide Molecule. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1963, 273, 275–289. [Google Scholar] [CrossRef]
- Raveendran, P.; Ikushima, Y.; Wallen, S.L. Polar Attributes of Supercritical Carbon Dioxide. Acc. Chem. Res. 2005, 38, 478–485. [Google Scholar] [CrossRef] [PubMed]
- Raveendran, P.; Wallen, S.L. Cooperative C-H···O Hydrogen Bonding in CO2-Lewis Base Complexes: Implications for Solvation in Supercritical CO2. J. Am. Chem. Soc. 2002, 124, 12590–12599. [Google Scholar] [CrossRef]
- Sahena, F.; Zaidul, I.S.M.; Jinap, S.; Karim, A.A.; Abbas, K.A.; Norulaini, N.A.N.; Omar, A.K.M. Application of supercritical CO2 in lipid extraction—A review. J. Food Eng. 2009, 95, 240–253. [Google Scholar] [CrossRef]
- Gouveia, L.; Nobre, B.P.; Marcelo, F.M.; Mrejen, S.; Cardoso, M.T.; Palavra, A.F.; Mendes, R.L. Functional food oil coloured by pigments extracted from microalgae with supercritical CO2. Food Chem. 2007, 101, 717–723. [Google Scholar] [CrossRef]
- De Marco, I.; Riemma, S.; Iannone, R. Life cycle assessment of supercritical CO2 extraction of caffeine from coffee beans. J. Supercrit. Fluids 2018, 133, 393–400. [Google Scholar] [CrossRef]
- Subramaniam, B.; Rajewski, R.A.; Snavely, K. Pharmaceutical processing with supercritical carbon dioxide. J. Pharm. Sci. 1997, 86, 885–890. [Google Scholar] [CrossRef]
- Bertucco, A.; Canu, P.; Devetta, L.; Zwahlen, A.G. Catalytic Hydrogenation in Supercritical CO2: Kinetic Measurements in a Gradientless Internal-Recycle Reactor. Ind. Eng. Chem. Res. 1997, 36, 2626–2633. [Google Scholar] [CrossRef]
- Blanchard, L.A.; Gu, Z.; Brennecke, J.F. High-Pressure Phase Behavior of Ionic Liquid/CO2 Systems. J. Phys. Chem. B 2001, 105, 2437–2444. [Google Scholar] [CrossRef]
- Rochelle, C.A.; Moore, Y.A. The Solubility of Supercritical CO2 into Pure Water and Synthetic Utsira Porewater; British Geological Survey: Nottingham, UK, 2002; 28p. [Google Scholar]
- Wang, Z.; Zhou, Q.; Guo, H.; Yang, P.; Lu, W. Determination of water solubility in supercritical CO2 from 313.15 to 473.15 K and from 10 to 50 MPa by in-situ quantitative Raman spectroscopy. Fluid Phase Equilibria 2018, 476, 170–178. [Google Scholar] [CrossRef]
- Regnault, O.; Lagneau, V.; Catalette, H.; Schneider, H. Étude expérimentale de la réactivité du CO2 supercritique vis-à-vis de phases minérales pures. Implications pour la séquestration géologique de CO2. C. R. Geosci. 2005, 337, 1331–1339. [Google Scholar] [CrossRef]
- Regnault, O.; Lagneau, V.; Schneider, H. Experimental measurement of portlandite carbonation kinetics with supercritical CO2. Chem. Geol. 2009, 265, 113–121. [Google Scholar] [CrossRef]
- Criscenti, L.J.; Cygan, R.T. Molecular Simulations of Carbon Dioxide and Water: Cation Solvation. Environ. Sci. Technol. 2013, 47, 87–94. [Google Scholar] [CrossRef]
- Rempel, K.U.; Liebscher, A.; Heinrich, W.; Schettler, G. An experimental investigation of trace element dissolution in carbon dioxide: Applications to the geological storage of CO2. Chem. Geol. 2011, 289, 224–234. [Google Scholar] [CrossRef]
- Di Noto, V.; Vezzù, K.; Conti, F.; Giffin, G.A.; Lavina, S.; Bertucco, A. Broadband Electric Spectroscopy at High CO2 Pressure: Dipole Moment of CO2 and Relaxation Phenomena of the CO2–Poly(vinyl chloride) System. J. Phys. Chem. B 2011, 115, 9014–9021. [Google Scholar] [CrossRef]
- Santosh, M.; Omori, S. CO2 flushing: A plate tectonic perspective. Gondwana Res. 2008, 13, 86–102. [Google Scholar] [CrossRef]
- Stewart, E.M.; Ague, J.J.; Ferry, J.M.; Schiffries, C.M.; Tao, R.B.; Terry, T.; Isson, T.T.; Noah, J.; Planavsky, N.J. Carbonation and decarbonation reactions: Implications for planetary habitability. Am. Mineral. 2019, 104, 1369–1380. [Google Scholar] [CrossRef]
- Gibbins, J.; Chalmers, H. Carbon capture and storage. Energy Policy 2000, 36, 4317–4322. [Google Scholar] [CrossRef]
- Zhang, M.; Zhan, S.; Jin, Z. Recovery mechanisms of hydrocarbon mixtures in organic and inorganic nanopores during pressure drawdown and CO2 injection from molecular perspectives. Chem. Eng. J. 2020, 382, 122808. [Google Scholar] [CrossRef]
- Pruess, K. On production behavior of enhanced geothermal systems with CO2 as working fluid. Energy Convers. Manag. 2008, 49, 1446–1454. [Google Scholar] [CrossRef]
- Borgia, A.; Pruess, K.; Kneafsey, T.J.; Oldenburg, C.M.; Pan, L. Simulation of CO2-EGS in a fractured reservoir with salt precipitation. Energy Procedia 2013, 37, 6617–6624. [Google Scholar] [CrossRef]
- Borgia, A.; Oldenburg, C.M.; Zhang, R.; Pan, L.; Daley, T.M.; Finsterle, S.; Ramakrishnan, T.S. Simulating CO2 injection into fractures and faults for Improved characterization of EGS sites. Geothermics 2017, 69, 189–201. [Google Scholar] [CrossRef]
- Leitner, W. The coordination chemistry of carbon dioxide and its relevance for catalysis: A critical survey. Coord. Chem. Rev. 1996, 153, 257–284. [Google Scholar] [CrossRef]
- Sato, H.; Matubayasi, N.; Nakahara, M.; Hirata, F. Which carbon oxide is more soluble? Ab initio study on carbon monoxide and dioxide in aqueous solution. Chem. Phys. Lett. 2000, 323, 257–262. [Google Scholar] [CrossRef]
- Xantheas, S.S. Ab initio studies of cyclic water clusters (H2O)n, n = 1–6. Analysis of many body interactions. J. Chem. Phys. 1994, 100, 7523. [Google Scholar] [CrossRef]
- Jena, N.R.; Mishra, P.C. An ab initio and density functional study of microsolvation of carbon dioxide in water clusters and formation carbonic acid. Theor. Chem. Acc. 2005, 114, 189–199. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, J.; Yu, Y.-X. Dielectric Constant and Density Dependence of the Structure of Supercritical Carbon Dioxide Using a New Modified Empirical Potential Model: A Monte Carlo Simulation. J. Phys. Chem. B 2005, 109, 13375–13382. [Google Scholar] [CrossRef]
- Cipriani, P.; Nardone, M.; Ricci, F.P.; Ricci, M.A. Orientational correlations in liquid and supercritical CO2: Neutron diffraction experiments and molecular dynamics simulations. Mol. Phys. 2001, 99, 301–308. [Google Scholar] [CrossRef]
- Saharay, M.; Balasubramanian, S. Enhanced Molecular Multipole Moments and Solvent Structure in Supercritical Carbon Dioxide. ChemPhysChem 2004, 5, 1442–1445. [Google Scholar] [CrossRef]
- Mi, W.; Ramos, P.; Maranhao, J.; Pavanello, M. Ab Initio Structure and Dynamics of CO2 at Supercritical Conditions. J. Phys. Chem. Lett. 2019, 10, 7554–7559. [Google Scholar] [CrossRef] [PubMed]
- Saharay, M.; Balasubramanian, S. Evolution of Intermolecular Structure and Dynamics in Supercritical Carbon Dioxide with Pressure: An ab Initio Molecular Dynamics Study. J. Phys. Chem. B 2007, 111, 387–392. [Google Scholar] [CrossRef] [PubMed]
- Anderson, K.E.; Mielke, S.L.; Siepmann, J.I.; Donald, G.; Truhlar, D.G. Bond Angle Distributions of Carbon Dioxide in the Gas, Supercritical, and Solid Phases. J. Phys. Chem. A 2009, 113, 2053–2059. [Google Scholar] [CrossRef] [PubMed]
- Adya, A.K.; Wormald, C.J. Intra and intermolecular structure in the condensed phases of ethylene, ethane and carbon dioxide by neutron diffraction. Mol. Phys. 1992, 77, 1217–1246. [Google Scholar] [CrossRef]
- Ishii, R.; Okazaki, S.; Odawara, O.; Okada, I.; Misawa, M.; Fukunaga, T. Structural study of supercritical carbon dioxide by neutron diffraction. Fluid Phase Equilibria 1995, 104, 291–304. [Google Scholar] [CrossRef]
- Silvestroni, P. Fondamenti di Chimica; College English Association: San Antonio, TX, USA, 1996; ISBN 8808084019. [Google Scholar]
- Wilmshurst, J.K. An Empirical Expression for Bond Dipole Moments. J. Phys. Chem. 1958, 62, 631–633. [Google Scholar] [CrossRef]
- Breneman, C.M.; Wiberg, K.B. Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis. J. Comp. Chem. 1990, 11, 361. [Google Scholar] [CrossRef]
- Schaef, H.T.; Loganathan, N.; Bowers, G.M.; Kirkpatrick, R.J.; Yazaydin, A.O.; Burton, S.D.; Hoyt, D.W.; Thanthiriwatte, K.S.; Dixon, D.A.; McGrail, B.P.; et al. Tipping Point for Expansion of Layered Aluminosilicates in Weakly Polar Solvents: Supercritical CO2. ACS Appl. Mater. Interfaces 2017, 9, 36783–36791. [Google Scholar] [CrossRef]
- Propp, W.A.; Carleson, T.E.; Wai, C.M.; Huang, S. Transport of Metal Sulfides in Supercritical Carbon Dioxide; Lockheed Idaho Technologies Co.: Idaho Falls, CO, USA, 1996. [Google Scholar] [CrossRef][Green Version]
- Sanguinito, S.; Goodman, A.; Tkach, M.; Kutchko, B.; Culp, J.; Natesakhawat, S.; Fazio, J.; Fukai, I.; Crandall, D. Quantifying dry supercritical CO2-induced changes of the Utica Shale. Fuel 2018, 226, 54–64. [Google Scholar] [CrossRef]
- Kwak, J.H.; Hu, J.Z.; Turcu, R.V.F.; Rosso, K.M.; Ilton, E.S.; Wang, C.; Sears, J.A.; Engelhard, M.H.; Felmy, A.R.; David, W.; et al. The role of H2O in the carbonation of forsterite in supercritical CO2. Int. J. Greenh. Gas Control. 2011, 5, 1081–1092. [Google Scholar] [CrossRef]
- Rahmani, O.; Highfield, J.; Junin, R.; Tyrer, M.; Pour, A.B. Experimental Investigation and Simplistic Geochemical Modeling of CO₂ Mineral Carbonation Using the Mount Tawai Peridotite. Molecules 2016, 21, 353. [Google Scholar] [CrossRef]
- Sugama, T.; Ecker, L.; Butcher, T. Carbonation of Rock Minerals by Supercritical Carbon Dioxide at 250 °C; Energy Resources Department/Energy Resources Division Brookhaven National Laboratory: Upton, LI, USA, 2010; p. 25. [Google Scholar] [CrossRef]
- Tutolo, B.M.; Luhmann, A.J.; Kong, X.Z.; Saar, M.O.; Seyfried, W.E., Jr. Experimental Observation of Permeability Changes In Dolomite at CO2 Sequestration Conditions. Environ. Sci. Technol. 2014, 48, 2445–2452. [Google Scholar] [CrossRef]
- Xu, T.; Pruess, K.; Apps, J. Numerical Studies of Fluid Rock Interaction in Enhanced Geothermal Systems (EGS) with CO2 as Working Fluid. In Proceedings of the Thirty-Third Workshop on Geothermal Reservoir Engineering Stanford University, Stanford, CA, USA, 28–30 January 2008. [Google Scholar]
- Lupton, J.; Butterfield, D.; Lilley, M.; Evans, L.; Nakamura, K.; Chadwick Jr., W.; Resing, J.; Embley, R.; Olson, E.; Proskurowski, G.; et al. Submarine venting of liquid carbon dioxide on a Mariana Arc volcano. Geochem. Geophys. Geosyst. 2006, 7, Q08007. [Google Scholar] [CrossRef]
- Chivas, A.R.; Barnes, I.; Evans, W.C.; Lupton, J.E.; Stone, J.O. Liquid carbon dioxide of magmatic origin and its role in volcanic eruptions. Nature 1987, 326, 587–589. [Google Scholar] [CrossRef]
- Beccaluva, L.; Bonatti, E.; Dupuy, C.; Ferrara, G.; Innocenti, F.; Lucchini, F.; Macera, P.; Petrini, R.; Rossi, P.L.; Serri, G.; et al. Geochemistry and Mineralogy of Volcanic Rocks from ODP Sites 650, 651, 655, and 654 in the Tyrrhenian Sea. Proc. Ocean. Drill. Program Sci. Results 1990, 107, 49–74. [Google Scholar] [CrossRef]
- Lauro, S.E.; Pettinelli, E.; Caprarelli, G.; Guallini, L.; Rossi, A.P.; Mattei, E.; Cosciotti, B.; Cicchetti, A.; Soldovieri, F.; Cartacci, M.; et al. Multiple subglacial water bodies below the south pole of Mars unveiled by new MARSIS data. Nat. Astron. 2020, 5, 63–70. [Google Scholar] [CrossRef]
- Booth, M.C.; Kieffer, H.H. Carbonate formation in Marslike environments. J. Geophys. Res. 1978, 83, 1809–1815. [Google Scholar] [CrossRef]
- Stephens, S.K.; Stevenson, D.J. Dry Carbonate Formation on Mars: A Plausible Sink for an Early Dense CO2 Atmosphere? In Proceedings of the Lunar and Planetary Science Conference, Houston, TX, USA, 12–18 March 1990; Volume 21, p. 56. [Google Scholar]
- Wray, J.J.; Murchie, S.L.; Bishop, J.L.; Ehlmann, B.L.; Milliken, R.E.; Wilhelm, M.B.; Seelos, K.D.; Chojnacki, M. Orbital evidence for more widespread carbonate-bearing rocks on Mars. J. Geophys. Res. Planets 2016, 121, 652–677. [Google Scholar] [CrossRef]
- Di Lorenzo, F.; Ruiz-Agudo, C.; Ibañez-Velasco, A.; Gil-San Millán, R.; Navarro, J.A.R.; Ruiz-Agudo, E.; Rodriguez-Navarro, C. The Carbonation of Wollastonite: A Model Reaction to Test Natural and Biomimetic Catalysts for Enhanced CO2 Sequestration. Minerals 2018, 8, 209. [Google Scholar] [CrossRef]
- Kelektsoglou, K. Carbon Capture and Storage: A Review of Mineral Storage of CO2 in Greece. Sustainability 2018, 10, 4400. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).