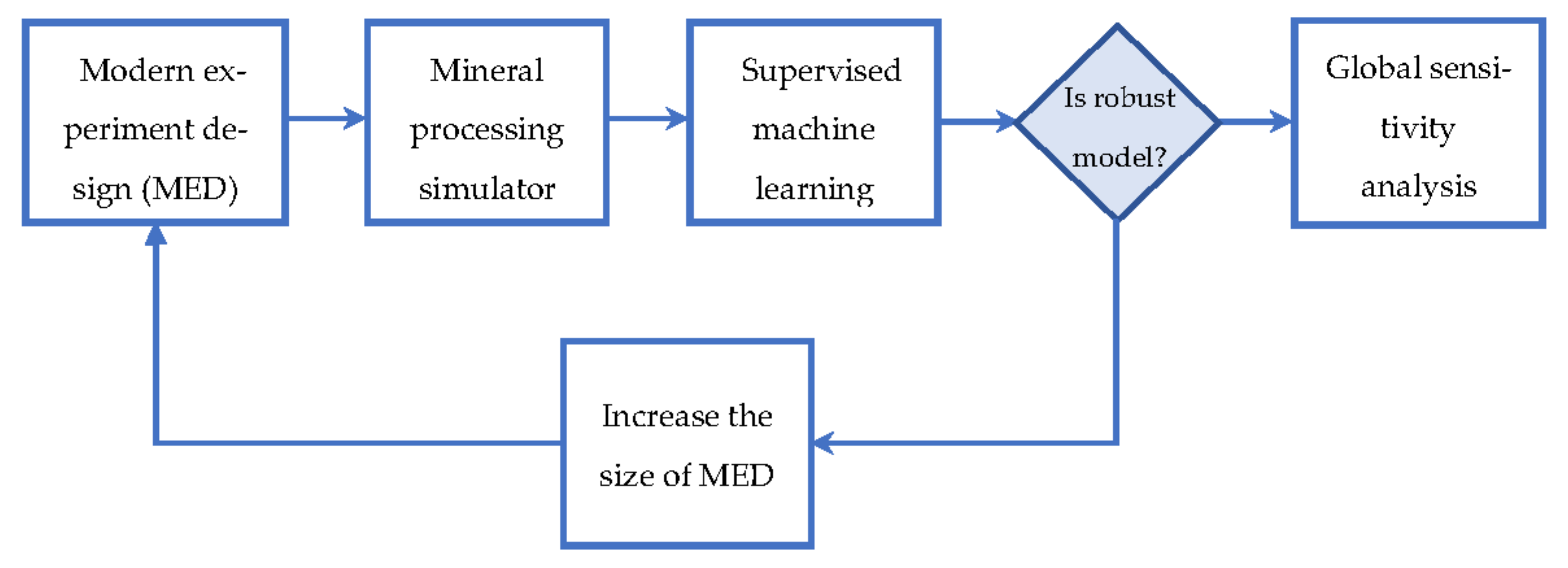
This section presents three examples to illustrate the applicability of the methodology proposed. It is worth mentioning that all the experiments were carried out in JupyterLab using R and Python kernels and a computer with an Intel Core i7 2.21 GHz and 16 GB of RAM.
3.1. SAG Mill: Batch Training
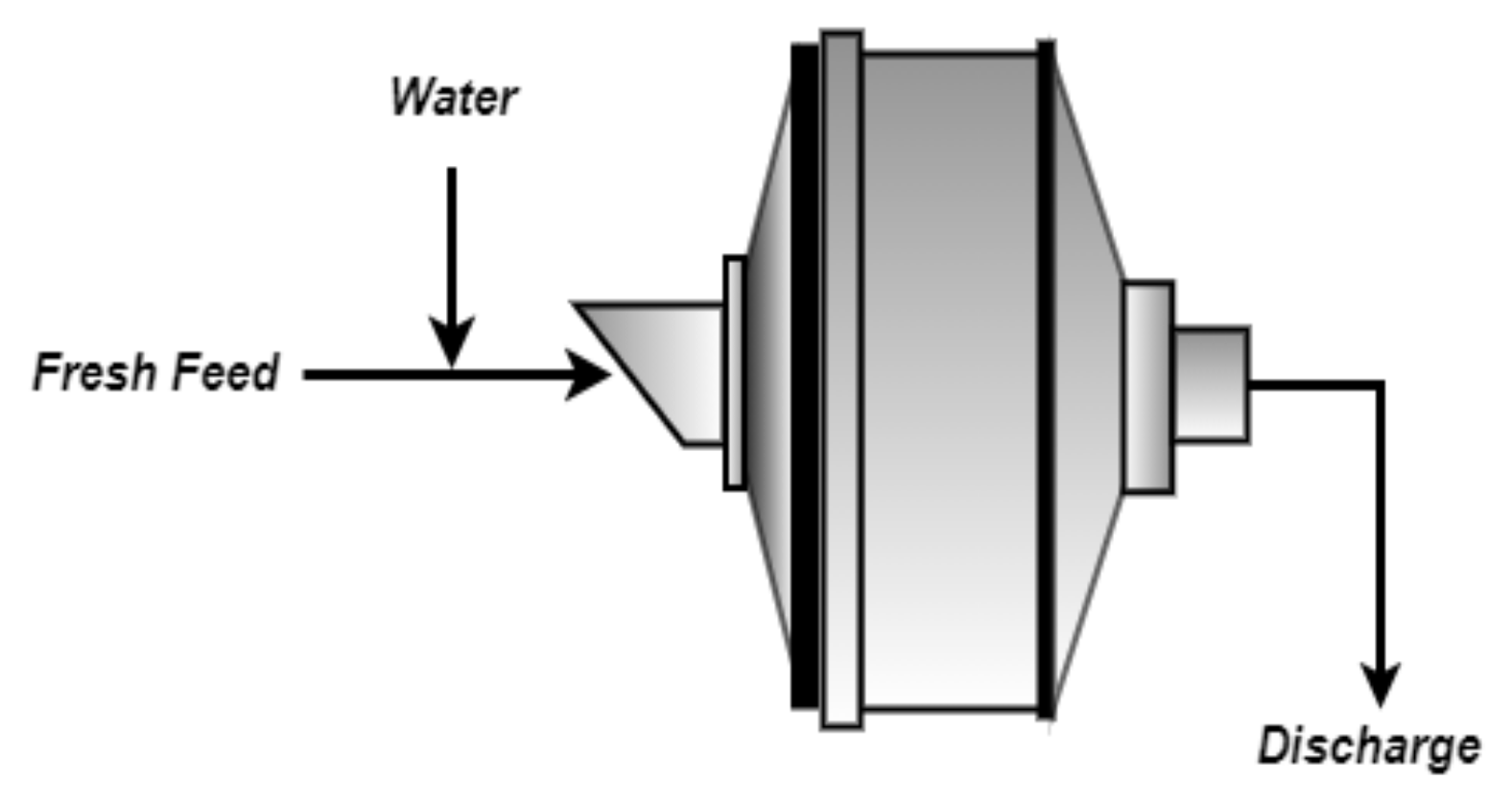
We considered the SAG mill shown in
Figure 2, modeled using mathematical expressions reported by [
9] and a model to estimate the ore hardness (
) in the feed. Specifically,
, where
;
is the ore hardness in the Mohs scale,
is minimum hardness in the Mohs scale,
is the maximum hardness in the Mohs scale,
is equal to 1.5, and
is equal to 0.5. For more detail on the hardness model, see [
38]. The grinding model was coded in the R programming language and solved via the nleqslv solver, assuming that the SAG mill behaved like a perfectly mixed reactor with first-order kinetics. The input variables considered in the model are shown in
Table 2.
The power consumption (
) and comminution specific energy (
were selected as the model output variables because of their relevance to the total cost in the mining industry, representing values between 60 to 80% of the electric costs. The distribution functions used to describe the uncertainty of the input variables are shown in
Table 2. The GSA was performed using the Sobol–Jansen function included in the sensitivity package for the R programming language. The Python programming language offers several libraries for carrying out GSA; however, they do not include the Sobol–Jansen method. Within this context, this method was coded by the author (see
Supplementary Material). The Sobol–Jansen method requires: (a) a mathematical model; (b) two subsamples of the same size; (c) a resampling method for estimating the variance of sensitivity indices. According to Pianosi et al. [
39], the sample size commonly used is 500 to 1000 [
20]. However, the researcher indicated that the sample size may vary significantly from one application to another. Therefore, a much larger sample might be needed to achieve reliable results. Additionally, the number of samples required to achieve stable sensitivity indices can vary from one input variable to another, with low sensitivity inputs usually converging faster than high sensitivity ones [
40]. In this first instance, a sample size equal to 1000 allows for the achievement of stable sensitivity indices. Therefore, the sample size used for carrying out GSA was 16,000 data. The bootstrapping technique consisting of random sampling with replacement from the original data was used as the resampling method. The number of resampling methods used was equal to 100, which is consistent with the literature.
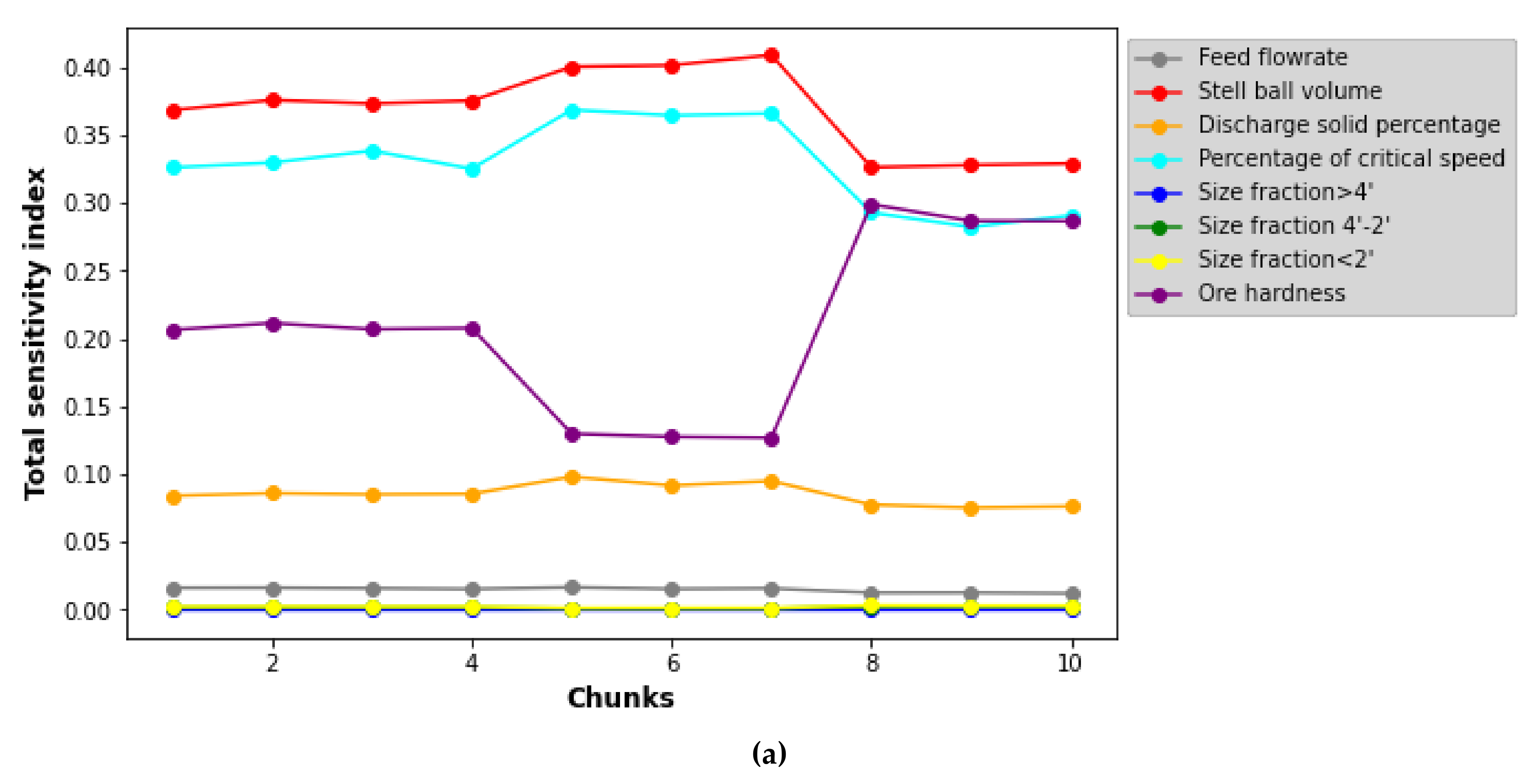
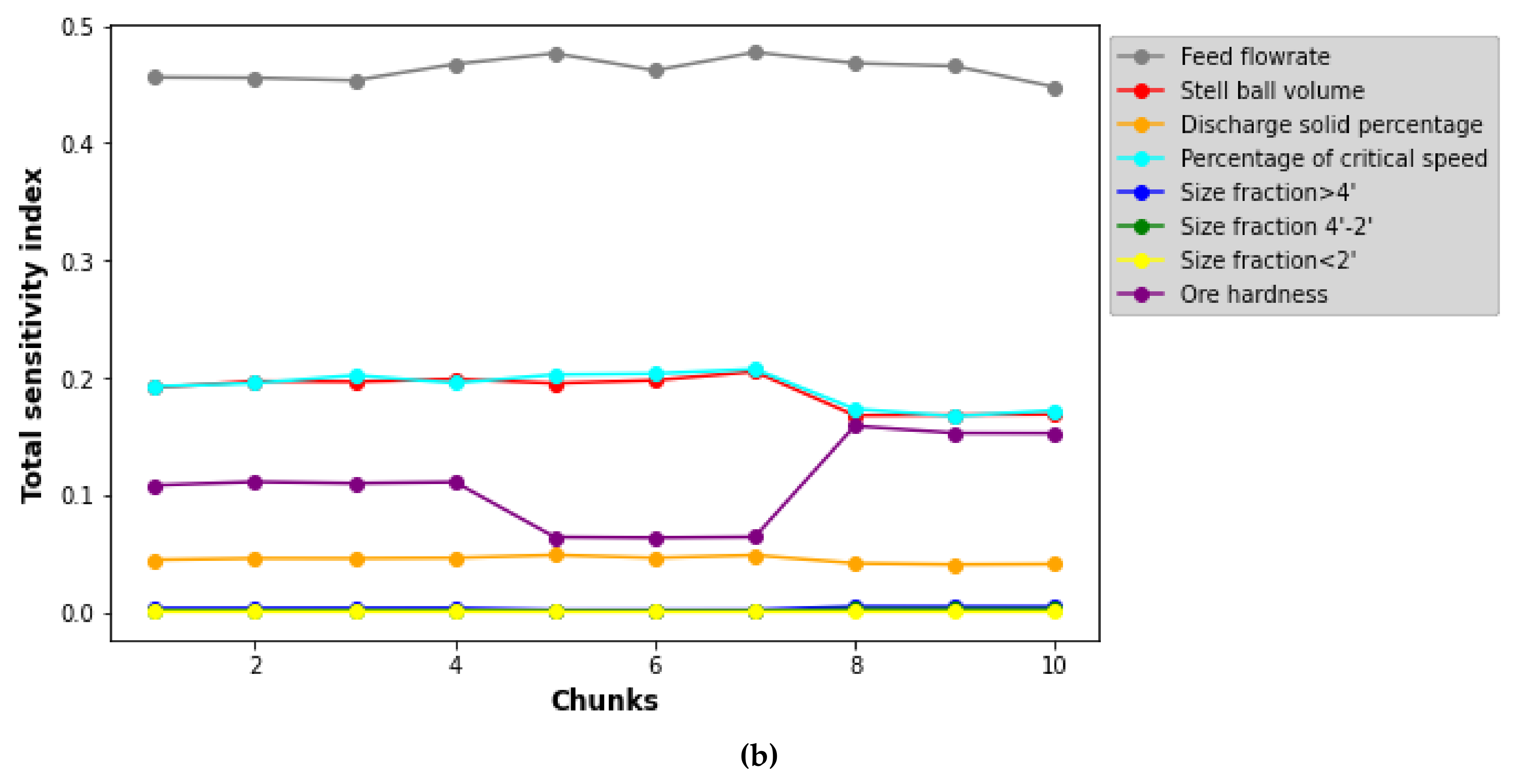
The execution time of the Sobol–Jansen function applied to the grinding model was approximately 18,500 s, revealing that the complexity of the model and sample size severely affected the applicability of this method, and consequently, the analysis of the results. To reduce the execution time, the flowchart presented in
Figure 1 was applied to construct SMs. In Step 1, the LHS sampling method was used to generate the operational conditions of the SAG mill. In Step 2, previous samples were used to simulate the grinding model. In Step 3, the samples, with their corresponding responses, were used to construct SMs, whose results are shown in
Figure 3.
Figure 3 shows the results obtained during the SML tool training and testing using 80 and 20% of the dataset, respectively. Here, the tools labeled with py and r were constructed in Python and R, respectively. Note that SML tool multiparameters were tuned via trial and error. For instance, for MLP, this procedure evaluated the effect of the multiparameters on its statistical performance, including the number of neurons by layer, activation function, training rate, training algorithm, and the number of layers.
Figure 3 reveals that as the dataset increased from 100 to 1000, and that R2 increased for both SML tool training and testing. This increase in samples helped to improve the capture of the SAG mill’s behavior on uncertainty space, and consequently, the SML tool’s performance. This figure shows that SVR-py, MLP-skl, LR-skl, ENR-py, RR-py, LAR-py, GPR-py, MLP-TensorFlow-py, MLP-r, SVR-r, LR-r, and ELM-DEA-r provided a better yield than RFR-py and RFR-r, but all exhibited an R2 greater than 0.8 when the simulation sample was equal to 1000; then, all SML tools moved to the next stage. Before they proceeded to the next step, note that RFR-r and RFR-py exhibited disparate performances. RFR, offered by the RandomForest package (RFR-r) and the scikit-learn library (RFR-p), is based on Breiman’s original version [
41] and Geurts et al. [
42], respectively. The latter consists of heavily randomizing both input variables and cut-point while splitting a tree node. In the extreme case, this approach randomly chooses a single input variable and cut-point at each node, building totally randomized trees whose structures are independent of the output variable values of the learning sample. Therefore, the RFR versions offered by scikit-learn and RandomForest differ, which could explain the disparity in their performance. In the case of RFR-r, its decreasing performance could be related to perturbations induced in the models by modifying the algorithm responsible for the search of the optimal split during tree growing [
42]. In this context, the researcher indicated that it is productive to somewhat deteriorate the algorithm’s “optimality” that seeks the best split locally at each tree node. In Step 4, the GSA was carried out using the Sobol–Jansen method and SMs, and their results are shown in
Figure 4 and
Figure 5.
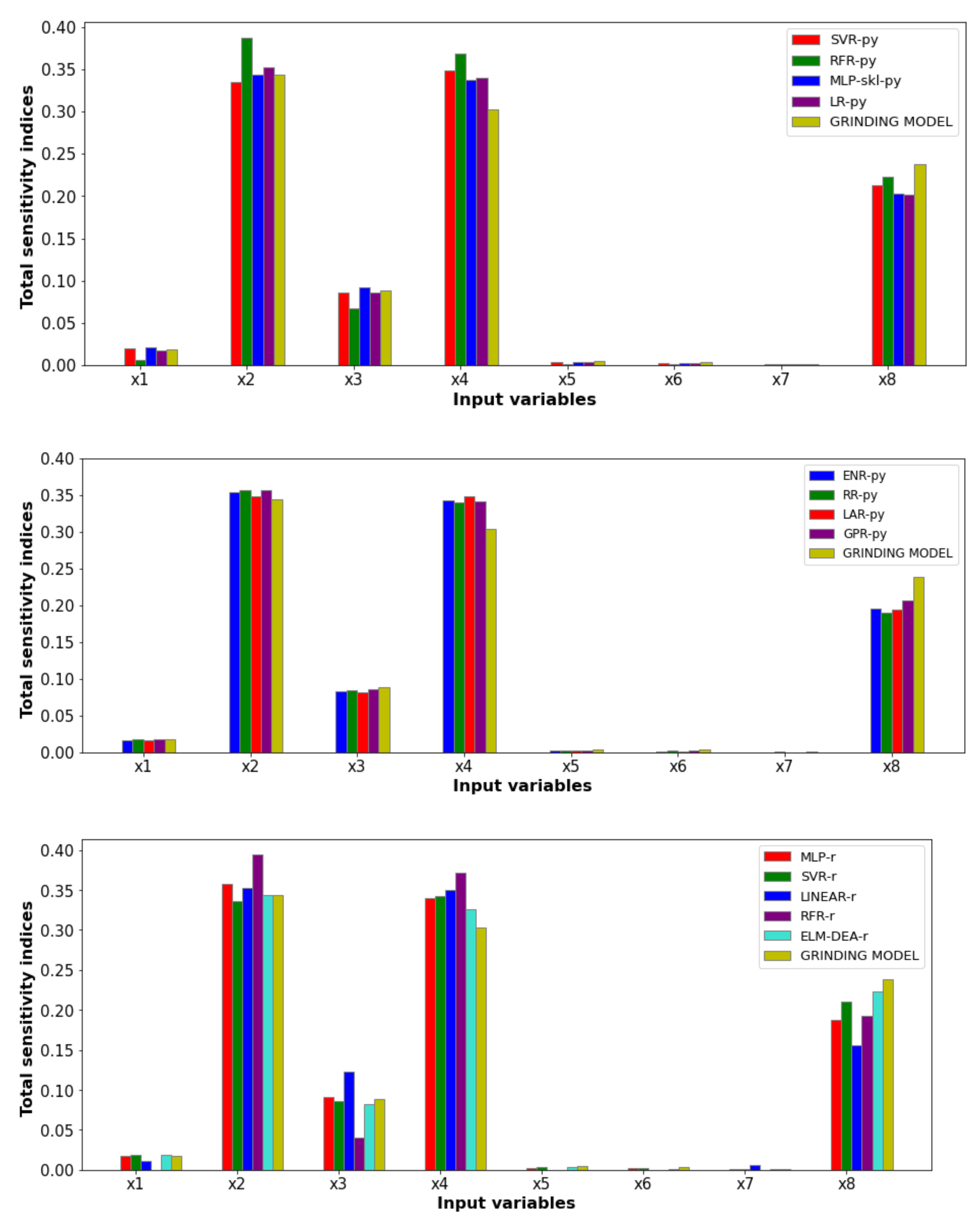
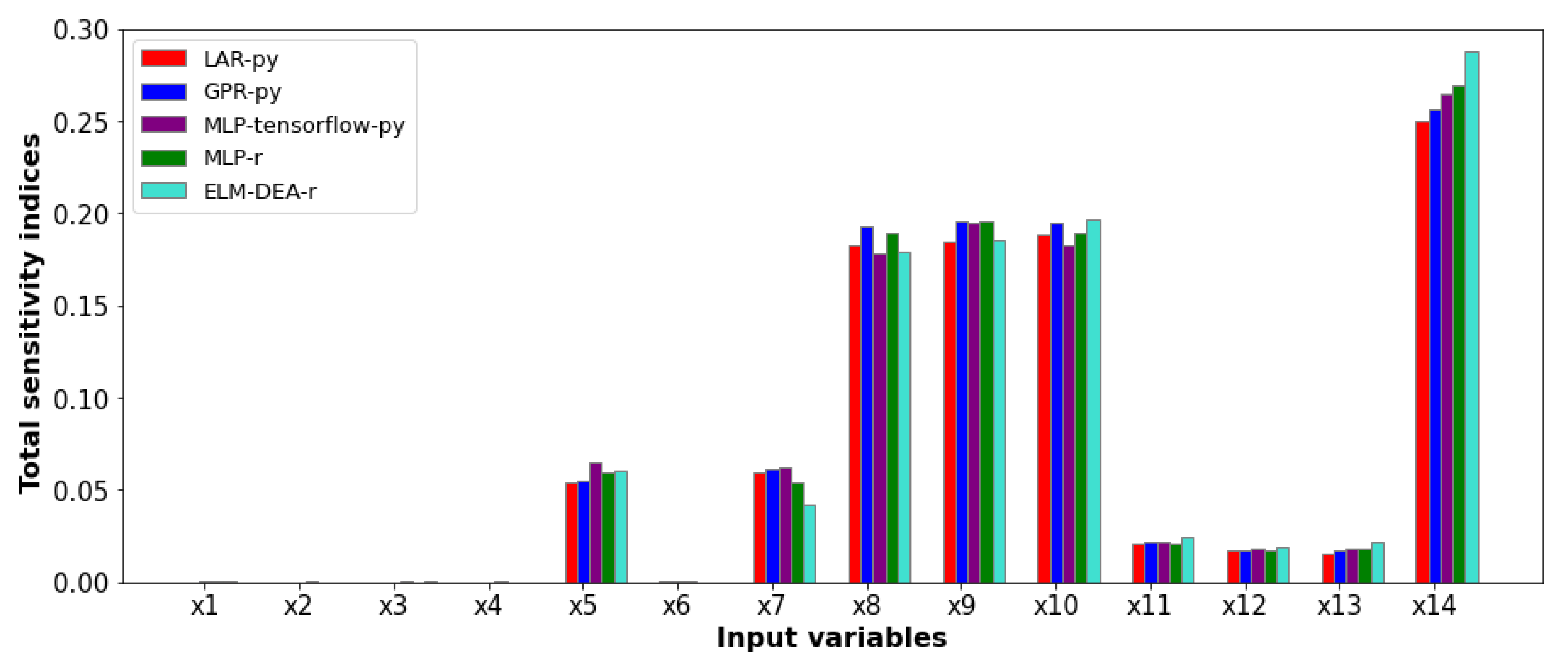
Figure 4 shows the total sensitivity indices provided by the Sobol–Jansen method for the surrogate and grinding models when the output variable was the power consumption. Here, we can see that the total sensitivity indices obtained from SM were similar to those obtained with the grinding model, highlighting the indices reached with the ELM-DEA surrogate model, which required more training time (approximately 600 s) owing to the stochastic nature of DEA. The GSA indicated that the influential input variables on power consumption were
and
. The equation used to estimate the power consumption included the first two input variables, explaining their high total Sobol index [
43].
influenced the ratio between the ore mass and water mass retained inside the mill, and therefore, the power consumption.
influenced the specific breakage rate, and consequently, the mass retained in the mill. The latter influenced a fraction of mill filling, and in turn, the power consumption (see [
9,
43]).
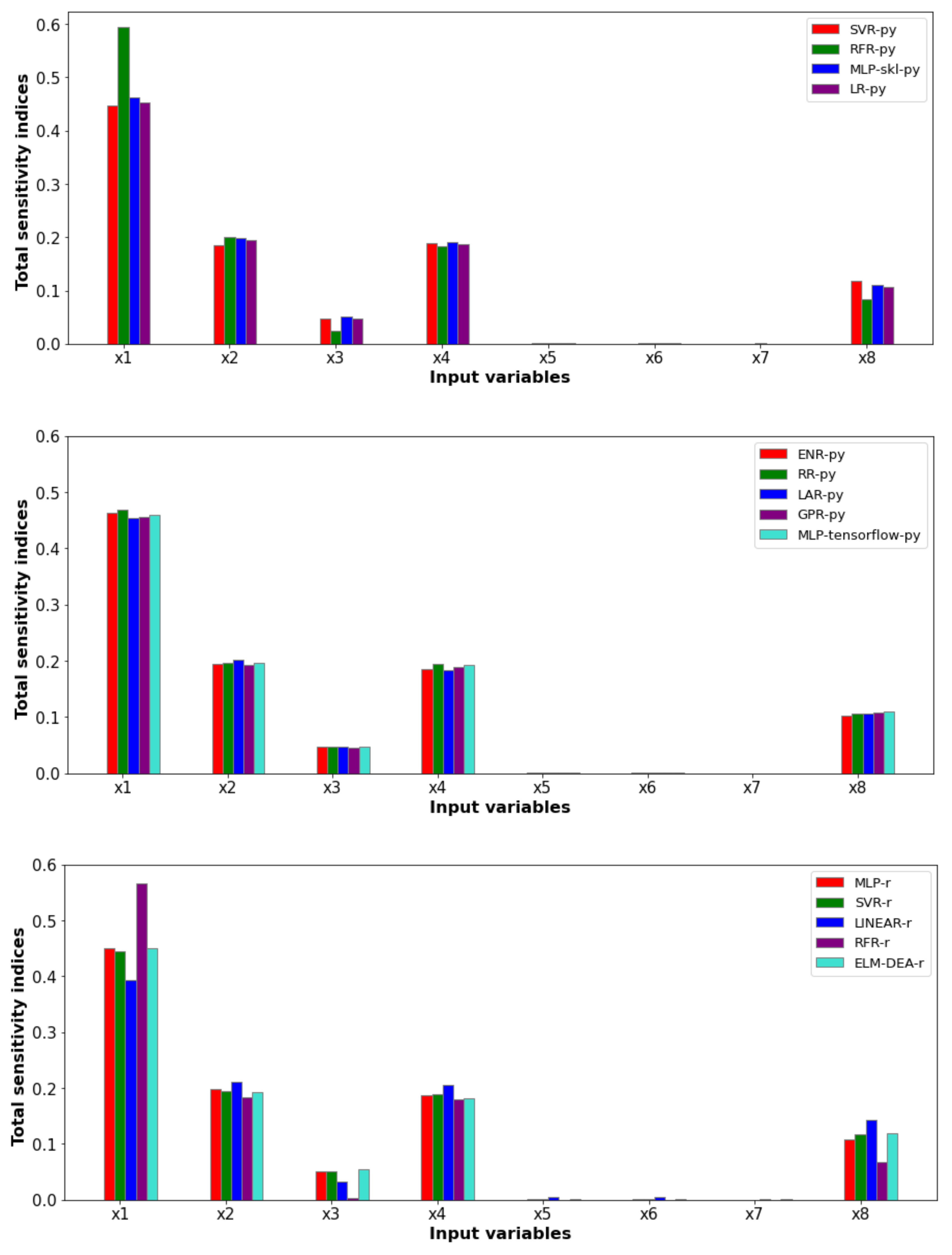
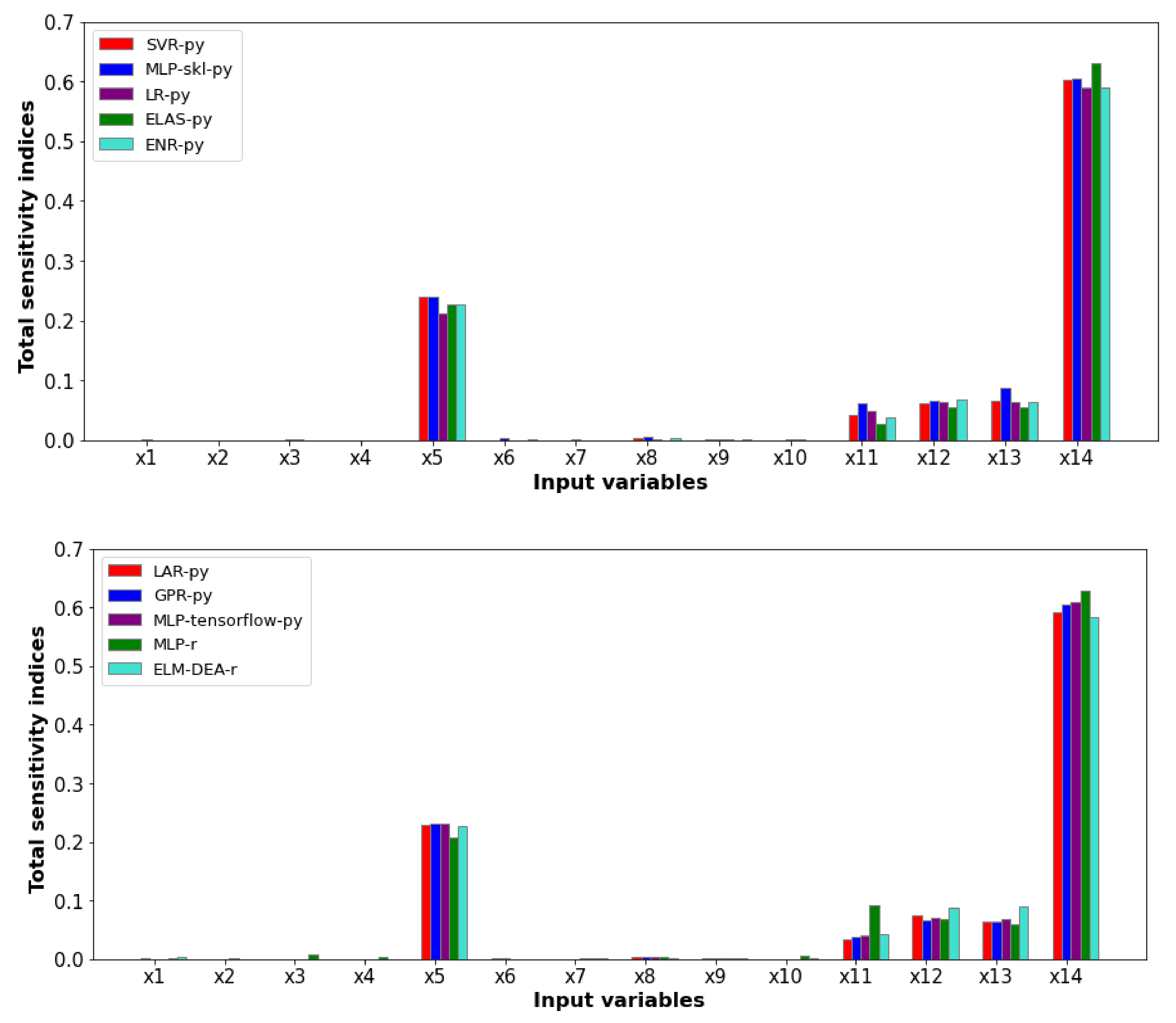
Figure 5 shows the total sensitivity indices provided by the Sobol–Jansen method for the SMs when the output variable was the comminution-specific energy. The latter was influenced mainly by
,
,
, and
. By definition,
directly affects the comminution-specific energy, explaining this input variable’s high total Sobol index.
and
, and
, directly and indirectly, affected the power consumption, respectively, and therefore the comminution-specific energy [
9,
38,
43]. An immediate result of the GSA was reducing the uncertainty space to (
, , , ,, , , and (
, , , ,, , , for the power consumption and comminution-specific energy, respectively. Therefore, optimizing the SAG mill’s outcomes must be made over the reduced spaces to achieve effective operational conditions and decrease the computational burden. Such optimization can be addressed via metaheuristic algorithms [
44].
Table 3 shows the execution time required to obtain total sensitivity indices by each tool, revealing significant computational gains by applying the proposed methodology. Note that the execution time was more significant for Python than R, indicating that the programming of the Sobol–Jansen method in Python must be improved.
3.2. Cell Bank: Batch Training
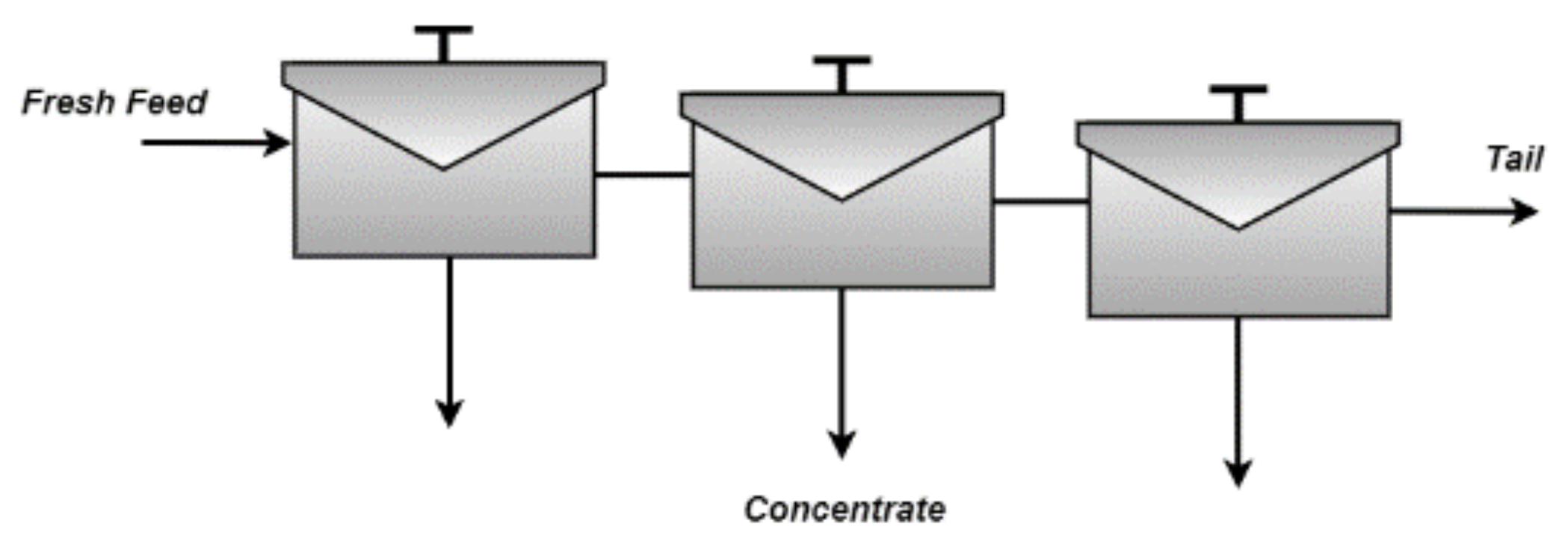
We considered the rougher bank shown in
Figure 6, modeled using the expressions proposed by Hu et al. [
45]. This model considered the entrained flotation recovery, the true flotation recovery, the sedimentation velocity of the particle, the viscosity of the slurry, and the particle size, among others. For this reason, the flotation model was challenging to solve. Under these conditions, this was coded in the GAMS software and solved using the BARON solver, which is widely used in optimization. The model input variables and their standard values (extracted from [
45]) are shown in
Table 4.
The copper recovery and concentrate grade were selected as the output variables of the cell bank. The distribution functions used to describe the uncertainty on the input variables are shown in
Table 4. Initially, the flotation model was solved considering some samples of the operational conditions, requiring an average of 10 s to solve one operational instance. The Sobol–Jansen method requires a large size sample and resample to provide reliable results. This way, the execution time of this analysis would ascend approximately to 28,000,000 s, obstructing the analysis of the outcomes. It is worth mentioning that the Sobol-Jansen method is unavailable in GAMS, and its programming in this software implies a challenge. Therefore, as it was seen in the previous application, it was necessary to develop an SM. In Step 1, the LHS sampling method was used to generate the operating conditions of the cell bank. In Step 2, previous samples were used to simulate the cell bank model. In Step 3, the samples with corresponding responses were utilized to develop SMs, which are shown in
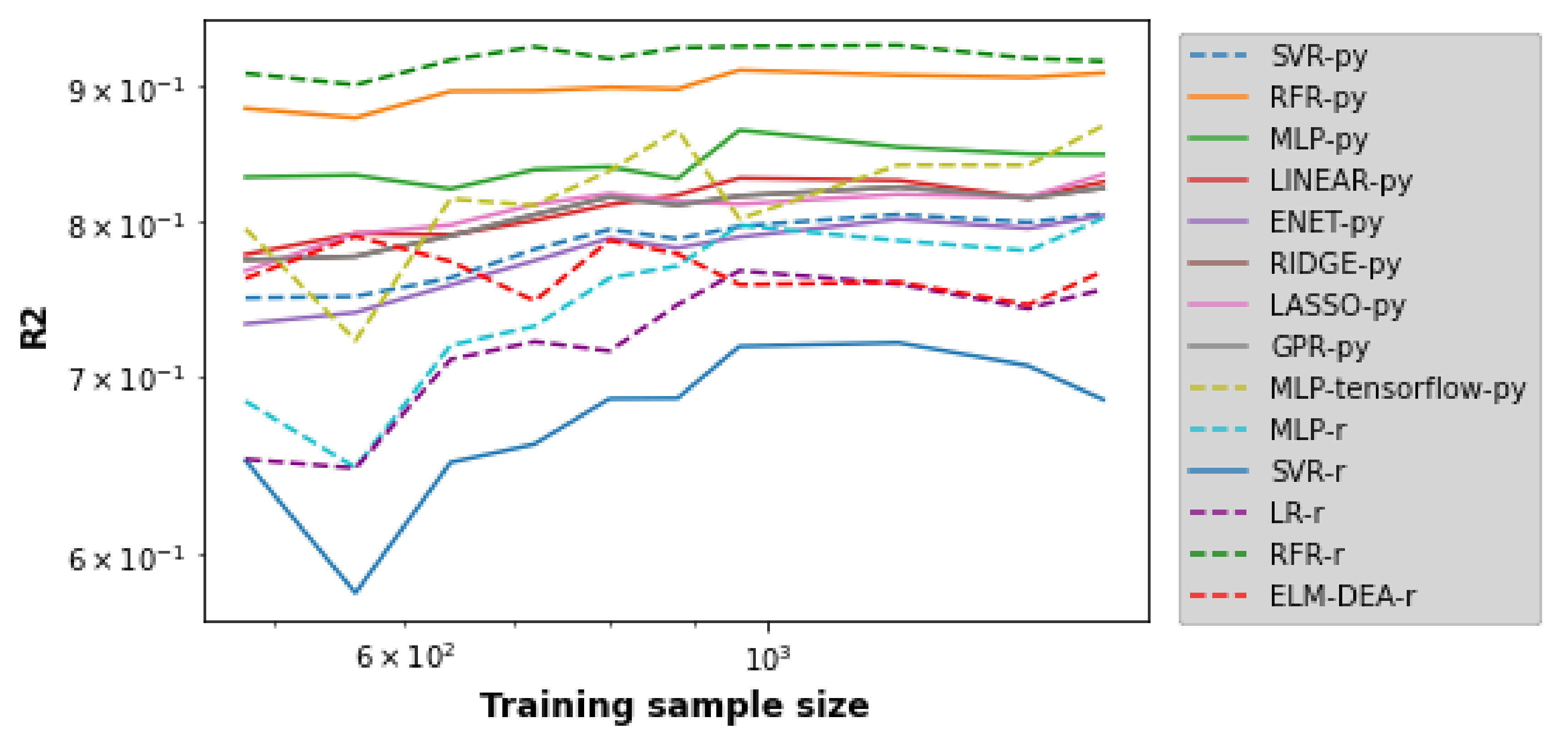
Figure 7.
Figure 7 shows the results obtained during the SML tool training and testing using 80 and 20% of the dataset, respectively. This figure does not show RFR-r because its performance was very poor; its inclusion was detrimental to achieving a good resolution of the performance of the rest of the SML tools. Again, the SML tool multiparameters were tuned via trial and error. In general,
Figure 7 reveals that as the dataset increased from 600 to 2000, R2 increased for both the SML tool training and testing. This increase in samples benefited the capture of the cell bank’s behavior regarding uncertainty space, and in turn, the SML tools’ performance. This figure shows that SVR-py, MLP-skl, LR-skl, ENR-py, RR-py, LAR-py, GPR-py, MLP-TensorFlow-py, MLP-r, and ELM-DEA-r provided an R2 close to 0.8 when the simulation sample was equal to 2000; then, they went to the next stage. In Step 4, the GSA was carried out using the Sobol–Jansen method and SMs, and the results are shown in
Figure 8 and
Figure 9.
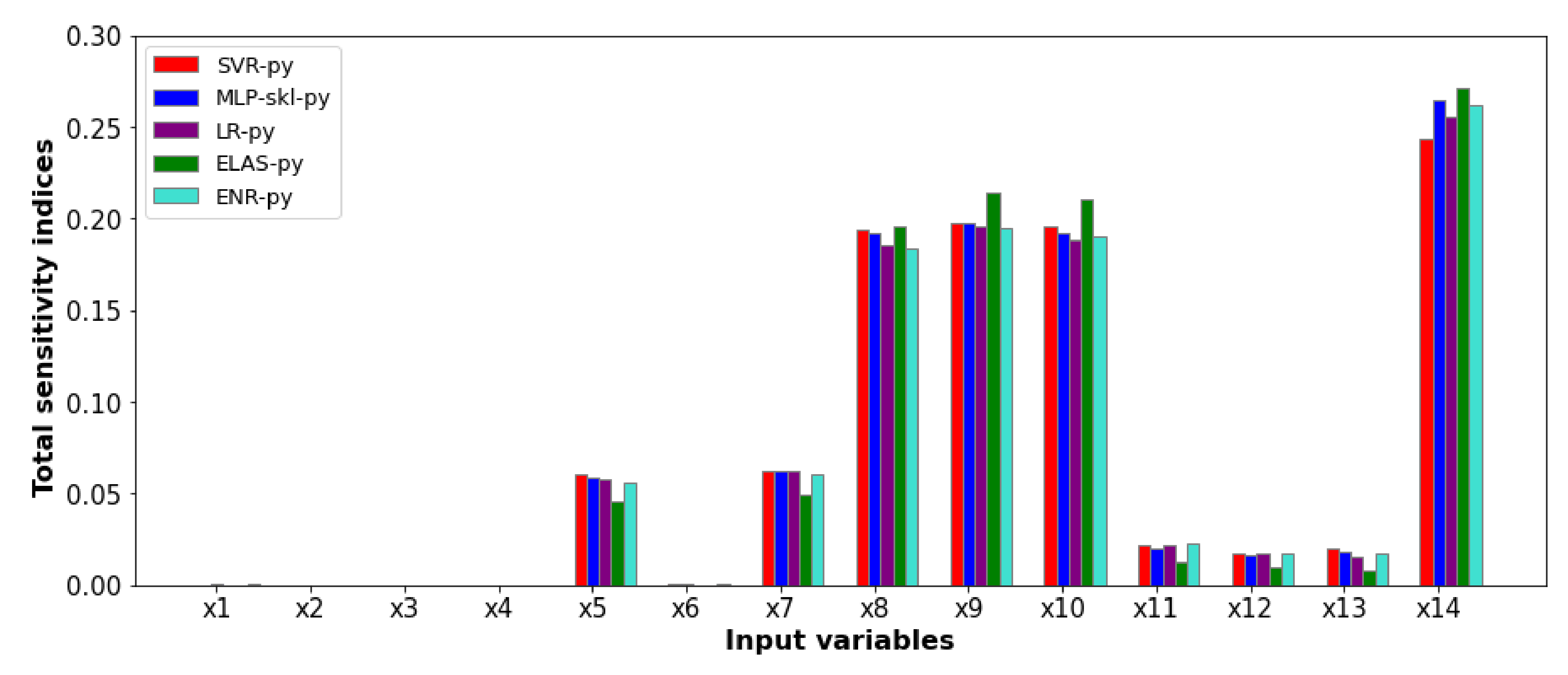
Figure 8 shows the total sensitivity indices provided by the Sobol–Jansen method for the SMs when the output variable was copper grade. Here, we see that the total sensitivity indices provided by GSA were similar. These indicated that
,
, and
influenced the cell bank’s copper grade. The particle size and superficial air velocity influenced the particle–bubble collision efficiency, and consequently, they influenced true and entrained flotation recoveries [
45,
46,
47,
48]. These results implied that the uncertainty space can be reduced to (
for the copper grade. In other words, the SM concerning copper grade can be reduced from 14-dimensional to 9-dimensional.
Figure 9 shows the total sensitivity indices for the SMs when the output variable was copper recovery. These indices were similar and indicated that
and
influenced the cell bank’s copper recovery. The flotation rate constant is directly related to the chalcopyrite mass flow present in the concentrate [
45]. Particle size directly influences the contact probability with the bubbles (“elephant curve”), as well as its settling velocity, and consequently, the true and entrainment flotation recoveries [
45,
47]. Thus, the SM concerning copper recovery can be simplified from 14-dimensional to 5-dimensional. Therefore, the Sobol–Jansen method allowed for simultaneously quantified results reported only from an experimental point of view. Input variables
,
, and
must be analyzed to optimize the cell bank copper grade, and
and
must be studied to optimize the copper recovery.
Table 5 shows the execution time required to obtain total sensitivity indices by each tool, revealing significant computational benefit by applying the methodology proposed. Again, the execution time was more significant for Python than R, revealing that the programming of the Sobol–Jansen method in Python must be enhanced.