Semi-Analytical Modeling of Geological Features Based Heterogeneous Reservoirs Using the Boundary Element Method
Abstract
:1. Introduction
2. Methodology
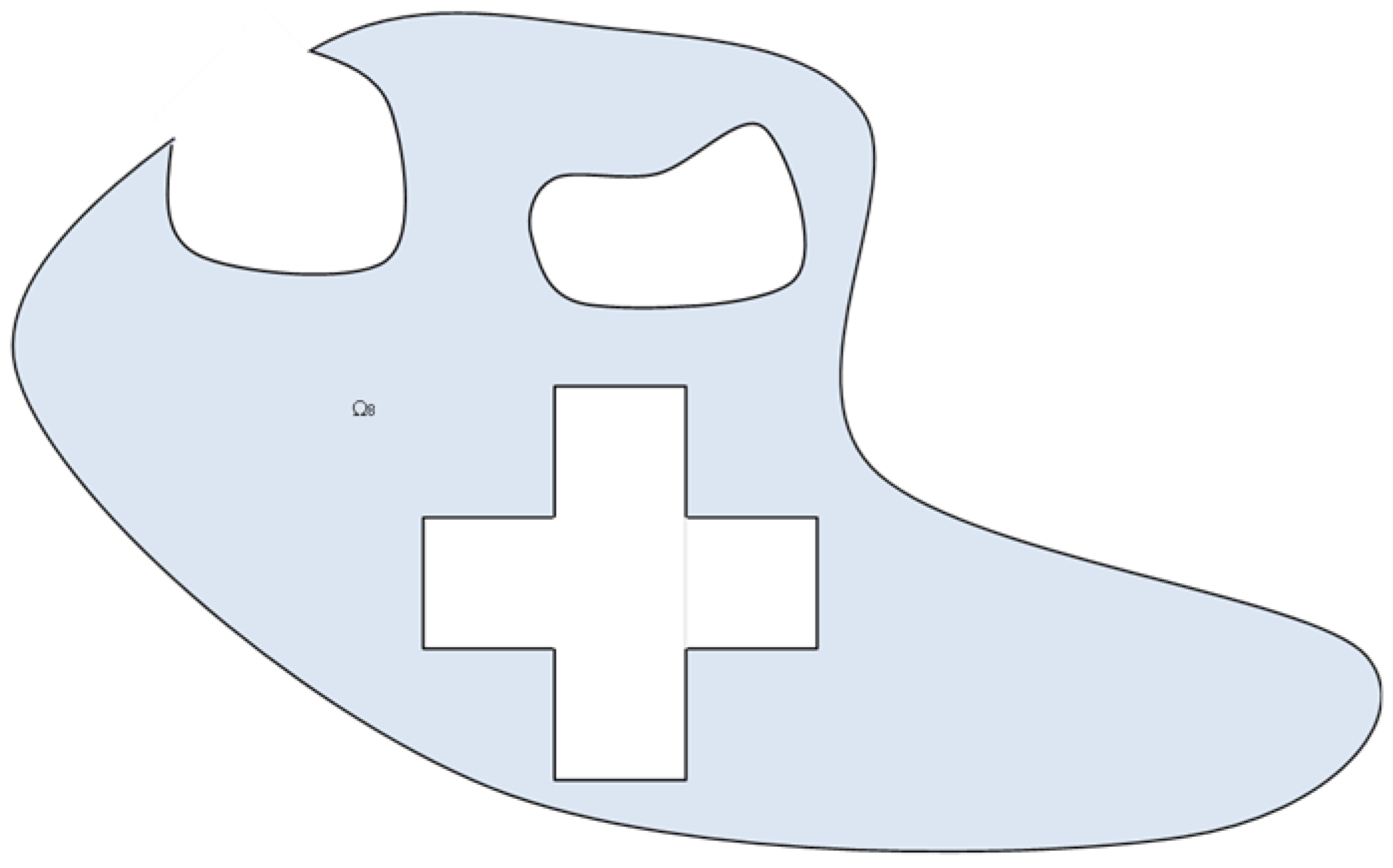
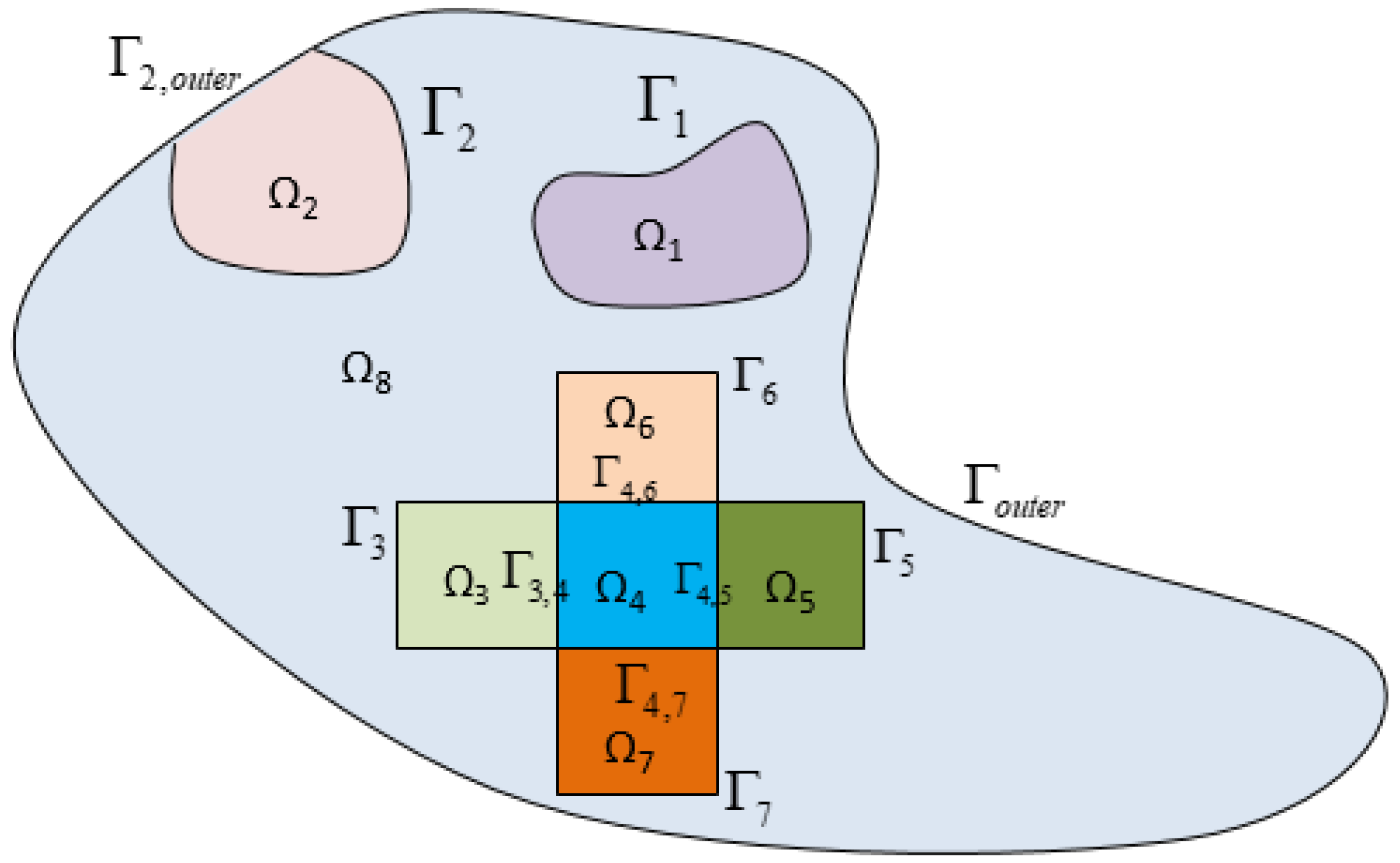
2.1. Complex Heterogeneous Reservoir Definition
2.2. Mathematical Descriptions
- Slightly compressible, single-phase fluid flow in each region was assumed.
- Rock and fluid properties in each region were considered uniform and static.
- Along the boundaries to be specified in the modeling process, the interfaces among all subsystems were treated as fully penetrated communicating planes with a uniform thickness of formation.
- Any two regions with interfaces that are in hydraulic contact with no flow resistance and the interfaces/boundaries between the two regions were static.
- Initial reservoir pressure was assumed uniform across the entire heterogeneous reservoir.
2.3. Pressure in Region 1 to 7
2.4. Pressure in Region 8
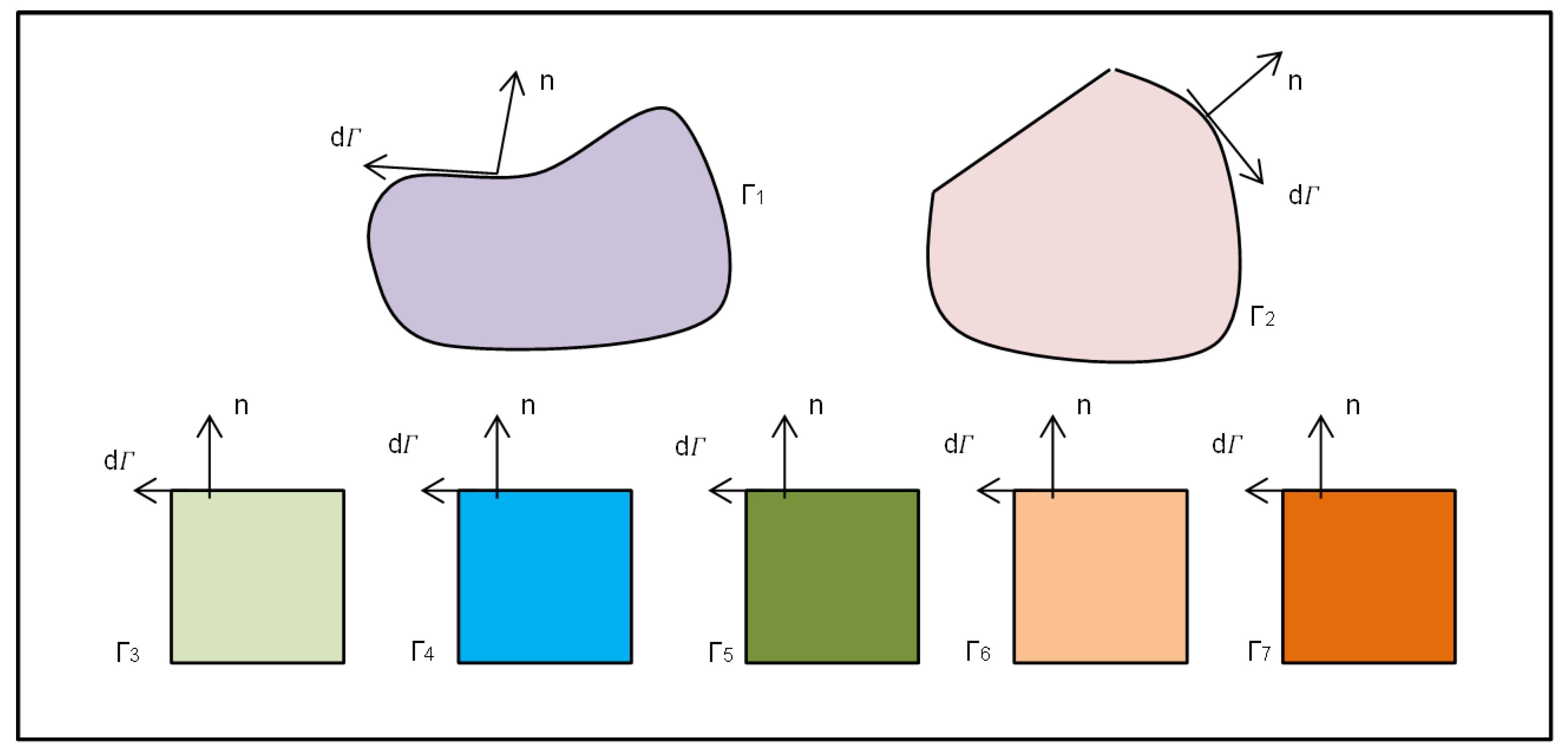
2.5. Boundary Discretization
2.6. Laplace Transformation
2.7. Linear Matrix Equations in Laplace Domain
3. Model Validity and Results
3.1. Scenario 1: Fully Compartmentalized Reservoir
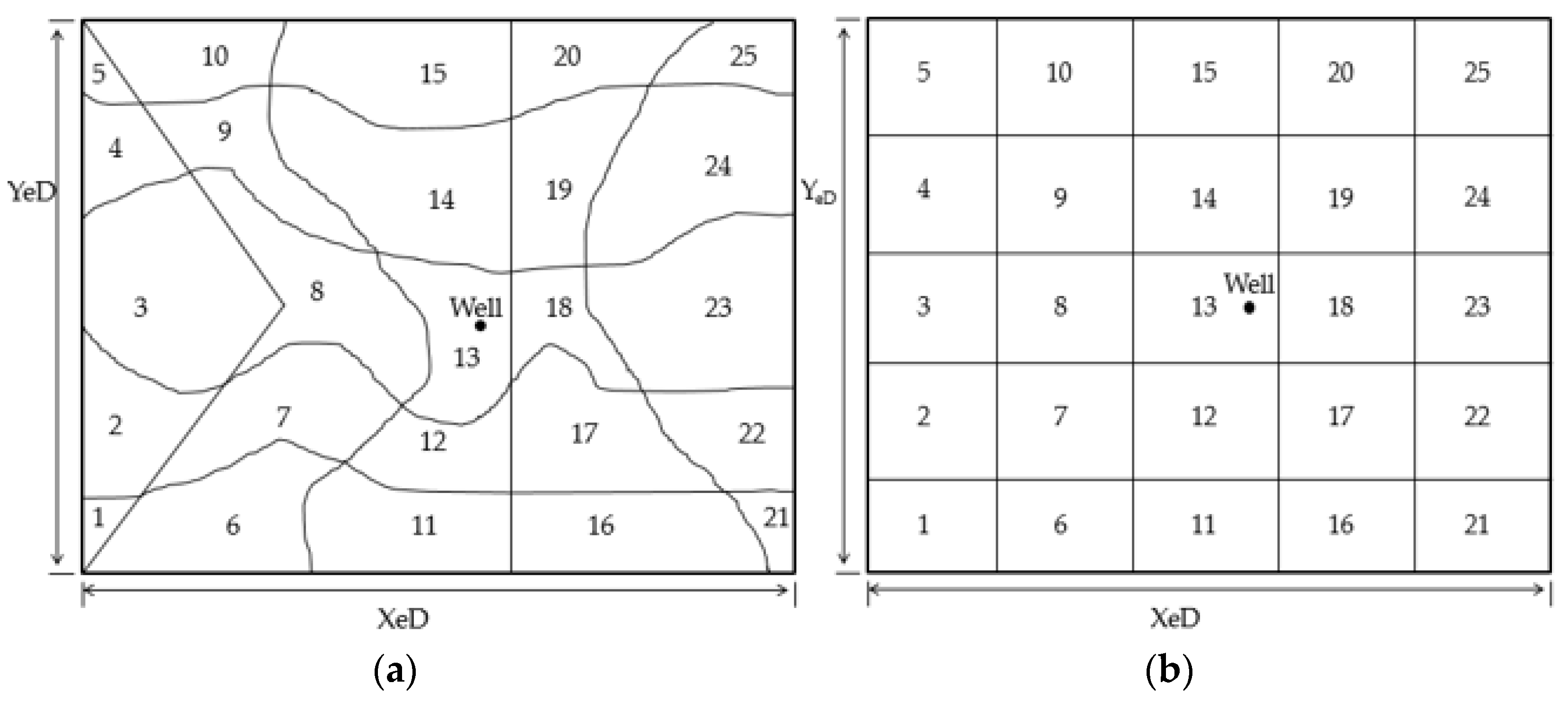
3.1.1. Scenario 1—1: Standard Reservoir with Discussion on Gridding
3.1.2. Scenarios 1—2: Linear Composite Reservoir
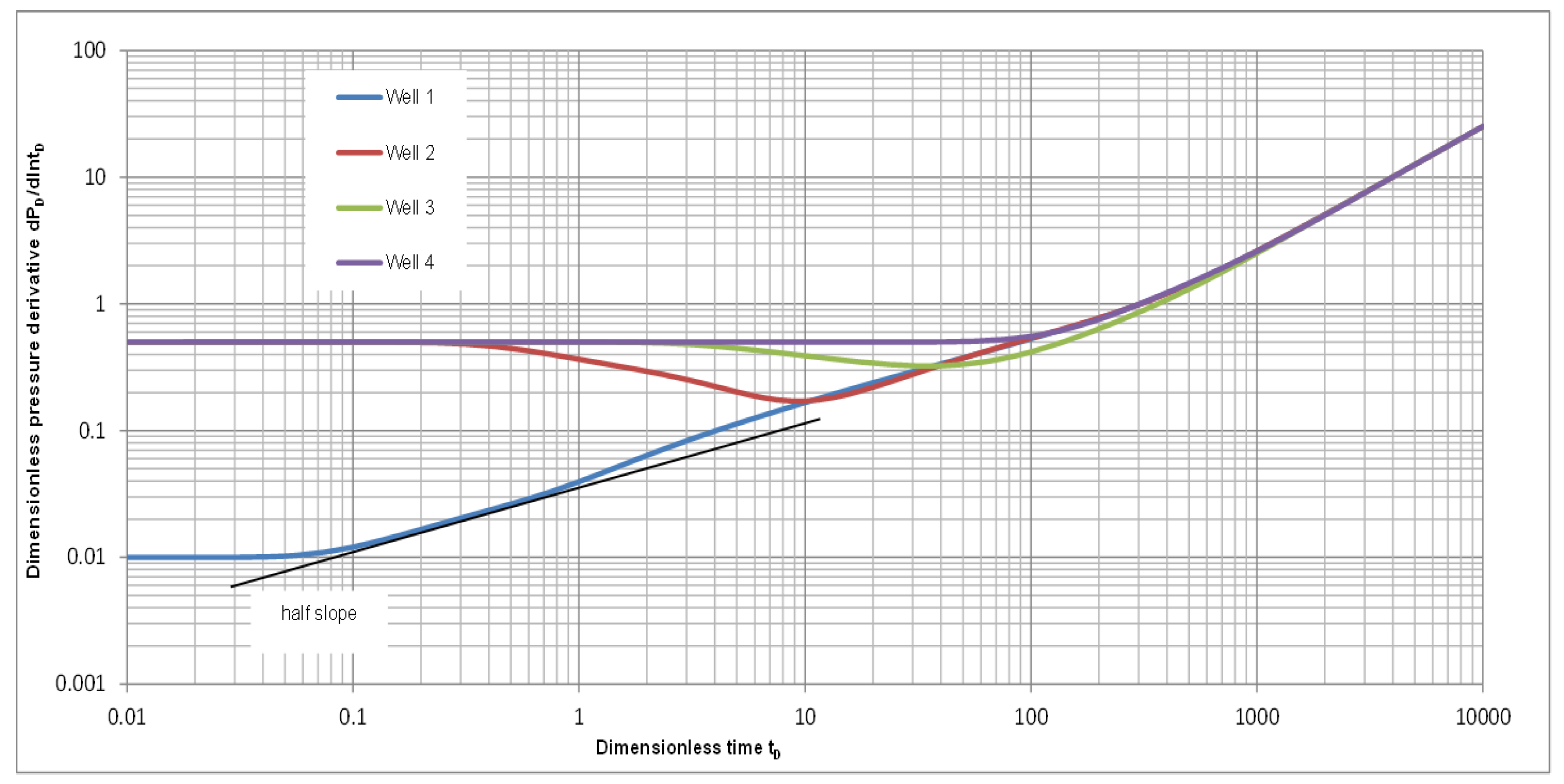
3.2. Reservoir with Multi-Scale Heterogeneities
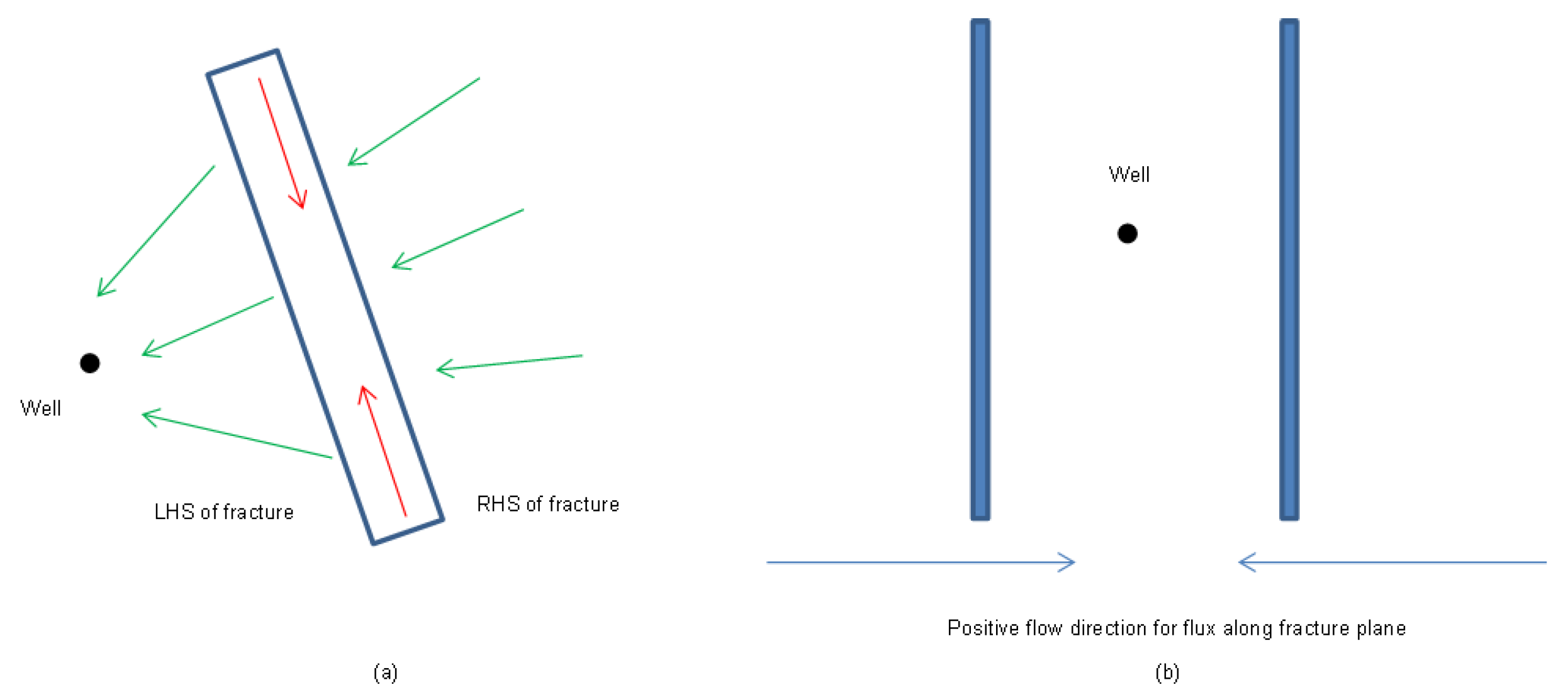
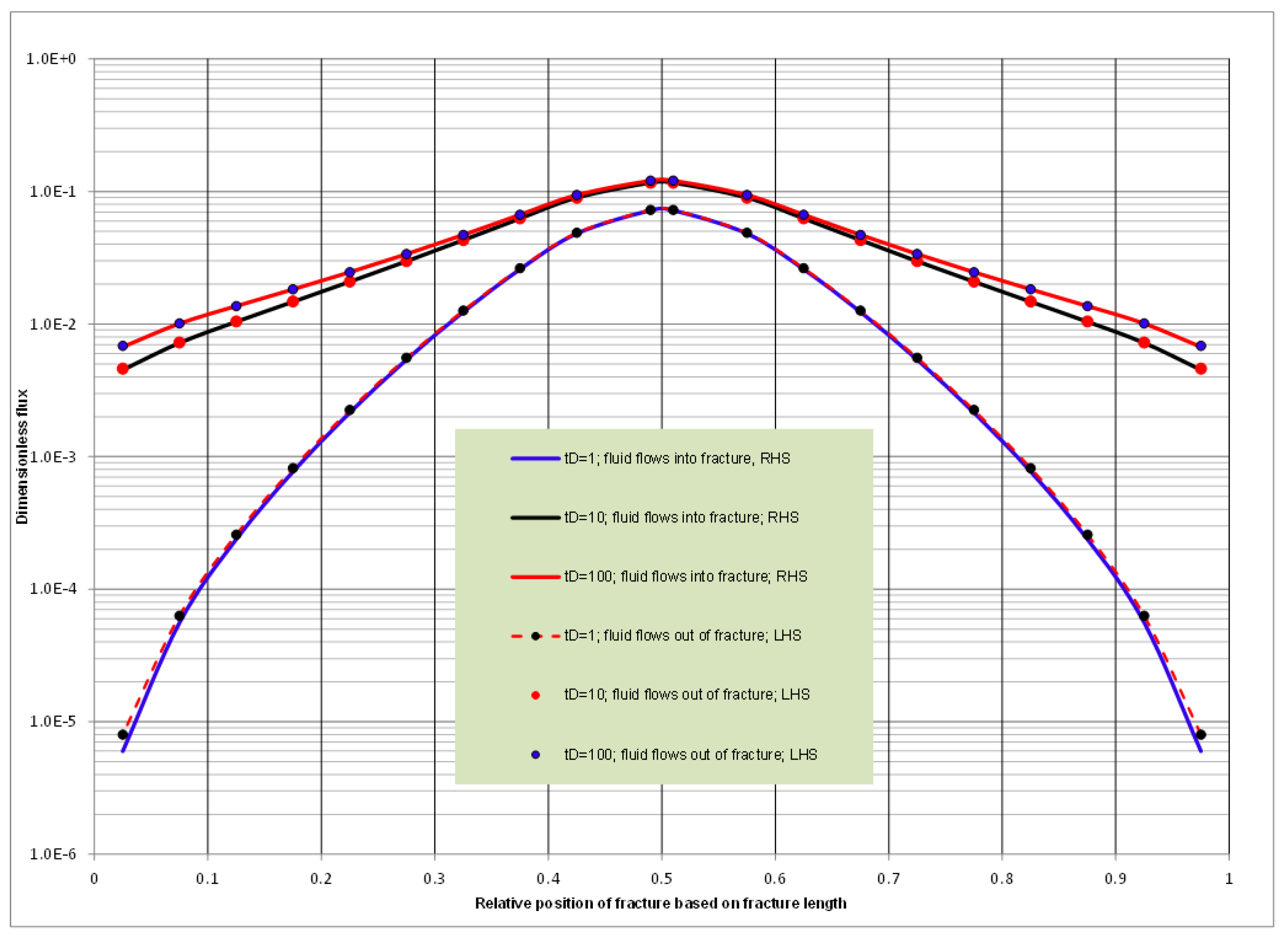
3.2.1. Scenario 2—1: A Reservoir with Two Isolated, Parallel, Natural Fractures
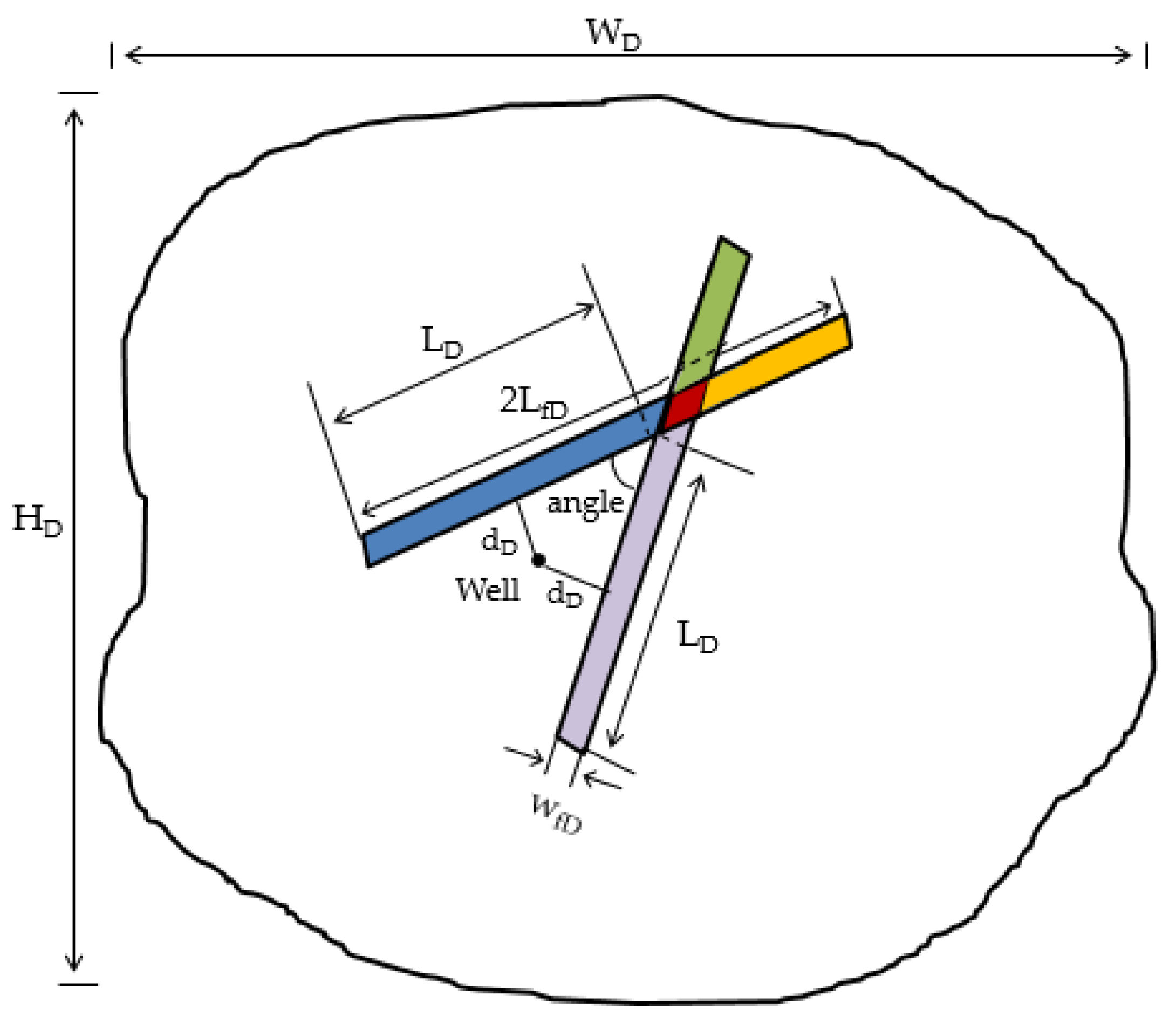
3.2.2. Scenario 2—2: A Reservoir with Two Isolated, Crossing, Natural Fractures
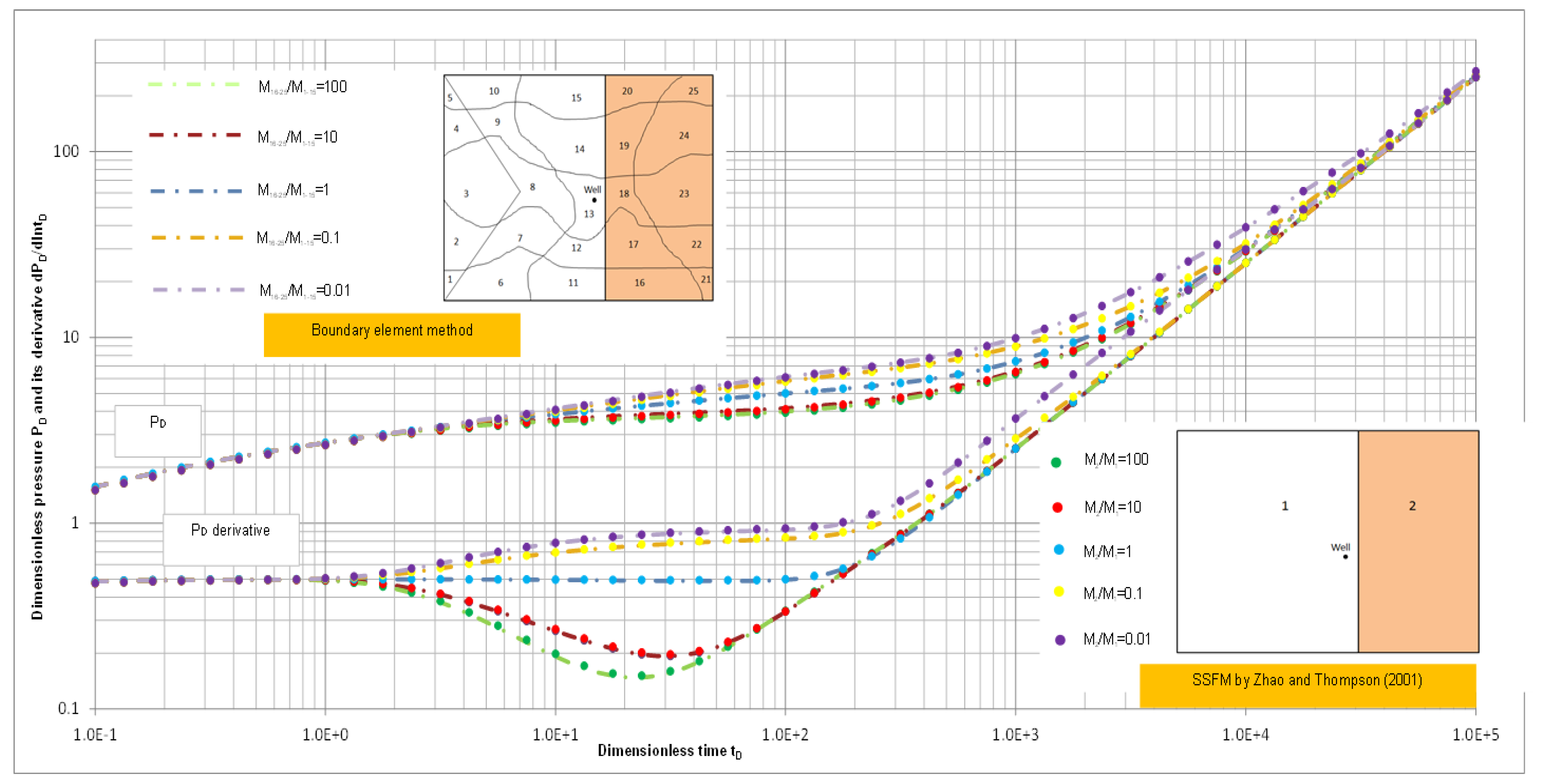
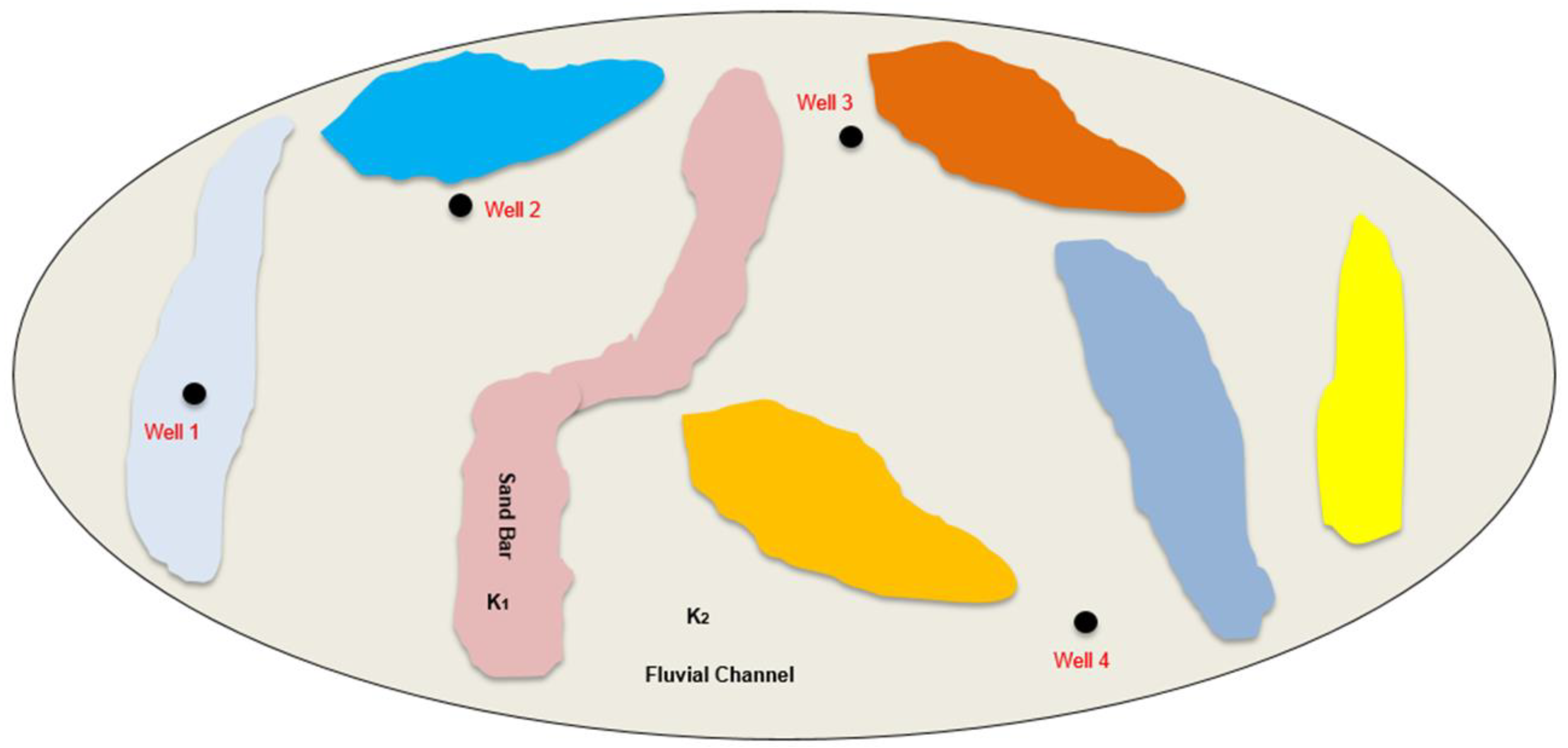
3.2.3. Scenario 2—3: Reservoir with Sandbars in Fluvial Channeling
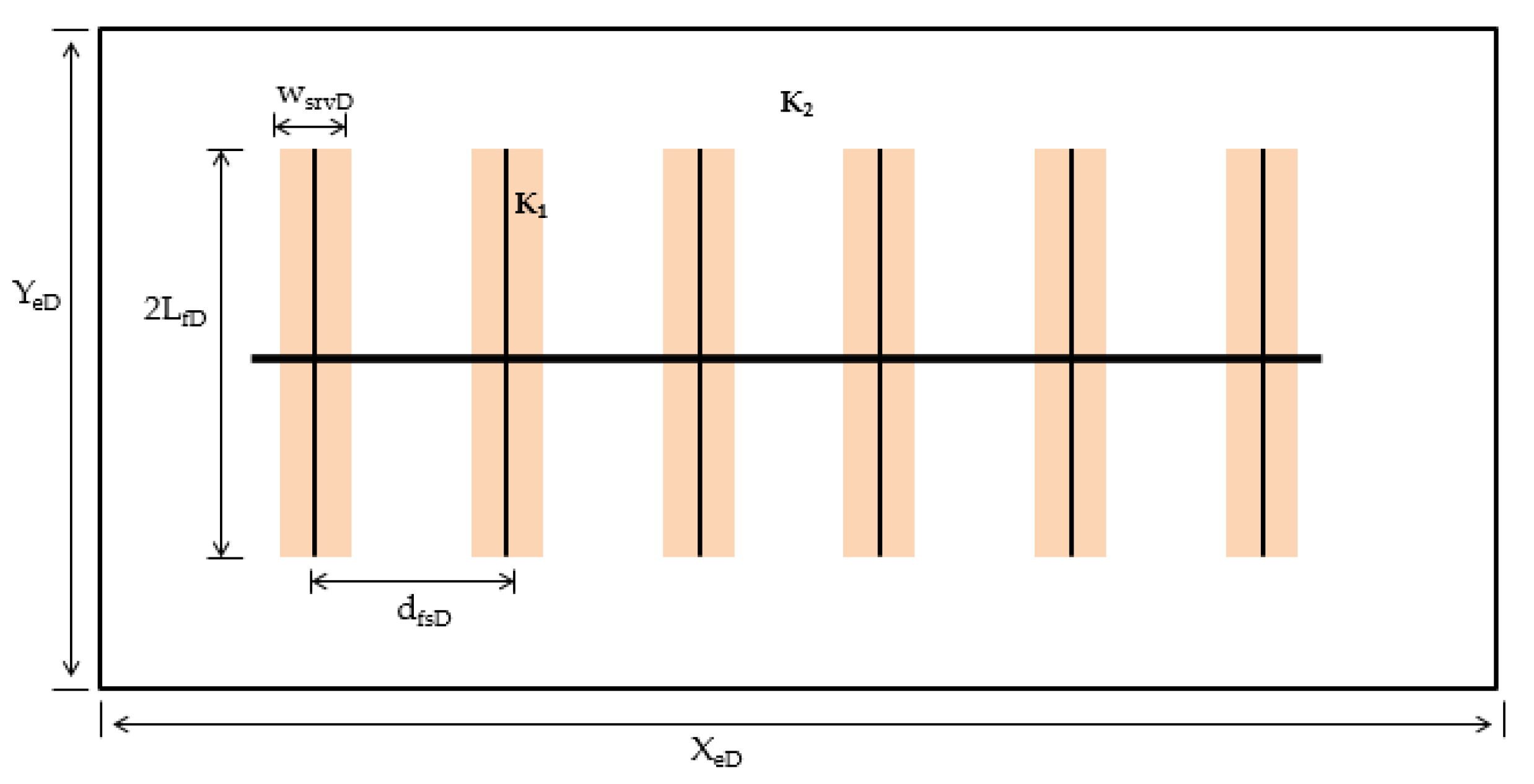
3.3. Scenario 3: Enhanced-Fracture-Region (ERF) Model
3.3.1. Effect of Local SRV Region Permeability
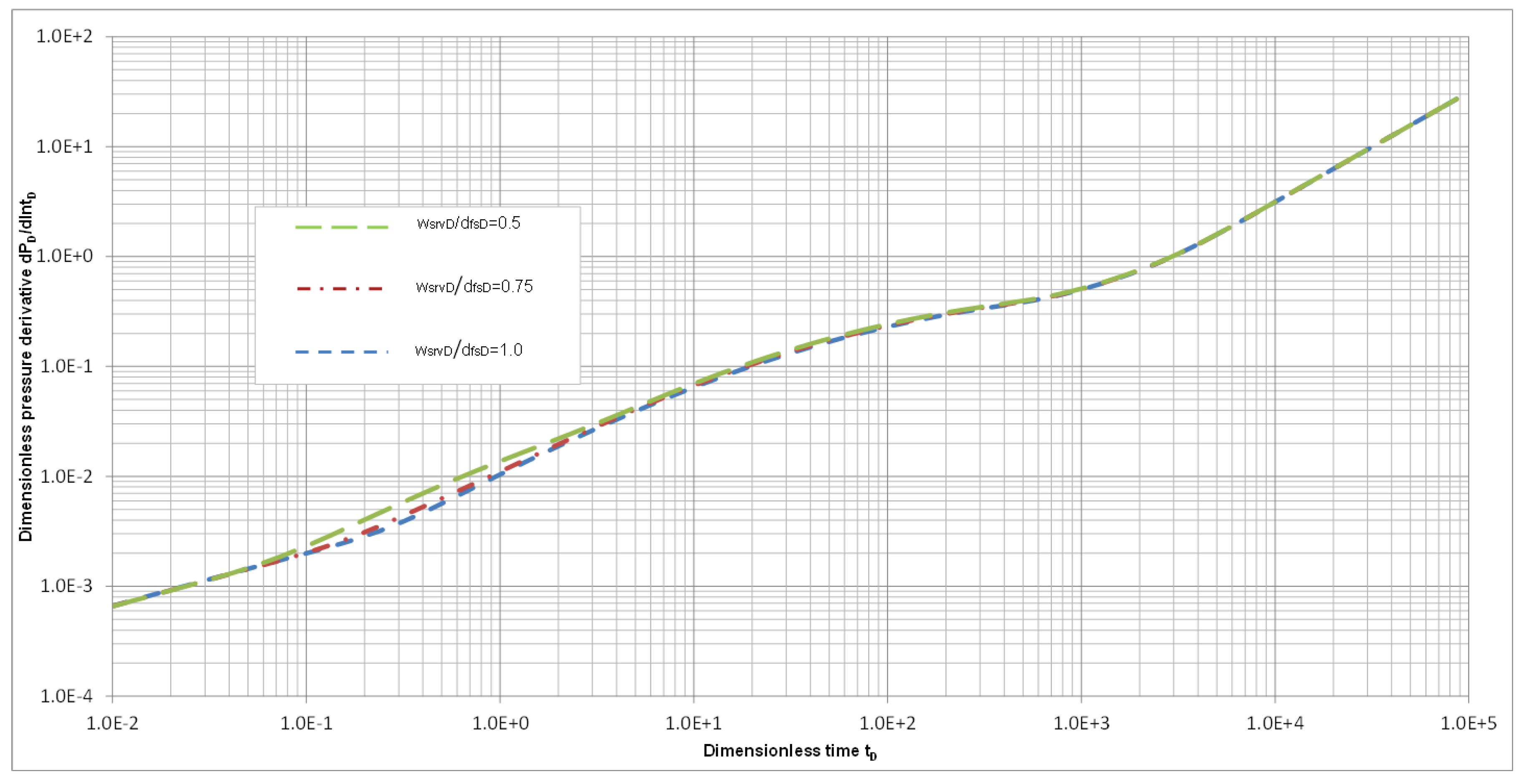
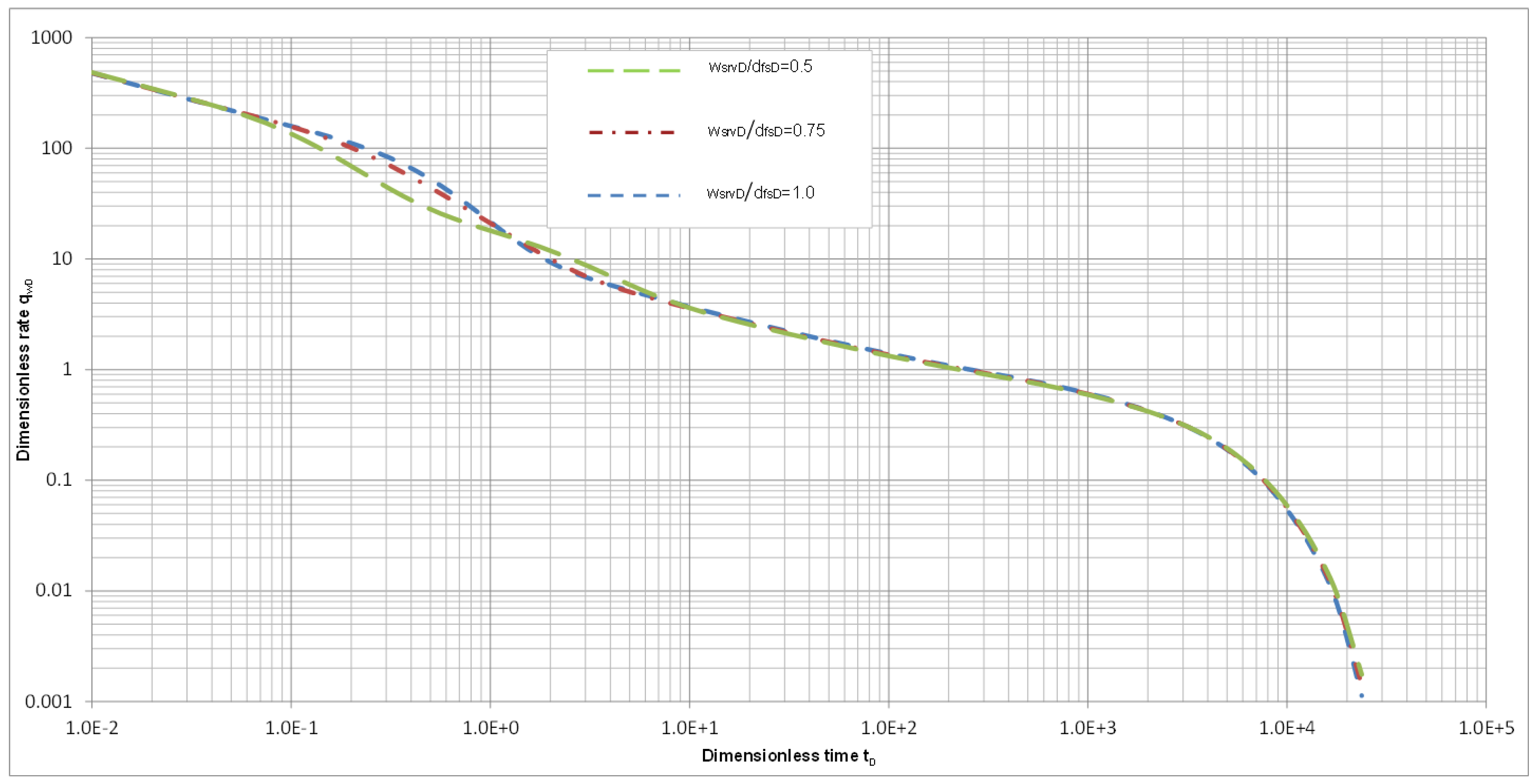
3.3.2. Effect of Local SRV Size
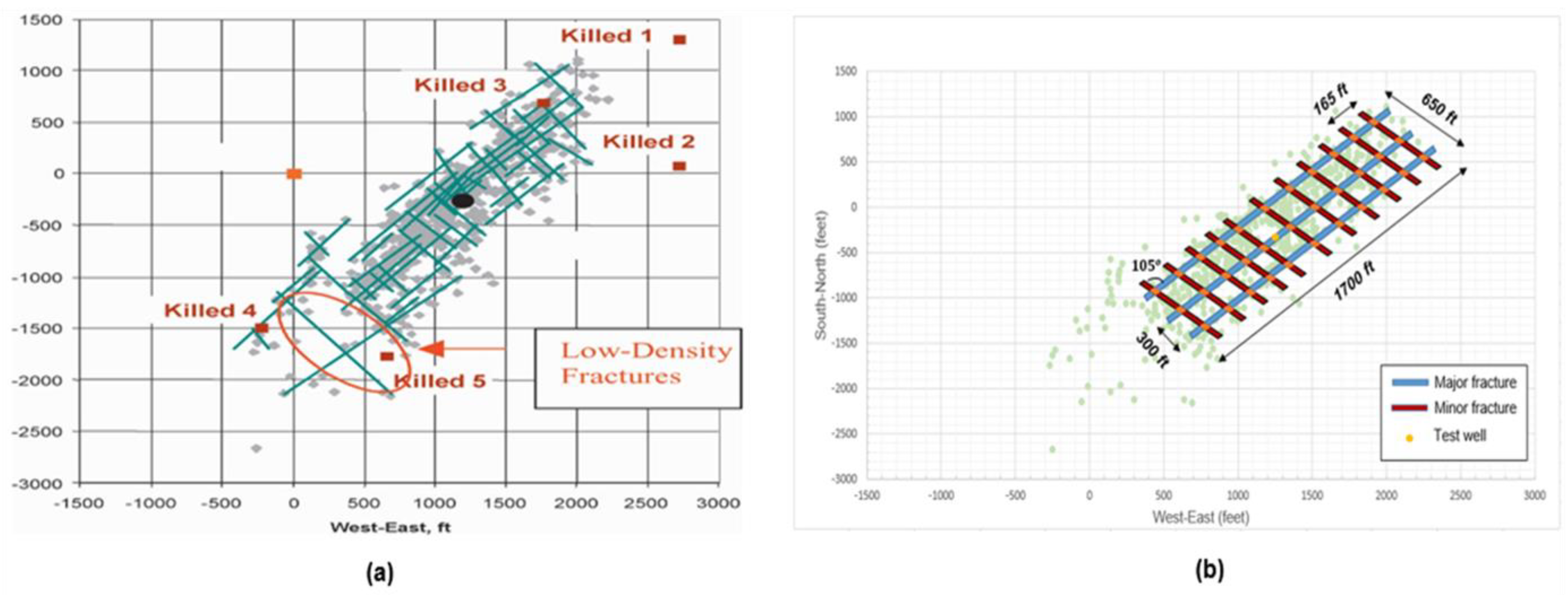
4. Field Case Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| =total compressibility of reservoir, 1/Pa | |
| =storativity, 1/Pa | |
| =diffusivity, m2/s | |
| =free-space Green’s function | |
| =reservoir vertical thickness, m | |
| =permeability, m2 | |
| L | =length, m |
| =fracture half-length, m | |
| =mobility, | |
| =the outward-pointing normal on a boundary element | |
| =discretized number of boundary element for a flow domain | |
| =discretized number of boundary element for a reservoir outer boundary directly surrounding the outer region | |
| =number of sources/sinks in a flow domain | |
| =pressure, Pa | |
| =rate of source/sink, | |
| =producing rate of well, | |
| =Laplace variable | |
| =time, s | |
| =horizontal coordinate, m | |
| =x coordinate of the source/sink point, m | |
| =horizontal coordinate, m | |
| =y coordinate of the source/sink point, m | |
| =local coordinate for boundary element, m | |
| =local coordinate for boundary element, m | |
| =reservoir diffusivity, | |
| =fluid viscosity, | |
| =time variable, s | |
| =porosity of the reservoir, fraction | |
| δ | =the Dirac delta function |
| =included angle between two boundary elements, or the term defined in Equation (3) | |
| =the function term defined in Equation (A23) | |
| =the function term defined in Equation (A24) | |
| =locally homogeneous domain | |
| =enclosed boundary for domain | |
| =reservoir outer boundary | |
| =the k-th boundary element | |
| Subscripts | |
| =boundary related term | |
| =initial | |
| =the j-th flow domain | |
| =the k-th boundary element | |
| m | =reservoir matrix |
| p | =primary fractures |
| ref | =reference system |
| s | =secondary fractures |
| =dimensionless term | |
| SRV | =stimulated reservoir volume |
Appendix A. Dimensionless Terms Defined
Appendix B. Pressure Solution Derivation of the Outer Region
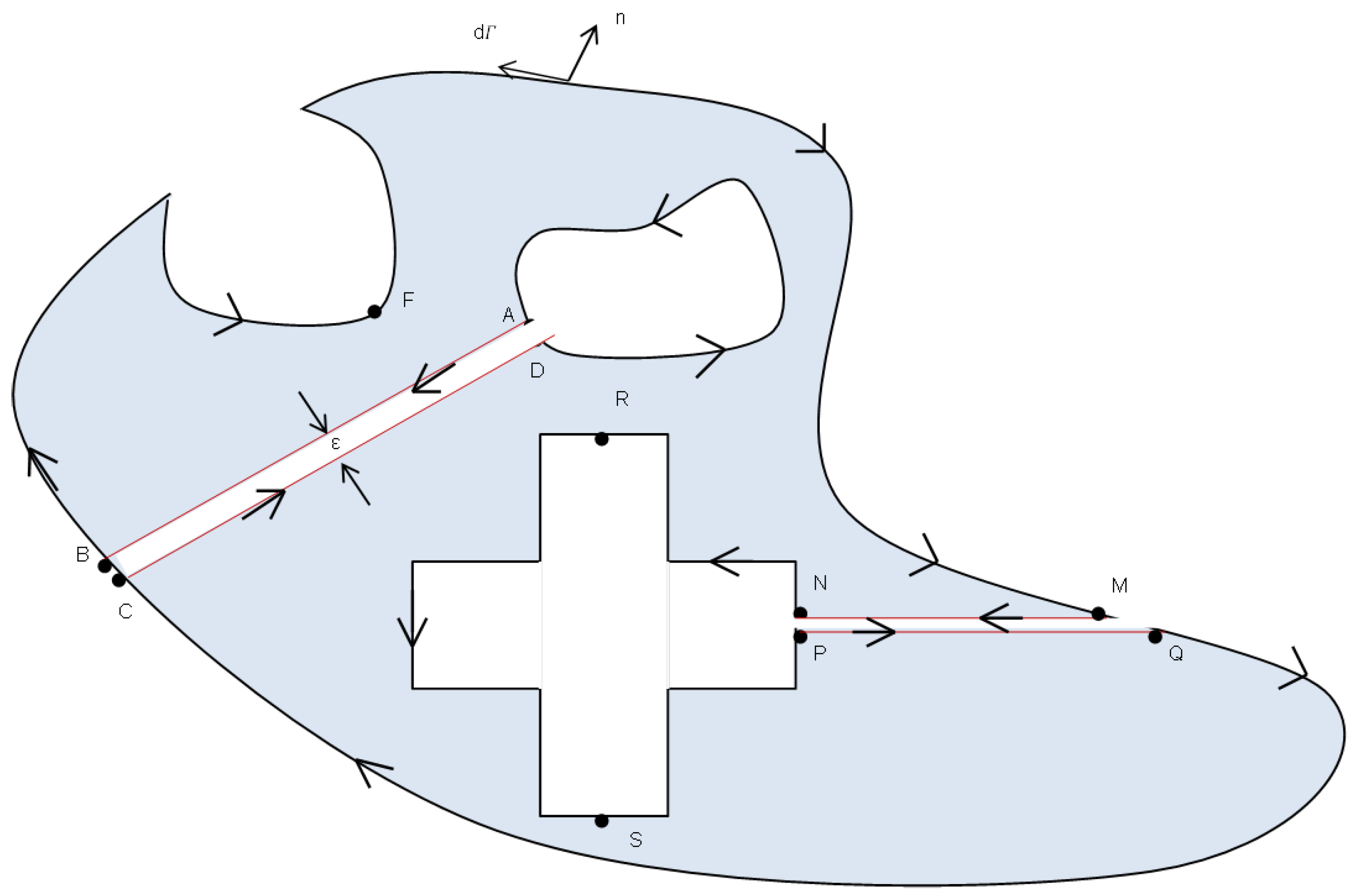
Appendix C. Pressure Solution in Discrete Form
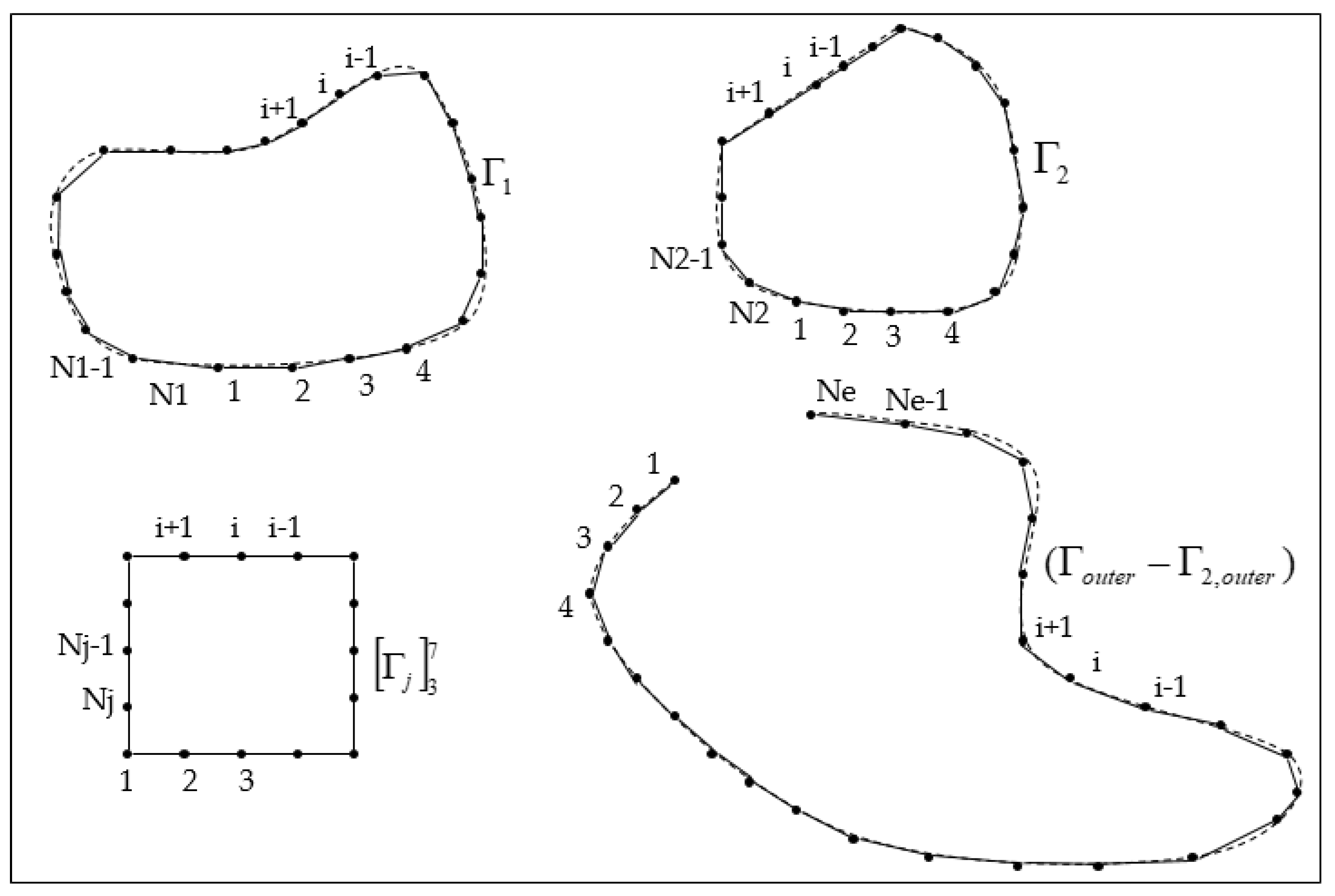
Pressure in Region 1 to 7 in Discrete Form
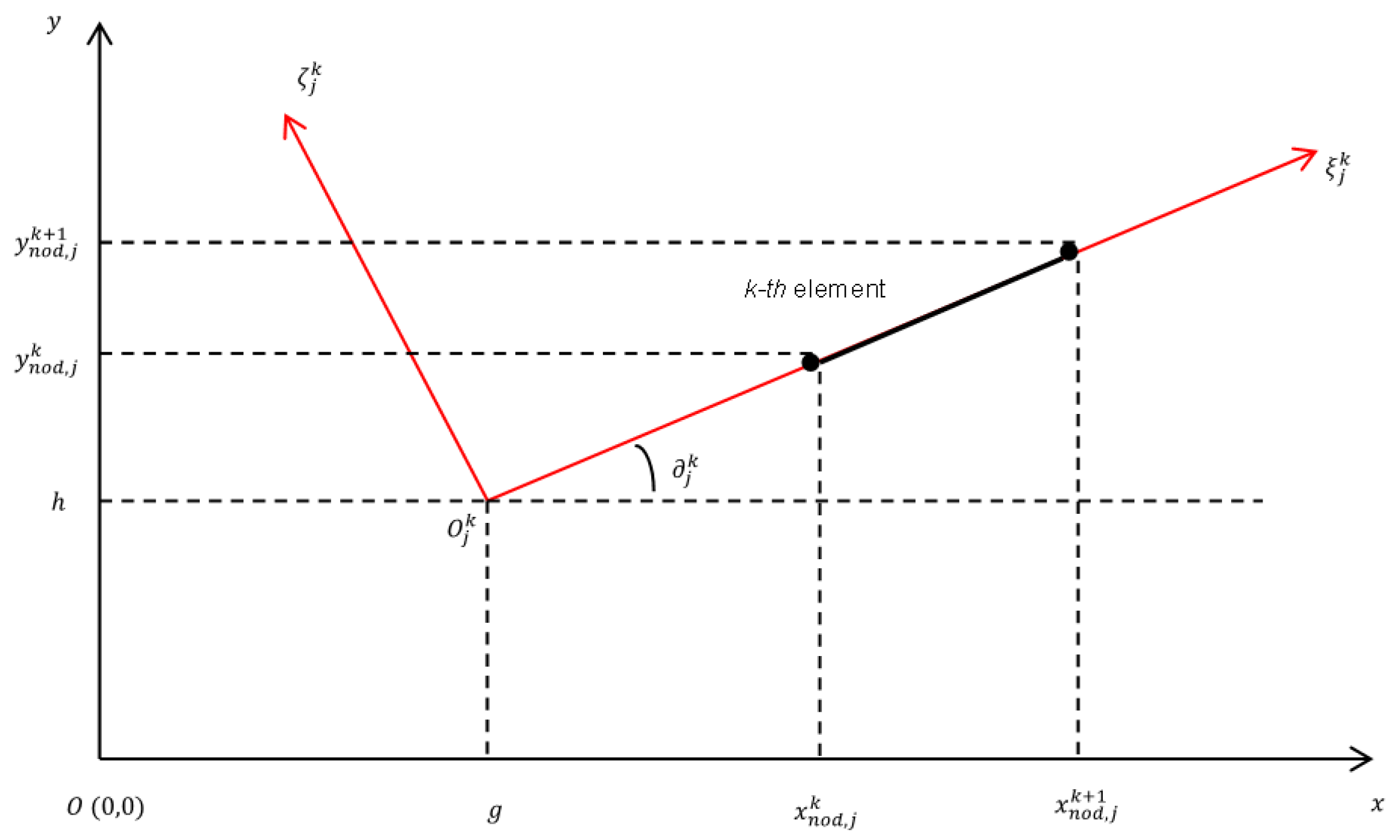
Pressure in Region 8 in Discrete Form
References
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Oxford at the Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Gringarten, A.C.; Ramey, H.J., Jr. The Use of Source and Green’s Functions in Solving Unsteady-Flow Problems in Reservoirs. Soc. Pet. Eng. J. 1973, 13, 285–296. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Ramey, H.J., Jr.; Raghavan, R. Unsteady-State Pressure Distributions Created by a Well With a Single Infinite-Conductivity Vertical Fracture. Soc. Pet. Eng. J. 1974, 14, 347–360. [Google Scholar] [CrossRef] [Green Version]
- Ozkan, E.; Raghavan, R. New Solutions for Well-Test-Analysis Problems: Part 1—Analytical Considerations. SPE Form. Eval. 1991, 6, 359–368. [Google Scholar] [CrossRef] [Green Version]
- Ozkan, E.; Raghavan, R. New Solutions for Well-Test-Analysis Problems: Part 2—Computational Considerations and Applications. SPE Form. Eval. 1991, 6, 369–378. [Google Scholar] [CrossRef]
- Ramey, H.J. Approximate Solutions For Unsteady LiquidFlow In Composite Reservoirs. J. Can. Pet. Technol. 1970, 9, 32–37. [Google Scholar] [CrossRef]
- Kuchuk, F.J.; Habashy, T. Pressure Behavior of Laterally Composite Reservoirs. SPE Form. Eval. 1997, 12, 47–56. [Google Scholar] [CrossRef]
- Basquet, R.; Alabert, F.G.; Caltagirone, J.P.; Batsale, J.C. A Semianalytical Approach for Productivity Evaluation of Complex Wells in Multilayered Reservoirs. SPE Reserv. Eval. Eng. 1999, 2, 503–513. [Google Scholar] [CrossRef]
- Medeiros, F.; Ozkan, E.; Kazemi, H. A Semianalytical Approach To Model Pressure Transients in Heterogeneous Reservoirs. SPE Reserv. Eval. Eng. 2010, 13, 341–358. [Google Scholar] [CrossRef]
- Zhao, G.; Thompson, L.G. Transient Pressure Analysis of Bounded Communicating Reservoirs. In Proceedings of the SPE Rocky Mountain Petroleum Technology Conference, Keystone, CO, USA, 21–23 May 2001. [Google Scholar] [CrossRef]
- Zhao, G.; Thompson, L.G. Semianalytical Modeling of Complex-Geometry Reservoirs. SPE Reserv. Eval. Eng. 2002, 5, 437–446. [Google Scholar] [CrossRef]
- Zhao, G.; Thompson, L.G. Transient Pressure Response of Fluvial Reservoir with Branching Channel and Splay. In Proceedings of the 2001 SPE Annual Technical Conference and Exhibition, New Orleans, LO, USA, 30 September–3 October 2001. [Google Scholar] [CrossRef]
- Zhao, G.; Thompson, L.G. Well Testing Analysis in Heterogeneous Reservoir Using Semi-Analytical Method. In Proceedings of the 55th Annual Technical Meeting, Canadian International Petroleum Conference (CIPC), Petroleum Society Canadian Institute of Mining, Metallurgy & Petroleum, Calgary Stampede Roundup Centre, Calgary, AB, Canada, 8–10 June 2004. [Google Scholar]
- Zhao, G. Reservoir Modeling Method. U.S. Patent 8,275,593, 25 September 2012. [Google Scholar]
- Kikani, J.; Horne, R.N. Pressure-Transient Analysis of Arbitrarily Shaped Reservoirs With the Boundary-Element Method. SPE Form. Eval. 1992, 7, 53–60. [Google Scholar] [CrossRef]
- Xiao, L.; Zhao, G.; Qing, H. A Compatible Boundary Element Approach with Geologic Modeling Techniques to Model Transient Fluid Flow in Heterogeneous Systems. J. Pet. Sci. Eng. 2017, 151, 318–329. [Google Scholar] [CrossRef]
- Wu, M.; Ding, M.; Yao, J.; Li, C.; Huang, Z.; Xu, S. Production-Performance Analysis of Composite Shale-Gas Reservoirs by the Boundary-Element Method. SPE Reserv. Eval. Eng. 2018, 22, 238–252. [Google Scholar] [CrossRef] [Green Version]
- Lennon, G.P.; Liu, P.L.-F.; Liggett, J.A. Boundary Integral Solutions to Three-Dimensional Unconfined Darcy’s Flow. Water Resour. Res. 1980, 16, 651–658. [Google Scholar] [CrossRef]
- Lafe, O.E.; Liggett, J.A.; Liu, P.L.-F. BEIM Solutions to Combinations of Leaky, Layered, Confined, Unconfined, Nonisotropic Aquifers. Water Resour. Res 1981, 17, 1431–1444. [Google Scholar] [CrossRef]
- Azevedo, J.P.S.; Wrobel, L.C. Non-Linear Heat Conduction in Composite Bodies: A Boundary Element Formulation. Int. J. Numer. Methods Eng. 1988, 26, 19–38. [Google Scholar] [CrossRef]
- Bialecki, R.; Kuhn, G. Boundary Solution of Heat Conduction Problems in Multizone Bodies of Non-Linear Materials. Int. J. Numer. Methods Eng. 1993, 36, 799–809. [Google Scholar] [CrossRef]
- Kikani, J.; Horne, R.N. Modeling Pressure-Transient Behavior of Sectionally Homogeneous Reservoirs by the Boundary-Element Method. SPE Form. Eval. 1993, 8, 145–152. [Google Scholar] [CrossRef]
- Layne, M.A.; Numbere, D.T.; Koederitz, L.F. Future Performance Prediction for Water Drive Gas Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3 October 1993. [Google Scholar] [CrossRef]
- Pecher, R.; Stanislav, J.F. Boundary Element Techniques in Petroleum Reservoir Simulation. J. Pet. Sci. Eng. 1997, 17, 353–366. [Google Scholar] [CrossRef]
- Xiao, L.; Zhao, G. Estimation of CHOPS Wormhole Coverage From Rate/Time Flow Behaviors. SPE Reserv. Eval. Eng. 2017, 20, 957–973. [Google Scholar] [CrossRef]
- Wu, Y.; Cheng, L.; Fang, S.; Huang, S.; Jia, P. A Green Element Method-Based Discrete Fracture Model for Simulation of the Transient Flow in Heterogeneous Fractured Porous Media. Adv. Water Resour. 2020, 136, 103489. [Google Scholar] [CrossRef]
- Su, C. Semi-Analytical Modeling of Fluid Flow in and Formation Evaluation of Unconventional Reservoir Using Boundary Integration Strategies. Dissertation, University of Regina, Saskatchewan, SK, Canada, 2018. [Google Scholar]
- Onur, M.; Reynolds, A.C. Numerical Laplace Transformation of Sampled Data for Well-Test Analysis. SPE Reserv. Eval. Eng. 1998, 1, 268–277. [Google Scholar] [CrossRef]
- Stehfest, H. Numerical Inversion of Laplace Transforms. Commun. ACM 1970, 13, 47. [Google Scholar] [CrossRef]
- Karimi-Fard, M.; Durlofsky, L.J. A General Gridding, Discretization, and Coarsening Methodology for Modeling Flow in Porous Formations With Discrete Geological Features. Adv. Water Resour. 2016, 96, 354–372. [Google Scholar] [CrossRef]
- Xu, Y.; Cavalcante Filho, J.S.; Yu, W.; Sepehrnoori, K. Discrete-Fracture Modeling of Complex Hydraulic-Fracture Geometries in Reservoir Simulators. SPE Reserv. Eval. Eng. 2016, 20, 403–422. [Google Scholar] [CrossRef]
- Zhao, G. Modeling Complex Natural Fracture Network in Heterogeneous Tight Formations Using Semi-Analytical Strategy. In Proceedings of the SPE Unconventional Resources Conference, Calgary, AB, Canada, 5 November 2013. [Google Scholar] [CrossRef]
- Stalgorova, E.; Mattar, L. Analytical Model for Unconventional Multifractured Composite Systems. SPE Reserv. Eval. Eng. 2013, 16, 246–256. [Google Scholar] [CrossRef]
- Chen, C.; Raghavan, R. On Some Characteristic Features of Fractured-Horizontal Wells and Conclusions Drawn Thereof. SPE Reserv. Eval. Eng. 2013, 16, 19–28. [Google Scholar] [CrossRef]
- Zhao, G. A Simplified Engineering Model Integrated Stimulated Reservoir Volume (SRV) and Tight Formation Characterization With Multistage Fractured Horizontal Wells. In Proceedings of the SPE Canadian Unconventional Resources Conference, Calgary, AB, Canada, 30 October 2012. [Google Scholar] [CrossRef]
- Fisher, M.K.; Wright, C.A.; Davidson, B.M.; Goodwin, A.K.; Fielder, E.O.; Buckler, W.S.; Steinsberger, N.P. Integrating Fracture Mapping Technologies to Optimize Stimulations in the Barnett Shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TA, USA, 29 September 2002. [Google Scholar] [CrossRef]


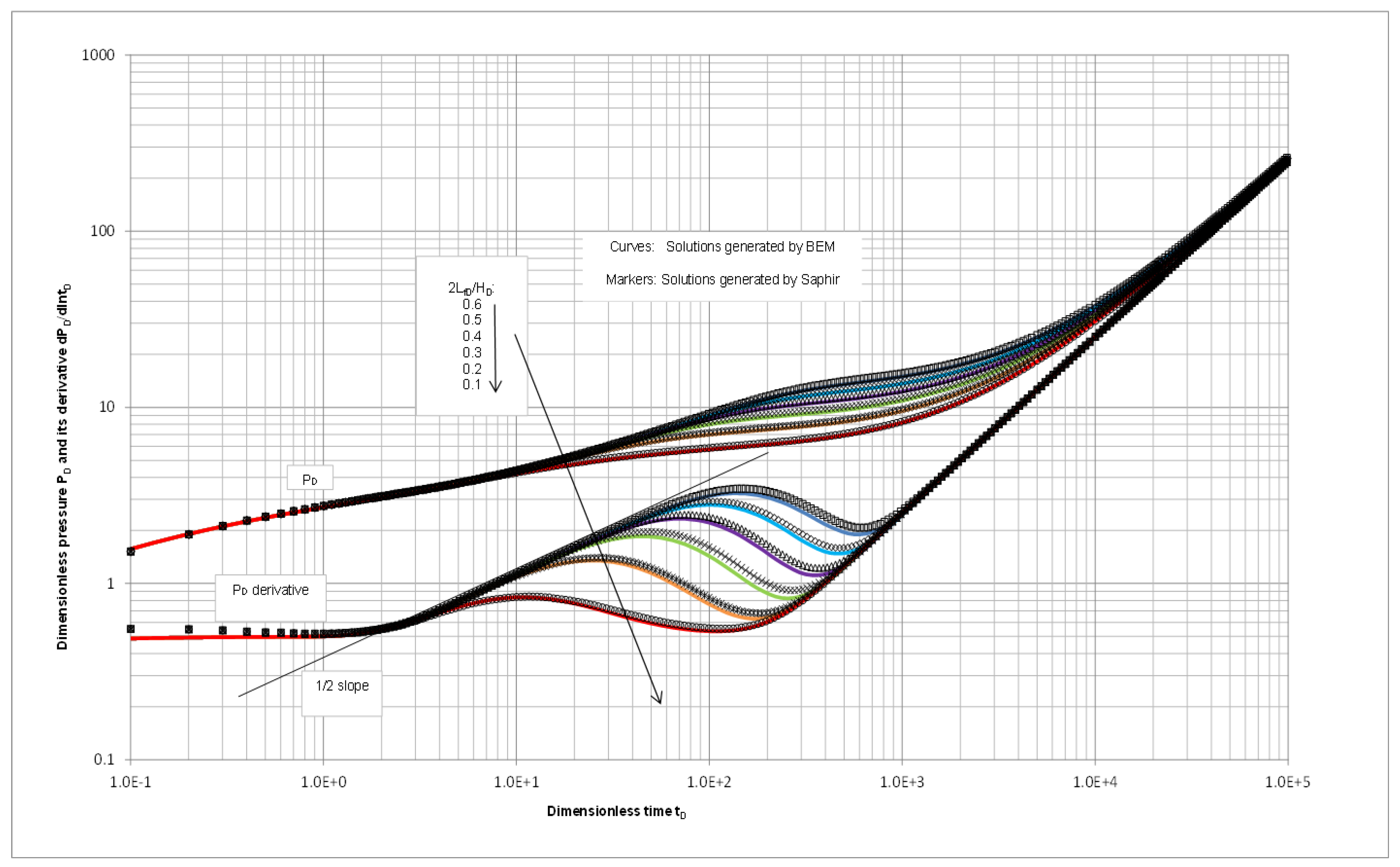
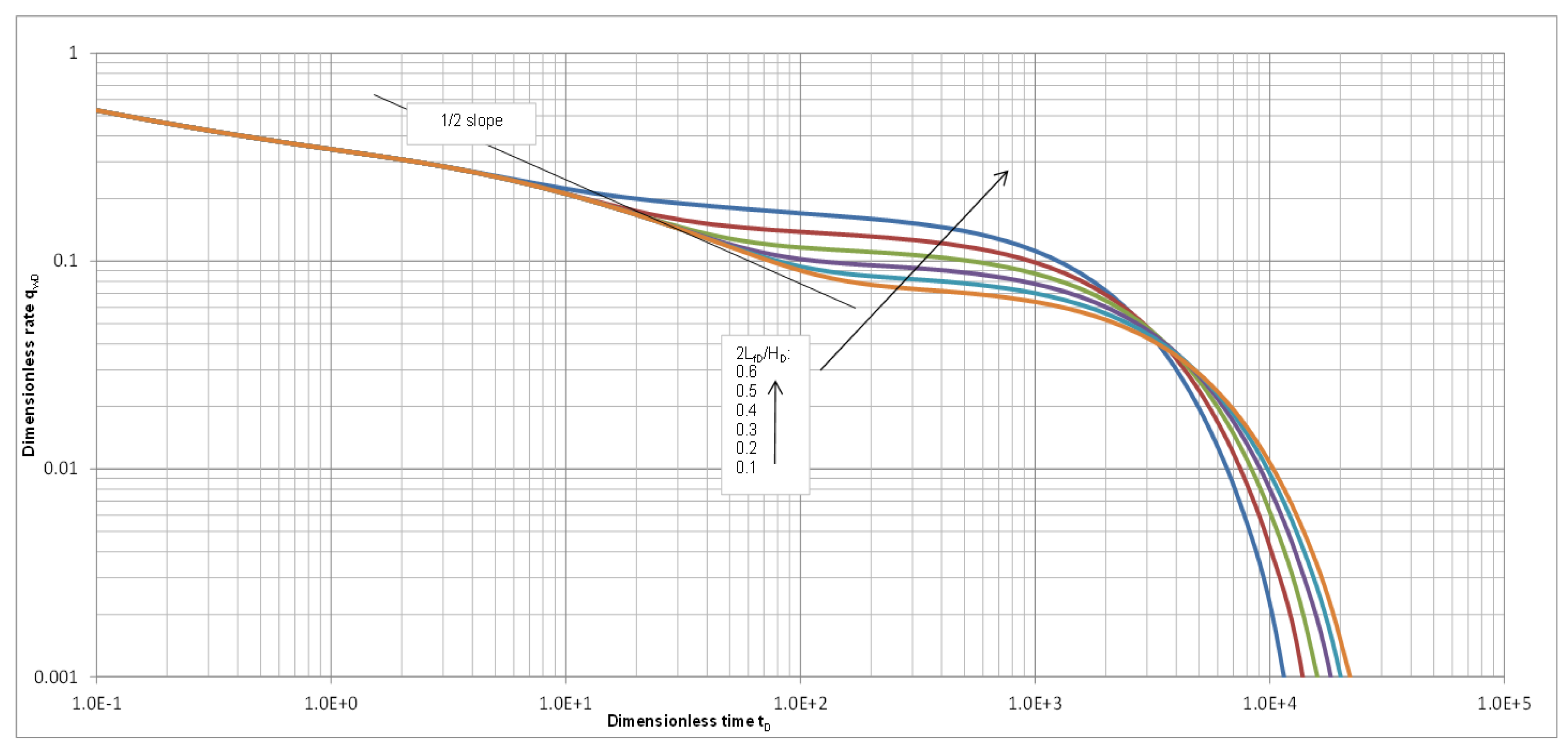
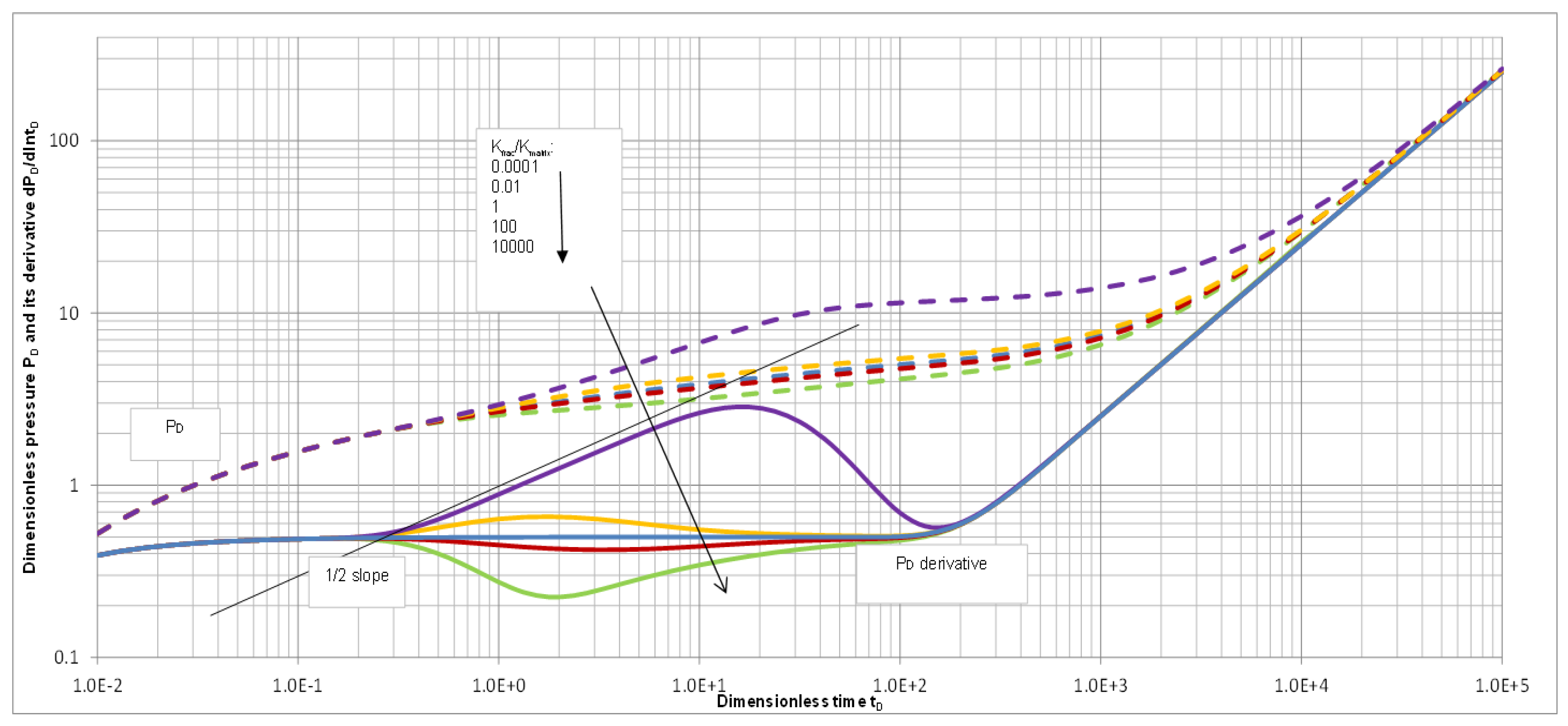
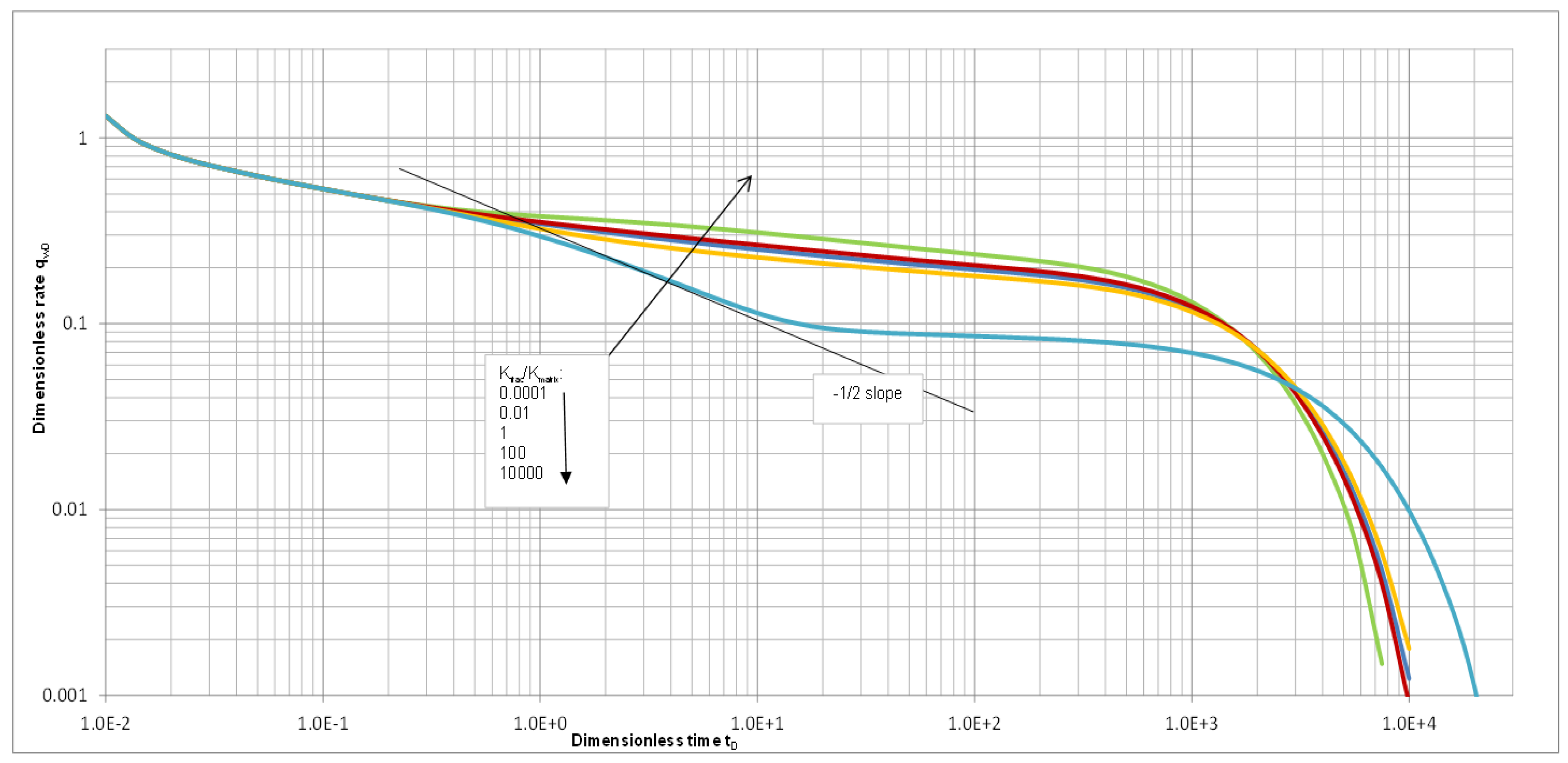





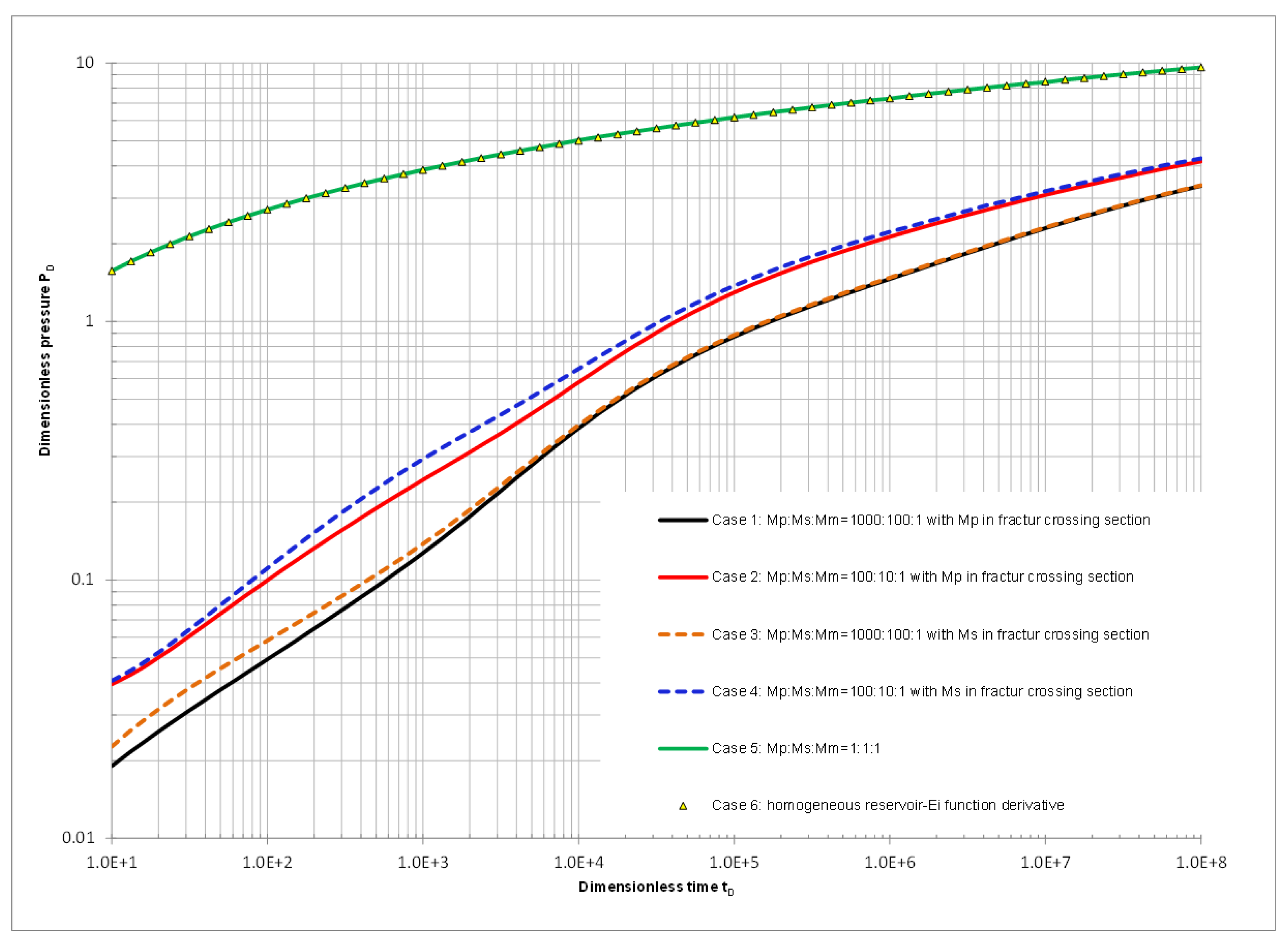
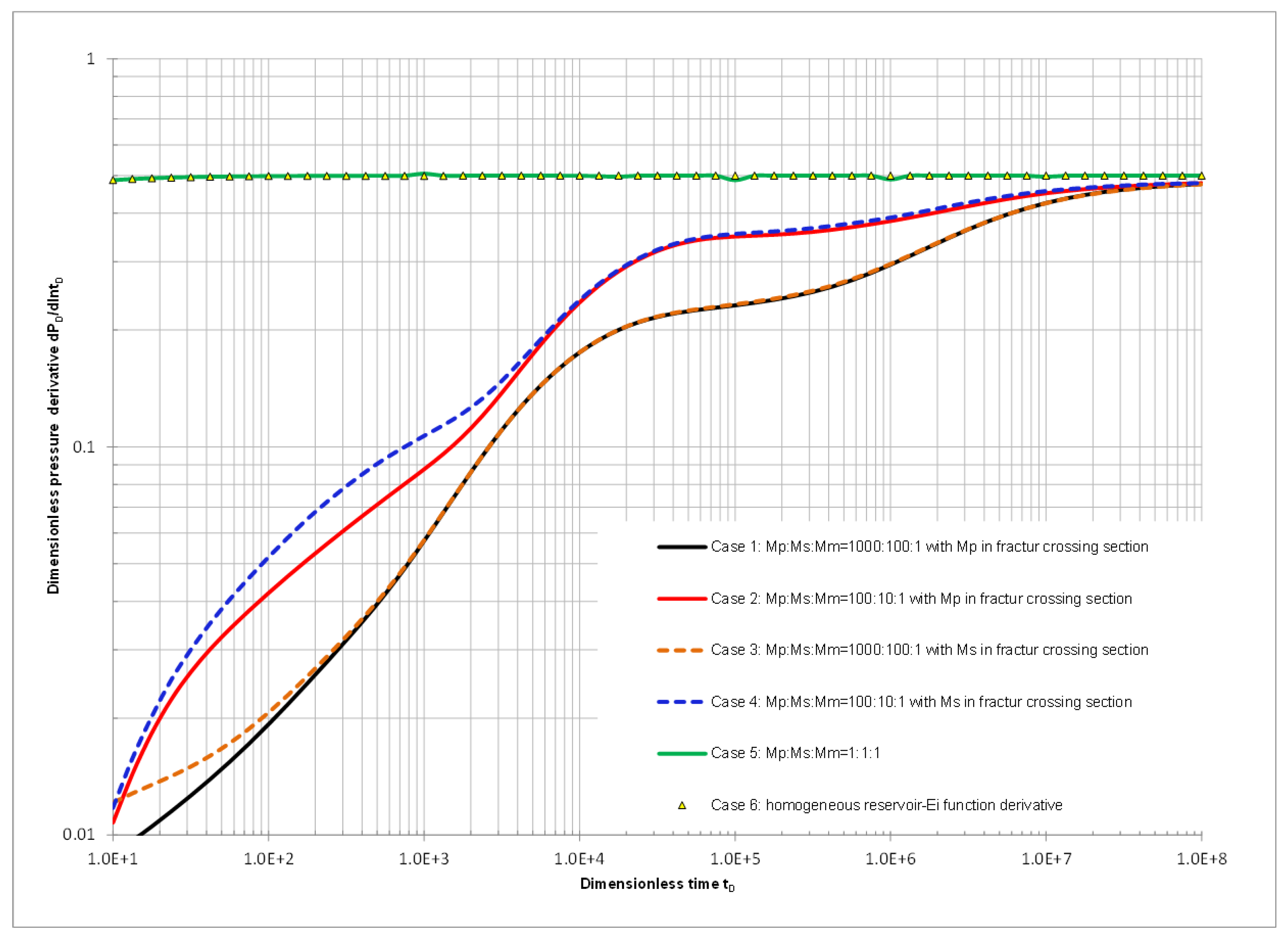
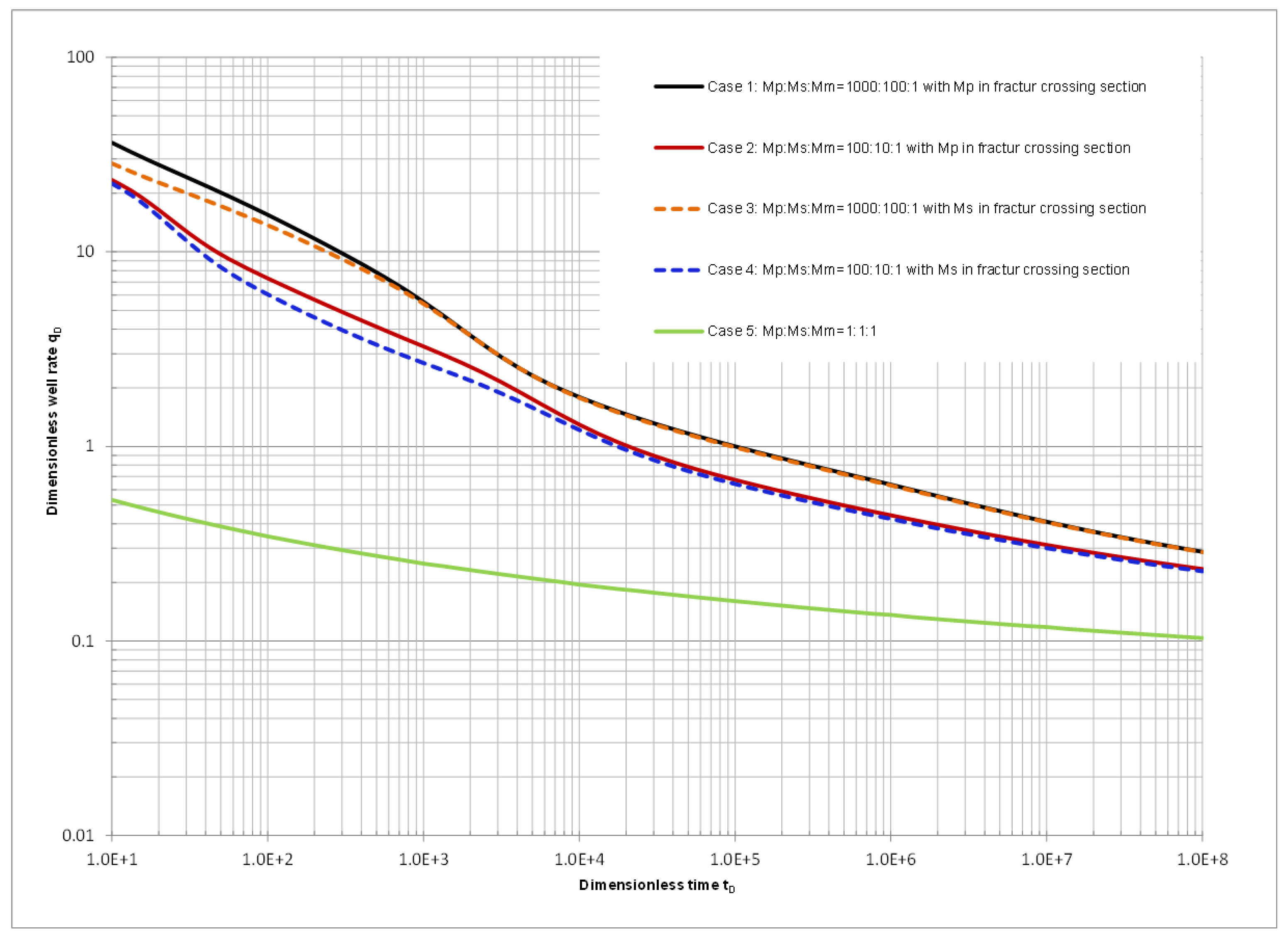
| Mobility Ratio Comparison of Mp:Ms:Mm | Mobility of Fracture Crossing Section | |
|---|---|---|
| Case 1 | 1000:100:1 | 1000 |
| Case 2 | 100:10:1 | 100 |
| Case 3 | 1000:100:1 | 100 |
| Case 4 | 100:10:1 | 10 |
| Case 5 | 1:1:1 | homogeneous |
| Case 6 | homogeneous reservoir | homogeneous |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, C.; Zhao, G.; Jin, Y.-C.; Yuan, W. Semi-Analytical Modeling of Geological Features Based Heterogeneous Reservoirs Using the Boundary Element Method. Minerals 2022, 12, 663. https://doi.org/10.3390/min12060663
Su C, Zhao G, Jin Y-C, Yuan W. Semi-Analytical Modeling of Geological Features Based Heterogeneous Reservoirs Using the Boundary Element Method. Minerals. 2022; 12(6):663. https://doi.org/10.3390/min12060663
Chicago/Turabian StyleSu, Chang, Gang Zhao, Yee-Chung Jin, and Wanju Yuan. 2022. "Semi-Analytical Modeling of Geological Features Based Heterogeneous Reservoirs Using the Boundary Element Method" Minerals 12, no. 6: 663. https://doi.org/10.3390/min12060663
APA StyleSu, C., Zhao, G., Jin, Y.-C., & Yuan, W. (2022). Semi-Analytical Modeling of Geological Features Based Heterogeneous Reservoirs Using the Boundary Element Method. Minerals, 12(6), 663. https://doi.org/10.3390/min12060663







