Abstract
Filtered tailing is a relatively-environmentally friendly technique due to the recovery of water during the process of dehydration. This technique was recently developed and therefore there are few studies available compared to research on conventional tailings. This work focuses on the behaviour of a filtered copper tailing under an unsaturated condition, studying the effect of self-compaction by self-weight which is triggered by the deposition process through 1D consolidation tests. In addition, the impact of confinement on the stiffness and shear strength was studied by means of unsaturated drained triaxial tests. The initial matric suction was determined based on soil-water characteristic curves for two initially loose dry densities and the water content at which the material leaves the dehydration process. The unsaturated consolidation tests showed that for vertical stresses above 100 kPa and with ratios between the applied matric suction and air entry value lower than twelve, the material approaches saturated condition, reaching up to 95% degree of saturation. On the other hand, for the unsaturated drained triaxial tests, the effect of the matric suction generates increases in the shear strength and the stiffness of the material up to 200% and 600%, respectively. However, the increase tends to disappear as confinement increases.
1. Introduction
The high consumption of water in the mining industry is a constant and relevant problem. Therefore, various mining waste disposal strategies, such as filtered tailings, are being developed to optimize and reduce water consumption. This type of tailing is considered to be high-density tailing [1] since they are subjected to a dehydration process and reach a solid concentration higher than 77% [2,3]. This dehydration process can be carried out by mechanical or vacuum filtration, and the material usually achieves a water content below its saturation condition. Therefore, the material cannot be pumped, and it must be transported to the site of collection or final disposal by means of conveyor belts or trucks [4].
High-density tailings, such as filtered tailings, are naturally subjected to a certain degree of desiccation in arid climates [1,5]. Therefore, these tailings should be characterized using the soil-water characteristic curve (SWCC) associated with the drying path used. According to Oldecop and Rodari [6], lower water content in mining waste deposits means structurally more stable deposits which are less vulnerable to seismic events and a lower probability of generating acid drainage. However, according to Ulrich and Coffin [7], eventual saturation and the consequent development of pore pressures can also occur in this type of deposit. In fact, Wilson and Robertson [8] warn that this new technique is not immune to potential failures, as two high-density tailing facilities have had problems in both design and operating conditions. Therefore, there is still a great need to advance on the understanding of the hydromechanical behaviour of these deposits, particularly about the rates and heights of deposition that ensure adequate performance [9].
Table 1 and Figure 1 show the existing filtered tailing facilities in Chile and their geographical locations according to the update carried out in 2020 by the National Geology and Mining Service (https://www.sernageomin.cl/datos-publicos-deposito-de-relaves, accessed on 25 February 2022). According to the information available in East and Fernandez [10] and Ulrich and Coffin [7], the second-largest project associated with this type of deposit worldwide is located in Chile; there are only 15 of these operations in the country, of which only seven are currently active. Therefore, this technology is relatively new compared to conventional deposition techniques, and it is necessary to study and evaluate the behaviour of filtered tailing deposits under unsaturated conditions during the construction, operation, and closure phases [11].

Table 1.
Facilities with filtered tailings in Chile.
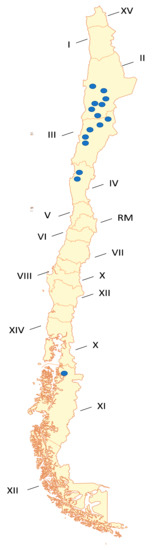
Figure 1.
Geographical locations of filtered tailing facilities in Chile.
The existing studies of filtered tailings have mainly focused on the analysis of hydromechanical properties and flow modelling [12,13], considerations and practical experiences for design, operation, and field evaluation [7,10,14,15,16,17] and studies on the hydrological behaviour and undrained resistance of mixed waste rock and filtered tailings [18,19,20]. However, there are very few studies on the eventual increase of the saturation by self-compaction or about shear strength decrease at long term, due to the increase of confinement that the material could reach.
This research is focused on the characterization of the hydromechanical behaviour of filtered copper tailings without mechanical compaction and the effects of the unsaturated condition in both long-term compressibility and shear strength. The analysis was carried out by studying stiffness and strength, through one-dimensional consolidation and drained triaxial tests in conditions of total and partial saturation. One-dimensional consolidation tests are performed to evaluate the increase in the saturation degree as a result of self-compaction, simulating accelerated deposition rates, and to study the evolution of the compressibility of the material as a function of the increase in matric suction due to the drying these materials present in the field [21]. On the other hand, triaxial tests quantify the impact on the shear strength and stiffness at long term under unsaturated conditions as a function of the confinement. The consolidation analysis was performed adopting the matric suction corresponding to the water content of the material when deposited in the disposal, and then the matric suction is increased to simulate in-situ drying. For triaxial path, the initial matric suction was selected to estimate the minimum impact that an eventual saturation would have on the shear strength of the material. The samples were extracted from fresh tailings from a copper sulphide mill plant concentrator located in northern Chile. This operation has a concentration by flotation plant which generates 18,000 tons of tailings per day.
2. Materials and Methods
2.1. Geotechnical Characterization of the Material
The main physical characteristics of the studied material are presented in Table 2, while the particle size distribution and the preparation densities are shown in Figure 2. The tested samples were made by the moist tamping method at densities corresponding to 86% and 81% of those obtained in the Standard Proctor test. These densities agree with the values reported from on-site tests carried out by the company that supplied the material and represents the loose condition of the material as it is piled up in the field. Furthermore, the water content of the samples was approximately 16% as indicated by the company.

Table 2.
Physical characteristics of filtered tailing.
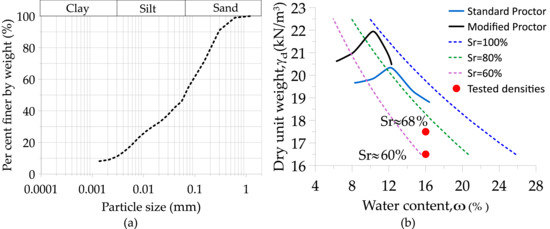
Figure 2.
(a) Particle size distribution of the material tested. (b) Water content and initial mounting dry unit weight.
Figure 3 shows the mineralogical composition of the material obtained by X-ray diffraction (XRD) using a Bruker D8 Advance diffractometer and a scan range between 10–80°. Qualitative analysis was performed through EVA and TOPAS software packages. This test shows the presence of hematite and albite, enhancers of acid drainage [27,28], and neutralizing minerals such as calcite, which consume the acid generated in mining deposits (acid mine drainage) through the formation of bicarbonate and carbonic acid [29].
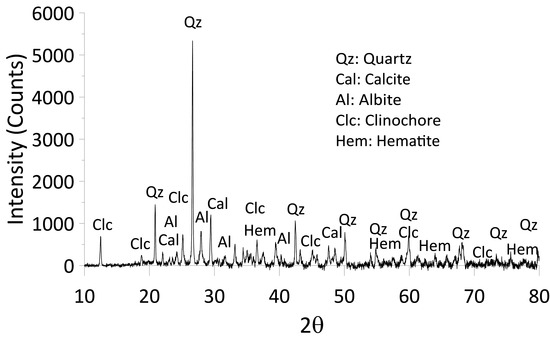
Figure 3.
Mineralogical composition of the studied material.
2.2. Acid Drainage Potential
Acid drainage is generated by the drying of material over a long time in an environment with abundant oxygen [30,31,32]; that is precisely the condition of the soil in all of the tests carried out, mainly due to the incorporation of air pressure necessary to impose a constant matric suction during the tests. The acid drainage phenomenon was experienced strongly in the first consolidation tests. To avoid this phenomenon, which leads to a reduction in the useful life of the equipment used, a leaching test was carried out on the material using water with an acidic pH (2) and a basic pH (10) (Table 3). These tests were conducted according to the following methodology: (i) 1 g of tailing material was prepared in 50 mL of solution (acidic or neutral water), (ii) the preparation was shaken on an orbital shaker for 1 h at 150 RPM and then filled up to 250 mL with the same solution; and (iii) the material was filtered on 8- to 12-μ cellulose filter papers and (iv) atomic absorption analysis was carried out. In this investigation, a Perkin Elmer AAnalyst 100® was used. The process is summarized as a flowchart in the Figure 4. As shown in Table 3, the use of water with an acidic pH (<7) triggers the generation of acid drainage and can be mitigated by using water with a basic pH. For this reason, the tests were then carried out with industrial water (with a pH of 7.3) provided by the same mining company. This water controlled the generation of acid drainage. However, as a precaution, at the end of each test, the water was circulated through high air entry porous discs (HAEPD) to clean any residual acid drainage generated during the execution of the test.

Table 3.
Leaching test results.
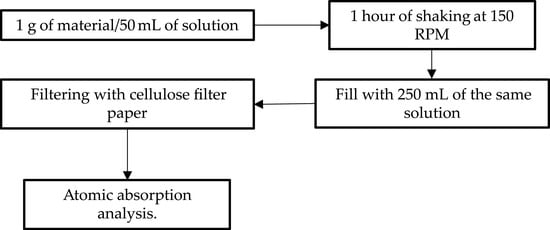
Figure 4.
Leaching test flowchart.
2.3. Experimental Program
The effect of the matric suction on the stiffness and compressibility of the material, and the potential increase in saturation under monotonic loading, were evaluated to replicate the stress path considering a hypothetical storage pile. The SWCC was constructed for the two target densities up to 1.6 MPa and then the matric suction was found as a function of the moisture content at which the material is deposited in field (16%). One-dimensional consolidation and drained triaxial tests were performed using the axis translation technique [33]. One-dimensional saturated and unsaturated consolidation tests were carried out with matric suctions from 50 kPa to 400 kPa, while unsaturated triaxial tests were subjected to matric suction of 50 kPa. The purpose of studying the material under the consolidation path with increasing suctions is to simulate the environmental drying effect of the material and assess the impact on the compressibility and the evolution of its saturation degree by the increase of vertical stress. Regarding the drained triaxial tests, the effect of the initial matric suction on the stiffness and the shear strength was evaluated at several confinement stresses, since the initial condition is the closest to the saturation condition which should correspond to the minimum shear strength of the material. Of course, the hydro-mechanical path in the field is more complex, since the environmental drying effect is added to the water flow inside the disposal due to self-compaction, increasing the humidity in the lower zones and drying the upper layers. Moreover, none of these effects are 1D. The simplified path explored in this work are intended to isolate these combined effects to improve the understanding the behavior of the material in the disposal. Figure 5 summarizes the experimental program.
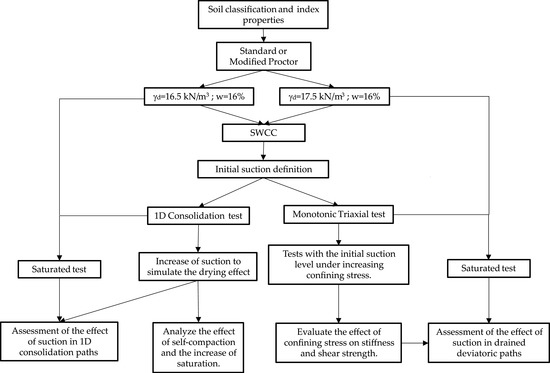
Figure 5.
Flowchart of the experimental program.
The construction of the SWCC was carried out with the following techniques: (i) a tensiometer was used from 0 to 90 kPa in a device that records weight and matric suction variations (commercial equipment manufactured by UGT) on samples of 72 mm of diameter and 61.4 mm of height; (ii) an automatic oedometer was used for the axis translation technique from 50 kPa to 400 kPa (commercial equipment manufactured GDS Instruments) on samples of 63 mm of diameter and 22 mm of height; (iii) the contact filter paper test [34] was used from 50 kPa to 1.6 MPa (using Whatman 42 filter paper); and (iv) the equilibrium vapor testing method was used to characterize the residual zone with values from 4 MPa to 110 MPa. For techniques (iii) and (iv), we used samples of 50 mm of diameter and 18 mm of height. In technique (iv), a hermetic desiccator instrument with high-precision load cells was developed to continuously monitor the variation in weight. The exchange of salts must be rapid to avoid a significant change of the temperature and relative humidity (RH) inside of the desiccator, which could modify the measurement of the weight. Figure 6 shows the combination of methods used to construct the SWCC.
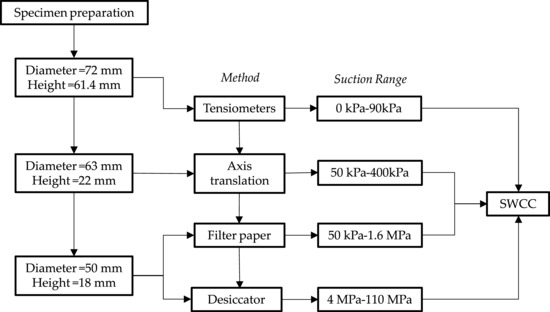
Figure 6.
Combination of methods to obtain SWCC.
In the present investigation, the samples inside of desiccator were dried in an oven for 24 h and then equilibrated with the salt reaching the highest moisture content, with the purpose to start from the wettest possible condition. The salt exchange time was less than two minutes, and the salts were exchanged in decreasing order with relative humidity to simulate the drying effect. Inside the desiccator, there were three samples for each test density (i.e., six samples) to ensure repeatability of the test. The temperature and relative humidity within the closed circuit were continuously monitored, and Kelvin’s law was used to determine the total suction [35] according to the following equation:
where is the density of water, R is the universal gas constant (8.31432 J/mol K°), T is the temperature inside of the desiccator, is the molecular mass of water vapor (18.016 g/mol), and RH is the relative humidity inside the desiccator. Figure 7 shows the equipment used to obtain the SWCCs through all of the methodologies mentioned above.

Figure 7.
Equipment used to obtain the SWCC. (a) Ku-pf; (b) GDS oedometer; (c) filter paper; (d) equilibrium vapor.
The residual zone is one of the most complex to characterize due to the high level of suction that must be achieved and quantified. To reach these levels of suction, the equilibrium vapor technique was used. Table 4 and Figure 8 shows the salts used for this technique and the moisture balance process for both densities. Figure 8 shows the average weight variation evolution of the samples that were placed in the desiccator (3 samples for each density). The salts were exchanged from the higher RH to the lower RH as shown in Table 4. Vertical lines indicate each salt replacement in the system. The results of the SWCC show that the combination of the four techniques is suitable for obtaining a continuous curve and consistent with the proposed models.

Table 4.
Salts used to determine the total suction by the equilibrium vapor technique.
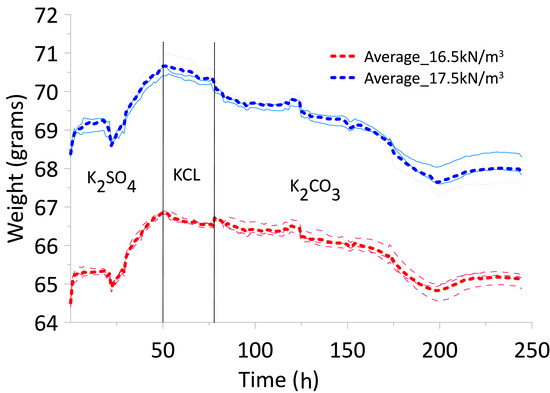
Figure 8.
Variations in weight relative to test duration and salts used for each density.
The tested specimens were 63 mm in diameter and 22 mm heigh for the oedometer and 50 mm in diameter and 100 mm heigh for the triaxial tests. Table 5 summarizes the tests carried out, where the matric suction ψ corresponds to the difference between the air pressure and the backpressure applied to the sample. The axis translation technique was applied using a porous stone with a high air entry value (HAEPD) of 1500 kPa until a variation of less than 0.0004 mm3/s was obtained [36]. This condition was considered equilibrium for this investigation. The time to reach this equilibrium depended on the permeability of the HAEPD, was well as the matric suction applied. This balance must be achieved at each stage of load increase.

Table 5.
Tests carried out under saturated and unsaturated conditions.
2.4. Conventions Considered for the Presentation of the Results
The measurement of the variation in the water within the sample () and its vertical deformation allow for calculating the degree of saturation (), the void ratio (), and the volumetric water content () throughout the consolidation and drained triaxial tests. The initial matric suction corresponds to the water content of the material deposited in the ground (16%) and according to the SWCC corresponding to 50 kPa (see Figure 10). This initial matric suction is, in principle, the most saturated condition that the material will have in the field since the evaporative drying process should prevail over the potential external water inputs. Indeed, most of this kind of deposits are located in the desert area of northern Chile where annual precipitation are in the range of 30 to 50 mm/year in average [37].
To determine the saturation in the consolidation tests, Equation (1) was used:
where is the initial volumetric water content for each test density, is the is the change in the volume of water within the specimen and is measured by the volumetric backpressure controller at each load increment, is the initial void volume, is the variation of the height of the specimen and is the cross-sectional area of specimen to test. The volumetric back pressure controller allows checking for any issues with the air diffusion through the high air entry porous stone and accurately measuring any change in the actual volume of water in the sample.
In triaxial tests and after an equilibrated state of consolidation, the shear loading phase was executed at a rate of 0.0015 mm/min, given the low permeability of the HAEPD, and up to 20% of axial deformation. To analyze the data the approach by Fredlund et al. [38] and the extended in mean net stress term by Wang et al. [39] was used. The equations are the following:
where q is the deviatoric stress, is the projection of the critical state line (CSL) in this plane, is the mean net stress, is the final intercept of this projection with the q axis, is the net confinement stress, is the cell pressure, is the air pressure applied to sample, and is the net principal stress. The change volume in the sample were obtained according to the following expressions:
where is the volume of solid for each test density.
The air volume () in the sample was obtained according to the gas law, thanks to the digital pressure/air volume controller used [40], according to the following expressions:
where is the system temperature, is the atmospheric pressure measured directly by the equipment, is the initial volume of air in the controller (after equilibrium was reached in the consolidation phase), is the air volume variation recorded by the controller, is the volume of air in the line connecting the upper cap with the outlet valve of the triaxial cell, and is the air volume in the line connecting the cell valve to the digital air pressure/volume controller. Figure 9 illustrates the designations of the different volumes in the previous expression.
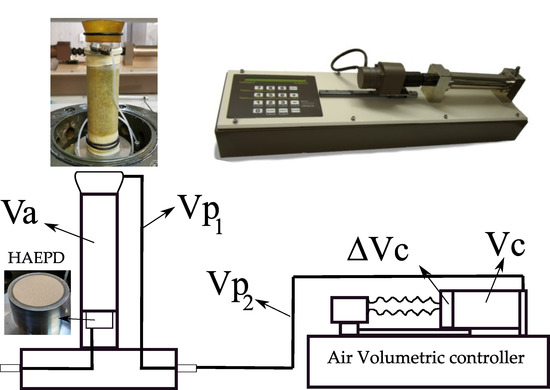
Figure 9.
Designations of different air volumes.
3. Results and Discussions
3.1. SWCC of Studies Densities
Figure 10 shows the SWCC as a function of the volumetric water content (the quotient between the volume of water and the total volume of of the sample), for the two dry densities proposed in this investigation and three commonly used adjustment models: Gardner [41], Van Genuchten [42], and Fredlund and Xing [43]. From Figure 10, comparing the denser material (17.5 kN/m3) with the looser material (16.5 kN/m3), the air entry value (AEV) decreased from 8 kPa to 4 kPa. The value of parameters of each curve are shown in Table 6. According to Vanapalli et al. [44], this point separates the material’s behavior from a saturated state to an unsaturated state, indicating that the denser material (17.5 kN/m3) remains in saturated behaviour in a wider range of suction than the looser material. However, over 700 kPa of suction, the behaviour of the materials with both densities were similar, resulting in very similar residual volumetric water content ().
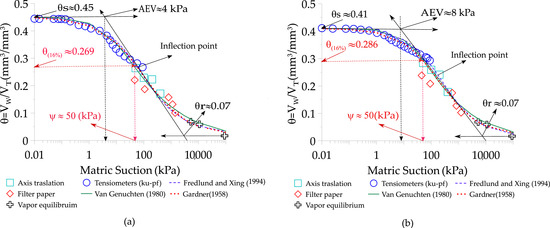
Figure 10.
Soil-water characteristic curves [41,42,43]. (a) Dry unit weight 16.5 kN/m3. (b) Dry unit weight 17.5 kN/m3.

Table 6.
SWCC adjustment parameters for each model. θs and θr are the volumetric contents of the saturated and residual water, respectively.
The impact of dry density on the properties of the water retention curve is related to the relative size of the pores. In the sample with the highest density, the pore size is relatively small, inducing a higher air entry value. Therefore, higher suction levels must be achieved for the same saturation degree regarding lower density [45,46]. On the other hand, Gao and Sun [47] and Cai et al. [48] indicated that samples with different dry densities showed very similar behaviours at significant levels of matric suction, a phenomenon that was observed above 700 kPa in this research.
3.2. Hydromechanical Behaviour of the Material at a Constant Matric Suction in the 1D Consolidation Test
Details of the 1D consolidations carried out are shown in Figure 11. Figure 11a,c show the evolution of the void ratio as a function of vertical stress, while Figure 11b,d show the evolution of saturation degree as the applied vertical stress increases. The compression (Cc) and expansion indexes (Cs) for both densities are displayed in Table 7. These indexes are considered apparent to differentiate them from those corresponding to a saturated condition.
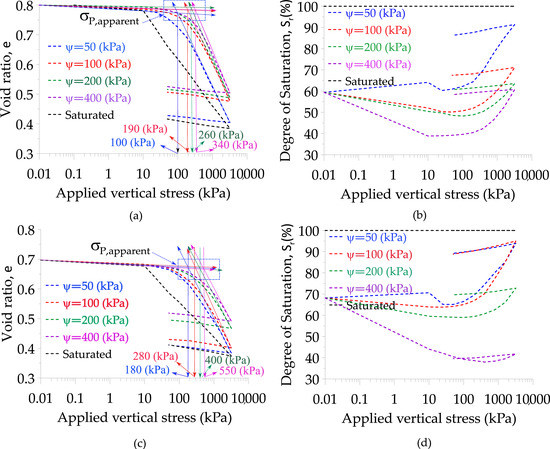
Figure 11.
1D consolidation tests and the degree of saturation reached. (a) Variation in the void ratio vs. vertical stress at a dry unit weight of 16.5 kN/m3. (b) Variation in the void ratio vs. vertical stress at a dry unit weight of 16.5 kN/m3. (c) Degree of saturation in each increment of vertical stress at a dry unit weight of 17.5 kN/m3. (d) Degree of saturation in each increment of vertical stress at a dry unit weight of 17.5 kN/m3.

Table 7.
Compression and expansion index as a function of matric suction.
The oedometric curves in saturated condition shows an approximately normally consolidated behavior (NC) in both dry densities. However the looser density has a compressibility index 26% larger than the highest dry density tested.
The effect of matric suction shows that when a matric suction exceeds the level of the air entry value, the soil becomes stiffer and the compressibility index is slightly reduced compared to the value at 50 kPa (up to 5% for an initial dry density of 16.5 kN/m3 and 16% for the dry density of 17.5 kN/m3, see Table 7). However, the effect on saturation is much more significant, reaching up to 95% for suctions in the range of 50 to 100 kPa and initial dry density of 17.5 kN/m3 since the lower void ratio. Also, it can be seen the contribution of the matric suction which shows a more clearly pre-consolidated “type” behavior.
Regarding the unloading, it was observed that the matric suction did not have a significant effect, and the expansion indexes were equivalent from a practical point of view to the one corresponding to the saturated condition. This may have occurred since the unloading was carried out at high stress (1600 kPa), and as the evolution of compressibility suggests, the material at that stress level has reached a particle arrangement corresponding to a pseudo-elastic behaviour under unloading. Regarding the effect of the density in the looser sample, the reduction in the void ratio reached approximately 50% of the preparation density if the matric suction did not exceed 50 kPa. In the denser sample, this value was closer to 40% but with matric suction up to 100 kPa.
In terms of the evolution of saturation, it was observed that the value remained stable up to approximately 100 to 200 kPa of vertical stress. However, for higher vertical stresses, the saturation increased at both densities. For a density of 17.5 kN/m3 and a vertical stress higher than 1600 kPa with matric suctions between 50 and 100 kPa, the material reached a saturation condition of up to 95%. For a density of 16.5 kN/m3, the saturation achieved was of about 90%, and only for a matric suction of 50 kPa. Hence, for a ratio between the matric suction and the air entry value of less than twelve (12), the material increases its saturation degree, reaching up to 95%. This behaviour has already been observed by other authors [49,50]. However, in those studies, the water content in the sample was correlated and not directly measured, in which differs from this investigation.
Compared to the lower density sample, the denser sample has less porosity, and the reorganization of the solid skeleton reduces the space available for water and therefore it is easier to increase its saturation. The comparison of the results at low suctions against the saturated condition indicated that when the saturation exceeded approximately 80%, the changes in the soil were such as those observed in the saturated condition with vertical stress greater than 800 kPa. This pattern was observed in the looser material at a matric suction of only 50 kPa, while for the denser material, this behaviour takes place at suctions from 50 kPa and 100 kPa.
Another way to quantify the effect of matric suction on the compressibility of the material is through the calculation of an apparent pre-consolidation stress using the Casagrande method for each curve. Since the material is remoulded and due to the matric suction, this pre-consolidation is considered apparent (σP,apparent). The results are presented in Figure 12, were the values of apparent pre-consolidation stresses correspond to the fit shown in Figure 11a,c. This curve shows an increase in apparent pre-consolidation stresses as matric suction increases, for both densities under study. The slope of this curve decreases with the increase suction, suggesting an asymptotic tendency at very high suction. According to our results, it is suggested to consider suction above 400 kPa to determine the maximum achievable apparent pre-consolidation stress. These results follow the same trend as those presented by Zou et al. [51] and Burton et al. [52]. However, they were obtained for natural soils at a constant moisture content.
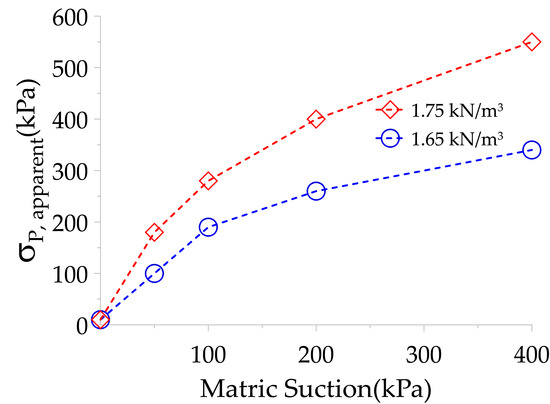
Figure 12.
Effect of matric suction on the apparent pre-consolidation stress.
3.3. Hydromechanical Behaviour of Material at a Constant Matric Suction in Drained Triaxial Tests
A series of drained triaxial tests of material at a constant matric suction were carried out to assess the influence on the stiffness and the shear strength. Figure 13 and Figure 14 present the results for the two initial densities studied and the results of the saturated condition as a reference. The tests were carried out at a constant matric suction of 50 kPa in accordance with the SWCC presented above and the humidity expected in the field. First, despite the saturation degree, a contractive behaviour was observed for all of the confinement imposed on the looser preparation (16.5 kN/m3). For the denser case, a slight dilative behaviour was observed at an axial deformation of approximately 6%. From the point of view of shear behaviour, both densities showed an increase in shear strength and stiffness, as suggested by other authors [31,53].
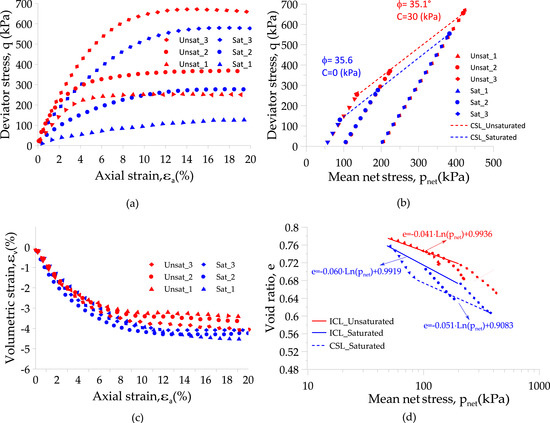
Figure 13.
Behavior of the soil studied at a dry unit weight of 16.5 kN/m3. (a) Diagram of stress relative to axial strain (q vs. εa). (b) Diagram of pnet vs. q. (c) Volumetric strain versus axial strain. (d) Diagram of pnet vs. void ratio during the shear phase.
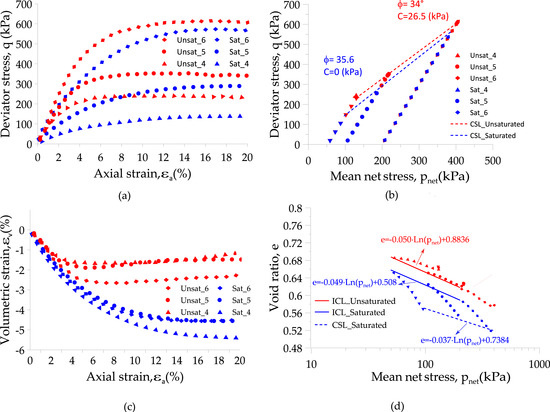
Figure 14.
Behavior of the soil studied at a dry unit weight of 17.5 kN/m3. (a) Diagram of stress versus axial strain (q vs. εa). (b) Diagram of pnet vs. q. (c) Volumetric strain versus axial strain. (d) Diagram of pnet vs. void ratio during the shear phase.
Figure 13b and Figure 14b shows the shear failure envelopes and their parameters for both preparation densities. A slight reduction in the friction angle was observed for both densities when a constant matric suction of 50 kPa is applied. In addition, an apparent cohesion of about 25–30 kPa appears due to applied matric suction. Figure 15 shows the initial and the evolution of the degree of saturation during the shearing showing that there is no significant variation in this stage. Nevertheless, the saturation increases with the confinement.
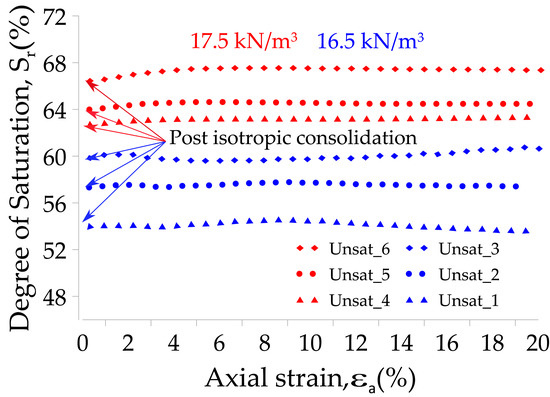
Figure 15.
Behavior of the saturation at both densities in the shear phase.
Regarding the isotropic consolidation line (ICL) in Figure 13d and Figure 14d, the effect of suction on its slope is only evident for the lower density case (16.5 kN/m3). For the denser case, the slopes are very similar suggesting that the effect of suction on compressibility becomes less relevant as the material has a stiffer soil skeleton. In the case of the large deformation states from the triaxial tests at failure, the trends are more erratic, and it is not obvious to distinguish a clear trend from these results. In general, changes in slopes with respect to the saturated case are observed for both initial densities.
Difference in stiffness and strength compared to the saturated condition tends to decrease as the confining pressure increases. To quantify this difference, Figure 16a,b shows the ratio between the secant modulus at 50% of the peak load (E50) and the large strain deviatoric stress under saturated and unsaturated conditions, respectively. These figures show that at confinements of about 50 kPa, the increase of stiffness and deviatoric stress could reach up to 600% and 200%, respectively, while at confinements of 200 kPa, the unsaturated condition is only approximately 180% more rigid with an increase of 20% the deviatoric stress for the dry density of 16.5 kN/m3. This behaviour was more evident for the preparation at a dry unit weight of 17.5 kN/m3 due to the increase of saturation in comparison with the lower density (see Figure 15). Then, by applying a matric suction closer to the air entry value, the material behavior approaches the saturated case. These effects were observed in the consolidation tests under the same level of matric suction (see Figure 11a,c).
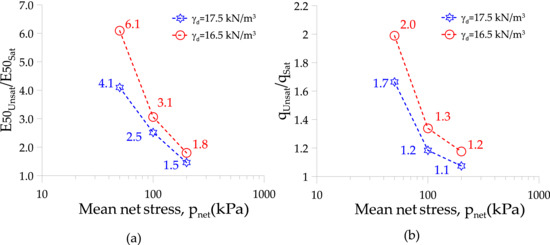
Figure 16.
Stiffness and large strain deviatoric stress ratios for the unsaturated vs. saturated conditions of both dry densities studied. (a) Modulus of stiffness at 50% maximum load. (b) Large strain deviatoric stress.
In this work the matric suctions were maintained as a constant to facilitate the interpretation of the results. However, in the field the material could receive external supplies of water due to climatic conditions or from flows within deposited dry stacks or also experience a more significant reduction in humidity in arid regions. Furthermore, in seismic countries such as Chile, there are also questions about the cyclic behaviour of this type of uncompacted tailing material. These and other factors are expected to be addressed in future phases of this research.
4. Conclusions
The response of the soil to the consolidation tests at a constant matric suction showed an increase in the apparent pre-consolidation stress as the matric suction increased. However, the soil became saturated, reaching values of up to 95% for matric suctions lower than twelve times the air entry value. These results allow a partial answer to some doubts raised by authors such as Ulrich and Coffin [7], Wilson and Robertson [8] and Fredlund and Houston [11] regarding a possible saturation at the base of this type of tailing deposit.
The contractive behaviour of the material in the unsaturated and initially loose con-ditions was not affected by a matric suction of 50 kPa, maintaining a predominantly contractive behaviour under drained triaxial paths. In addition, the stiffness and large strain deviatoric stress of the material increases up to 600% and 200%, respectively, for confining pressures below 100 kPa. However, above 200 kPa of confining, these differences were less significant, and the behavior approaches saturated condition.
From the point of view of the deposition of the material in the field and assuming that the expected matric suction is around 50 kPa, it can be inferred that to avoid a behaviour close to saturation, the deposition height should not exceed 40 m. This means that a confinement below 800 kPa must be achieved to guarantee a saturation degree of the material below 70%. Naturally, this analysis does not consider the external or internal water contributions to the disposal by the flow from upper layers, so this is only a first rough approximation.
Finally, it is possible to conclude that the hydromechanical behaviour of an un-saturated filtered tailing under loose conditions and monotonic drained loading does not prevent the increase of its degree of saturation due to increase of confinement stress. Therefore, the maximum deposition height should be limited and constantly monitored.
Author Contributions
Conceptualization, E.S.R. and R.G.S.; methodology, E.S.R., R.G.S. and J.C.-T.; formal analysis, R.G.S.; investigation, R.G.S.; resources, E.S.R., R.G.S.; data curation, R.G.S.; writing—original draft preparation, R.G.S.; writing—review and editing, E.S.R. and J.C.-T.; supervision, E.S.R. and J.C.-T.; project administration, E.S.R.; funding acquisition, E.S.R. and R.G.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been supported by CODELCO, through the Piensa Minería scholarship year 2019, the Pontificia Universidad Católica de Chile, through its doctoral scholarship, the National Research Center for Integrated Natural Disaster Management (CONICYT/FONDAP/15110017) and the FONDEQUIP EQM150024 project. The third author acknowledges the funding given by the Research Vice-presidency of the Universidad Militar Nueva Granada, Colombia, through the Project IMP-ING-2932.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
To Sergio Barrera for supplying the filtered tailing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Simms, P. 2013 colloquium of the Canadian geotechnical society: Geotechnical and geoenvironmental behaviour of high-density tailings. Can. Geotech. J. 2016, 54, 455–468. [Google Scholar] [CrossRef] [Green Version]
- Lara Montani, J.; Pornillos, E.; Munoz, H. Geotechnical-Geochemical and operational considerations for the application ofdry stacking tailings deposits—State ofthe art. In Proceedings of the 16th International Seminar on Paste and Thickened Tailings, Belo Horizonte, Brazil, 17–19 June 2013; pp. 249–260. [Google Scholar]
- Weatherwx, T.W.; Kipara, A. Paste operations training at Barrick’s Bulyanhulu Gold Mine. In Proceedings of the 13th International Conference on Paste and Thickened Tailings, Toronto, ON, Canada, 3–6 May 2010; pp. 41–50. [Google Scholar]
- Davies, M.P.; Rice, S. An alternative to conventional tailing management—“Dry stack” filtered tailings. In Proceedings of the 8th International Conference on Tailings and Mine Waste’01, Fort Collins, CO, USA, 15–18 January 2001; pp. 411–420. [Google Scholar]
- Daliri, F.; Simms, P.; Sivathayalan, S. Shear and dewatering behaviour of densified gold tailings in a laboratory simulation of multi-layer deposition. Can. Geotech. J. 2016, 53, 1246–1257. [Google Scholar] [CrossRef]
- Oldecop, L.; Rodari, G. Unsaturated Soil Mechanics in Mining. In Proceedings of the Pan Am Unsaturated Soils, Dallas, TX, USA, 12–15 November 2017; pp. 257–280. [Google Scholar]
- Ulrich, B.; Coffin, J. Considerations for Tailings Facility Design and Operation Using Filtered Tailings Summary of Significant Operating Filtered Tailings Operations. In Proceedings of the 16th International Seminar on Paste and Thickened Tailings, Belo Horizonte, Brazil, 17–20 June 2013; pp. 201–210. [Google Scholar]
- Wilson, G.W.; Robertson, A.M. The Value of Failure. Geotech. News 2015, 33, 24–28. [Google Scholar]
- Ulrich, B. Practical thoughts regarding filtered tailings. In Proceedings of the 22th International Conference on Tailings and Mine Waste, Cape Town, South Africa, 8–10 May 2019; pp. 71–79. [Google Scholar]
- East, D.; Fernandez, R. Managing Water to Minimize Risk in Tailings Storage Facility Design, Construction, and Operation. Mine Water Environ. 2021, 40, 36–41. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Houston, S.L. Interpretation of soil-water characteristic curves when volume change occurs as soil suction is changed. In Proceedings of the 1st Pan-American Conference on Unsaturated Soils, Cartagena de Indias, Colombia, 20–22 February 2013; pp. 15–31. [Google Scholar]
- Bussière, B. Colloquium 2004: Hydrogeotechnical properties of hard rock tailings from metal mines and emerging geoenvironmental disposal approaches. Can. Geotech. J. 2007, 44, 1019–1052. [Google Scholar] [CrossRef]
- Sánchez, J.A.; Beltra, L.N.; Trujillo-Vela, M.G.; Larrahondo, J.M. Flows of Liquefied Filtered Tailings: Laboratory-Scale Physical and Numerical Modeling. Int. J. Civ. Eng. 2020, 18, 393–404. [Google Scholar] [CrossRef]
- Crystal, C.; Hore, C.; Ezama, I. Filter-Pressed Dry Stacking: Design Considerations Based on Practical Experience. In Proceedings of the 22th International Conference on Tailings and Mine Waste, Keystone, CO, USA, 30 September–2 October 2018; pp. 209–219. [Google Scholar]
- Hore, C.; Luppnow, D. Karara Iron Ore TSF—Design considerations for a unique large scale dry stack facility. In Proceedings of the 18th International Conference on Tailings and Mine Waste, Keystone, CO, USA, 5–8 October 2014; pp. 293–304. [Google Scholar]
- Robertson, P.K.; Da Fonseca, A.V.; Ulrich, B.; Coffin, J. Characterization of unsaturated mine waste: A case history. Can. Geotech. J. 2017, 54, 1752–1761. [Google Scholar] [CrossRef] [Green Version]
- Whatnall, O.; Barber, K.; Robinson, P. Tailings Filtration Using Viper Filtration Technology—A Case Study. Min. Metall. Explor. 2021, 38, 1297–1303. [Google Scholar] [CrossRef]
- Borja, R.N.; Bareither, C.A. Shear Behavior of Waste Rock and Filtered Tailings Mixtures. In Proceedings of the Geo-Congress 2020: Geotechnical Earthquake Engineering and Special Topics, Minneapolis, MI, USA, 25–28 February 2020; pp. 872–880. [Google Scholar]
- Gorakhki, M.R.H.; Bareither, C.A.; Scalia, J.; Aparicio, M. Hydrologic and Environmental Behavior of Geo Waste and Waste Rock in Field Experimental Piles. Min. Metall. Explor. 2021, 38, 1339–1354. [Google Scholar] [CrossRef]
- Ulrich, B.; Coffin, J. Combined tailings and mine waste. In Proceedings of the Tailings and Mine Waste, Vancouver, BC, Canada, 26–28 October 2015; pp. 83–92. [Google Scholar]
- Lee, K.; Sills, G. The consolidation of a soil stratum, including self-weight effects and large strains. Int. J. Numer. Anal. Methods Geomech. 1981, 5, 405–428. [Google Scholar] [CrossRef]
- ASTM Standard D854-14; ASTM Standard Test Methods for Specific Gravity of Soil Solids by Water Pycnometer. ASTM Int.: West Conshohocken, PA, USA, 2014.
- ASTM Standard D2487-17e1; ASTM Standard Practice for Classification of Coils for Engineering Purposes (Unified Soil Classification System). ASTM Int.: West Conshohocken, PA, USA, 2017.
- ASTM Standard D4318-17e1; ASTM Standard Test Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils. ASTM Int.: West Conshohocken, PA, USA, 2017.
- ASTM Standard D1557-12; ASTM Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Modified Effort. ASTM Int.: West Conshohocken, PA, USA, 2012.
- ASTM Standard D698-12; ASTM Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Standard Effort. ASTM Int.: West Conshohocken, PA, USA, 2012.
- Dold, B. Evolution of acid mine drainage formation in sulphidic mine tailings. Minerals 2014, 4, 621–641. [Google Scholar] [CrossRef] [Green Version]
- Murray, J.; Nordstrom, D.K.; Dold, B.; Kirschbaum, A. Seasonal fluctuations and geochemical modeling of acid mine drainage in the semi-arid Puna region: The Pan de Azúcar Pb–Ag–Zn mine, Argentina. J. South. Am. Earth Sci. 2021, 109, 103197. [Google Scholar] [CrossRef]
- Akcil, A.; Koldas, S. Acid Mine Drainage (AMD): Causes, treatment and case studies. J. Clean. Prod. 2006, 14, 1139–1145. [Google Scholar] [CrossRef]
- Daliri, F.; Paul, S.; Siva, S. A Comparison of Different Laboratory Techniques to Simulate Stress and Moisture History of Hard Rock Mine Tailings. In Proceedings of the Tailings and Mine Waste 2011 Conference, Vancouver, BC, Canada, 6–9 November 2011; pp. 163–175. [Google Scholar]
- Daliri, F.; Kim, H.; Simms, P.; Sivathayalan, S. Influence of desiccation and overconsolidation on monotonic and cyclic shear response of thickened gold tailings. In Proceedings of the 14th Pan-American Conference on Soil Mechanics and Geotechnical Engineering, Toronto, ON, Canada, 2–6 October 2011; pp. 1–8. [Google Scholar]
- Simms, P.; Grabinsky, M.; Zhan, G. Modelling evaporation of paste tailings from the Bulyanhulu mine. Can. Geotech. J. 2007, 44, 1417–1432. [Google Scholar] [CrossRef]
- Hilf, J.W. An Investigation of Pore-Water in Compacted Cohesive Soils. Technical Memo. No. 654. Ph.D. Thesis, Bureau of Reclamation, Design and Construction Division, U.S. Department of the Interior, Denver, CO, USA, 1956. [Google Scholar]
- ASTM Standard D5298-16; ASTM Standard Test Method for Measurement of Soil Potential (Suction) Using Filter Paper. ASTM Int.: West Conshohocken, PA, USA, 2016. [CrossRef]
- Edlefsen, N.E.; Alfred, B.C.A. Thermodynamics of soil moisture. Hilgardia 1943, 15, 31–298. [Google Scholar] [CrossRef] [Green Version]
- Hoyos, L.R.; Pérez-Ruiz, D.D.; Puppala, A.J. Modeling Unsaturated Soil Response under Suction-Controlled True Triaxial Stress Paths. Int. J. Geomech. 2012, 12, 292–308. [Google Scholar] [CrossRef]
- Schumacher, V.; Comin, A.; Sarricolea, P.; Meseguer-ruiz, O. Comparison between observations and gridded data sets over complex terrain in the Chilean Andes: Precipitation and temperature. Int. J. Climatol. 2020, 40, 5266–5288. [Google Scholar] [CrossRef]
- Fredlund, D.; Morgenstern, N.; Widger, R. The shear strength of unsaturated soils. Can. Geotech. J. 1978, 15, 313–321. [Google Scholar] [CrossRef]
- Wang, Q.; Pufahl, D.; Fredlund, D. A study of critical state on an unsaturated silty soil. Can. Geotech. J. 2002, 39, 213–218. [Google Scholar] [CrossRef]
- Adams, B.A.; Wulfsohn, D.; Fredlund, D.G. Air volume change measurement in unsaturated soil testing using a digital pressure-volume controller. Geotech. Test. J. 1996, 19, 12–21. [Google Scholar] [CrossRef]
- Gardner, W. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Vanapalli, S.K.; Fredlund, D.G.; Pufahl, D.E.; Clifton, A.W. Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 1996, 33, 379–392. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rajardo, H.; Frdlund, M.D. Unsaturated Soil Mechanics in Engineering Practice; Wiley Online Library: Hoboken, NJ, USA, 2012; ISBN 978111813359. [Google Scholar]
- Heshmati, A.A.; Motahari, M.R. Modeling the Dependency of Suction Stress Characteristic Curve on Void Ratio in Unsaturated Soils. KSCE J. Civ. Eng. 2015, 19, 91–97. [Google Scholar] [CrossRef]
- Gao, Y.; Sun, D. Soil-water retention behavior of compacted soil with different densities over a wide suction range and its prediction. Comput. Geotech. 2017, 91, 17–26. [Google Scholar] [CrossRef]
- Cai, G.; Zhou, A.; Sheng, D. Permeability function for unsaturated soils with different initial densities. Can. Geotech. J. 2014, 51, 1456–1467. [Google Scholar] [CrossRef]
- Roy, S.; Rajesh, S. Test apparatus for rapid determination of soil-water retention curve under isotropic loading condition. Geotech. Test. J. 2021, 44, 255–273. [Google Scholar] [CrossRef]
- Islam, T.; Kodikara, J. Interpretation of the loading—Wetting behaviour of compacted. Can. Geotech. J. 2016, 805, 783–805. [Google Scholar] [CrossRef] [Green Version]
- Zou, W.; Han, Z.; Vanapalli, S.K.; Zhang, J.; Zhao, G. Predicting volumetric behavior of compacted clays during compression. Appl. Clay Sci. 2018, 156, 116–125. [Google Scholar] [CrossRef]
- Burton, G.; Pineda, J.; Sheng, D.; Airey, D.; Zhang, F. Exploring one-dimensional compression of compacted clay under constant degree of saturation paths. Geotechnique 2016, 66, 435–440. [Google Scholar] [CrossRef]
- Kimoto, S.; Oka, F.; Fukutani, J.; Yabuki, T.; Nakashima, K. Monotonic and cyclic behavior of unsaturated sandy soil under drained and fully undrained conditions. Soils Found. 2011, 51, 663–681. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).