Study on Explicit–Implicit Simulation and In-Situ Measurement of Floor Failure Law in Extra-Thick Coal Seams
Abstract
:1. Introduction
2. Numerical Simulation Method
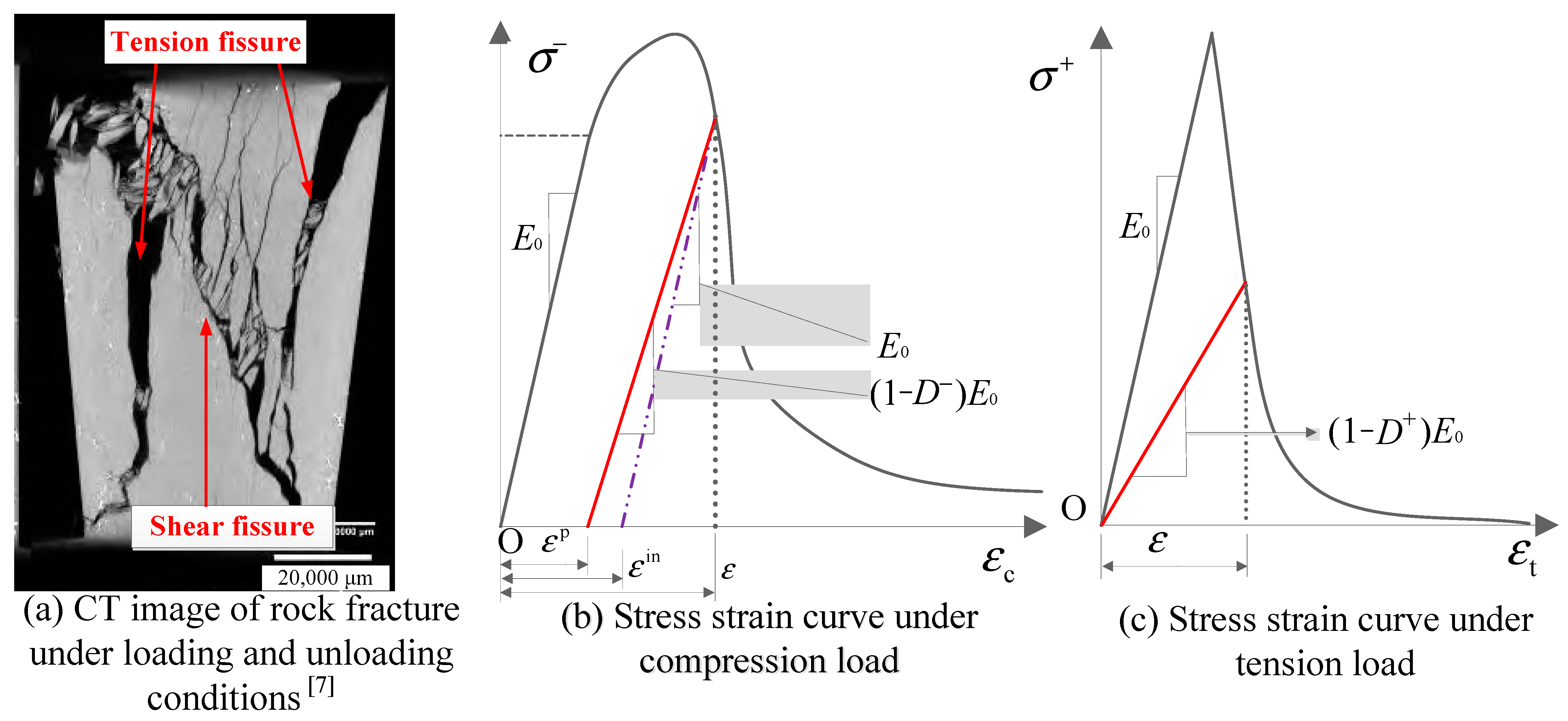
2.1. Plastic Damage Constitutive Relation under Cyclic Loading and Unloading
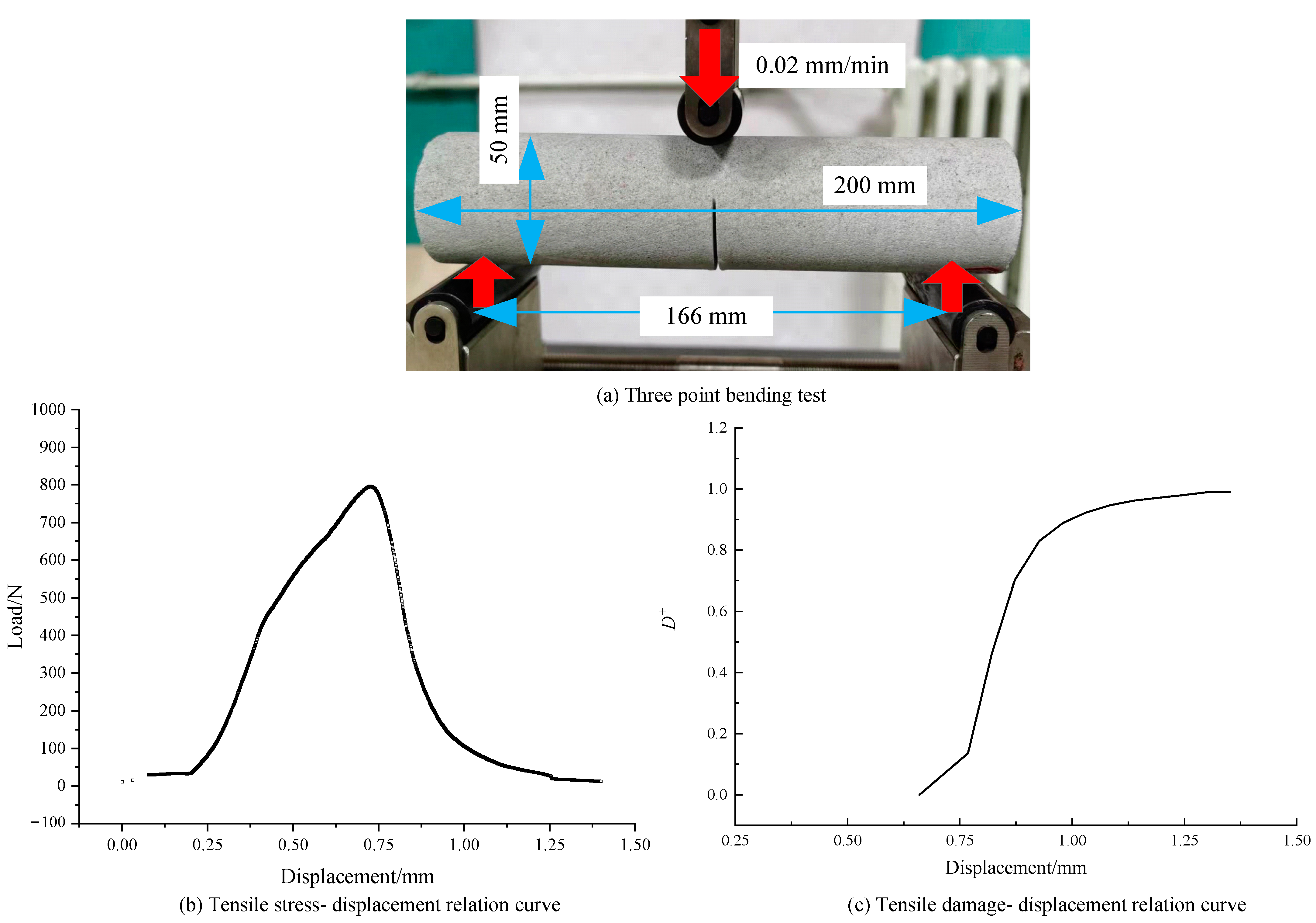
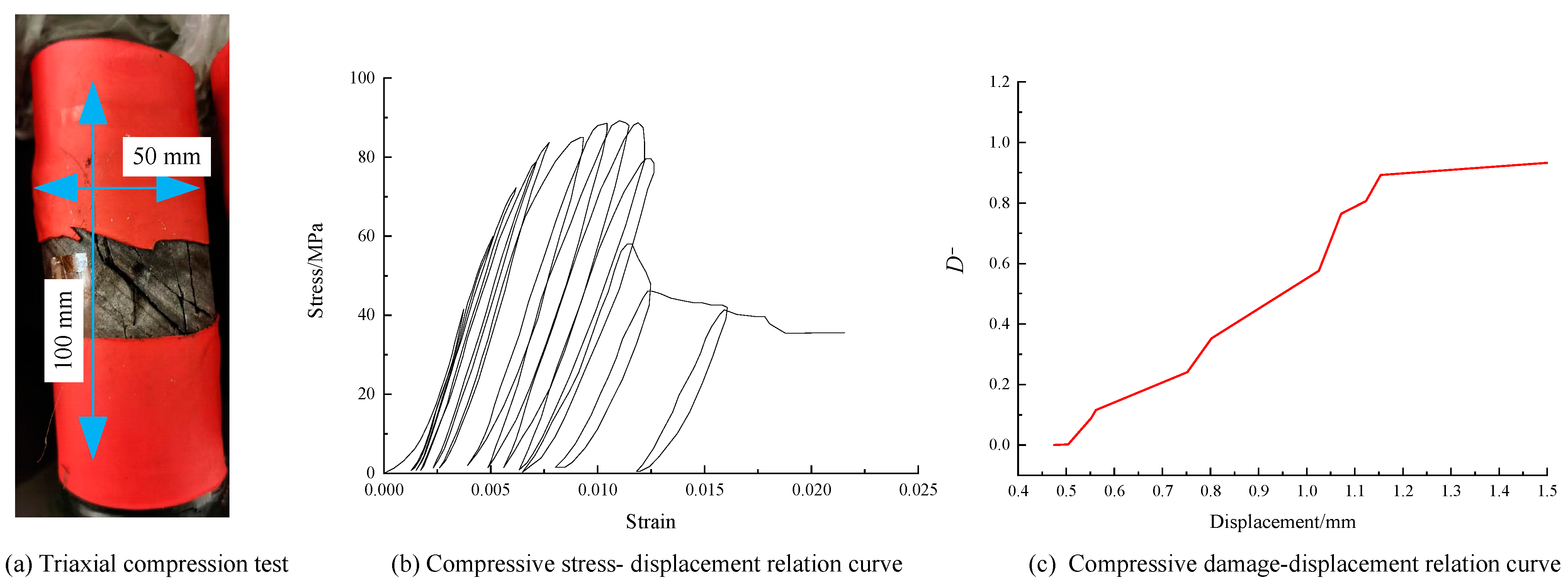
2.2. Parameter Identification
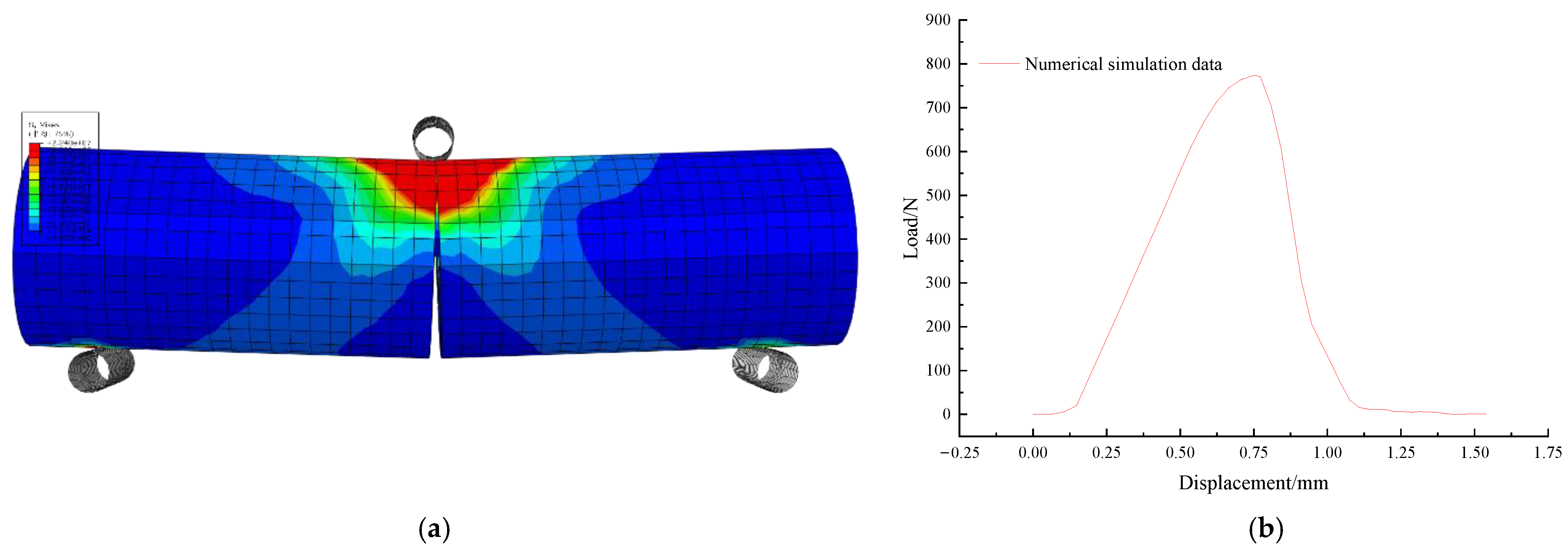
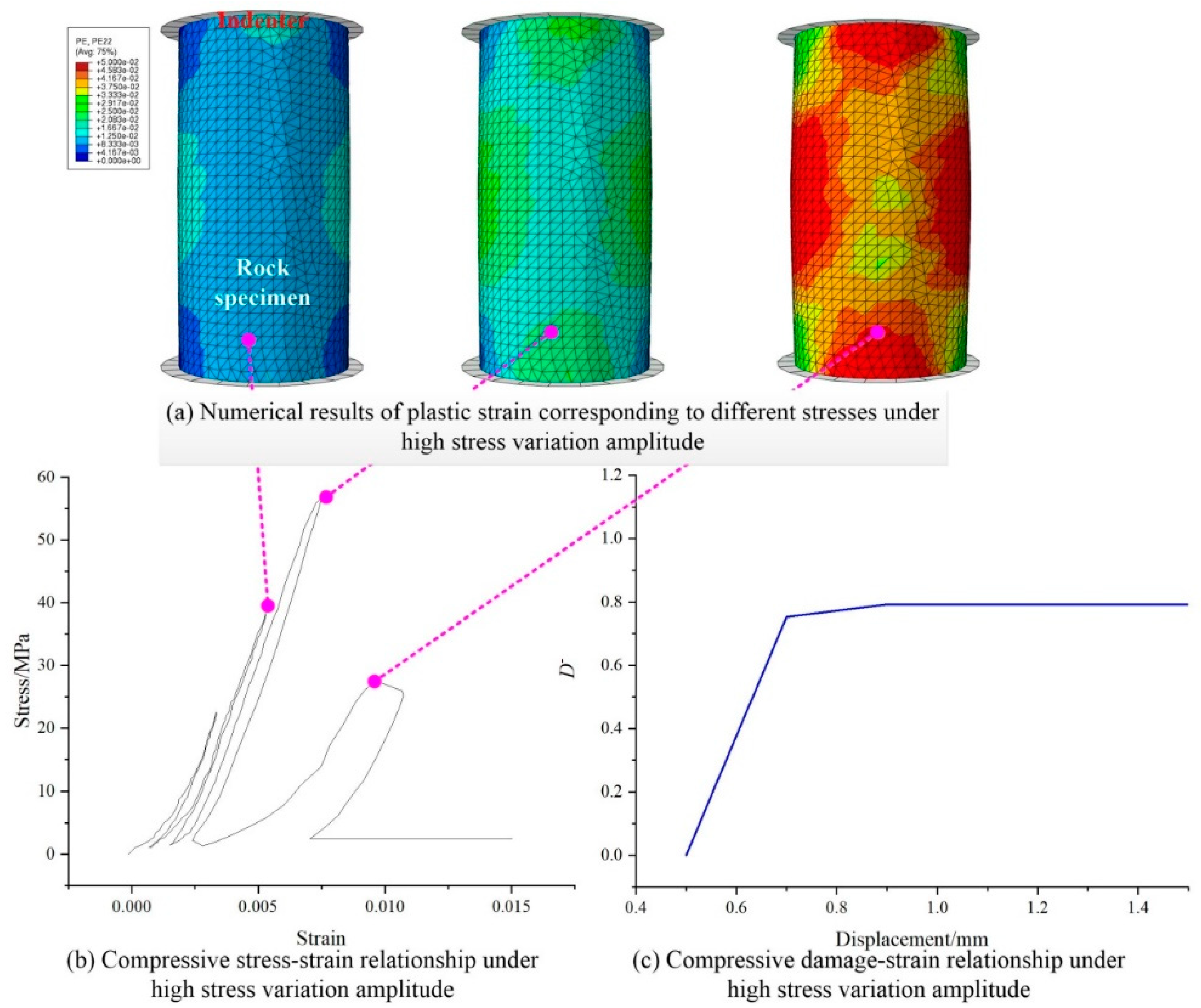
2.3. Verification of Constitutive Equations under High Stress Variation Amplitude
3. Numerical Simulation
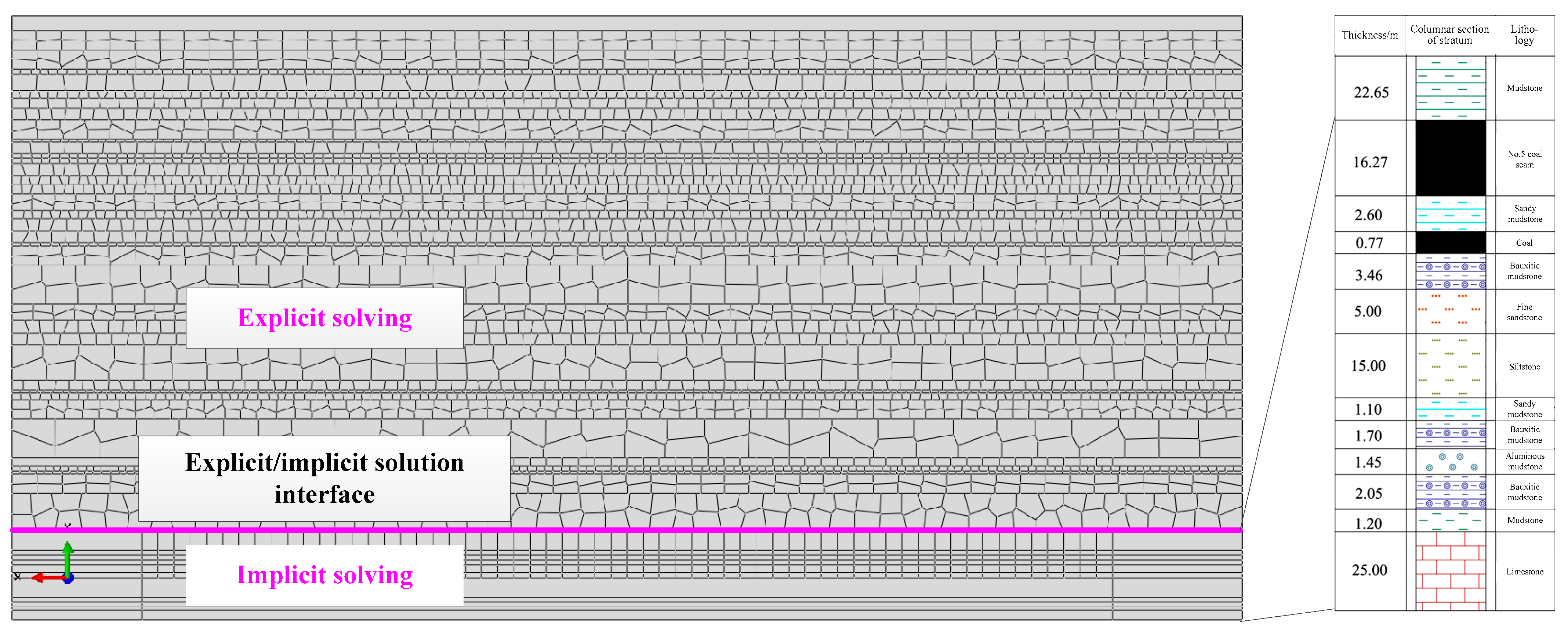
3.1. Geological Characteristics and Numerical Calculation Model of Yushupo Mine
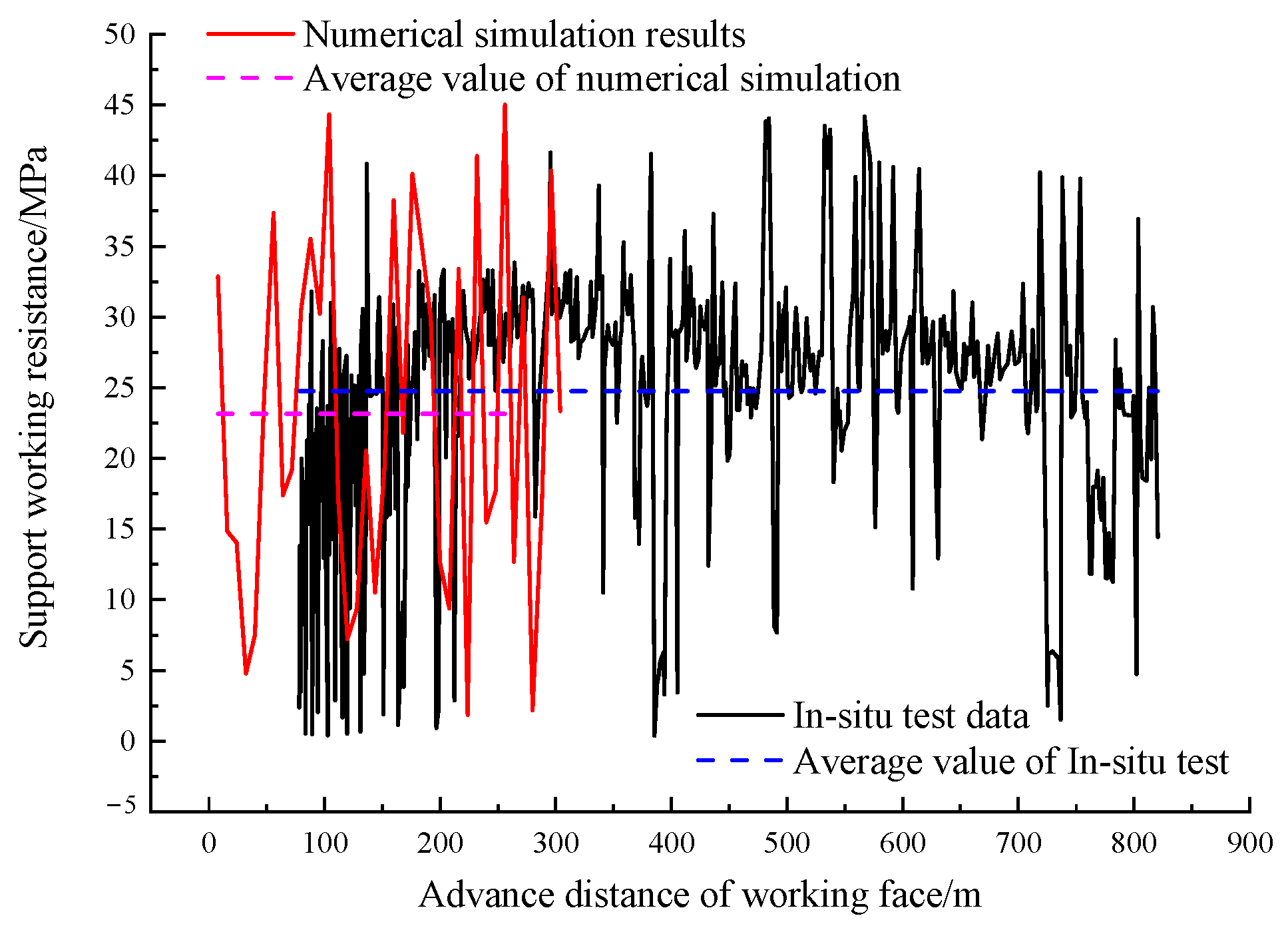
3.2. Numerical Simulation Results
4. In-Situ Tests
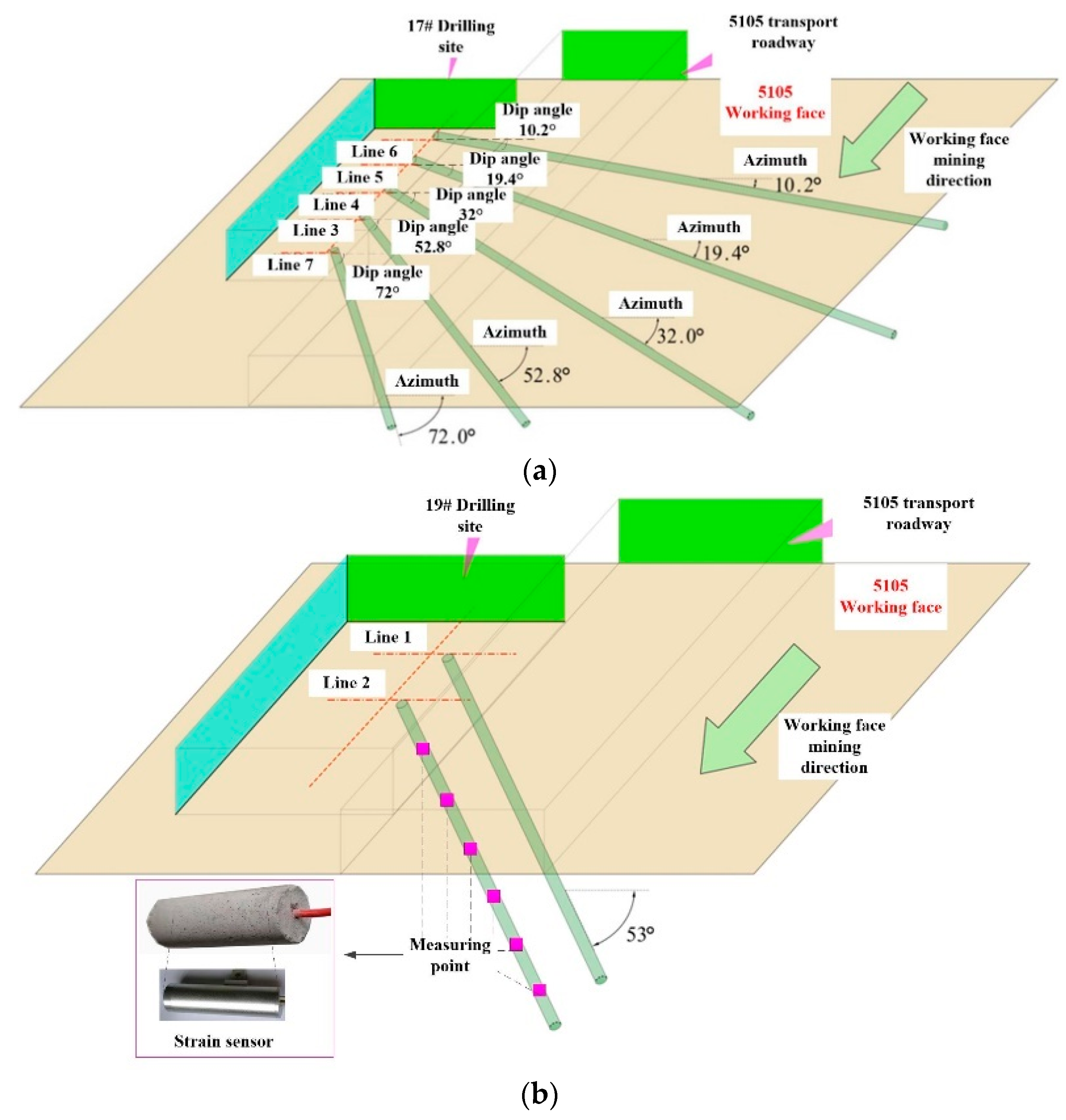
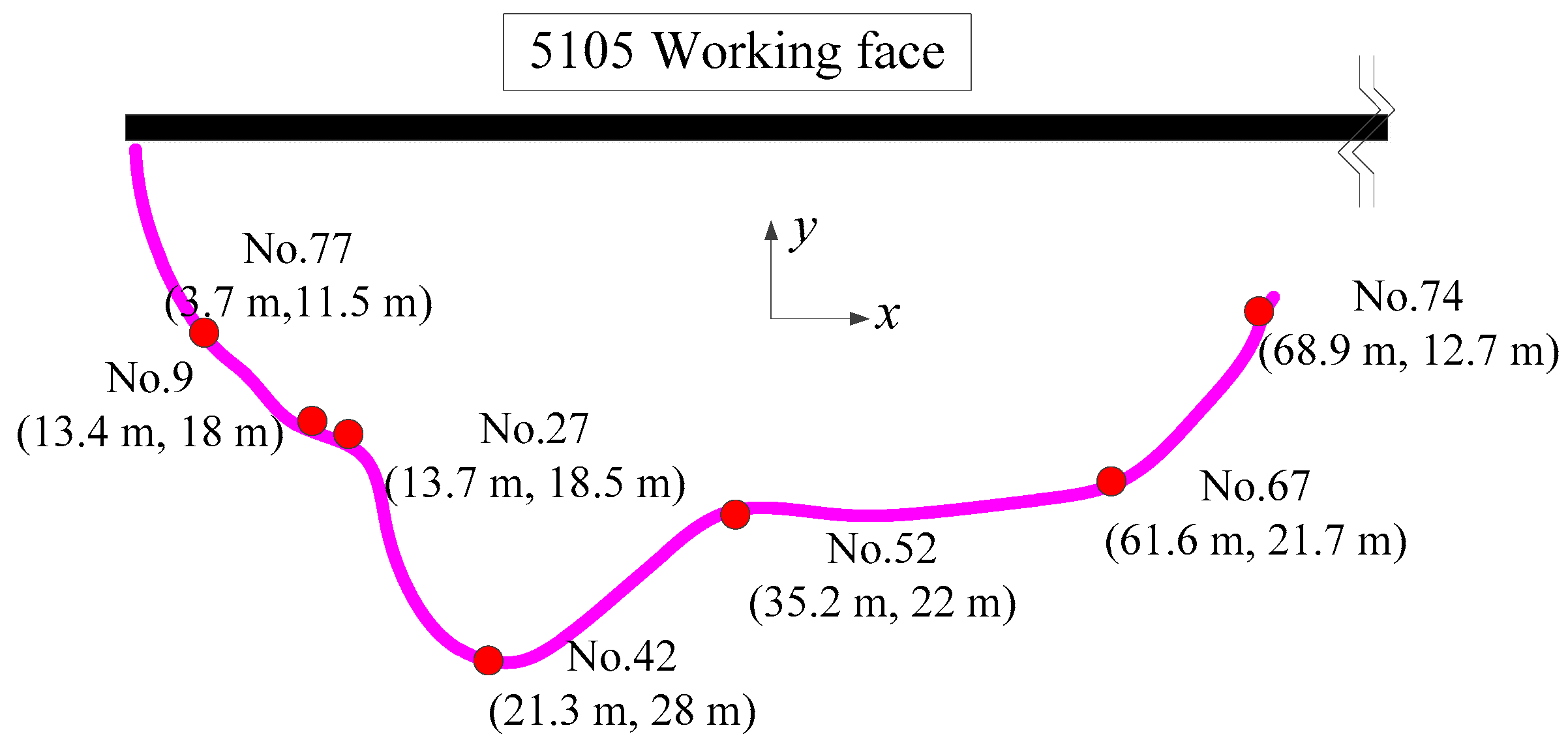
4.1. Measured Process
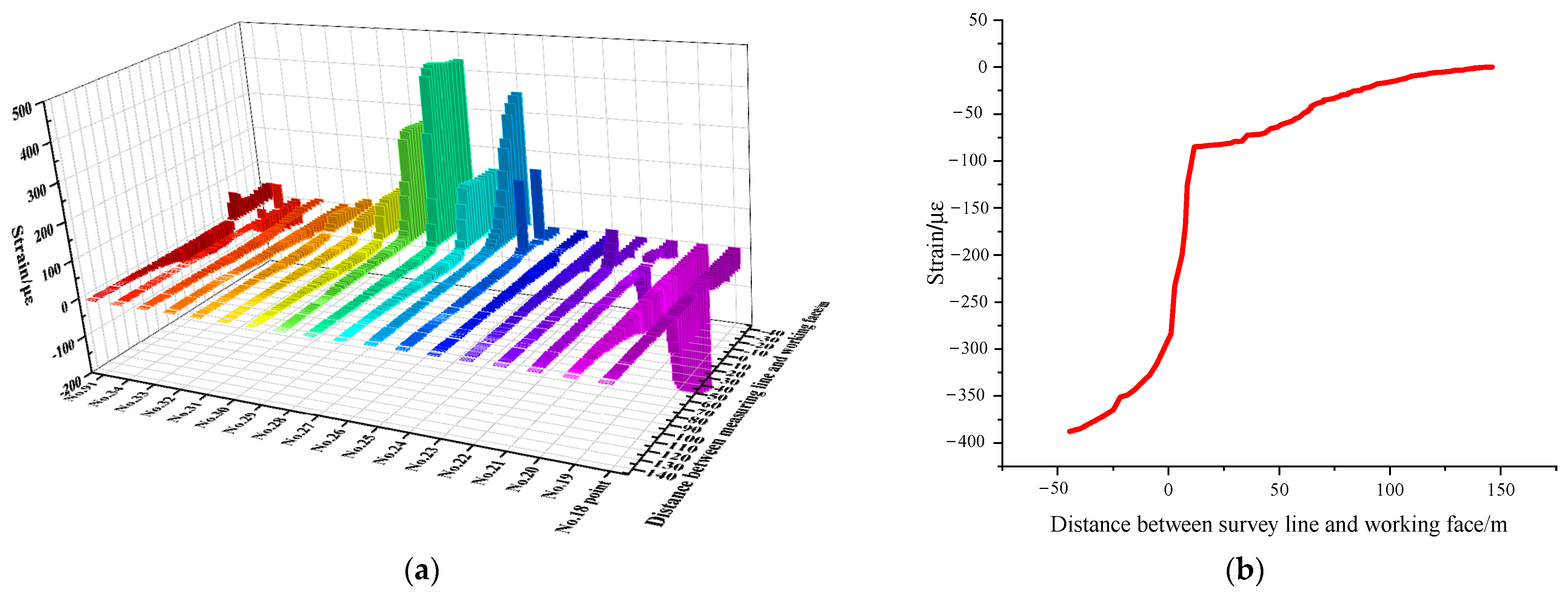
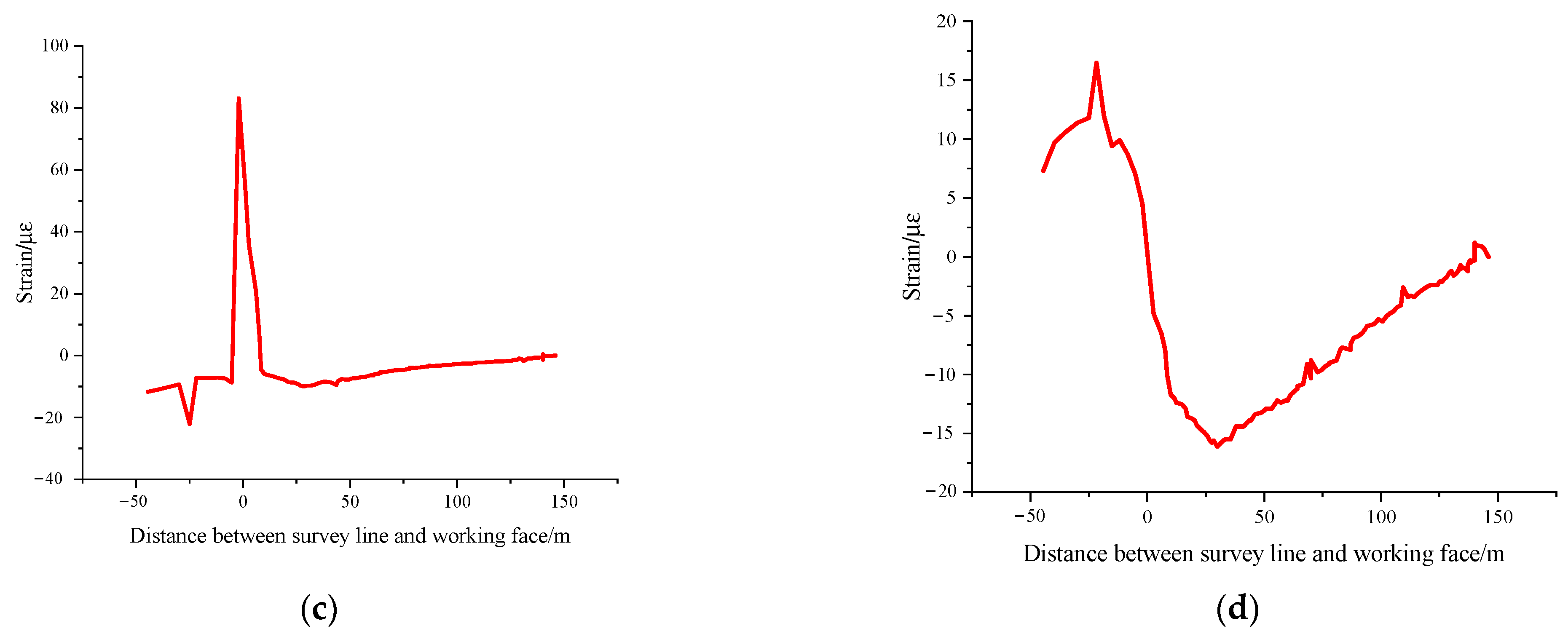
4.2. Measured Results and Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, Y.; Jiang, S.; Zhao, Y.; Li, H.; He, G.; Li, L. Life-cycle-based water footprint assessment of coal-fired power generation in China. J. Clean. Prod. 2020, 254, 120098. [Google Scholar] [CrossRef]
- Varis, O.; Vakkilainen, P. China’s 8 challenges to water resources management in the first quarter of the 21st Century. Geomorphology 2001, 41, 93–104. [Google Scholar] [CrossRef]
- Shen, N.; Pang, A.; Li, C.; Liu, K. Study on ecological compensation mechanism of Xin’an spring water source protection zone in Shanxi Province, China. Procedia Environ. Sci. 2010, 2, 1063–1073. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.Y.; Jiang, Z.Q.; Hou, H.L.; Xiao, W.G.; Yao, P. Analytical model and application of stress distribution on mining coal floor. J. Chin. Univ. Min. Technol. 2008, 18, 13–17. [Google Scholar] [CrossRef]
- Zhang, P.S.; Yan, W.; Zhang, W.Q.; Shen, B.T.; Wang, H. Mechanism of water inrush due to damage of floor and fault activation induced by mining coal seam with fault defects under fluid-solid coupling mode. Chin. J. Geotech. Eng. 2016, 38, 877–889. [Google Scholar]
- Zhu, W.C.; Wei, C.H. Numerical simulation on mining-induced water inrushes related to geologic structures using a damage-based hydromechanical model. Environ. Earth Sci. 2011, 62, 43–54. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, P.; Ou, Y.; Yao, D.; Tian, Y. Analytical stress analysis method of interbedded coal and rock floor over confined water: A study on mining failure depth. J. Appl. Geophys. 2022, 204, 104720. [Google Scholar] [CrossRef]
- Song, W.; Liang, Z. Theoretical and numerical investigations on mining-induced fault activation and groundwater outburst of coal seam floor. Bull. Eng. Geol. Environ. 2021, 80, 5757–5768. [Google Scholar] [CrossRef]
- Chen, Y.; Tang, L. Main controlling factors to determine depth of failure zone in complete floor of coal seam based on field measurements. Arab. J. Geosci. 2022, 15, 101. [Google Scholar] [CrossRef]
- Shi, S.; Miao, Y.; Wu, H.; Xu, Z.; Liu, C. The Stress Evolution of Adjacent Working Faces Passing through an Abandoned Roadway and the Damage Depth of the Floor. Energies 2022, 15, 5824. [Google Scholar] [CrossRef]
- Ma, K.; Sun, X.Y.; Tang, C.A.; Yuan, F.Z.; Wang, S.J.; Chen, T. Floor water inrush analysis based on mechanical failure characters and microseismic monitoring. Tunn. Undergr. Space Technol. 2021, 108, 103698. [Google Scholar] [CrossRef]
- Li, A.; Liu, Y.; Mou, L.; Li, K. Numerical analysis and case study on the mitigation of mining damage to the floor of no. 5 coal seam of Taiyuan Group by grouting. J. South. Afr. Inst. Min. Metall. 2018, 118, 461–470. [Google Scholar] [CrossRef]
- Mei, Q.I.U.; Longqing, S.H.I.; Xiaoge, Y.U.; Weifu, G.A.O.; Yongkui, S.H.I. On preventing the high pressure water-inrush from floor with paste-like backfill mining. J. Min. Saf. Eng. 2016, 33, 409–414+422. [Google Scholar]
- Li, H.; Bai, H.; Wu, J.; Meng, Q.; Ma, K.; Wu, L.; Meng, F.; Wang, S. A set of methods to predict water inrush from an ordovician karst aquifer: A case study from the Chengzhuang mine, China. Mine Water Environ. 2019, 38, 39–48. [Google Scholar] [CrossRef]
- Xue, W.F.; Wang, S.J.; Huang, K.J.; Ji, R.J.; Liu, M.L.; Ren, Y.L.; Xi, X.P.; Wang, F. Theoretical analysis and field measurement of floor failure in gob side entry of cutting roof in confined water mine area. J. China Coal Soc. 2020, 45, 581–588. [Google Scholar]
- Hou, E.K.; Fan, J.C.; Xie, X.S.; Long, T.W.; Zhuang, H.L.; Wang, J.H.; Fan, Z.G. Development characteristics of water-conducting fractured zone in deep coal seam based on microseismic monitoring. Coal Geol. Explor. 2020, 48, 89–96. [Google Scholar]
- Duan, H. Analysis on Failure Features and Failure Depth of Coal Seam Floor During Mining Process. Coal Sci. Technol. 2014, 42, 17–20. [Google Scholar]
- Liu, X.; Chai, Z.; Liu, X.; Yang, Z.; Xin, Z. Study on pore fracture propagation and unloading failure characteristics of siltite under cyclic loads. J. China Coal Soc. 2022, 47 (Suppl. 1), 77–89. [Google Scholar]
- Enakoutsa, K. New applications of a generalized Hooke’s law for second gradient materials. Theor. Appl. Mech. Lett. 2015, 5, 129–133. [Google Scholar] [CrossRef] [Green Version]
- Meng, Q.; Zhang, M.; Han, L.; Pu, H.; Nie, T. Effects of acoustic emission and energy evolution of rock specimens under the uniaxial cyclic loading and unloading compression. Rock Mech. Rock Eng. 2016, 49, 3873–3886. [Google Scholar] [CrossRef]
- Steinke, C.; Kaliske, M. A phase-field crack model based on directional stress decomposition. Comput. Mech. 2019, 63, 1019–1046. [Google Scholar] [CrossRef]
- Rubin, M.B. A new approach to modeling the thermomechanical, orthotropic, elastic-inelastic response of soft materials. Mech. Soft Mater. 2019, 1, 3. [Google Scholar] [CrossRef] [Green Version]
- Komar, L.A.; Svistkov, A.L. Thermodynamics of Elastic Material with Relaxing Heat Flux. Mech. Solids 2020, 55, 584–588. [Google Scholar] [CrossRef]
- Li, H.; Liang, W.; Wang, J.; Cao, W.; Wu, P.; Ma, K.; Wei, J.; Li, J. Research on main controlling factors and its influencing laws on hydraulic fracture network in the fractured soft and low-permeability coal. J. Nat. Gas Sci. Eng. 2021, 95, 104147. [Google Scholar] [CrossRef]
- Li, A.; Ma, Q.; Lian, Y.; Ma, L.; Mu, Q.; Chen, J. Numerical simulation and experimental study on floor failure mechanism of typical working face in thick coal seam in Chenghe mining area of Weibei, China. Environ. Earth Sci. 2020, 79, 118. [Google Scholar] [CrossRef]
- Meng, X.; Liu, W.; Zhao, J.; Ding, X. In situ investigation and numerical simulation of the failure depth of an inclined coal seam floor: A case study. Mine Water Environ. 2019, 38, 686–694. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, S.; Wang, Z.; Li, F. Deformation and failure of floor in mine with soft coal, soft floor, hard roof and varying thicknesses of coal seam. Eng. Fail. Anal. 2020, 115, 104653. [Google Scholar] [CrossRef]
- Hu, Y.; Li, W.; Wang, Q.; Liu, S.; Wang, Z. Study on failure depth of coal seam floor in deep mining. Environ. Earth Sci. 2019, 78, 697. [Google Scholar] [CrossRef]





| E0/GPa | μ | ψ/° | σB/σU | ||
|---|---|---|---|---|---|
| 6.58 | 0.19 | 28 | 1.32 | 3.85 | 31.50 |
| Drilling Site | Line Number | Number of Measuring Points | Measuring Point Number | Measure-Point Distance/m |
|---|---|---|---|---|
| J19 | 1 | 18 | 18–34, 91 | 2.0 |
| 2 | 18 | 1–7, 90 | 2.2 | |
| J17 | 3 | 11 | 35–45 | 3.3 |
| 4 | 14 | 46–58 | 4.2 | |
| 5 | 14 | 59–72 | 6.1 | |
| 6 | 3 | 73–75 | 33.4 | |
| 7 | 14 | 76–89 | 1.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, G.; Wang, Z.; Qu, S.; Li, H.; Zhou, Y.; Lyu, H.; He, Y. Study on Explicit–Implicit Simulation and In-Situ Measurement of Floor Failure Law in Extra-Thick Coal Seams. Minerals 2022, 12, 1511. https://doi.org/10.3390/min12121511
Guo G, Wang Z, Qu S, Li H, Zhou Y, Lyu H, He Y. Study on Explicit–Implicit Simulation and In-Situ Measurement of Floor Failure Law in Extra-Thick Coal Seams. Minerals. 2022; 12(12):1511. https://doi.org/10.3390/min12121511
Chicago/Turabian StyleGuo, Guoqiang, Zhimin Wang, Shaobo Qu, Hao Li, Yang Zhou, Hanjiang Lyu, and Yuan He. 2022. "Study on Explicit–Implicit Simulation and In-Situ Measurement of Floor Failure Law in Extra-Thick Coal Seams" Minerals 12, no. 12: 1511. https://doi.org/10.3390/min12121511
APA StyleGuo, G., Wang, Z., Qu, S., Li, H., Zhou, Y., Lyu, H., & He, Y. (2022). Study on Explicit–Implicit Simulation and In-Situ Measurement of Floor Failure Law in Extra-Thick Coal Seams. Minerals, 12(12), 1511. https://doi.org/10.3390/min12121511






