Estimation of Final Product Concentration in Metalic Ores Using Convolutional Neural Networks
Abstract
1. Introduction
1.1. Grain Size Distribution—State of the Art
1.2. Chemical Composition
1.3. Aim of the Article
1.4. General Model Description
2. Materials and Methods
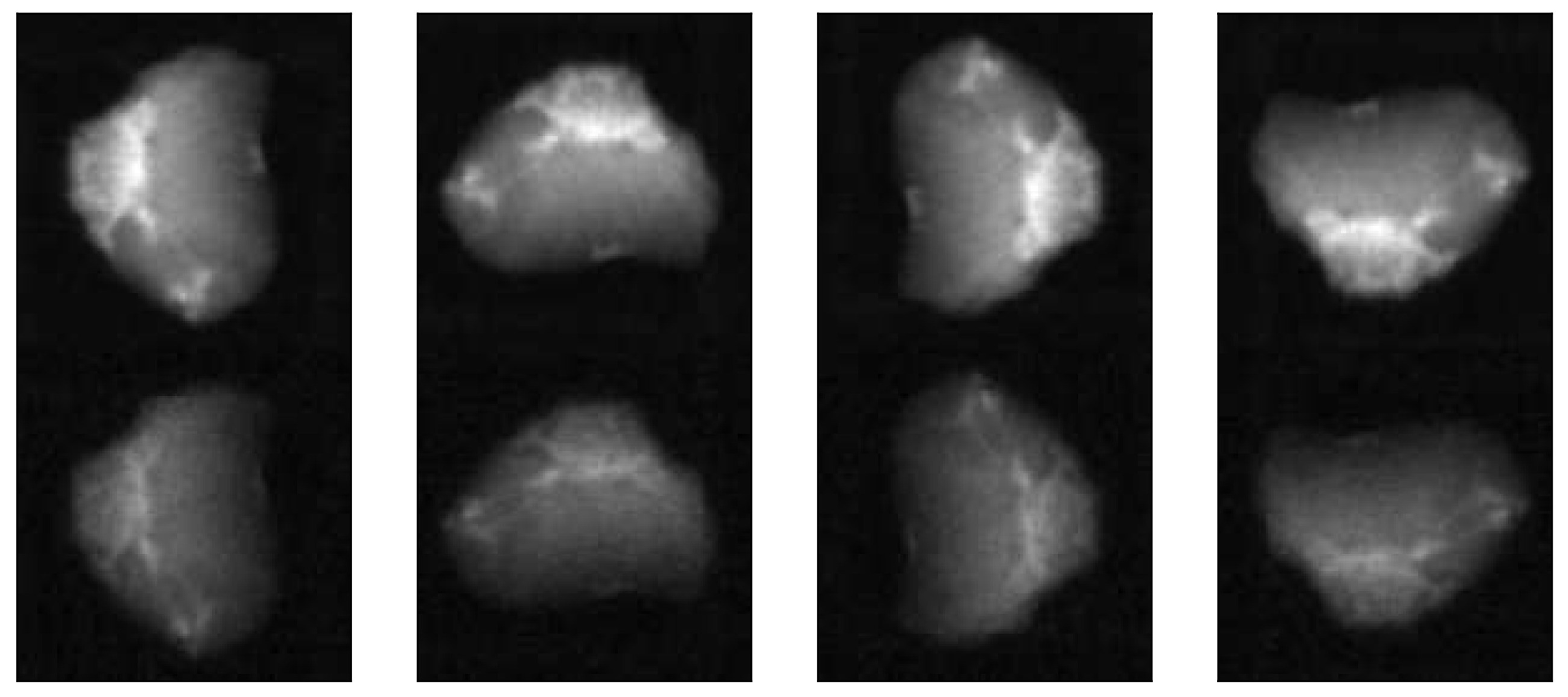
2.1. Data Description
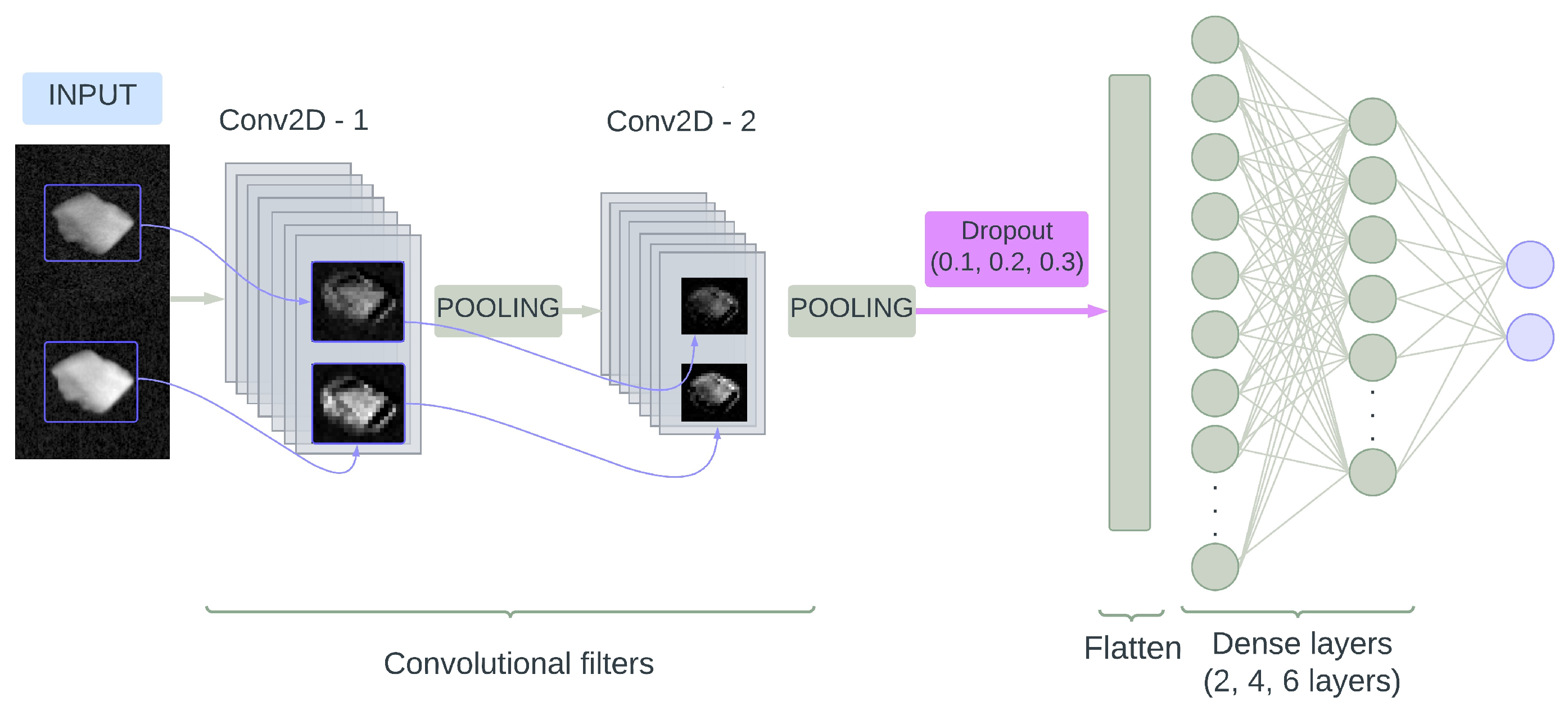
2.2. Model Description
2.3. Structure Optimization Procedure
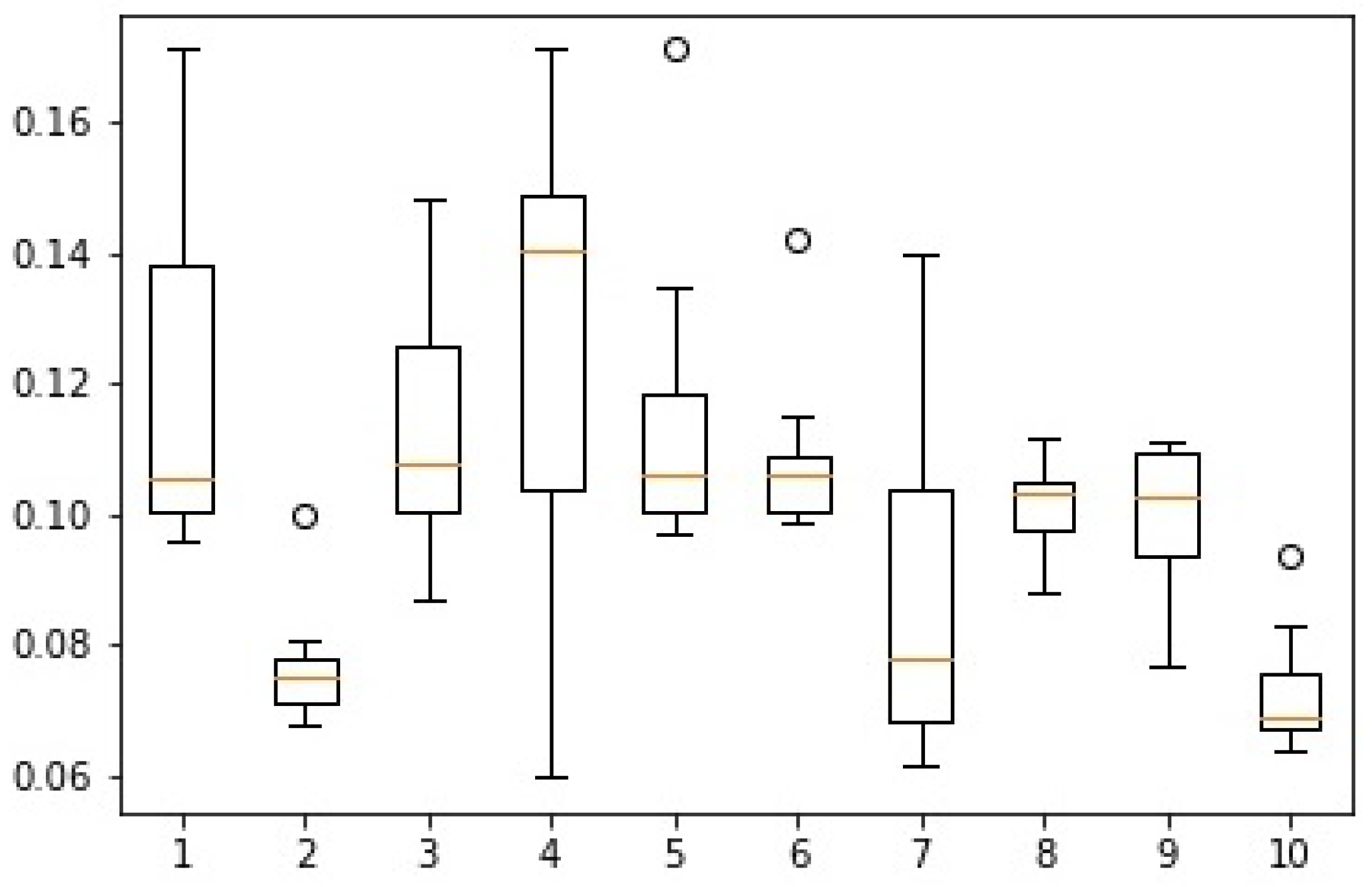
3. Results
4. Discussion
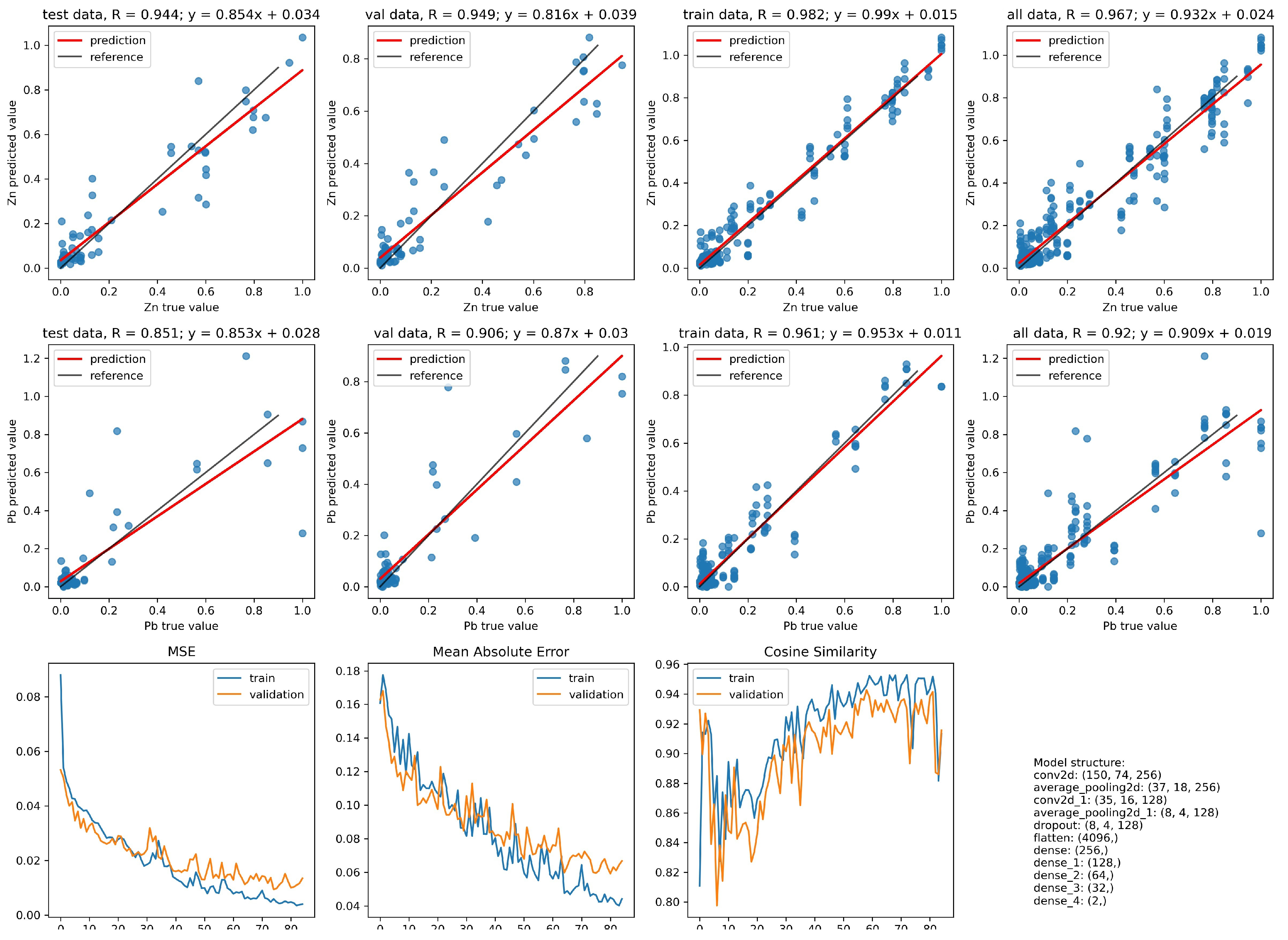
- In the case of identifying the value of the zinc content in the grain, the network with the index 10 is characterized by a better convergence to the results with the values obtained from the chemical analysis. The improvement in convergence in this case is at the level of 5%.
- When identifying the value of the lead content in the grain, the network with the index 2 has a slightly better convergence than the network with the index 10. However, this disproportion is not as significant as it was in the case of zinc content for the network with the index 10.
- In case of identifying the value of the zinc content in the grain:
- The network with the index 10 is characterized by more than a twice lower maximum error. The number of occurrences of this error for both networks is so marginal that the situation is negligible.
- The network with the index 10 in relation to the network with the index 2, for most of the analyzed cases, has twice the convergence of the output values with respect to the targets.
- In the case of identifying the value of the lead content in the grain:
- The network with index 10 is characterized by a smaller maximum error compared with the network with index 2. The occurrence of this error for both networks takes place at a level so marginal that it is negligible.
- Network errors with indexes 2 and 10 for most of the analyzed cases are in the range between 0 and 0.06.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yeshi, K.; Wangdi, T.; Qusar, N.; Nettles, J.; Craig, S.R.; Schrempf, M.; Wangchuk, P. Geopharmaceuticals of Himalayan Sowa Rigpa medicine: Ethnopharmacological uses, mineral diversity, chemical identification and current utilization in Bhutan. J. Ethnopharmacol. 2018, 223, 99–112. [Google Scholar] [CrossRef] [PubMed]
- Rustom, L.E.; Poellmann, M.J.; Johnson, A.J.W. Mineralization in micropores of calcium phosphate scaffolds. Acta Biomater. 2019, 83, 435–455. [Google Scholar] [CrossRef]
- Gierz, Ł.; Markowski, P.; Chmielewski, P. Validation of an image-analysis-based method of measurement of the overall dimensions of seeds. J. Phys. Conf. Ser. 2021, 1736, 012007. [Google Scholar] [CrossRef]
- Gierz, Ł. The method and a stand for measuring aerodynamic forces in every plane on the basis of an image analysis. Proc. SPIE—Int. Soc. Opt. Eng. 2019, 11179, 111793F. [Google Scholar] [CrossRef]
- Gierz, Ł.; Gierz, S.; Koszela, K.; Fojud, A.; Boniecki, P.; Gawałek, J. Validation of a photogrammetric method for evaluating seed potato cover by a chemical agent. In Proceedings of the International Society for Optical Engineering, Shanghai, China, 11–14 May 2018; Volume 108064. [Google Scholar] [CrossRef]
- Przybył, K.; Gawałek, J.; Gierz, L.; Łukomski, M.; Zaborowicz, M.; Boniecki, P. Recognition of color changes in strawberry juice powders using self-organizing feature map. Proc. SPIE 2018, 10806, 1080621. [Google Scholar] [CrossRef]
- Yen, Y.K.; Lin, C.L.; Miller, J.D. Particle overlap and segregation problems in on-line coarse particle size measurement. Powder Technol. 1998, 98, 1–12. [Google Scholar] [CrossRef]
- Hahne, R.; Pålsson, B.I.; Samskog, P.O. Ore characterisation for—-And simulation of—-Primary autogenous grinding. Miner. Eng. 2003, 16, 13–19. [Google Scholar] [CrossRef]
- Tessier, J.; Duchesne, C.; Bartolacci, G. On-line multivariate image analysis of run-of-mine ore for control of grinding and mineral processing plants. In Proceedings of the International Conference on Mineral Processing, Modeling, Simulation and Control (MPMSC), Sudbury, ON, Canada, 6–7 June 2006; Volume 2006, pp. 175–189. [Google Scholar]
- Ko, Y.D.; Shang, H. A neural network-based soft sensor for particle size distribution using image analysis. Powder Technol. 2011, 212, 359–366. [Google Scholar] [CrossRef]
- Lange, T.B. Real-time measurement of the size distribution of rocks on a conveyor belt. IFAC Proc. Vol. 1988, 21, 25–34. [Google Scholar] [CrossRef]
- Lin, C.L.; Miller, J.D. The development of a PC, image-based, on-line particle-size analyzer. Min. Metall. Explor. 1993, 10, 29–35. [Google Scholar] [CrossRef]
- Singh, V.; Rao, S.M. Application of image processing and radial basis neural network techniques for ore sorting and ore classification. Miner. Eng. 2005, 18, 1412–1420. [Google Scholar] [CrossRef]
- Al-Sammarraie, M.A.J.; Gierz, Ł.; Przybył, K.; Koszela, K.; Szychta, M.; Brzykcy, J.; Baranowska, H.M. Predicting Fruit’s Sweetness Using Artificial Intelligence—Case Study: Orange. Appl. Sci. 2022, 12, 8233. [Google Scholar] [CrossRef]
- Hamzeloo, E.; Massinaei, M.; Mehrshad, N. Estimation of particle size distribution on an industrial conveyor belt using image analysis and neural networks. Powder Technol. 2014, 261, 185–190. [Google Scholar] [CrossRef]
- Thurley, M.J.; Andersson, T. An industrial 3D vision system for size measurement of iron ore green pellets using morphological image segmentation. Miner. Eng. 2008, 21, 405–415. [Google Scholar] [CrossRef]
- Williams, R.A.; Luke, S.P.; Ostrowski, K.L.; Bennett, M.A. Measurement of bulk particulates on belt conveyor using dielectric tomography. Chem. Eng. J. 2000, 77, 57–63. [Google Scholar] [CrossRef]
- Skoczylas, A.; Anufriiev, S.; Stefaniak, P. Oversized ore pieces detection method based on computer vision and sound processing for validation of vibrational signals in diagnostics of mining screen. In Proceedings of the International Multidisciplinary Scientific GeoConference: SGEM, Albena, Bulgaria, 18–24 August 2020; Volume 20, pp. 829–839. [Google Scholar]
- Ma, X.; Zhang, P.; Man, X.; Ou, L. A new belt ore image segmentation method based on the convolutional neural network and the image-processing technology. Minerals 2020, 10, 1115. [Google Scholar] [CrossRef]
- Gierz, Ł.; Przybył, K.; Koszela, K.; Duda, A.; Ostrowicz, W. The Use of Image Analysis to Detect Seed Contamination—A Case Study of Triticale. Sensors 2021, 21, 151. [Google Scholar] [CrossRef]
- Stachowiak, M.; Koperska, W.; Stefaniak, P.; Skoczylas, A.; Anufriiev, S. Procedures of detecting damage to a conveyor belt with use of an inspection legged robot for deep mine infrastructure. Minerals 2021, 11, 1040. [Google Scholar] [CrossRef]
- Dabek, P.; Szrek, J.; Zimroz, R.; Wodecki, J. An Automatic Procedure for Overheated Idler Detection in Belt Conveyors Using Fusion of Infrared and RGB Images Acquired during UGV Robot Inspection. Energies 2022, 15, 601. [Google Scholar] [CrossRef]
- Oestreich, J.M.; Tolley, W.K.; Rice, D.A. The development of a color sensor system to measure mineral compositions. Miner. Eng. 1995, 8, 31–39. [Google Scholar] [CrossRef]
- Petersen, K.R.P.; Aldrich, C.; Van Deventer, J.S.J. Analysis of ore particles based on textural pattern recognition. Miner. Eng. 1998, 11, 959–977. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Y.; Wang, Q. Synthetic informational mineral resource prediction: Case study in Chifeng Region, Inner Mongolia, China. Earth Sci. Front. 2008, 15, 18–26. [Google Scholar] [CrossRef]
- Ślipek, B.; Młynarczuk, M. Application of pattern recognition methods to automatic identification of microscopic images of rocks registered under different polarization and lighting conditions. Geol. Geophys. Environ. 2013, 39, 373. [Google Scholar] [CrossRef][Green Version]
- Shu, L.; McIsaac, K.; Osinski, G.R.; Francis, R. Unsupervised feature learning for autonomous rock image classification. Comput. Geosci. 2017, 106, 10–17. [Google Scholar] [CrossRef]
- Kitzig, M.C.; Kepic, A.; Grant, A. Near real-time classification of iron ore lithology by applying fuzzy inference systems to petrophysical downhole data. Minerals 2018, 8, 276. [Google Scholar] [CrossRef]
- Liu, C.; Li, M.; Zhang, Y.; Han, S.; Zhu, Y. An enhanced rock mineral recognition method integrating a deep learning model and clustering algorithm. Minerals 2019, 9, 516. [Google Scholar] [CrossRef]
- Murtagh, F.; Qiao, X.; Crookes, D.; Walsh, P.; Basheer, P.A.; Long, A.; Starck, J.L. A machine vision approach to the grading of crushed aggregate. Mach. Vis. Appl. 2005, 16, 229–235. [Google Scholar] [CrossRef]
- Tessier, J.; Duchesne, C.; Bartolacci, G. A machine vision approach to on-line estimation of run-of-mine ore composition on conveyor belts. Miner. Eng. 2007, 20, 1129–1144. [Google Scholar] [CrossRef]
- Dudzik, M.; Stręk, A.M. ANN Architecture Specifications for Modelling of Open-Cell Aluminum under Compression. Math. Probl. Eng. 2020, 2020, 2834317. [Google Scholar] [CrossRef]
- Dudzik, M.; Romanska-Zapala, A.; Bomberg, M. A Neural Network for Monitoring and Characterization of Buildings with Environmental Quality Management, Part 1: Verification under Steady State Conditions. Energies 2020, 13, 3469. [Google Scholar] [CrossRef]
- Dudzik, M. Towards Characterization of Indoor Environment in Smart Buildings: Modelling PMV Index Using Neural Network with One Hidden Layer. Sustainability 2020, 12, 6749. [Google Scholar] [CrossRef]
- Talos Library. Available online: https://pypi.org/project/talos/ (accessed on 30 May 2022).
- Maximum Pooling. Available online: https://www.kaggle.com/code/ryanholbrook/maximum-pooling (accessed on 30 May 2022).
- Shin, Y.; Shin, S. Rock Classification in a Vanadiferous Titanomagnetite Deposit Based on Supervised Machine Learning. Minerals 2022, 12, 461. [Google Scholar] [CrossRef]

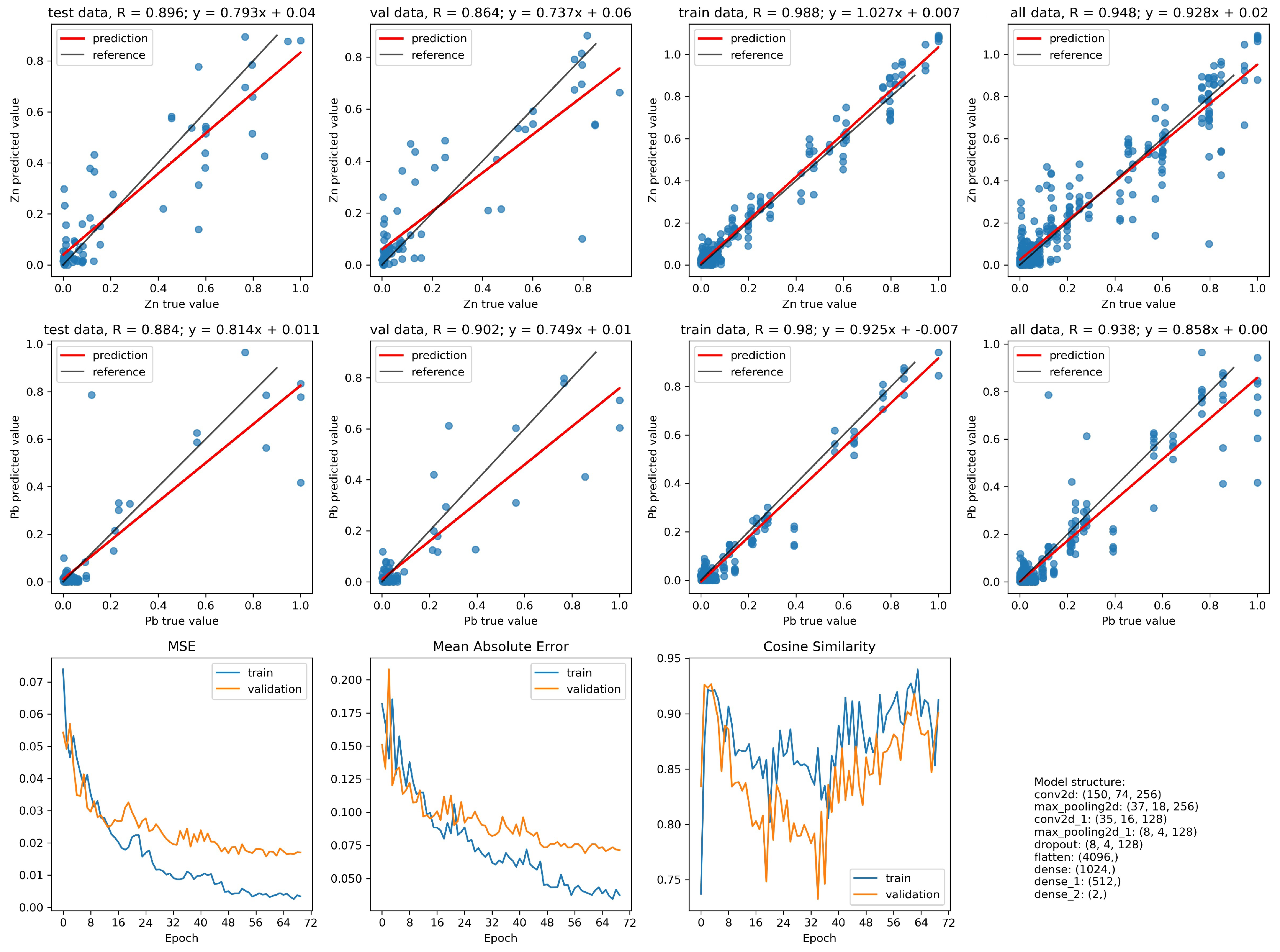
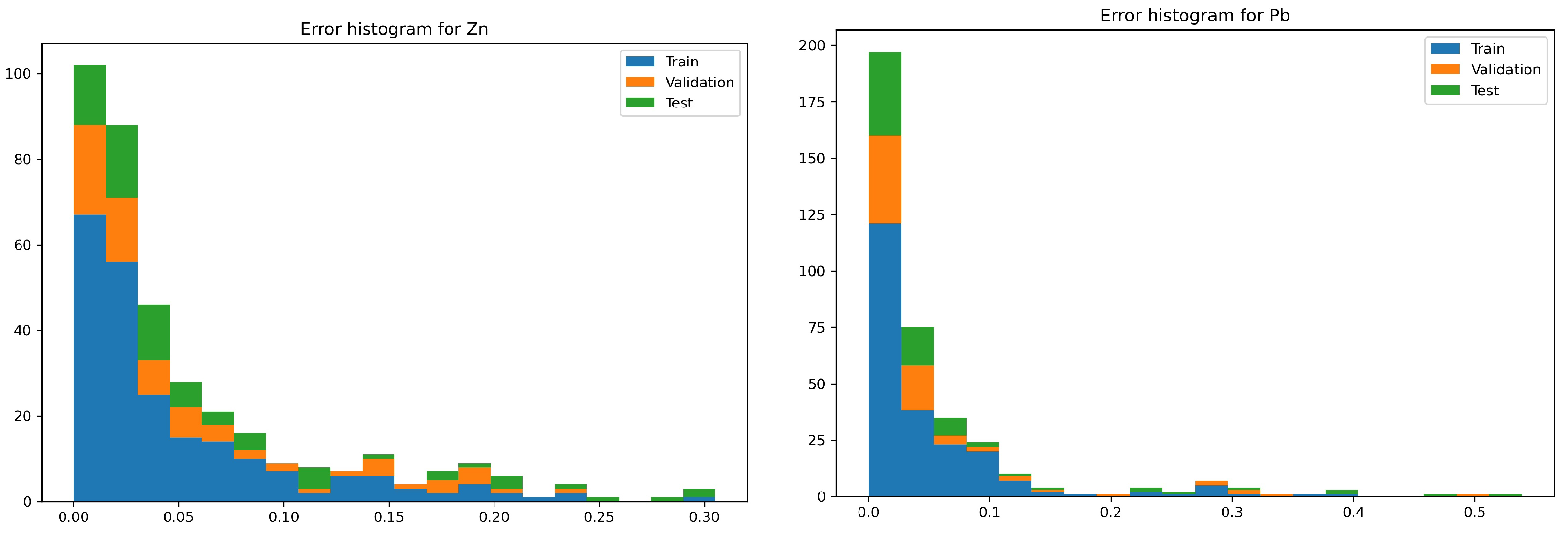
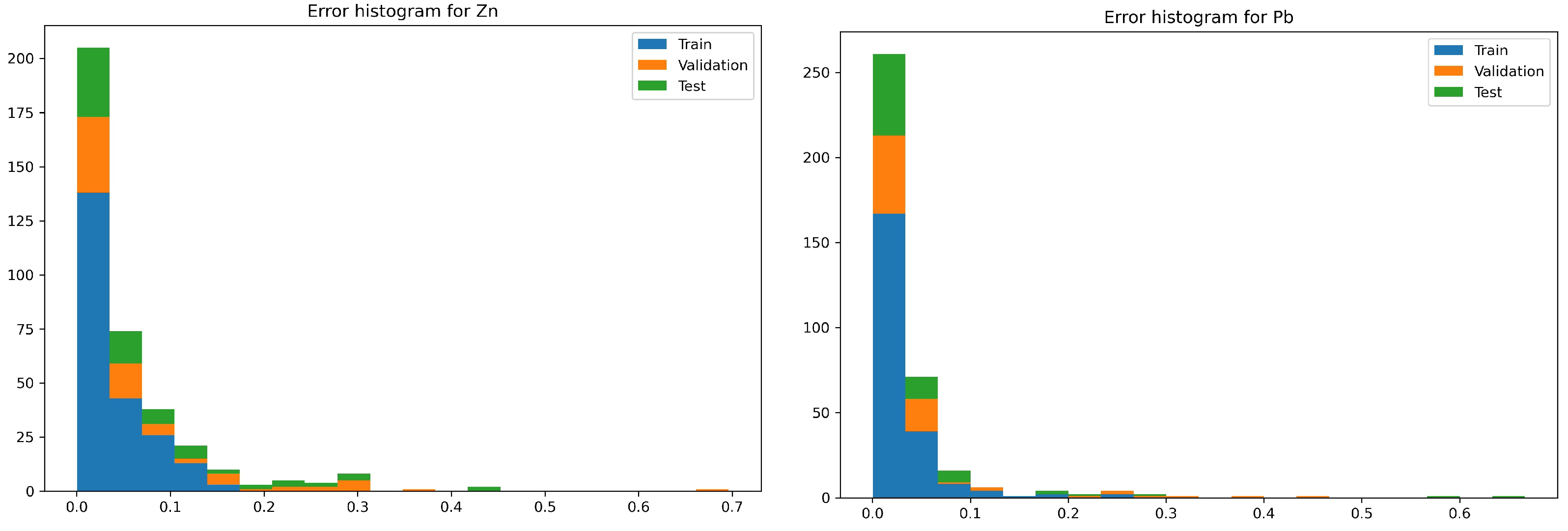
| Optimized Parameter | Value Range |
|---|---|
| Number of filters in the first convolutional layer | 64, 128, 256, 512 |
| Pooling layers type | MaxPooling, AveragePooling |
| Pooling size | 2 × 2, 4 × 4 |
| Dropout | 0.1, 0.2, 0.3 |
| Optimizer | Adam, Stochastic Gradient Descent, RMSProp, Ftrl |
| Loss function | Mean Squared Error, Mean Squared Logarithmic Error, Cosine Similarity, Huber, LogCosh |
| Number of neurons in the first dense layer | 1024, 512, 256 |
| Number of dense layers | 2, 4, 6 |
| Dense layers divider | 2, 4 |
| Dense layers activation function | ReLU, Sigmoid, Tanh |
| Structure Number | Conv. Layers | Pooling Type | Dropout | Dense Layers | Activation Function | Optimizer |
|---|---|---|---|---|---|---|
| 1 | 64, 32 | Max, (4, 4) | 0.2 | 1024, 512, 256, 128, 64, 32 | ReLU | RMSprop |
| 2 | 256, 128 | Max, (4, 4) | 0.2 | 1024, 512 | ReLU | Adam |
| 3 | 64, 32 | Max, (4, 4) | 0.2 | 256, 128, 64, 32, 16, 8 | ReLU | RMSprop |
| 4 | 64, 32 | Max, (4, 4) | 0.1 | 1024, 256, 64, 16, 4, 2 | ReLU | Adam |
| 5 | 128, 64 | Max, (4, 4) | 0.3 | 512, 256, 128, 64 | ReLU | RMSprop |
| 6 | 64. 32 | Max, (4, 4) | 0.2 | 512, 256, 128, 64 | ReLU | RMSprop |
| 7 | 256, 128 | Average, (2, 2) | 0.2 | 1024, 256, 64, 16 | ReLU | Adam |
| 8 | 64, 32 | Max, (4, 4) | 0.3 | 512, 128 | ReLU | RMSprop |
| 9 | 64, 32 | Max, (4, 4) | 0.1 | 256, 64 | ReLU | RMSprop |
| 10 | 256, 128 | Average, (4, 4) | 0.1 | 256, 128, 64, 32 | ReLU | Adam |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Progorowicz, J.; Skoczylas, A.; Anufriiev, S.; Dudzik, M.; Stefaniak, P. Estimation of Final Product Concentration in Metalic Ores Using Convolutional Neural Networks. Minerals 2022, 12, 1480. https://doi.org/10.3390/min12121480
Progorowicz J, Skoczylas A, Anufriiev S, Dudzik M, Stefaniak P. Estimation of Final Product Concentration in Metalic Ores Using Convolutional Neural Networks. Minerals. 2022; 12(12):1480. https://doi.org/10.3390/min12121480
Chicago/Turabian StyleProgorowicz, Jakub, Artur Skoczylas, Sergii Anufriiev, Marek Dudzik, and Paweł Stefaniak. 2022. "Estimation of Final Product Concentration in Metalic Ores Using Convolutional Neural Networks" Minerals 12, no. 12: 1480. https://doi.org/10.3390/min12121480
APA StyleProgorowicz, J., Skoczylas, A., Anufriiev, S., Dudzik, M., & Stefaniak, P. (2022). Estimation of Final Product Concentration in Metalic Ores Using Convolutional Neural Networks. Minerals, 12(12), 1480. https://doi.org/10.3390/min12121480






