Study of the Reaction Mechanisms during the Thermal Decomposition of Arsenic Sulfide (V) at High Temperatures under Non-Isothermal Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample
2.2. No-Isothermal
2.3. Interrupted Tests
2.4. Gas Treatment
3. Results and Discussion
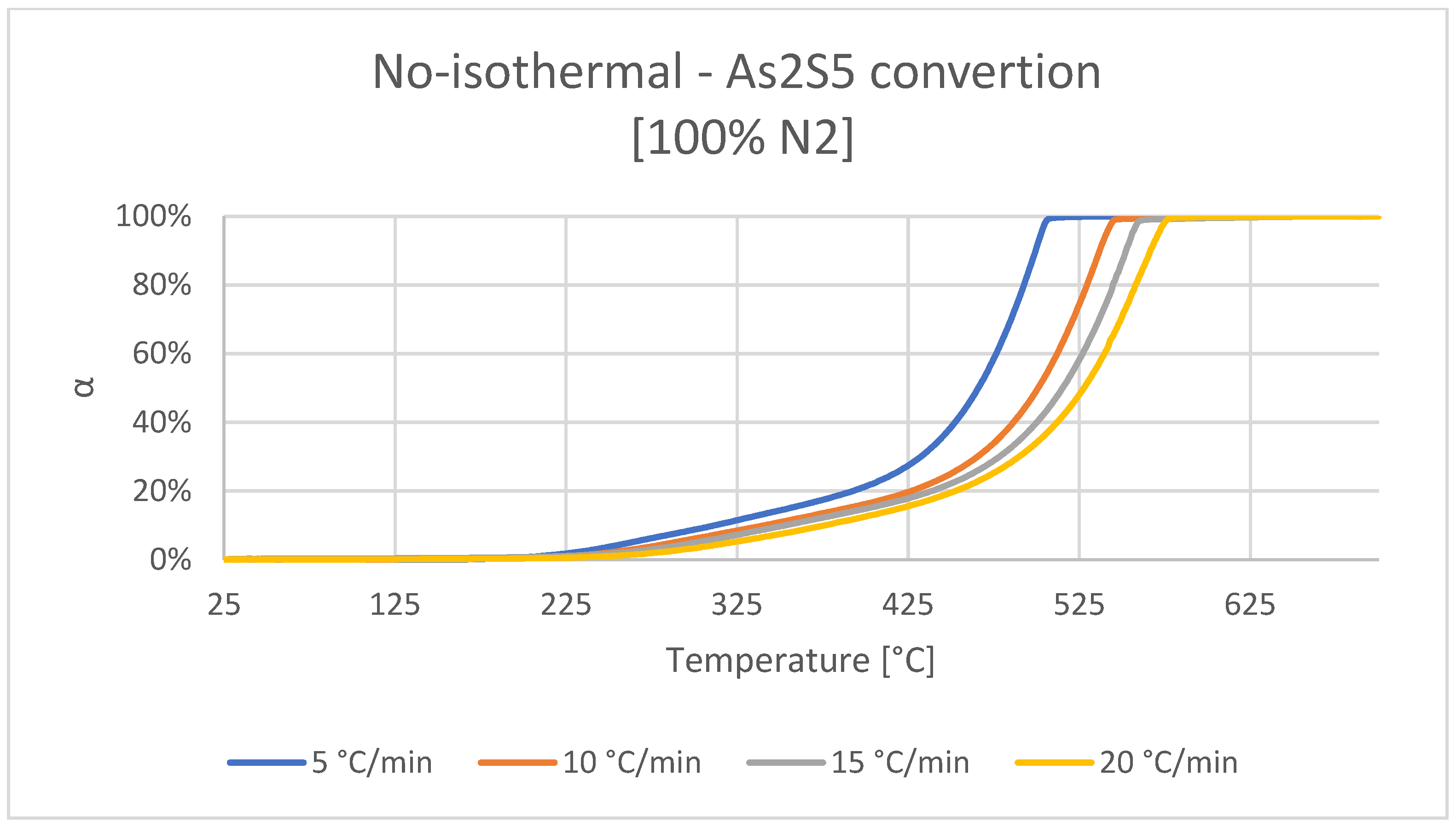
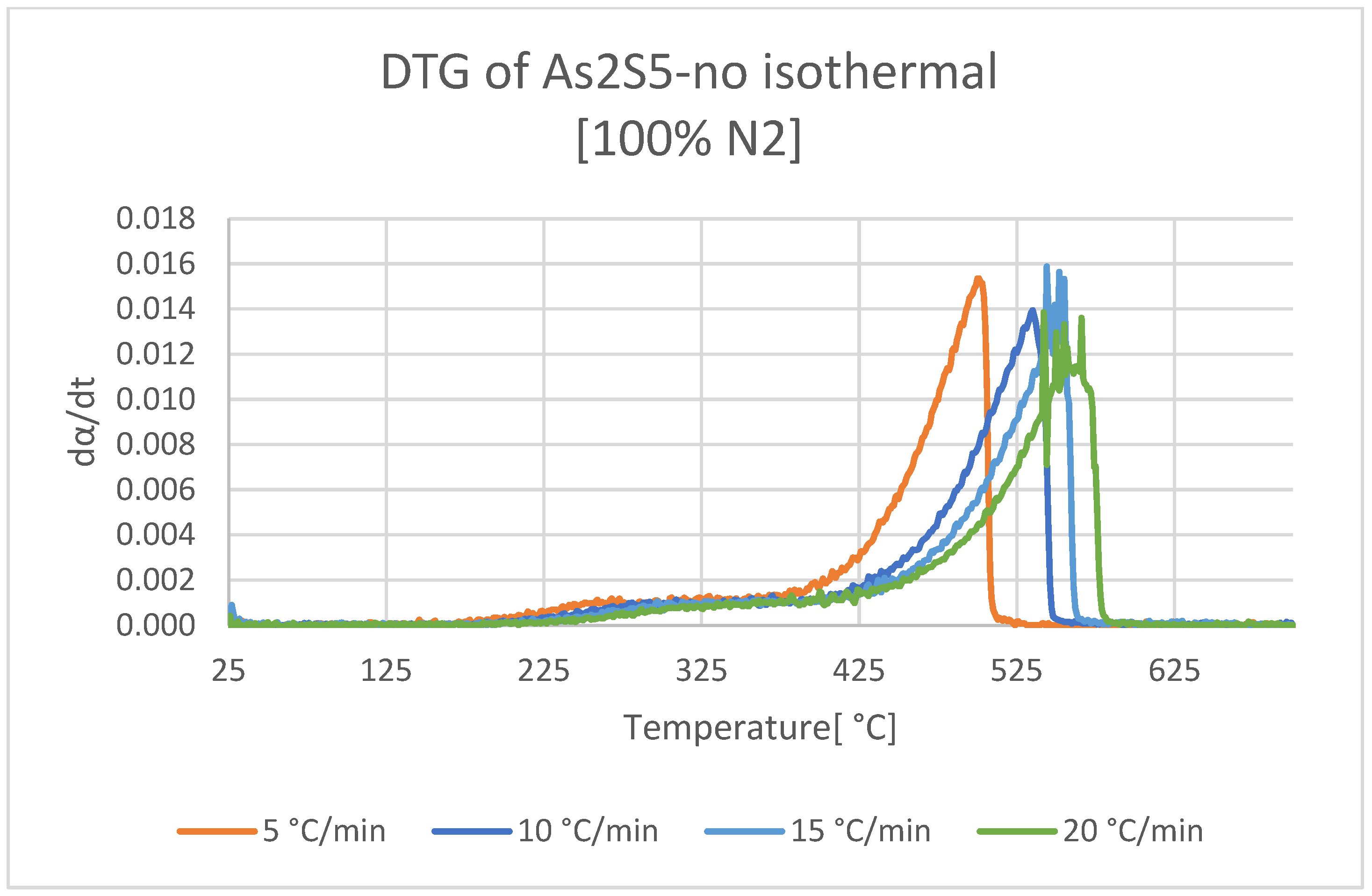
3.1. Decomposition of As2S5 in Neutral Atmosphere
3.2. Kinetic Parameters
3.2.1. Kissinger
3.2.2. Ozawa
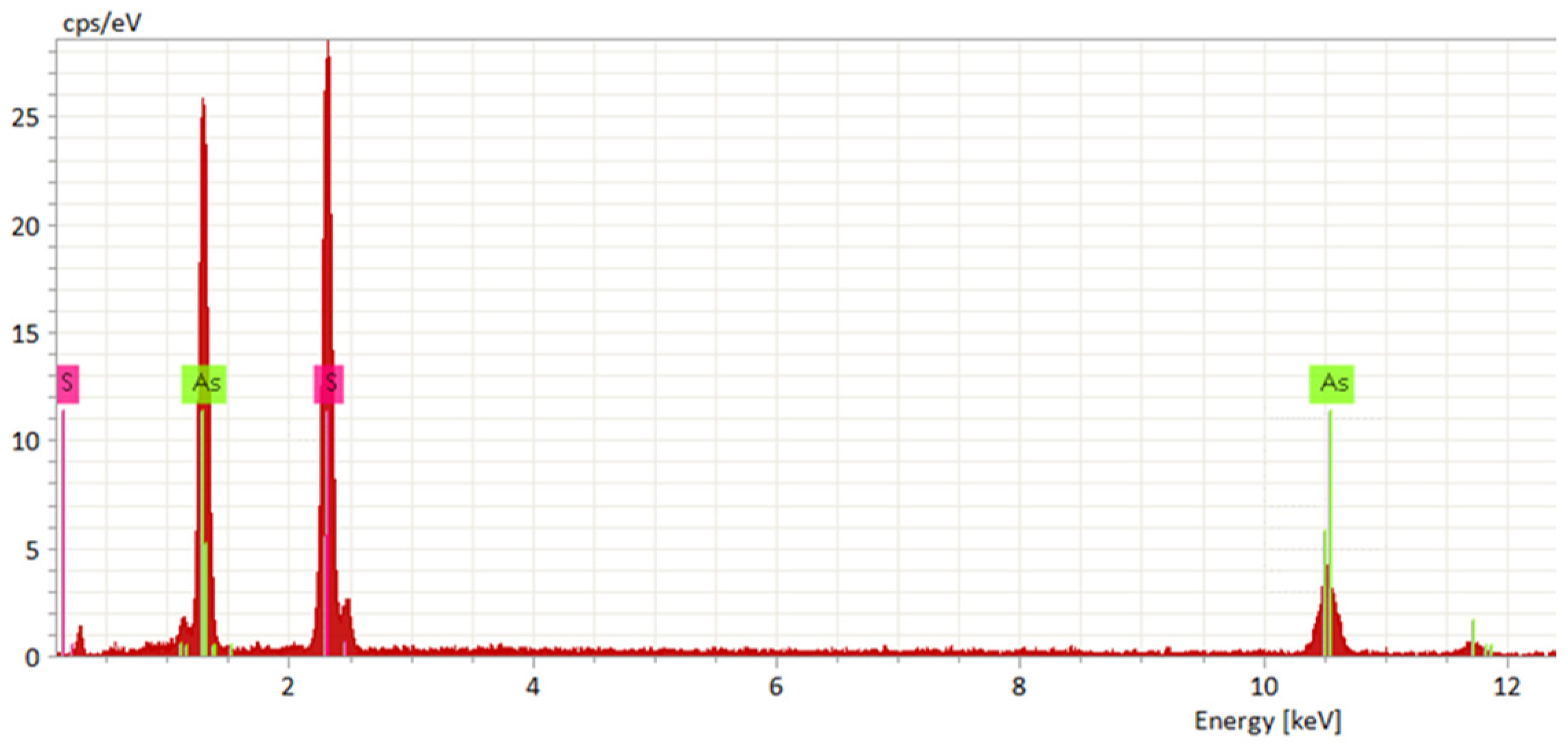
3.3. Analysis of Products
- The As2S5 sample when subjected to an increase in temperature releases sulfur, transforming into As2S3, a stable phase at higher temperatures;
- Subsequently, by visual inspection, it was verified that at 250 °C, there are no solids present, only a molten phase; and, given that at 300 °C, the SEM-EDS analysis detected the presence of As2S5 and As2S3, it is inferred that the molten phase is a mixture of As2S5 (l) and As2S3 (l);
- After complete conversion of As2S5 to As2S3, SEM-EDS analysis does not detect the presence of another phase between 300 and 500 °C; and
- Finally, at 500 °C, the formation of a molten As3S4 phase is detected, which has not been reported as part of the reaction mechanism in the literature. Therefore, the test was performed in duplicate and the same phase was detected; however, since it is consistent with the theory [11] of the formation of a stable phase at high temperatures and release of elemental sulfur, it is concluded that it is possible that As3S4 is a metastable transition phase, detected due to the rapid cooling in liquid nitrogen of the interrupted tests.
3.4. Reaction Mechanism for As2S5
- First, decomposition between 200 and 450 °C; parallel volatilization of sulfur in the sample, along with the transformation of As2S5 to As2S3 with the sulfur release.
- Second, decomposition between 450 and 575 °C; the formation of a molten phase of metastable As2S3 and As3S4, the latter formed from the decomposition of As2S3 (l) releasing elemental sulfur. Furthermore, in this temperature range, the respective volatilizations of As2S3 (g) -As4S6 (g)- from As2S3 (l), and As4S4 (g) from As3S4 (l) can be found, until a complete conversion of the sample to the gas phase.
- Finally, the overall reaction describing the thermal decomposition of As2S5 for a bed of 100% −500 μm particles, with a P80 = 232 μm, is as follows:
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sichen, D.; Seetharaman, S. Modelling of gas-solid and solid-solid reaction kinetics. In Proceedings of the Sohn International Symposium Advanced Processing of Metals and Materials, San Diego, CA, USA, 27–31 August 2006. [Google Scholar]
- Barnes, P. Reactions in the Solid State; Bamford, C.H., Tipper, C.F.H., Eds.; (Comprehensive Chemical Kinetics); Elsevier: Amsterdam, The Netherlands, 1980; Volume 22. [Google Scholar]
- Yuanhua, F. Cinética y Mecanismos de Vaporización de Sulfuros de Arsénicos desde concentrados de cobre. Master’s Thesis, Universidad de Concepción, Concepción, Chile, 1997. [Google Scholar]
- Vershinin, A.D.; Selivanov, E.N. Thermal expansion of arsenopyrite in helium and air. Inorg. Mater. 2000, 36, 551–555. [Google Scholar] [CrossRef]
- Berg, L.G.; Shlyapkina, E.N. Characteristic features of sulphide mineral DTA. J. Therm. Anal. 1975, 8, 417–426. [Google Scholar] [CrossRef]
- Johnson, G.K.; Papatheodorou, G.N.; Johnson, C.E. The enthalpies of formation and high-temperature thermodynamic functions of As4S4 and As2S3. J. Chem. Thermodyn. 1980, 12, 545–557. [Google Scholar] [CrossRef]
- Štrbac, N.; Mihajlović, I.; Minić, D.; Živković, D.; Živković, Ž. Kinetics and mechanism of arsenic sulfides oxidation December 2008. J. Min. Metall. Sect. B Metall. 2009, 45, 59–67. [Google Scholar] [CrossRef]
- Kissinger, H.E. Variation of peak temperature with heating rate in differential thermal analysis. J. Res. Natl. Bur. Stand. 1956, 57, 217. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction Kinetics in Differential Thermal Analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Ozawa, T. A New Method of Analyzing Thermogravimetric Data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
- Dunn, J.G. The oxidation of sulphide minerals. Thermochim. Acta 1997, 300, 127–139. [Google Scholar] [CrossRef]
- Vijayan, P.P.; Puglia, D.; Jyothishkumar, P.; Kenny, J.M.; Thomas, S. Effect of nanoclay and carboxyl-terminated (butadiene-co-acrylonitrile) (CTBN) rubber on the reaction induced phase separation and cure kinetics of epoxy/cyclic anhydride system. J. Mater. Sci. 2012, 47, 5241–5253. [Google Scholar] [CrossRef]
- Castro, K.; Balladares, E.; Jerez, O.; Pérez-Tello, M.; Aracena, Á. Behavior of As/AsxSy in neutral and oxidizing atmospheres at high temperatures—An overview. Metals 2022, 12, 457. [Google Scholar] [CrossRef]
- HSC Chemistry®[Software], version 8.2.0, Metso:Outotec. 2022. Available online: https://www.mogroup.com/portfolio/hsc-chemistry/ (accessed on 4 January 2022).
- Mihajlović, N.; Štrbac, N.; Živković, Ž.; Ilić, I. Kinetics and mechanism of As2S2 oxidation. J. Serb. Chem. Soc. 2005, 70, 869–877. [Google Scholar] [CrossRef]
- Pankratz, L.B.; Mrazek, R.V.; Robert, V. Thermodynamic Properties of Elements and Oxides; U.S. Dept. of the Interior, Bureau of Mines: Washington, DC, USA, 1982.
- Weisenberg, I.J.; Bakshi, P.S.; Vervaert, A.E. Arsenic Distribution and Control in Copper Smelters. JOM 1979, 31, 38–44. [Google Scholar] [CrossRef]
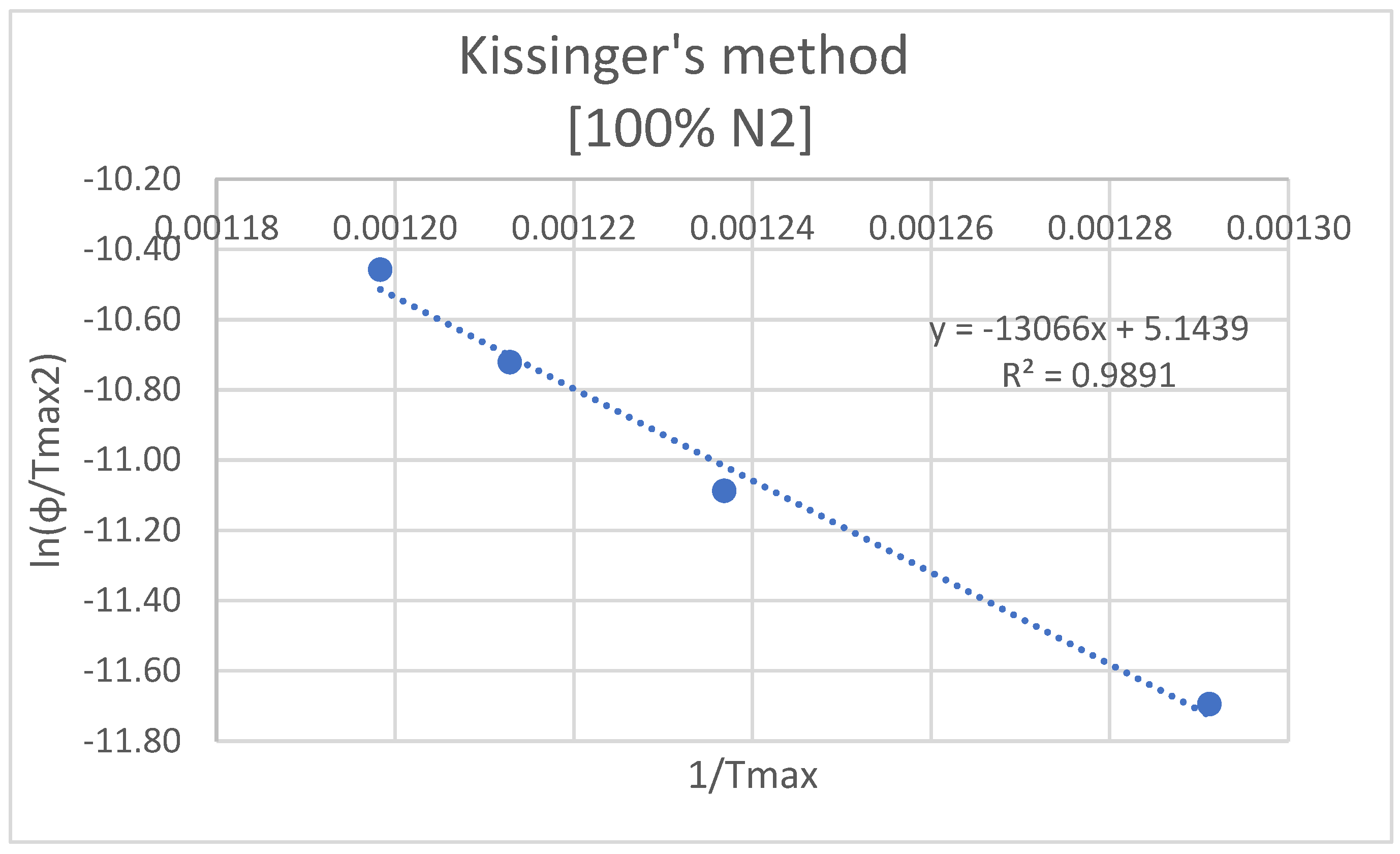


| ф [K/min] | Tmax [K] | ln(ф/T2max) | 1/Tmax | A [1/s] | k [1/s] |
|---|---|---|---|---|---|
| 5 | 774.50 | −11.69 | 1.29 × 10−3 | 3.73 × 104 | 1.76 × 10−3 |
| 10 | 808.50 | −11.09 | 1.24 × 10−3 | 3.73 × 104 | 3.58 × 10−3 |
| 15 | 824.50 | −10.72 | 1.21 × 10−3 | 3.73 × 104 | 4.89 × 10−3 |
| 20 | 834.50 | −10.46 | 1.20 × 10−3 | 3.73 × 104 | 5.92 × 10−3 |
| Ea= 108.63 kJ/mol | |||||
| α [%] | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|
| Ea [kJ/mol] | 66.80 | 88.77 | 102.37 | 103.95 | 104.57 | 105.05 | 105.80 | 106.47 | 105.81 | 108.78 |
| Temperature °C | SEM-EDS wt.-% As | SEM-EDS wt.-% S | Theoretical wt.-% As | Theoretical wt.-% S | Phase Represented |
|---|---|---|---|---|---|
| 25 | 50.73 | 49.27 | 48.31 | 51.69 | As2S5 |
| 250 | 60.73 | 39.27 | 60.90 | 39.09 | As2S3 |
| 250 | 49.11 | 50.89 | 48.31 | 51.69 | As2S5 |
| 300 | 57.66 | 42.34 | 60.90 | 39.09 | As2S3 |
| 300 | 45.76 | 54.24 | 48.31 | 51.69 | As2S5 |
| 400 | 59.45 | 40.55 | 60.90 | 39.09 | As2S3 |
| 450 | 59.15 | 40.85 | 60.90 | 39.09 | As2S3 |
| 500 | 59.37 | 40.63 | 60.90 | 39.09 | As2S3 |
| 500 | 64.38 | 35.62 | 63.67 | 36.33 | As3S4 |
| 500 | 62.24 | 37.76 | 63.67 | 36.33 | As3S4 |
| Thermal Decomposition | ||
|---|---|---|
| Temperature (°C) | Chemical Reaction | Equilibrium Constant K(T) |
| 200 | 2As2S5 = 4AsS(g) + 3S2(g) | 1.623 × 10−81 |
| 2As2S5 = 2As2(g) + 5S2(g) | 1.240 × 10−73 | |
| 2As2S5 = As4(g) + 5S2(g) | 1.210 × 10−56 | |
| 2As2S5 = As4S4(g) + 3S2(g) | 6.768 × 10−28 | |
| 2As2S5 = As2S3(g) + S2(g) | 9.083 × 10−12 | |
| 300 | 2As2S5 = 4AsS(g) + 3S2(g) | 2.972 × 10−55 |
| 2As2S5 = 2As2(g) + 5S2(g) | 4.553 × 10−49 | |
| 2As2S5 = As4(g) + 5S2(g) | 2.103 × 10−36 | |
| 2As2S5 = As4S4(g) + 3S2(g) | 1.130 × 10−15 | |
| 2As2S5 = As2S3(g) + S2(g) | 2.505 × 10−6 | |
| 400 | 2As2S5 = 4AsS(g) + 3S2(g) | 1.968 × 10−36 |
| 2As2S5 = 2As2(g) + 5S2(g) | 1.848 × 10−31 | |
| 2As2S5 = As4(g) + 5S2(g) | 7.985 × 10−22 | |
| 2As2S5 = As4S4(g) + 3S2(g) | 1.074 × 10−6 | |
| 2As2S5 = As2S3(g) + S2(g) | 2.569 × 10−2 | |
| 500 | 2As2S5 = 4AsS(g) + 3S2(g) | 3.295 × 10−22 |
| 2As2S5 = 2As2(g) + 5S2(g) | 3.772 × 10−18 | |
| 2As2S5 = As4(g) + 5S2(g) | 9.431 × 10−11 | |
| 2As2S5 = As4S4(g) + 3S2(g) | 9.447 | |
| 2As2S5 = As2S3(g) + S2(g) | 3.343 × 101 | |
| 600 | 2As2S5 = 4AsS(g) + 3S2(g) | 4.944 × 10−11 |
| 2As2S5 = 2As2(g) + 5S2(g) | 1.089 × 10−7 | |
| 2As2S5 = As4(g) + 5S2(g) | 5.203 × 10−2 | |
| 2As2S5 = As4S4(g) + 3S2(g) | 3.577 × 106 | |
| 2As2S5 = As2S3(g) + S2(g) | 1.084 × 104 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castro, K.; Balladares, E.; Jerez, O.; Pérez-Tello, M.; Aracena, Á. Study of the Reaction Mechanisms during the Thermal Decomposition of Arsenic Sulfide (V) at High Temperatures under Non-Isothermal Conditions. Minerals 2022, 12, 1379. https://doi.org/10.3390/min12111379
Castro K, Balladares E, Jerez O, Pérez-Tello M, Aracena Á. Study of the Reaction Mechanisms during the Thermal Decomposition of Arsenic Sulfide (V) at High Temperatures under Non-Isothermal Conditions. Minerals. 2022; 12(11):1379. https://doi.org/10.3390/min12111379
Chicago/Turabian StyleCastro, Kristhobal, Eduardo Balladares, Oscar Jerez, Manuel Pérez-Tello, and Álvaro Aracena. 2022. "Study of the Reaction Mechanisms during the Thermal Decomposition of Arsenic Sulfide (V) at High Temperatures under Non-Isothermal Conditions" Minerals 12, no. 11: 1379. https://doi.org/10.3390/min12111379
APA StyleCastro, K., Balladares, E., Jerez, O., Pérez-Tello, M., & Aracena, Á. (2022). Study of the Reaction Mechanisms during the Thermal Decomposition of Arsenic Sulfide (V) at High Temperatures under Non-Isothermal Conditions. Minerals, 12(11), 1379. https://doi.org/10.3390/min12111379








