3D Mineral Prospectivity Mapping of Zaozigou Gold Deposit, West Qinling, China: Machine Learning-Based Mineral Prediction
Abstract
1. Introduction
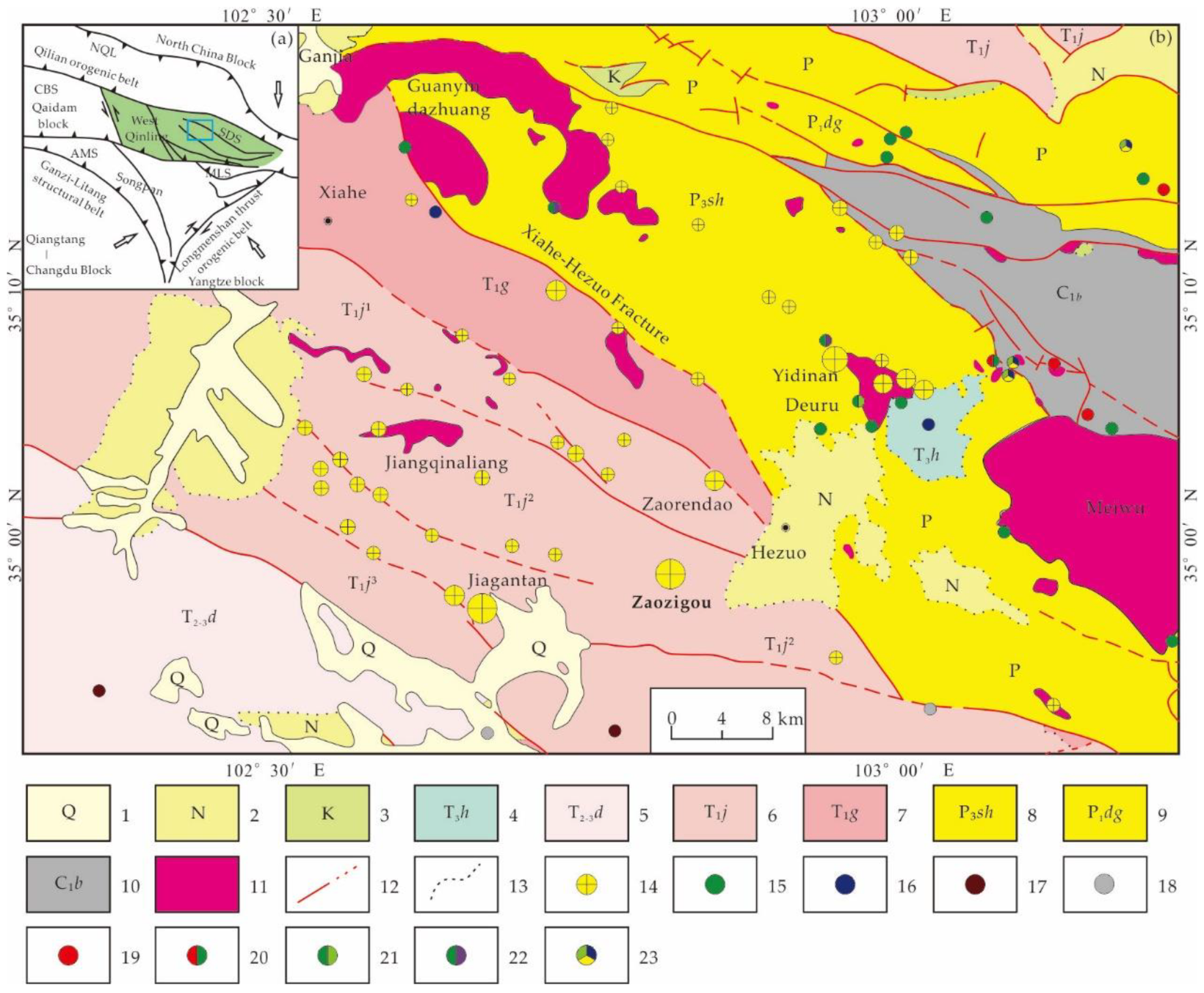
2. Geological Setting and Datasets
2.1. Geological Setting
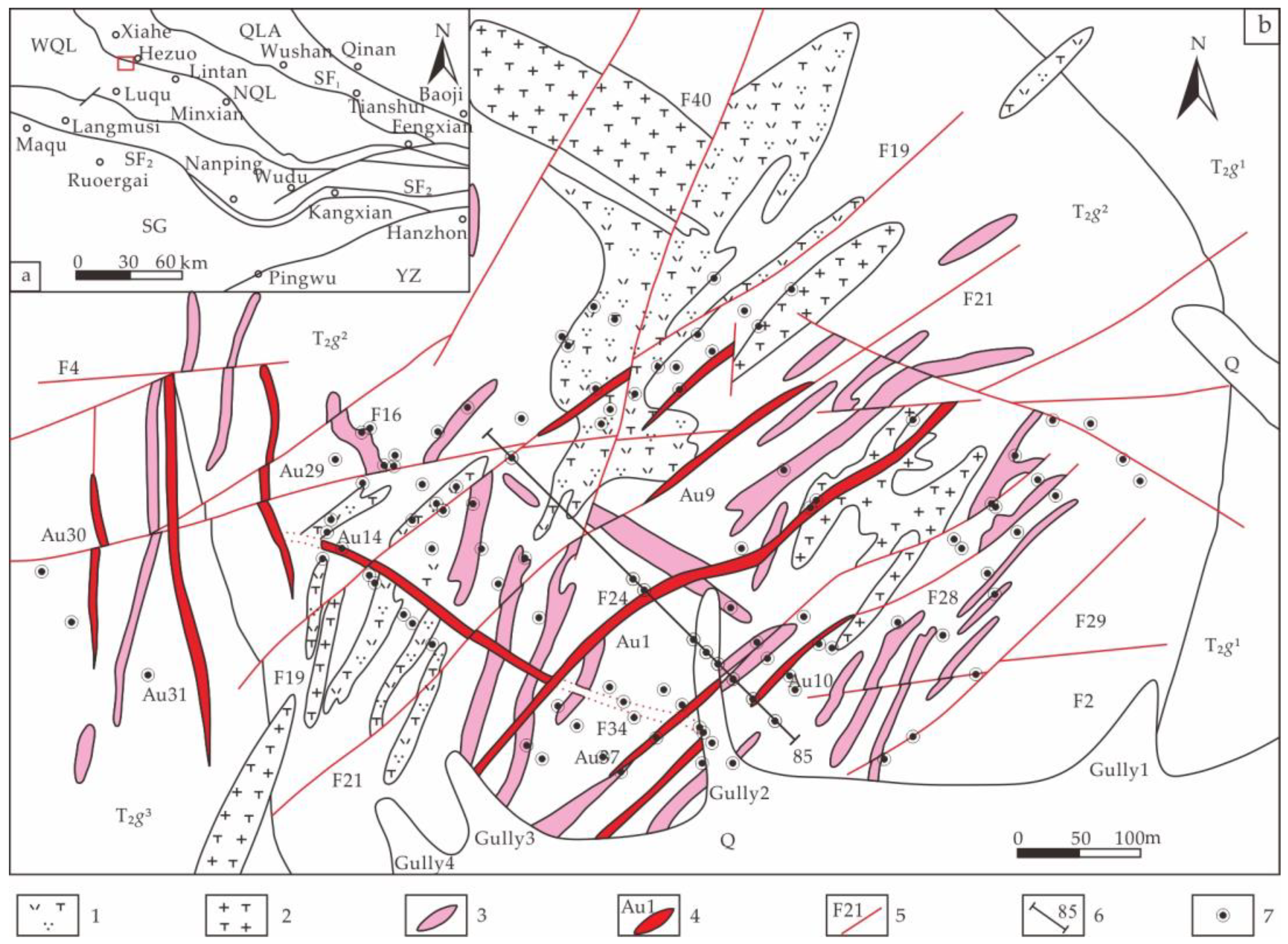
2.2. Datesets Description
3. Methodology
3.1. Concentration-Volume (C-V) Model
3.2. Compositional Data Analysis
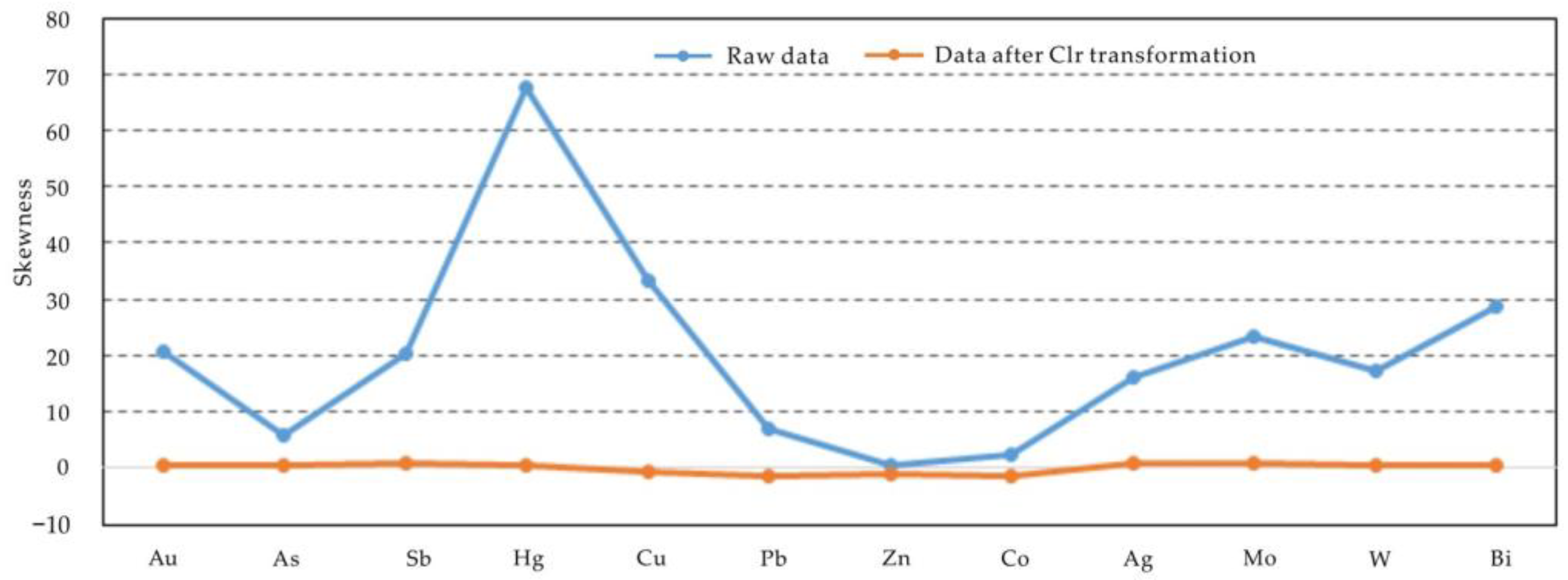
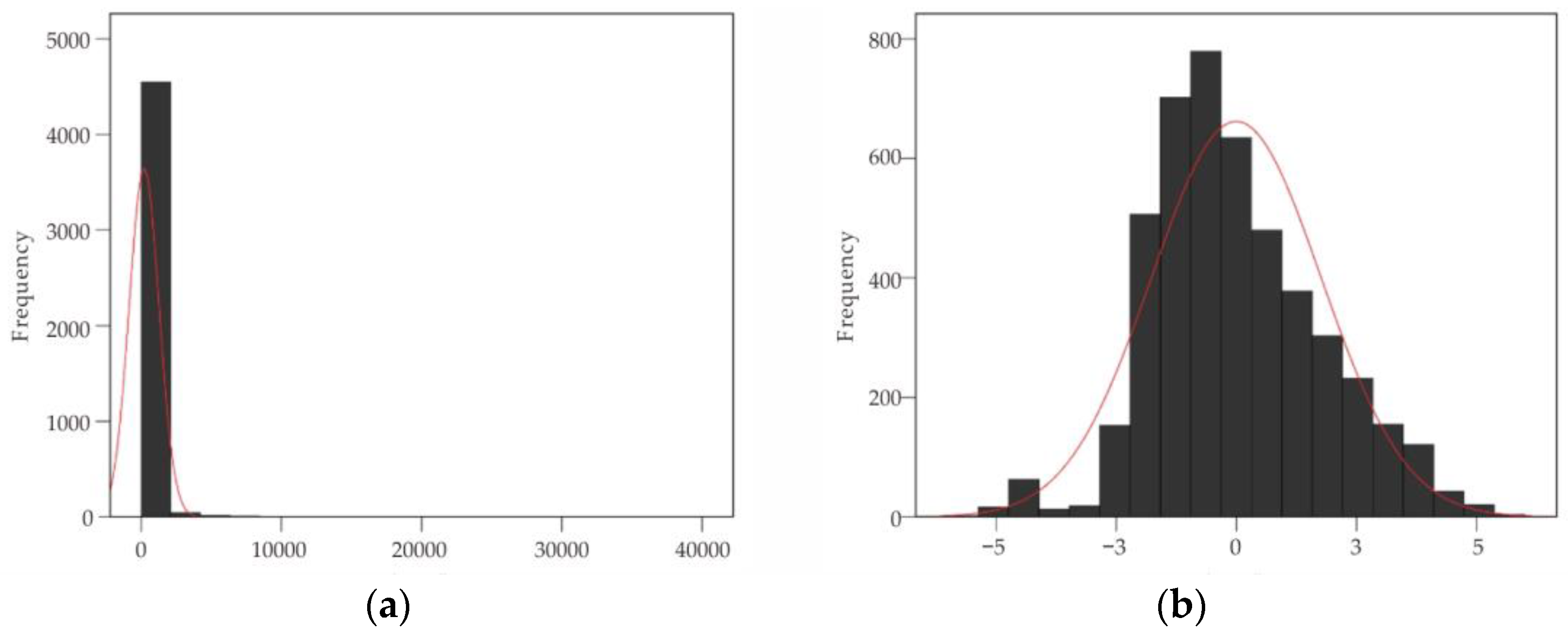
3.2.1. Central Log-Ratio Transformation (clr)
3.2.2. Sequential Binary Partition (SBP)
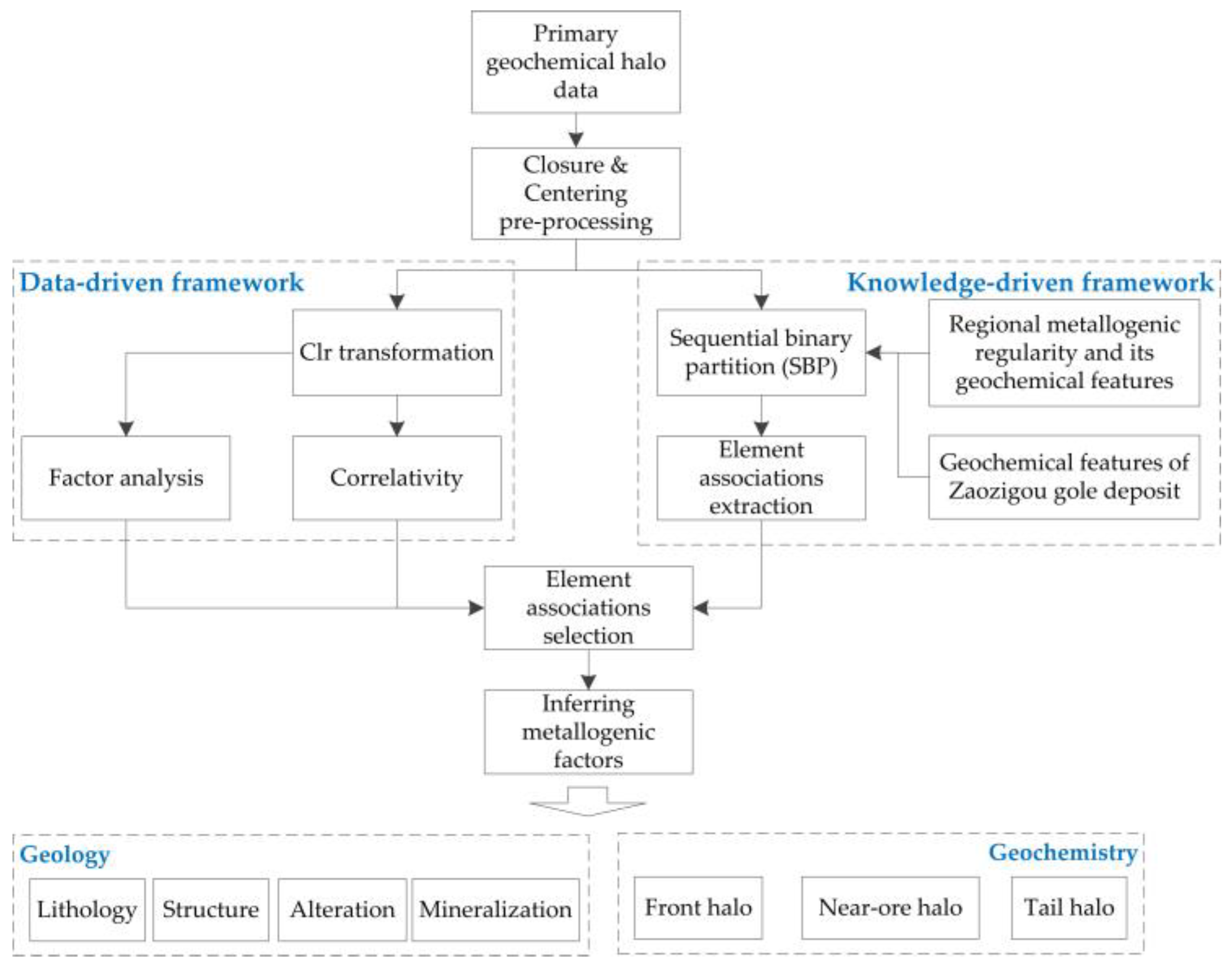
3.2.3. Geochemical Compositional Data Analysis Framework Based on CoDA
3.3. Machine Learning-Based Quantitative Mineral Prediction Methods
3.3.1. MaxEnt Model
3.3.2. Gaussian Mixture Model (GMM)
- Initializing the k multivariate Gaussian distributions and their weights.
- Estimating the posterior probability of each sample generated by each component according to Bayes’ theorem.
- Updating the mean vector, covariance matrix and the weights according to the step 2.
- Repeating steps 2–3 until the increase in the likelihood function has been less than the convergence threshold, or the maximum number of iterations is reached.
- For each sample point, calculating its posterior probability of belonging to each cluster according to Bayes’ theorem and classifying the sample into the cluster with the largest posterior probability.
4. Results
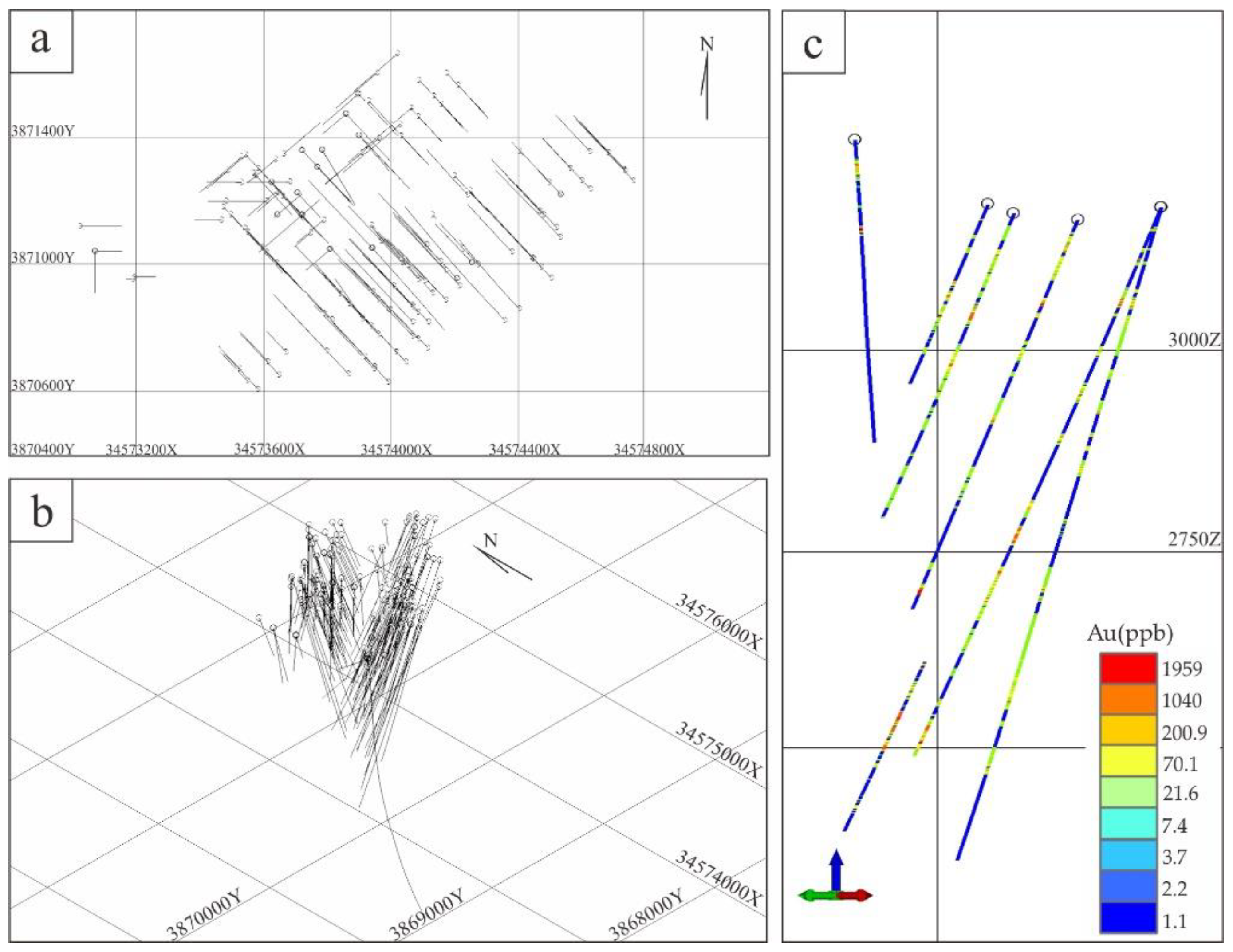
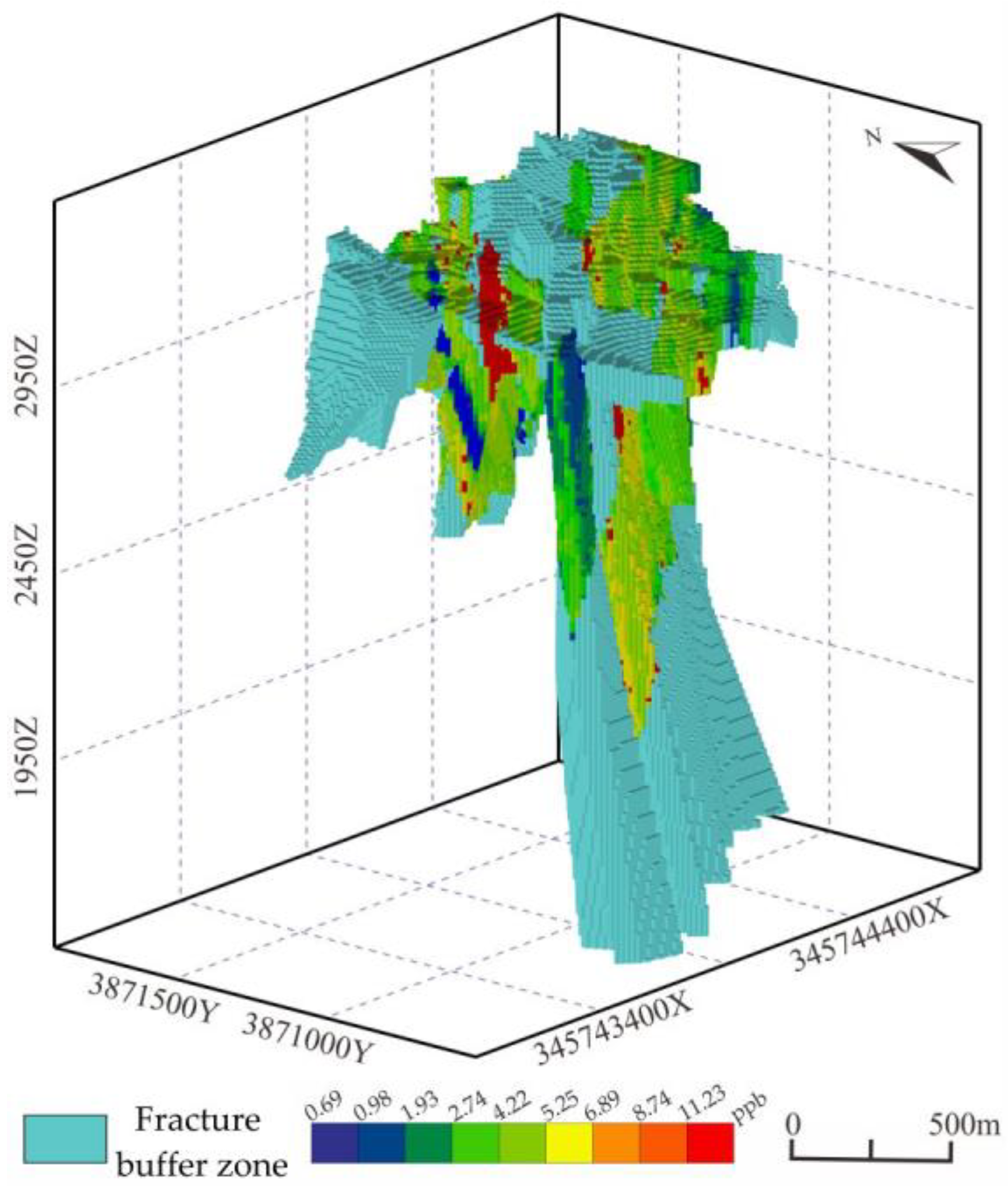
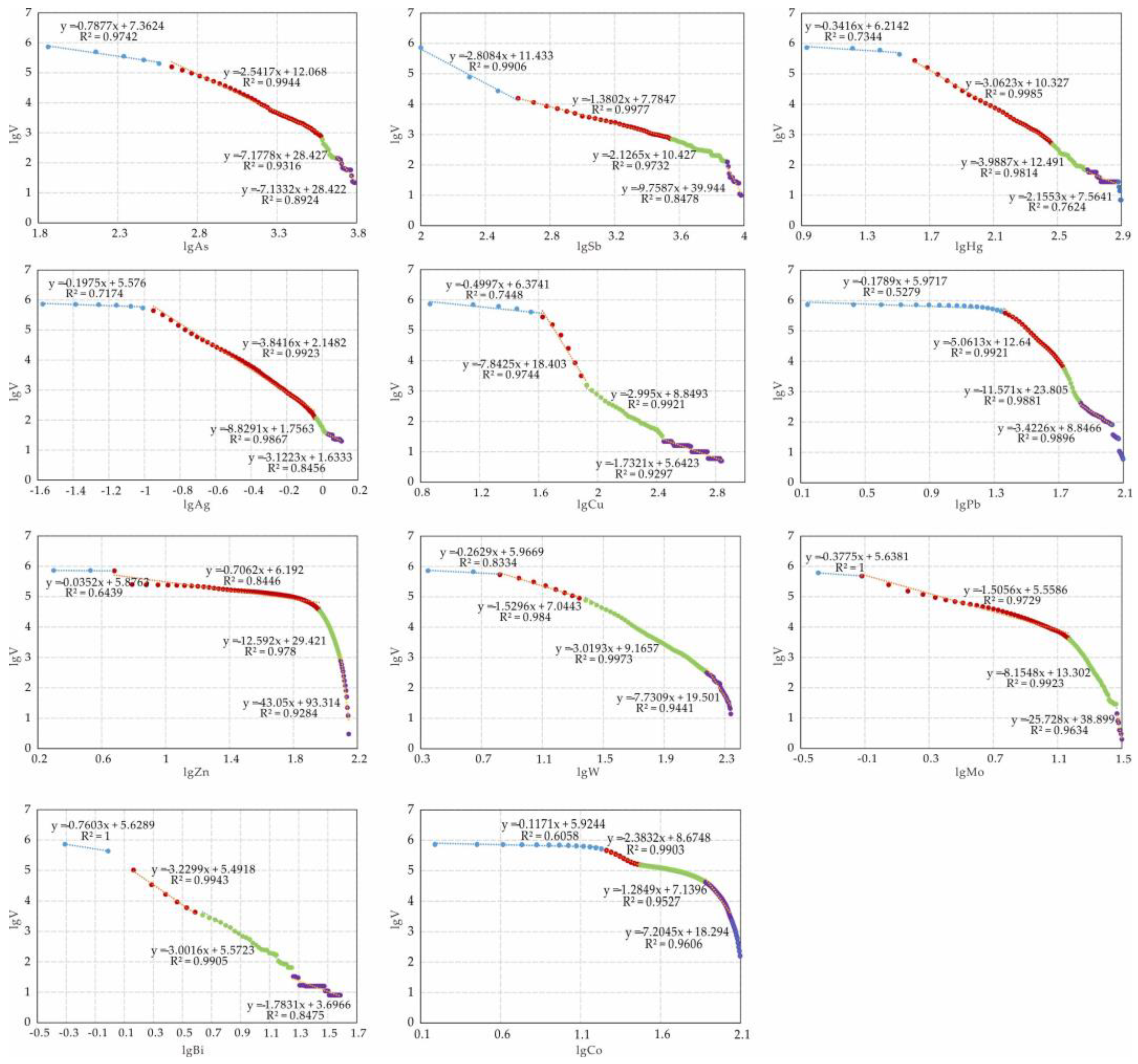
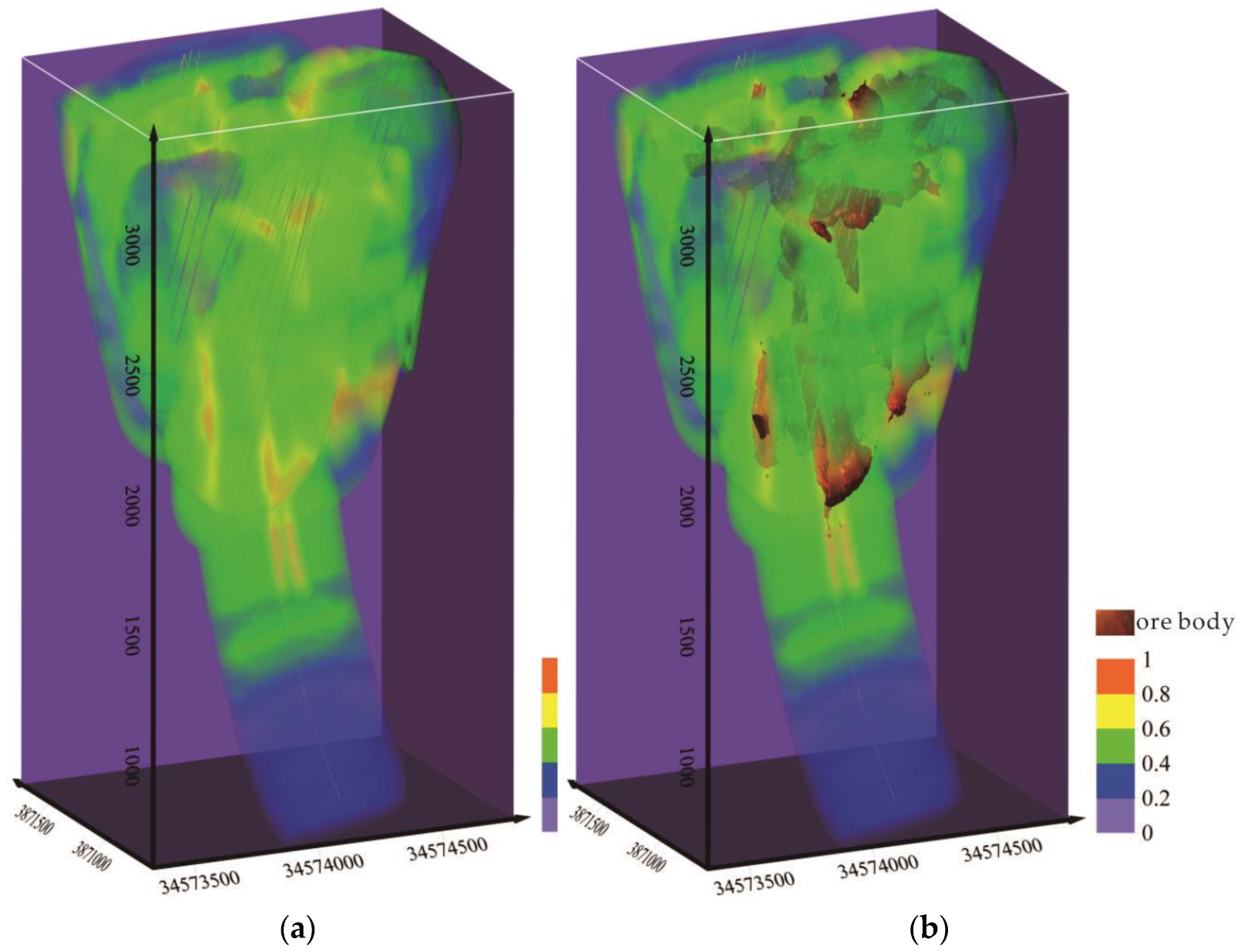
4.1. Three-Dimensional Primary Geochemical Halo Anomaly Data Volume Modeling Based on the C-V Model
4.2. Data-Driven CoDA and Its Based Element Association Extraction
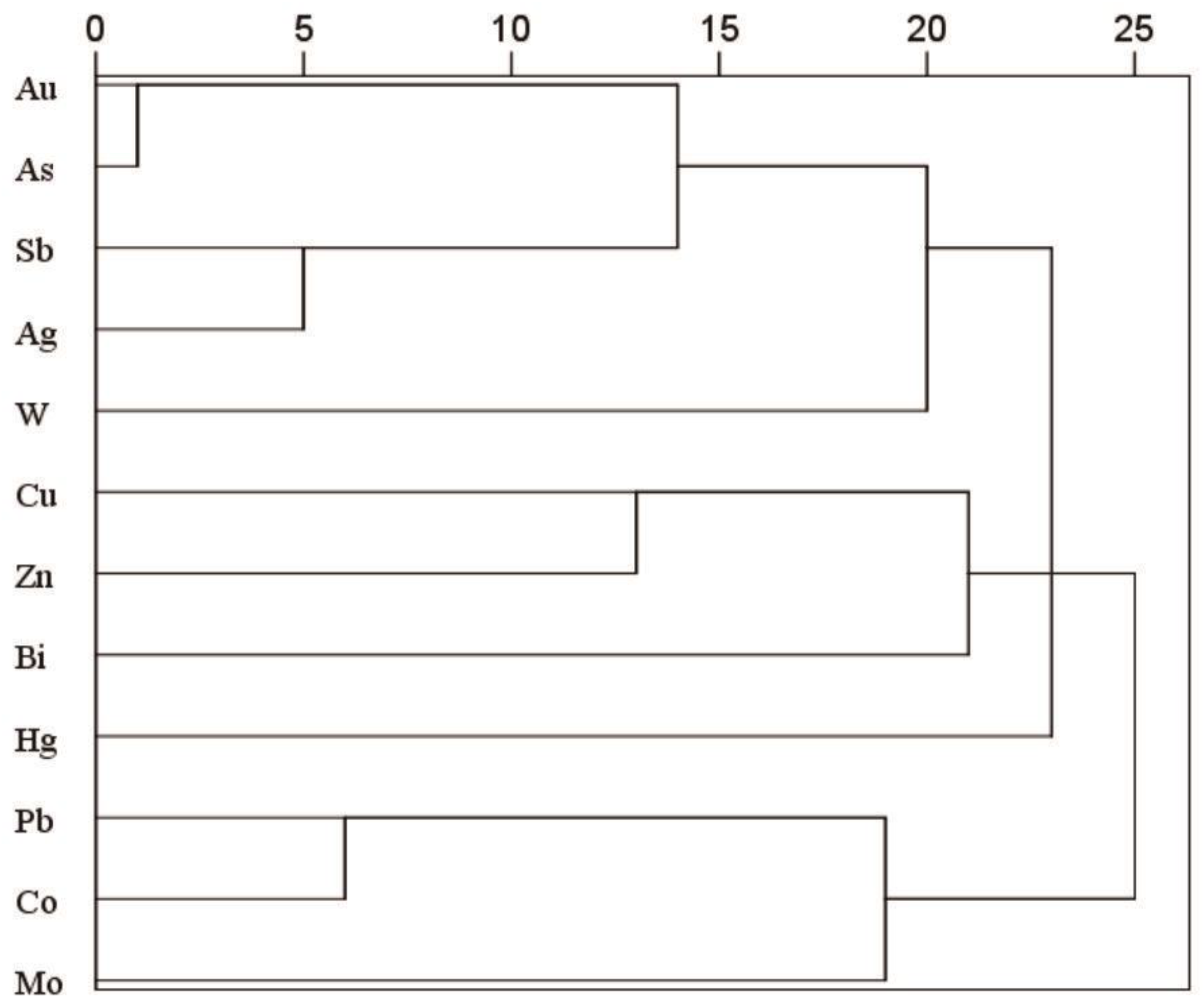
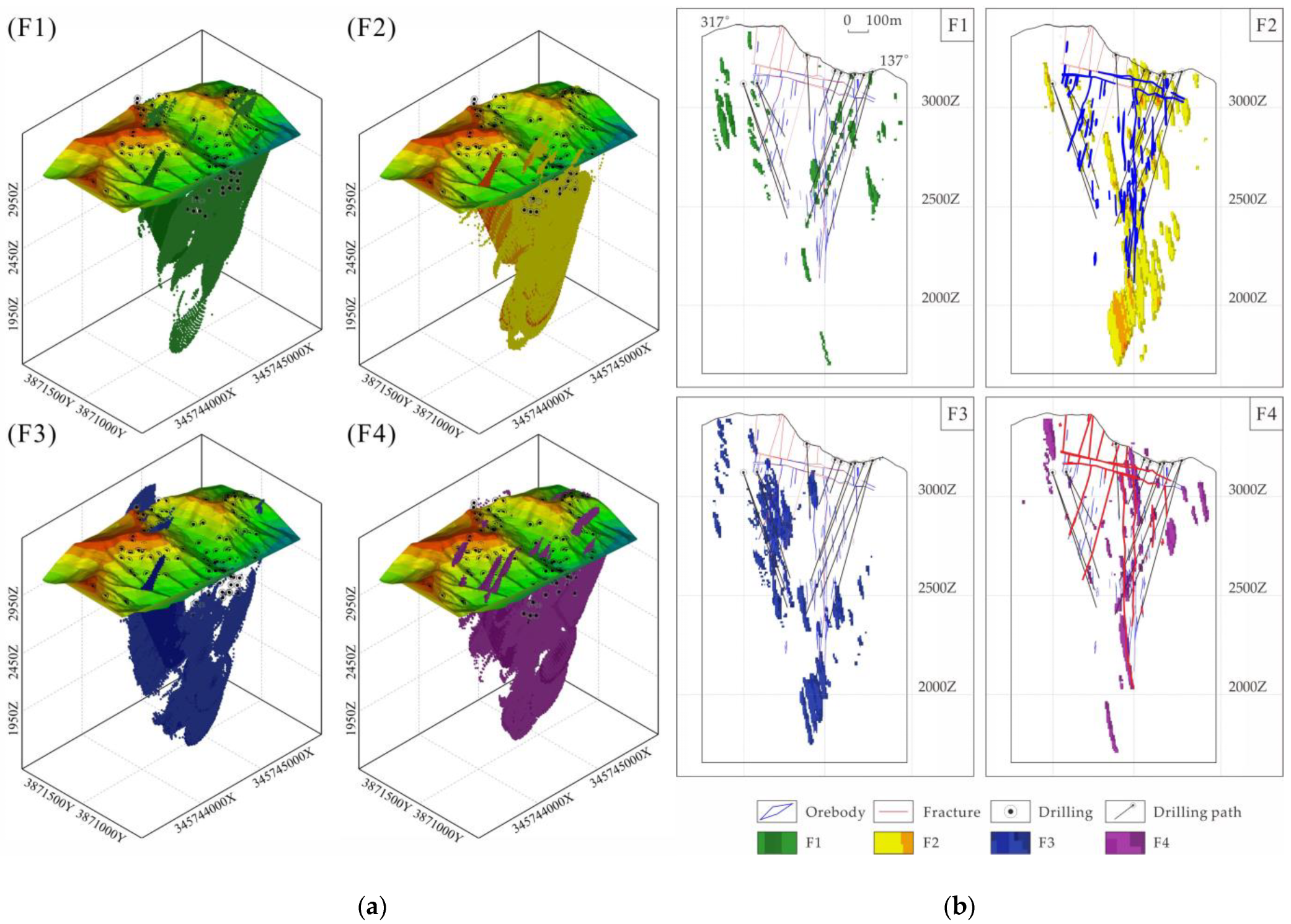
4.2.1. Correlation Analysis
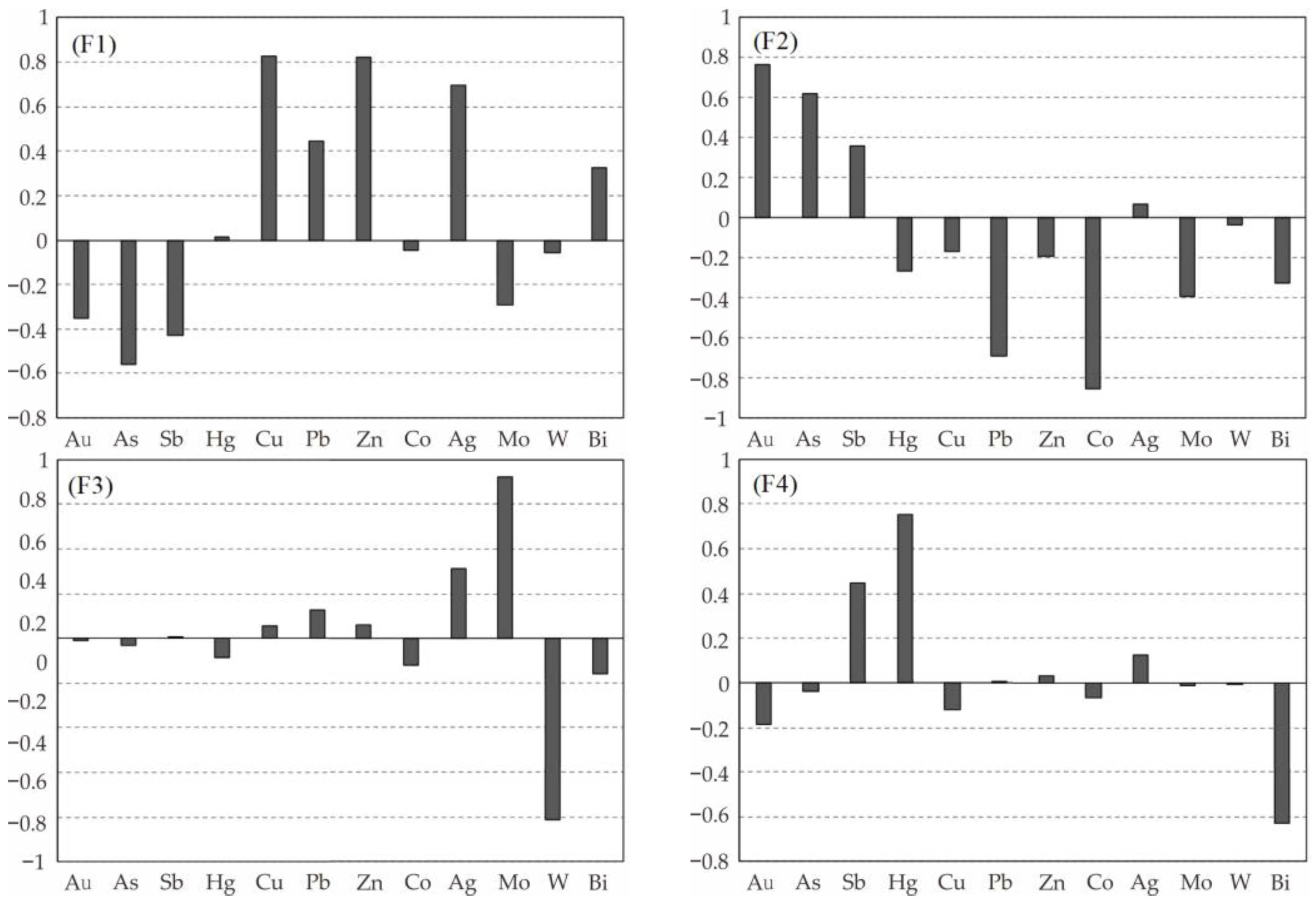
4.2.2. Element Associations Identification Based on clr-Biplot
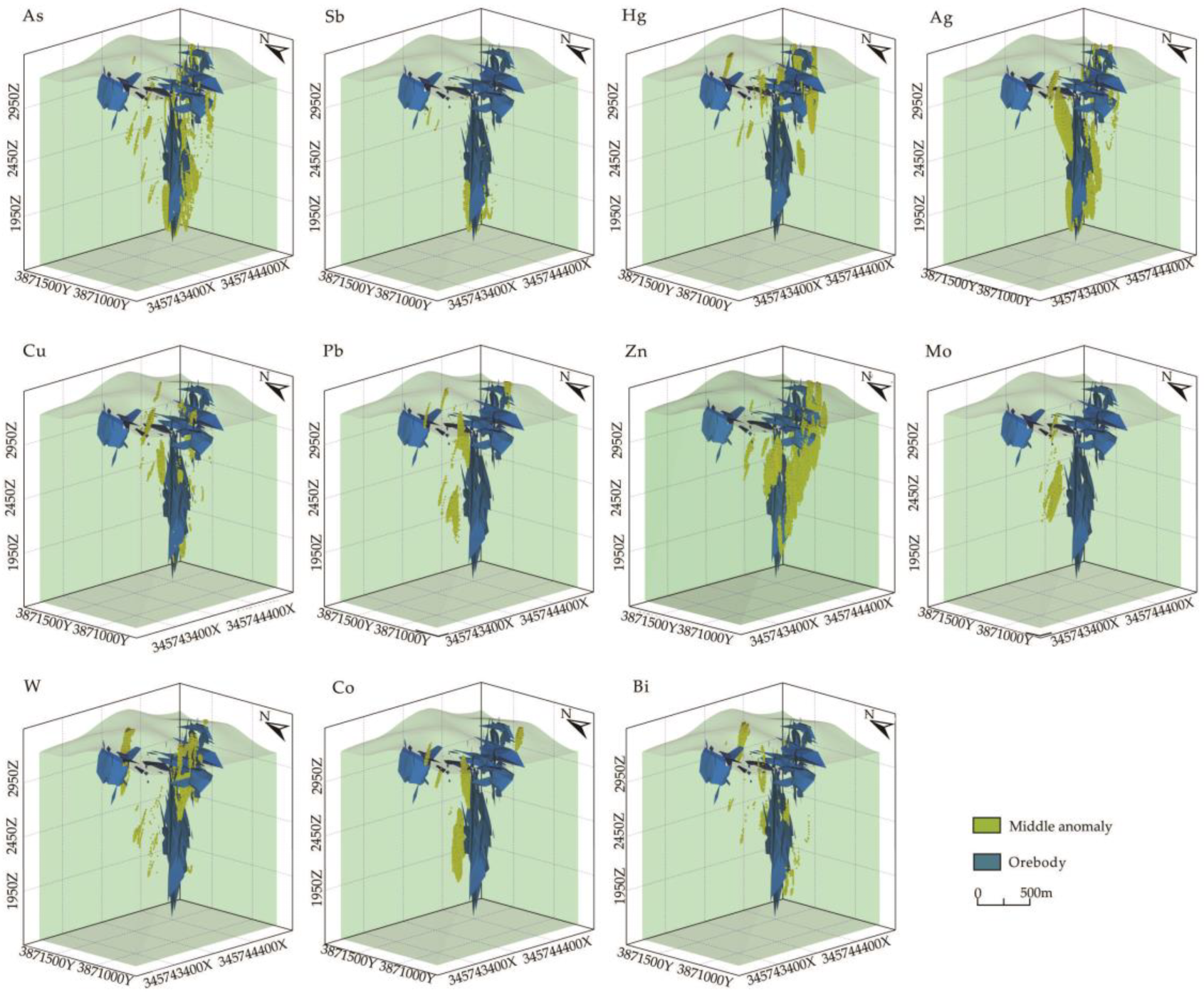
4.3. Knowledge-Driven CoDA and Its Based Element Association Extraction
- 1.
- In the mid-shallow part and the deeper part of elevation at 2500 m, As, Sb and Hg are concentrated as the front halo of the orebodies. The anomalies of Au, Ag, Cu, Pb and Zn linked to sulphurs (pyrite, arsenopyrite, galena and covelline) and are superposed with the orebodies and can be regarded as the near-ore halo elements. At the shallow position of 2500 m, the anomaly locations of W, Mo and Bi linked to magmatism are at the tail of the orebodies, which can be regarded as the tail halo element association.
- 2.
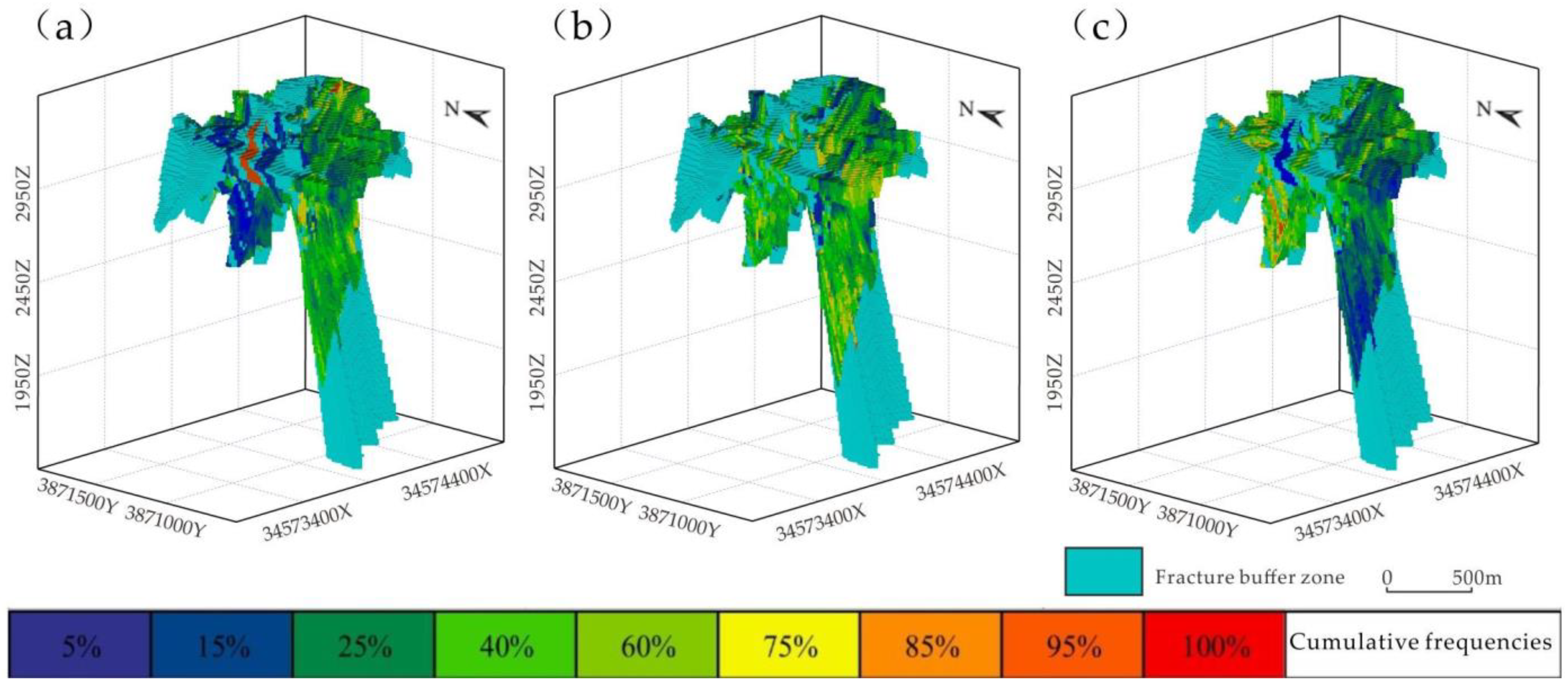
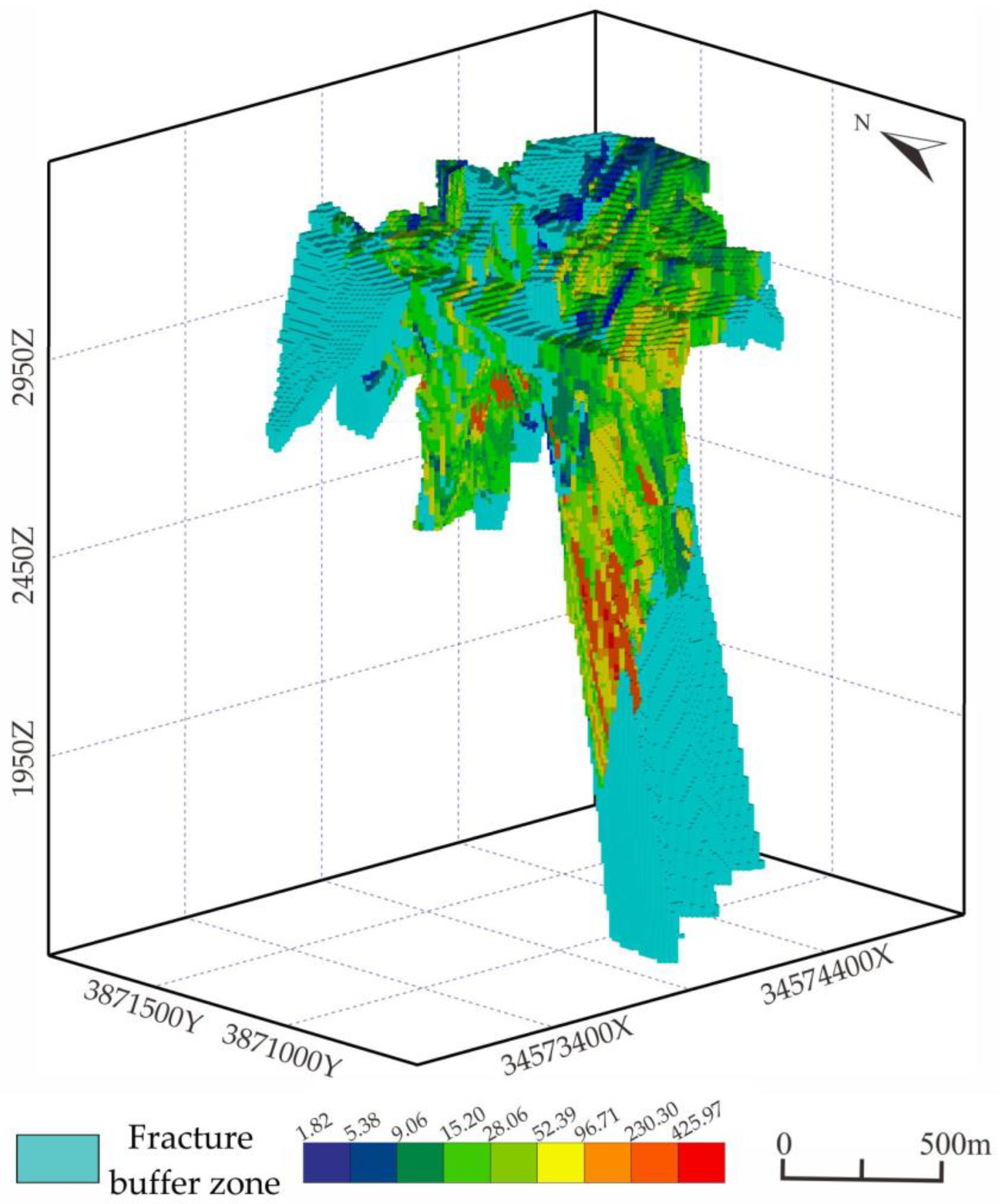
- In terms of Au, its anomalies are controlled by fractures observably, and observable fractures certainly cross-cut orebodies. Especially, the abnormal intensity is larger along the depth indicating the deep mineralization.
4.4. Geological and Geochemical Quantitative Prediction Model at Depth of Zaozigou Gold Deposit
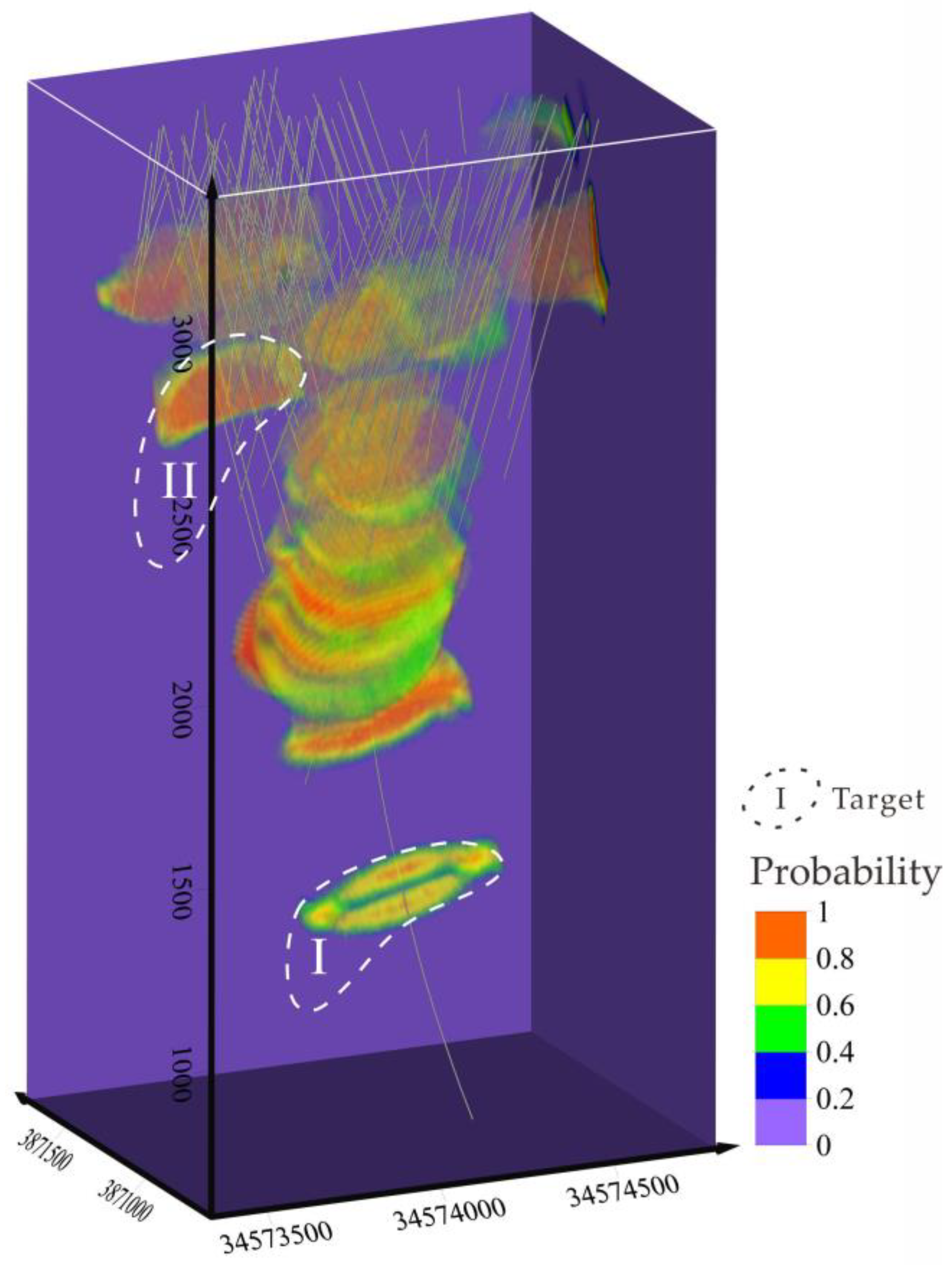
4.5. Three-Dimensional MPM Based on Machine Learning
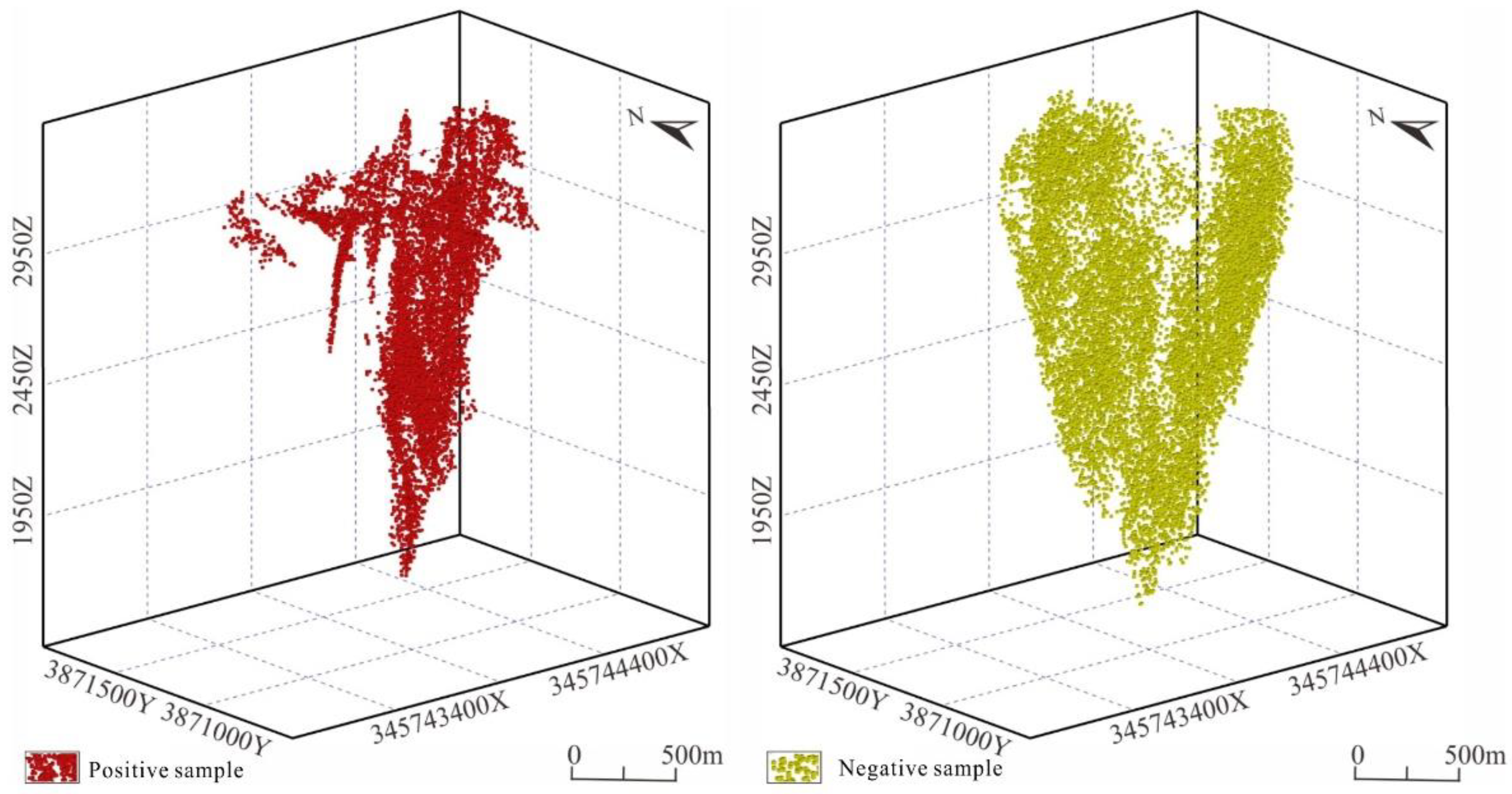
4.5.1. Training Sample Construction
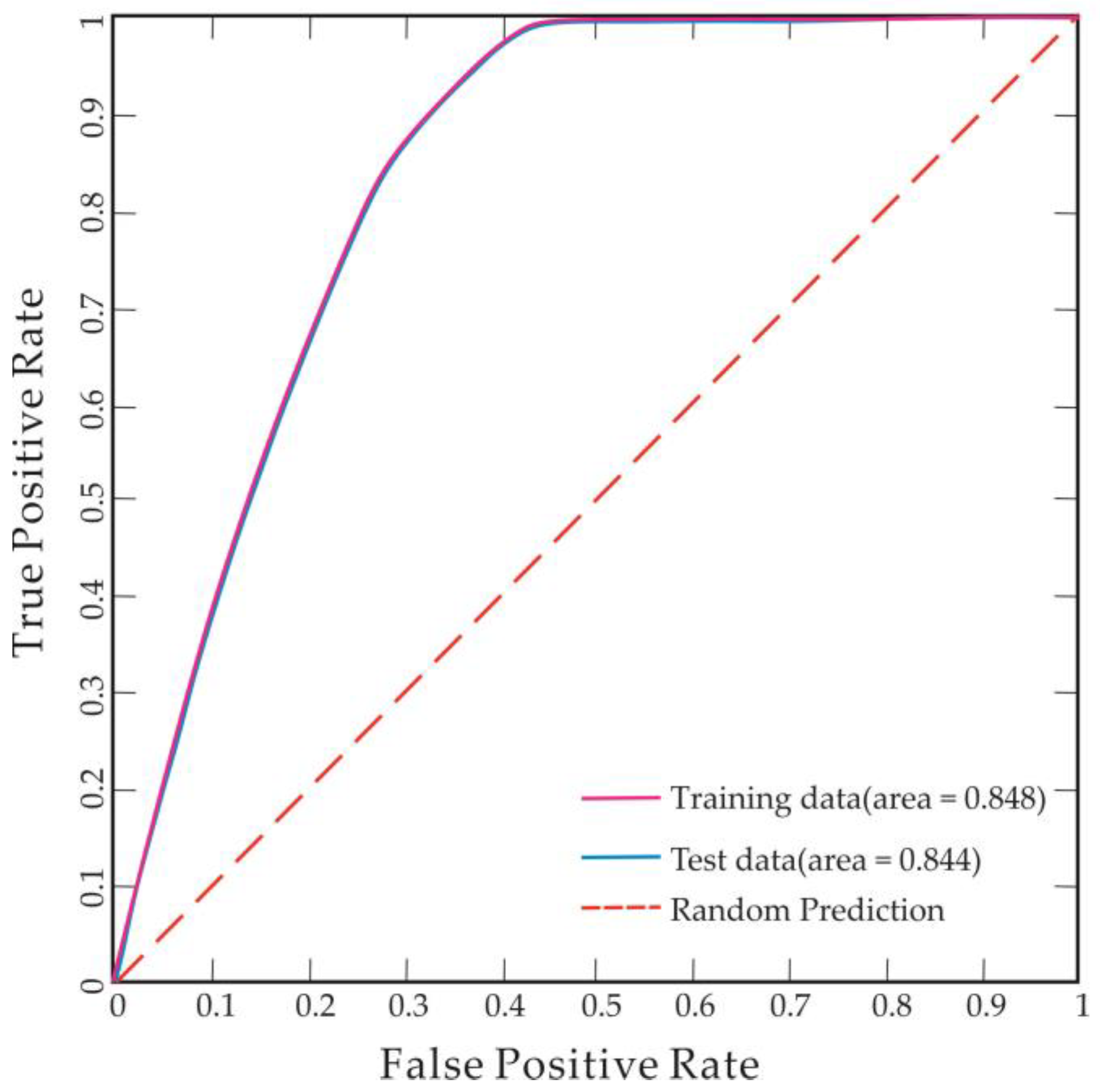
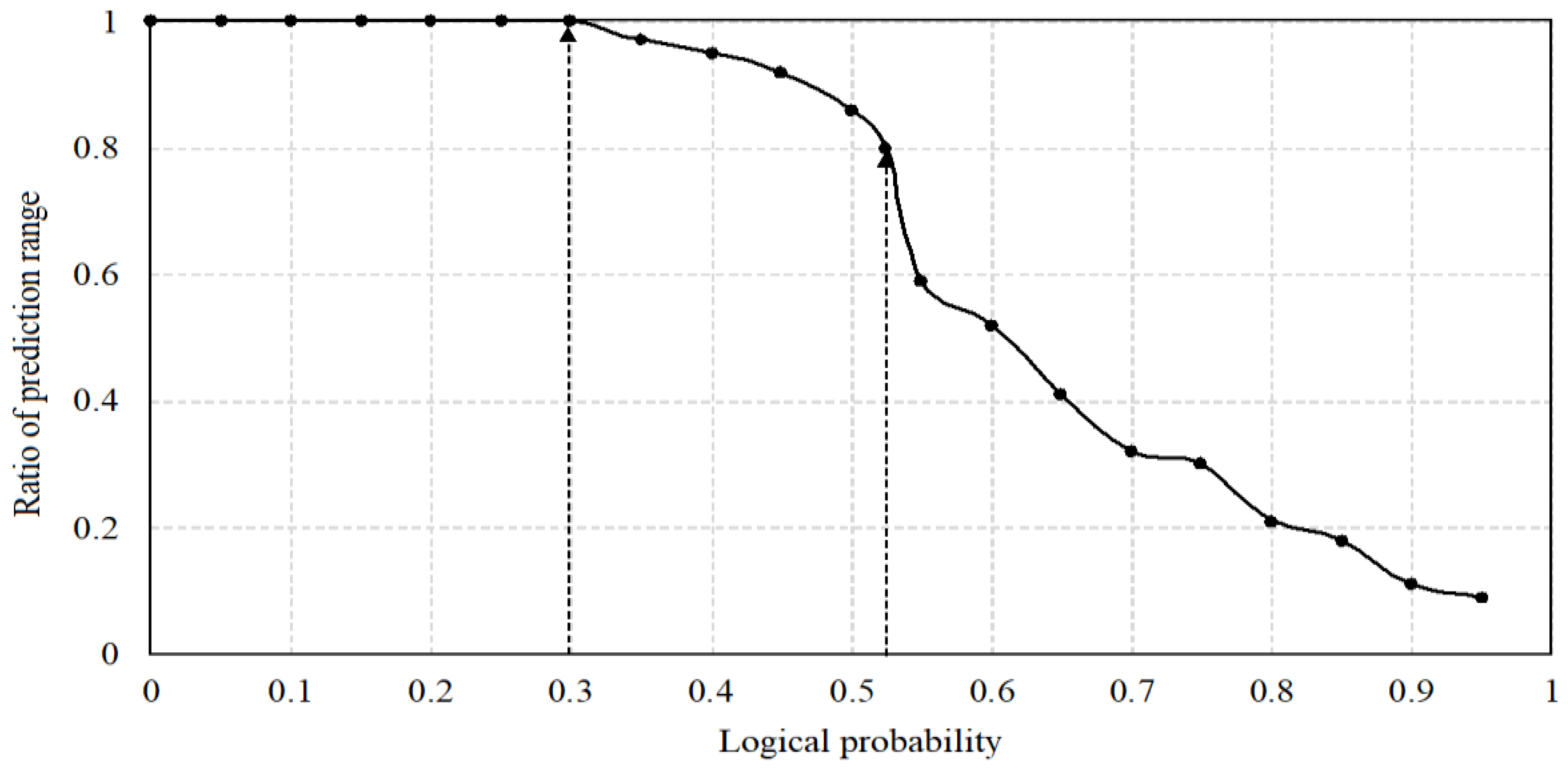
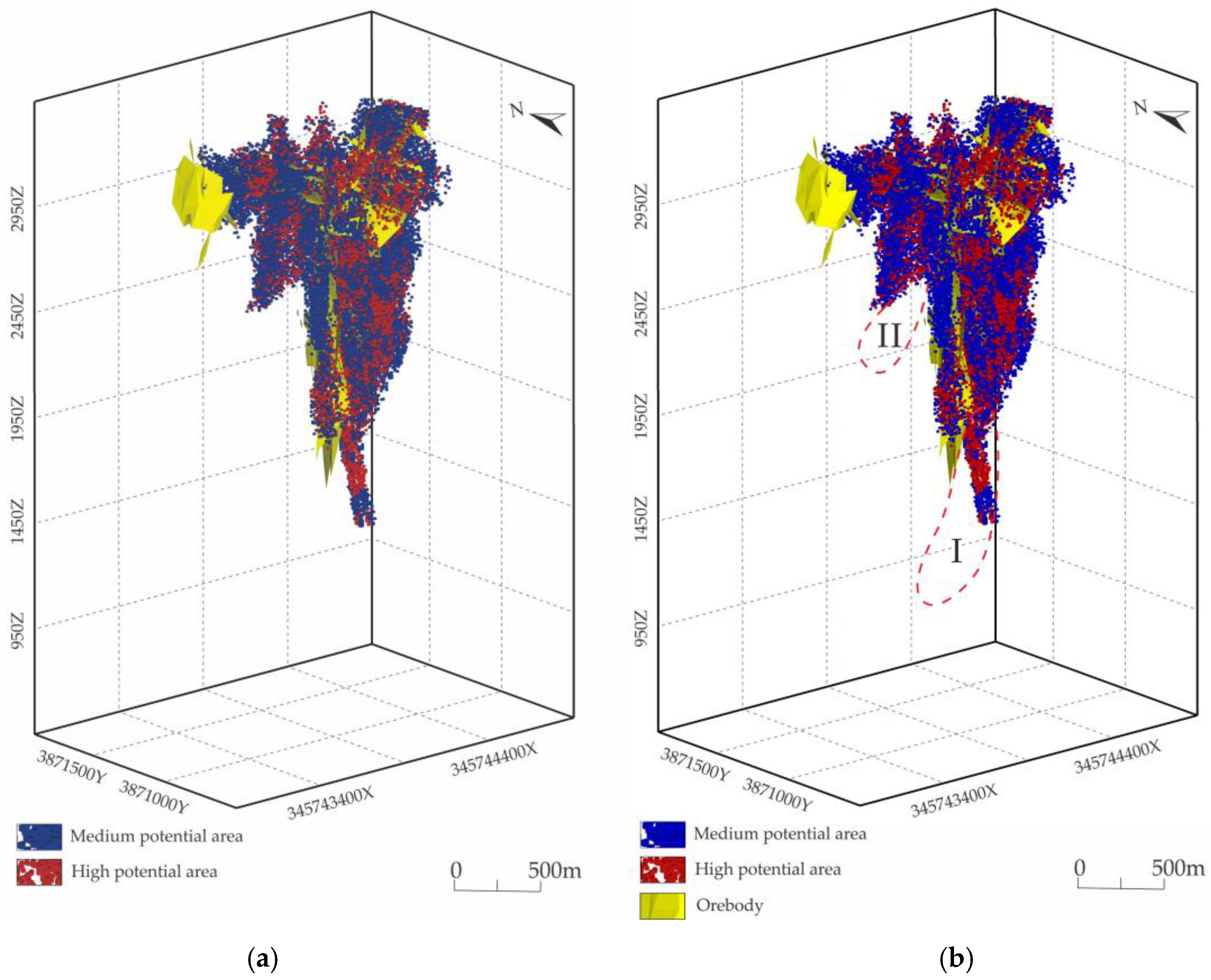
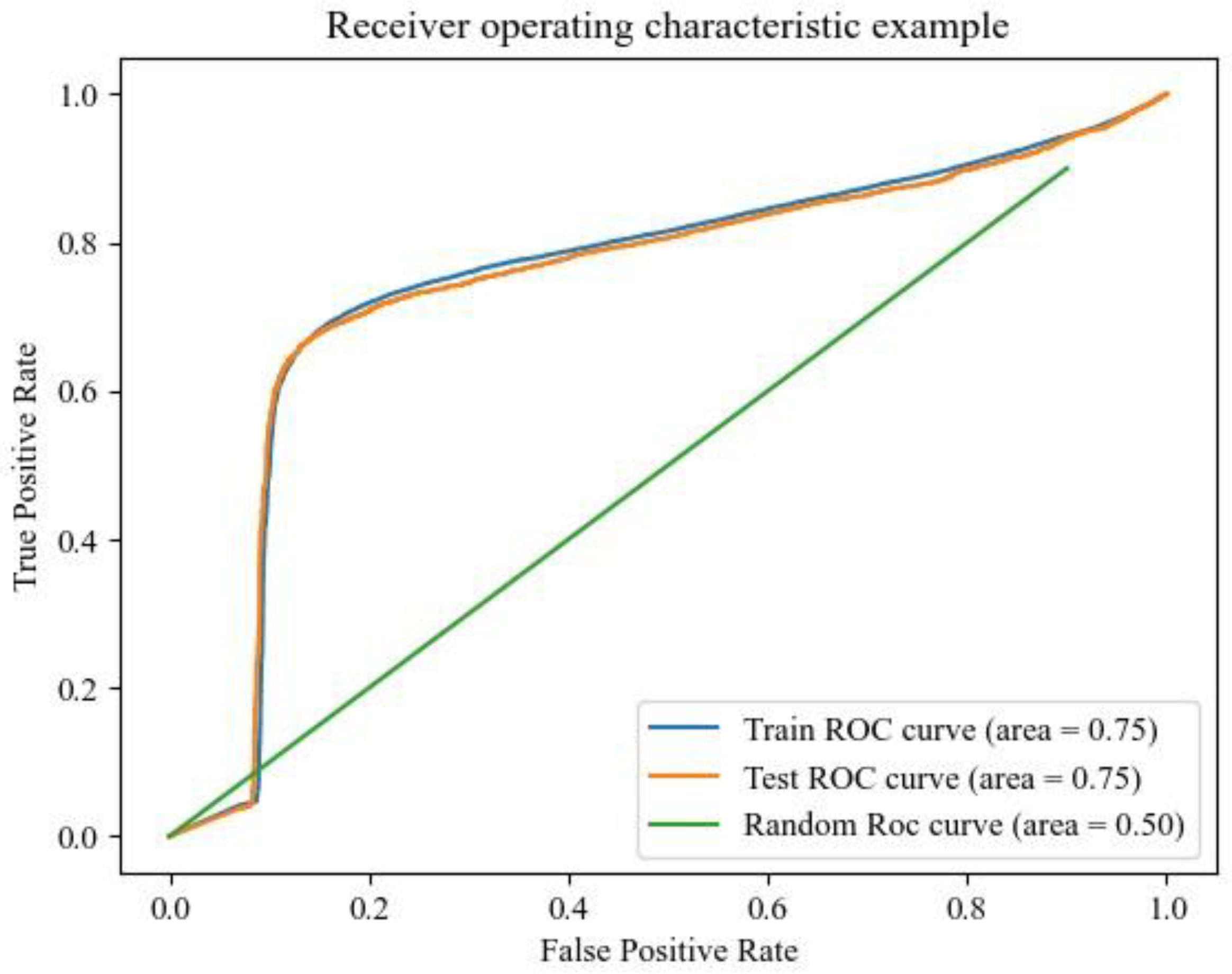
4.5.2. Three-Dimensional MPM and Uncertainty Evaluation of MaxEnt Model
4.5.3. Three-Dimensional MPM and Uncertainty Evaluation of GMM
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, S.C.; Yang, Y.H.; Yan, G.S.; Li, J.C. Study of large and Giant Gold Deposits: Quantitative Prognosis Method in China. Geol. Rev. 2000, 46, 17–24, (In Chinese with English Abstract). [Google Scholar]
- Zhao, P.D. “Three-Component” Quantitative Resource Prediction and Assessments: Theory and Practice of Digital Mineral Prospecting. Earth Sci. 2002, 27, 482–489, (In Chinese with English Abstract). [Google Scholar]
- Zhao, P.D. Quantitative mineral prediction and deep mineral exploration. Earth Sci. Front. 2007, 14, 1–10, (In Chinese with English Abstract). [Google Scholar]
- Xiao, K.Y.; Zhao, P.D. A Preliminary Discussion on Basic Problems and Researching Programming of the Large Scale Metallogenetic Prognosis. Miner. Explor. 1994, 3, 49–56, (In Chinese with English Abstract). [Google Scholar]
- Xiao, K.Y.; Zhang, X.H.; Chen, Z.H.; Song, G.Y.; Ge, Y.; Liu, D.L.; Wang, S.L.; Ning, S.N.; Cao, Y. Comparison of Method of Weights of Evidence and Information. Comput. Tech. Geophys. Geochem. Explor. 1999, 21, 223–226, (In Chinese with English Abstract). [Google Scholar]
- Xiao, K.Y.; Zhu, Y.S.; Song, G.Y. Quantitative Evaluation of Mineral Resources GIS. Geol. China. 2000, 278, 29–32. (In Chinese) [Google Scholar]
- Xiao, K.Y.; Chen, X.G.; Li, N.; Zou, W.; Sun, L. 3D visualization technology for geological and mineral exploration evaluation and software development for prospectors. Miner. Depos. 2010, 29, 758–760. (In Chinese) [Google Scholar]
- Xiao, K.Y.; Li, N.; Sun, L.; Zou, W.; Li, Y. Large scale 3D mineral prediction methods and channels based on 3D information technology. J. Geol. 2012, 36, 229–236, (In Chinese with English Abstract). [Google Scholar]
- Xiao, K.Y.; Li, N.; Sun, L.; Zou, W.; Li, Y. 3D Digital Mineral Deposit Model Establishment Method and Its Application. Miner. Deposits 2012, 31, 929–930. (In Chinese) [Google Scholar]
- Xiao, K.Y.; Sun, L.; Li, N.; Wang, K.; Fan, J.F.; Ding, J.H. Mineral resources assessment under the thought of big data. Geol. Bull. China 2015, 34, 1266–1272, (In Chinese with English Abstract). [Google Scholar]
- Chen, J.P.; Chen, Y.; Zeng, M. 3D positioning and quantitative pre-diction of the Koktokay No. 3 pegmatite dike, Xinjiang, China, based on the digital mineral deposit model. Geol. Bull. China 2008, 27, 552–559, (In Chinese with English Abstract). [Google Scholar]
- Chen, J.P.; Lv, P.; Wu, W.; Zhao, J.; Hu, Q. A 3D method for predicting blind orebodies, based on a 3D visualization model and its application. Earth Sci. Front. 2007, 14, 56–65, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Chen, J.P.; Wang, C.N.; Shang, B.C.; Shi, R. Three-Dimensional Metallogenic Prediction in Yongmei Region Based on Digital Ore Deposit Model. Sci. Technol. Manag. Land Resour. 2012, 29, 14–20, (In Chinese with English Abstract). [Google Scholar]
- Chen, J.P.; Yu, M.; Yu, P.P.; Shang, B.C.; Zheng, X.; Wang, L.M. Method and Practice of 3D Geological Modeling at Key Metallogenic Belt with Large and Medium Scale. Acta Geol. Sin. 2014, 88, 1187–1195, (In Chinese with English Abstract). [Google Scholar]
- Lv, P. Cube Predicting Model Based 3D Predicting Methods of Blind Orebody and Software Development. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2007. (In Chinese with English Abstract). [Google Scholar]
- Zhang, S.H. Deep Learning foe Mineral Prospectivity Mapping of Lala-type Copper Deposit in the Huili Region, Sichuan. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2020. (In Chinese with English Abstract). [Google Scholar]
- Zhang, S.H.; Xiao, K.Y. Random Forest—Based Mineralization Prediction of the Lala—Type Cu Deposit in the Huili Area, Sichuan Province. Geol. Explor. 2020, 56, 239–252, (In Chinese with English Abstract). [Google Scholar]
- Mao, X.C.; Tang, Y.H.; Deng, H. Three-dimensional morphological analysis method for geologic bodies and its application. J. Cent. South Univ. Sci. Technol. 2012, 43, 588–595, (In Chinese with English Abstract). [Google Scholar]
- Mao, X.C.; Tang, Y.H.; Lai, J.Q.; Zou, Y.H.; Chen, J.; Peng, S.L.; Shao, Y.J. Three Dimensional Structure of Metallogenic Geologic Bodies in the Fenghuangshan Ore Field and Ore-controlling Geological Factors. J. Geol. 2011, 85, 1507–1518, (In Chinese with English Abstract). [Google Scholar]
- Mao, X.C.; Wang, Q.; Chen, J.; Deng, H.; Liu, Z.K.; Wang, J.L.; Chen, J.P.; Xiao, K.Y. Three-dimensional Modeling of Deep Metallogenic Structure in Northwestern Jiaodong Peninsula and Its Gold Prospecting Significance. Acta Geol. Sin. 2020, 41, 166–178, (In Chinese with English Abstract). [Google Scholar]
- Mao, X.C.; Zhang, M.M.; Deng, H.; Zou, Y.H.; Chen, J. 3D Visualization Prediction Method for Concealed Ore Bodies in the Deep. Mining Area. J. Geol. 2016, 40, 363–371, (In Chinese with English Abstract). [Google Scholar]
- Mao, X.C.; Zou, Y.H.; Chen, J.; Lai, J.Q.; Peng, S.L.; Shao, Y.J.; Shu, Z.M.; Lv, J.W.; Lv, C.Y. Three-dimensional visual prediction of concealed ore bodies in the deep and marginal parts of crisis mines: A case study of the Fenghuangshan ore field in Tongling, Anhui, China. Geol. Bull. China 2010, 29, 401–413, (In Chinese with English Abstract). [Google Scholar]
- Xiang, J.; Chen, J.P.; Xiao, K.Y.; Li, S.; Zhang, Z.P.; Zhang, Y. 3D metallogenic prediction based on machine learning: A case study of the Lala copper deposit in Sichuan Province. Geol. Bull. China 2019, 38, 2010–2021, (In Chinese with English Abstract). [Google Scholar]
- Yuan, F.; Li, X.H.; Zhang, M.M.; Jia, C.; Hu, X.Y. Research Progress of 3D Prospectivity Modeling. Gansu Geol. 2018, 27, 32–36, (In Chinese with English Abstract). [Google Scholar]
- Yuan, F.; Zhang, M.M.; Li, X.H.; Ge, C.; Lu, S.M.; Li, J.S.; Zhou, Y.Z.; Lan, X.Y. Prospectivity modeling: From two dimension to three-dimension. Acta Petrol. Sin. 2019, 35, 3863–3874, (In Chinese with English Abstract). [Google Scholar]
- Cheng, Q.M. What are Mathematical Geosciences and its frontiers? Earth Sci. Front. 2021, 28, 6–25, (In Chinese with English Abstract). [Google Scholar]
- Cheng, Q.; Agterberg, F.P.; Ballantyne, S.B. The separation of geochemical anomalies from background by fractal methods. J. Geochem. Explor. 1994, 51, 109–130. [Google Scholar] [CrossRef]
- Cheng, Q.M. Multifractality and spatial statistics. Comput. Geosci. 1999, 25, 949–961. [Google Scholar] [CrossRef]
- Chen, Z.J.; Cheng, Q.M.; Cheng, J.G.; Xie, S.Y. A novel iterative approach for mapping local singularities from geochemical data. Nonlinear Process. Geophys. 2007, 14, 317–324. [Google Scholar] [CrossRef][Green Version]
- Cheng, Q.M. Modeling local scaling properties for multiscale mapping. Vadose Zone J. 2008, 7, 525–532. [Google Scholar] [CrossRef]
- Cheng, Q.M.; Agterberg, F. Multifractals and singularity analysis in mineral exploration and environmental assessment. J. Geochem. Explor. 2018, 189, 1. [Google Scholar] [CrossRef]
- Cheng, Q.M. Multifractal and Geostatistic Methods for Characterizing Local Structure and Singularity Properties of Exploration Geochemical Anomalies. Earth Sci. 2001, 26, 161–166, (In Chinese with English Abstract). [Google Scholar]
- Carranza, E.J.M. Geochemical Anomaly and Mineral Prospectivity Mapping in GIS. In Handbook of Exploration and Environmental Geochemistry; Elsevier: Amsterdam, The Netherlands, 2009; p. 11. [Google Scholar]
- Afzal, P.; Alghalandis, Y.F.; Khakzad, A.; Moarefvand, P.; Omran, N.R. Delineation of mineralization zones in porphyry Cu deposits by fractal concentration–volume modeling. J. Geochem. Explor. 2011, 108, 220–232. [Google Scholar] [CrossRef]
- Zuo, R.G.; Wang, J.; Chen, G.X.; Yang, M.G. Identification of weak anomalies: A multifractal perspective. J. Geochem. Explor. 2014, 148, 12–24. [Google Scholar] [CrossRef]
- Chen, Y.L. Mineral potential mapping with a restricted Boltzmann machine. Ore Geol. Rev. 2015, 71, 749–760. [Google Scholar] [CrossRef]
- Chen, Y.L.; Wu, W. Mapping mineral prospectivity using an extreme learning machine regression. Ore Geol. Rev. 2017, 80, 200–213. [Google Scholar] [CrossRef]
- Cheng, Q.M.; Zhang, S.Y.; Zuo, R.G.; Chen, Z.J.; Xie, S.Y.; Xia, Q.L.; Xu, D.Y.; Yao, L.Q. Progress of multifractal filtering techniques and their applications in geochemical information extraction. Earth Sci. Front. 2009, 16, 185–198, (In Chinese with English Abstract). [Google Scholar]
- Xiang, Z.L. Study on 3D Geological Modeling method and Prospecting Prediction of Deep Comprehensive Information in Mining area. Ph.D. Thesis, Henan Polytechnic University, JiaoZuo, China, 2019. (In Chinese with English Abstract). [Google Scholar]
- Chen, Y.Q.; Zhang, S.Y.; Xia, Q.L.; Li, W.C.; Lu, Y.X.; Huang, J.N. Application of Multi Fractal Filtering to Extraction of Geochemical Anomalies from Multi Geochemical Backgrounds: A Case Study of the Southern Section of “Sanjiang Ore-Forming Zone”, Southwestern China. Earth Sci. 2006, 31, 861–866, (In Chinese with English Abstract). [Google Scholar]
- Sun, Z.J. Multifractal Method of Geochem Ical Threshold in Mineral Exploration. Comput. Tech. Geophys. Geochem. Explor. 2007, 29, 54–57+94, (In Chinese with English Abstract). [Google Scholar]
- Li, X.H. 3D Prospectivity Modeling for Concealed Orebody and System Development. Ph.D. Thesis, Hefei University Of Technology, Hefei, China, 2015. (In Chinese with English Abstract). [Google Scholar]
- Chen, G.X. Identifying Weak But Complex Geophysical and Geochemical Anomalies Caused by Buried Ore Bodies Using Fractal and Wavelet Methods. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2016. (In Chinese with English Abstract). [Google Scholar]
- Liu, S.F. Fractal Analysis on Geochemical Distribution and Anomaly Separation in the Guangxi Zhuang Autonomous Region. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2017. (In Chinese with English Abstract). [Google Scholar]
- Carranza, E.J.M.; Zuo, R. Introduction to the thematic issue: Analysis of exploration geochemical data for mapping of anomalies. Geochem. Explor. Env. Anal. 2017, 17, 183–185. [Google Scholar] [CrossRef]
- Zuo, R.G.; Cheng, Q.M.; Xia, Q.L. Application of fractal models to characterization of vertical distribution of geochemical element concentration. J. Geochem. Explor. 2009, 102, 37–43. [Google Scholar] [CrossRef]
- Delavar, S.T.; Afzal, P.; Borg, G.; Rasa, I.; Lotfi, M.; Omran, N.R. Delineation of mineralization zones using concentration-volume fractal method in Pb-Zn carbonate hosted deposits. J. Geochem. Explor. 2012, 118, 98–110. [Google Scholar] [CrossRef]
- Pearson, K. On a Form of Spurious Correlation Which May Arise When Indices Are Used in the Measurement of Organs. Proc. R. Soc. Lond. 1897, 60, 489–502. [Google Scholar]
- Chayes, F. On correlation between variables of constant sum. J. Geophys. Res. 1960, 65, 4185–4193. [Google Scholar] [CrossRef]
- Egozcue, J.J.; Pawlowsky-Glahn, V. Groups of Parts and Their Balances in Compositional Data Analysis. Math. Geol. 2005, 37, 795–828. [Google Scholar] [CrossRef]
- Pawlowsky-Glahn, V.; Egozcue, J.J. Exploring Compositional Data with the CoDa-Dendrogram. Austrian J. Stat. 2011, 40, 103–113. [Google Scholar]
- Zhou, D. Geological Compositional Data Analysis: Difficulties and Solutions. Earth Sci. 1998, 23, 41–46, (In Chinese with English Abstract). [Google Scholar]
- Carranza, E.J.M. Analysis and mapping of geochemical anomalies using logratio-transformed stream sediment data with censored values. J. Geochem. Explor. 2011, 110, 167–185. [Google Scholar] [CrossRef]
- Grunsky, E.C.; Mueller, U.A.; Corrigan, D. A study of the lake sediment geochemistry of the Melville Peninsula using multivariate methods: Applications for predictive geological mapping. J. Geochem. Explor. 2014, 141, 15–41. [Google Scholar] [CrossRef]
- Parent, L.E.; Parent, S.T.; Ziadi, N. Biogeochemistry of soil inorganic and organic phosphorus: A compositional analysis with balances. J. Geochem. Explor. 2014, 141, 52–60. [Google Scholar] [CrossRef]
- Wang, W.L.; Zhao, J.; Cheng, Q.M. Mapping of Fe mineralization-associated geochemical signatures using logratio transformed stream sediment geochemical data in eastern Tianshan, China. J. Geochem. Explor. 2014, 141, 6–14. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Geochemical Mineral Exploration: Should We Use Enrichment Factors or Log-Ratios. Nat. Resour. Res. 2016, 26, 411–428. [Google Scholar] [CrossRef]
- Mckinley, J.M.; Grunsky, E.; Mueller, U. Environmental Monitoring and Peat Assessment Using Multivariate Analysis of Regional-Scale Geochemical Data. Math. Geosci. 2017, 50, 235–246. [Google Scholar] [CrossRef]
- Reimann, C.; Filzmoser, P.; Hron, K.; Kynlová, P.; Garrett, R.G. A new method for correlation analysis of compositional (environmental) data—A worked example. Sci. Total Environ. 2017, 607, 965–971. [Google Scholar] [CrossRef] [PubMed]
- Thiombane, M.; Martín-Fernández, J.; Albanese, S.; Lima, A.; Doherty, A.; Vivo, B.D. Exploratory analysis of multi-element geochemical patterns in soil from the Sarno River Basin (Campania region, southern Italy) through compositional data analysis (CODA). J. Geochem. Explor. 2018, 195, 110–120. [Google Scholar] [CrossRef]
- Aitchison, J. The statistical analysis of compositional data. J. R. Stat. Soc. B 1982, 44, 139–177. [Google Scholar] [CrossRef]
- Buccianti, A.; Lima, A.; Albanese, S.; Cannatelli, C.; Esposito, R.; Vivo, B.D. Exploring topsoil geochemistry from the CoDA (Compositional Data Analysis) perspective: The multi-element data archive of the Campania Region (Southern Italy). J. Geochem. Explor. 2015, 159, 302–316. [Google Scholar] [CrossRef]
- Mckinley, J.M.; Hron, K.; Grunsky, E.C.; Reimann, C.; Tolosana-Delgado, R. The single component geochemical map: Fact or fiction. J. Geochem. Explor. 2016, 162, 16–28. [Google Scholar] [CrossRef]
- Buccianti, A.; Lima, A.; Albanese, S.; DeVivo, B. Measuring the change under compositional data analysis (CoDA): Insight on the dynamics of geochemical systems. J. Geochem. Explor. 2018, 189, 100–108. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, Q.M.; Zhou, K.F. New Insights into Element Distribution Patterns in Geochemistry: A Perspective from Fractal Density. Nat. Resour. Res. 2018, 28, 5–29. [Google Scholar] [CrossRef]
- Zheng, W.B.; Liu, B.L.; McKinley, J.M.; Cooper, M.R.; Wang, L. Geology and geochemistry-based metallogenic exploration model for the eastern Tethys Himalayan metallogenic belt, Tibet. J. Geochem. Explor. 2021, 224, 106743. [Google Scholar] [CrossRef]
- Liu, Y.; Carranza, E.J.M.; Xia, Q. Developments in Quantitative Assessment and Modeling of Mineral Resource Potential: An Overview. Nat. Resour. Res. 2022, 31, 1825–1840. [Google Scholar] [CrossRef]
- Agterberg, F. Principles of Probabilistic Regional Mineral Resource Estimation. Earth Sci. 2011, 36, 189–200. [Google Scholar]
- Zhou, Y.Z.; Chen, S.; Zhang, Q.; Xiao, F.; Wang, S.G.; Liu, Y.P.; Jiao, S.T. Advances and Prospects of Big Data and Mathematical Geoscience. Acta Petrol. Sin. 2018, 34, 255–263, (In Chinese with English Abstract). [Google Scholar]
- Zhou, Y.Z.; Wang, J.; Zuo, R.G.; Xiao, F.; Shen, W.J.; Wang, S.G. Machine learning, deep learning and Python language in field of geology. Acta Petrol. Sin. 2018, 34, 3173–3178, (In Chinese with English Abstract). [Google Scholar]
- Zhou, Y.Z.; Zuo, R.G.; Liu, G.; Yuan, F.; Mao, X.C.; Guo, Y.J.; Liao, J.; Liu, Y.P. The Great-leap-forward Development of Mathematical Geoscience During 2010–2019: Big Data and Artificial Intelligence Algorithm Are Changing Mathematical Geoscience. Bull. Miner. Petrol. Geochem. 2021, 40, 556–573+777, (In Chinese with English Abstract). [Google Scholar]
- Zuo, R.G. Deep Learning-Based Mining and Integration of Deep-Level Mineralization Information. Bull. Miner. Petrol. Geochem. 2019, 38, 53–60, (In Chinese with English Abstract). [Google Scholar]
- Zuo, R.G.; Peng, Y.; Li, T.; Xiong, Y.H. Challenges of Geological Prospecting Big Data Mining and Integration Using Deep Learning Algorithms. Earth Sci. 2021, 46, 350–358, (In Chinese with English Abstract). [Google Scholar]
- Zuo, R.G.; Carranza, E.J.M. Support vector machine: A tool for mapping mineral prospectivity. Comput. Geosci. 2011, 37, 1967–1975. [Google Scholar] [CrossRef]
- Shabankareh, M.; Hezarkhani, A. Application of support vector machines for copper potential mapping in Kerman region, Iran. J. Afr. Earth Sci. 2016, 128, 116–126. [Google Scholar] [CrossRef]
- Zhang, S.; Xiao, K.Y.; Carranza, E.J.M.; Yang, F. Maximum Entropy and Random Forest Modeling of Mineral Potential: Analysis of Gold Prospectivity in the Hezuo–Meiwu District, West Qinling Orogen, China. Nat. Resour. Res. 2018, 28, 645–664. [Google Scholar] [CrossRef]
- Sun, T.; Chen, F.; Zhong, L.X.; Liu, W.M.; Wang, Y. GIS-based mineral prospectivity mapping using machine learning methods: A case study from Tongling ore district, eastern China. Ore Geol. Rev. 2019, 109, 26–49. [Google Scholar] [CrossRef]
- Wang, J.; Zuo, R.G.; Xiong, Y.H. Mapping Mineral Prospectivity via Semi-supervised Random Forest. Nat. Resour. Res. 2019, 29, 189–202. [Google Scholar] [CrossRef]
- Sun, T.; Li, H.; Wu, K.X.; Chen, F.; Hu, Z.J. Data-Driven Predictive Modelling of Mineral Prospectivity Using Machine Learning and Deep Learning Methods: A Case Study from Southern Jiangxi Province, China. Minerals 2020, 10, 102. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Zuo, R.G.; Dong, Y.N. Mapping Himalayan leucogranites using a hybrid method of metric learning and support vector machine. Comput. Geosci. 2020, 138, 104455. [Google Scholar] [CrossRef]
- Chen, J.; Mao, X.C.; Liu, Z.K.; Deng, H. Three-dimensional Metallogenic Prediction Based on Random Forest Classification Algorithm for the Dayingezhuang Gold Deposit. Geotecton. Metallog. 2020, 44, 231–241, (In Chinese with English Abstract). [Google Scholar]
- Li, C.B.; Xiao, K.Y.; Li, N.; Song, X.L.; Zhang, S.; Wang, K.; Chu, W.K.; Cao, R. A Comparative Study of Support Vector Machine, Random Forest and Artificial Neural Network Machine Learning Algorithms in Geochemical Anomaly Information Extraction. Acta Geosci. Sin. 2020, 41, 309–319, (In Chinese with English Abstract). [Google Scholar]
- Wang, Y.; Zhou, Y.Z.; Xiao, F.; Wang, J.; Wang, K.Q.; Yu, X.T. Numerical Metallogenic Modelling and Support Vector Machine Methods Applied to Predict Deep Mineralization: A Case Study from the Fankou Pb-Zn Ore Deposit in Northern Guangdong. Geotecton. Metallog. 2020, 44, 222–230, (In Chinese with English Abstract). [Google Scholar]
- Li, S.; Chen, J.P.; Liu, C.; Wang, Y. Mineral Prospectivity Prediction via Convolutional Neural Networks Based on Geological Big Data. J. Earth Sci. 2021, 32, 327–347. [Google Scholar] [CrossRef]
- Zhang, S.; Carranza, E.J.M.; Wei, H.T.; Xiao, K.Y.; Yang, F.; Xiang, J.; Zhang, S.H.; Xu, Y. Data-driven Mineral Prospectivity Mapping by Joint Application of Unsupervised Convolutional Auto-encoder Network and Supervised Convolutional Neural Network. Nat. Resour. Res. 2021, 30, 1011–1031. [Google Scholar] [CrossRef]
- Zhou, Y.Z.; Li, P.X.; Wang, S.G.; Xiao, F.; Li, J.Z.; Gao, L. Research Progress on Big Data and Intelligent Modelling of Mineral Deposits. Bull. Miner. Petrol. Geochem. 2017, 36, 327–331+344, (In Chinese with English Abstract). [Google Scholar]
- Singer, D.A.; Kouda, R. Application of a feed forward neural network in the search for Kuroko deposits in the Hokuroku District. Math. Geol. 1996, 28, 1017–1023. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Zuo, R.G.; Xiong, Y.H. Geodata science and geochemical mapping. J. Geochem. Explor. 2019, 209, 106431. [Google Scholar] [CrossRef]
- Xiong, Y.H.; Zuo, R.G. Robust Feature Extraction for Geochemical Anomaly Recognition Using a Stacked Convolutional Denoising Autoencoder. Math. Geosci. 2021, 54, 623–644. [Google Scholar] [CrossRef]
- Gao, Y. Mineral Prospecting Information Mining and Mapping Mineral Prospectivity for Copper Polymetallic Mineralization in Southwest Fujian Province, China. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2019. (In Chinese with English Abstract). [Google Scholar]
- Zuo, R.G. Geodata Science-Based Mineral Prospectivity Mapping: A Review. Nat. Resour. Res. 2020, 29, 3415–3424. [Google Scholar] [CrossRef]
- Li, T.; Zuo, R.G.; Xiong, Y.H.; Peng, Y. Random-Drop Data Augmentation of Deep Convolutional Neural Network for Mineral Prospectivity Mapping. Nat. Resour. Res. 2020, 30, 27–38. [Google Scholar] [CrossRef]
- Cai, H.H.; Xu, Y.Y.; Li, Z.X.; Cao, H.H.; Feng, Y.X.; Chen, S.Q.; Li, Y.S. The division of metallogenic prospective areas based onconvolutional neural network model: A case study of the Daqiao gold polymetallic deposit. Geol. Bull. China 2019, 38, 1999–2009, (In Chinese with English Abstract). [Google Scholar]
- Wang, Z.Y. Mapping of Himalaya Leucogranites Based on Metric Learning. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2020. (In Chinese with English Abstract). [Google Scholar]
- Deng, H.; Wei, Y.F.; Chen, J.; Liu, Z.K.; Yu, S.Y.; Mao, X.C. Three-dimensional prospectivity mapping and quantitative analysis of structural ore-controlling factors in Jiaojia Auore-belt with attention convolutional neural networks. J. Cent. South Univ. 2021, 52, 3003–3014, (In Chinese with English Abstract). [Google Scholar]
- Deng, H.; Zheng, Y.; Chen, J.; Wei, Y.F.; Mao, X.C. Deep Learning-based 3D Prediction Model for the Dayingezhuang Gold Deposit, Shandong Province. Acta Geosci. Sin. 2020, 41, 157–165, (In Chinese with English Abstract). [Google Scholar]
- Zhang, Z.J.; Cheng, Q.M.; Yang, J.; Wu, G.P.; Ge, Y.Z. Machine Learning for Mineral Prospectivity: A Case Study of Iron-polymetallic Mineral Prospectivity in Southwestern Fujian. Earth Sci. Front. 2021, 28, 221–235, (In Chinese with English Abstract). [Google Scholar]
- Feng, Y.M.; Cao, X.Z.; Zhang, E.P.; Hu, Y.X.; Pan, X.P.; Yang, J.L.; Jia, Q.Z.; Li, W.M. Tectonic Evolution Framework and Nature of The West Qinling Orogenic Belt. Northwest. Geol. 2003, 36, 1–10, (In Chinese with English Abstract). [Google Scholar]
- Wei, L.X. Tectonic Evolution and Mineralization of Zaozigou Gold Deposit, Gansu Province. Master’s Thesis, China University of Geosciences, Beijing, China, 2015. (In Chinese with English Abstract). [Google Scholar]
- Zeng, J.J.; Li, K.N.; Yan, K.; Wei, L.L.; Huo, X.D.; Zhang, J.P. Tectonic Setting and Provenance characteristics of the Lower Triassic Jiangligou Formation in West Qinling—Constraints from Geochemistry of Clastic Rock and zircon U-Pb Geochronology of Detrital Zircon. Geol. Rev. 2021, 67, 1–15, (In Chinese with English Abstract). [Google Scholar]
- Li, Z.B.; Liu, Z.Y.; Li, R. Geochemical Characteristics and metallogenic Potential Analysis of Daheba Formation in Ta-Ga Area of Gansu Province. Contrib. Geol. Miner. Resour. Res. 2021, 36, 187–194, (In Chinese with English Abstract). [Google Scholar]
- Chen, Y.; Wang, K.J. Geological Features and Ore Prospecting Indicators of Sishangou Silver Deposit. Gansu. Metal. 2015, 37, 108–111, (In Chinese with English Abstract). [Google Scholar]
- Di, P.F. Geochemistry and Ore-Forming Mechanism on Zaozigou gold deposit in Xiahe-Hezuo, West Qinling, China. Ph.D. Thesis, Lanzhou University, Lanzhou, China, 2018. (In Chinese with English Abstract). [Google Scholar]
- Li, K.N.; Li, H.R.; Liu, B.C.; Yan, K.; Jia, R.Y.; Wei, L.L. Geochemical characteristics of TTG Dick rock and the Relation with Gold Mineralization in West Qinling Mountain. Sci. Technol. Eng. 2019, 19, 52–65, (In Chinese with English Abstract). [Google Scholar]
- Kang, S.S. Geological Characteristics and Prospecting Criteria of Nanmougou Copper Deposit, Gansu Province. Gansu. Metal. 2018, 40, 79–85, (In Chinese with English Abstract). [Google Scholar]
- Kang, S.S.; Dou, X.G.; Zhi, C.; Wu, X.L. Geochemical Characteristics and Genetic Analysis of the Namugou Copper Deposit in Sunan County, Gansu. Gansu. Metal. 2019, 41, 65–72, (In Chinese with English Abstract). [Google Scholar]
- Liu, Y. Relationship between Intermediate-acid Dike Rock and Gold Mineralization of the Zaozigou Deposit, Gansu Province. Master’s Thesis, Chang’an University, Xi’an, China, 2013. (In Chinese with English Abstract). [Google Scholar]
- Hu, J.Q. Mineral Control Factors, Metallogenic Law and Prospecting Direction of Integrated Gold Mine Exploration Area in Shilijba-Yangshan Area of Gansu Province. Gansu. Sci. Technol. 2018, 34, 27–33. (In Chinese) [Google Scholar]
- Zhao, J.Z.; Chen, G.Z.; Liang, Z.L.; Zhao, J.C. Ore-body Geochemical Features of Zaozigou Gold Deposit. Gansu. Geol. 2013, 22, 38–43, (In Chinese with English Abstract). [Google Scholar]
- Lu, J. Study on Characteristics and Ore-host Regularity of Gold Mineral in the Western Qinling Region, Gansu Province. Master’s Thesis, China University of Geosciences, Beijing, China, 2016. (In Chinese with English Abstract). [Google Scholar]
- Zhang, Y.N.; Liang, Z.L.; Qiu, K.F.; Ma, S.H.; Wang, J.L. Overview on the Metallogenesis of Zaozigou gold deposit in the West Qinling Orogen. Miner. Explor. 2020, 11, 28–39, (In Chinese with English Abstract). [Google Scholar]
- Tang, L.; Lin, C.G.; Cheng, Z.Z.; Jia, R.Y.; Li, H.R.; Li, K.N. 3D Characteristics of Primary Halo and Deep Prospecting Prediction in The Zaozigou Gold Deposit, Hezuo City, Gansu Province. Geol. Bull. China 2020, 39, 1173–1181, (In Chinese with English Abstract). [Google Scholar]
- Chen, G.Z.; Wang, J.L.; Liang, Z.L.; Li, P.B.; Ma, H.S.; Zhang, Y.N. Analysis of Geological Structures in Zaozigou Gold Deposit of Gansu Province. Gansu. Geol. 2013, 22, 50–57, (In Chinese with English Abstract). [Google Scholar]
- Chen, G.Z.; Liang, M.L.; Wang, J.L.; Zhang, Y.N.; Li, P.B. Characteristics and Deep Prediction of Primary Superimposed Halos in The Zaozigou Gold Deposit of Hezuo, Gansu Province. Geophys. Geochem. Explor. 2014, 38, 268–277, (In Chinese with English Abstract). [Google Scholar]
- Jin, D.G.; Liu, B.C.; Chen, Y.Y.; Liang, Z.L. Spatial Distribution of Gold Bodies in Zaozigou Mine of Gansu Province. Gansu. Geol. 2015, 24, 25–30+41, (In Chinese with English Abstract). [Google Scholar]
- Zhu, F.; Wang, G.W. Study on Grade Model of Gansu Zaozigou Gold Mine Based on Geological Statistics. Acta Mineral. Sin. 2015, 35, 1065–1066. (In Chinese) [Google Scholar]
- Chen, G.Z.; Li, L.N.; Zhang, Y.N.; Ma, H.S.; Liang, Z.L.; Wu, X.M. Characteristics of fluid inclusions and deposit formation in Zaozigou gold mine. In Proceedings of the The 15th Annual Academic Conference of Chinese Society for Mineralogy, Petrology and Geochemistry, Changchun, China, 24 June 2015. [Google Scholar]
- Wu, X.M. Study on Geological Characteristics and Metallogenic Regularity of the Gelouang Gold Deposit. Master’s Thesis, Lanzhou University, Lanzhou, China, 2018. (In Chinese with English Abstract). [Google Scholar]
- Liu, H.T.; Jiang, Y.M.; Wu, T.J.; Chang, D.L. Application of singularity analysis to geochemical anomaly recognization in Chifeng area. Contrib. Geol. Miner. Resour. Res. 2011, 26, 341–344, (In Chinese with English Abstract). [Google Scholar]
- Wang, Y. The Application of Fractal Theory in Geophysical Research. Master’s Thesis, Chang’an University, Xi’an, China, 2013. (In Chinese with English Abstract). [Google Scholar]
- Filzmoser, P.; Hron, K.; Reimann, C. Univariate statistical analysis of environmental (compositional) data: Problems and possibilities. Sci. Total Environ. 2009, 407, 6100–6108. [Google Scholar] [CrossRef]
- Wang, L.; Liu, B.L.; McKinley, J.M.; Cooper, M.R.; Li, C.; Kong, Y.H.; Shan, M.X. Compositional data analysis of regional geochemical data in the Lhasa area of Tibet, China. Appl. Geochem. 2021, 135, 105108. [Google Scholar] [CrossRef]
- Zheng, W.B.; Liu, B.L.; Tang, J.X.; McKinley, J.M.; Cooper, M.R.; Tang, P.; Lin, B.; Li, C.; Wang, L.; Zhang, D. Exploration indicators of the Jiama porphyry–skarn deposit, southern Tibet, China. J. Geochem. Explor. 2022, 236, 106982. [Google Scholar] [CrossRef]
- Zuo, R.G. Identification of weak geochemical anomalies using robust neighborhood statistics coupled with GIS in covered areas. J. Geochem. Explor. 2014, 136, 93–101. [Google Scholar] [CrossRef]
- Liu, Y. The Study of Regional Geochemistry Data Analysis and Metallogenic Information Fusion Models. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2015. (In Chinese with English Abstract). [Google Scholar]
- Prado, E.; Filho, C.; Carranza, E.; Motta, J.G. Modeling of Cu-Au Prospectivity in the Carajás mineral province (Brazil) through Machine Learning: Dealing with Imbalanced Training Data. Ore Geol. Rev. 2020, 124, 103611. [Google Scholar] [CrossRef]
- Brown, W.M.; Gedeon, T.D.; Groves, D.I.; Barnes, R.G. Artificial neural networks: A new method for mineral prospectivity mapping. Aust. J. Earth Sci. 2000, 47, 757–770. [Google Scholar] [CrossRef]
- Skabar, A. Mineral potential mapping using feed-forward neural networks. In Proceedings of the International Joint Conference on Neural Networks IEEE, Portland, OR, USA, 20–24 July 2003. [Google Scholar]
- Leite, E.P.; Filho, C. Probabilistic neural networks applied to mineral potential mapping for platinum group elements in the Serra Leste region, Carajás Mineral Province, Brazil. Comput. Geosci. 2009, 35, 675–687. [Google Scholar] [CrossRef]
- Leite, E.P.; de Souza, C.R. Artificial neural networks applied to mineral potential mapping for copper-gold mineralizations in the Carajás Mineral Province, Brazil. Geophys. Prospect. 2009, 57, 1049–1065. [Google Scholar] [CrossRef]
- Abedi, M.; Norouzi, G.H.; Bahroudi, A. Support vector machine for multi-classification of mineral prospectivity areas. Comput. Geosci. 2012, 9, 272–283. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Chica-Olmo, M.; Chica-Rivas, M. Predictive modelling of gold potential with the integration of multisource information based on random forest: A case study on the Rodalquilar area, Southern Spain. Int. J. Geogr. Inf. Sci. 2014, 28, 1336–1354. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, Z.J.; Xiong, Y.H.; Zuo, R.G. Mapping mineral prospectivity for Cu polymetallic mineralization in southwest Fujian Province, China. Ore Geol. Rev. 2016, 75, 16–28. [Google Scholar] [CrossRef]
- Geranian, H.; Tabatabaei, S.H.; Asadi, H.H.; Carranza, E.J.M. Application of Discriminant Analysis and Support Vector Machine in Mapping Gold Potential Areas for Further Drilling in the Sari-Gunay Gold Deposit, NW Iran. Nat. Resour. Res. 2016, 25, 145–159. [Google Scholar] [CrossRef]
- Xie, S. Research on the prediction of potential suitable distribution of Biomphalaria straminea in Guangdong Province. Master’s Thesis, South China Agricultural University, Guangzhou, China, 2017. (In Chinese with English Abstract). [Google Scholar]
- Xu, C. Distribution of Vehicle Free Flow Speeds Based on Gaussian Mixture Model. J. Highw. Transp. Res. Dev. Chin. Ed. 2012, 19, 132–158, (In Chinese with English Abstract). [Google Scholar]
- Matheron, G. Kriging or polynomial interpolation procedures? Trans. Can. Inst. Min. Metal. 1967, 70, 240–244. [Google Scholar]
- Journel, A.G.; Huijbregts, C.J. Mining Geostatistics; Academic Press: London, UK, 1978. [Google Scholar]
- Cressie, N. The origins of kriging. Math. Geosci. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- Wang, H.; Lineweaver, C.H. Chemical Complementarity between the Gas Phase of the Interstellar Medium and the Rocky Material of Our Planetary System. In Proceedings of the 15th Australian Space Research Conference, Canberra, Australia, 29 September–1 October 2016; pp. 173–182. [Google Scholar]
- Ye, T.Z. Theoretical Framework of Synthetic Geological Information Prediction Techniques and Methods for Mineral Deposit Models. J. Jilin Univ. Earth Sci. Ed. 2013, 43, 1053–1072, (In Chinese with English Abstract). [Google Scholar]
- Beus, A.A.; Grigorian, S.V. Geochemical Exploration Methods for Mineral Deposits; Applied Publishing Ltd.: Wilmette, IL, USA, 1977; pp. 31–270. [Google Scholar]
- Levinson, A.A. Introduction to Exploration Geochemistry; Applied Publishing Ltd.: Wilmette, IL, USA, 1974; p. 612. [Google Scholar]
- Rabeaut, O.; Legault, M.; Cheilletz, A.; Jébrak, M.; Royer, J.J.; Cheng, L.Z. Gold Potential of a Hidden Archean Fault Zone: The Case of the Cadillac–Larder Lake Fault. Explor. Min. Geol. 2010, 19, 99–116. [Google Scholar] [CrossRef]
- Mejia-Herrera, P.; Royer, J.J.; Caumon, G.; Cheilletz, A. Curvature Attribute from Surface-Restoration as Predictor Variable in Kupferschiefer Copper Potentials: An Example from the Fore-Sudetic Region. Nat. Resour. Res. 2015, 24, 275–290. [Google Scholar] [CrossRef]
- Li, B.B.; Liu, B.L.; Guo, K.; Li, C.; Wang, B. Application of a Maximum Entropy Model for Mineral Prospectivity Maps. Minerals 2019, 9, 556. [Google Scholar] [CrossRef]
- Kong, W.X.; Li, X.H.; Zou, H.F. Optimization of Maximum Entropy Model in Species Distribution Prediction. J. Appl. Ecol. 2019, 30, 2116–2128, (In Chinese with English Abstract). [Google Scholar]
- Elith, J.; Phillips, S.J.; Hastie, T.; Dudik, M.; Chee, Y.E.; Yates, C.J. A statistical explanation of MaxEnt for ecologists. Divers. Distrib. 2013, 17, 43–57. [Google Scholar] [CrossRef]
- Radosavljevic, A.; Anderson, R.P. Making better MAXENT models of species distributions: Complexity, overfitting and evaluation. J. Biogeogr. 2013, 41, 629–643. [Google Scholar] [CrossRef]
- Caumon, G.; Collon-Drouaillet, P.; De Veslud, C.L.C.; Viseur, S.; Sausse, J. Surface-based 3D modeling of geological structures. Math. Geosci. 2009, 41, 927–945. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, G.; Li, X.; Zhang, Z.; Li, Y. A corner-point-grid-based voxelization method for the complex geological structure model with folds. J. Vis. 2017, 20, 875–888. [Google Scholar] [CrossRef]
- Yarus, J.M.; Chambers, R.L. Stochastic Modeling and Geostatistics: Principles, Methods, and Case Studies; American Association of Petroleum Geologists: Tulsa, OK, USA, 1994; p. 379. [Google Scholar]
- Chen, Q.; Liu, G.; Ma, X.; Li, X.; He, Z. 3D stochastic modeling framework for Quaternary sediments using multiple-point statistics: A case study in Minjiang Estuary area, southeast China. Comput. Geosci. 2019, 136, 104404. [Google Scholar] [CrossRef]
- Chen, Q.; Mariethoz, G.; Liu, G.; Comunian, A.; Ma, X. Locality-based 3-D multiple-point statistics reconstruction using 2-D geological cross sections. Hydrol. Earth Syst. Sci. 2018, 22, 6547–6566. [Google Scholar] [CrossRef]
- Gueting, N.; Caers, J.; Comunian, A.; Vanderborght, J.; Englert, A. Reconstruction of three-dimensional aquifer heterogeneity from two-dimensional geophysical data. Math. Geosci. 2018, 50, 53–75. [Google Scholar] [CrossRef]
- Mahmud, K.; Mariethoz, G.; Baker, A.; Treble, P.C. Hydrological characterization of cave drip waters in a porous limestone: Golgotha Cave, Western Australia. Hydrol. Earth Syst. Sci. 2018, 22, 977–988. [Google Scholar] [CrossRef]
- Feng, W.; Yin, Y.; Zhang, C.; Duan, T.; Zhang, W.; Hou, G.; Zhao, L. A training image optimal selecting method based on composite correlation coefficient ranking for multiple-point geostatistics. J. Petrol. Sci. Eng. 2019, 179, 292–311. [Google Scholar] [CrossRef]
- Cui, Z.; Chen, Q.; Liu, G.; Mariethoz, G.; Ma, X. Hybrid parallel framework for multiple-point geostatistics on tianhe-2: A robust solution for large-scale simulation. Comput. Geosci. 2021, 157, 104923. [Google Scholar] [CrossRef]
- Chen, Q.; Cui, Z.; Liu, G.; Yang, Z.; Ma, X. Deep convolutional generative adversarial networks for modeling complex hydrological structures in Monte-Carlo simulation. J. Hydrol. 2022, 610, 127970. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, Q.; Cui, Z.; Liu, G.; Dong, S.; Tian, Y. Automatic reconstruction method of 3D geological models based on deep convolutional generative adversarial networks. Comput. Geosci. 2022, 26, 1135–1150. [Google Scholar] [CrossRef]
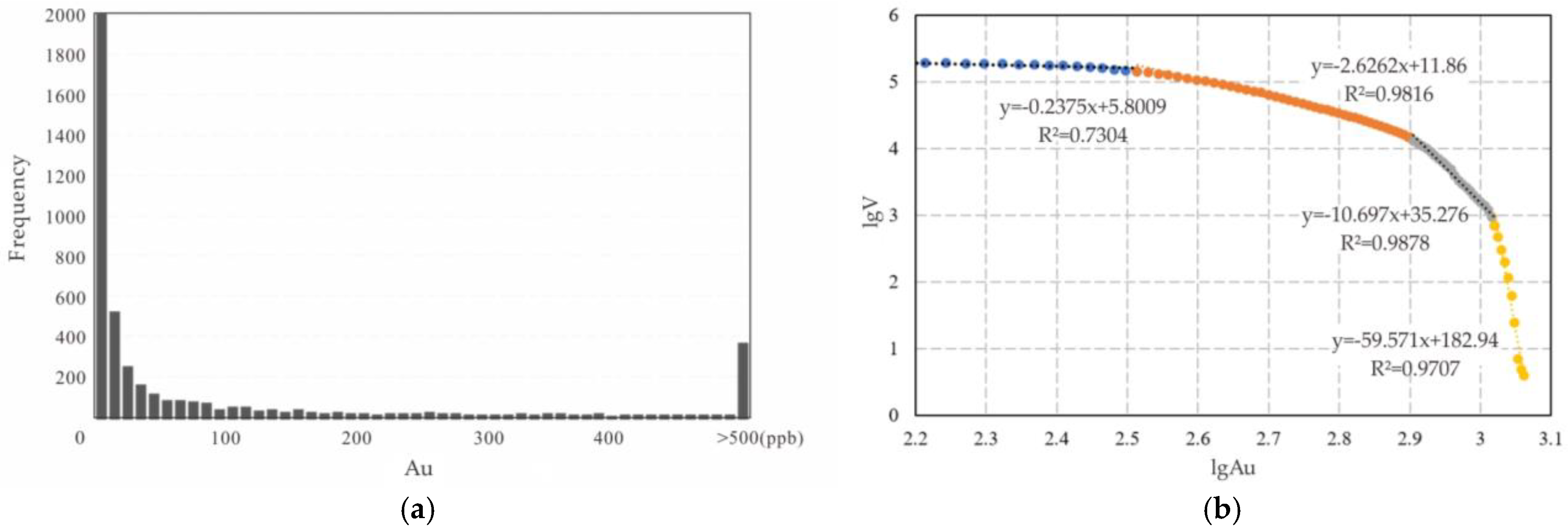

| Anomaly Classes | Fractal Dimension | R Square (R2) | Inflection Point | Au (ppb) |
|---|---|---|---|---|
| Background area | 0.2375 | 0.7304 | 1.0876 | 12.2349 |
| Outer anomalies | 2.6262 | 0.9816 | 2.5137 | 326.3623 |
| Middle anomaly | 10.697 | 0.9878 | 2.9049 | 803.3411 |
| Internal anomaly | 59.571 | 0.9707 | 3.0202 | 1047.6108 |
| Element | Anomaly Classes | Fractal Dimension | R Square (R2) | Inflection Point | Cut-Off Value |
|---|---|---|---|---|---|
| As | Background area | 0.7877 | 0.9742 | 1.8621 | 72.7949 |
| Outer anomalies | 2.5417 | 0.9944 | 2.5595 | 362.653 | |
| Middle anomaly | 7.1778 | 0.9316 | 3.5762 | 3768.486 | |
| Internal anomaly | 7.1332 | 0.8924 | 3.6731 | 4710.524 | |
| Sb | Background area | 2.8084 | 0.9906 | 2.0003 | 100.091 |
| Outer anomalies | 1.3802 | 0.9977 | 2.6022 | 400.0882 | |
| Middle anomaly | 2.1265 | 0.9732 | −0.4559 | 3500.06 | |
| Internal anomaly | 9.7587 | 0.8478 | −0.1079 | 7800 | |
| Hg | Background area | 0.3416 | 0.7344 | 0.9318 | 8.5462 |
| Outer anomalies | 3.0623 | 0.9985 | 1.5123 | 32.5296 | |
| Middle anomaly | 3.9887 | 0.9814 | 2.4599 | 288.3531 | |
| Internal anomaly | 2.1553 | 0.7624 | 2.6814 | 480.2207 | |
| Ag | Background area | 0.1975 | 0.7174 | −1.5708 | 0.0289 |
| Outer anomalies | 3.8416 | 0.9923 | −1.0079 | 0.0982 | |
| Middle anomaly | 8.8291 | 0.9867 | −0.0403 | 0.9114 | |
| Internal anomaly | −3.1223 | 0.8456 | 0.0287 | 1.0683 | |
| Cu | Background area | 0.4997 | 0.7448 | 0.864 | 7.312 |
| Outer anomalies | 7.8425 | 0.9744 | 1.6271 | 42.372 | |
| Middle anomaly | 2.995 | 0.9921 | 1.9266 | 84.444 | |
| Internal anomaly | 1.7321 | 0.9297 | 2.4374 | 273.768 | |
| Pb | Background area | 0.1789 | 0.5279 | 0.1436 | 1.392 |
| Outer anomalies | 5.0613 | 0.9921 | 1.3684 | 23.356 | |
| Middle anomaly | 11.571 | 0.9881 | 1.7353 | 54.364 | |
| Internal anomaly | 3.4226 | 0.9896 | 1.8362 | 68.576 | |
| Zn | Background area | 0.0352 | 0.6439 | 0.2996 | 1.993 |
| Outer anomalies | 0.7062 | 0.8446 | 0.7904 | 6.172 | |
| Middle anomaly | 12.592 | 0.978 | 1.9663 | 92.538 | |
| Internal anomaly | 43.05 | 0.9284 | 2.0954 | 124.577 | |
| W | Background area | 0.2629 | 0.8334 | 0.3484 | 2.2303 |
| Outer anomalies | 1.5296 | 0.984 | 0.8215 | 6.6297 | |
| Middle anomaly | 3.0193 | 0.9973 | 1.343 | 22.0275 | |
| Internal anomaly | 7.7309 | 0.9441 | 2.175 | 149.6098 | |
| Mo | Background area | 0.3775 | 1 | −0.3907 | 0.4067 |
| Outer anomalies | 1.5056 | 0.9729 | −0.1184 | 0.7614 | |
| Middle anomaly | 8.1548 | 0.9923 | 1.1745 | 14.9466 | |
| Internal anomaly | 25.728 | 0.9634 | 1.4696 | 29.4864 | |
| Bi | Background area | 0.7603 | 1 | −0.3087 | 0.4913 |
| Outer anomalies | 3.2299 | 0.9943 | −0.0116 | 0.9737 | |
| Middle anomaly | 3.0016 | 0.9905 | 1.2518 | 3.8681 | |
| Internal anomaly | 1.7831 | 0.8475 | 1.5919 | 17.8579 | |
| Co | Background area | 0.1171 | 0.6058 | 0.1909 | 1.5524 |
| Outer anomalies | 2.3832 | 0.9903 | 1.2625 | 18.3011 | |
| Middle anomaly | 1.2849 | 0.9527 | 1.4756 | 29.8963 | |
| Internal anomaly | 7.2045 | 0.9606 | 1.8749 | 74.9889 |
| Ore-Forming Factor | Description | Prediction Indicator | Variables |
|---|---|---|---|
| Geology | Fracture | Influence range of fracture | 30 m buffer zone |
| Element association of fracture | Hg-Sb (F4) | ||
| Geochemistry | Ore-forming element | Geochemical anomaly | Au |
| Primary geochemical halo | Element association of near-ore halo | Au-Ag-Cu-Pb-Zn (B2) | |
| Geochemical parameter (Front halo/tail halo) | As-Sb-Hg(B1)/W-Bi-Co-Mo (B3) |
| Prediction Indicator | Rate of Contribution (%) |
|---|---|
| Au | 77.6 |
| 30m buffer zone | 13 |
| Au-Ag-Cu-Pb-Zn (B2) | 7.7 |
| Hg-Sb (F4) | 0.9 |
| As-Sb-Hg(B1)/W-Bi-Co-Mo(B3) | 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, Y.; Chen, G.; Liu, B.; Xie, M.; Yu, Z.; Li, C.; Wu, Y.; Gao, Y.; Zha, S.; Zhang, H.; et al. 3D Mineral Prospectivity Mapping of Zaozigou Gold Deposit, West Qinling, China: Machine Learning-Based Mineral Prediction. Minerals 2022, 12, 1361. https://doi.org/10.3390/min12111361
Kong Y, Chen G, Liu B, Xie M, Yu Z, Li C, Wu Y, Gao Y, Zha S, Zhang H, et al. 3D Mineral Prospectivity Mapping of Zaozigou Gold Deposit, West Qinling, China: Machine Learning-Based Mineral Prediction. Minerals. 2022; 12(11):1361. https://doi.org/10.3390/min12111361
Chicago/Turabian StyleKong, Yunhui, Guodong Chen, Bingli Liu, Miao Xie, Zhengbo Yu, Cheng Li, Yixiao Wu, Yaxin Gao, Shuai Zha, Hanyuan Zhang, and et al. 2022. "3D Mineral Prospectivity Mapping of Zaozigou Gold Deposit, West Qinling, China: Machine Learning-Based Mineral Prediction" Minerals 12, no. 11: 1361. https://doi.org/10.3390/min12111361
APA StyleKong, Y., Chen, G., Liu, B., Xie, M., Yu, Z., Li, C., Wu, Y., Gao, Y., Zha, S., Zhang, H., Wang, L., & Tang, R. (2022). 3D Mineral Prospectivity Mapping of Zaozigou Gold Deposit, West Qinling, China: Machine Learning-Based Mineral Prediction. Minerals, 12(11), 1361. https://doi.org/10.3390/min12111361





