Molecule Diffusion Behavior of Tritium and Selenium in Mongolia Clay Rock by Numerical Analysis of the Spatial and Temporal Variation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theory of Through-Diffusion
2.2. Experiments
2.2.1. Clay Rocks and Liquids
2.2.2. Batch Tests
2.2.3. Sorption Kinetic Experiments
2.2.4. Sorption Isotherm Experiments
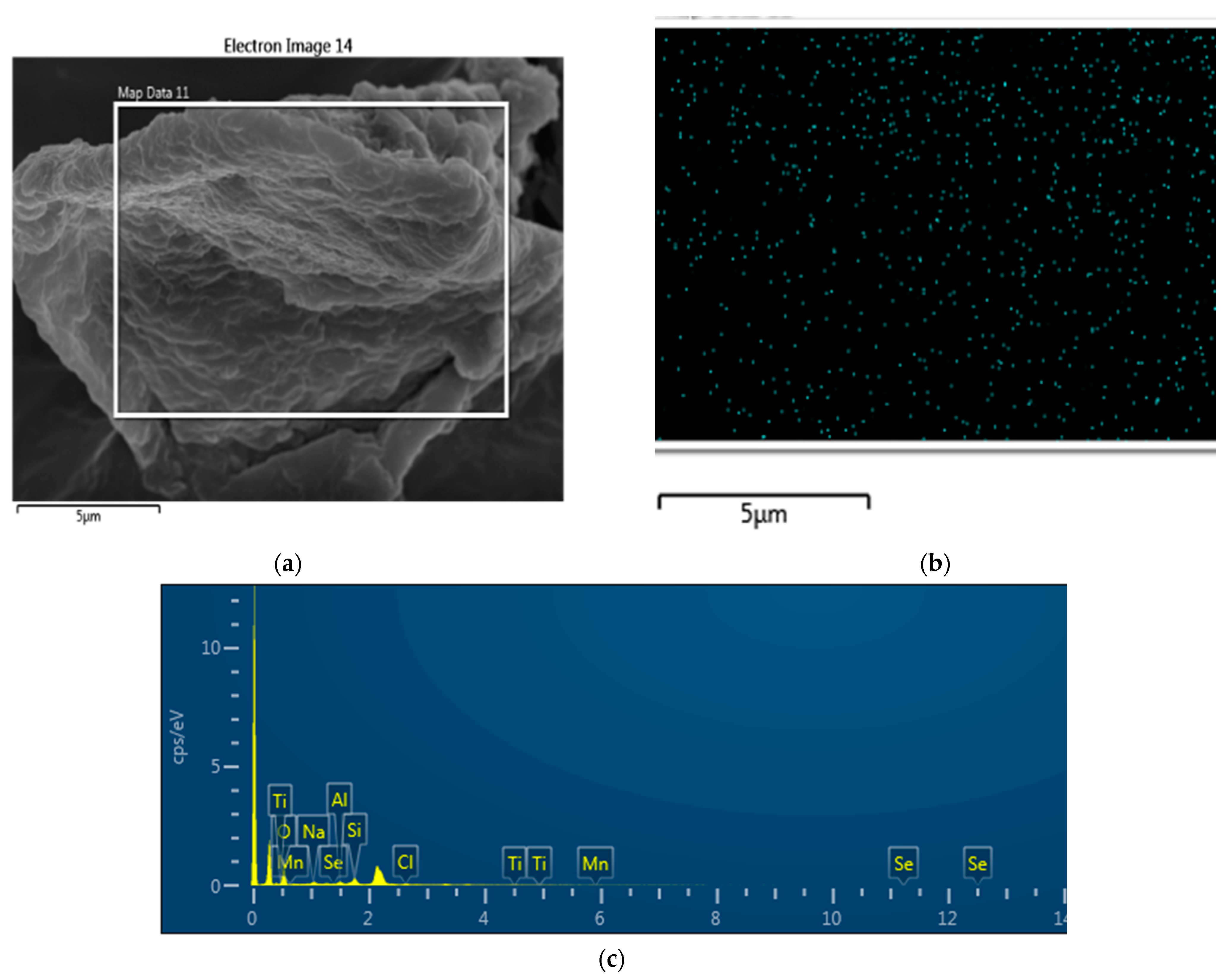
2.2.5. Microanalysis and Elemental Analysis (SEM–EDS Experiments)
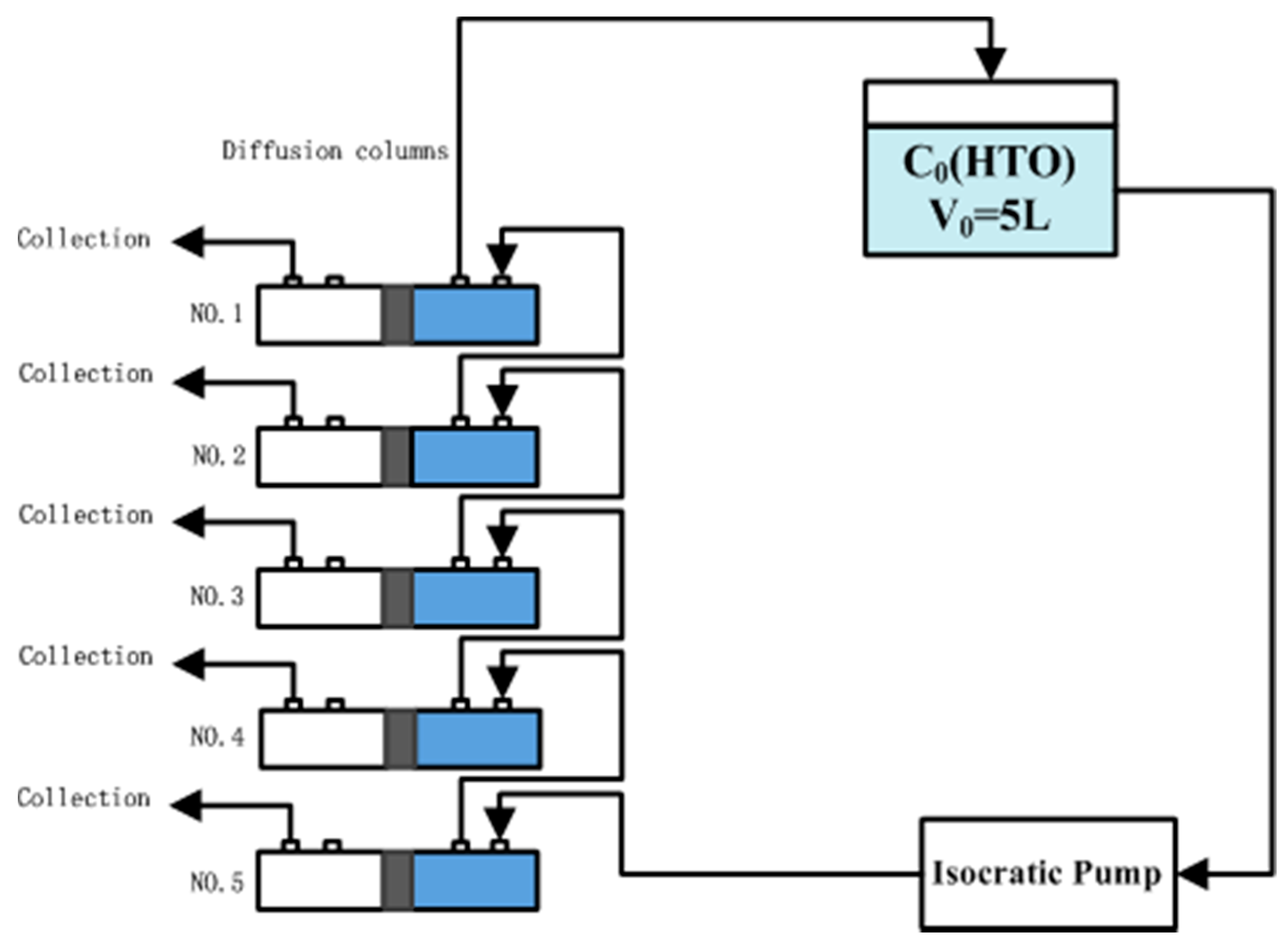
2.3. Through-Diffusion Experiments (TD): Column Tests
2.3.1. Water Saturation
2.3.2. Nonreactive Tests—HTO
2.3.3. Reactive Tests—Selenium (Se(IV))
3. Results
3.1. Batch Sorption Tests: One- and Two-Site Kinetic Fitting and Langmuir Isotherm
3.2. Microanalysis and Elemental Analysis for Se Sorption on TMS Clay Rocks
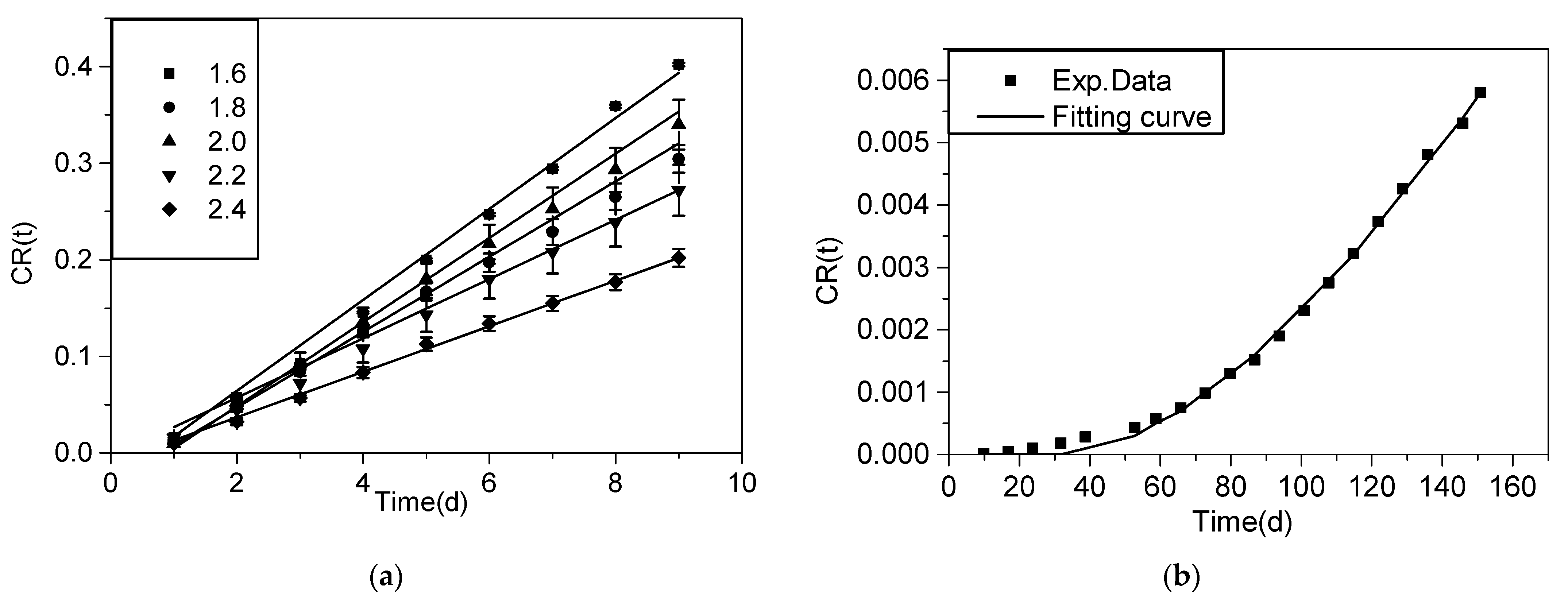
3.3. Diffusion Coefficients of HTO and Se for TMS Clay Rocks
3.4. Spatial and Temporal Variation with Various Diffusion Coefficients by Numerical Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ahn, J.; Apted, M.J. Preface—Geological Repository Systems for Safe. Disposal of Spent Nuclear Fuels and Radioactive Waste, 2nd ed.; Woodhead Publishing, Elsevier: Sawston, UK, 2017; pp. xxiii–xxvi. [Google Scholar]
- Seby, F.; Potin-Gautier, M.; Giffaut, E.; Donard, O.F.X. Assessing the speciation and the biogeochemical processes affecting the mobility of selenium from a geological repository of radioactive wastes to the biosphere. Analusis 1998, 26, 193–197. [Google Scholar] [CrossRef] [Green Version]
- Deniau, I.; Devol-Brown, I.; Derenne, S.; Behar, F.; Largeau, C. Comparison of the bulk geochemical features and thermal reactivity of kerogens from Mol (Boom Clay), Bure (Callovo-Oxfordian argillite) and Tournemire (Toarcian shales) underground research laboratories. Sci. Total Environ. 2008, 389, 475–485. [Google Scholar] [CrossRef] [PubMed]
- Descostes, M.; Blin, V.; Bazer-Bachi, F.; Meier, P.; Grenut, B.; Radwan, J.; Schlegel, M.L.; Buschaert, S.; Coelho, D.; Tevissen, E. Diffusion of anionic species in callovo-oxfordian argillites and oxfordian limestones (Meuse/Haute–Marne, France). Appl. Geochem. 2008, 23, 655–677. [Google Scholar] [CrossRef]
- Guo, Z.J.; Chen, Z.Y.; Wu, W.S.; Liu, C.L.; Chen, T.; Tian, W.Y.; Li, C. Adsorption of Se(IV) onto Beishan granite. Acta Phys.-Chim. Sin. 2011, 27, 2222–2226. [Google Scholar]
- Jin, Q.; Wang, G.; Ge, M.; Chen, Z.; Wu, W.; Guo, Z. The adsorption of Eu(III) and Am(III) on Beishan granite: XPS, EPMA, batch and modeling study. Appl. Geochem. 2014, 47, 17–24. [Google Scholar] [CrossRef]
- Jiang, T.; Yao, J.; Zhou, D.; Bao, L.J.; Zhang, Y.; Chen, X.; Fan, X.H. Effect of temperature on sorption of Np(IV)/Np(V) on beishan granite. J. Nucl. Radiochem. 2011, 33, 25–31. [Google Scholar]
- Tao, C.; Tian, W.Y.; Sun, M.; Li, C.; Liu, X.Y.; Wang, L.H.; Wang, X.Y.; Liu, C.L. Influence of silver halide additives on the sorption of iodine-125 on Beishan granite powder. Chin. J. Inorg. Chem. 2009, 25, 761–766. [Google Scholar]
- Li, C.; Liu, X.Y.; Chen, T.; Tian, W.Y.; Zheng, Z.; Wang, L.H.; Liu, C.L. The influence of pH on the sorption and diffusion of 99TcO4− in Beishan granite. Int. J. Chem. Aspects Nucl. Sci. Technol. 2012, 100, 449–456. [Google Scholar]
- Hu, H.Y.; Liu, X.D.; Yang, T.; Wang, G.B.; Huo, L. Experimental study and mechanism analysis on mechanical properties of clay rocks in Tamusu area. Geotech. Investig. Surv. 2014, 12, 9–13. [Google Scholar]
- Altmann, S.; Tournassat, C.; Goutelard, F.; Parneix, J.C.; Gimmi, T.; Maes, N. Diffusion-driven transport in clayrock formations. Appl. Geochem. 2012, 27, 463–478. [Google Scholar] [CrossRef]
- Appelo, C.A.J.; Van Loon, L.R.; Wersin, P. Multicomponent diffusion of a suite of tracers (Hto, Cl, Br, I, na, sr, Cs) in a sample of opalinus Clay. Geochim. Cosmochim. Acta 2010, 74, 1201–1219. [Google Scholar] [CrossRef]
- Yuan, G.X.; Zhang, L.Q.; Zeng, Q.L. Prediction of rock mass quality in target depth for Tamusu area of Alxa pre-selected region for geological disposal of high-level nuclear waste. J. Eng. Geol. 2018, 26, 1690–1700. [Google Scholar]
- Jörg, G.; Bühnemann, R.; Hollas, S.; Kivel, N.; Kossert, K.; Winckel, S.V.; Gostomski, C.L.V. Preparation of radiochemically pure Se-79 and highly precise de-termination of its half-life. Appl. Radiat. Isot. 2010, 68, 2339–2351. [Google Scholar] [CrossRef]
- Tsai, T.L.; Lee, C.P.; Lin, T.Y.; Wei, H.J.; Men, L.C. Evaluation of sorption and diffusion behavior of selenium in crushed granite by through-diffusion column tests. J. Radioanal. Nucl. Chem. 2010, 285, 733–739. [Google Scholar] [CrossRef]
- Wang, B.T.; Lee, C.P.; Wu, M.C.; Tsai, T.L.; Tsai, S.C.; Hsu, K.C. Novel Method for Analyzing Transport Parameters in Through-Diffusion Tests. J. Environ. Radioact. 2019, 196, 125–132. [Google Scholar] [CrossRef] [PubMed]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- García-Gutiérrez, M.; Cormenzana, J.L.; Missana, T.; Mingarro, M.; Molinero, J. Overview of laboratory methods employed for obtaining diffusion coefficients in FEBEX compacted bentonite. J. Iber. Geol. 2006, 32, 37–53. [Google Scholar]
- Lee, C.P.; Lan, P.L.; Jan, Y.L.; Wei, Y.Y.; Teng, S.P.; Hsu, C.N. Sorption and diffusion of HTO and cesium in crushed granite compacted to different lengths. J. Radioanal. Nucl. Chem. 2008, 275, 371–378. [Google Scholar] [CrossRef]
- Lee, C.P.; Wu, M.C.; Tsai, T.L.; Wei, H.J.; Men, L.C.; Lin, T.Y. Comparative study on retardation behavior of Cs in crushed and intact rocks: Two potential repository host rocks in the Taiwan area. J. Radioanal. Nucl. Chem. 2012, 293, 579–586. [Google Scholar] [CrossRef]
- Lee, C.P.; Wei, Y.Y.; Tsai, S.C.; Teng, S.P.; Hsu, C.N. Diffusion of cesium and selenium in mudrock. J. Radioanal. Nucl. Chem. 2009, 275, 761–768. [Google Scholar] [CrossRef]
- Wu, H.; Huang, W.; Duan, Z.Q.; Luo, M.B.; Wang, Z.F.; Hua, R. Investigation of Se(IV) diffusion in compacted Tamusu clay by capillary. J. Radioanal. Nucl. Chem. 2020. [Google Scholar] [CrossRef]
- He, H.Y.; Liu, J.; Dong, Y.; Li, H.H.; Zhao, S.W.; Wang, J.; Jia, M.L.; Zhang, H.; Liao, J.L.; Yang, Y.Y.; et al. Sorption of selenite on Tamusu clay in simulated groundwater with high. J. Environ. Radioact. 2019, 203, 210–219. [Google Scholar] [CrossRef] [PubMed]
- ASTM C1733-10, Standard Test Method for Distribution Coefficients of Inorganic Species by the Batch Method; ASTM International: West Conshohocken, PA, USA, 2010.
- Lee, C.P.; Kuo, Y.M.; Tsai, S.C.; Wei, Y.Y.; Teng, S.P.; Hsu, C.N. Numerical analysis for characterizing the sorption/desorption of cesium in crushed granite. J. Radioanal. Nucl. Chem. 2008, 275, 343–349. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, H.; Lee, C.P.; Luo, M.; Hua, R.; Liu, W.; Kong, J.; Hu, Y. Diffusion behavior of Se(IV) in Tamusu clayrock core by through-diffusion method. J. Radioanal. Nucl. Chem. 2021, 329, 149–158. [Google Scholar] [CrossRef]
- Kang, M.L.; Chen, F.R.; Wu, S.J.; Yang, Y.G.; Bruggeman, C.; Charlet, L. Effect of pH on Aqueous Se(IV) Reduction by Pyrite. Environ. Sci. Technol. 2011, 45, 2704–2710. [Google Scholar] [CrossRef]
- Ervanne, H.; Hakanen, M.; Lehto, J. Selenium sorption on clays in synthetic groundwaters representing crystalline bedrock conditions. J. Radioanal. Nucl. Chem. 2016, 307, 1365–1373. [Google Scholar] [CrossRef]
- Bruggeman, C.; Vancluysen, J.; Maes, A. New selenium solution speciation method by ion chromatography +gamma counting and its application to FeS2-controlled reducing conditions. Radiochim. Acta 2002, 90, 629–635. [Google Scholar] [CrossRef]
- Kong, J.; Lee, C.P.; Sun, Y.; Hua, R.; Liu, W.; Wang, Z.; Li, Y.; Wang, Y. Anion exclusion and sorption effect for compacted bentonite: The dependency of diffusion coefficients and capacity of HTO and Se(IV). J. Radioanal. Nucl. Chem. 2021, 328, 717–725. [Google Scholar] [CrossRef]


| Item. Type RN | 1 | 2 | |||||
|---|---|---|---|---|---|---|---|
| Compacted Powder | Intact Rocks | ||||||
| HTO | Se(IV) | ||||||
| Column | No. 1 | No. 2 | No. 3 | No. 4 | No. 5 | No.6 | |
| Bulk density | 1.6 | 1.8 | 2.0 | 2.2 | 2.4 | - | |
| Initial HTO activity A0 (dpm/mL)/Se Conc. Co (ppm) | HTO: 40 dpm/mL (V0 = 5000 mL) | Se(IV): 3000 ppm | |||||
| Parameters | Sorption | |
|---|---|---|
| 1-Site | 2-Site | |
| Ce | 7.85 × 10−1 | 7.76 × 10−1 |
| λ1 | 4.88 × 100 | 1.02 × 101 |
| λ2 | - | 1.86 × 10−1 |
| f | - | 7.67 × 10−1 |
| LSE | 3.48 × 10−3 | 3.29 × 10−4 |
| Parameter | K | M (mol/g) | R-Squared |
|---|---|---|---|
| Se(IV) | 3.67 × 102 | 1.75 × 10−4 | 0.9261 |
| Item | HTO | Se | ||||
|---|---|---|---|---|---|---|
| No. 1 (1.6) | No. 2 (1.8) | No. 3 (2.0) | No. 4 (2.2) | No. 5 (2.4) | No. 6 (-) | |
| α | 0.4074 | 0.3330 | 0.2593 | 0.1852 | 0.1111 | 2.9546 |
| Da × 10−10 (m2/s) | 1.92 | 1.77 | 2.49 | 2.84 | 3.53 | 0.011 |
| De × 10−11 (m2/s) | 7.81 | 5.89 | 6.47 | 5.25 | 3.92 | 0.324 |
| Kd (mL/g) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.10 |
| td | 16.67 | 15.29 | 21.55 | 24.51 | 40.50 | 1.34 |
| R-squared | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.97 |
| Da (m2/s) | T (Days) in Temporal Variation | T (Days) in Spatial Variation (x = 0.299 cm) |
|---|---|---|
| 1.00 × 10−10 | 0.25 | 0.46 |
| 1.00 × 10−11 | 2.25 | 4.70 |
| 1.00 × 10−12 | 18.0 | 46.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-P.; Hu, Y.; Tien, N.-C.; Tsai, S.-C.; Shi, Y.; Liu, W.; Kong, J.; Sun, Y. Molecule Diffusion Behavior of Tritium and Selenium in Mongolia Clay Rock by Numerical Analysis of the Spatial and Temporal Variation. Minerals 2021, 11, 875. https://doi.org/10.3390/min11080875
Lee C-P, Hu Y, Tien N-C, Tsai S-C, Shi Y, Liu W, Kong J, Sun Y. Molecule Diffusion Behavior of Tritium and Selenium in Mongolia Clay Rock by Numerical Analysis of the Spatial and Temporal Variation. Minerals. 2021; 11(8):875. https://doi.org/10.3390/min11080875
Chicago/Turabian StyleLee, Chuan-Pin, Yanqin Hu, Neng-Chuan Tien, Shih-Chin Tsai, Yunfeng Shi, Weigang Liu, Jie Kong, and Yuzhen Sun. 2021. "Molecule Diffusion Behavior of Tritium and Selenium in Mongolia Clay Rock by Numerical Analysis of the Spatial and Temporal Variation" Minerals 11, no. 8: 875. https://doi.org/10.3390/min11080875
APA StyleLee, C.-P., Hu, Y., Tien, N.-C., Tsai, S.-C., Shi, Y., Liu, W., Kong, J., & Sun, Y. (2021). Molecule Diffusion Behavior of Tritium and Selenium in Mongolia Clay Rock by Numerical Analysis of the Spatial and Temporal Variation. Minerals, 11(8), 875. https://doi.org/10.3390/min11080875






