Applied Machine Learning for Geometallurgical Throughput Prediction—A Case Study Using Production Data at the Tropicana Gold Mining Complex
Abstract
:1. Introduction
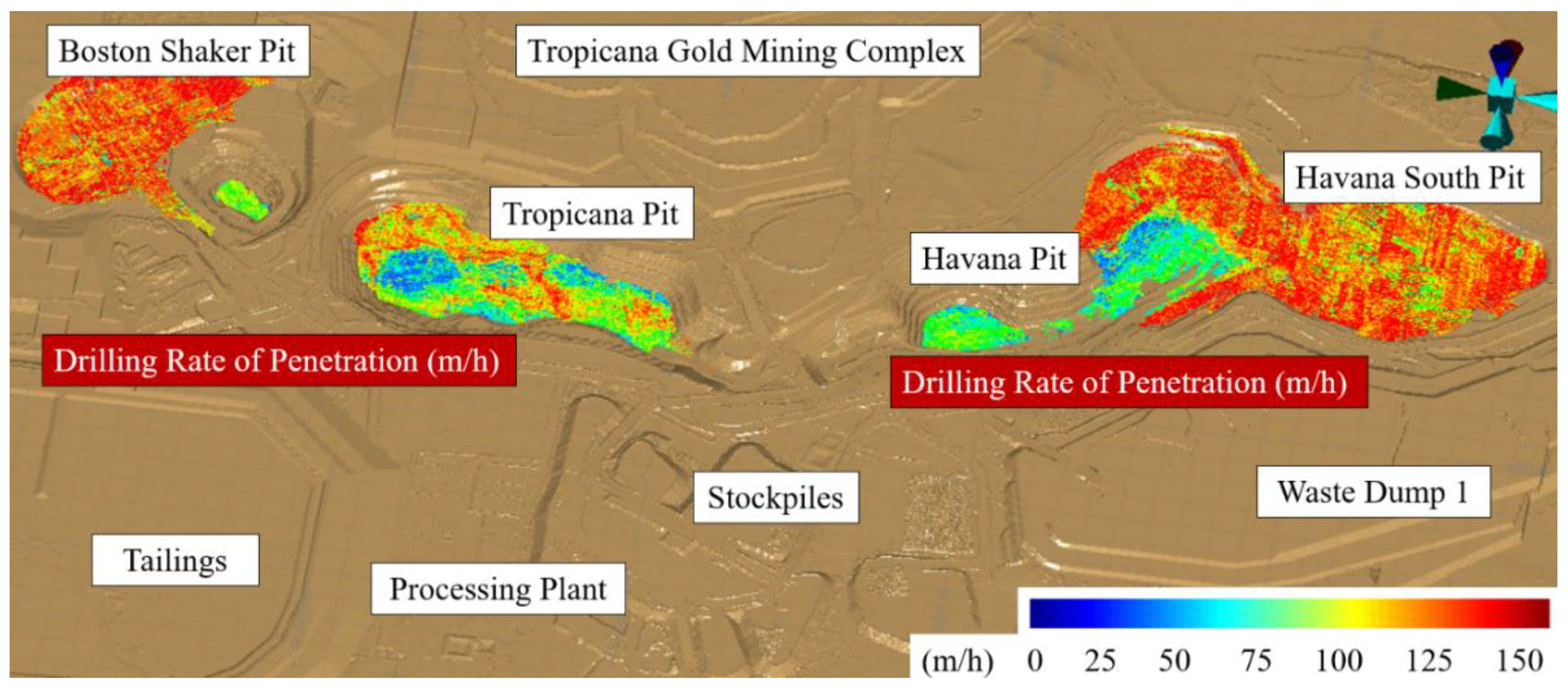
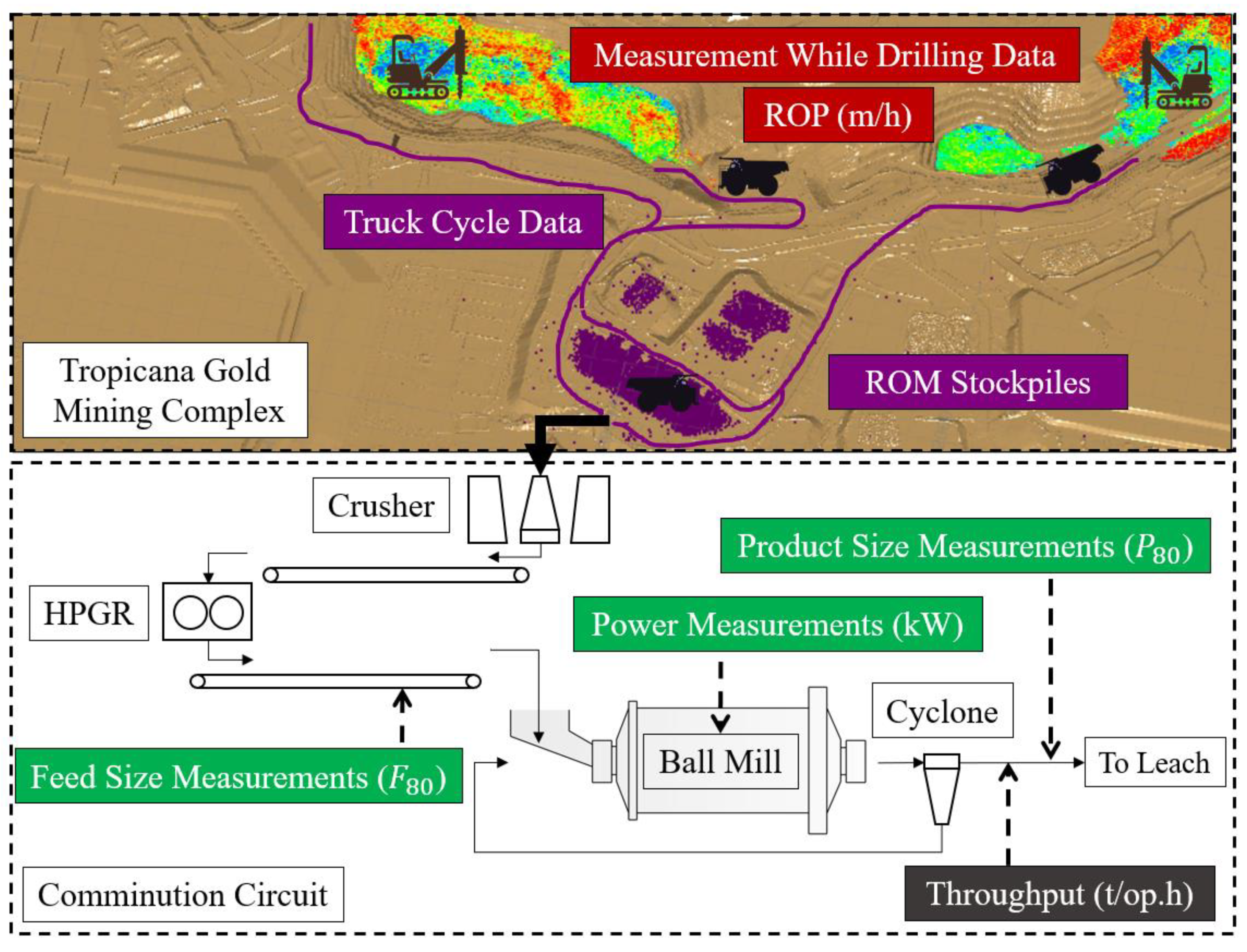
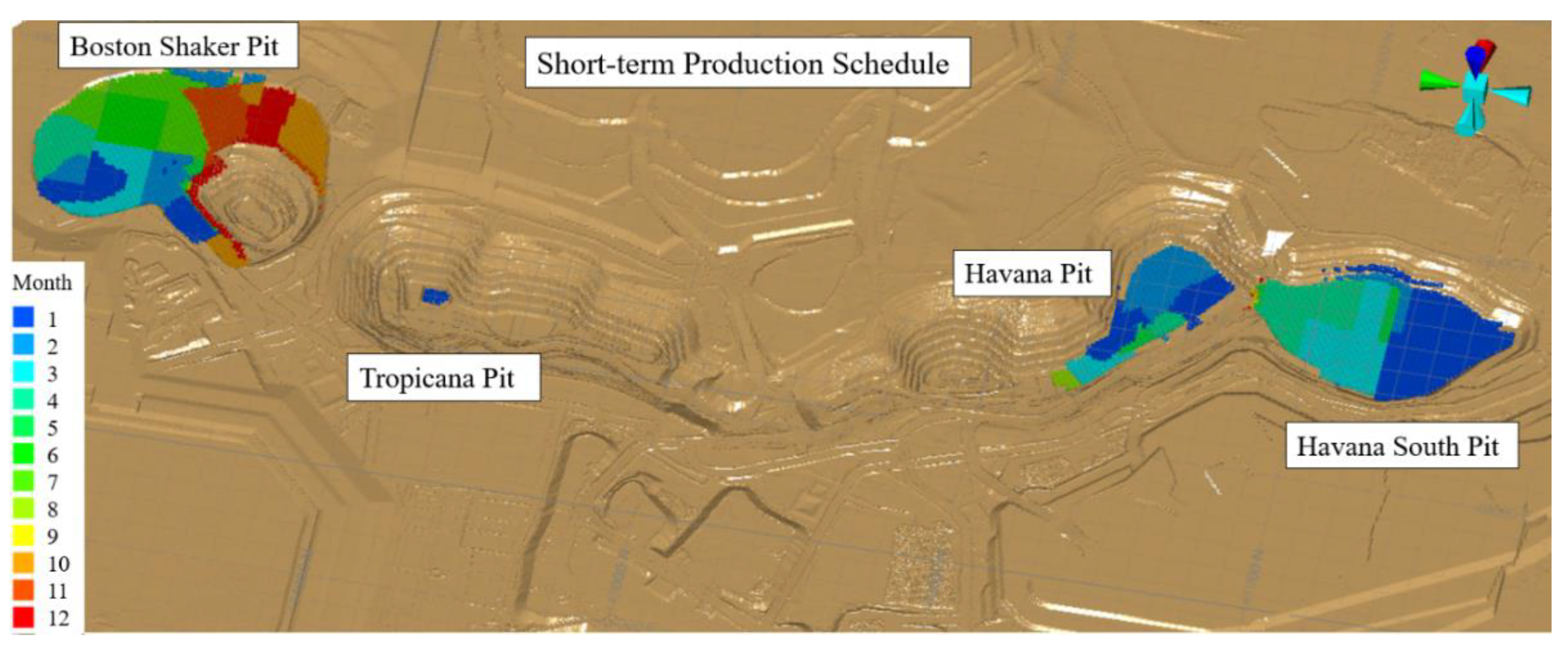
2. The Tropicana Gold Mining Complex and Utilized Production Data for Ball Mill Throughput Prediction
3. Application of Supervised Machine Learning for Throughput Prediction
3.1. Neural Networks
3.2. Dataset and Statistical Analysis
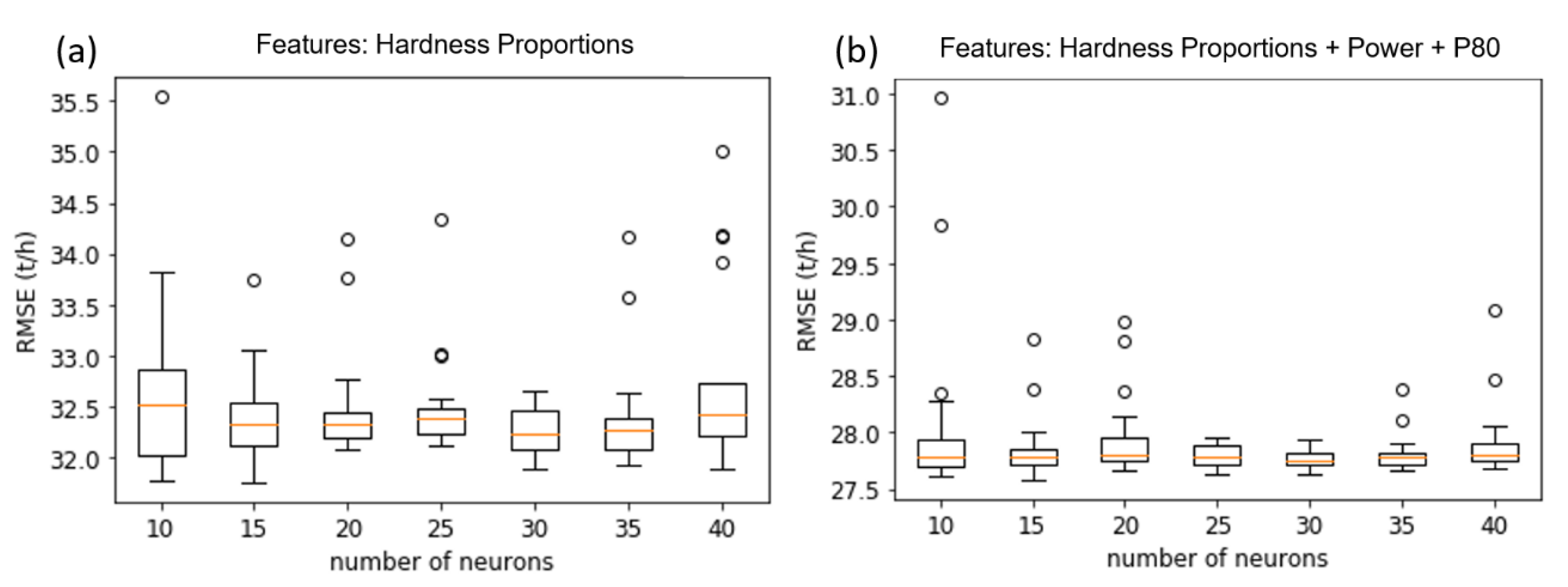
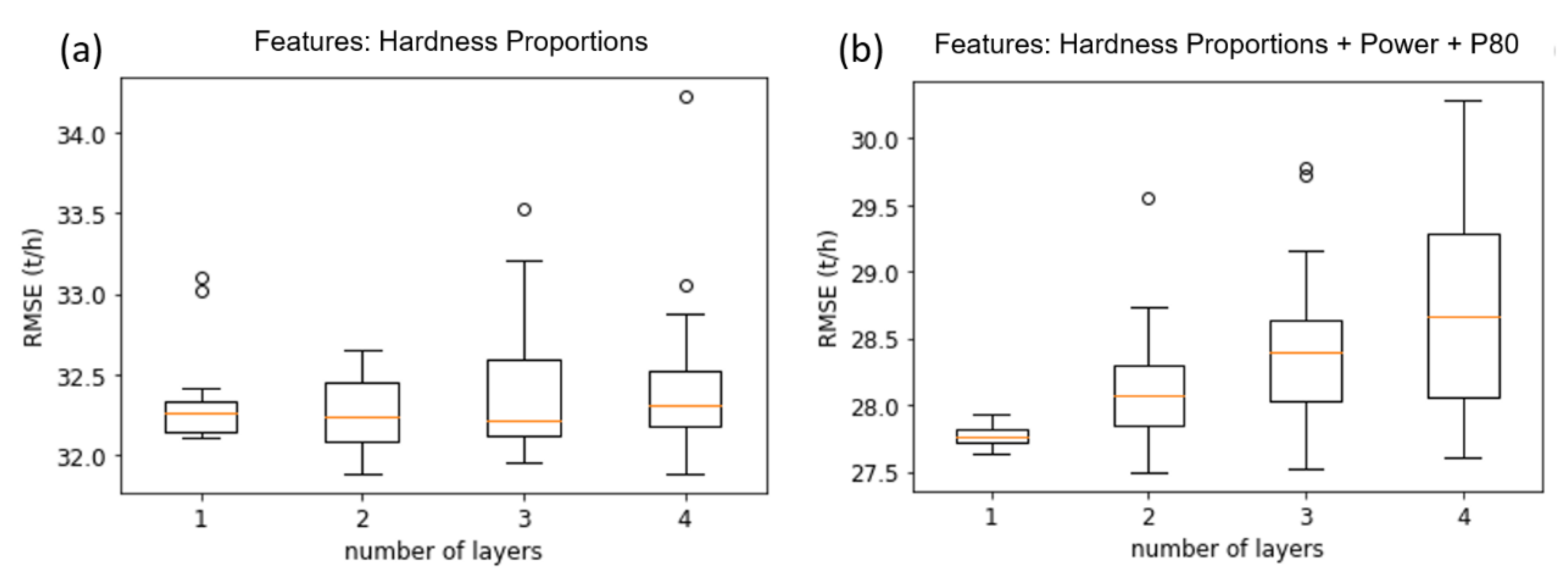
3.3. Network Architecture and Hyperparameter Search
Number of Layers and Neurons
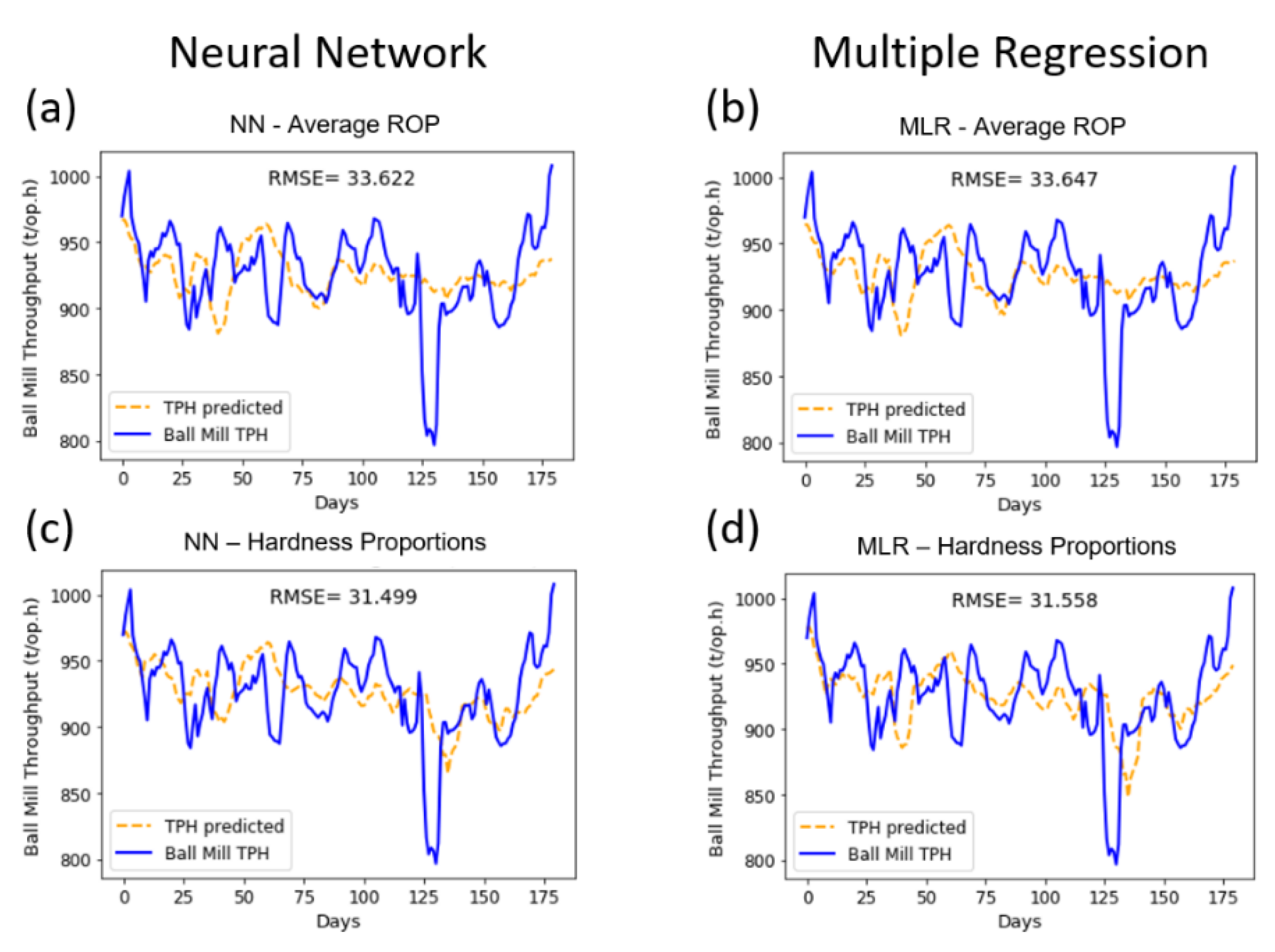
4. Results and Analysis
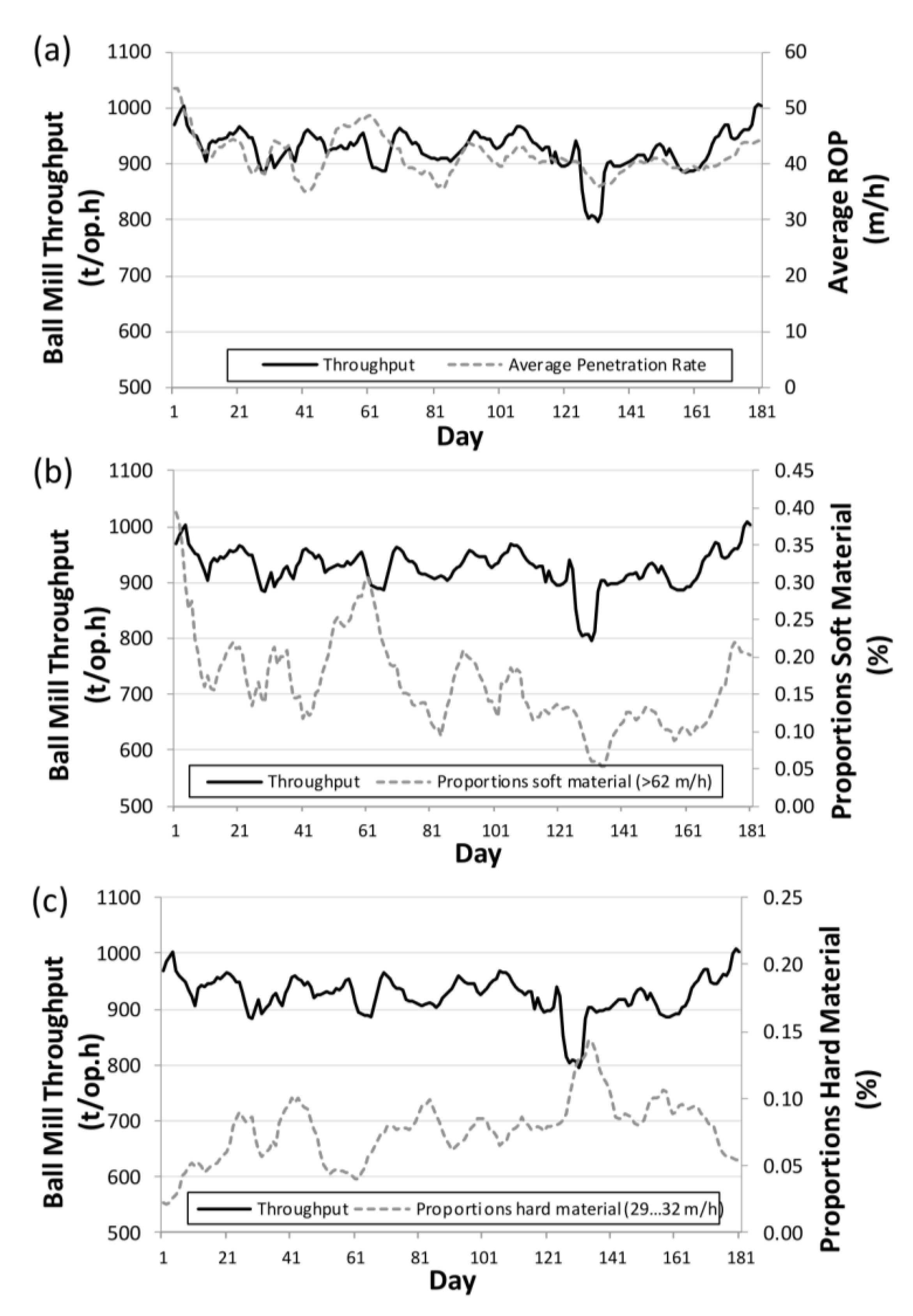
4.1. Hardness-Related Variables (Effect of Non-Additivity)
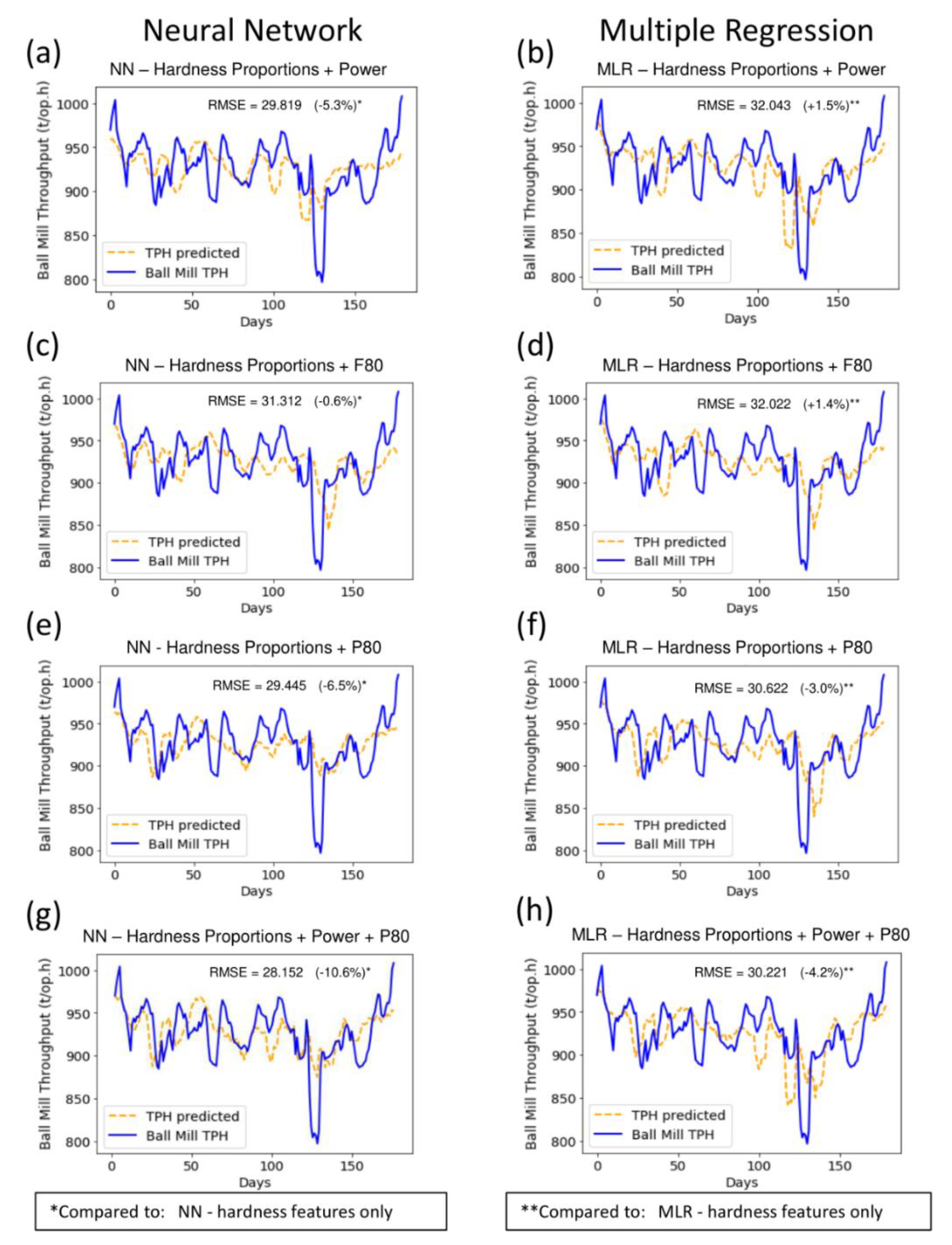
4.2. Effect of Comminution Variables on Prediction
4.2.1. Ball Mill Power
4.2.2. Particle Sizes
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moradi Afrapoli, A.; Askari-Nasab, H. Mining Fleet Management Systems: A Review of Models and Algorithms. Int. J. Min. Reclam. Environ. 2017, 33, 42–60. [Google Scholar] [CrossRef]
- Rai, P.; Schunnesson, H.; Lindqvist, P.A.; Kumar, U. An Overview on Measurement-While-Drilling Technique and Its Scope in Excavation Industry. J. Inst. Eng. Ser. D 2015, 96, 57–66. [Google Scholar] [CrossRef]
- Lessard, J.; De Bakker, J.; McHugh, L. Development of Ore Sorting and Its Impact on Mineral Processing Economics. Miner. Eng. 2014, 65, 88–97. [Google Scholar] [CrossRef]
- Williams, S.R. A Historical Perspective of the Application and Success of Geometallurgical Methodologies. In Proceedings of the Second AusIMM International Geometallurgy Conference, Brisbane, Australia, 30 September—2 October 2013; AusIMM: Carlton, Australia, 2013; pp. 37–47. [Google Scholar]
- Dobby, G.; Bennett, C.; Kosick, G. Advances in SAG Circuit Design and Simulation Applied: The Mine Block Model. In Proceedings of the International Autogenous and Semi-Autogenous Grinding Technology—SAG 2001, Vancouver, BC, Canada, 30 September—3 October 2001; Volume 4, pp. 221–234. [Google Scholar]
- Bueno, M.; Foggiatto, B.; Lane, G. Geometallurgy Applied in Comminution to Minimize Design Risks. In Proceedings of the 6th International Conference Autogenous and Semi-Autogenous Grinding and High Pressure Grinding Roll Technology, Vancouver, BC, Canada, September 2015; University of British Columbia (UBC): Vancouver, BC, Canada, 2015; Volume 40, pp. 1–19. [Google Scholar]
- McKay, N.; Vann, J.; Ware, W.; Morley, W.; Hodkiewicz, P. Strategic and Tactical Geometallurgy—A Systematic Process to Add and Sustain Resource Value. In Proceedings of the Third AUSIMM International Geometallurgy Conference, Perth, Australia, 15–16 June 2016; AusIMM: Carlton, Australia; pp. 29–36. [Google Scholar]
- Mwanga, A.; Rosenkranz, J.; Lamberg, P. Testing of Ore Comminution Behavior in the Geometallurgical Context—A Review. Minerals 2015, 5, 276–297. [Google Scholar] [CrossRef] [Green Version]
- Bond, F.C. The Third Theory of Comminution. Trans. AIME Min. Eng. 1952, 193, 484–494. [Google Scholar]
- Bond, F.C. Crushing & Grinding Calculations Part 1. Br. Chem. Eng. 1961, 6, 378–385. [Google Scholar]
- Starkey, J.; Dobby, G. Application of the MinnovEX SAG Power Index at Five Canadian SAG Plants. Autogenous Semi Autogenous Grind. 1996, 345–360. [Google Scholar]
- Morrell, S. Predicting the Specific Energy of Autogenous and Semi-Autogenous Mills from Small Diameter Drill Core Samples. Miner. Eng. 2004, 17, 447–451. [Google Scholar] [CrossRef]
- Amelunxen, P.; Berrios, P.; Rodriguez, E. The SAG Grindability Index Test. Miner. Eng. 2014, 55, 42–51. [Google Scholar] [CrossRef]
- Dominy, S.C.; O’Connor, L.; Parbhakar-Fox, A.; Glass, H.J.; Purevgerel, S. Geometallurgy—A Route to More Resilient Mine Operations. Minerals 2018, 8, 560. [Google Scholar] [CrossRef] [Green Version]
- Flores, L. Hardness Model and Reconciliation of Throughput Models to Plant Results at Minera Escondida Ltda., Chile. SGS Miner. Serv. Tech. Bull. 2005, 5, 1–14. [Google Scholar]
- Bulled, D.; Leriche, T.; Blake, M.; Thompson, J.; Wilkie, T. Improved Production Forecasting through Geometallurgical Modeling at Iron Ore Company of Canada. In Proceedings of the 41st Annual Meeting of Canadian Mineral Processors, Ottawa, ON, Canada, 20–22 January 2009; pp. 279–295. [Google Scholar]
- Keeney, L.; Walters, S.G.; Kojovic, T. Geometallurgical Mapping and Modelling of Comminution Performance at the Cadia East Porphyry Deposit. In Proceedings of the First AusIMM International Geometallurgy Conference, Brisbane, Australia, 5–7 September 2011; AusIMM: Carlton, Australia, 2011; pp. 5–7. [Google Scholar]
- Alruiz, O.M.; Morrell, S.; Suazo, C.J.; Naranjo, A. A Novel Approach to the Geometallurgical Modelling of the Collahuasi Grinding Circuit. Miner. Eng. 2009, 22, 1060–1067. [Google Scholar] [CrossRef]
- Keeney, L.; Walters, S.G. A Methodology for Geometallurgical Mapping and Orebody Modelling. In Proceedings of the First AusIMM International Geometallurgy Conference, Brisbane, Australia, 5–7 September 2011; AusIMM: Carlton, Australia, 2011; pp. 217–225. [Google Scholar]
- Morales, N.; Seguel, S.; Cáceres, A.; Jélvez, E.; Alarcón, M. Incorporation of Geometallurgical Attributes and Geological Uncertainty into Long-Term Open-Pit Mine Planning. Minerals 2019, 9, 108. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Dimitrakopoulos, R. Application of Simultaneous Stochastic Optimization with Geometallurgical Decisions at a Copper–Gold Mining Complex. Min. Technol. Trans. Inst. Min. Metall. 2019, 128, 88–105. [Google Scholar] [CrossRef] [Green Version]
- Yan, D.; Eaton, R. Breakage Properties of Ore Blends. Miner. Eng. 1994, 7, 185–199. [Google Scholar] [CrossRef]
- Amelunxen, P. The Application of the SAG Power Index to Ore Body Hardness Characterization for the Design and Optimization of Autogenous Grinding Circuits. Master’s Thesis, McGill University, Montreal, QC, Canada, 2003. [Google Scholar]
- Garrido, M.; Ortiz, J.M.; Villaseca, F.; Kracht, W.; Townley, B.; Miranda, R. Change of Support Using Non-Additive Variables with Gibbs Sampler: Application to Metallurgical Recovery of Sulphide Ores. Comput. Geosci. 2019, 122, 68–76. [Google Scholar] [CrossRef]
- Deutsch, J.L.; Palmer, K.; Deutsch, C.V.; Szymanski, J.; Etsell, T.H. Spatial Modeling of Geometallurgical Properties: Techniques and a Case Study. Nat. Resour. Res. 2016, 25, 161–181. [Google Scholar] [CrossRef]
- Deutsch, C.V. Geostatistical Modelling of Geometallurgical Variables—Problems and Solutions. In Proceedings of the Second AusIMM International Geometallurgy Conference, Brisbane, Australia, 30 September–2 October 2013; AusIMM: Carlton, Australia, 2013; pp. 7–15. [Google Scholar]
- van den Boogaart, K.G.; Konsulke, S.; Tolosana-Delgado, R. Non-Linear Geostatistics for Geometallurgical Optimisation. In Proceedings of the Second AusIMM International Geometallurgy Conference, Brisbane, Australia, 30 September–2 October 2013; AusIMM: Carlton, Australia, 2013; pp. 253–257. [Google Scholar]
- Ortiz, J.M.; Kracht, W.; Pamparana, G.; Haas, J. Optimization of a SAG Mill Energy System: Integrating Rock Hardness, Solar Irradiation, Climate Change, and Demand-Side Management. Math. Geosci. 2020, 52, 355–379. [Google Scholar] [CrossRef]
- Kumar, A.; Dimitrakopoulos, R. Production Scheduling in Industrial Mining Complexes with Incoming New Information Using Tree Search and Deep Reinforcement Learning. Appl. Soft Comput. 2021, 110, 107644. [Google Scholar] [CrossRef]
- Both, C.; Dimitrakopoulos, R. Integrating Geometallurgical Ball Mill Throughput Predictions into Short-Term Stochastic Production Scheduling in Mining Complexes. Int. J. Min. Sci. Technol. 2021, 1–37, accepted. [Google Scholar]
- Goodfellow, R.C.; Dimitrakopoulos, R. Global Optimization of Open Pit Mining Complexes with Uncertainty. Appl. Soft. Comput. J. 2016, 40, 292–304. [Google Scholar] [CrossRef]
- Montiel, L.; Dimitrakopoulos, R. Optimizing Mining Complexes with Multiple Processing and Transportation Alternatives: An Uncertainty-Based Approach. Eur. J. Oper. Res. 2015, 247, 166–178. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Kim, K. Use of Drilling Performance to Improve Rock-Breakage Efficiencies: A Part of Mine-to-Mill Optimization Studies in a Hard-Rock Mine. Int. J. Min. Sci. Technol. 2020, 30, 179–188. [Google Scholar] [CrossRef]
- Vezhapparambu, V.; Eidsvik, J.; Ellefmo, S. Rock Classification Using Multivariate Analysis of Measurement While Drilling Data: Towards a Better Sampling Strategy. Minerals 2018, 8, 384. [Google Scholar] [CrossRef] [Green Version]
- Wambeke, T.; Elder, D.; Miller, A.; Benndorf, J.; Peattie, R. Real-Time Reconciliation of a Geometallurgical Model Based on Ball Mill Performance Measurements—A Pilot Study at the Tropicana Gold Mine. Min. Technol. 2018, 127, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Horner, P.C.; Sherrell, F.W. The Application of Air-Flush Rotary Percussion Drilling Techniques in Site Investigation. Q. J. Eng. Geol. 1977, 10, 207–220. [Google Scholar] [CrossRef]
- Sugawara, J.; Yue, Z.; Tham, L.; Law, K.; Lee, C. Weathered Rock Characterization Using Drilling Parameters. Can. Geotech. J. 2003, 40, 661–668. [Google Scholar] [CrossRef] [Green Version]
- Yue, Z.Q.; Lee, C.F.; Law, K.T.; Tham, L.G. Automatic Monitoring of Rotary-Percussive Drilling for Ground Characterization-Illustrated by a Case Example in Hong Kong. Int. J. Rock Mech. Min. Sci. 2004, 41, 573–612. [Google Scholar] [CrossRef]
- Rosenblatt, F. The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [Green Version]
- Hornik, K.; Stichcombe, M.; White, H. Multilayer Feedforward Networks. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Hornik, K. Approximation Capabilities of Multilayer Feedforward Networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Bengio, Y.; Grandvalet, Y. No Unbiased Estimator of the Variance of K-Fold Cross-Validation. J. Mach. Learn. Res. 2004, 5, 1089–1105. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning. Bayesian Forecast. Dyn. Model. 2009, 1, 1–694. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.V.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Journal of Machine Learning Research: Preface. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the Limited Memory BFGS Method for Large Scale Optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef] [Green Version]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Carrasco, P.; Chilès, J.-P.; Séguret, S. Additivity, Metallurgical Recovery, and Grade. In Proceedings of the 8th International Geostatistics Congress, Santiago, Chile, 1–5 December 2008; p. 10. [Google Scholar]
- Coward, S.; Vann, J.; Dunham, S.; Steward, M. The Primary-Response Framework for Geometallurgical Variables. In Proceedings of the Seventh International Mining Geology Conference Proceedings, Perth, Australia, 17–19 August 2009; AusIMM: Carlton, Australia, 2009; pp. 109–113. [Google Scholar]
- Both, C.; Dimitrakopoulos, R. Joint Stochastic Short-Term Production Scheduling and Fleet Management Optimization for Mining Complexes. Optim. Eng. 2020, 21, 1717–1743. [Google Scholar] [CrossRef] [Green Version]


| Average ROP (m/h) | Ball Mill Power (kW) | Ball Mill Utilization (%) | Ball Mill Throughput (t/op.h) | |||
|---|---|---|---|---|---|---|
| Minimum | 35.0 | 9996 | 0.7 | 76.5 | 10.3 | 796.4 |
| Mean | 41.4 | 13,002 | 1.0 | 83.3 | 13.1 | 926.5 |
| Maximum | 53.6 | 13,435 | 1.0 | 93.2 | 15.0 | 1007.9 |
| Std. Dev. | 3.45 | 685.9 | 0.052 | 3.12 | 1.00 | 34.8 |
| Coeff. of Var. (CV) | 0.083 | 0.053 | 0.053 | 0.037 | 0.077 | 0.038 |
| Skewness | 0.88 | −3.01 | −3.03 | 0.57 | −0.36 | −1.07 |
| Kurtosis | 1.20 | 9.26 | 9.30 | 0.94 | −0.13 | 3.05 |
| Count | 181 | 181 | 181 | 176 | 153 | 181 |
| No. | Category | Feature | Unit | Pearson’s Correlation Coefficient to Ball Mill Throughput |
|---|---|---|---|---|
| A1 | Ore hardness using average pen-rate values | Average ROP | (m/h) | 0.44 |
| B1 | (Harder material) | <26 m/h | (%) | −0.274 |
| B2 | Ore hardness expressed by proportions of penetration rate intervals | 26–29 m/h | (%) | −0.370 |
| B3 | 29–32 m/h | (%) | −0.525 | |
| B4 | 32–35 m/h | (%) | −0.361 | |
| B5 | 35–38 m/h | (%) | −0.416 | |
| B6 | 38–42 m/h | (%) | −0.318 | |
| B7 | 42–46 m/h | (%) | 0.028 | |
| B8 | 46–53 m/h | (%) | 0.356 | |
| B9 | 53–62 m/h | (%) | 0.386 | |
| B10 | (Softer Material) | >62 m/h | (%) | 0.498 |
| C1 | Measurements in the comminution circuit | Feed size F80 | (mm) | 0.046 |
| C2 | Product size P80 | (μm) | 0.063 | |
| C3 | Power | (kW) | 0.382 | |
| C4 | Mill Utilization | (%) | 0.374 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Both, C.; Dimitrakopoulos, R. Applied Machine Learning for Geometallurgical Throughput Prediction—A Case Study Using Production Data at the Tropicana Gold Mining Complex. Minerals 2021, 11, 1257. https://doi.org/10.3390/min11111257
Both C, Dimitrakopoulos R. Applied Machine Learning for Geometallurgical Throughput Prediction—A Case Study Using Production Data at the Tropicana Gold Mining Complex. Minerals. 2021; 11(11):1257. https://doi.org/10.3390/min11111257
Chicago/Turabian StyleBoth, Christian, and Roussos Dimitrakopoulos. 2021. "Applied Machine Learning for Geometallurgical Throughput Prediction—A Case Study Using Production Data at the Tropicana Gold Mining Complex" Minerals 11, no. 11: 1257. https://doi.org/10.3390/min11111257
APA StyleBoth, C., & Dimitrakopoulos, R. (2021). Applied Machine Learning for Geometallurgical Throughput Prediction—A Case Study Using Production Data at the Tropicana Gold Mining Complex. Minerals, 11(11), 1257. https://doi.org/10.3390/min11111257







