Structure and Stability of Iron Fluoride at High Pressure–Temperature and Implication for a New Reservoir of Fluorine in the Deep Earth
Abstract
1. Introduction
2. Methods
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McDonough, W.F.; Sun, S. The composition of the Earth. Chem. Geol. 1995, 120, 223–253. [Google Scholar] [CrossRef]
- Dingwell, D.B.; Mysen, B.O. Effects of water and fluorine on the viscosity of albite melt at high pressure: A preliminary investigation. Earth Planet. Sci. Lett. 1985, 74, 266–274. [Google Scholar] [CrossRef]
- Filiberto, J.; Wood, J.; Dasgupta, R.; Shimizu, N.; Le, L.; Treiman, A.H. Effect of fluorine on near-liquidus phase equilibria of a Fe–Mg rich basalt. Chem. Geol. 2012, 312, 118–126. [Google Scholar] [CrossRef]
- Kovalenko, V.; Naumov, V.; Girnis, A.; Dorofeeva, V.; Yarmolyuk, V. Composition and chemical structure of oceanic mantle plumes. Petrology 2006, 14, 452–476. [Google Scholar] [CrossRef]
- Joachim, B.; Stechern, A.; Ludwig, T.; Konzetti, J.; Pawley, A.; Ruzié, L.; Burgess, R.; Ballentine, C.J. Effect of water on the fluorine and chlorine partitioning behavior between olivine and silicate melts. Contrib. Mineral. Petrol. 2017, 172, 15. [Google Scholar] [CrossRef]
- Koga, K.T.; Rose-Koga, E.F. Fluorine in the Earth and the solar system, where does it come from and can it be found? C. R. Chimie 2018, 21, 749–756. [Google Scholar] [CrossRef]
- Bromiley, D.W.; Kohn, S.C. Comparisons between fluoride and hydroxide incorporation in nominally anhydrous and fluorine-free mantle minerals. Geochim. Cosmochim. Acta 2007, 71, A124. [Google Scholar]
- Bernini, D.; Wiedenbeck, M.; Dolejš, D.; Keppler, H. Partitioning of halogens between mantle minerals and aqueous fluids: Implications for the fluid flow regime in subduction zones. Contrib. Mineral. Petrol. 2012, 165, 117–128. [Google Scholar] [CrossRef]
- Gruützner, T.; Klemme, S.; Rohrbach, A.; Gervasoni, F.; Berndt, J. The role of F-clinohumite in volatile recycling processes in subduction zones. Geology 2017, 45, 443–446. [Google Scholar] [CrossRef]
- Dalou, C.; Koga, K.T.; Shimizu, N.; Boulon, J.; Devidal, J.-L. Experimental determination of F and Cl partitioning between lherzolite and basaltic melt. Contrib. Mineral. Petrol. 2012, 163, 591–609. [Google Scholar] [CrossRef]
- Gruützner, T.; Klemme, S.; Rohrbach, A.; Gervasoni, F.; Berndt, J. The effect of fluorine on the stability of wadsleyite: Implications for the nature and depths of the transition zone in the Earth’s mantle. Earth Planet. Sci. Lett. 2018, 482, 236–244. [Google Scholar]
- Yoshino, T.; Jaseem, V. Fluorine solubility in bridgmanite: A potential fluorine reservoir in the Earth’s mantle. Earth Planet. Sci. Lett. 2018, 504, 106–114. [Google Scholar] [CrossRef]
- Kaminsky, F.V.; Wirth, R.; Schreiber, A. Carbonatitic inclusions in Deep Mantle diamond from Juina, Brazil: New minerals in the carbonate-halide association. Can. Mineral. 2013, 51, 669–688. [Google Scholar] [CrossRef]
- Kaminsky, F.V.; Ryabchikov, I.D.; Wirth, R. A primary natrocarbonatitic association in the Deep Earth. Miner. Petrol. 2016, 110, 387–398. [Google Scholar] [CrossRef]
- Du, X.P.; Wang, Z.; Wang, H.; Iitaka, T.; Pan, Y.; Wang, H.; Tse, J.S. Structures and Stability of Iron Halides at the Earth’s Mantle and Core Pressures: Implications for the Missing Halogen Paradox. ACS Earth Space Chem. 2018, 2, 711–719. [Google Scholar] [CrossRef]
- Andrault, D.; Muñoz, M.; Pesce, G.; Cerantola, V.; Chumakov, A.; Kantor, I.; Pascarelli, S.; Rüffer, R.; Hennet, L. Large oxygen excess in the primitive mantle could be the source of the Great Oxygenation Event. Geochem. Perspect. Lett. 2018, 6, 5–10. [Google Scholar] [CrossRef]
- Frost, D.J.; Mann, U.; Asahara, Y.; Rubie, D.C. The redox state of the mantle during and just after core formation. Philos. Trans. A. Math. Phys. Eng. Sci. 2008, 366, 4315–4337. [Google Scholar] [CrossRef]
- Jørgensen, J.-E.; Staun Olsen, J.; Gerward, L. Compression mechanism of GaF3 and FeF3: A high-pressure X-ray diffraction study. High Press. Res. 2010, 30, 634–642. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 2010, 82, 94116. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, Z.; Wang, Y.; Zou, G.; Mao, H.; Ma, Y. Spiral Chain O4 Form of Dense Oxygen. Proc. Natl. Acad. Sci. USA. 2012, 109, 751–753. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lv, J.; Zhu, L.; Lu, S.; Yin, K.; Li, Q.; Wang, H.; Zhang, L.; Ma, Y. Materials discovery via CALYPSO methodology. J. Phys. Condens. Matter. 2015, 27, 203203. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Borstad, G.M.; Liu, H.; Guńka, P.A.; Guerette, M.; Dolyniuk, J.-A.; Meng, Y.; Greenberg, E.; Prakapenka, V.B.; Chaloux, B.L.; et al. Carbon-boron clathrates as a new class of sp3-bonded framework materials. Sci. Adv. 2020, 6, eaay8361. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Jephcoat, A.P.; Mao, H.-K.; Bell, P.M. Hydrothermal Experiment Techniques, 1st ed.; Wiley-Interscience: Hoboken, NJ, USA, 1987. [Google Scholar]
- Meng, Y.; Hrubiak, R.; Rod, E.; Boehler, R.; Shen, G. New developments in laser-heated diamond anvil cell with in situ synchrotron x-ray diffraction at High Pressure Collaborative Access Team. Rev. Sci. Instrum. 2015, 86, 072201. [Google Scholar] [CrossRef]
- Yuan, H.; Zhang, L. In situ determination of crystal structure and chemistry of minerals at Earth’s deep lower mantle conditions. Matter Radiat. Extremes 2017, 2, 117–128. [Google Scholar] [CrossRef]
- Fei, Y.; Ricolleau, A.; Frank, M.; Mibe, K.; Shen, G.; Prakapenka, V. Toward an internally consistent pressure scale. Proc. Natl. Acad. Sci. USA 2007, 104, 9182–9186. [Google Scholar] [CrossRef]
- Nishi, M.; Irifune, T.; Tsuchiya, J.; Tange, Y.; Nishihara, Y.; Fujino, K.; Higo, Y. Stability of hydrous silicate at high pressures and water transport to the deep lower mantle. Nat. Geosci. 2014, 7, 224–227. [Google Scholar] [CrossRef]
- Pépin, C.M.; Dewaele, A.; Geneste, G.; Loubeyre, P.; Mezouar, M. New Iron Hydrides under High Pressure. Phys. Rev. Lett. 2014, 113, 265504. [Google Scholar] [CrossRef] [PubMed]
- Pépin, C.M.; Geneste, G.; Dewaele, A.; Mezouar, M.; Loubeyre, P. Synthesis of FeH5: A layered structure with atomic hydrogen slabs. Science 2017, 357, 382–385. [Google Scholar] [CrossRef] [PubMed]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Hazen, R.M.; Yang, H.; Prewitt, C.T.; Gasparik, T. Crystal chemistry of superfluorous phase B (Mg10Si3O14F4), implications for the role of fluorine in the mantle. Am. Mineral. 1997, 82, 647–650. [Google Scholar] [CrossRef]
- Zhu, S.-C.; Hu, Q.; Mao, W.L.; Mao, H.-K.; Sheng, H. Hydrogen-bond symmetrization breakdown and dehydrogenation mechanism of FeO2H at high pressure. J. Am. Chem. Sci. 2017, 139, 12129–12132. [Google Scholar] [CrossRef]
- Lin, Y.; Hu, Q.; Meng, Y.; Walter, M.; Mao, H.-K. Evidence for the stability of ultrahydrous stishovite in Earth’s lower mantle. Proc. Nat. Acad. Sci. USA 2020, 117, 184–189. [Google Scholar] [CrossRef]
- Hu, Q.; Kim, D.Y.; Yang, W.; Yang, L.; Meng, Y.; Zhang, L.; Mao, H.-K. FeO2 and FeOOH under deep lower-mantle conditions and Earth’s oxygen-hydrogen cycles. Nature 2016, 534, 241–244. [Google Scholar] [CrossRef]
- Hu, Q.; Liu, J.; Chen, J.; Yan, B.; Meng, Y.; Prakapenka, V.B.; Mao, W.L.; Mao, H.-K. Mineralogy of the deep lower mantle in the presence of H2O. Natl. Sci. Rev. 2020. [Google Scholar] [CrossRef]
- Mao, H.-K.; Mao, W.L. Key problems of the four-dimensional Earth system. Matter Radiat. Extremes 2020, 5, 038102. [Google Scholar] [CrossRef]
- Kaminsky, F.V. Water in the Earth’s lower mantle. Geochem. Int. 2018, 56, 1117–1134. [Google Scholar] [CrossRef]
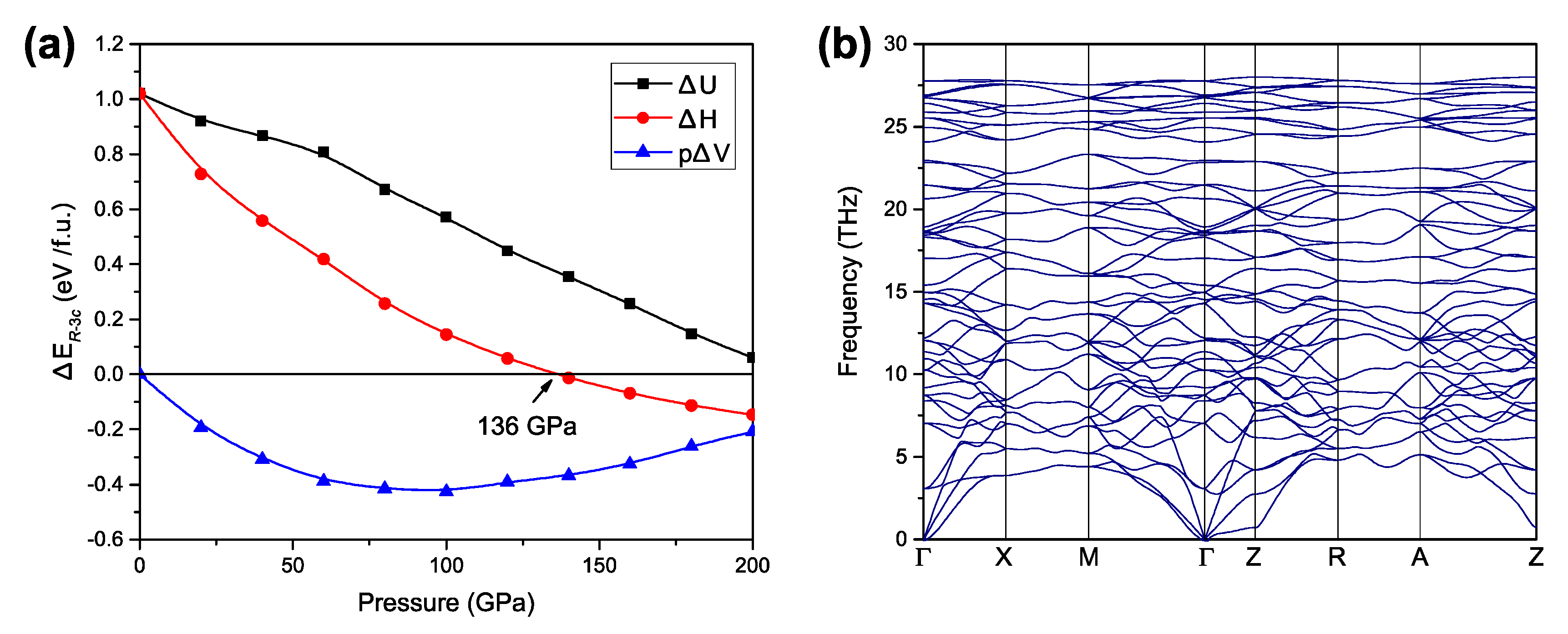
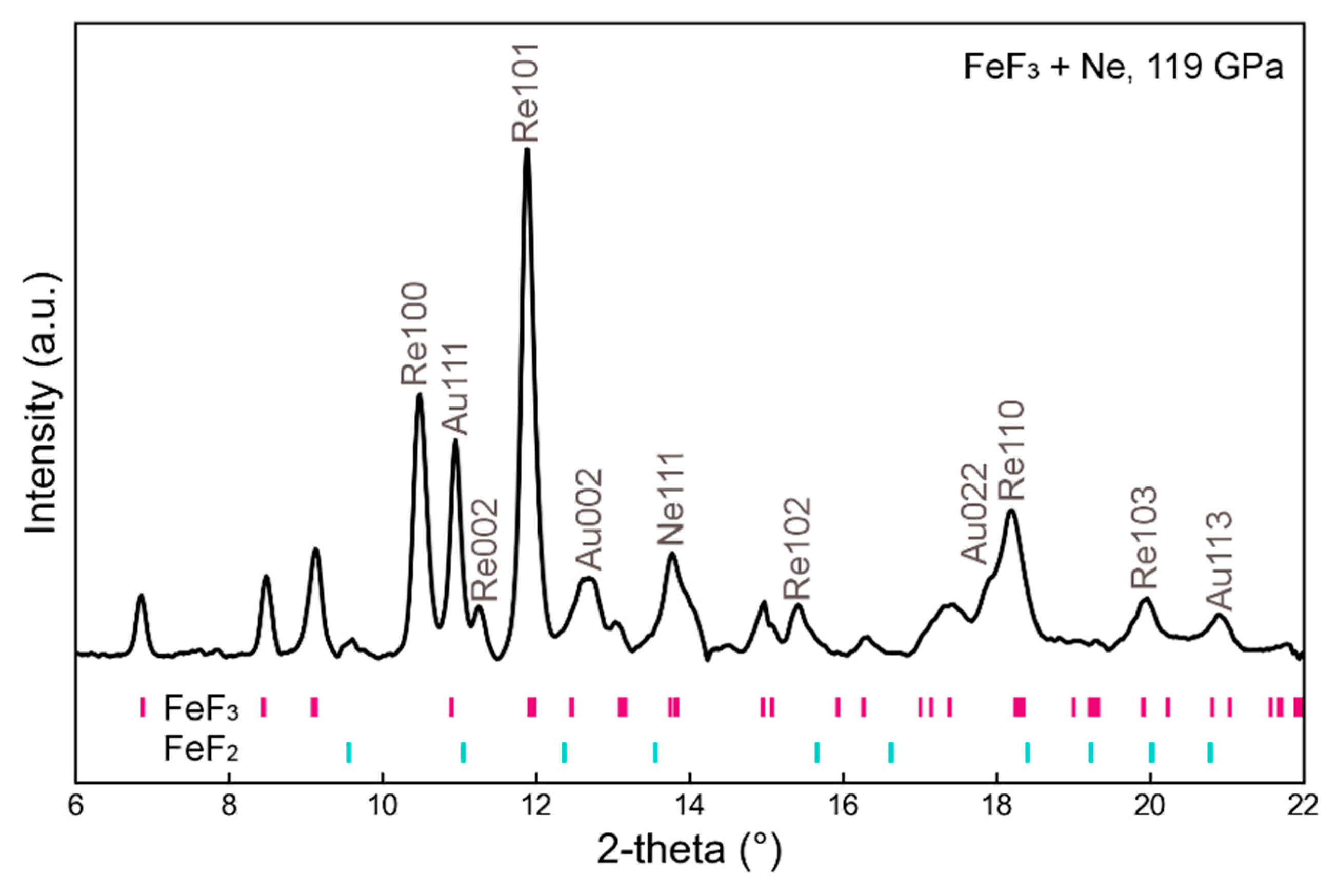
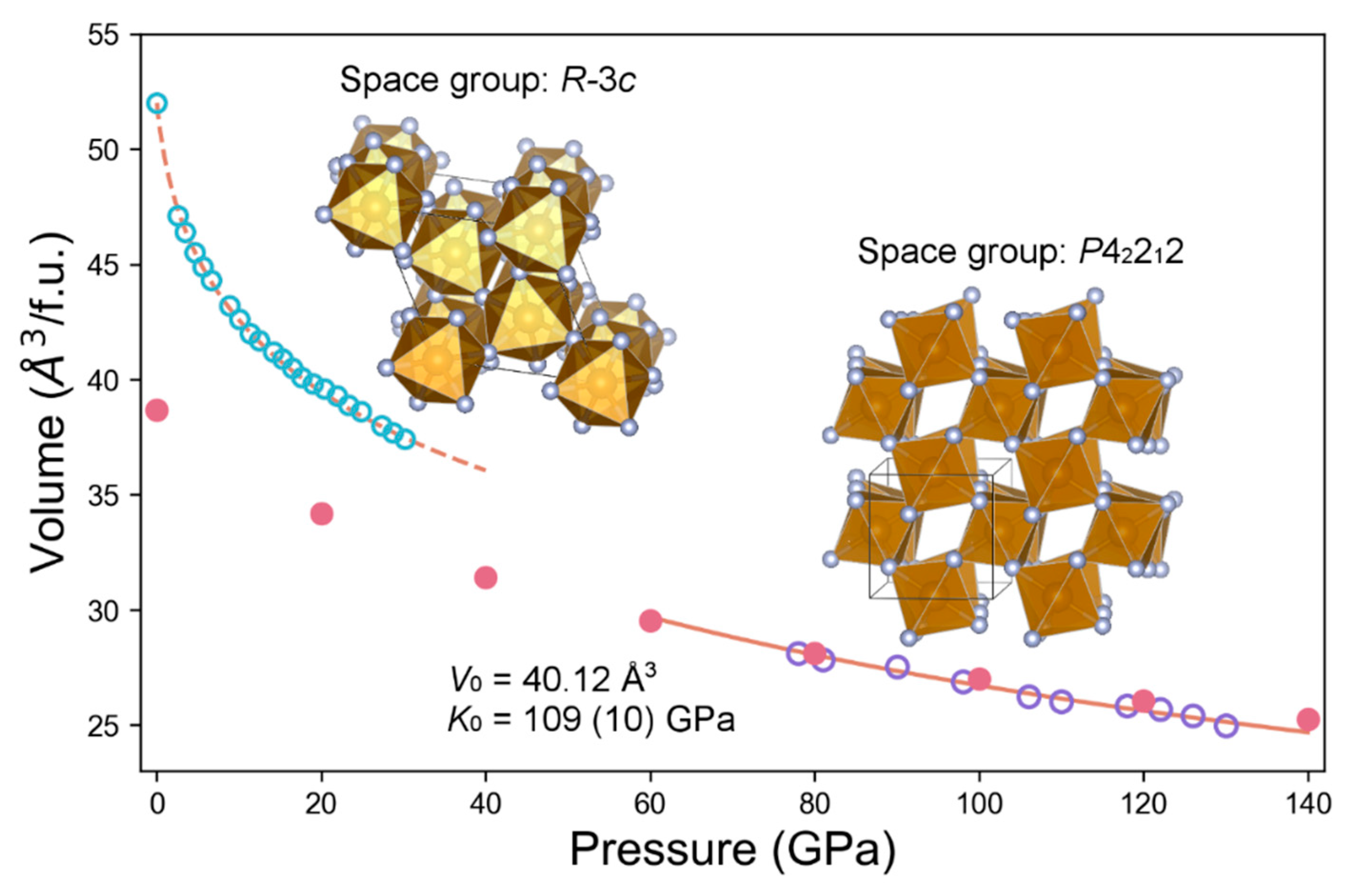
| P (GPa) | a (Å) | c (Å) | V/(Å3/f.u.) | Density (g/cm3) |
|---|---|---|---|---|
| 78 | 4.010(2) | 6.992(2) | 28.11(2) | 6.501(5) |
| 81 | 3.993(2) | 6.980(2) | 27.83(3) | 6.567(7) |
| 90 | 3.983(2) | 6.939(4) | 27.52(2) | 6.639(5) |
| 98 | 3.949(2) | 6.896(3) | 26.88(2) | 6.799(5) |
| 106 | 3.919(1) | 6.836(4) | 26.25(2) | 6.962(5) |
| 110 | 3.910(1) | 6.806(4) | 26.01(2) | 7.026(5) |
| 118 | 3.905(1) | 6.778(3) | 25.84(2) | 7.072(6) |
| 122 | 3.884(1) | 6.765(4) | 25.69(2) | 7.113(6) |
| 126 | 3.878(1) | 6.756(4) | 25.40(2) | 7.193(6) |
| 130 | 3.854(1) | 6.725(4) | 24.98(2) | 7.316(6) |
| P (GPa) | a (Å) | c (Å) | V (Å3/f.u.) | Density (g/cm3) |
|---|---|---|---|---|
| 0 | 4.435 | 7.867 | 38.68 | 4.853 |
| 20 | 4.290 | 7.425 | 34.17 | 5.493 |
| 40 | 4.205 | 7.104 | 31.40 | 5.978 |
| 60 | 4.138 | 6.901 | 29.54 | 6.354 |
| 80 | 4.083 | 6.747 | 28.12 | 6.675 |
| 100 | 4.037 | 6.625 | 26.99 | 6.955 |
| 120 | 3.996 | 6.527 | 26.06 | 7.203 |
| 140 | 3.961 | 6.442 | 25.26 | 7.431 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Hu, Q.; Zhu, L.; Meng, Y. Structure and Stability of Iron Fluoride at High Pressure–Temperature and Implication for a New Reservoir of Fluorine in the Deep Earth. Minerals 2020, 10, 783. https://doi.org/10.3390/min10090783
Lin Y, Hu Q, Zhu L, Meng Y. Structure and Stability of Iron Fluoride at High Pressure–Temperature and Implication for a New Reservoir of Fluorine in the Deep Earth. Minerals. 2020; 10(9):783. https://doi.org/10.3390/min10090783
Chicago/Turabian StyleLin, Yanhao, Qingyang Hu, Li Zhu, and Yue Meng. 2020. "Structure and Stability of Iron Fluoride at High Pressure–Temperature and Implication for a New Reservoir of Fluorine in the Deep Earth" Minerals 10, no. 9: 783. https://doi.org/10.3390/min10090783
APA StyleLin, Y., Hu, Q., Zhu, L., & Meng, Y. (2020). Structure and Stability of Iron Fluoride at High Pressure–Temperature and Implication for a New Reservoir of Fluorine in the Deep Earth. Minerals, 10(9), 783. https://doi.org/10.3390/min10090783






