Assessing the Combined Effect of Water Temperature and Complex Water Matrices on Xanthate Adsorption Using Multiple Linear Regression
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Mineral Sample Preparation
2.1.2. Plant Water
2.2. Adsorption Experimental Procedure
2.3. Experimental Design
3. Results
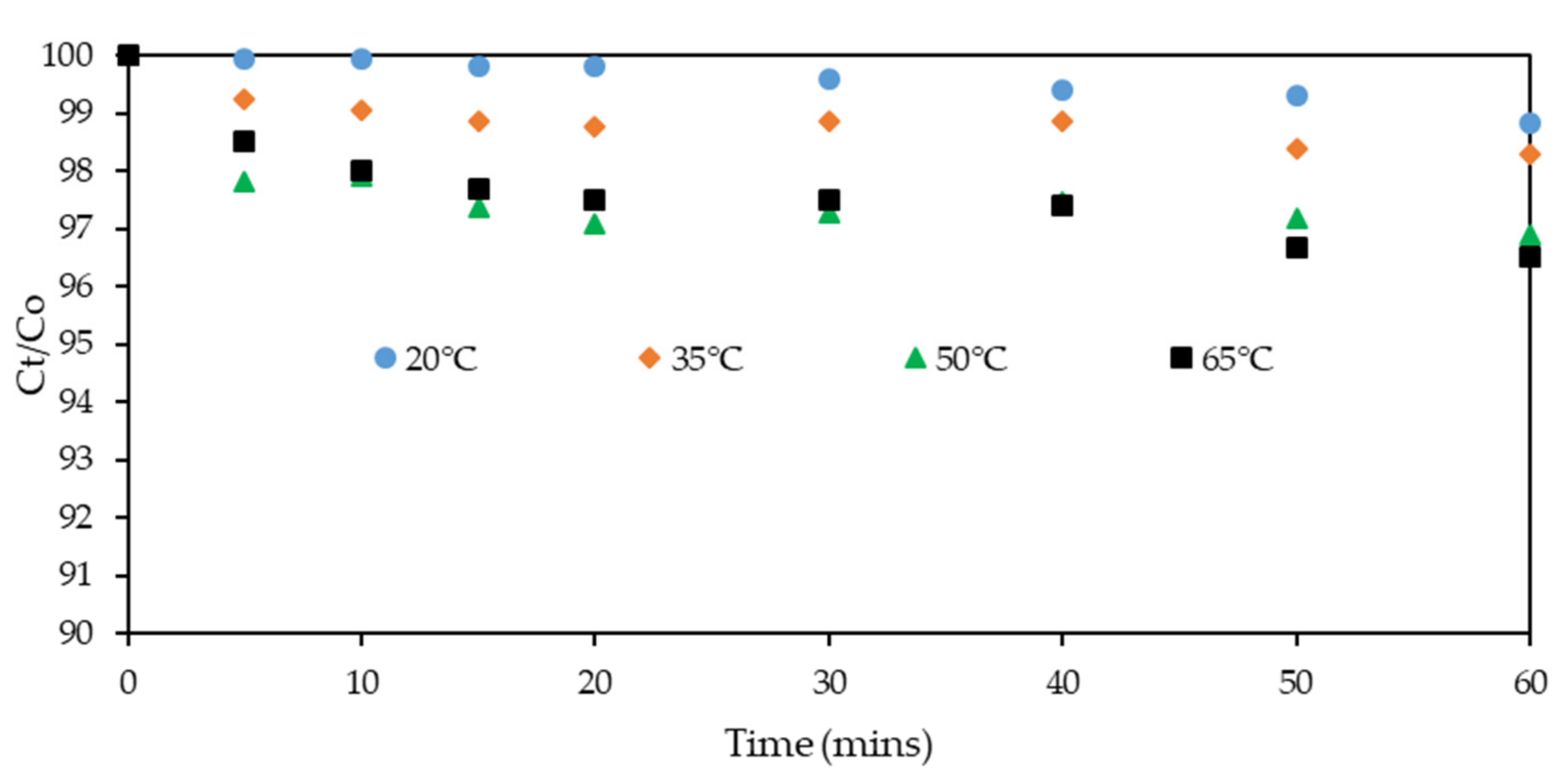
3.1. Effect of Temperature on Xanthate Solution Degradation
3.2. Xanthate Adsorption on Chalcopyrite
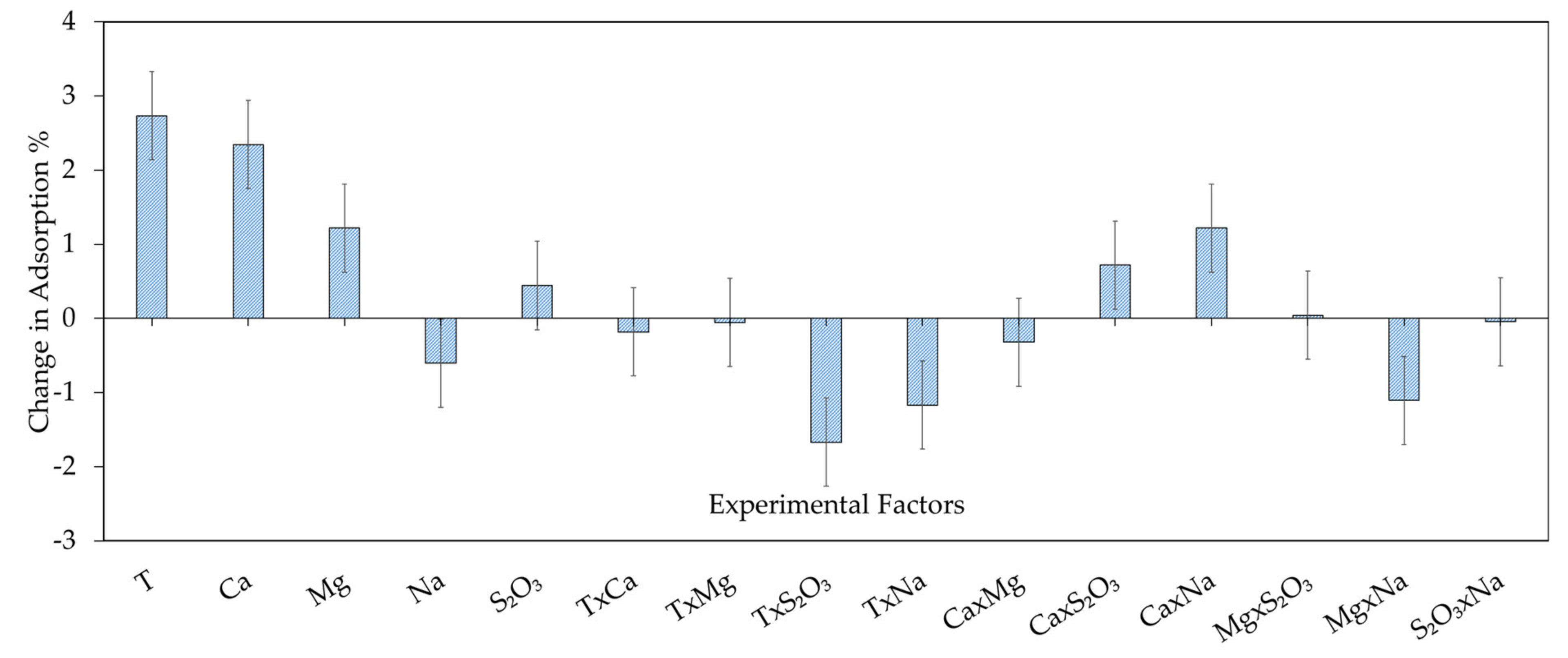
3.2.1. Xanthate Adsorption on Chalcopyrite—Model Development and Model Analysis
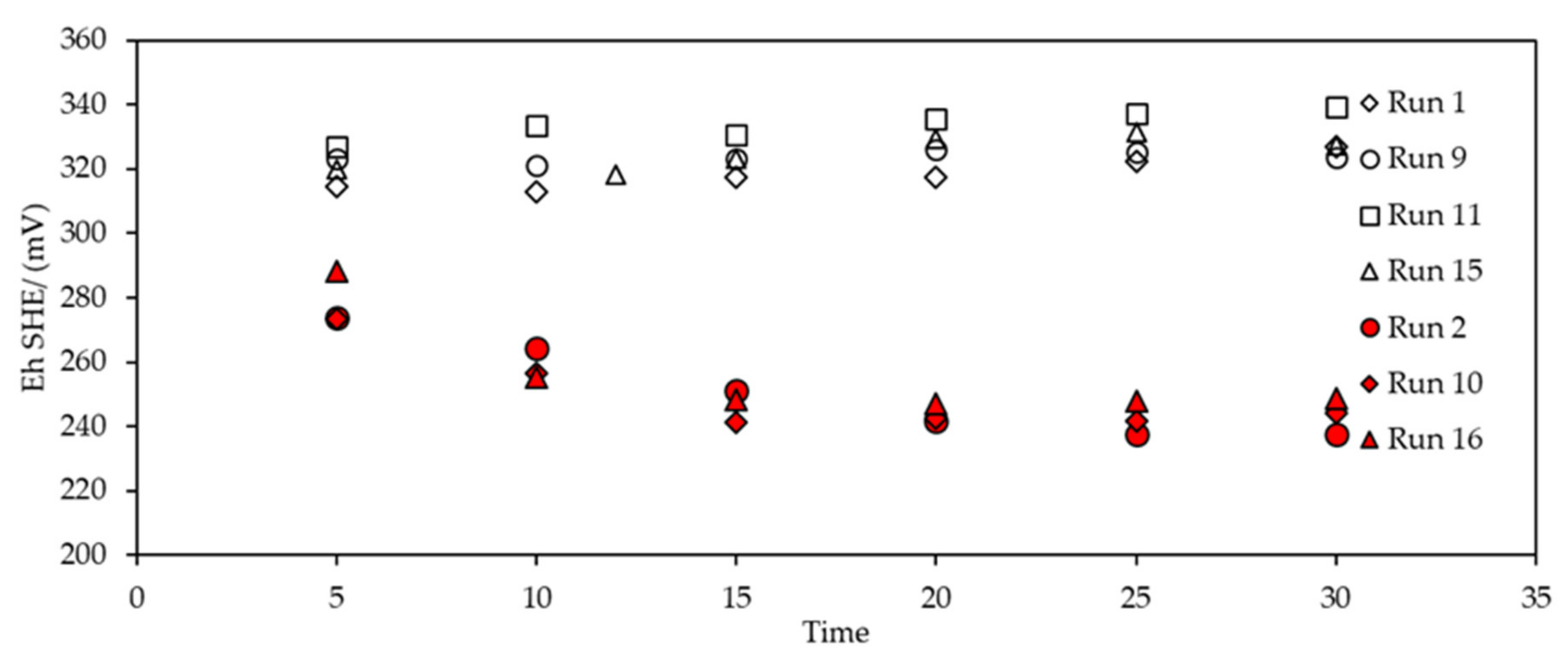
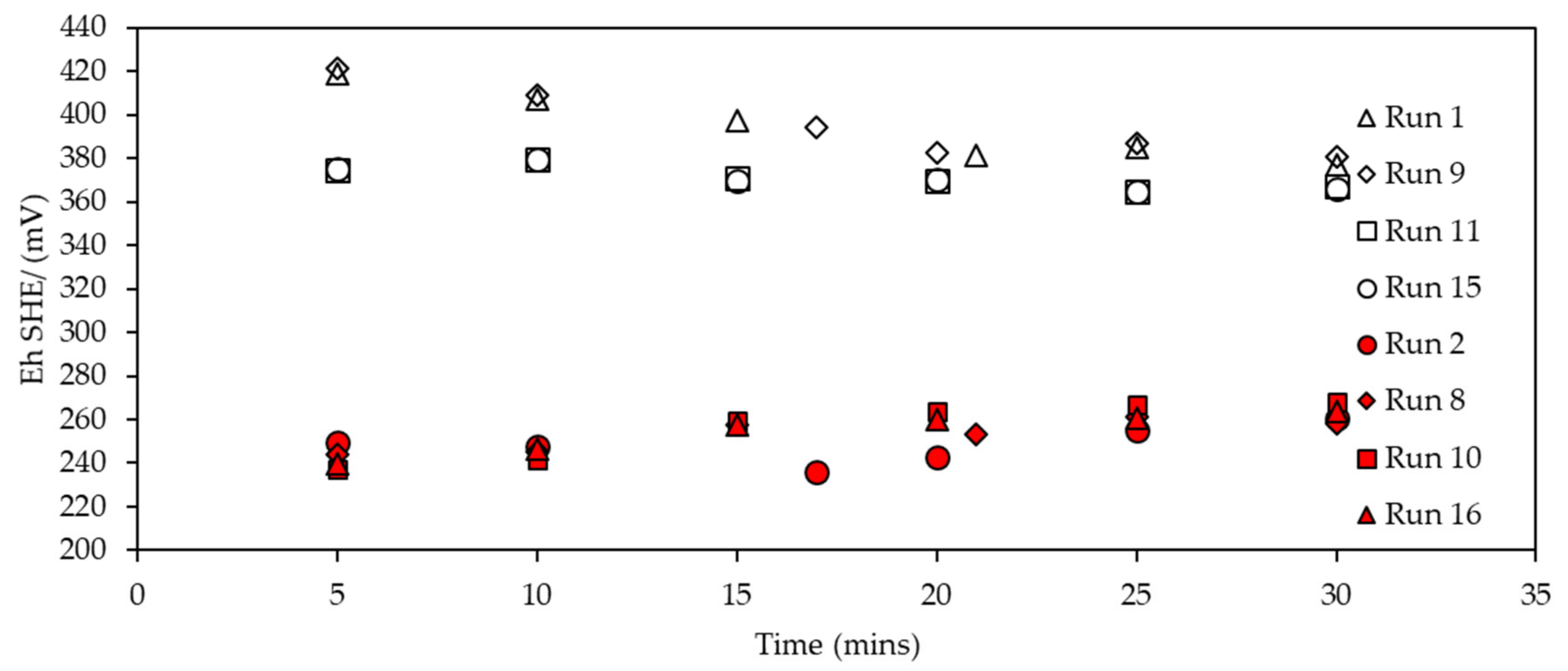
3.2.2. Eh Monitoring during SIBX Adsorption onto Chalcopyrite
3.2.3. Xanthate Adsorption on Chalcopyrite—Discussion of Experimental Observations
3.3. Xanthate Adsorption on Enriched Pentlandite
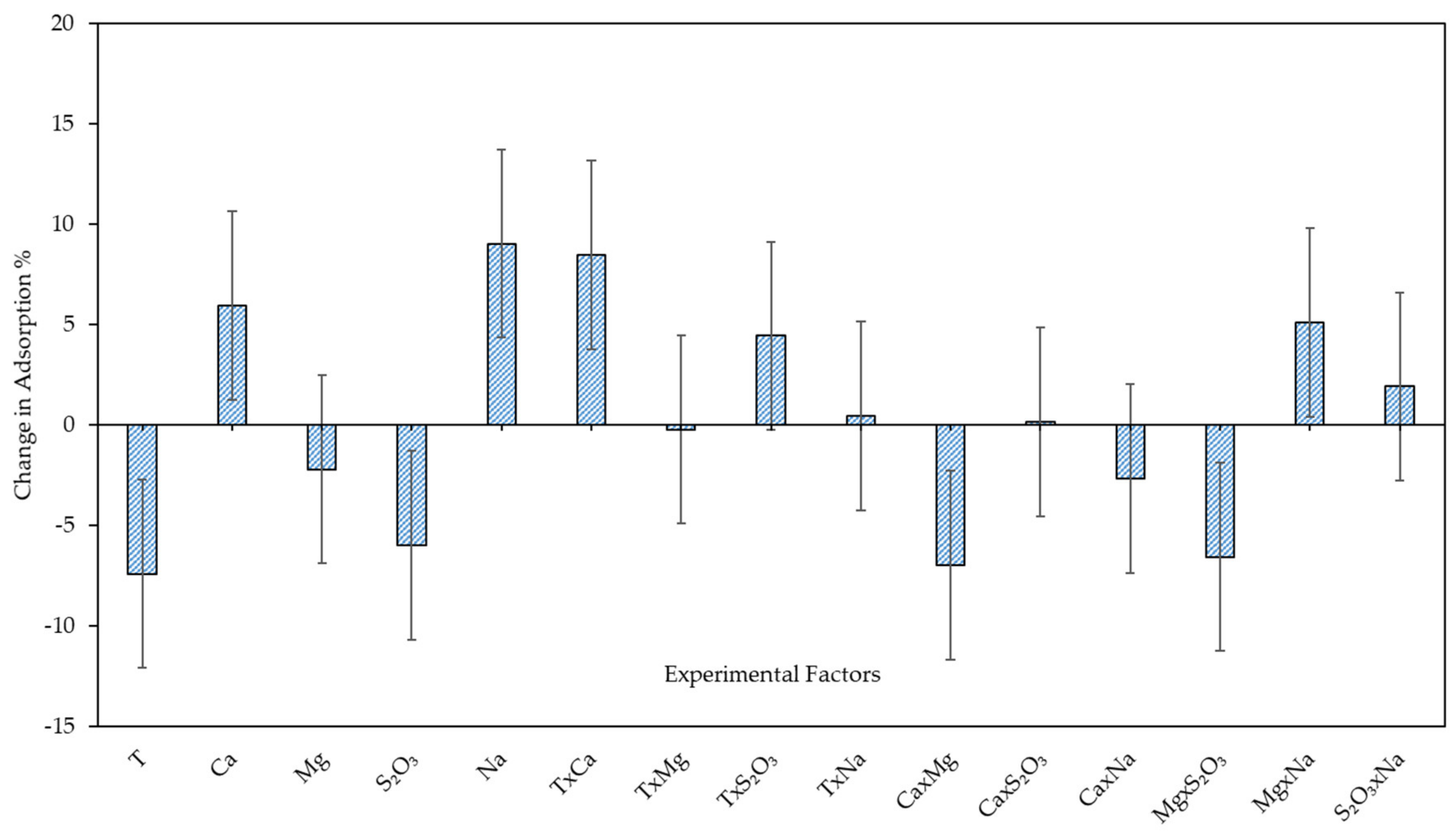
3.3.1. Xanthate Adsorption on Enriched Pentlandite—Model Development and Model Analysis
3.3.2. Eh Monitoring during Collector Adsorption on Enriched Pentlandite
3.3.3. Xanthate Adsorption on Enriched Pentlandite—Discussion of Experimental Observations
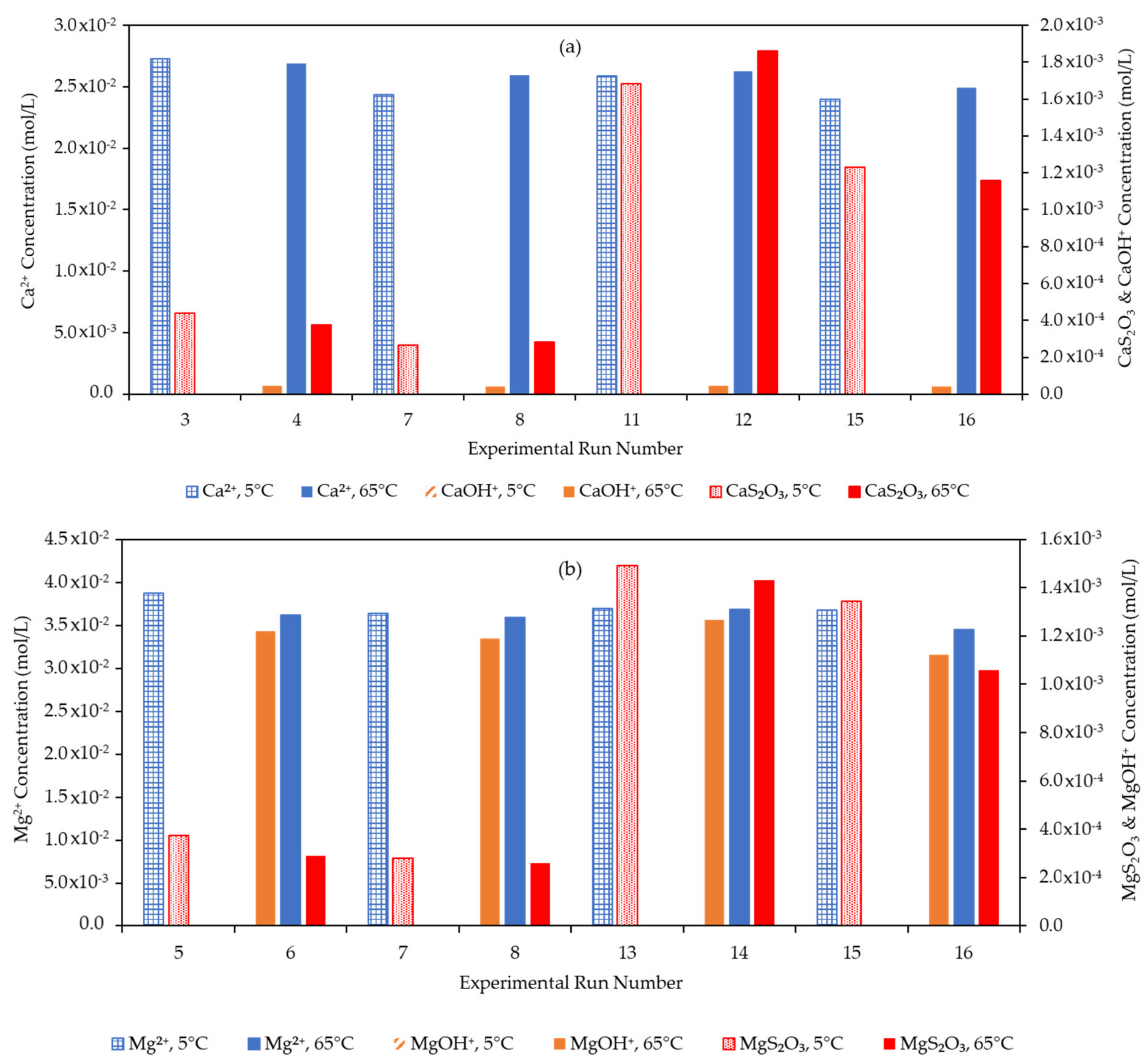
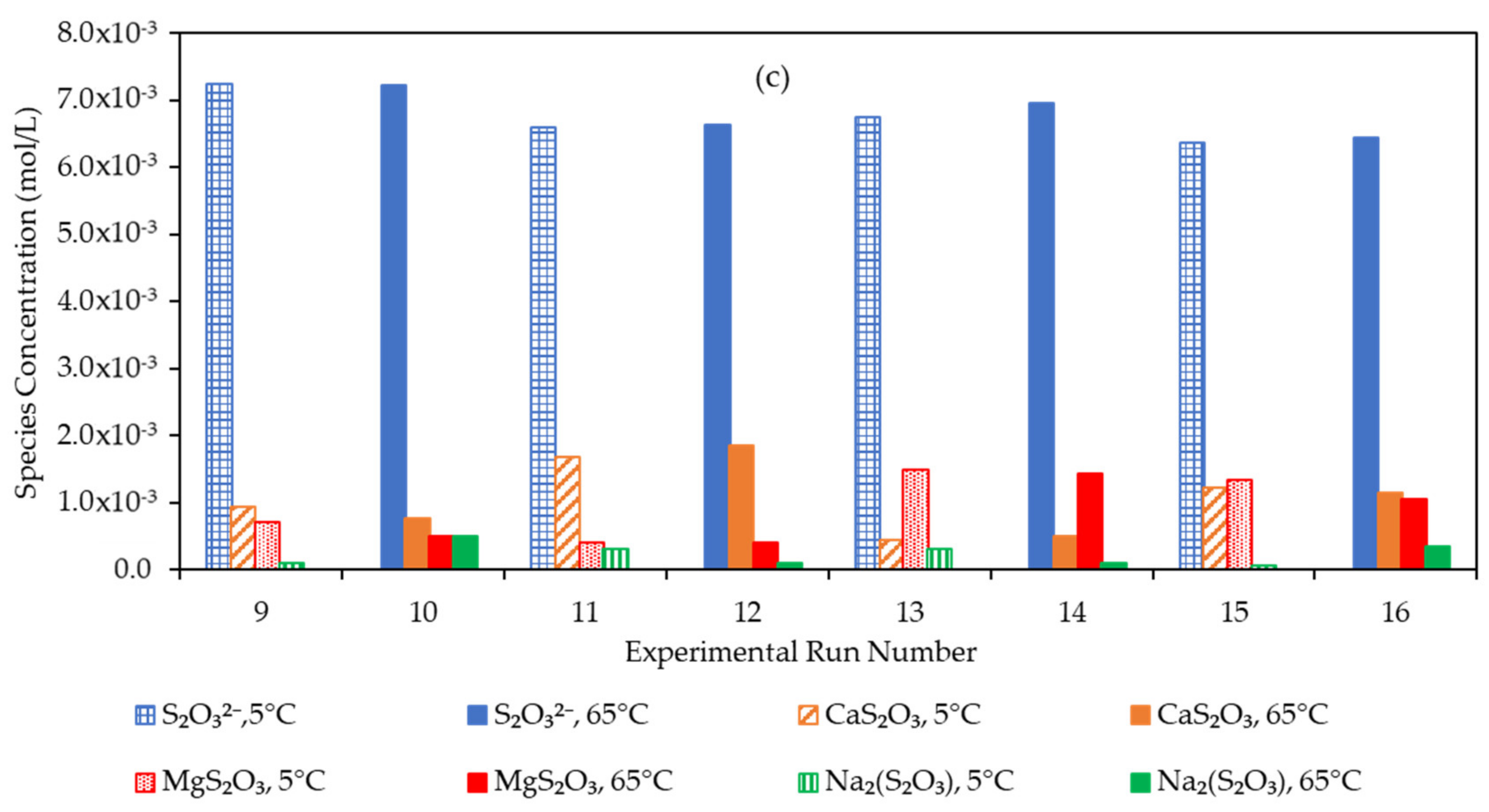
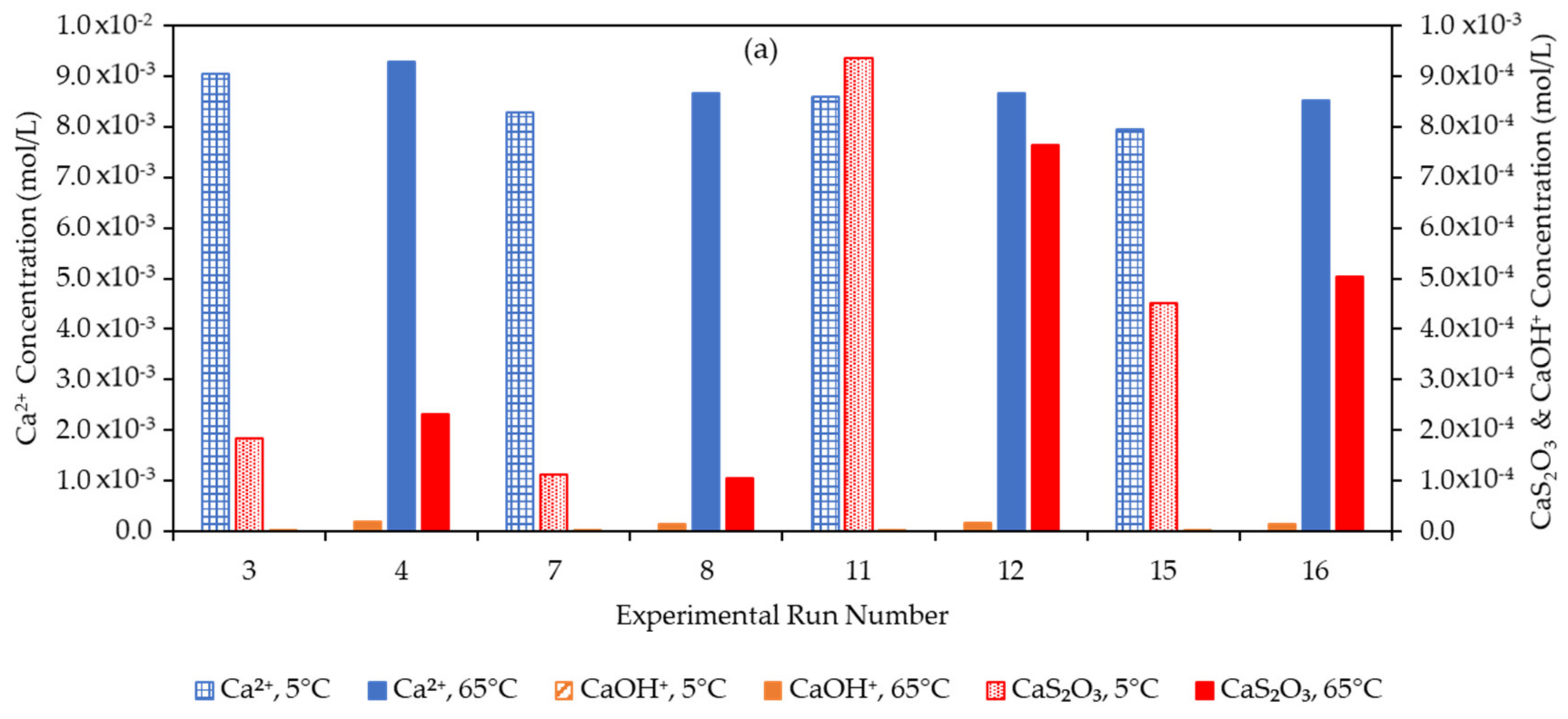
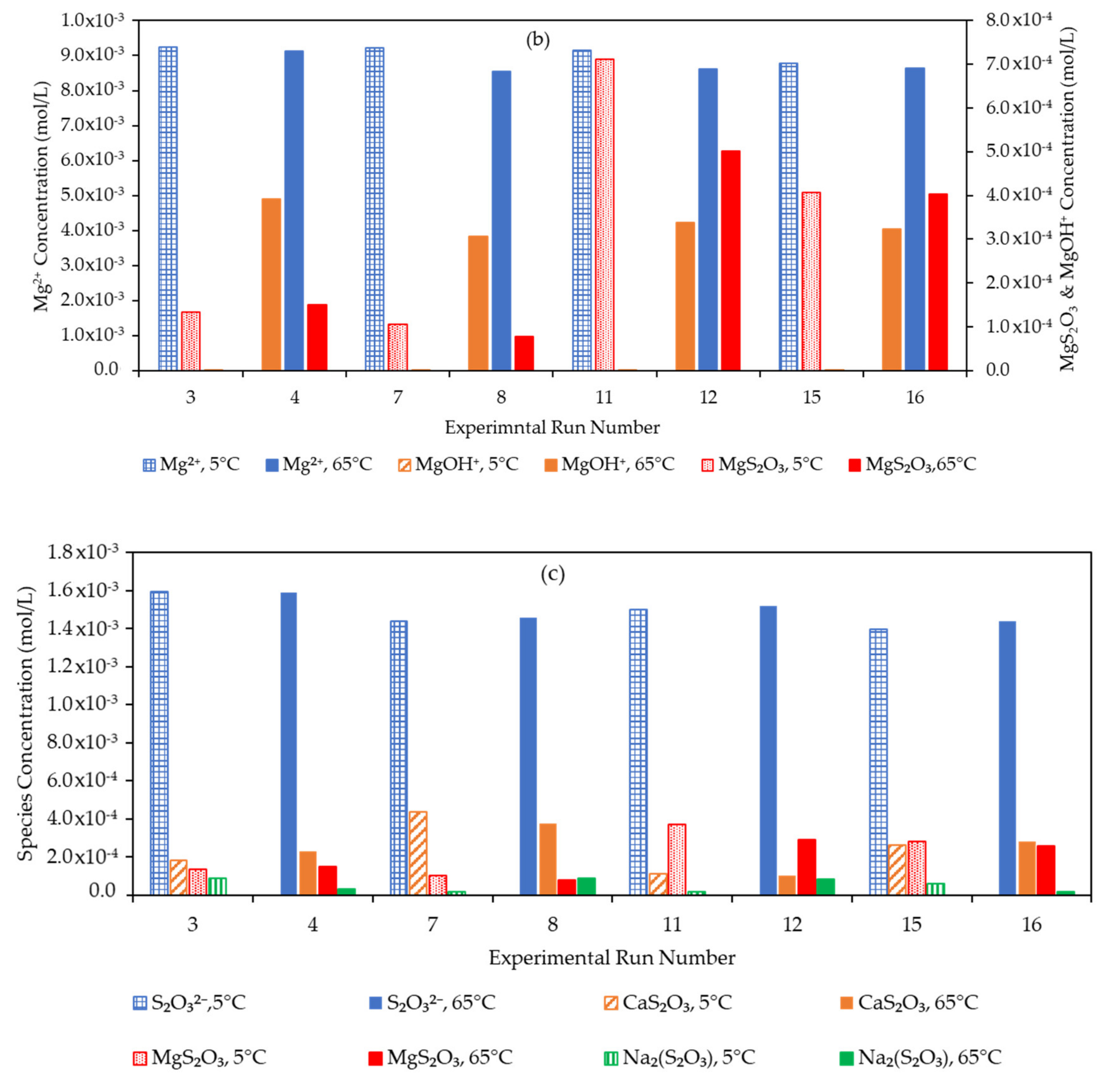
3.4. Effect of the Water Matrix on Electrolyte Speciation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schumann, R.; Levay, G.; Ametov, I. Impact of Recycling on Process Water Qauality in Mineral Processing. In Proceedings of the Water in Mining Conference, Perth, Australia, 15–17 September 2009; pp. 79–86. [Google Scholar]
- Liu, W.; Moran, C.J.; Vink, S. A Review of the Effect of Water Quality on Flotation. Miner. Eng. 2013, 53, 91–100. [Google Scholar] [CrossRef]
- Levay, G.; Smart, R.; Skinner, W. The Impact of Water Quality on Flotation Performance. J. S. Afr. Inst. Min. Metall. 2001, 1, 69–76. [Google Scholar]
- Albrecht, T.W.J.; Addai-Mensah, J.; Fornasiero, D. Critical Copper Concentration in Sphalerite Flotation: Effect of Temperature and Collector. Int. J. Miner. Process. 2016, 146, 15–22. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Pascoe, R.D. Effect of Temperature on Coal Flotation Performance—A Review. Miner. Process. Extr. Metall. Rev. 2005, 26, 31–61. [Google Scholar] [CrossRef]
- Lin, I. The Effect of Seasonal Variations in Temperature on the Performance of Mineral Processing Plants. Miner. Eng. 1989, 2, 47–54. [Google Scholar] [CrossRef]
- O’Connor, C.T.; Dunne, R.C.; Botelho de Sousa, A.M.R. The Effect of Temperature on the Flotation of Pyrite. J. S. Afr. Inst. Min. Metall. 1984, 84, 389–394. [Google Scholar]
- Moses, C.O.; Nordstrom, K.D.; Herman, J.S.; Mills, A.L. Aqueous Pyrite Oxidation by Dissolved Oxygen and by Ferric Iron. Geochim. Cosmochim. Acta 1987, 51, 1561–1571. [Google Scholar] [CrossRef]
- Gibson, C.E.; Kelebek, S. International Journal of Mineral Processing Sensitivity of Pentlandite Fl Otation in Complex Sul Fi de Ores towards PH Control by Lime versus Soda Ash: Effect on Ore Type. Int. J. Miner. Process. 2014, 127, 44–51. [Google Scholar] [CrossRef]
- Jiang, L.; Krasowska, M.; Fornasiero, D.; Ralston, J.; Koh, P. Electrostatic Attraction between a Hydrophilic Solid and a Bubble. Phys. Chem. Chem. Phys. 2010, 12, 14527–14533. [Google Scholar] [CrossRef]
- Grano, S.R.; Prestidge, C.A.; Ralston, J. Solution Interaction of Ethyl Xanthate and Sulphite and Its Effect on Galena Flotation and Xanthate Adsorption. Int. J. Miner. Process. 1997, 52, 161–186. [Google Scholar] [CrossRef]
- Mäkelä, M. Experimental Design and Response Surface Methodology in Energy Applications: A Tutorial Review. Energy Convers. Manag. 2017, 151, 630–640. [Google Scholar] [CrossRef]
- Paulo, F.; Santos, L. Design of Experiments for Microencapsulation Applications: A Review. Mater. Sci. Eng. C 2017, 77, 1327–1340. [Google Scholar] [CrossRef] [PubMed]
- Kharia, A.A.; Singhai, A.K. Screening of Most Effective Variables for Development of Gastroretentive Mucoadhesive Nanoparticles by Taguchi Design. ISRN Nanomater. 2013, 2013, 1–8. [Google Scholar] [CrossRef][Green Version]
- Brereton, R.G.; Araujo, P.W. Experimental Design I. Screening. TrAC Trends Anal. Chem. 1996, 15, 26–31. [Google Scholar] [CrossRef]
- Dauneau, P.; Perez-Martinez, G. Fractional Factorial Design and Multiple Linear Regression to Optimise Extraction of Volatiles from a Lactobacillus Plantarum Bacterial Suspension Using Purge and Trap. J. Chromatogr. A 1997, 775, 225–230. [Google Scholar] [CrossRef]
- Kiralj, R.; Ferreira, M. Basic Validation Procedures for Regression Models in QSAR and QSPR Studies: Theory and Application. J. Braz. Chem. Soc. 2009, 20, 770–787. [Google Scholar] [CrossRef]
- Ebert, R.-U.; Kühne, R.; Wang, B.; Schüürmann, G.; Chen, J. External Validation and Prediction Employing the Predictive Squared Correlation Coefficient—Test Set Activity Mean vs Training Set Activity Mean. J. Chem. Inf. Model. 2008, 48, 2140–2145. [Google Scholar] [CrossRef]
- Chimonyo, W.; Corin, K.C.; Wiese, J.G.; O’Connor, C.T. The Use of Oxidising Agents for Control of Electrochemical Potential in Flotation. Miner. Eng. 2017, 109, 135–143. [Google Scholar] [CrossRef]
- Ekmeki, Z.; Becker, M.; Tekes, E.B.; Bradshaw, D. The Relationship between the Electrochemical, Mineralogical and Flotation Characteristics of Pyrrhotite Samples from Different Ni Ores. J. Electroanal. Chem. 2010, 647, 133–143. [Google Scholar] [CrossRef]
- Woods, R. The Oxidation of Ethyl Xanthate on Platinum, Gold, Copper, and Galena Electrodes. Relation to the Mechanism of Mineral Flotation. J. Phys. Chem. 1971, 75, 354–362. [Google Scholar] [CrossRef]
- Trahar, W.J.; Guy, P.J. The Effects of Oxidation and Mineral Interaction of Sulphide Flotation. In Flotation of Sulphide Minerals; Forssberg, K.S., Ed.; Elsevier B.V.: Amsterdam, The Netherlands, 1985; pp. 91–110. [Google Scholar]
- Hu, Y.; Sun, W.; Wang, D. Electrochemistry of Flotation of Sulphide Minerals; Hu, Y., Wei, S., Dianzuo, W., Eds.; Tsinghua University Press: Beijing, China, 2009. [Google Scholar]
- Mustafa, S.; Hamid, A.; Naeem, A. Temperature Effect on Xanthate Sorption by Chalcopyrite. J. Colloid Interface Sci. 2004, 275, 368–375. [Google Scholar] [CrossRef] [PubMed]
- An, D.; Zhang, J. A Study of Temperature Effect on the Xanthate’s Performance during Chalcopyrite Flotation. Minerals 2020, 10, 426. [Google Scholar] [CrossRef]
- Dávila-Pulido, G.I.; Uribe-Salas, A.; Álvarez-Silva, M.; López-Saucedo, F. The Role of Calcium in Xanthate Adsorption onto Sphalerite. Miner. Eng. 2015, 71, 113–119. [Google Scholar] [CrossRef]
- Bulut, G.; Yenial, Ü. Effects of Major Ions in Recycled Water on Sulfide Minerals Flotation. Miner. Metall. Process. 2016, 33, 137–143. [Google Scholar] [CrossRef]
- Eliseev, N.I.; Kirbitova, N.V. Chalcopyrite and Pyrite Depression with a Mixture of Hyposulfite and Copper Sulfate. Sov. J. Non Ferr. Met. 1984, 1, 125–126. [Google Scholar]
- Petrus, H.T.B.M.; Hirajima, T.; Sasaki, K.; Okamoto, H. Effects of Sodium Thiosulphate on Chalcopyrite and Tennantite: An Insight for Alternative Separation Technique. Int. J. Miner. Process. 2012, 102–103, 116–123. [Google Scholar] [CrossRef]
- Kirjavainen, V.; Schreithofer, N.; Heiskanen, K. Effect of Calcium and Thiosulfate Ions on Flotation Selectivity of Nickel-Copper Ores. Miner. Eng. 2002, 15, 1–5. [Google Scholar] [CrossRef]
- Strong, A.; Yan, D.; Dunne, R. The Detection of Xanthate in Solution and on Sulfide Surfaces to Help Understand and Improve Mineral Separation on Industrial Plants. In Centenary of Flotation Symposium; Australasian Institute of Mining and Metallurgy: Brisbane, QLD, Australia, 2005; pp. 619–624. [Google Scholar]
- Miller, J.D.; Li, J.; Davidtz, J.C.; Vos, F. A Review of Pyrrhotite Flotation Chemistry in the Processing of PGM Ores. Miner. Eng. 2005, 18, 855–865. [Google Scholar] [CrossRef]
- Buswell, A.M.; Nicol, M.J. Some Aspects of the Electrochemistry of Pyrrhotite. J. Appl. Electrochem. 2002, 32, 1321–1329. [Google Scholar] [CrossRef]
- Kerr, A. An Overview of Recent Developments in Flotation Technology and Plant Practice for Nickel Ores. In Mineral Processing, Plant Design, Practice and Control Proceedings; Mular, A.L., Halbe, D.N., Barratt, D.J., Eds.; Society for Mining, Metallurgy and Exploration: Littleton, CO, USA, 2002; pp. 142–1158. [Google Scholar]
- Schreithofer, N. Effect of Calcium and Thiosulphate on Flotability and Xanthate Chemistry of Pentlandite Ion Real Ore System. Doctoral Dissertation, University of Miskolc, Miskolc, Hungary, 1998. [Google Scholar]
- Hodgson, M.; Agar, G.E. Electrochemical Investigations into the Flotation Chemistry of Pentlandite and Pyrrhotite: Process Water and Xanthate Interactions. Can. Metall. Q. 1989, 28, 189–198. [Google Scholar] [CrossRef]
- Mustafa, S.; Hamid, A.; Naeem, A. Xanthate Adsorption Studies on Chalcopyrite Ore. Int. J. Miner. Process. 2004, 74, 317–325. [Google Scholar] [CrossRef]
| Sample | Mineral Phases | Purity (%) |
|---|---|---|
| Chalcopyrite | Chalcopyrite | 80 |
| Quartz | 13 | |
| Sphalerite | 3 | |
| Other non-sulphide minerals | 4 | |
| Enriched Pentlandite | Pentlandite | 25 |
| Pyrrhotite | 11 | |
| Talc | 16 | |
| Amphiboles | 11 | |
| Other non-sulphide minerals | 37 |
| Experiment | Actual Level of Variables | Response | |||||
|---|---|---|---|---|---|---|---|
| Run Order | T(°C) | Ca2+ (mg/L) | Mg2+ (mg/L) | S2O32− (mg/L) | Na+ (mg/L) | Extent of Adsorption: Chalcopyrite (%) | Extent of Adsorption: Pentlandite (%) |
| 1 | 5 | 200 | 200 | 200 | 1000 | 80.4 | 87.5 |
| 2 | 65 | 200 | 200 | 200 | 200 | 90.7 | 38 |
| 3 | 5 | 1000 | 200 | 200 | 200 | 80.9 | 93 |
| 4 | 65 | 1000 | 200 | 200 | 1000 | 93.3 | 85.4 |
| 5 | 5 | 200 | 1000 | 200 | 200 | 84.4 | 92 |
| 6 | 65 | 200 | 1000 | 200 | 1000 | 88.0 | 80.7 |
| 7 | 5 | 1000 | 1000 | 200 | 1000 | 86.7 | 96.2 |
| 8 | 65 | 1000 | 1000 | 200 | 200 | 95.6 | 69.9 |
| 9 | 5 | 200 | 200 | 1000 | 200 | 82.2 | 67.2 |
| 10 | 65 | 200 | 200 | 1000 | 1000 | 83.6 | 61.8 |
| 11 | 5 | 1000 | 200 | 1000 | 1000 | 92.9 | 87.2 |
| 12 | 65 | 1000 | 200 | 1000 | 200 | 91.1 | 92.3 |
| 13 | 5 | 200 | 1000 | 1000 | 1000 | 84.4 | 90.4 |
| 14 | 65 | 200 | 1000 | 1000 | 200 | 92.4 | 29.7 |
| 15 | 5 | 1000 | 1000 | 1000 | 200 | 91.1 | 40.5 |
| 16 | 65 | 1000 | 1000 | 1000 | 1000 | 92.0 | 78 |
| 17 | 35 | 600 | 600 | 600 | 600 | 88.0 | 81.3 |
| 18 | 35 | 600 | 600 | 600 | 600 | 89.3 | 80.9 |
| 19 | 35 | 600 | 600 | 600 | 600 | 87.6 | 80.1 |
| Factor | Confounding Pattern |
|---|---|
| T | Ca2+ × Mg2+ × S2O32− × Na+ |
| Ca2+ | T × Mg2+ × S2O32− × Na+ |
| Mg2+ | T × Ca2+× S2O32− × Na+ |
| Na+ | T × Ca2+ × Mg2+ × S2O32− |
| S2O32− | T × Ca2+ × Mg2+ × Na+ |
| T × Ca2+ | Mg2+ × S2O32− × Na+ |
| T × Mg2+ | Ca2+ × S2O32− × Na+ |
| T × S2O32− | Ca2+ × Mg2+ × Na+ |
| T × Na+ | Ca2+ × Mg2+ × S2O32− |
| Ca2+ × Mg2+ | T × Na+ × S2O32− |
| Ca2+ × S2O32− | T × Na+ × Mg2+ |
| Ca2+ × Na+ | T × S2O32− × Mg2+ |
| Mg2+ × S2O32− | T × Na+ × Ca2+ |
| Mg2+ × Na+ | T × S2O32− × Ca2+ |
| S2O32− × Na+ | T × Mg2+ × Ca2+ |
| Term | Coefficients | P Values |
|---|---|---|
| Constant | 88.14 | 1.39 × 10−19 |
| T | 2.73 | 2.88 × 10−7 |
| Ca2+ | 2.34 | 9.41 × 10−7 |
| Mg2+ | 1.22 | 1.19 × 10−4 |
| S2O32− | −0.44 | 0.0086 |
| Na+ | 0.61 | 0.035 |
| T × S2O32− | −1.67 | 1.23 × 10−5 |
| T × Na+ | −1.17 | 1.59 × 10−4 |
| Ca2+ × S2O32− | 0.72 | 0.0033 |
| Ca2+ × Na+ | 1.22 | 1.19 × 10−4 |
| Mg2+ × Na+ | −1.11 | 2.31 × 10−4 |
| R2pred = 0.934 | R2 = 0.989 | R2Adj = 0.978 |
| ANOVA TABLE: Chalcopyrite Adsorption Tests | |||||
|---|---|---|---|---|---|
| Parameter | DF | Sum of Squares (SS) | Mean Square (Variance) | F Value | P Value |
| Total Corrected | 18 | 362 | 20.1 | ||
| Regression | 10 | 358 | 35.8 | 72.0 | 0 |
| Residual | 8 | 3.94 | 0.49 | ||
| Lack of Fit | 6 | 2.36 | 0.39 | 0.5 | 0.785 |
| Pure Error | 2 | 1.58 | 0.79 | ||
| Term | Coefficients | P Value |
|---|---|---|
| Constant | 75.37 | 1.77 × 10−11 |
| T | −7.39 | 0.0055 |
| Ca2+ | 5.95 | 0.017 |
| Mg2+ | −2.19 | 0.31 |
| S2O32− | −5.98 | 0.017 |
| Na+ | 9.04 | 0.0016 |
| T × S2O32− | 4.45 | 0.017 |
| T × Ca2+ | 8.48 | 0.0025 |
| Ca2+ × Mg2+ | −6.98 | 0.0076 |
| Mg2+ × S2O32− | −6.55 | 0.011 |
| Mg2+ × Na+ | 5.11 | 0.033 |
| R2pred = 0.72 | R2 = 0.96 | R2Adj = 0.91 |
| ANOVA TABLE: Chalcopyrite Adsorption Tests | |||||
|---|---|---|---|---|---|
| Parameters | DF | Sum of Squares (SS) | Mean Square (Variance) | F Value | P Value |
| Total Corrected | 18 | 7024 | 390 | ||
| Regression | 10 | 6743 | 674 | 19.22 | 0.001 |
| Residual | 8 | 280 | 35 | ||
| Lack of Fit | 6 | 279 | 46 | 124.92 | 0.008 |
| Pure Error | 2 | 0.75 | 0.37 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mhonde, N.; Schreithofer, N.; Corin, K.; Mäkelä, M. Assessing the Combined Effect of Water Temperature and Complex Water Matrices on Xanthate Adsorption Using Multiple Linear Regression. Minerals 2020, 10, 733. https://doi.org/10.3390/min10090733
Mhonde N, Schreithofer N, Corin K, Mäkelä M. Assessing the Combined Effect of Water Temperature and Complex Water Matrices on Xanthate Adsorption Using Multiple Linear Regression. Minerals. 2020; 10(9):733. https://doi.org/10.3390/min10090733
Chicago/Turabian StyleMhonde, Ngoni, Nora Schreithofer, Kirsten Corin, and Mikko Mäkelä. 2020. "Assessing the Combined Effect of Water Temperature and Complex Water Matrices on Xanthate Adsorption Using Multiple Linear Regression" Minerals 10, no. 9: 733. https://doi.org/10.3390/min10090733
APA StyleMhonde, N., Schreithofer, N., Corin, K., & Mäkelä, M. (2020). Assessing the Combined Effect of Water Temperature and Complex Water Matrices on Xanthate Adsorption Using Multiple Linear Regression. Minerals, 10(9), 733. https://doi.org/10.3390/min10090733






