IR Features of Hydrous Mg2SiO4-Ringwoodite, Unannealed and Annealed at 200–600 °C and 1 atm, with Implications to Hydrogen Defects and Water-Coupled Cation Disorder
Abstract
1. Introduction
2. Experimental and Analytical Methods
2.1. Synthesizing Mg-Rw Crystals at High P
2.2. Preparing Single-Crystal Thin Sections
2.3. Annealing Single-Crystal Thin Sections at 1 atm
2.4. Unpolarized Transmission IR Measurements
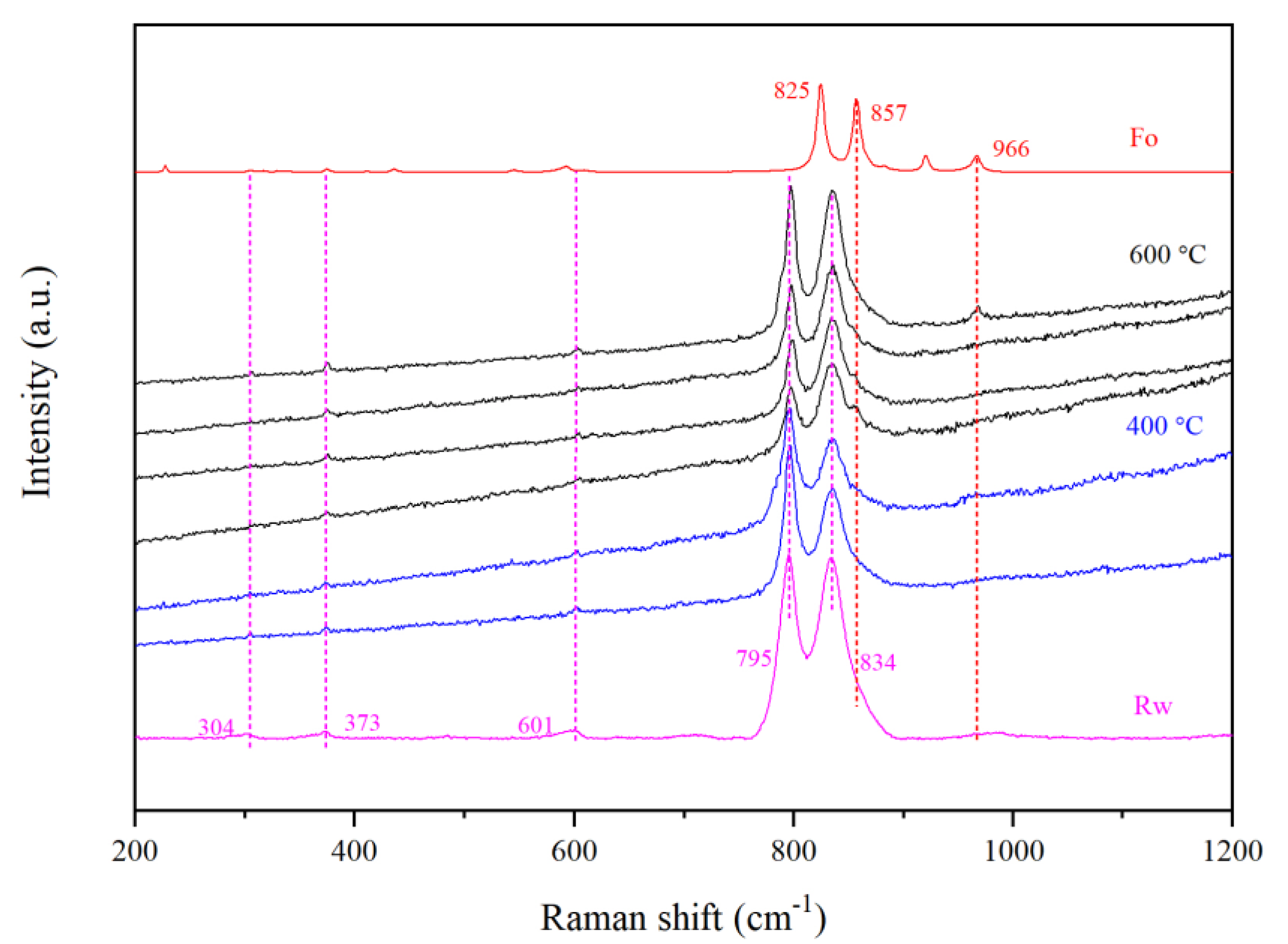
2.5. Unpolarized Raman Spectroscopic Characterizations
2.6. Quantifying Water Content of Mg-Rw
3. Results and Discussions
3.1. Fundamentals, Combinations/Overtones, Thickness Estimates and Water Quantifications
3.2. IR Peaks for Water in Mg-Rw without Anealing
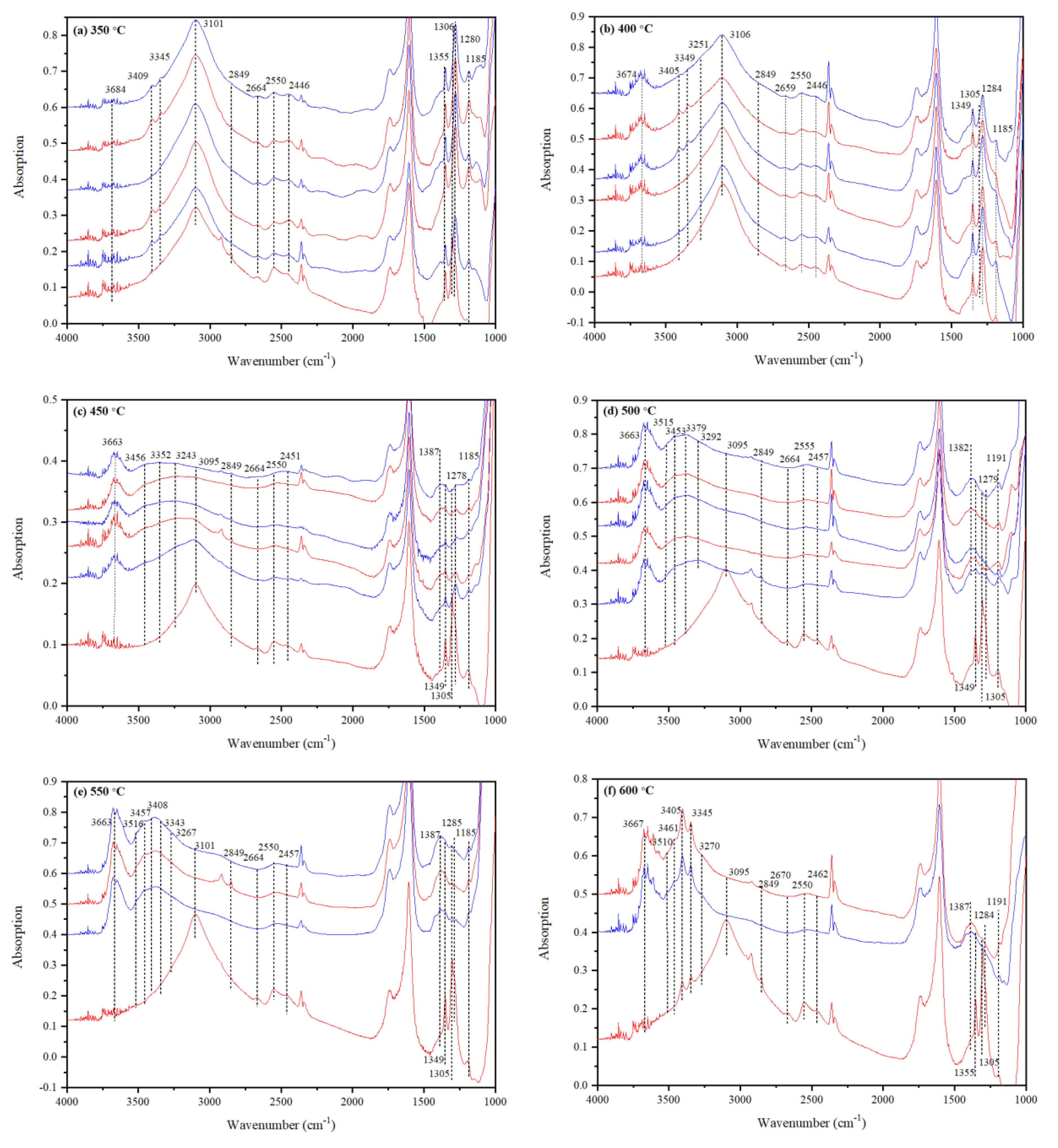
3.3. IR Features of Water in Annealed Mg-Rw
3.3.1. IR Features of Water in low-H2O Mg-Rw Annealed at 200, 250 and 300 °C
3.3.2. IR Features of Water in Intermediate-H2O Mg-Rw Annealed at 350 °C
3.3.3. IR Features of Water in Intermediate-H2O Mg-Rw Annealed at 400 °C
3.3.4. IR Features of Water in Intermediate-H2O Mg-Rw Annealed at 450 °C
3.3.5. IR Features of Water in Intermediate-H2O Mg-Rw Annealed at 500 °C
3.3.6. IR Features of Water in Intermediate-H2O Mg-Rw Annealed at 550 °C
3.3.7. IR Features of Water in Intermediate-H2O Mg-Rw Annealed at 600 °C
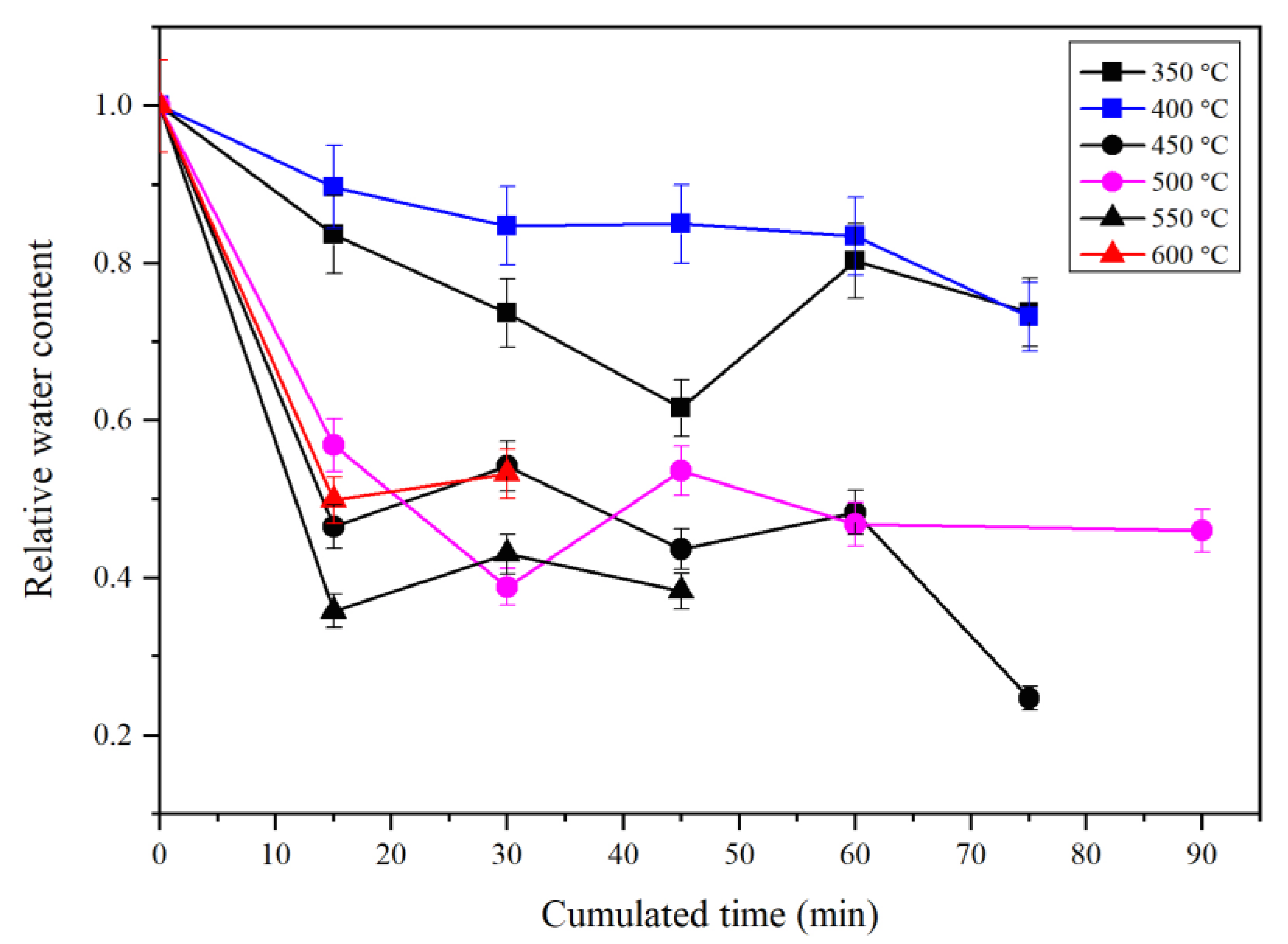
3.3.8. IR Features of Water in Mg-Rw Annealed at Different T: A Summary
3.4. Hydrogen Defects and Its IR Features in Mg-Rw at High P-T Conditions
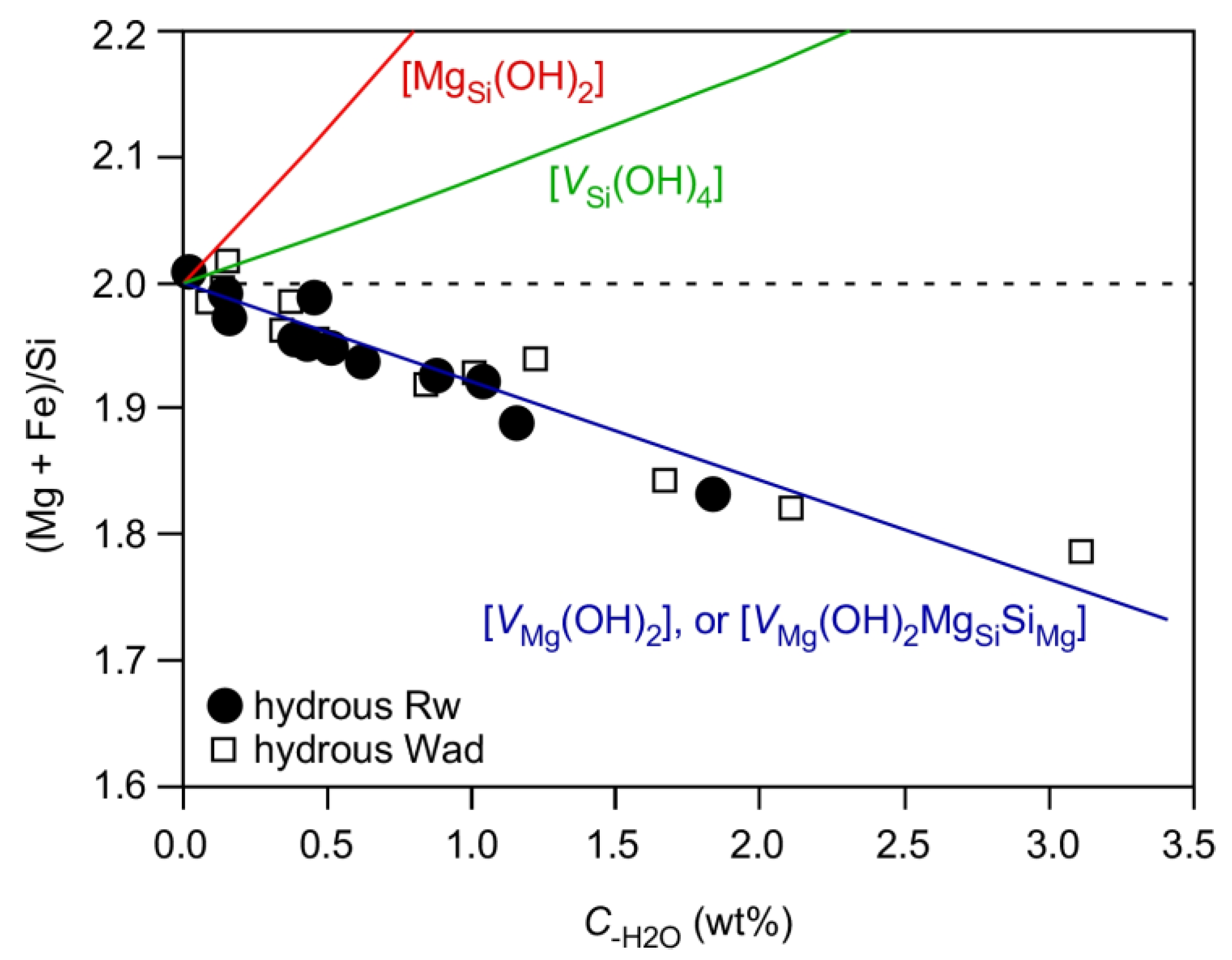
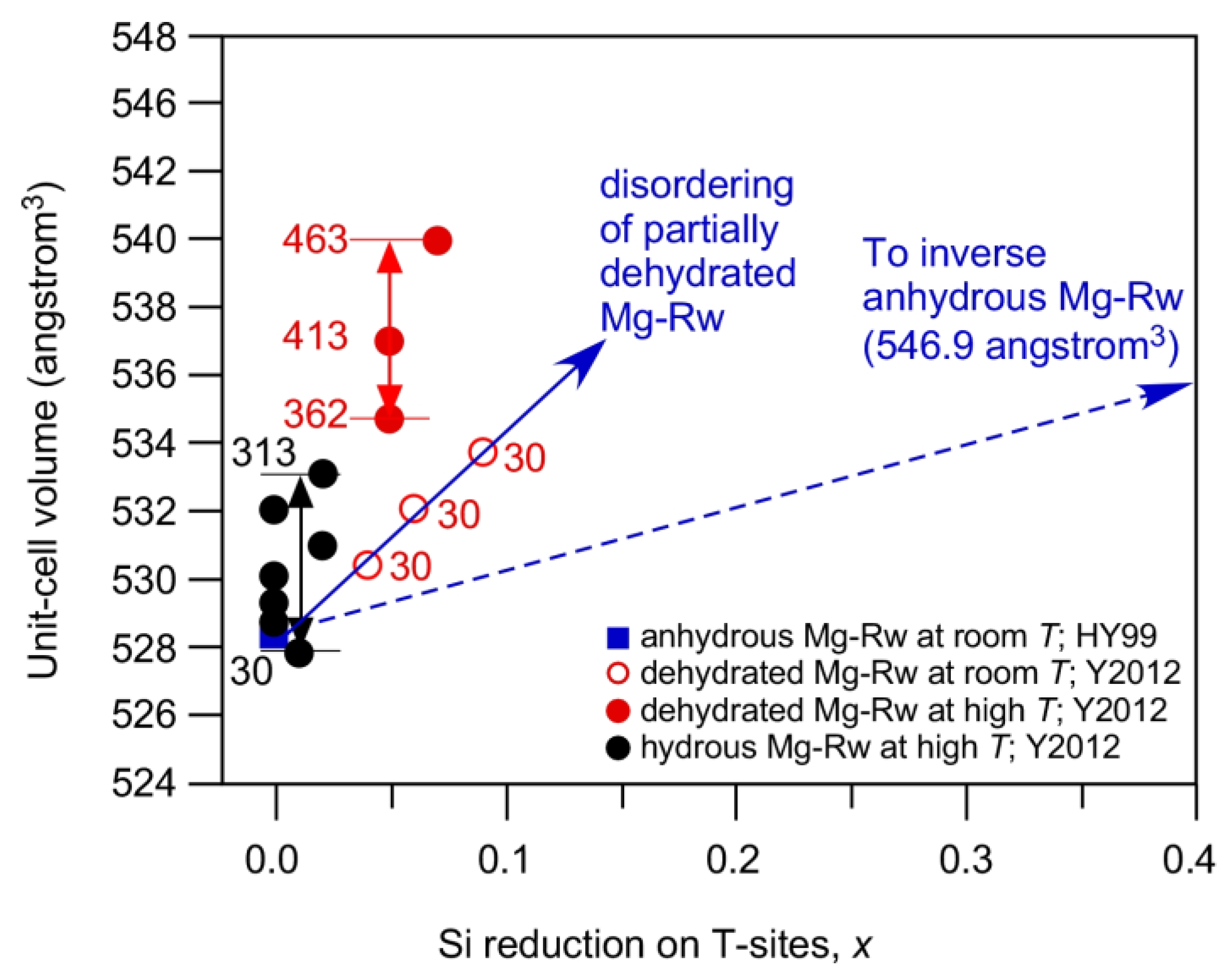
3.5. Water-Coupled Cation Disorder in Mg-Rw and Its Influences
4. Conclusions
- With extensive IR spectroscopic measurements performed on a large number of thin sections of different thickness and different CH2O, we have found at least up to ~15 IR water peaks for hydrous Mg-Rw quenched from conventional high-P experiments, suggesting multiple types of hydrogen defects in the Rw structure.
- There are many significant variations in the IR spectra of hydrous Mg-Rw at high T, as observed from thin sections annealed and quickly quenched from different T to room T. The major variations include an absorption enhancement of the peak at ~3680 cm−1, some new peaks occurring at ~3510 and 3461 cm−1 and significant absorption reductions of the peaks at ~2550 cm−1, signifying hydrogen migration among different crystallographic sites and rearrangement of the O-H dipoles in hydrous Rw at high T.
- The IR peaks at ~3680, 3650–3000 and 3000–2000 cm−1 have been attributed to the hydrogen defects [VSi(OH)4], [VMg(OH)2MgSiSiMg] and [VMg(OH)2], respectively. The hydrogen defects [VMg(OH)2MgSiSiMg] are dominant in hydrous Rw at high P-T conditions, in good agreement with the chemical characteristics of hydrous Rw. Both the defects [VSi(OH)4] and the defects [VMg(OH)2] may play minor roles whereas the defects [MgSi(OH)2] may not operate at all.
- Substantial amounts of cation disorder should be present in hydrous Rw, as required by the formation of the hydrogen defects [VMg(OH)2MgSiSiMg]. The Mg-Si disorder may have very large effects on the physical and chemical properties, as exampled by the effects on the unit-cell volume and thermal expansivity. These effects should be carefully investigated in future.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Anderson, D.L.; Bass, J.D. Transition region of the Earth’s upper mantle. Nature 1986, 320, 321–328. [Google Scholar] [CrossRef]
- Irifune, T.; Ringwood, A.E. Phase transformation in primitive MORB and pyrolite compositions to 25 GPa and some geophysical implications. High Press. Res. Miner. Phys. 1987, 39, 235–246. [Google Scholar]
- Fei, Y.; Bertka, C.M. Phase transitions in the Earth’s mantle and mantle mineralogy. Mantle Petrol. 1999, 6, 189–207. [Google Scholar]
- Frost, D.J. The upper mantle and transition zone. Elements 2008, 4, 171–176. [Google Scholar] [CrossRef]
- Hazen, R.M. Comparative compressibilities of silicate spinels: anomalous behavior of (Mg,Fe)2SiO4. Science 1993, 259, 206–209. [Google Scholar] [CrossRef]
- Higo, Y.; Inoue, T.; Li, B.; Irifune, T.; Liebermann, R.C. The effect of iron on the elastic properties of ringwoodite at high pressure. Phys. Earth Planet. Inter. 2006, 159, 276–285. [Google Scholar] [CrossRef]
- Liu, X.; Xiong, Z.; Chang, L.; He, Q.; Wang, F.; Shieh, S.R.; Wu, C.; Li, B.; Zhang, L. Anhydrous ringwoodites in the mantle transition zone: their bulk modulus, solid solution behavior, compositional variation, and sound velocity feature. Solid Earth Sci. 2016, 1, 28–47. [Google Scholar] [CrossRef]
- Hazen, R.M.; Yang, H. Effects of cation substitution and order-disorder on P-V-T equations of state of cubic spinels. Am. Miner. 1999, 84, 1956–1960. [Google Scholar] [CrossRef]
- Li, L.; Carrez, P.; Weidner, D. Effect of cation ordering and pressure on spinel elasticity by ab initio simulation. Am. Miner. 2007, 92, 174–178. [Google Scholar] [CrossRef]
- Liu, L.; Liu, X.; Bao, X.; He, Q.; Yan, W.; Ma, Y.; He, M.; Tao, R.; Zou, R. Si-disordering in MgAl2O4-spinel under high P-T conditions, with implications for Si-Mg disorder in Mg2SiO4-ringwoodite. Minerals 2018, 8, 210. [Google Scholar] [CrossRef]
- Ohtani, E.; Mizobata, H.; Yurimoto, H. Stability of dense hydrous magnesium silicate phases in the systems Mg2SiO4-H2O and MgSiO3-H2O at pressures up to 27 GPa. Phys. Chem. Miner. 2000, 27, 533–544. [Google Scholar] [CrossRef]
- Fei, H.; Katsura, T. High water solubility of ringwoodite at mantle transition zone temperature. Earth Planet. Sci. Lett. 2020, 531, 115987. [Google Scholar] [CrossRef]
- Kohlstedt, D.L.; Keppler, H.; Rubie, D.C. Solubility of water in the α, β and γ phases of (Mg,Fe)2 SiO4. Contrib. Miner. Pet. 1996, 123, 345–357. [Google Scholar] [CrossRef]
- Inoue, T.; Weidner, D.J.; A Northrup, P.; Parise, J.B. Elastic properties of hydrous ringwoodite (γ-phase) in Mg2SiO4. Earth Planet. Sci. Lett. 1998, 160, 107–113. [Google Scholar] [CrossRef]
- Yusa, H.; Inoue, T.; Ohishi, Y. Isothermal compressibility of hydrous ringwoodite and its relation to the mantle discontinuities. Geophys. Res. Lett. 2000, 27, 413–416. [Google Scholar] [CrossRef]
- Koch-Müller, M.; Rhede, D.; Schulz, R.; Wirth, R. Breakdown of hydrous ringwoodite to pyroxene and spinelloid at high P and T and oxidizing conditions. Phys. Chem. Miner. 2008, 36, 329–341. [Google Scholar] [CrossRef]
- Ghosh, S.; Ohtani, E.; Litasov, K.; Suzuki, A.; Dobson, D.P.; Funakoshi, K. Effect of water in depleted mantle on post-spinel transition and implication for 660km seismic discontinuity. Earth Planet. Sci. Lett. 2013, 371, 103–111. [Google Scholar] [CrossRef]
- Litasov, K.D.; Ohtani, E. Effect of water on the phase relations in Earth’s mantle and deep water cycle—Special Paper. Geol. Soc. Am. 2007, 421, 115–156. [Google Scholar]
- Schmandt, B.; Jacobsen, S.; Becker, T.W.; Liu, Z.; Dueker, K.G. Dehydration melting at the top of the lower mantle. Science 2014, 344, 1265–1268. [Google Scholar] [CrossRef]
- Suzuki, I.; Ohtani, E.; Kumazawa, M. Thermal expansion of modified spinel, γ-Mg2SiO4. J. Phys. Earth 1980, 28, 273–280. [Google Scholar] [CrossRef]
- Inoue, T.; Tanimoto, Y.; Irifune, T.; Suzuki, T.; Fukui, H.; Ohtaka, O. Thermal expansion of wadsleyite, ringwoodite, hydrous wadsleyite and hydrous ringwoodite. Phys. Earth Planet. Inter. 2004, 143–144, 279–290. [Google Scholar] [CrossRef]
- Ye, Y.; Schwering, R.A.; Smyth, J. Effects of hydration on thermal expansion of forsterite, wadsleyite, and ringwoodite at ambient pressure. Am. Miner. 2009, 94, 899–904. [Google Scholar] [CrossRef]
- Ye, Y.; Brown, D.A.; Smyth, J.; Panero, W.R.; Jacobsen, S.; Chang, Y.-Y.; Townsend, J.P.; Thomas, S.-M.; Hauri, E.H.; Dera, P.; et al. Compressibility and thermal expansion of hydrous ringwoodite with 2.5(3) wt% H2O. Am. Miner. 2012, 97, 573–582. [Google Scholar] [CrossRef]
- Jacobsen, S.D.; Smyth, J.R.; Spetzler, H.; Holl, C.M.; Frost, D.J. Sound velocities and elastic constants of iron-bearing hydrous ringwoodite. Phys. Earth Planet. Inter. 2004, 143–144, 47–56. [Google Scholar] [CrossRef]
- Chang, Y.-Y.; Jacobsen, S.; Bina, C.R.; Thomas, S.-M.; Smyth, J.R.; Frost, D.J.; Ballaran, T.B.; McCammon, C.A.; Hauri, E.H.; Inoue, T.; et al. Comparative compressibility of hydrous wadsleyite and ringwoodite: Effect of H2O and implications for detecting water in the transition zone. J. Geophys. Res. Solid Earth 2015, 120, 8259–8280. [Google Scholar] [CrossRef]
- Chen, J.; Weidner, D.; Vaughan, M.; Inoue, T.; Wu, Y. Strength and water weakening of mantle minerals, olivine, wadsleyite and ringwoodite. Geophys. Res. Lett. 1998, 25, 575–578. [Google Scholar] [CrossRef]
- Kavner, A. Elasticity and strength of hydrous ringwoodite at high pressure. Earth Planet. Sci. Lett. 2003, 214, 645–654. [Google Scholar] [CrossRef]
- Fei, H.; Yamazaki, D.; Sakurai, M.; Miyajima, N.; Ohfuji, H.; Katsura, T.; Yamamoto, T. A nearly water-saturated mantle transition zone inferred from mineral viscosity. Sci. Adv. 2017, 3, e1603024. [Google Scholar] [CrossRef]
- Wang, J.; Sinogeikin, S.V.; Inoue, T.; Bass, J.D. Elastic properties of hydrous ringwoodite. Am. Miner. 2003, 88, 1608–1611. [Google Scholar] [CrossRef]
- Mao, Z.; Lin, J.-F.; Jacobsen, S.D.; Duffy, T.S.; Chang, Y.-Y.; Smyth, J.R.; Frost, D.J.; Hauri, E.H.; Prakapenka, V.B. Sound velocities of hydrous ringwoodite at 16 GPa and 673 K. Earth Planet. Sci. Lett. 2012, 331–332, 112–119. [Google Scholar] [CrossRef]
- Schulze, K.; Marquardt, H.; Kawazoe, T.; Boffa Ballaran, T.; McCammon, C.; Koch-Müller, M.; Kurnosov, A.; Marquardt, K. Seismically invisible water in Earth’s transition zone? Earth Planet. Sci. Lett. 2018, 498, 9–16. [Google Scholar] [CrossRef]
- Huang, X.; Xu, Y.; Karato, S.-I. Water content in the transition zone from electrical conductivity of wadsleyite and ringwoodite. Nature 2005, 434, 746–749. [Google Scholar] [CrossRef] [PubMed]
- Yoshino, T.; Matsuzaki, T.; Shatskiy, A.; Katsura, T. The effect of water on the electrical conductivity of olivine aggregates and its implications for the electrical structure of the upper mantle. Earth Planet. Sci. Lett. 2009, 288, 291–300. [Google Scholar] [CrossRef]
- Zhang, B.; Yoshino, T.; Zhao, C. The effect of water on Fe-Mg interdiffusion rates in ringwoodite and implications for the electrical conductivity in the mantle transition zone. J. Geophys. Res. Solid Earth 2019, 124, 2510–2524. [Google Scholar] [CrossRef]
- Keppler, H.; Smyth, J.R. Optical and near infrared spectra of ringwoodite to 21.5 GPa: Implications for radiative heat transport in the mantle. Am. Miner. 2005, 90, 1209–1212. [Google Scholar] [CrossRef]
- Thomas, S.-M.; Bina, C.R.; Jacobsen, S.; Goncharov, A.F. Radiative heat transfer in a hydrous mantle transition zone. Earth Planet. Sci. Lett. 2012, 357, 130–136. [Google Scholar] [CrossRef]
- Pearson, D.G.; Brenker, F.E.; Nestola, F.; McNeill, J.; Nasdala, L.; Hutchison, M.T.; Matveev, S.; Mather, K.; Silversmit, G.; Schmitz, S.; et al. Hydrous mantle transition zone indicated by ringwoodite included within diamond. Nature 2014, 507, 221–224. [Google Scholar] [CrossRef]
- Thomas, S.-M.; Jacobsen, S.; Bina, C.R.; Reichart, P.; Moser, M.; Hauri, E.H.; Koch-Müller, M.; Smyth, J.; Dollinger, G. Quantification of water in hydrous ringwoodite. Front. Earth Sci. 2015, 2, 38. [Google Scholar] [CrossRef]
- Blanchard, M.; Wright, K.; Gale, J.D. A computer simulation study of OH defects in Mg2SiO4 and Mg2GeO4 spinels. Phys. Chem. Miner. 2005, 32, 585–593. [Google Scholar] [CrossRef]
- Blanchard, M.; Balan, E.; Wright, K. Incorporation of water in iron-free ringwoodite: A first-principles study. Am. Miner. 2009, 94, 83–89. [Google Scholar] [CrossRef]
- Li, L.; Brodholt, J.; Alfè, D. Structure and elasticity of hydrous ringwoodite: A first principle investigation. Phys. Earth Planet. Inter. 2009, 177, 103–115. [Google Scholar] [CrossRef]
- Panero, W.R. First principles determination of the structure and elasticity of hydrous ringwoodite. J. Geophys. Res. Space Phys. 2010, 115, 03203. [Google Scholar] [CrossRef]
- Kudoh, Y.; Kuribayashi, T.; Mizobata, H.; Ohtani, E. Structure and cation disorder of hydrous ringwoodite, γ-Mg1.89 Si0.98 H0.30 O4. Phys. Chem. Miner. 2000, 27, 474–479. [Google Scholar] [CrossRef]
- Smyth, J.R.; Holl, C.M.; Frost, D.J.; Jacobsen, S.; Langenhorst, F.; McCammon, C. Structural systematics of hydrous ringwoodite and water in Earth’s interior. Am. Miner. 2003, 88, 1402–1407. [Google Scholar] [CrossRef]
- Purevjav, N.; Okuchi, T.; Tomioka, N.; Abe, J.; Harjo, S. Hydrogen site analysis of hydrous ringwoodite in mantle transition zone by pulsed neutron diffraction. Geophys. Res. Lett. 2014, 41, 6718–6724. [Google Scholar] [CrossRef]
- Liu, L.; Lin, C.-C.; Mernagh, T.P.; Inoue, T. Raman spectra of hydrous γ-Mg2SiO4 at various pressures and temperatures. Phys. Chem. Miner. 2002, 29, 181–187. [Google Scholar] [CrossRef]
- Kleppe, A.K.; Jephcoat, A.P.; Smyth, J.; Frost, D.J. On protons, iron and the high-pressure behavior of ringwoodite. Geophys. Res. Lett. 2002, 29, 171–174. [Google Scholar] [CrossRef]
- Kleppe, A.K.; Jephcoat, A.P.; Smyth, J.R. Raman spectroscopy study of hydrous γ-Mg2SiO4 to 56.5 GPa. Phys. Chem. Miner. 2002, 29, 473–476. [Google Scholar] [CrossRef]
- Bolfan-Casanova, N. Water partitioning between nominally anhydrous minerals in the MgO–SiO2–H2O system up to 24 GPa: Implications for the distribution of water in the Earth’s mantle. Earth Planet. Sci. Lett. 2000, 182, 209–221. [Google Scholar] [CrossRef]
- Litasov, K.; Ohtani, E. Stability of various hydrous phases in CMAS pyrolite-H2O system up to 25 GPa. Phys. Chem. Miner. 2003, 30, 147–156. [Google Scholar] [CrossRef]
- Chamorro Pérez, E.M.; Daniel, I.; Chervin, J.-C.; Dumas, P.; Bass, J.D.; Inoue, T. Synchrotron IR study of hydrous ringwoodite (γ-Mg2SiO4) up to 30 GPa. Phys. Chem. Miner. 2006, 33, 502–510. [Google Scholar] [CrossRef]
- Mrosko, M.; Lenz, S.; McCammon, C.A.; Taran, M.; Wirth, R.; Koch-Müller, M. Hydrogen incorporation and the oxidation state of iron in ringwoodite: A spectroscopic study. Am. Miner. 2013, 98, 629–636. [Google Scholar] [CrossRef]
- Panero, W.R.; Smyth, J.; Pigott, J.S.; Liu, Z.; Frost, D.J. Hydrous ringwoodite to 5 K and 35 GPa: Multiple hydrogen bonding sites resolved with FTIR spectroscopy. Am. Miner. 2013, 98, 637–642. [Google Scholar] [CrossRef]
- Yang, X.; Keppler, H.; Dubrovinsky, L.; Kurnosov, A. In-situ infrared spectra of hydroxyl in wadsleyite and ringwoodite at high pressure and high temperature. Am. Miner. 2014, 99, 724–729. [Google Scholar] [CrossRef]
- Stebbins, J.F.; Smyth, J.; Panero, W.R.; Frost, D.J. Forsterite, hydrous and anhydrous wadsleyite and ringwoodite (Mg2SiO4): 29Si NMR results for chemical shift anisotropy, spin-lattice relaxation, and mechanism of hydration. Am. Miner. 2009, 94, 905–915. [Google Scholar] [CrossRef]
- Bolfan-Casanova, N.; Schiavi, F.; Novella, D.; Bureau, H.; Raepsaet, C.; Khodja, H.; Demouchy, S. Examination of water quantification and incorporation in transition zone minerals: wadsleyite, ringwoodite and phase D using ERDA (Elastic Recoil Detection Analysis). Front. Earth Sci. 2018, 6, 75. [Google Scholar] [CrossRef]
- Koch-Müller, M.; Rhede, D. IR absorption coefficients for water in nominally anhydrous high-pressure minerals. Am. Miner. 2010, 95, 770–775. [Google Scholar] [CrossRef]
- Rossman, G.R. Chapter 6. Vibrational spectroscopy of hydrous components. Spectrosc. Methods Mineral. Geol. 1988, 18, 193–206. [Google Scholar] [CrossRef]
- Rossman, G. Analytical methods for measuring water in nominally anhydrous minerals. Rev. Miner. Geochem. 2006, 62, 1–28. [Google Scholar] [CrossRef]
- McMillan, P.F.; Hofmeister, A.M. Infrared and Raman spectroscopy. Rev. Mineral. 1988, 18, 99–159. [Google Scholar]
- Libowitzky, E.; Beran, A.; Papp, G. IR spectroscopic characterisation of hydrous species in minerals. Spectrosc. Methods Mineral. 2004, 6, 227–279. [Google Scholar] [CrossRef]
- Hofmeister, A.; Mao, H. Evaluation of shear moduli and other properties of silicates with the spinel structure from IR spectroscopy. Am. Miner. 2001, 86, 622–639. [Google Scholar] [CrossRef]
- Ma, Y.; Yan, W.; Sun, Q.; Liu, X. Raman and infrared spectroscopic quantification of the carbonate concentration in K2CO3 aqueous solutions with water as an internal standard. Geosci. Front. 2020. [Google Scholar] [CrossRef]
- Kovács, I.; O’Neill, H.S.C.; Hermann, J.; Hauri, E.H. Site-specific infrared O-H absorption coefficients for water substitution into olivine. Am. Miner. 2010, 95, 292–299. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.; Zheng, H.; Zhang, L. Anharmonic vibration of the SiO4 tetrahedron in olivine at temperatures in the subduction zone: An infrared absorbance spectroscopic study. Acta Petrol. Sin. 2015, 31, 1891–1900. [Google Scholar]
- Liu, X.; Ma, Y.; He, Q.; He, M. Some IR features of SiO4 and OH in coesite, and its amorphization and dehydration at ambient pressure. J. Asian Earth Sci. 2017, 148, 315–323. [Google Scholar] [CrossRef]
- Libowitzky, E.; Rossman, G. An IR absorption calibration for water in minerals. Am. Miner. 1997, 82, 1111–1115. [Google Scholar] [CrossRef]
- He, M.; Yan, W.; Chang, Y.-D.; Liu, K.; Liu, X. Fundamental infrared absorption features of α-quartz: An unpolarized single-crystal absorption infrared spectroscopic study. Vib. Spectrosc. 2019, 101, 52–63. [Google Scholar] [CrossRef]
- Lu, A.; Li, Y.; Ding, H.; Xu, X.; Li, Y.; Ren, G.; Liang, J.; Liu, Y.; Hong, H.; Chen, N.; et al. Photoelectric conversion on Earth’s surface via widespread Fe- and Mn-mineral coatings. Proc. Natl. Acad. Sci. USA 2019, 116, 9741–9746. [Google Scholar] [CrossRef]
- Bolfan-Casanova, N.; Keppler, H.; Rubie, D.C. Water partitioning at 660 km depth and evidence for very low water solubility in magnesium silicate perovskite. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Yu, Y.G.; Wentzcovitch, R.M. Density functional study of vibrational and thermodynamic properties of ringwoodite. J. Geophys. Res. Space Phys. 2006, 111, 12202. [Google Scholar] [CrossRef]
- Akaogi, M.; Ross, N.L.; McMillan, P.; Navrotsky, A. The Mg2SiO4 polymorphs (olivine, modified spinel and spinel)-thermodynamic properties from oxide melt solution calorimetry, phase relations, and models of lattice vibrations. Am. Mineral. 1984, 69, 499–512. [Google Scholar]
- Binns, R. (Mg,Fe)2SiO4 spinel in a meteorite. Phys. Earth Planet. Inter. 1970, 3, 156–160. [Google Scholar] [CrossRef]
- Koch-Müller, M.; Speziale, S.; Deon, F.; Mrosko, M.; Schade, U. Stress-induced proton disorder in hydrous ringwoodite. Phys. Chem. Miner. 2010, 38, 65–73. [Google Scholar] [CrossRef]
- Shinoda, K.; Aikawa, N. Polarized infrared absorbance spectra of an optically anisotropic crystal: Application to the orientation of the OH− dipole in quartz. Phys. Chem. Miner. 1993, 20, 308–314. [Google Scholar] [CrossRef]
- Liu, X.; O’Neill, H.S.C.; Berry, A.J. The effects of small amounts of H2O, CO2 and Na2O on the partial melting of spinel lherzolite in the system CaO-MgO-Al2O3-SiO2 ± H2O ± CO2 ± Na2O at 1.1 GPa. J. Petrol. 2006, 47, 409–434. [Google Scholar] [CrossRef]
- Ganskow, G.; Ballaran, T.B.; Langenhorst, F. Effect of iron on the compressibility of hydrous ringwoodite. Am. Miner. 2010, 95, 747–753. [Google Scholar] [CrossRef]
- Bolfan-Casanova, N. Water in the Earth’s mantle. Miner. Mag. 2005, 69, 229–257. [Google Scholar] [CrossRef]
- Sasaki, S.; Prewitt, C.T.; Sato, Y.; Ito, E. Single-crystal X ray study of γ Mg2SiO4. J. Geophys. Res. Space Phys. 1982, 87, 7829–7832. [Google Scholar] [CrossRef]
- Hudson, R.L.; Gerakines, P.A.; Ferrante, R.F. IR spectra and properties of solid acetone, an interstellar and cometary molecule. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 193, 33–39. [Google Scholar] [CrossRef]
- Zhang, Y.; Belcher, R.; Ihinger, P.; Wang, L.; Xu, Z.; Newman, S. New calibration of infrared measurement of dissolved water in rhyolitic glasses. Geochim. Cosmochim. Acta 1997, 61, 3089–3100. [Google Scholar] [CrossRef]
- Scott, H.P.; Williams, Q. An infrared spectroscopic study of lawsonite to 20 GPa. Phys. Chem. Miner. 1999, 26, 437–445. [Google Scholar] [CrossRef]
- Lehmann, K.; Smith, A.M. Where does overtone intensity come from? J. Chem. Phys. 1990, 93, 6140–6147. [Google Scholar] [CrossRef]
- Matveev, S.; O’Neill, H.S.C.; Ballhaus, C.; Taylor, W.R.; Green, D. Effect of silica activity on OH-IR spectra of olivine: Implications for low-aSiO2 mantle metasomatism. J. Pet. 2001, 42, 721–729. [Google Scholar] [CrossRef]
- Mosenfelder, J.L.; Deligne, N.; Asimow, P.D.; Rossman, G. Hydrogen incorporation in olivine from 2–12 GPa. Am. Miner. 2006, 91, 285–294. [Google Scholar] [CrossRef]
- Liu, D.; Wang, S.; Smyth, J.R.; Zhang, J.; Wang, X.; Zhu, X.; Ye, Y. In situ infrared spectra for hydrous forsterite up to 1243 K: Hydration effect on thermodynamic properties. Minerals 2019, 9, 512. [Google Scholar] [CrossRef]
- Wang, Y.; He, M.; Yan, W.; Yang, M.; Liu, X. Jianite: Massive dunite solely made of virtually pure forsterite from Ji’an County, Jilin Province, Northeast China. Minerals 2020, 10, 220. [Google Scholar] [CrossRef]
- Paterson, M.S. The determination of hydroxyl by infrared absorption in quartz, silicate glasses and similar materials. Bull. Minéral. 1982, 105, 20–29. [Google Scholar] [CrossRef]
- Kubicki, J.D.; Sykes, D.; Rossman, G. Calculated trends of oh infrared stretching vibrations with composition and structure in aluminosilicate molecules. Phys. Chem. Miner. 1993, 20, 425–432. [Google Scholar] [CrossRef]
- Balan, E.; Refson, K.; Blanchard, M.; Delattre, S.; Lazzeri, M.; Ingrin, J.; Mauri, F.; Wright, K.; Winkler, B. Theoretical infrared absorption coefficient of OH groups in minerals. Am. Miner. 2008, 93, 950–953. [Google Scholar] [CrossRef]
- Kudoh, Y. Structural relation of hydrous ringwoodite to hydrous wadsleyite. Phys. Chem. Miner. 2001, 28, 523–530. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, X. Kinetics and thermodynamics of Mg-Al disorder in MgAl2O4-spinel: A review. Molecules 2019, 24, 1704. [Google Scholar] [CrossRef]
- Nakamoto, K.; Margoshes, M.; Rundle, R.E. Stretching frequencies as a function of distances in hydrogen bonds. J. Am. Chem. Soc. 1955, 77, 6480–6486. [Google Scholar] [CrossRef]
- Libowitzky, E. Correlation of O-H stretching frequencies and O-H…O hydrogen bond lengths in minerals. Mon. Chem. Chem. Mon. 1999, 130, 1047–1059. [Google Scholar] [CrossRef]
- Kiefer, B.; Stixrude, L.; Wentzcovitch, R. Normal and inverse ringwoodite at high pressures. Am. Miner. 1999, 84, 288–293. [Google Scholar] [CrossRef]
- Panero, W.R. Cation disorder in ringwoodite and its effects on wave speeds in the Earth’s transition zone. J. Geophys. Res. 2008, 113, B10204. [Google Scholar] [CrossRef]
- Liu, L.; Ma, Y.; Yan, W.; Liu, X. Trace element partitioning between MgAl2O4-spinel and carbonatitic silicate melt from 3 to 6 GPa, with emphasis on the role of cation order-disorder. Solid Earth Sci. 2019, 4, 43–65. [Google Scholar] [CrossRef]
- Hazen, R.P.; Downs, R.T.; Finger, L.W.; Ko, J. Crystal chemistry of ferromagnesian silicate spinels: Evidence for Mg-Si disorder. Am. Mineral. 1993, 78, 1320–1323. [Google Scholar]
- Stebbins, J.F.; Panero, W.R.; Smyth, J.; Frost, D.J. Forsterite, wadsleyite, and ringwoodite (Mg2SiO4): 29Si NMR constraints on structural disorder and effects of paramagnetic impurity ions. Am. Miner. 2009, 94, 626–629. [Google Scholar] [CrossRef]
- Taran, M.; Koch-Müller, M.; Wirth, R.; Abs-Wurmbach, I.; Rhede, D.; Greshake, A. Spectroscopic studies of synthetic and natural ringwoodite, γ-(Mg, Fe)2SiO4. Phys. Chem. Miner. 2008, 36, 217–232. [Google Scholar] [CrossRef]
- Ohtani, E.; Kimura, Y.; Kimura, M.; Takata, T.; Kondo, T.; Kubo, T. Formation of high-pressure minerals in shocked L6 chondrite Yamato 791384: Constraints on shock conditions and parent body size. Earth Planet. Sci. Lett. 2004, 227, 505–515. [Google Scholar] [CrossRef]
- Liu, X. Phase relations in the system KAlSi3O8–NaAlSi3O8 at high pressure–high temperature conditions and their implication for the petrogenesis of lingunite. Earth Planet. Sci. Lett. 2006, 246, 317–325. [Google Scholar] [CrossRef]
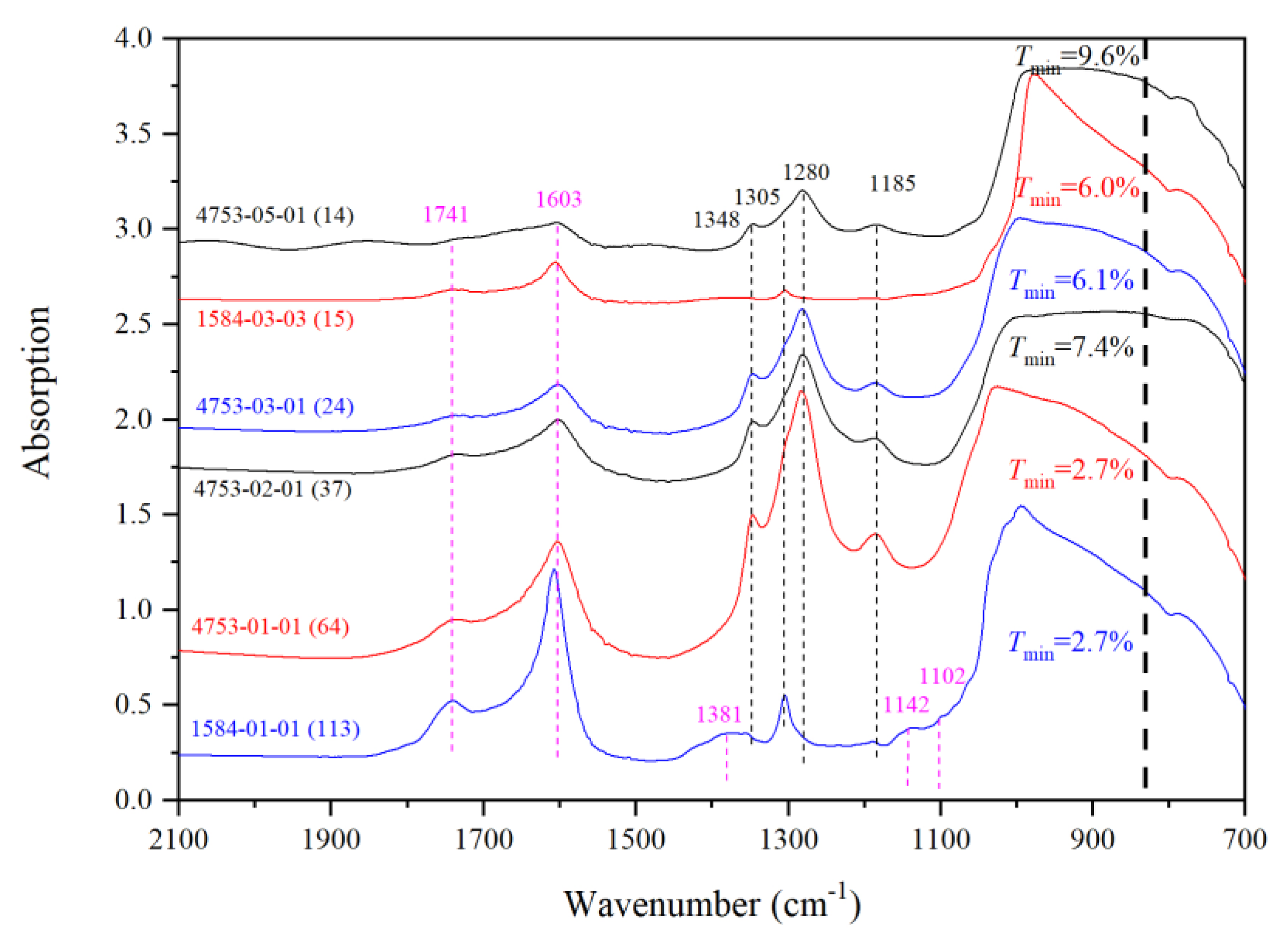
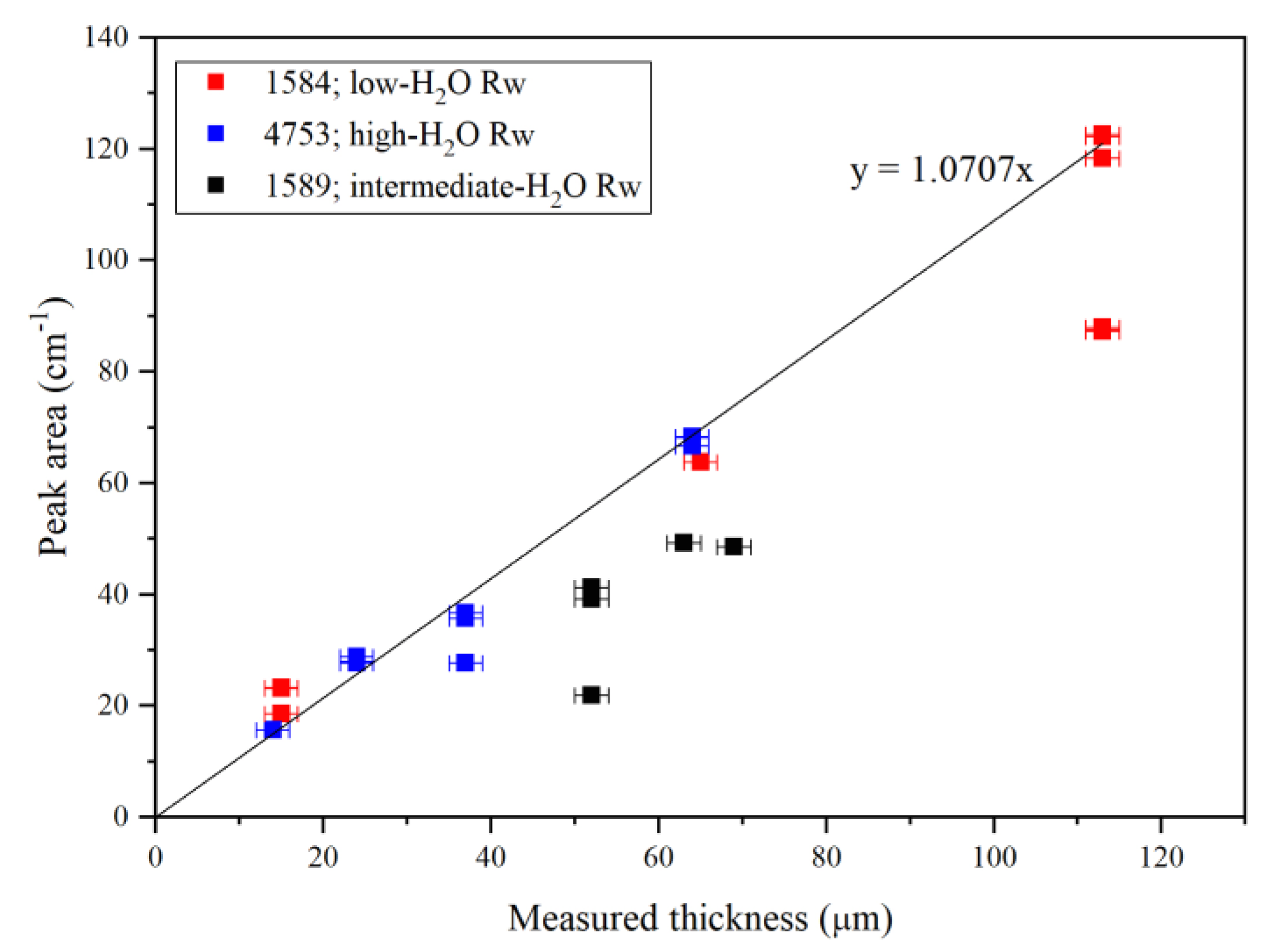
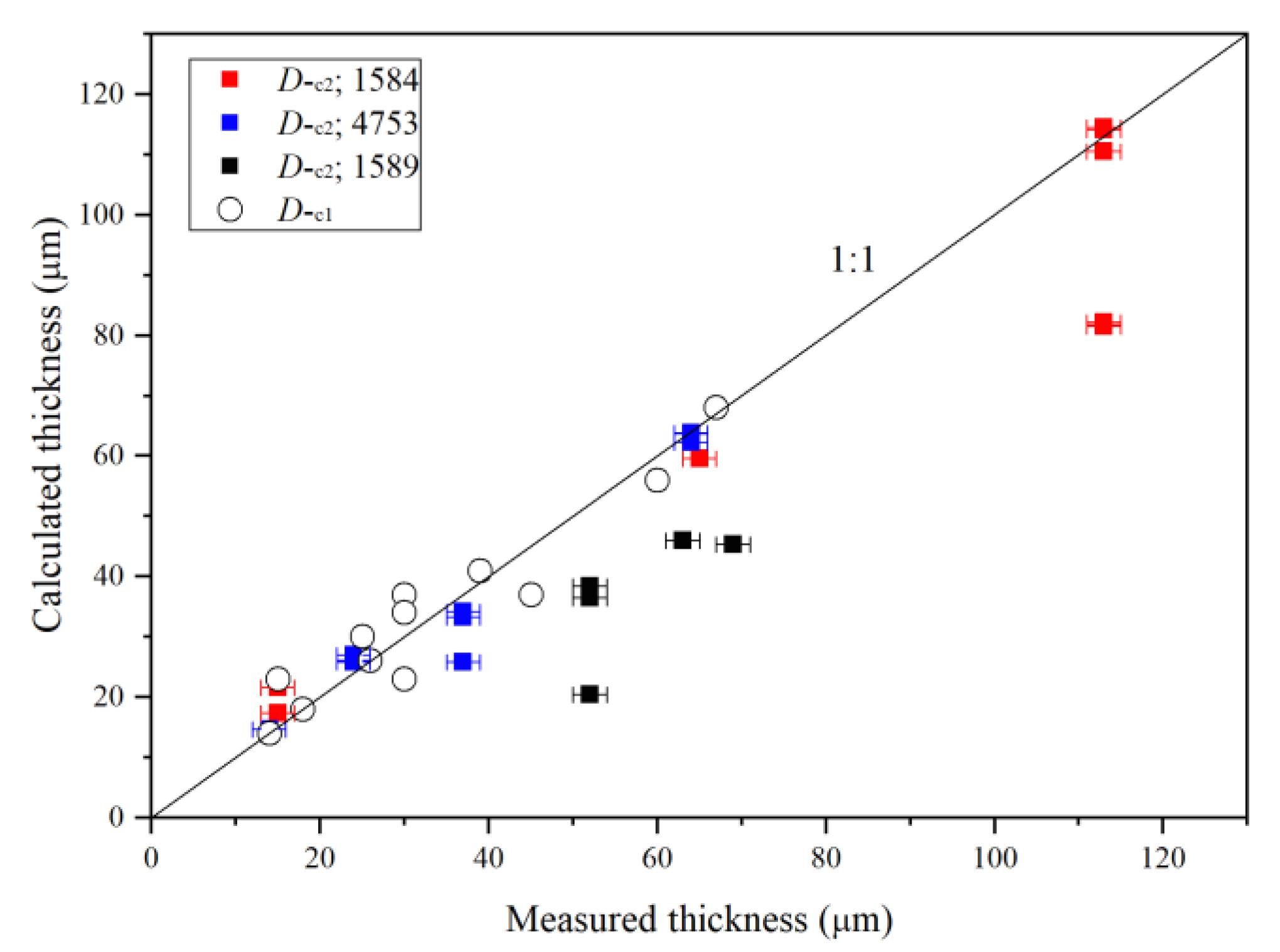
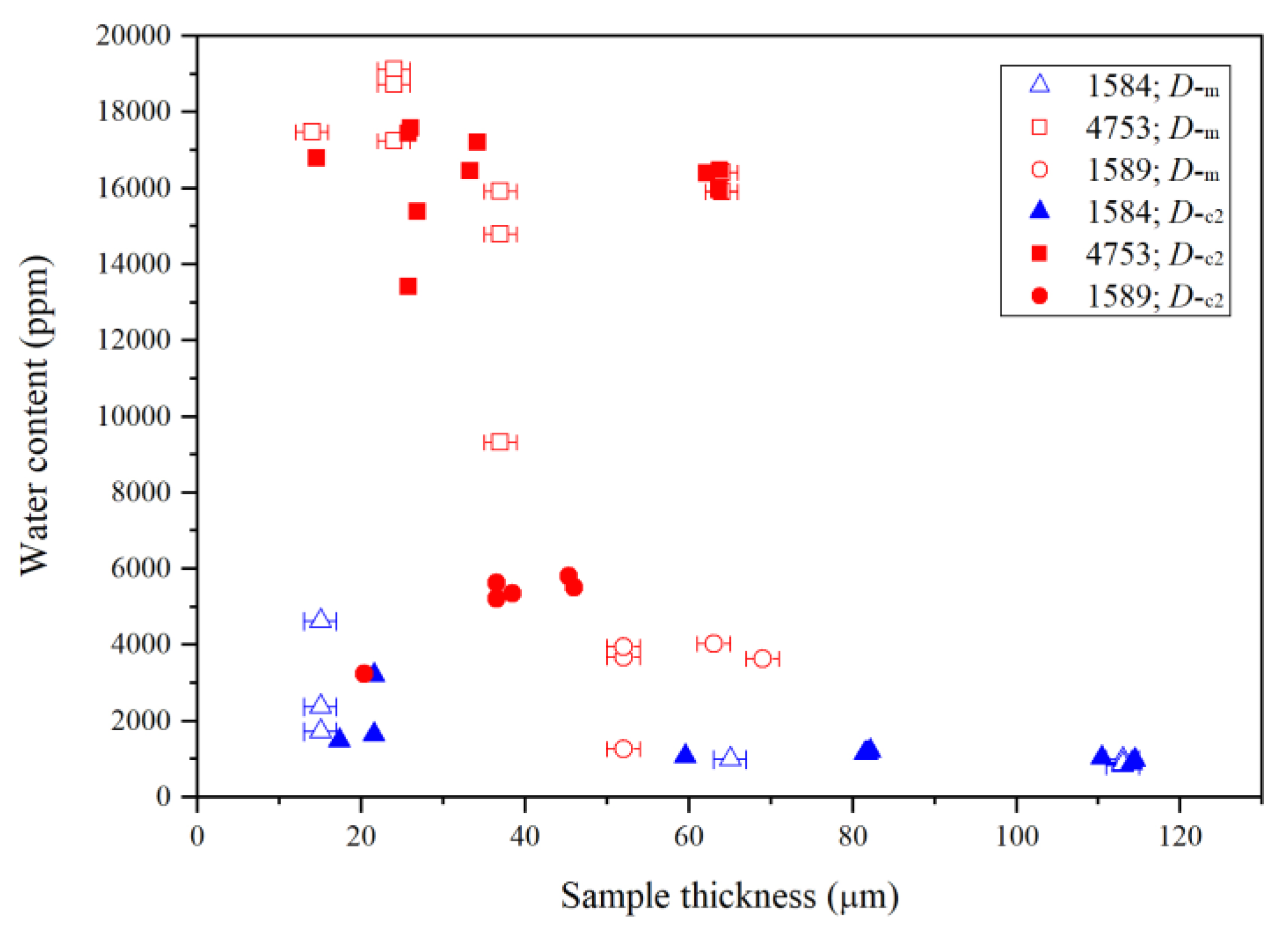

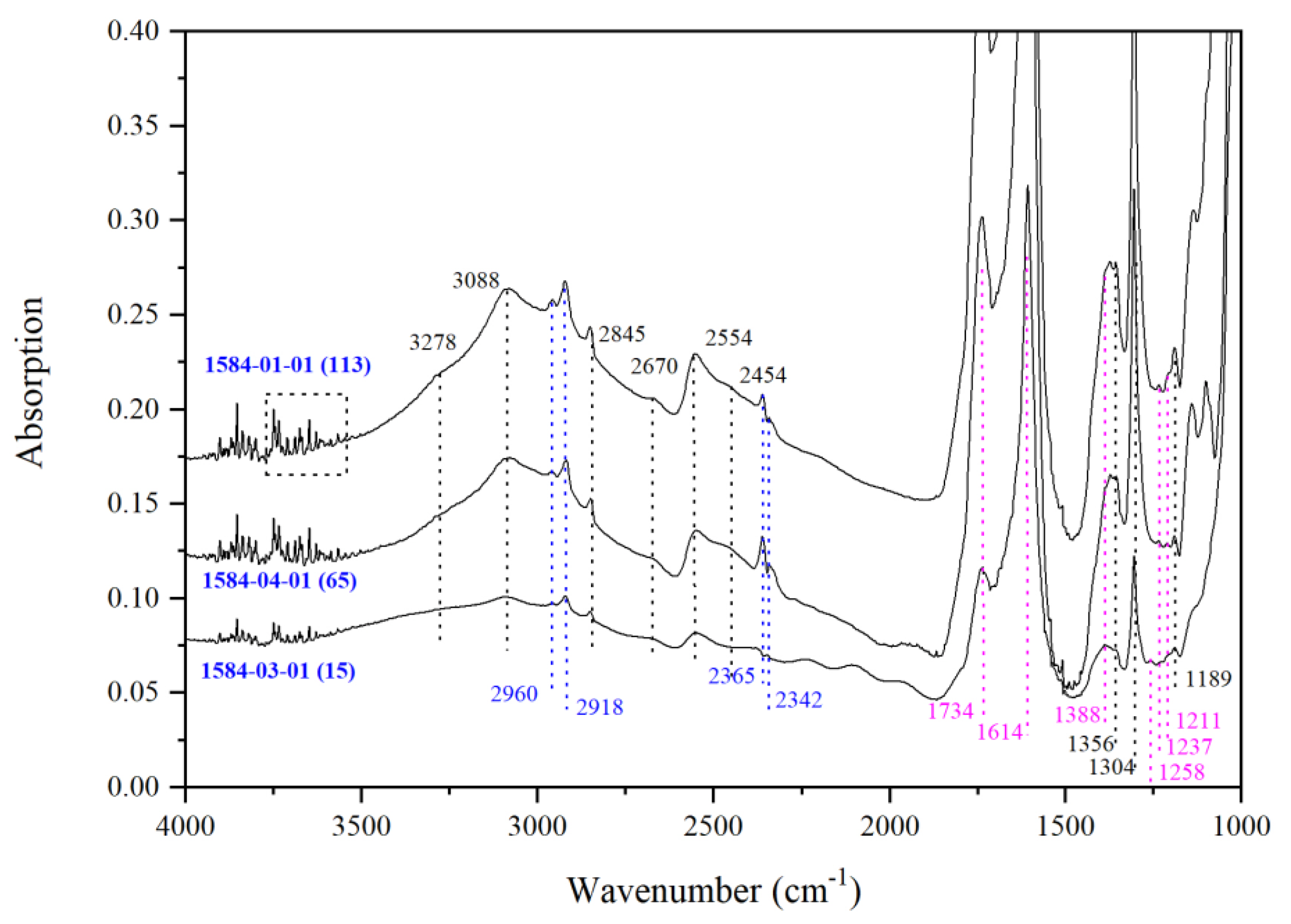
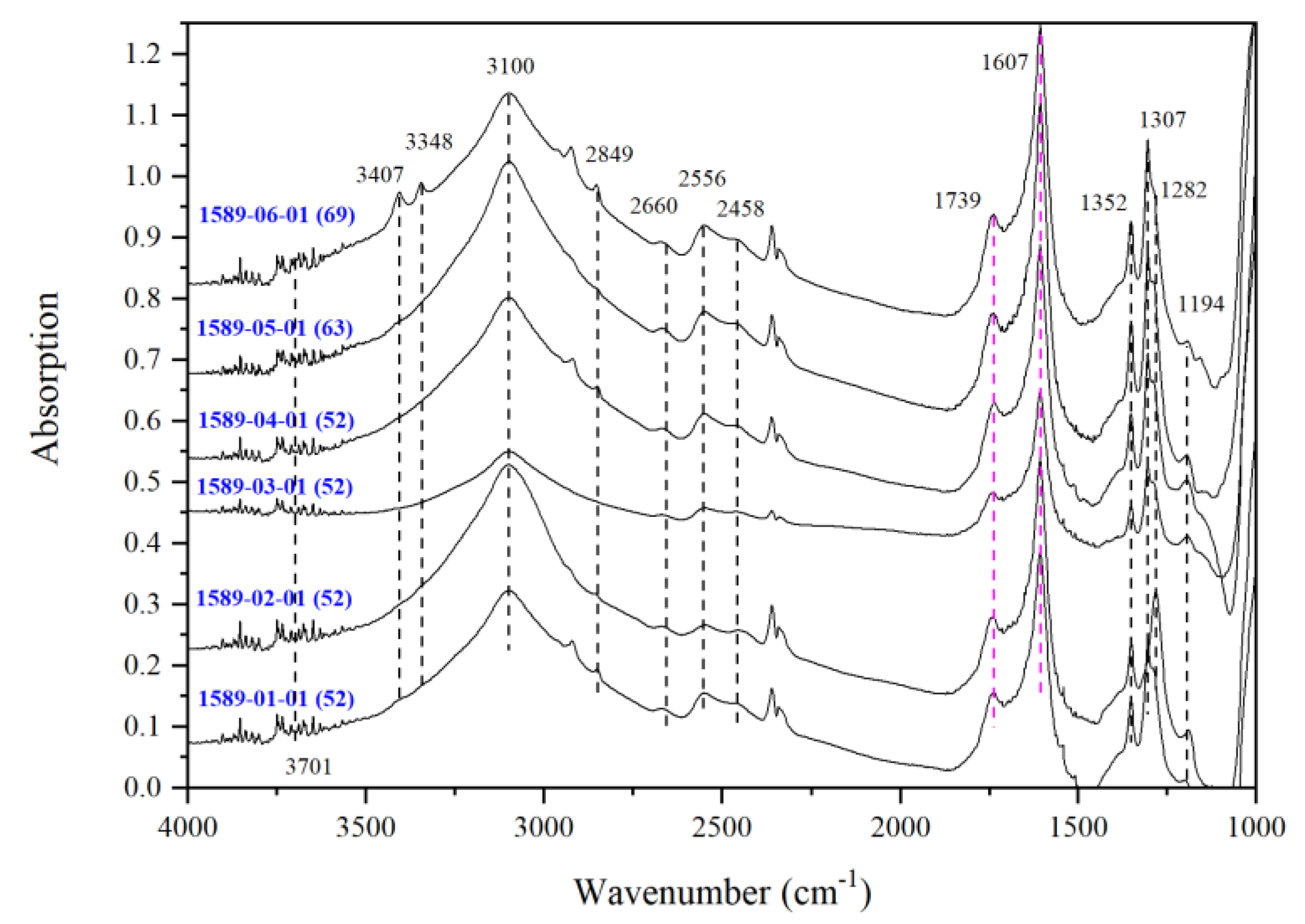
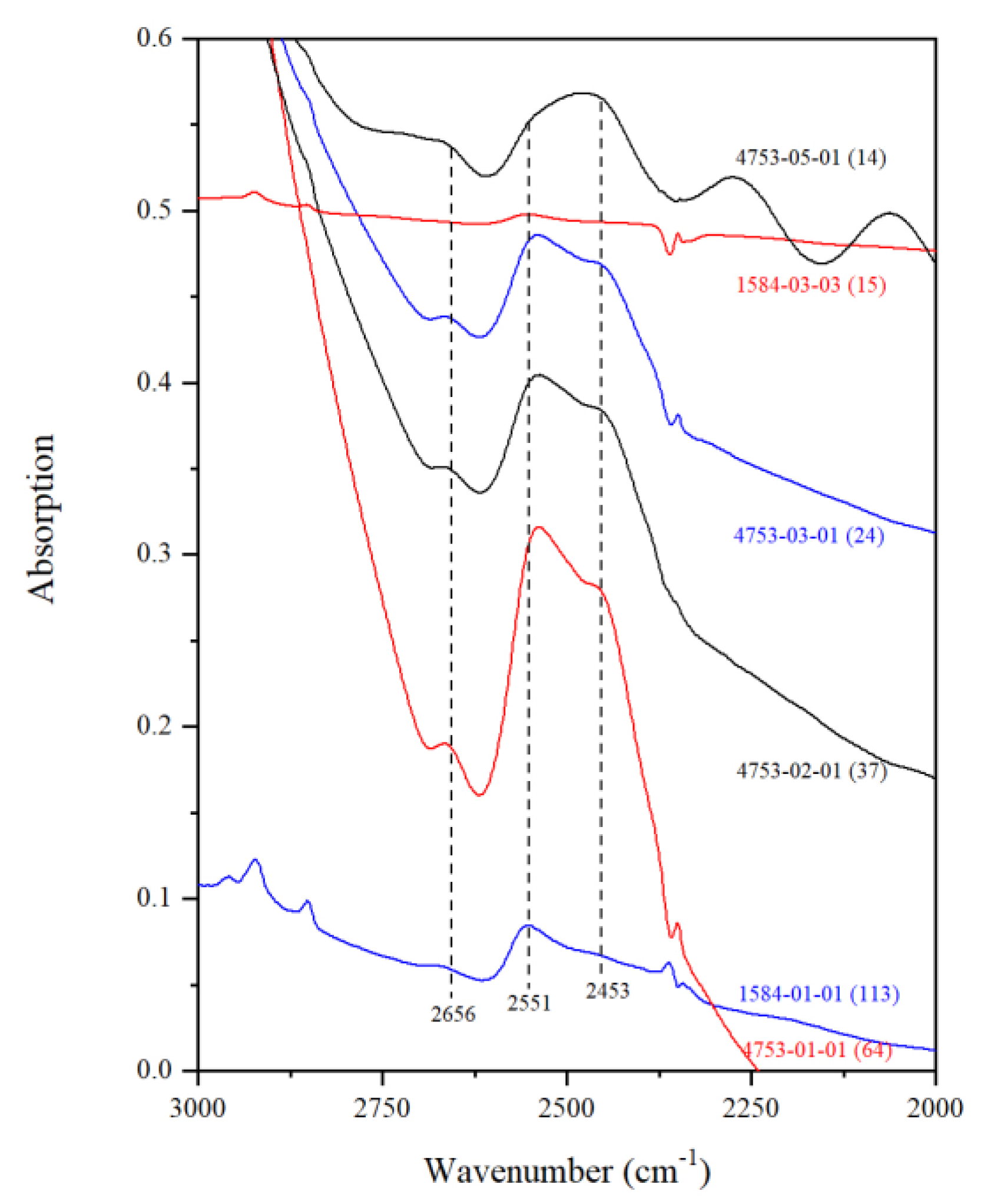
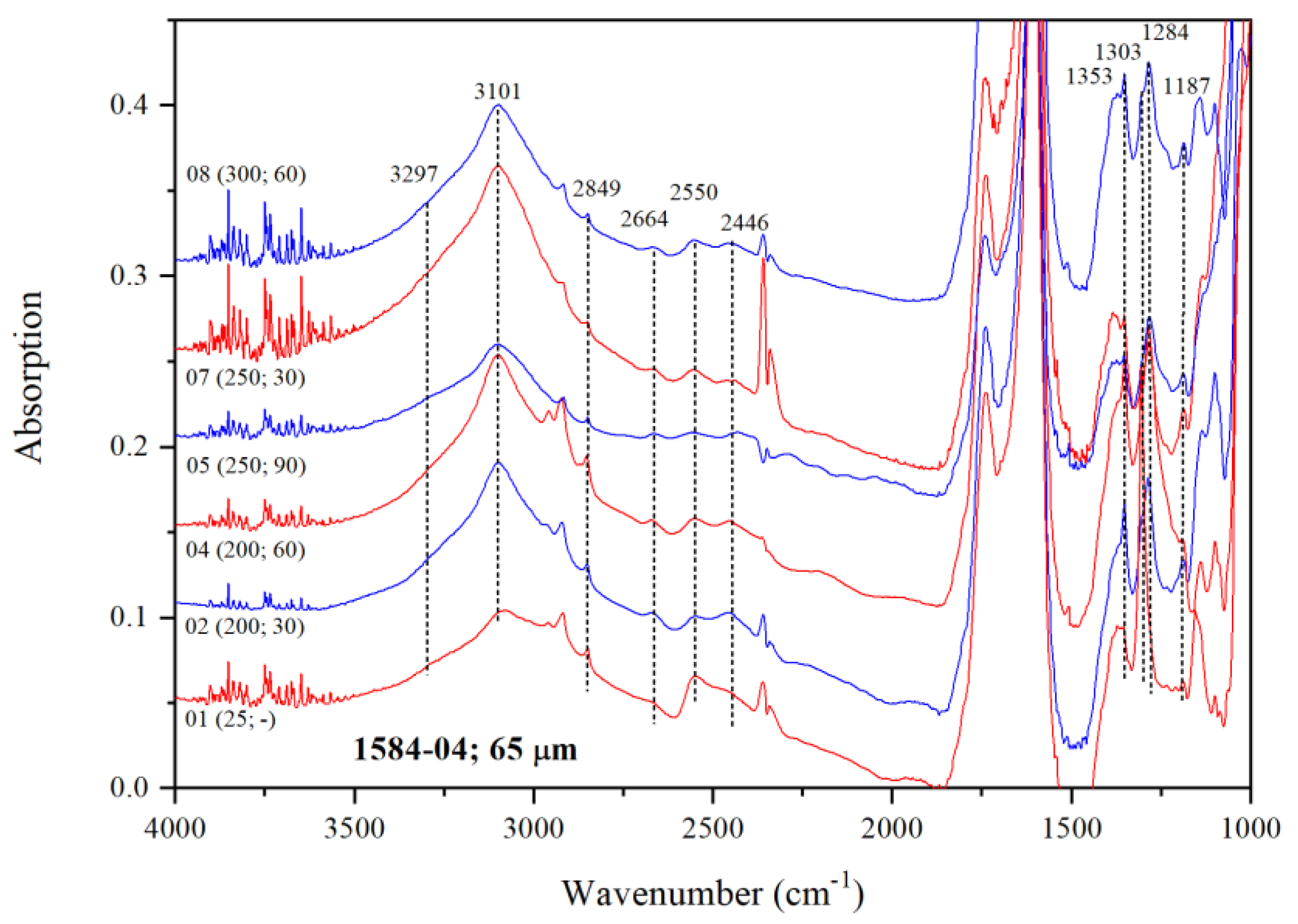
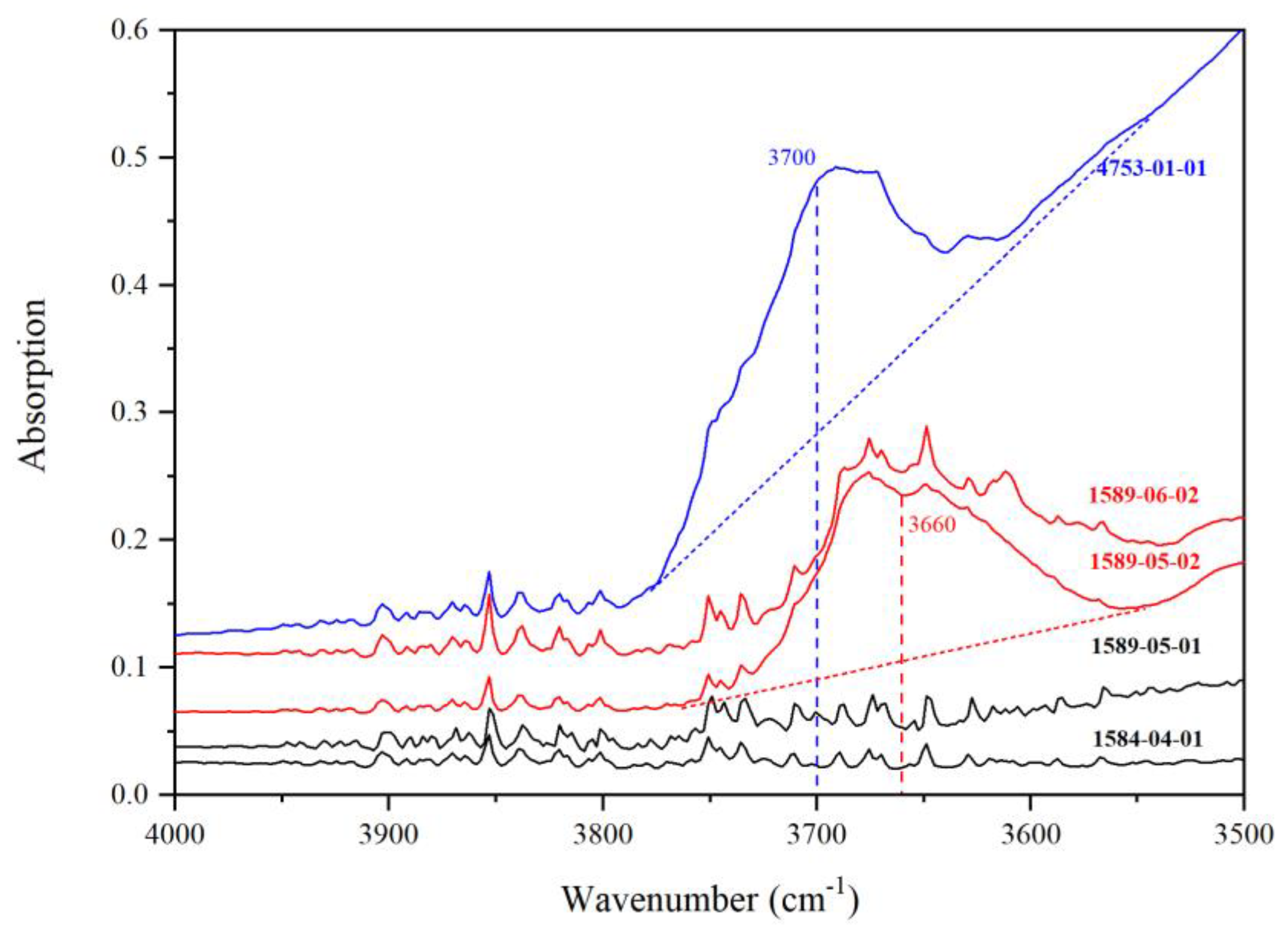
| Run | Crystal | Dma | IR | A1850–1500b | Dc2c | A3730–2000b | CH2O |
|---|---|---|---|---|---|---|---|
| # | # | (μm) | # | (cm−1) | (μm) | (cm−1) | (ppm) |
| 1584 | 01 | 113 | 1584-01-01 | 87.45 | 81.7 | 70.31 | 1149 |
| 1584-01-02 | 87.23 | 81.5 | 70.27 | 1151 | |||
| 1584-01-03 | 122.55 | 114.5 | 83.4 | 972 | |||
| 1584-01-04 | 122.12 | 114.1 | 76.5 | 895 | |||
| 1584-01-05 | 118.33 | 110.5 | 84.35 | 1019 | |||
| 1584-01-06 | 87.92 | 82.1 | 74.05 | 1204 | |||
| 03 | 15 | 1584-03-01 | 23.13 | 21.6 | 51.86 | 3203 d | |
| 1584-03-02 | 23.16 | 21.6 | 26.56 | 1639 | |||
| 1584-03-03 | 18.52 | 17.3 | 19.23 | 1483 | |||
| 04 | 65 | 1584-04-01 | 63.67 | 59.5 | 53.92 | 1210 | |
| 1589 | 01 | 52 | 1589-01-01 | 39.06 | 36.5 | 148.14 | 5418 |
| 02 | 52 | 1589-02-01 | 39.05 | 36.5 | 158.25 | 5791 | |
| 03 | 52 | 1589-03-01 | 21.83 | 20.4 | 45.16 | 2956 d | |
| 04 | 52 | 1589-04-01 | 41.17 | 38.4 | 150.08 | 5209 | |
| 05 | 63 | 1589-05-01 | 49.24 | 46 | 186.67 | 5416 | |
| 06 | 69 | 1589-06-01 | 48.47 | 45.3 | 192.16 | 5665 | |
| 4753 | 01 | 64 | 01/01/4753 | 68.2 | 63.7 | 761.8 | 15,961 |
| 02/01/4753 | 68.26 | 63.8 | 786.64 | 16,465 | |||
| 03/01/4753 | 66.55 | 62.2 | 763.63 | 16,394 | |||
| 02 | 37 | 01/02/4753 | 36.65 | 34.2 | 441.28 | 17,206 | |
| 02/02/4753 | 27.58 | 25.8 | 258.63 | 13,401 | |||
| 03/02/4753 | 35.64 | 33.3 | 410.19 | 16,447 | |||
| 03 | 24 | 01/03/4753 | 27.93 | 26.1 | 343.54 | 17,577 | |
| 02/03/4753 | 27.58 | 25.8 | 336.52 | 17,435 | |||
| 03/03/4753 | 28.79 | 26.9 | 310.11 | 15,390 | |||
| 05 | 14 | 01/05/4753 | 15.61 | 14.6 | 183.38 | 16,789 |
| Crystal | Dma | T | t | IR | A1850–1500b | Dc2c | A3730–2000b | CH2O |
|---|---|---|---|---|---|---|---|---|
| # | (μm) | (°C) | (min) | # | (cm−1) | (μm) | (cm−1) | (ppm) |
| Crystals from Run 1584 | ||||||||
| 04 | 65 | 200 | 30 | 1584-04-02 | 64.34 | 60.1 | 57.5 | 1277 |
| 200 | 60 | 1584-04-04 | 72.13 | 67.4 | 58.44 | 1158 | ||
| 250 | 90 | 1584-04-05 | 41.35 | 38.6 | 34.11 | 1179 | ||
| 250 | 30 | 1584-04-07 | 61.37 | 57.3 | 69.05 | 1608 | ||
| 300 | 60 | 1584-04-08 | 60.36 | 56.4 | 50.2 | 1188 | ||
| Crystals from Run 1589 | ||||||||
| 01 | 52 | 350 | 15 | 1589-01-02 | 31.43 | 29.4 | 101.19 | 4600 |
| 350 | 15 | 1589-01-03 | 39.23 | 36.6 | 111.28 | 4053 | ||
| 350 | 15 | 1589-01-04 | 39.23 | 36.6 | 93.03 | 3388 | ||
| 350 | 15 | 1589-01-05 | 38.79 | 36.2 | 119.87 | 4415 | ||
| 350 | 15 | 1589-01-06 | 36.67 | 34.2 | 104.08 | 4056 | ||
| 02 | 52 | 400 | 15 | 1589-02-02 | 39.99 | 37.3 | 138.04 | 4932 |
| 400 | 15 | 1589-02-03 | 38.96 | 36.4 | 127.11 | 4662 | ||
| 400 | 15 | 1589-02-04 | 38.76 | 36.2 | 126.81 | 4675 | ||
| 400 | 15 | 1589-02-05 | 34.51 | 32.2 | 110.9 | 4591 | ||
| 400 | 15 | 1589-02-06 | 40.87 | 38.2 | 115.11 | 4025 | ||
| 03 d | 52 | 450 | 15 | 1589-03-02 | 19.62 | 18.3 | 35.13 | 2558 |
| 450 | 15 | 1589-03-03 | 19.89 | 18.6 | 41.53 | 2983 | ||
| 450 | 15 | 1589-03-04 | 20.85 | 19.5 | 35.04 | 2401 | ||
| 450 | 15 | 1589-03-05 | 21.76 | 20.3 | 40.49 | 2659 | ||
| 450 | 15 | 1589-03-06 | 19.53 | 18.2 | 18.58 | 1359 | ||
| 04 | 52 | 500 | 15 | 1589-04-02 | 39.41 | 36.8 | 86.33 | 3130 |
| 500 | 15 | 1589-04-03 | 35.05 | 32.7 | 52.46 | 2138 | ||
| 500 | 15 | 1589-04-04 | 36.98 | 34.5 | 76.35 | 2950 | ||
| 500 | 15 | 1589-04-05 | 35.17 | 32.8 | 63.39 | 2575 | ||
| 500 | 30 | 1589-04-06 | 39.37 | 36.8 | 69.7 | 2530 | ||
| 05 | 63 | 550 | 15 | 1589-05-02 | 60.7 | 56.7 | 83.66 | 1969 |
| 550 | 15 | 1589-05-03 | 62.49 | 58.4 | 103.49 | 2367 | ||
| 550 | 15 | 1589-05-04 | 63.16 | 59 | 93.24 | 2109 | ||
| 06 | 69 | 600 | 15 | 1589-06-02 | 39.35 | 36.8 | 75.54 | 2743 |
| 600 | 15 | 1589-06-03 | 46.19 | 43.1 | 94.62 | 2927 | ||
| Study/Run | D/CH2Oa | IR Peaks (cm−1) at Ambient P and T | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mg-Rw as synthesized from conventional high-P experiments | |||||||||||||||||||||
| B03/H1302 | 50/0.21 | 3700 | - | - | - | - | - | - | - | - | 3120 | - | - | 2540 | - | - | - | - | - | - | - |
| B00/H892 | 45/0.78 | 3695 | - | - | - | - | - | - | - | - | 3120 | - | - | - | 2455 | 1347 | - | 1286 | 1191 | - | |
| P13/SZ0817 b | 20/1.0 | - | - | - | - | - | - | - | - | (3273)3127(3088) | - | - | - | - | - | - | - | - | - | - | - |
| Y14/- | 30/1.1 | 3695 | - | - | - | - | - | - | - | - | 3115 | - | - | 2550 | 2472 | - | - | - | - | - | - |
| C06/load 2 c | 16/1.7 | 3668 | - | - | - | - | - | - | - | - | 3151 | - | - | 2543 | 2460 | - | 1349 | - | 1279 | - | 1184 |
| Y12/SZ0820 | 30/1.77 | 3688 | 3598 | - | - | - | - | - | - | - | 3127 | 2830 | 2654 | 2538 | 2350 | - | - | - | - | - | - |
| P13/SZ0820 | 25/1.77 | 3662 | - | - | - | - | - | - | - | - | 3122 | - | - | - | - | 1352 | - | - | 1286 | - | 1176 |
| T15/SZ0820 d | 84/1.77 | 3670 | - | 3568 | - | - | 3412 | - | - | - | 3130 | 2809 | - | 2504 | - | - | - | - | - | - | - |
| TS/1584 | -/0.10 | - | - | - | - | - | - | - | - | 3278 | 3088 | 2845 | 2670 | 2554 | 2454 | 1356 | - | 1304 | - | 1189 | - |
| TS/1589 | -/0.55 | 3701 | - | - | - | - | 3407 | - | 3348 | - | 3100 | 2849 | 2660 | 2556 | 2448 | 1352 | - | 1307 | 1282 | 1194 | - |
| TS/4753 | -/1.63 | 3682 | - | - | - | - | - | - | - | - | 3118 | - | 2663 | 2538 | 2445 | - | 1347 | - | 1281 | - | 1186 |
| Mg-Rw as further annealed at high 600 °C and 1 atm | |||||||||||||||||||||
| TS/1589 | -/0.55 | 3667 | - | - | 3510 | 3461 | 3405 | - | 3345 | 3270 | - | 2849 | - | 2500 | 2448 | 1387 | - | 1307 | 1284 | 1191 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Sui, Z.; Fei, H.; Yan, W.; Ma, Y.; Ye, Y. IR Features of Hydrous Mg2SiO4-Ringwoodite, Unannealed and Annealed at 200–600 °C and 1 atm, with Implications to Hydrogen Defects and Water-Coupled Cation Disorder. Minerals 2020, 10, 499. https://doi.org/10.3390/min10060499
Liu X, Sui Z, Fei H, Yan W, Ma Y, Ye Y. IR Features of Hydrous Mg2SiO4-Ringwoodite, Unannealed and Annealed at 200–600 °C and 1 atm, with Implications to Hydrogen Defects and Water-Coupled Cation Disorder. Minerals. 2020; 10(6):499. https://doi.org/10.3390/min10060499
Chicago/Turabian StyleLiu, Xi, Zhaoyang Sui, Hongzhan Fei, Wei Yan, Yunlu Ma, and Yu Ye. 2020. "IR Features of Hydrous Mg2SiO4-Ringwoodite, Unannealed and Annealed at 200–600 °C and 1 atm, with Implications to Hydrogen Defects and Water-Coupled Cation Disorder" Minerals 10, no. 6: 499. https://doi.org/10.3390/min10060499
APA StyleLiu, X., Sui, Z., Fei, H., Yan, W., Ma, Y., & Ye, Y. (2020). IR Features of Hydrous Mg2SiO4-Ringwoodite, Unannealed and Annealed at 200–600 °C and 1 atm, with Implications to Hydrogen Defects and Water-Coupled Cation Disorder. Minerals, 10(6), 499. https://doi.org/10.3390/min10060499





