The Role of Barite in the Post-Mining Stabilization of Radium-226: A Modeling Contribution for Sequential Extractions
Abstract
1. Introduction
2. Materials and Methods
2.1. An Example of Sequential Extractions Targeting U and 226Ra in Mill Tailings
2.1.1. Study on Bois Noirs Limouzat Tailings
2.1.2. Selection of Samples for this Study
2.1.3. Identification of the Minerals of Interest in the Mineral Assemblage for the Sequential Extractions Modeling
2.2. Development of the Model
2.3. Model Construction for the Sequential Extractions on Bois Noirs Limouzat Mill Tailing Samples
2.3.1. Mineral Quantities
- For the optimum model: from the quantities of total aqueous SO4, total aqueous Ba and total aqueous Fe respectively that were extracted during the sequential extractions. This “optimum model” will be discussed in the Results Section 3;
- For the bulk model: only from the bulk analysis of the samples. The quantity of ferrihydrite was determined using the total Fe content of the bulk samples measured by chemical analysis, the quantity of gypsum from the total sulfur (S) content and the quantity of barite from the total Ba content. This “bulk model” will be discussed in the Discussion Section 4.1.
2.3.2. Building the Initial State of the Model for the Tailing Samples
2.3.3. Modeling the Extraction Steps
2.4. Test Model for the Mineral Reactivity Towards Each of the Reactants
3. Results
3.1. The Reactivity of the Minerals with Each Reactant
3.2. Understanding the Sequential Extraction of Tailing Samples through Modeling
3.2.1. Behavior of the Major Elements
Ca, SO42−, Ba
Fe
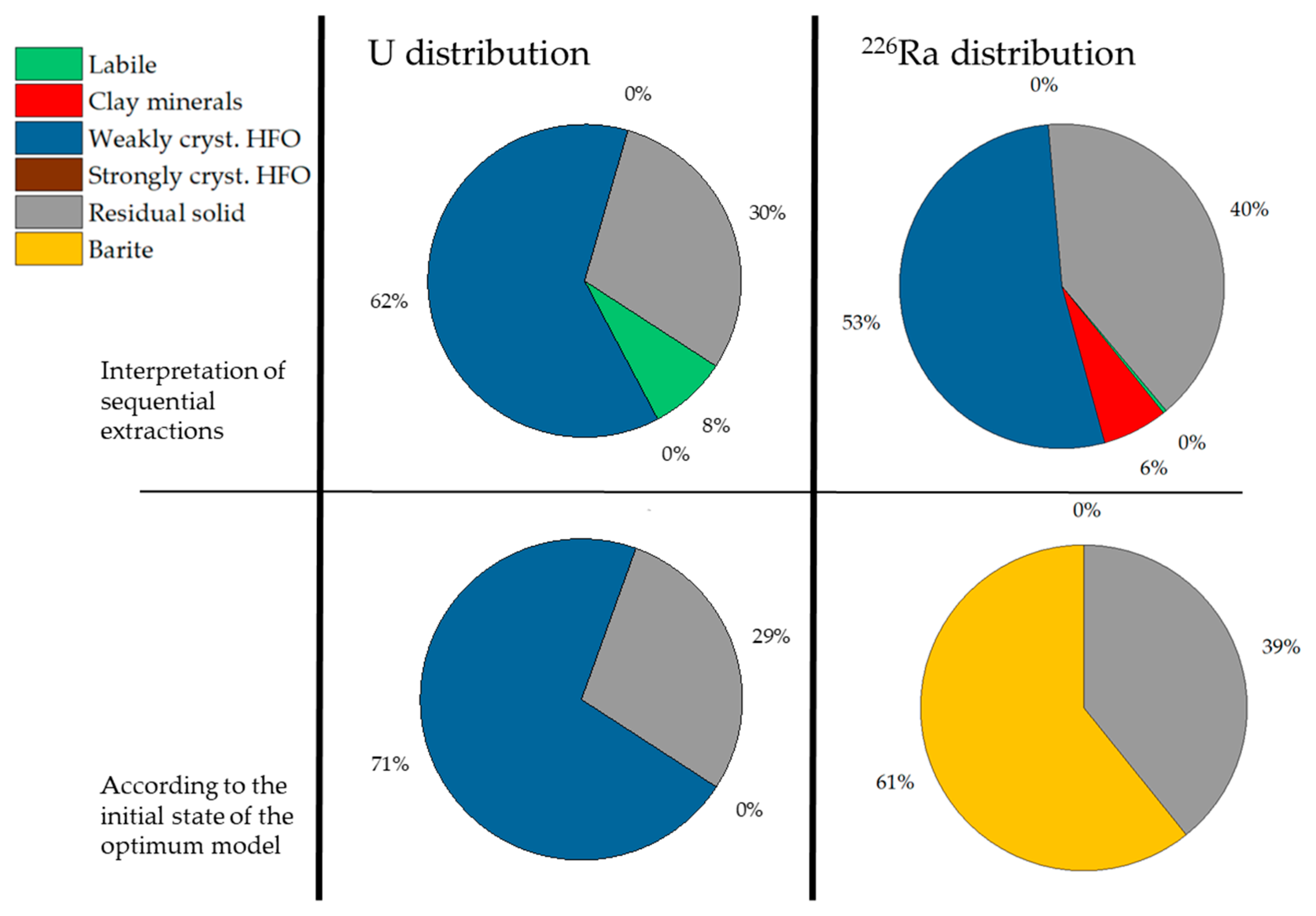
3.2.2. Trace and Ultra-Trace Elements Behavior and Distribution: U and 226Ra
U
226. Ra
4. Discussion
4.1. Building the Model with Less Data: A Sensitivity Study
- the experimental results with
- the results obtained from the sequential extraction model presented previously—the “optimum model” built upon the mineral quantities derived from experimental leaching data—and with
- the results of this modeling of sequential extractions—the “bulk model” can be found for sample C1P3B in Figure 5, and for samples C1P5H and C1P11B in Supplementary Materials Section 6.1.
4.2. Field Application: A Different Interpretation on the Origin of Extractable 226Ra in Tailing Samples
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ballini, M.; Chautard, C.; Nos, J.; Phrommavanh, V.; Beaucaire, C.; Besançon, C.; Boizard, A.; Cathelineau, M.; Peiffert, C.; Vercouter, T.; et al. A multi-scalar study of the long-term reactivity of uranium mill tailings (Bellezane, France). J. Environ. Radioact. 2020, 218, 106223. [Google Scholar] [CrossRef] [PubMed]
- Phan, T.T.; Capo, R.C.; Stewart, B.W.; Graney, J.R.; Johnson, J.D.; Sharma, S.; Toro, J. Trace metal distribution and mobility in drill cuttings and produced waters from Marcellus Shale gas extraction: Uranium, arsenic, barium. Appl. Geochem. 2015, 60, 89–103. [Google Scholar] [CrossRef]
- Van Sice, K.; Cravotta, C.A.; McDevitta, B.; Taskera, T.L.; Landisc, J.D.; Puhra, J.; Warnera, N.R. Radium attenuation and mobilization in stream sediments following oil and gas wastewater disposal in western Pennsylvania. Appl. Geochem. 2018, 98, 393–403. [Google Scholar] [CrossRef]
- Liu, D.J.; Hendry, M.J. Controls on 226Ra during raffinate neutralization at the Key Lake uranium mill, Saskatchewan, Canada. Appl. Geochem. 2011, 26, 2113–2120. [Google Scholar] [CrossRef]
- Benĕs, P.; Sedláček, J.; Šebesta, F.; Šandrik, R.; John, J. Method of selective dissolution for characterization of radium and barium in natural and waste waters. Water Res. 1981, 15, 1299–1304. [Google Scholar] [CrossRef]
- Tessier, A.; Campbell, P.G.C.; Bisso, M. Sequential extraction procedure for the speciation of particulate trace metals. Anal. Chem. 1979, 51, 844–851. [Google Scholar] [CrossRef]
- Schultz, M.K.; Burnetta, W.C.; Inn, K.G.W. Evaluation of a sequential extraction method for determining actinide fractionation in soils and sediments. J. Environ. Radioact. 1998, 40, 155–174. [Google Scholar] [CrossRef]
- Perez-Moreno, S.M.; Gazquez, M.J.; Perez-Lopez, R.; Bolivar, J.P. Validation of the BCR sequential extraction procedure for natural radionuclides. Chemosphere 2018, 198, 397–408. [Google Scholar] [CrossRef]
- Virtanen, S.; Vaaramaa, K.; Lehto, J. Fractionation of U, Th, Ra and Pb from boreal forest soils by sequential extractions. Appl. Geochem. 2013, 38, 1–9. [Google Scholar] [CrossRef]
- Bacon, J.; Davidson, C. Is there a future for sequential chemical extraction? Analyst 2008, 133, 25–46. [Google Scholar] [CrossRef]
- Kheboian, C.; Bauer, C.F. Accuracy of selective extraction procedures for metal speciation in model aquatic sediments. Anal. Chem. 1987, 59, 1417–1423. [Google Scholar] [CrossRef]
- Leermakers, M.; Mbachou, B.E.; Husson, A.; Lagneau, V.; Descostes, M. An alternative sequential extraction scheme for the determination of trace elements in ferrihydrite rich sediments. Talanta 2019, 199, 80–88. [Google Scholar] [CrossRef] [PubMed]
- Blanco, P.; Vera Tomé, F.; Lozano, J.C. Sequential extraction for radionuclide fractionation in soil samples: A comparative study. Appl. Radiat. Isot. 2004, 610–611, 345–350. [Google Scholar] [CrossRef] [PubMed]
- Dodd, J.; Large, D.J.; Fortey, N.J.; Milodowski, A.E.; Kemp, S. A petrographic investigation of two sequential extraction techniques applied to anaerobic canal bed mud. Environ. Geochem. Health 2000, 22, 281–296. [Google Scholar] [CrossRef]
- Gleyzes, C.; Tellier, S.; Astruc, M. Fractionation studies of trace elements in contaminated soils and sediments: A review of sequential extraction procedures. Trends Analyt. Chem. 2002, 21, 451–467. [Google Scholar] [CrossRef]
- Vandenhove, H.; Vanhoudt, N.; Duquène, L.; Autunes, K.; Wannijn, J. Comparison of two sequential extraction procedures for uranium fractionation in contaminated soils. J. Environ. Radioact. 2014, 137, 1–9. [Google Scholar] [CrossRef]
- Ouyang, B.; Renock, D.J.; Ajemigbitse, M. a.; Van Sice, K.; Warner, N.R.; Landisa, J.D.; Feng, X. Radium in hydraulic fracturing wastewater: Distribution in suspended solids and implications to its treatment by sulfate co-precipitation. Environ. Sci. Process. Impacts 2019, 21, 339–351. [Google Scholar] [CrossRef]
- Somot, S. Radium, Uranium et Métaux dans les Résidus de Traitement Dynamique, Acide et Alcalin, de Minerais d’uranium. Ph.D. Thesis, Université Henri Poincaré, Nancy, France, 1997. [Google Scholar]
- Kersten, M.; Förstner, U. Chemical fractionation of heavy metals in anoxic estuarine and coastal sediments. Water Sci. Technol. 1986, 18, 121–130. [Google Scholar] [CrossRef]
- Menozzi, D.; Dosseto, A.; Kinsley, L. Assessing the effect of sequential extraction on the uranium-series isotopic composition of a basaltic weathering profile. Chem. Geol. 2016, 446, 126–137. [Google Scholar] [CrossRef]
- Gontier, A. Quantification de l’altération dans les sols par les déséquilibres radioactifs: Approche sur sol total et phases minérales séparées. Ph.D. Thesis, Université de Strasbourg, Strasbourg, France, 2014. [Google Scholar]
- Chautard, C.; Beaucaire, C.; Gérard, M.; Roy, R.; Savoye, S.; Descostes, M. Geochemical characterization of U tailings: U and 226Ra retention (Bois Noirs Limouzat, France). J. Environ. Radioact. 2020, 218, 106251. [Google Scholar] [CrossRef]
- Renock, D.J.; Landis, J.D.; Sharma, M. Reductive weathering of black shale and release of barium during hydraulic fracturing. Appl. Geochem. 2016, 65, 73–86. [Google Scholar] [CrossRef]
- Regenspurg, S.; Margot-Roquier, C.; Harfouche, M.; Froidevaux, P.; Steinmann, P.; Junier, P.; Bernier-Latmani, R. Speciation of naturally-accumulated uranium in an organic-rich soil of an alpine region (Switzerland). Geochim. Cosmochim. Acta 2010, 74, 2083–2098. [Google Scholar] [CrossRef]
- Shaw, S.A.; Hendry, M.J.; Essilfie-Dughan, J.; Kotzer, T.; Wallschläger, D. Distribution, characterization, and geochemical controls of elements of concern in uranium mine tailings, Key Lake, Saskatchewan, Canada. Appl. Geochem. 2011, 26, 2044–2056. [Google Scholar] [CrossRef]
- Stewart, B.W.; Chapman, E.C.; Capo, R.C.; Johnson, J.D.; Graney, J.R.; Kirby, C.S.; Schroeder, K.T. Origin of brines, salts and carbonate from shales of the Marcellus Formation: Evidence from geochemical and Sr isotope study of sequentially extracted fluids. Appl. Geochem. 2015, 60, 78–88. [Google Scholar] [CrossRef]
- IAEA. Management of NORM Residues; IAEA-TECDOC-1712: Vienna, Austria, 2013; ISBN 978-92-0-142710-6. [Google Scholar]
- Meija, J.; Coplen, T.B.; Berglund, M.; Brand, W.A.; De Bièvre, P.; Gröning, M.; Holden, N.E.; Irrgeher, J.; Loss, R.D.; Walczyk, T.; et al. Isotopic Compositions of the Elements 2013 (IUPAC Technical Report). Pure Appl. Chem. 2016, 88, 293–306. [Google Scholar] [CrossRef]
- IRSN. Radium-226; Radioprotection: Radionucléides; IRSN: Fontenay-aux-Roses, France, 2014. [Google Scholar]
- Karsten, L.; Michalik, B.; Wiegand, J. Availability of radium isotopes and heavy metals from scales and tailings of Polish hard coal mining. J. Environ. Radioact. 2007, 94, 137–150. [Google Scholar]
- Rowan, E.L.; Engle, M.A.; Kirby, C.S.; Kraemer, T.F. Radium Content of Oil- and Gas-Field Produced Waters in the Northern Appalachian Basin (USA): Summary and Discussion of Data; U.S. Geological Survey: Reston, VA, USA, 2011.
- Cuney, M. The extreme diversity of uranium deposits. Miner. Depos. 2008, 44, 3–9. [Google Scholar] [CrossRef]
- Cuney, M. World-class unconformity-related uranium deposits: Key factors for their genesis. In Proceedings of the Mineral Deposit Research: Meeting the Global Challenge, Beijing, China, 18–21 August 2005; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Cuney, M. Geologic environment, mineralogy, and fluid inclusions of the Bois Noirs-Limouzat uranium vein, Forez, France. Econ. Geol. 1978, 73, 1567–1610. [Google Scholar] [CrossRef]
- Pagel, M.; Mao, J.; Bierlein, F.P. Uranium deposits in the Arlit area (Niger). In Mineral Deposit Research: Meeting the Global Challenge; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Nirdosh, I.; Muthuswami, S.V.; Baird, M.H.I. Radium in uranium mill tailing – Some observations on retention and removal. Hydrometallurgy 1984, 12, 151–176. [Google Scholar] [CrossRef]
- Robertson, J.; Hendry, M.J.; Kotzer, T.; Hughes, K.A. Geochemistry of uranium mill tailings in the Athabasca Basin, Saskatchewan, Canada: A review. Crit. Rev. Environ. Sci. Technol. 2019, 29, 1237–1293. [Google Scholar] [CrossRef]
- Fesenko, S.; Carvalho, F.; Martin, P.; Moore, W.S.; Yankovic, T. Radium in the Environment. In The Environmental Behaviour of Radium: Revised Edition; IAEA: Vienna, Austria, 2014; pp. 33–105. [Google Scholar]
- Molinari, J.; Snodgrass, W.J. The Chemistry and Radiochemistry of Radium and the Other Elements of the Uranium and Thorium Natural Decay Series. In The Environmental Behaviour of Radium; IAEA Technical Report Series No. 310; IAEA: Vienna, Austria, 1990; Volume 1, pp. 11–56. ISBN 92-0-125090-8. [Google Scholar]
- Ames, L.L.; McGarrah, J.E.; Walker, B.A. Sorption or uranium and radium by biotite, muscovite and phlogopite. Clays Clay Miner. 1983, 32, 343–351. [Google Scholar] [CrossRef]
- Reinoso-Maset, E.; Ly, J. Study of uranium(VI) and radium(II) sorption at trace level on kaolinite using a multisite ion exchange model. J. Environ. Radioact. 2016, 157, 136–148. [Google Scholar] [CrossRef] [PubMed]
- Robin, V.; Tertre, E.; Beaufort, D.; Regnault, O.; Sardini, P.; Descostes, M. Ion exchange reactions of major inorganic cations (H+, Na+, Ca2+, Mg2+ and K+) on beidellite: Experimental results and new thermodynamic database. Toward a better prediction of contaminant mobility in natural environments. Appl. Geochem. 2015, 59, 74–84. [Google Scholar] [CrossRef]
- Nirdosh, I.; Trembley, W.B.; Johnson, C.R. Adsorption-Desorption Studies on the 226Ra-Hydrated Metal Oxide Systems. Hydrometallurgy 1990, 24, 237–248. [Google Scholar] [CrossRef]
- Sajih, M.; Bryan, N.D.; Livens, F.R.; Vaughan, D.J.; Descostes, M.; Phrommavanh, V.; Nos, J.; Morris, K. Adsorption of radium and barium on goethite and ferrihydrite: A kinetic and surface complexation modelling study. Geochim. Cosmochim. Acta 2014, 146, 150–163. [Google Scholar] [CrossRef]
- Bordelet, G.; Beaucaire, C.; Phrommavanh, V.; Descostes, M. Chemical reactivity of natural peat towards U and Ra. Chemosphere 2018, 202, 651–660. [Google Scholar] [CrossRef]
- Doerner, H.A.; Hoskins, W.M. Co-precipitation of radium and barium sulfates. J. Am. Chem. Soc. 1925, 47, 662–675. [Google Scholar] [CrossRef]
- Curie, M. Radium and the New Concepts in Chemistry. Nobel Lecture. 1911. [Google Scholar]
- Lestini, L.; Beaucaire, C.; Vercouter, T.; Ballini, M.; Descostes, M. Role of trace elements in the 226-radium incorporation in sulfate minerals (gypsum and celestite). ACS Earth Space Chem. 2019, 3, 295–304. [Google Scholar] [CrossRef]
- USGS Fact Sheet FS-142-99. Naturally Occurring Radioactive Materials (NORM) in Produced Water and Oil-Field Equipment—An Issue for the Energy Industry; USGS: Denver, CO, USA, 1999.
- Grundl, T.; Cape, M. Geochemical factors controlling radium activity in a sandstone aquifer. Ground Water 2006, 4, 518–527. [Google Scholar] [CrossRef]
- Brandt, F.; Curti, E.; Klinkenberg, M.; Rozov, K.; Bosbach, D. Replacement of barite by a (Ba,Ra)SO4 solid solution at close-to-equilibrium conditions: A combined experimental and theoretical study. Geochim. Cosmochim. Acta 2015, 155, 1–15. [Google Scholar] [CrossRef]
- Somot, S.; Pagel, M.; Thiry, J. Spéciation du radium dans les résidus de traitement acide de mineai d’uranium de l’Ecarpière (Vendée–France). Compte-rendu de l’Académie des Sciences, Sciences de la terre et des planètes (Earth Planet. Sci.) 1997, 325, 111–118. [Google Scholar]
- Abdelouas, A. Uranium mill tailings: Geochemistry, mineralogy, and environmental impact. Elements 2006, 2, 335–341. [Google Scholar] [CrossRef]
- Stieff, L.R. The characterization of uranium mill tailings using alpha-sensitive nuclear emulsions. In Proceedings of the 7th Symposium on Management of Uranium Mill Tailings, Low-Level Waste and Hazardous Waste, Fort Collins, CA, USA, 6–8 February 1985. [Google Scholar]
- Wagman, D.D.; Evans, W.H.; Parker, V.B.; Schumm, R.H.; Halow, I.; Bailey, S.M.; Churney, K.L.; Nuttall, R.L. The NBS Tables of chemical thermodynamic properties. Selected values for inorganic and C1 and C2 organic substances in SI units. J. Phys. Chem. Ref. Data 1982, 1, 407. [Google Scholar]
- Rutten, A.; de Lange, G.J. A novel selective extraction of barite, and its application to eastern Mediterranean sediments. Earth Planet. Sci. Lett. 2002, 198, 11–24. [Google Scholar] [CrossRef]
- Van Beek, P. Utilisation de la barytine sédimentaire marine pour les études paléocéanographiques de l’Holocène. Ph.D. Thesis, Université Paris VI, Paris, France, 2001. [Google Scholar]
- Eagle, M.; Paytan, A.; Arrigo, K.R.; van Dijken, G.; Murray, R.W. A comparaison between excess barium and barite as indicators of carbon export. Paleoceanogr. Paleoclimatol. 2003, 18, 1021. [Google Scholar]
- Sato, A.; Mori, N.; Takakura, M.; Notoya, S. Examination of analytical conditions for trace elements based on the detection limit for EPMA (WDS). JEOL News 2007, 42, 46–52. [Google Scholar]
- Batanova, V.G.; Sobolev, A.V.; Magnin, V. Trace element analysis by EPMA in geosciences: Detection limit, precision and accuracy. IOP Conf. Ser. Mater. Sci. Eng. 2018, 304, 012001. [Google Scholar] [CrossRef]
- Goulden, W.D. The geochemical distribution of radium-226 in Cluff Lake uranium mill tailings. Master’s Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 1997. [Google Scholar]
- Bunzl, K.; Kretner, R.; Schramel, P.; Szeles, M.; Winkler, R. Speciation of 238U, 226Ra, 210Pb, 228Ra, and stable Pb in the soil near an exhaust ventilating shaft of a uranium mine. Geoderma 1995, 67, 45–53. [Google Scholar] [CrossRef]
- Landis, J.D.; Sharma, M.; Renock, D.; Niu, D. Rapid desorption of radium isotopes from black shale during hydraulic fracturing. 1. Source phases that control the release of Ra from Marcellus Shale. Chem. Geol. 2018, 496, 1–13. [Google Scholar] [CrossRef]
- Gnanapragasam, E.K.; Lewis, B.-A.G. Elastic stain energy and the distribution coefficient of radum in solid solutions with calcium salts. Geochim. Cosmochim. Acta 1995, 59, 5103–5111. [Google Scholar] [CrossRef]
- Yoshida, Y.; Nakazawa, T.; Yoshikawa, H.; Nakanishi, T. Partition coefficient of Ra in gypsum. J. Radioanal. Nucl. Chem. 2009, 280, 541–545. [Google Scholar] [CrossRef]
- Parkhust, D.L.; Appelo, C.A.J. User’s Guide to PHREEQC Version2: A Computer Program for Speciation, Batch-reaction, One Dimensional Transport and Inverse Geochemical Calculations; Water-Resources Investigations; U.S. Departpment of the Interior, USGS: Denver, CO, USA, 1999.
- Combes, P.; Schmitt, J.M. Etude Hydrologique et Géochimique du Site Minier Des Bois Noirs; CIG Paris School of Mines: Fontainebleau, France, 2006. [Google Scholar]
- Tertre, E.; Ferrage, E.; Bihannic, I.; Michot, L.J.; Prêt, D. Influence of the ionic strength and solid/solution ratio on Ca(II)-for-Na+ exchange on montmorillonite. Part 2: Understanding the effect of the m/V ratio. Implications for pore water composition and element transport in natural media. J. Colloid Interface Sci. 2011, 363, 334–347. [Google Scholar] [CrossRef] [PubMed]
- Reinoso-Maset, E.; Ly, J. Study of major ions sorption equilibria to characterize the ion exchange properties of kaolinite. J. Chem. Eng. Data 2014, 59, 4000–4009. [Google Scholar] [CrossRef]
- Schwertmann, U. Solubility and dissolution of iron oxides. Plant Soil 1991, 130, 1–25. [Google Scholar] [CrossRef]
- Dzombak, D.A.; Morel, F.M.M. Surface Complexation Modelling. Hydrous Ferric Oxide; John Wiley & Sons: Hoboken, NJ, USA, 1990. [Google Scholar]
- Nos, J.; Boizard, A.; Peiffert, C.; Cathelineau, M.; Phrommavanh, V.; Descostes, M. Caractérisation et Réactivité des Résidus de Traitement Issus de L’exploitation des Minerais D’uranium en France (Lavaugrasse, Bellezane, Ribière, Cellier); Projet Envir@Mines–PNGMDR 2; AREVA: Paris, France, 2014. [Google Scholar]
- Reiller, P.; Descostes, M. Development and application of the thermodynamic database PRODATA dedicated to the monitoring of mining activities from exploration to remediation. Chemosphere 2020, 251, 126301. [Google Scholar] [CrossRef]
- Mahoney, J.; Cadle, S.; Jakubowski, R. Uranyl adsorption onto hydrous ferric oxides—A re-evaluation for the diffuse layer model database. Environ. Sci. Technol. 2009, 43, 9260–9266. [Google Scholar] [CrossRef]
- Gossuin, Y.; Colet, J.-M.; Roch, A.; Muller, R.N.; Gillis, P. Cesium Adsorption in Hydrated Iron Oxide Particles Suspensions: An NMR Study. J. Magn. Reson. 2002, 157, 132–136. [Google Scholar] [CrossRef]
- Robin, V.; Tertre, E.; Beaucaire, C.; Regnault, O.; Descostes, M. Experimental data and assessment of predictive modeling for radium ion-exchange on beidellite, a swelling clay mineral with a tetrahedral charge. Appl. Geochem. 2017, 85, 1–9. [Google Scholar] [CrossRef]
- Tertre, E. Détermination d’une Base de Données Opérationnelle Relative à L’adsorption sur les Minéraux Argileux; AREVA: Paris, France, 2017. [Google Scholar]
- Pabalan, R.T.; Turner, D.R. Uranium(6+) sorption on montmorillonite: Experimental and surface complexation modeling study. Aquat. Geochem. 1997, 2, 203–226. [Google Scholar] [CrossRef]
- Tertre, E.; Beaucaire, C.; Coreau, N.; Juery, A. Modeling of Zn sorption onto clayey sediments using a multi-site and multi-component ion-exchange model. Appl. Geochem. 2009, 24, 1852–1861. [Google Scholar] [CrossRef]
- Curti, E.; Fujiwara, K.; Iijima, K.; Tits, J.; Cuesta, C.; Kitamura, A.; Glaus, M.A.; Müller, W. Radium uptake during barite recrystallization at 23 ± 2 °C as a function of solution composition: An experimental 133Ba and 226Ra tracer study. Geochim. Cosmochim. Acta 2010, 74, 3553–3570. [Google Scholar] [CrossRef]
- Langmuir, D.; Reise, A.C. The thermodynamic properties of radium. Geochim. Cosmochim. Acta 1985, 49, 1593–1601. [Google Scholar] [CrossRef]
- Zhang, T.; Gregory, K.; Hammack, R.W.; Vidic, R.D. Co-precipitation of radium with barium and strontium sulfate and its impact on the fate of radium during treatment of produced water from unconventional gas extraction. Environ. Sci. Technol. 2014, 48, 4596–4603. [Google Scholar] [CrossRef] [PubMed]
- Chuiton, G.; Sanchez, B. Etude de la Composition Chimique de l’eau Interstitielle des sédiments du Grand Bassin du Forez; Gestion des résidus du Forez—Analyses sur produits carottés; Institut de Protection et de Sûreté Nucléaire—CEA: Fontenay-aux-Roses, France, 1984. [Google Scholar]
- Blount, C. Barite solubilities and thermodynamic quantities up to 300 °C and 1400 bars. Am. Mineral. 1977, 62, 9–10. [Google Scholar]
- Atun, G.; Bascetin, E. Adsorption of barium on kaolinite, illite and montmorillonite at various ionic strengths. Radiochimica Acta 2003, 91, 223–228. [Google Scholar] [CrossRef]
- Eylem, C.; Erten, H.N.; Göktürk, H. Sorption of barium on kaolinite, montmorillonite and chlorite. Analyst 1989, 114, 351–353. [Google Scholar] [CrossRef]
- Zhang, P.; Brady, P.; Arthur, S.; Zhou, W.Q.; Sawyer, D.; Hesterberg, D. Adsorption of barium (II) on montmorillonite: An EXAFS study. Colloids Surf. A Physicochem. Eng. Asp. 2001, 190, 239–249. [Google Scholar] [CrossRef]
- COGEMA. Site des Bois Noirs Limouzat-Situation Actuelle et Etudes d’hypothèses d’améliorations Pour Assurer Une Sécurité Durable; COGEMA: Paris, France, 1998. [Google Scholar]
- Sardini, P.; Angileri, A.; Descostes, M.; Duval, S.; Oger, T.; Partier, P.; Rividi, N.; Siitari-Kauppi, M.; Toubon, H.; Donnard, J. Quantitative autoradiography of alpha particle emission in geo-materials using the BeaverTM system. Nucl. Instrum. Methods Phys. Res. A 2016, 833, 15–22. [Google Scholar] [CrossRef]
- Angileri, A.; Sardini, P.; Donnard, J.; Duval, S.; Lefeuvre, H.; Oger, T.; Partier, P.; Rividi, N.; Siitari-Kauppi, M.; Toubon, H.; et al. Mapping 238U decay chain equilibrium state in thin sections of geo-materials by digital autoradiography and microprobe analysis. Appl. Radiat. Isot. 2018, 140, 228–237. [Google Scholar] [CrossRef]
- Angileri, A.; Sardini, P.; Beaufort, D.; Amiard, G.; Beaufort, M.F.; Nicolai, J.; Siitari-Kauppi, M.; Descostes, M. Mobility of daughter elements of 238U decay chain during leaching by In Situ Recovery (ISR): New insights from digital autoradiography. J. Environ. Radioact. 2020, 220–221, 106274. [Google Scholar] [CrossRef]
- Billon, S.; Sardini, P.; Angileri, A.; Beaucaire, C.; Parneix, J.-C.; Siitari-Kauppi, M.; Descostes, M. Quantitative imaging of 226Ra ultratrace distribution using electronic autoradiography: case of doped celestines. J. Environ. Radioact. 2020, 217, 106211. [Google Scholar] [CrossRef] [PubMed]

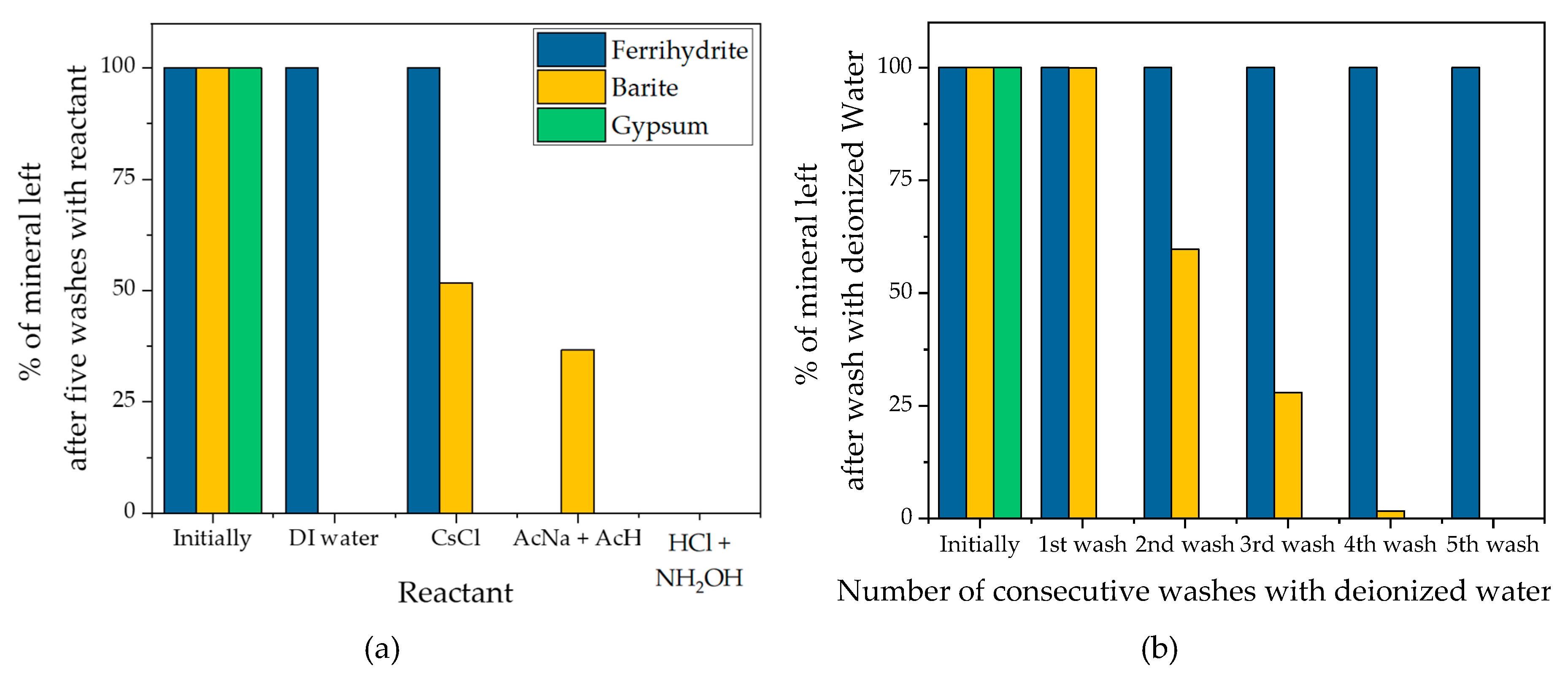
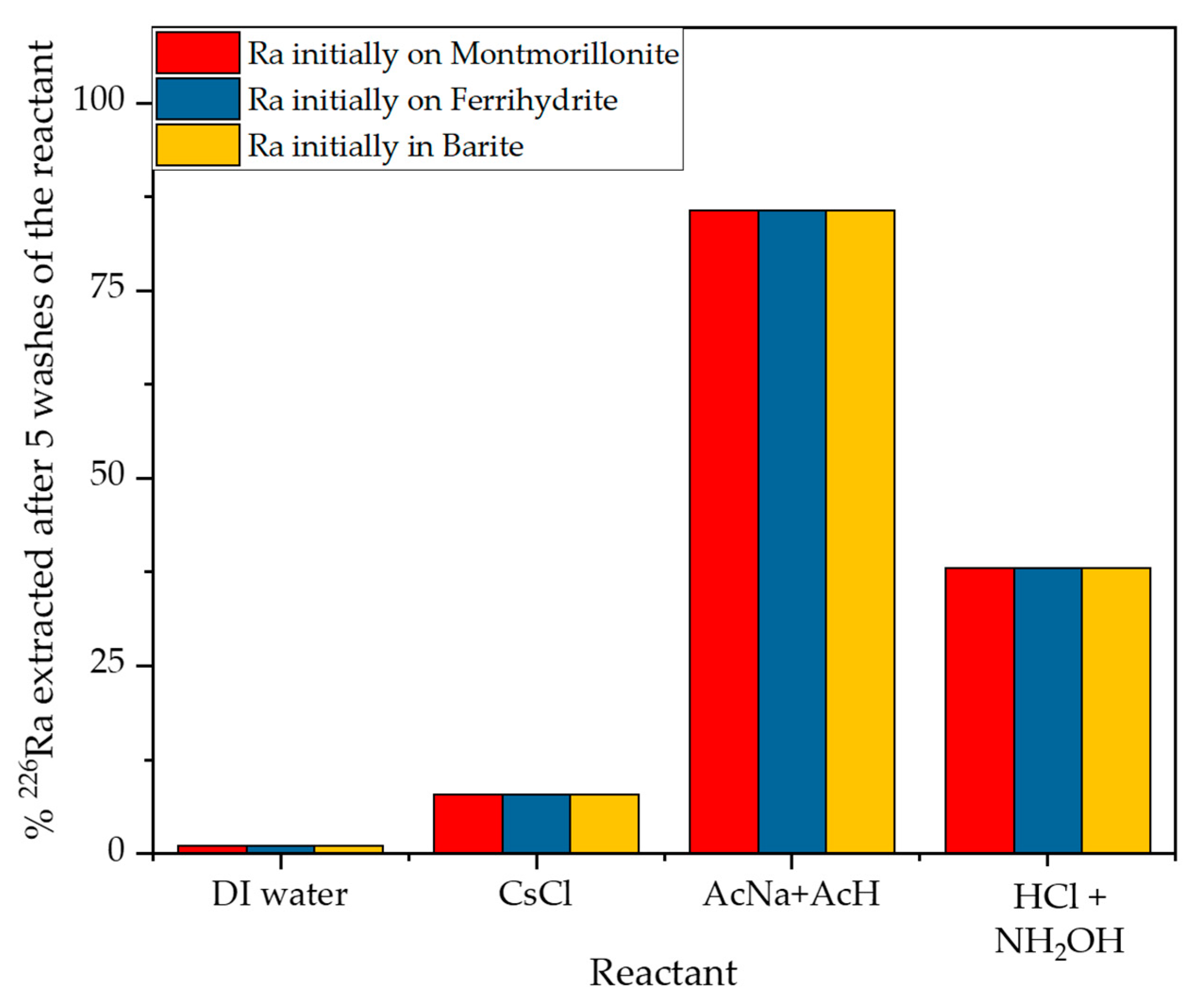
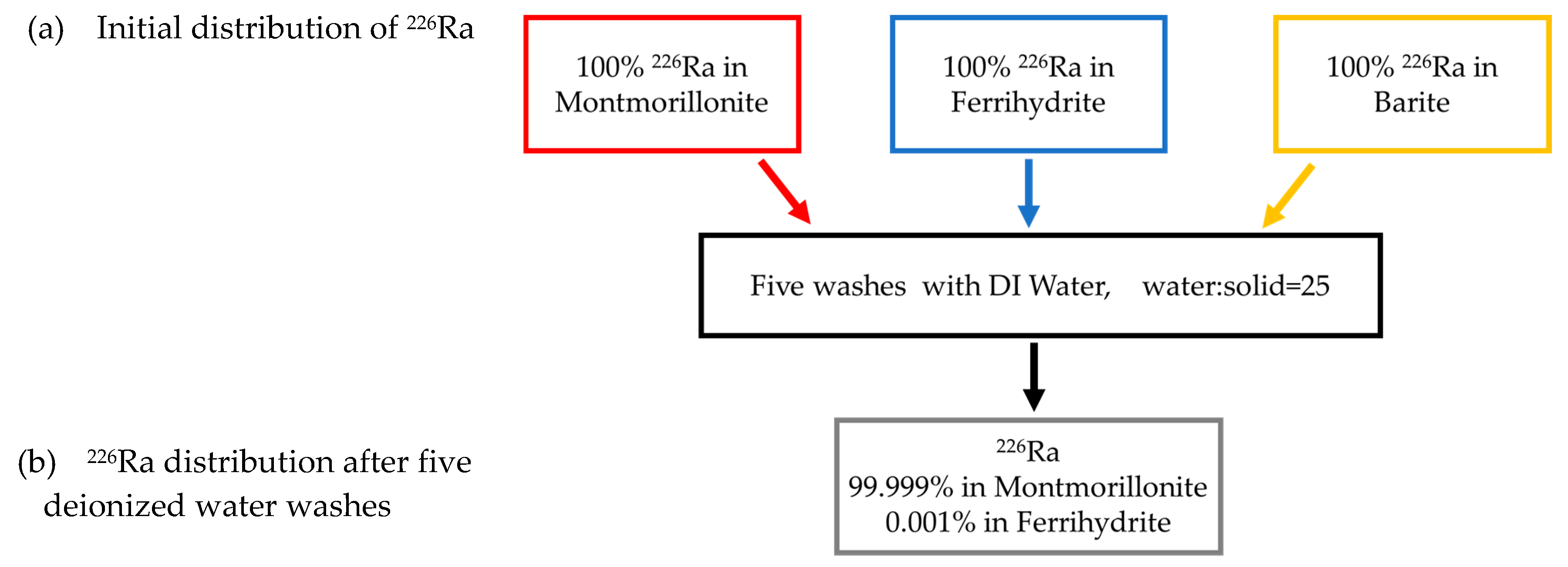
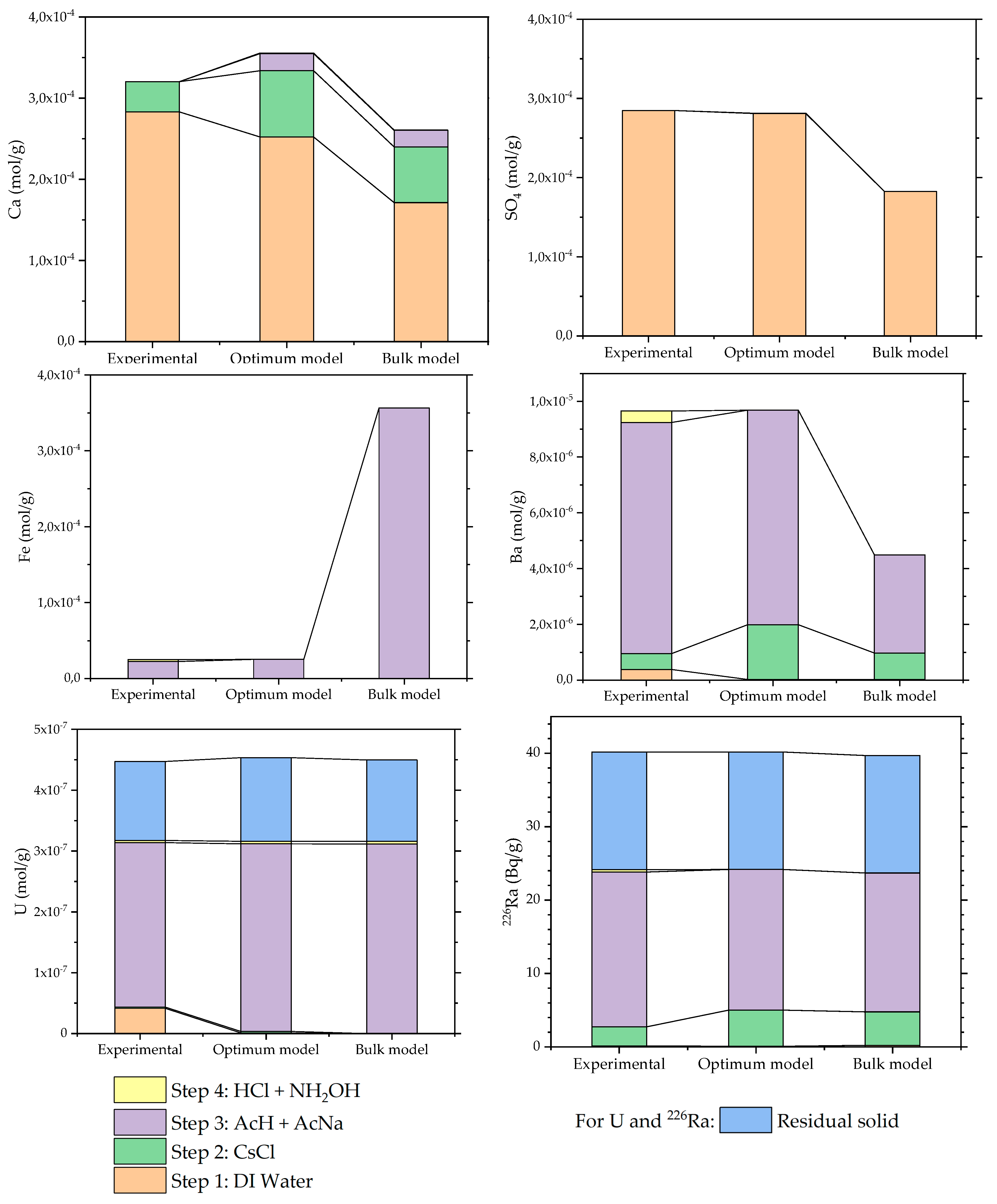
| Step | Reactant Used | |
|---|---|---|
| Experimental Study [22] | Modeling (This Study) | |
| 1—targeting soluble phases | 40 mL deionized water | 40 mL pure water in equilibrium with atmospheric CO2 |
| 2—targeting elements sorbed on clay minerals | 40 mL 10−2 M CsCl | 40 mL 10−2 M CsCl solution in equilibrium with atmospheric CO2 |
| 3—targeting carbonates and weakly crystallized ferric oxyhydroxides | 40 mL solution 1 M sodium acetate in 25% acetic acid, pH = 4 | 40 mL solution pH fixed at 4 solution concentrations: Na: 1 M Acetate: 5.2 M (1 M from sodium acetate, 4.2 M from 25% acetic acid) |
| 4—targeting strongly crystallized ferric oxyhydroxides | 40 mL solution NH2OH 0.04 M under the form of hydroxylamine hydrochloride + hydrochloric acid to fix pH = 2 | 40 mL solution solution concentrations: Cl: 0.05 M (0.04 M for hydroxylamine hydrochloride + 0.01 M for HCl to pH = 2) Solution in equilibrium with H2 gas phase fixing Eh = −3 V/SHE |
| Minerals | Observations | As Considered in the Model |
|---|---|---|
| Primary minerals | Quartz predominant, K-feldspar and plagioclases | Not considered |
| Clay minerals | Kaolinite, smectite, chlorite | Included as montmorillonite |
| Micas | Biotite, muscovite | Included as montmorillonite |
| Sulfate minerals | Gypsum, barite | Included |
| Sulfides | Partly oxidized pyrites | Included as ferrihydrite |
| Oxides/oxyhydroxides | Secondary iron oxyhydroxydes: ferrihydrite and goethite | Included as ferrihydrite |
| U-minerals | Uraninites included in quartz, apatites, monazites, uranyl phosphates | Considered as refractory part of U, not included |
| Sample | Gypsum (mol/g) | Ferrihydrite (mol/g) | Barite (mol/g) | Montmorillonite (g/g) | |||
|---|---|---|---|---|---|---|---|
| Optimum Model | Bulk Model | Optimum Model | Bulk Model | Optimum Model | BULK MODEL | Both Models | |
| C1P3B | 2.8 × 10−4 | 1.69 × 10−4 | 2.5 × 10−5 | 3.6 × 10−4 | 1.1 × 10−5 | 5.1 × 10−6 | 0.37 |
| C1P5H | 1.4 × 10−4 | 2.35 × 10−4 | 4.0 × 10−5 | 4.1 × 10−4 | 2.9 × 10−6 | 2.1 × 10−6 | 0.43 |
| C1P11B | 5.8 × 10−5 | 8.1 × 10−5 | 2.0 × 10−5 | 3.6 × 10−4 | 3.9 × 10−6 | 2.1 × 10−6 | 0.47 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Besançon, C.; Chautard, C.; Beaucaire, C.; Savoye, S.; Sardini, P.; Gérard, M.; Descostes, M. The Role of Barite in the Post-Mining Stabilization of Radium-226: A Modeling Contribution for Sequential Extractions. Minerals 2020, 10, 497. https://doi.org/10.3390/min10060497
Besançon C, Chautard C, Beaucaire C, Savoye S, Sardini P, Gérard M, Descostes M. The Role of Barite in the Post-Mining Stabilization of Radium-226: A Modeling Contribution for Sequential Extractions. Minerals. 2020; 10(6):497. https://doi.org/10.3390/min10060497
Chicago/Turabian StyleBesançon, Clémence, Camille Chautard, Catherine Beaucaire, Sébastien Savoye, Paul Sardini, Martine Gérard, and Michael Descostes. 2020. "The Role of Barite in the Post-Mining Stabilization of Radium-226: A Modeling Contribution for Sequential Extractions" Minerals 10, no. 6: 497. https://doi.org/10.3390/min10060497
APA StyleBesançon, C., Chautard, C., Beaucaire, C., Savoye, S., Sardini, P., Gérard, M., & Descostes, M. (2020). The Role of Barite in the Post-Mining Stabilization of Radium-226: A Modeling Contribution for Sequential Extractions. Minerals, 10(6), 497. https://doi.org/10.3390/min10060497






