Abstract
The hemispherical temperature (HT) is the most important indicator representing ash fusion temperatures (AFTs) in the Polish industry to assess the suitability of coal for combustion as well as gasification purposes. It is important, for safe operation and energy saving, to know or to be able to predict value of this parameter. In this study a non-linear model predicting the HT value, based on ash oxides content for 360 coal samples from the Upper Silesian Coal Basin, was developed. The proposed model was established using the machine learning method—extreme gradient boosting (XGBoost) regressor. An important feature of models based on the XGBoost algorithm is the ability to determine the impact of individual input parameters on the predicted value using the feature importance (FI) technique. This method allowed the determination of ash oxides having the greatest impact on the projected HT. Then, the partial dependence plots (PDP) technique was used to visualize the effect of individual oxides on the predicted value. The results indicate that proposed model could estimate value of HT with high accuracy. The coefficient of determination (R2) of the prediction has reached satisfactory value of 0.88.
1. Introduction
Ash fusion temperatures (AFTs) are widely used to characterize the ash fusibility, which is a basic characteristic to assess the propensity of ash to slagging and fouling processes during combustion at high temperatures [1,2]. The formation of slag in combustion processes is responsible for significant operational and maintenance problems [3]. This may result in increased costs and reduced process efficiency. AFTs are an important parameters because they also determines the behavior of coal ash in the other processes of coal conversion e.g., coal gasification, liquefaction and ash-utilization [4,5,6].
Determination of AFTs is based on measurements of the dimensional changes of an ash cone as a function of temperature during which four characteristic temperature points are identified under both oxidizing and reducing conditions [7,8,9]. These points define the temperature range in which the ash melting process takes place. Details of the ash fusion test, like the shape and size of samples and the way of their preparation, are defined by standard used in Poland—PN-ISO 540:2001. Specific temperature points are described in Table 1.

Table 1.
Ash fusion temperatures (AFTs) according to the PN-ISO 540:2001 standard.
An AFTs measurement is generally expensive, time consuming and hard to repeat because it could generate an error during laboratory analysis [10,11]. Moreover, the ash fusion laboratory test has been questioned as it is more like a quantitative observation [12]. Despite the shortcomings, AFTs are still widely used to assess the deposition characteristics of coal. Therefore, it is important to know, or be able to predict, the ash fusibility characteristics of a coal before it is fed to the boiler or reactor [13].
A number of studies have been carried out to predict AFTs of the coal ash using various methods. In the literature, there are three main directions of research aimed at forecasting AFTs. Many of them have focused on empirical or statistical correlations between AFTs and ash composition [6,8,14,15,16,17,18,19]. In most cases various regression analysis were used in order to find correlations between AFTs and coal ash composition. For instance, Özbayoglu et al. [17] showed that non-linear correlations are better than linear correlations for estimating AFTs of Turkish coals. Non-linear correlations were developed by using the chemical composition of ash (eight oxides) and coal parameters such as ash content, specific gravity, Hardgrove index and mineral matter content. Lolja et al. [16] analyzed the ash fusion temperatures for Albanian coals using oxides analysis from various perspectives. It was reconfirmed that AFTs were decreased by an increase in the basic oxide content.
As an alternative for empirical and statistical methods Huggins et al. [14] proposed equilibrium phase diagrams to determine liquid temperatures that parallel the fusion temperatures of the formed ash. Further research was carried out by Jak [8] using thermodynamic modeling of phase equilibria to characterize the behavior of coal mineral matter and predict AFTs.
Another direction of research is the use of machine learning methods to predict AFTs [11,20,21,22,23,24,25,26,27,28,29]. The most frequently techniques used were artificial neural networks (ANNs) and support vector machine (SVM). Yin et al. [27] and Miao et al. [22] used a back propagation neural network models on Chinese coals in order to predict AFTs. In the first case seven inputs were used. In the second case different numbers of inputs and hidden layers were tested and the model giving the best results was chosen. Karimi et al. [21] applied the adaptive neuro-fuzzy inference system (ANFIS) method on samples of US coals. As a model input different combinations of metal oxides where used. The SVM method was used to create the AFTs predictive model by Gao et al. [20]. The parameters of SVM were optimized by the improved ant colony algorithm. Recently, Xiao et al. [26] have used the SVM model optimized by the grey-wolf algorithm. The purpose of the study was to predict IDT and investigate how SO3 as an input parameter affects prediction performance.
Despite many studies devoted to prediction and finding the relationship between ash composition and AFTs, this issue is still not fully recognized and requires further research and improvement. For example, methods like ANN and SVM are classified as black box models. The main drawback of these types of models is that they cannot lead to any new knowledge about the process. The results cannot be checked in any simple way, as no additional information is available from the model. In other words, they are unable to reveal the complicated relationship between ash oxides and AFTs.
Vassilev et al. [4] specified the hemispherical temperature (HT) as the major ash fusion temperature measurement, which correspond significant melting of the most minerals (resulting from the intensive solution of the more refractory components) and some changes of flow properties and viscosity of the plastic phases. In Poland, the HT value among the AFTs characteristics is the most desirable parameter when determining the coal supply specifications for combustion processes. Especially, stoker-fired boilers for private users are designed to burn coal with a specific HT. This value also forms the basis of the Polish coal classification due to ash fusibility (easily, medium and difficult fusible) [30].
Therefore, the aim of this study was to create predicting model of HT using machine learning method—extreme gradient boosting (XGBoost) regressor [31]. It is a specific implementation (uses more accurate approximations) of the gradient boosting method, which is an ensemble learner. The effectiveness of XGBoost method has been proven by better performance than other machine learning methods on a variety of benchmark datasets [32].
An important feature of models based on XGBoost algorithm is the ability to determine the impact of individual input parameters on the predicted value using the feature importance (FI) technique. This could allow the determination of ash oxides having the greatest impact on the predicted HT. The main advantage of FI is the ability to capture non-linear relationships between parameters. Other methods of determining the significance of individual input terms such as, linear regression models, can only represent linear relationships. In this case, manual non-linearity modeling is needed, which is difficult to find. XGBoost is able to automatically calculate both linear and non-linear dependency between variables. In addition, the partial dependence plots (PDP) technique [33] was used to achieve a graphical representation of the marginal effect that a particular variable has on the ensemble predictions ignoring the rest of the variables. It is important that PDP is not a representation of the dataset values, it is a representation of the ensemble results, therefore it allowed us to investigate whether the relationship between the particular oxides and a predicted HT is linear, monotonic or more complex. Together, these two techniques enable the in-depth interpretation of machine learning black box models.
The predictive model was established for 360 samples of Polish coals. Ash content varies widely from country to country and even regions of a particular country [16,34]. Therefore, coals from different geological areas could reveal distinct ash fusibility due to their different coal-forming environment and different composition of the mineral matter [35]. This study focuses on Polish coals from the Upper Silesian Coal Basin. To our knowledge it is the first comprehensive analysis of Polish coal ashes and its influence on AFTs. Therefore, this investigation can be useful through comparative analysis with results of other basin studies.
2. Materials and Methods
2.1. Data Set
A set of 360 samples of Polish hard coals, acquired from various mines of the Upper Silesian Coal Basin (USCB), was the subject of the analyses presented in this work. USCB is one of the most intensively mined areas in Europe. The area of USCB is located in Poland and in the Czech Republic. Within the Polish territory (Figure 1) the area of the Upper Silesian Coal Basin is estimated at about 5600 km2. There are 144 documented hard coal deposits, including 43 deposits under exploitation, 54 undeveloped deposits and 47 abandoned deposits [36].
Figure 1.
Location of the Upper Silesian Coal Basin.
For each sample following parameters were determined:
- Ash chemical composition (content of the following oxides: SiO2, Al2O3, Fe2O3, CaO, MgO, Na2O, K2O, SO3, TiO2, P2O5 and Mn3O4) according to standard ISO 13605:2018,
- Hemispherical temperature of ash (HT) in a reducing atmosphere (mixture of CO:CO2 in a ratio of 3:2) according to standard PN-ISO 540:2001.
The analyses of the samples were carried out in the accredited laboratory of the Department of Solid Fuel Quality Assessment at the Central Mining Institute, Poland. Descriptive statistics of above mentioned parameters in an analyzed set of samples are presented in Table 2. Histogram of hemispherical temperatures in an analyzed set of samples is shown in Figure 2.

Table 2.
Descriptive statistics of coal parameters in an analyzed set of samples.
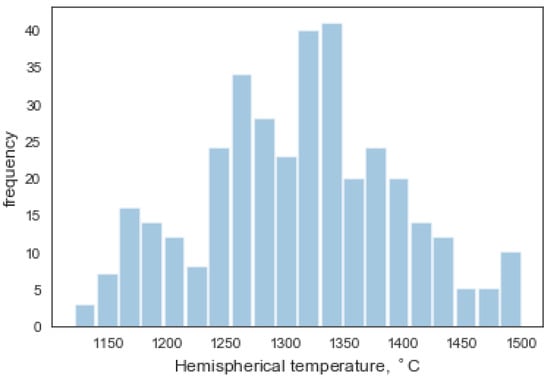
Figure 2.
Histogram of hemispherical temperature in analyzed samples.
2.2. Extreme Gradient Boosting (XGBoost)
XGBoost, short of extreme gradient boosting, [31] is an algorithm extending technique of gradient boosted decision trees. The basic idea of boosting is to combine a series of weak prediction models to a single, strong learner. Models are added to ensemble sequentially, in order to correct the errors made by existing learners [37]. The gradient boosting approach enhances the flexibility of boosting technique by employing gradient descent algorithm to minimize errors in sequential models [38].
A simple gradient boosting method is characterized by highly accurate estimations, but on the other hand, that technique is prone to over-fitting. XGBoost algorithm overcomes this limitation, by adding a regularization term into the objective function [31]:
This is an example of an equation:
where:
- yi—real value,
- —the prediction at the r-th round,
- gr—term denoting structure of decision tree,
- —loss function,
- n—number of training examples,
- —regularization term, given by formula:
- T—number of leaves,
- ω—weight of the leaves,
- λ and γ are coefficients, with default values set as λ = 1, γ = 0.
2.3. Feature Importance (FI)
Individual input predictors are rarely equally important in practical data mining problems. Usually only a few features have a significant impact on the output. The vast majority of predictors are irrelevant and might as well not be included in the model [39].
Feature importance (FI) is the statistical significance of the feature with respect to its impact on the generated model. Feature importance is explicitly calculated for each feature in the dataset, allowing them to be ordered and compared. The higher is relative importance of given attribute, the more significant is its impact on the output of the model.
Feature importance score is determined after the boosted trees are constructed. For a single decision tree D importance of predictor xj is calculated as [40]:
where the summation is over the non-terminal nodes t (non-leaves) of the J-terminal node tree D, vt is the splitting variable associated with node t, and is the corresponding empirical improvement in squared error as a result of using predictor xj as a splitting variable in the non-terminal node t.
Then, the feature importance is averaged across all of M decision trees within the model [33]:
2.4. Partial Dependence Plots (PDP)
The partial dependence plots (PDP) attempts to show the marginal effect of a given feature on the predicted outcome of a machine learning model, by plotting the average model outcome in terms of different values of that feature [33]. Hence, while the feature importance specifies what input features most affect prediction, PDP visualizes how a given variable affect prediction.
Given the output f(x) of the machine learning model, the partial dependence function for the chosen predictor is defined by the following formula [33,41]:
where:
- S—chosen predictor,
- C—the complement set of S (containing all other predictors),
- —feature vectors,
- —marginal probability density of .
Equation (5) can be estimated from a set of training data:
where:
- —the values of that occur in the training sample.
The partial dependence plots is a method with a global character. This technique considers all record and allows one to draw conclusions about the global relationship between the analyzed input variable and the predicted output [41].
2.5. Model Evaluation
The performance of predictive model was evaluated through the following metrics:
- Mean absolute error (MAE):
- Root mean squared error (RMSE):
- Coefficient of determination R2:
where:
- yi—the actual value of the dependent variable,
- di—the value of the dependent variable determined from the model,
- —the arithmetic mean of the actual values of the dependent variable.
2.6. Software
Data preparation, variable importance, development of predictive model and its evaluation were carried out using the Python programming language and its libraries dedicated to data analysis, machine learning and visualization (Pandas, Scikit-Learn, Matplotlib, Seaborn, XGBoost and pdpbox).
3. Results and Discussion
3.1. Feature Importance
A benefit of using ensembles of decision tree methods like XGBoost is that they can automatically provide estimates of feature importance from a trained predictive model. The effect of 11 different ash components (oxides) on the output of the model was investigated using the FI measure (Figure 3). The results showed that Al2O3 had the most significant influence on HT prediction, then respectively–Fe2O3, SO3, Na2O and CaO. These results were in a good agreement with previous studies concerning the relationship between ash composition and AFTs. Vassilev et al. [4] examined the impact of chemical and mineral composition of coals ashes on fusibility. According to them oxides of Si, Al, Fe, Ca and S had the main contribution for values of hemispherical temperature.
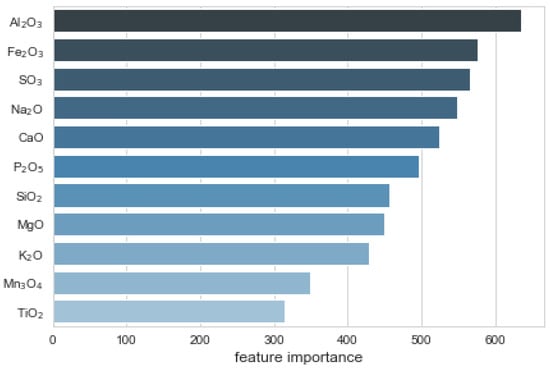
Figure 3.
Feature importance for predicting model of hemispherical temperature (HT).
It is well known that, acidic oxides (SiO2 and Al2O3) form a polymer structure that increase AFTs, while basic oxides (Fe2O3, CaO, MgO, Na2O and K2O) have a tendency to break the network structure, which decreases AFTs [18,42]. However, the fusibility of the coal may decrease to the minimum first and then increase as the content of flux increases [43].
3.2. Determining the Optimal Values of Model Hyperparameters
Every hyperparameter has a significant impact on the model performance. Therefore, their correct setting is crucial for the accuracy of the prediction. In this study, model hyperparameters were estimated using the grid search procedure. Grid search is the process of performing hyperparameters tuning that will methodically build and evaluate a model for each combination of algorithm hyperparameters specified in a grid. Grid search was additionally optimized by k-fold cross validation. This technique is widely used to evaluate performance of a model by handling the variance problem of the result set. The number of folds to use for cross-validation was set to 5. It was proved that for the following parameters the model performance was the best:
- n_estimators = 200—refers to number of trees in the ensemble,
- learning_rate = 0.08—step size shrinkage used in update to prevents overfitting,
- gamma = 0.3—minimum loss reduction required to make a further partition on a leaf node of the tree,
- subsample = 0.95—controls the number of samples (observations) supplied to a tree,
- min_child_weight = 1.5—the minimum number of instances required in a child node,
- colsample_bytree = 0.8—controls the number of features (variables) supplied to a tree,
- max_depth = 8—controls the depth of the tree.
3.3. Evaluation of the Model
The performance of the XGBoost model for prediction of HT was as follows:
- mean absolute error: 21.71,
- Root mean squared error: 29.16,
- R2: 0.88.
It is assumed that the smaller MAE and RMSE values indicate the model is more accurate. In the case of the R2 measure, which is one of the most popular indicators, the closer the value is to 1, the more accurate the model. Results show that the model could predict the HT with satisfactory efficiency. This was confirmed by the observations of the Figure 4, where individual points were arranged along the regression line.
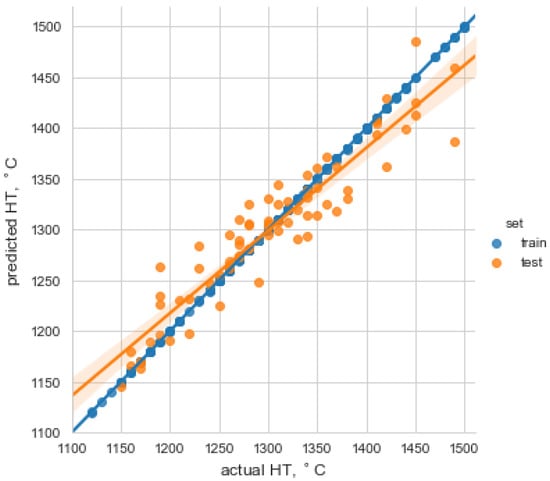
Figure 4.
Graphical comparison of experimental HT with those estimated by the XGBoost model for training and testing data.
To assess the performance of the proposed XGBoost model, two other typical predictive techniques were examined for the estimation of HT:
- Support vector regression (SVR) with RBF (radial basis function) kernel function, hyperparameters of that model were determined with grid search procedure: C = 1, ε = 0.01, γ = 10,
- Multiple linear regression (MLR), the coefficients of the model were determined by the least mean square algorithm.
In order to compare these two techniques with the XGBoost model the R2 metric was applied. Results (Table 3) indicated, that the proposed XGBoost model outperformed the other methods, as it had the highest value of R2 metric. However, while the effectiveness of another machine learning technique as SMV was also satisfactory (R2 = 0.83), the performance of the linear regression model was low (R2 = 0.34). This means that the linear relationships between the analyzed input variables and the predicted HT were very weak.

Table 3.
The results of examined methods for prediction of HT.
The learning curve of the developed XGBoost model is presented in Figure 5. The shape and dynamics of the learning curve allows you to determine the correctness of the behavior of the machine learning model. There are three typical dynamics observed in learning curves: underfit, overfit and good fit. A good fit is noticed on the learning curve when a training and testing loss decreases to a point of stability with a minimal gap between the two final loss values.
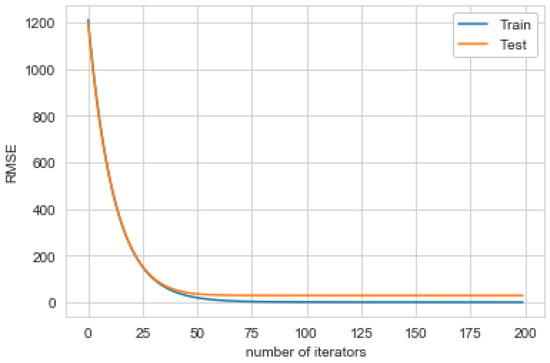
Figure 5.
Learning curve of the presented the XGBoost model.
3.4. Model Interpretation Using PDPs (Partial Dependence Plots)
Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 show partial dependence plots for oxides having the greatest impact on the HT prediction (according to Figure 3)—Al2O3, Fe2O3, SO3, Na2O, CaO and SiO2 (which in percentage is the main component of ash). The blue areas in the plots indicate the extent of uncertainty.
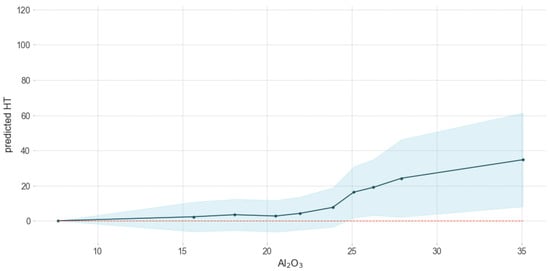
Figure 6.
Influence of Al2O3 on predicted HT.
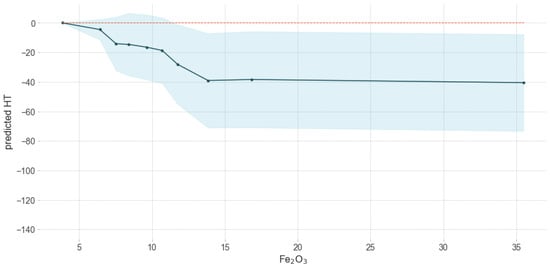
Figure 7.
Influence of Fe2O3 on predicted HT.
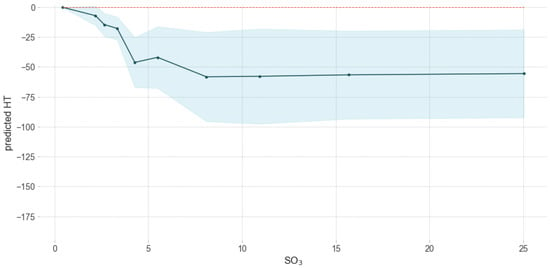
Figure 8.
Influence of SO3 on predicted HT.
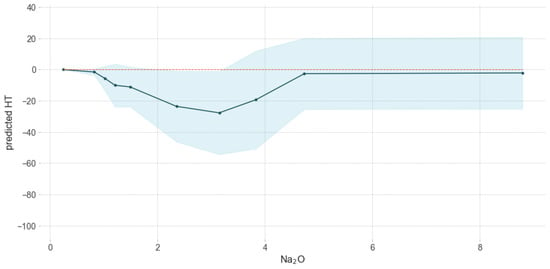
Figure 9.
Influence of Na2O on predicted HT.
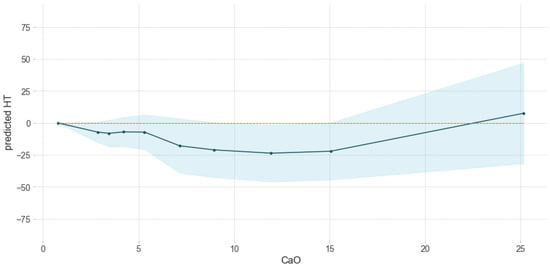
Figure 10.
Influence of CaO on predicted HT.
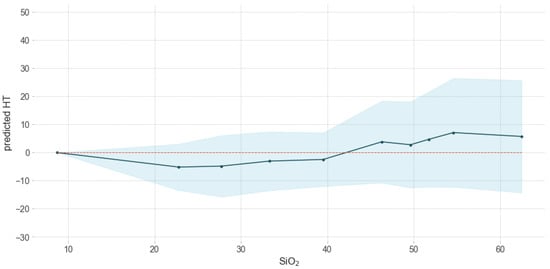
Figure 11.
Influence of SiO2 on predicted HT.
The HT of coals increased, as the content of Al2O3 in the ash became higher. However, a significant increase of fusibility was observed when the Al2O3 content in the ash was higher than about 25% (Figure 6).
Generally, as the Fe2O3 content increased, HT of coal samples decreased. However, when the concentration of Fe2O3 exceeded about 13%, the changes of HT were not significant (Figure 7). The decrease fusibility connected with the increase in Fe2O3 content was also described in other works [1,43].
The HT of coals decreased, as the content of SO3 became higher. A significant reduction of HT was observed when the content of SO3 was in the range 0–5. Meanwhile the concentration of SO3 exceeded about 10%, the changes of HT were not significant (Figure 8).
However, it should be indicated that SO3 did not exist in isolation in coal ash minerals, but together with other elements (Ca, Mg) in the sulfate form. Therefore, the cations in the chemical compounds had an effect on slag chemistry, not SO3 itself.
For the analyzed sample set, the ash fusion temperature decreased as the concentration of Na2O in the ash increased. However, this trend was reversed when the Na2O content exceeded 3%. An amount of Na2O in ash higher than about 5% no longer contributed to changes in HT (Figure 9).
It can be seen that the HT of the coal decreased with the increase of the CaO content until reaching the minimum around 12% content of CaO. Then fusibility increased gradually with the increase of the CaO content (Figure 10). Similar results were also presented in other works, among others [1,43].
SiO2 is a main component of coal ash. However, SiO2 fraction did not significantly affect the predicted HT (Figure 11).
4. Conclusions
- The aim of this study was to create a HT prediction model. The machine learning method was used for this purpose—XGBoost regressor, well known to provide better solutions than other machine learning algorithms.
- The effect of 11 different ash components (oxides) on HT prediction was investigated using the feature importance technique. The results showed that Al2O3 had the most significant influence on HT prediction, then respectively, Fe2O3, SO3, Na2O and CaO.
- The partial dependence plots technique was used to examine whether the relationship between the particular oxide and a predicted HT was linear, monotonic or more complex. It was revealed that:
- ○
- HT of coals increased, as the content of Al2O3 in the ash became higher. However, a significant increase of fusibility was observed when the Al2O3 content in the ash was higher than about 25%.
- ○
- The ash fusion temperature decreased as the concentration of Na2O in the ash increased. However, this trend was reversed when the Na2O content exceeded 3%. An amount of Na2O in ash higher than about 5% no longer contributed to changes in HT.
- ○
- As the Fe2O3 content increased, HT of coal samples decreased. However, when the concentration of Fe2O3 exceeded about 13%, the changes of HT were not significant.
- ○
- It can be seen that HT of the coal decreased with the increase of the CaO content until reaching the minimum around 12% content of CaO. Then fusibility increased gradually with the increase of the CaO content.
- ○
- HT of coals decreased, as the content of SO3 became higher. A significant reduction of HT was observed when the content of SO3 was in range of 0–5%. Meanwhile the concentration of SO3 exceeded about 10%, the changes of HT were not significant. However, it should be indicated that SO3 did not exist in isolation in coal ash minerals, but together with other elements (Ca, Mg) in the sulfate form. Therefore, the cations in the chemical compounds had an effect on slag chemistry, not SO3 itself.
- ○
- SiO2 fraction did not significantly affect the predicted HT.
- Results showed that the model created in this study could predict the HT with satisfactory efficiency R2 equal to 0.88. Finally, the results proved that XGBoost could be used as a reliable method for predicting HT.
Author Contributions
Conceptualization, M.R.; methodology, M.R. and A.Ż.; software, M.R. and A.Ż.; validation, A.Ż.; formal analysis, M.R. and A.Ż.; investigation, L.R.; writing—original draft preparation, M.R.; writing—review and editing, A.Ż.; visualization, M.R. and A.Ż., resources, L.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ministry of Science and Higher Education, Poland, grant number 11326019.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, B.; He, Q.; Jiang, Z.; Xu, R.; Hu, B. Relationship between coal ash composition and ash fusion temperatures. Fuel 2013, 105, 293–300. [Google Scholar] [CrossRef]
- Vassileva, G.C.; Vassilev, S.V. Relations between Ash-Fusion Temperatures and Chemical and Mineral Composition of Some Bulgarian Coals. Comptes Rendus l’Academie Bulg. Sci. 2002, 55, 6–61. [Google Scholar]
- Sharma, A.; Saikia, A.; Khare, P.; Dutta, D.K.; Baruah, B.P. The chemical composition of tertiary Indian coal ash and its combustion behaviour—A statistical approach: Part 2. J. Earth Syst. Sci. 2014, 123, 1439–1449. [Google Scholar] [CrossRef]
- Vassilev, S.V.; Kitano, K.; Takeda, S.; Tsurue, T. Influence of mineral and chemical composition of coal ashes on their fusibility. Fuel Process. Technol. 1995, 45, 27–51. [Google Scholar] [CrossRef]
- Van Dyk, J.C.; Keyser, M.J.; Van Zyl, J.W. Suitability of feedstocks for the Sasol–Lurgi fixed bed dry bottom gasification process. In Proceedings of the Gasification Technologies Conference, San Francisco, CA, USA, 7–10 October 2001. [Google Scholar]
- Seggiani, M. Empirical correlations of the ash fusion temperatures and temperature of critical viscosity for coal and biomass ashes. Fuel 1999, 78, 1121–1125. [Google Scholar] [CrossRef]
- Gray, V.R. Prediction of ash fusion temperature from ash composition for some New Zealand coals. Fuel 1987, 66, 1230–1239. [Google Scholar] [CrossRef]
- Jak, E. Prediction of coal ash fusion temperatures with the F*A*C*T thermodynamic computer package. Fuel 2002, 81, 1655–1668. [Google Scholar] [CrossRef]
- Luxsanayotin, A.; Pipatmanomai, S.; Bhattacharya, S. Effect of mineral oxides on slag formation tendency of Mae Moh lignites. Songklanakarin J. Sci. Technol. 2010, 32, 403–412. [Google Scholar]
- Li, F.; Yu, B.; Wang, G.; Fan, H.; Wang, T.; Guo, M.; Fang, Y. Investigation on improve ash fusion temperature (AFT) of low-AFT coal by biomass addition. Fuel Process. Technol. 2019, 191, 11–19. [Google Scholar] [CrossRef]
- Yazdani, S.; Hadavandi, E.; Chelgani, S.C. Rule-Based Intelligent System for Variable Importance Measurement and Prediction of Ash Fusion Indexes. Energy Fuels 2017, 32, 329–335. [Google Scholar] [CrossRef]
- Goni, C.; Helle, S.; Garcia, X.; Gordon, A.; Parra, R.; Kelm, U.; Jimenez, R.; Alfaro, G. Coal blend combustion: Fusibility ranking from mineral matter composition. Fuel 2003, 82, 2087–2095. [Google Scholar] [CrossRef]
- Carpenter, A. Coal Blending for Power Stations; IEA Coal Research: London, UK, 1995. [Google Scholar]
- Huggins, F.E.; Kosmack, D.A.; Huffman, G.P. Correlation between ash-fusion temperatures and ternary equilibrium phase diagrams. Fuel 1981, 60, 577–584. [Google Scholar] [CrossRef]
- Lloyd, W.G.; Riley, J.T.; Zhou, S.; Risen, M.A.; Tibbitts, R.L. Ash fusion temperatures under oxidizing conditions. Energy Fuels 1993, 7, 490–494. [Google Scholar] [CrossRef]
- Lolja, S.A.; Haxhi, H.; Dhimitri, R.; Drushku, S.; Malja, A. Correlation between ash fusion temperatures and chemical composition in Albanian coal ashes. Fuel 2002, 81, 2257–2261. [Google Scholar] [CrossRef]
- Özbayoğlu, G.; Özbayoğlu, M.E. A new approach for the prediction of ash fusion temperatures: A case study using Turkish Lignites. Fuel 2006, 85, 545–562. [Google Scholar] [CrossRef]
- Shi, W.J.; Kong, L.X.; Bai, J.; Xu, J.; Li, W.C.; Bai, Z.Q.; Li, W. Effect of CaO/Fe2O3 on fusion behaviors of coal ash at high temperatures. Fuel Process. Technol. 2018, 181, 18–24. [Google Scholar] [CrossRef]
- Winegartner, E.C.; Rhodes, B.T. An empirical study of the relation of chemical properties to ash fusion temperatures. J. Eng. Power 1975, 97, 395–403. [Google Scholar] [CrossRef]
- Gao, F.; Han, P.; Zhai, Y.J.; Chen, L.X. Application of support vector machine and ant colony algorithm in optimization of coal ash fusion temperature. In Proceedings of the 2011 International Conference on Machine Learning and Cybernetics, Guilin, China, 10–13 July 2011; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Karimi, S.; Jorjani, E.; Chelgani, S.C.; Mesroghli, S. Multivariable regression and adaptive neurofuzzy inference system predictions of ash fusion temperatures using ash chemical composition of us coals. J. Fuels 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Miao, S.; Jiang, Q.; Zhou, H.; Shi, J.; Cao, Z. Modelling and prediction of coal ash fusion temperature based on BP neural network. In MATEC Web of Conferences Volume 40 (2016), Proceedings of the 2015 International Conference on Mechanical Engineering and Electrical Systems (ICMES 2015), Singapore, 16–18 December 2015; Chang, G.A., Ma, M., Arumuga Perumal, S., Chen, G., Eds.; EDP Sciences: Les Ulis, France, 2016; pp. 5–10. [Google Scholar]
- Sasi, T.; Mighani, M.; Örs, E.; Tawani, R.; Gräbner, M. Prediction of ash fusion behavior from coal ash composition for entrained-flow gasification. Fuel Process. Technol. 2018, 176, 64–75. [Google Scholar] [CrossRef]
- Seggiani, M.; Pannocchia, G. Prediction of coal ash thermal properties using partial least-squares regression. Ind. Eng. Chem. Res. 2003, 42, 4919–4926. [Google Scholar] [CrossRef]
- Tambe, S.S.; Naniwadekar, M.; Tiwary, S.; Mukherjee, A.; Das, T.B. Prediction of coal ash fusion temperatures using computational intelligence based models. Int. J. Coal Sci. Technol. 2018, 5, 486–507. [Google Scholar] [CrossRef]
- Xiao, H.; Chen, Y.; Dou, C.; Ru, Y.; Cai, L.; Zhang, C.; Kang, Z.; Sun, B. Prediction of ash-deformation temperature based on grey-wolf algorithm and support-vector machine. Fuel 2019, 241, 304–310. [Google Scholar] [CrossRef]
- Yin, C.; Luo, Z.; Ni, M.; Cen, K. Predicting coal ash fusion temperature with a back-propagation neural network model. Fuel 1998, 77, 1777–1782. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, Z.; Wu, X. Prediction of coal ash fusion temperature by least squares support vector machine model. Energy Fuels 2010, 24, 3066–3071. [Google Scholar] [CrossRef]
- Żogała, A.; Rzychoń, M.; Łączny, M.J.; Róg, L. Selection of optimal coal blends in terms of ash fusion temperatures using Support Vector Machine (SVM) classifier—A case study for Polish coals. Physicochem. Probl. Miner. Process. 2019, 55, 1311–1322. [Google Scholar] [CrossRef]
- Mielecki, T. Studies on Coal Examination and Properties (In Polish); Silesia Publishing House: Katowice, Poland, 1971. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Krishnapuram, B., Ed.; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Machine Learning Wins The Higgs Challenge. Available online: http://cds.cern.ch/journal/CERNBulletin/2014/49/News%20Articles/1972036 (accessed on 8 January 2020).
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. Available online: https://www.jstor.org/stable/2699986 (accessed on 8 January 2020). [CrossRef]
- Basu, S.; Debnath, A.K. Power Plant Instrumentation and Control Handbook: A Guide to Thermal Power Plants, 1st ed.; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar] [CrossRef]
- Tomeczek, J.; Palugniok, H. Kinetics of mineral matter transformation during coal combustion. Fuel 2002, 81, 1251–1258. [Google Scholar] [CrossRef]
- Szuflicki, M.; Malon, A.; Tymiński, M. The Balance of Mineral Resources Deposits in Poland (In Polish); Polish Geological Institute—National Research Institute: Warsaw, Poland, 2019. [Google Scholar]
- Marsland, S. Machine Learning: An Algorithmic Perspective, 2nd ed.; Taylor & Francis Inc.: Milton Park, UK, 2014. [Google Scholar]
- Natekin, A.; Knoll, A. Gradient Boosting Machines, A Tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, Data Mining, Inference and Prediction, 2nd ed.; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Wadsworth Inc.: Belmont, TN, USA, 1984. [Google Scholar]
- Molnar, C. Interpretable Machine Learning, A Guide for Making Black Box Models Explainable; Version Dated, 10; Munich, Germany, 2018; ISBN 9780244768522. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 18 January 2020).
- Vorres, K.S. Melting behavior of coal ash materials from coal ash composition. Div. Fuel Chem. 1977, 22, 118. [Google Scholar]
- Liu, C.; Bai, Y.; Yan, L.; Zuo, Y.; Wang, Y.; Li, F. Impact of alkaline oxide on coal ash fusion temperature. Int. J. Oil Gas Coal Technol. 2014, 8, 79. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).