Application of GETFLOWS Coupled with Chemical Reactions to Arsenic Removal through Ferrihydrite Coprecipitation in an Artificial Wetland of a Japanese Closed Mine
Abstract
1. Introduction
2. Materials and Methods
2.1. Field Survey and Analysis
2.2. Simulation Model Using GETFLOWS
2.3. Kinetics Model
2.4. Surface Complexation Model
3. Results and Discussion
3.1. Field Survey
3.2. X-ray Diffraction Analysis
3.3. Geofluid Analysis
3.4. Quantitative Modeling
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dold, B. Evolution of Acid Mine Drainage Formation in Sulphidic Mine Tailings. Minerals 2014, 4, 621–641. [Google Scholar] [CrossRef]
- Johnson, D.B.; Hallberg, K.B. Acid mine drainage remediation options: A review. Sci. Total. Environ. 2005, 338, 3–14. [Google Scholar] [CrossRef]
- Akcil, A.; Koldas, S. Acid Mine Drainage (AMD): Causes, treatment and case studies. J. Clean. Prod. 2006, 14, 1139–1145. [Google Scholar] [CrossRef]
- Kato, T.; Yagisawa, M.; Matsuoka, M.; Tokoro, C.; Sakakibara, T.; Hayashi, K. Quantitative Modeling Incorporating Surface Complexation for the Treatment of Acid Mine Drainage. Kagaku Kogaku Ronbunshu 2017, 43, 207–212. [Google Scholar] [CrossRef][Green Version]
- Tokoro, C.; Kadokura, M.; Kato, T. Mechanism of arsenate coprecipitation at the solid/liquid interface of ferrihydrite: A perspective review. Adv. Powder Technol. 2020, 31, 859–866. [Google Scholar] [CrossRef]
- Al Mamun, A.; Morita, M.; Matsuoka, M.; Tokoro, C. Sorption mechanisms of chromate with coprecipitated ferrihydrite in aqueous solution. J. Hazard. Mater. 2017, 334, 142–149. [Google Scholar] [CrossRef]
- Tokoro, C.; Sakakibara, T.; Suzuki, S. Mechanism investigation and surface complexation modeling of zinc sorption on aluminum hydroxide in adsorption/coprecipitation processes. Chem. Eng. J. 2015, 279, 86–92. [Google Scholar] [CrossRef]
- Ueda, H.; Masuda, N. An Analysis on Mine Drainage Treatment Cost and the Technical Development to Prevent Mine Pollution. Shigen-to-Sozai 2005, 121, 323–329. [Google Scholar] [CrossRef]
- Otsuka, H.; Murakami, S.; Yamatomi, J.; Koide, R.; Tokoro, C. A predictive model for the future treatment of acid mine drainage with regression analysis and geochemical modeling. J. MMIJ 2014, 130, 488–493. [Google Scholar] [CrossRef][Green Version]
- Koide, R.; Tokoro, C.; Murakami, S.; Adachi, T.; Takahashi, A. A Model for Prediction of Neutralizer Usage and Sludge Generation in the Treatment of Acid Mine Drainage from Abandoned Mines: Case Studies in Japan. Mine Water Environ. 2012, 31, 287. [Google Scholar] [CrossRef]
- Kato, T.; Fukushima, R.; Giuseppe, G.; Sato, K.; Yamagata, S.; Tokoro, C. Quantitative Modeling Incorporating Surface Complexation for Zinc Removal Using Leaf Mold. J. Soc. Powder Technol. Jpn. 2019, 56, 136–141. [Google Scholar] [CrossRef][Green Version]
- Gazea, B.; Adam, K.; Kontopoulos, A. A review of passive systems for the treatment of acid mine drainage. Miner. Eng. 1996, 9, 23–42. [Google Scholar] [CrossRef]
- Tiruta-Barna, L.; Schiopu, N. Modelling inorganic biocide emission from treated wood in water. J. Hazard. Mater. 2011, 192, 1476–1483. [Google Scholar] [CrossRef] [PubMed]
- Fagervold, S.K.; Chai, Y.; Davis, J.W.; Wilken, M.; Cornelissen, G.; Ghosh, U. Bioaccumulation of Polychlorinated Dibenzo-p-Dioxins/Dibenzofurans inE. fetidafrom Floodplain Soils and the Effect of Activated Carbon Amendment. Environ. Sci. Technol. 2010, 44, 5546–5552. [Google Scholar] [CrossRef]
- Johnson, B.T.; Petty, J.D.; Huckins, J.N.; Lee, K.; Gauthier, J. Hazard assessment of a simulated oil spill on intertidal areas of the St. Lawrence River with SPMD-TOX. Environ. Toxicol. 2004, 19, 329–335. [Google Scholar] [CrossRef]
- Valente, T.M.; Antunes, M.; Braga, A.S.; Prudêncio, M.I.; Marques, R.; Pamplona, J. Mineralogical attenuation for metallic remediation in a passive system for mine water treatment. Environ. Earth Sci. 2011, 66, 39–54. [Google Scholar] [CrossRef]
- Furuta, S.; Ito, K.; Ishimori, Y. Measurements of radon around closed uranium mines. J. Environ. Radioact. 2002, 62, 97–114. [Google Scholar] [CrossRef]
- Ishimori, Y. Time-integrated monitoring of radon progeny around a closed uranium mine in Japan. J. Environ. Radioact. 2007, 93, 51–61. [Google Scholar] [CrossRef]
- Watanabe, K. Geochemical behavior of iron and manganese ions in the Ningyo-toge uranium deposit district, southwest Japan. Chem. Geol. 1987, 60, 299–307. [Google Scholar] [CrossRef]
- Kitamura, A.; Kurikami, H.; Sakuma, K.; Malins, A.; Okumura, M.; Machida, M.; Mori, K.; Tada, K.; Tawara, Y.; Kobayashi, T.; et al. Redistribution and export of contaminated sediment within eastern Fukushima Prefecture due to typhoon flooding. Earth Surf. Process. Landforms 2016, 41, 1708–1726. [Google Scholar] [CrossRef]
- Sakuma, K.; Kitamura, A.; Malins, A.; Kurikami, H.; Machida, M.; Mori, K.; Tada, K.; Kobayashi, T.; Tawara, Y.; Tosaka, H. Characteristics of radio-cesium transport and discharge between different basins near to the Fukushima Dai-ichi Nuclear Power Plant after heavy rainfall events. J. Environ. Radioact. 2017, 169, 137–150. [Google Scholar] [CrossRef] [PubMed]
- Sakuma, K.; Malins, A.; Funaki, H.; Kurikami, H.; Niizato, T.; Nakanishi, T.; Mori, K.; Tada, K.; Kobayashi, T.; Kitamura, A.; et al. Evaluation of sediment and 137Cs redistribution in the Oginosawa River catchment near the Fukushima Dai-ichi Nuclear Power Plant using integrated watershed modeling. J. Environ. Radioact. 2017, 182, 44–51. [Google Scholar] [CrossRef] [PubMed]
- Nagayasu, T.; Taki, T.; Fukushima, S. History and current situation of mine water treatment in Nigyo-toge uranium mine. JAEA Technol. 2017, 31, 1–74. [Google Scholar]
- Furusho, Y.; Ono, M.; Yamada, M.; Ohashi, K.; Kitade, T.; Kuriyama, K.; Ohta, S.; Inoue, Y.; Motomizu, S. Advanced Solid Phase Extraction for Inorganic Analysis and Its Applications. Bunseki Kagaku 2008, 57, 969–989. [Google Scholar] [CrossRef][Green Version]
- Tosaka, H.; Ito, K.; Furuno, T. Fully coupled formulation of surface flow with 2-phase subsurface flow for hydrological simulation. Hydrol. Process. 2000, 14, 449–464. [Google Scholar] [CrossRef]
- Mori, K.; Tada, K.; Tawara, Y.; Ohno, K.; Asami, M.; Kosaka, K.; Tosaka, H. Integrated watershed modeling for simulation of spatiotemporal redistribution of post-fallout radionuclides: Application in radiocesium fate and transport processes derived from the Fukushima accidents. Environ. Model. Softw. 2015, 72, 126–146. [Google Scholar] [CrossRef]
- Tosaka, H.; Matsumoto, Y. An efficient reservoir simulation by the successive explicitization process. J. Jpn. Assoc. Pet. Technol. 1987, 52, 307–313. [Google Scholar] [CrossRef]
- Tawara, Y.; Hazart, A.; Mori, K.; Tada, K.; Shimura, T.; Sato, S.; Yamamoto, S.; Asano, H.; Namiki, K. Extended two-phase flow model with mechanical capability to simulate gas migration in bentonite. Geol. Soc. Lond. Spéc. Publ. 2014, 400, 545–562. [Google Scholar] [CrossRef]
- Singer, P.C.; Stumm, W. Acidic Mine Drainage: The Rate-Determining Step. Science 1970, 167, 1121–1123. [Google Scholar] [CrossRef]
- Oscarson, D.W.; Huang, P.M.; Hammer, U.T.; Liaw, W.K. Oxidation and sorption of arsenite by manganese dioxide as influenced by surface coatings of iron and aluminum oxides and calcium carbonate. Water Air Soil Pollut. 1983, 20, 233–244. [Google Scholar] [CrossRef]
- Bednar, A.; Garbarino, J.; Ranville, J.; Wildeman, T. Effects of iron on arsenic speciation and redox chemistry in acid mine water. J. Geochem. Explor. 2005, 85, 55–62. [Google Scholar] [CrossRef]
- Kiskira, K.; Papirio, S.; Van Hullebusch, E.D.; Esposito, G. Fe(II)-mediated autotrophic denitrification: A new bioprocess for iron bioprecipitation/biorecovery and simultaneous treatment of nitrate-containing wastewaters. Int. Biodeterior. Biodegrad. 2017, 119, 631–648. [Google Scholar] [CrossRef]
- Parga, J.R.; Cocke, D.L.; Valenzuela-Garcia, J.L.; Gomes, J.A.; Kesmez, M.; Irwin, G.; Moreno, H.; Weir, M. Arsenic removal via electrocoagulation from heavy metal contaminated groundwater in La Comarca Lagunera México. J. Hazard. Mater. 2005, 124, 247–254. [Google Scholar] [CrossRef] [PubMed]
- Ahoranta, S.H.; Kokko, M.; Papirio, S.; Ozkaya, B.; Puhakka, J.A. Arsenic removal from acidic solutions with biogenic ferric precipitates. J. Hazard. Mater. 2016, 306, 124–132. [Google Scholar] [CrossRef]
- Tokoro, C.; Yatsugi, Y.; Koga, H.; Owada, S. Sorption Mechanisms of Arsenate during Coprecipitation with Ferrihydrite in Aqueous Solution. Environ. Sci. Technol. 2010, 44, 638–643. [Google Scholar] [CrossRef]
- Allison, J.D.; Brown, D.S.; Novo-Gradac, K.J. Minteqa2/prodefa2—A geochemical assessment model for environmental systems: User manual supplement for version 4.0. Environ. Res. Lab. 1998, 4, 43–74. [Google Scholar]
- Cole, W.F.; Lancucki, C.J. A refinement of the crystal structure of gypsum CaSO4∙2H2O. Acta Cryst. 1974, B30, 921–929. [Google Scholar] [CrossRef]
- Jia, Y.; Xu, L.; Fang, Z.; Demopoulos, G.P. Observation of Surface Precipitation of Arsenate on Ferrihydrite. Environ. Sci. Technol. 2006, 40, 3248–3253. [Google Scholar] [CrossRef]
- Jia, Y.; Xu, L.; Wang, X.; Demopoulos, G.P. Infrared spectroscopic and X-ray diffraction characterization of the nature of adsorbed arsenate on ferrihydrite. Geochim. Cosmochim. Acta 2007, 71, 1643–1654. [Google Scholar] [CrossRef]
- Fukushi, K.; Sasaki, M.; Sato, T.; Yanase, N.; Amano, H.; Ikeda, H. A natural attenuation of arsenic in drainage from an abandoned arsenic mine dump. Appl. Geochem. 2003, 18, 1267–1278. [Google Scholar] [CrossRef]
- Bigham, J.; Schwertmann, U.; Traina, S.; Winland, R.; Wolf, M. Schwertmannite and the chemical modeling of iron in acid sulfate waters. Geochim. Cosmochim. Acta 1996, 60, 2111–2121. [Google Scholar] [CrossRef]
- Cornell, R.M.; Schwertmann, H.C.U. The Iron Oxides: Structure, Properties, Reactions, Occurences and Uses, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003; pp. 345–364. ISBN 9783527302741. [Google Scholar]
- Perez, J.P.H.; Freeman, H.; Schuessler, J.A.; Benning, L.G. The interfacial reactivity of arsenic species with green rust sulfate (GRSO4). Sci. Total. Environ. 2019, 648, 1161–1170. [Google Scholar] [CrossRef] [PubMed]
- Al Mamun, A.; Onoguchi, A.; Granata, G.; Tokoro, C. Role of pH in green rust preparation and chromate removal from water. Appl. Clay Sci. 2018, 165, 205–213. [Google Scholar] [CrossRef]
- Onoguchi, A.; Granata, G.; Haraguchi, D.; Hayashi, H.; Tokoro, C. Kinetics and mechanism of selenate and selenite removal in solution by green rust-sulfate. R. Soc. Open Sci. 2019, 6, 182147. [Google Scholar] [CrossRef] [PubMed]
- Kiskira, K.; Papirio, S.; Mascolo, M.C.; Fourdrin, C.; Pechaud, Y.; Van Hullebusch, E.D.; Esposito, G. Mineral characterization of the biogenic Fe(III)(hydr)oxides produced during Fe(II)-driven denitrification with Cu, Ni and Zn. Sci. Total. Environ. 2019, 687, 401–412. [Google Scholar] [CrossRef]
- Senko, J.M.; Dewers, T.A.; Krumholz, L.R. Effect of Oxidation Rate and Fe(II) State on Microbial Nitrate-Dependent Fe(III) Mineral Formation. Appl. Environ. Microbiol. 2005, 71, 7172–7177. [Google Scholar] [CrossRef]
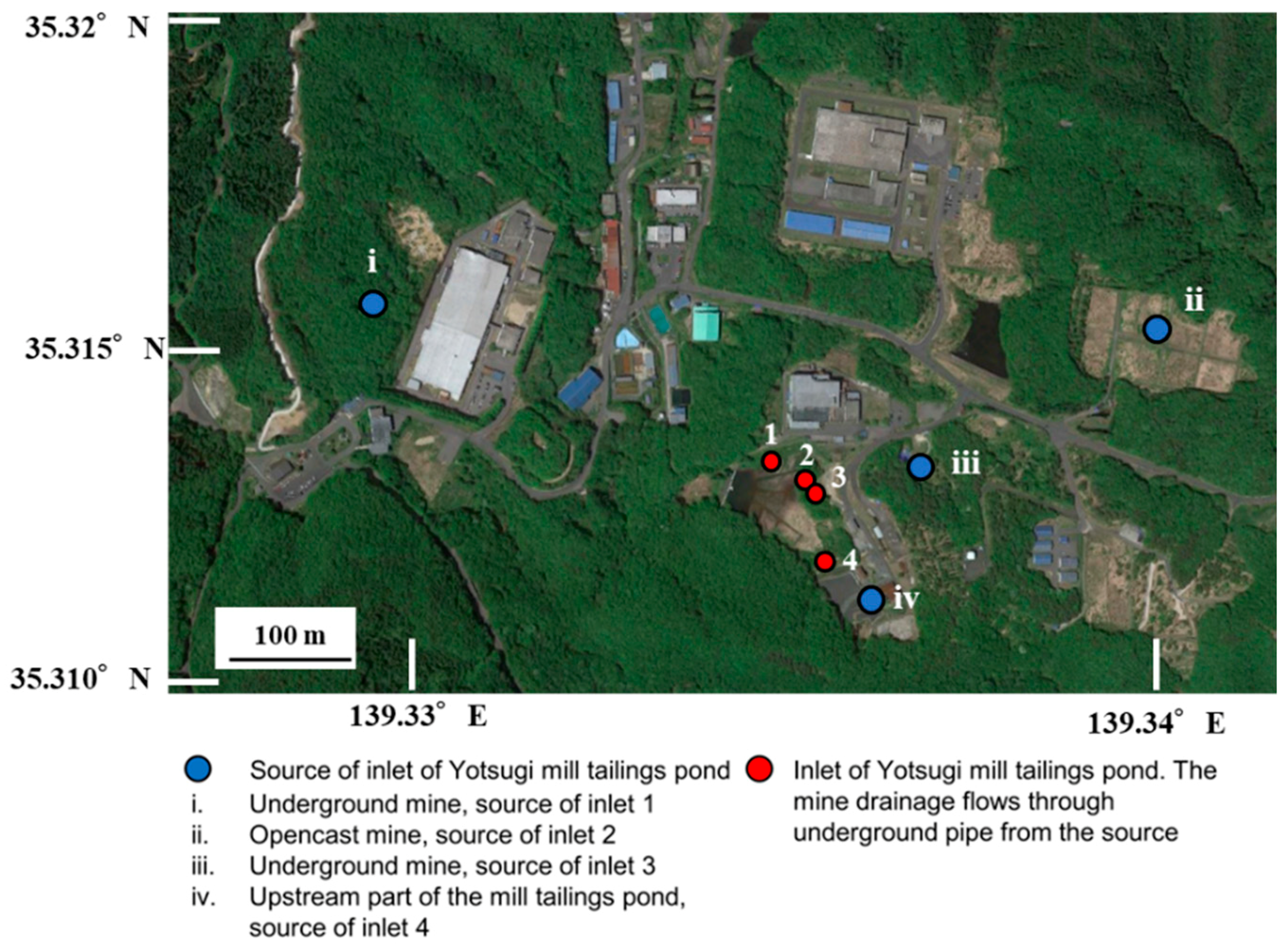
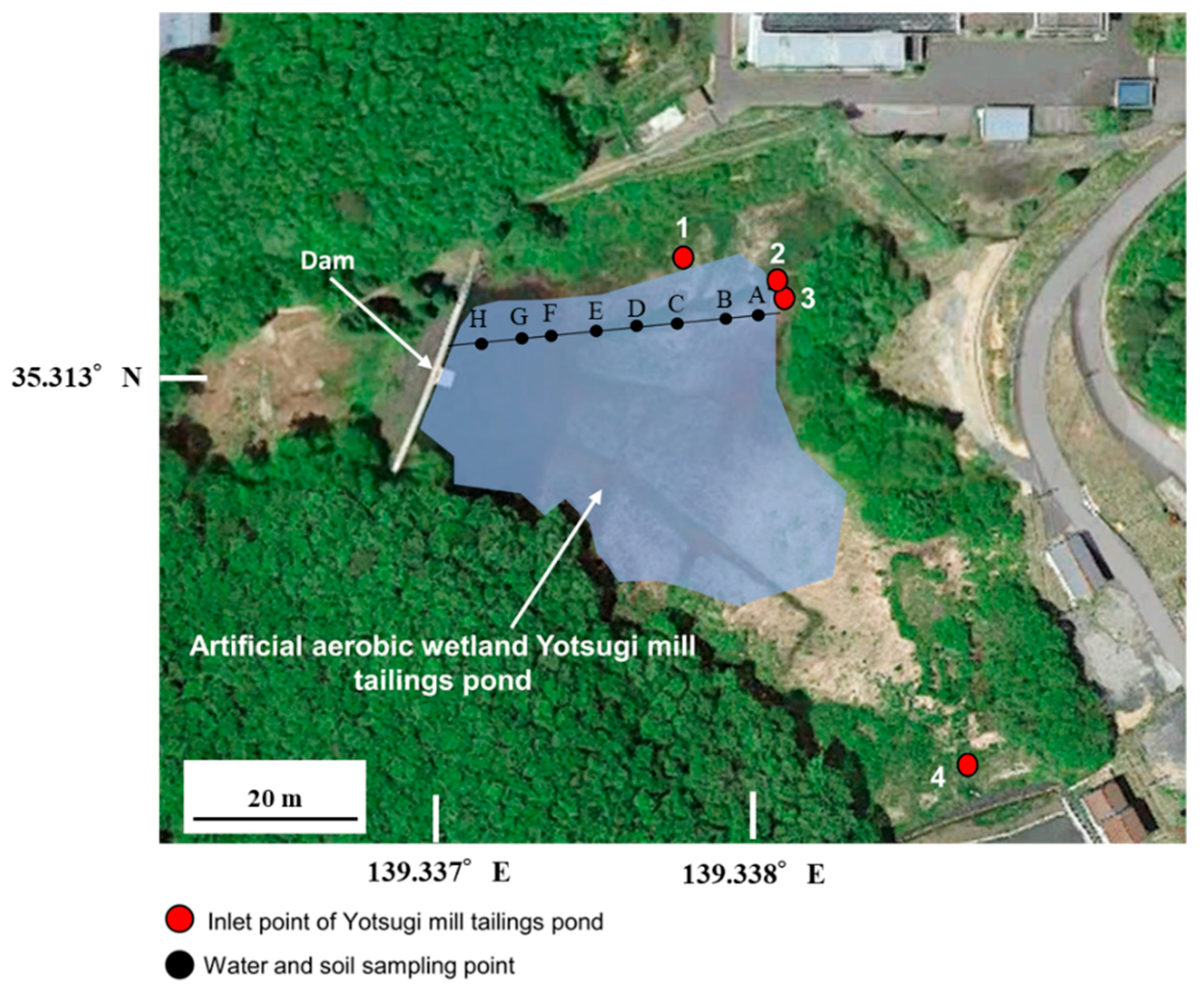
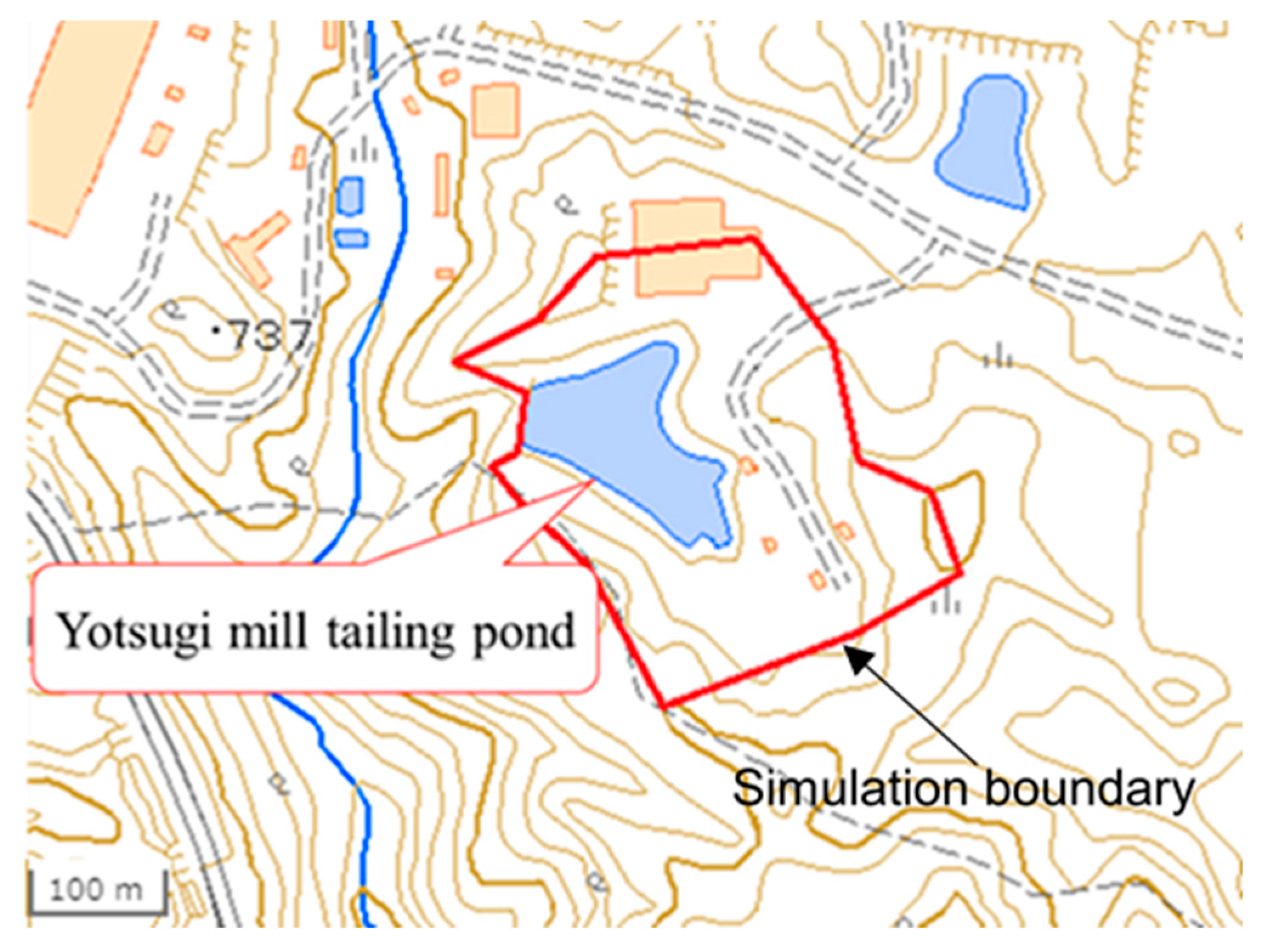
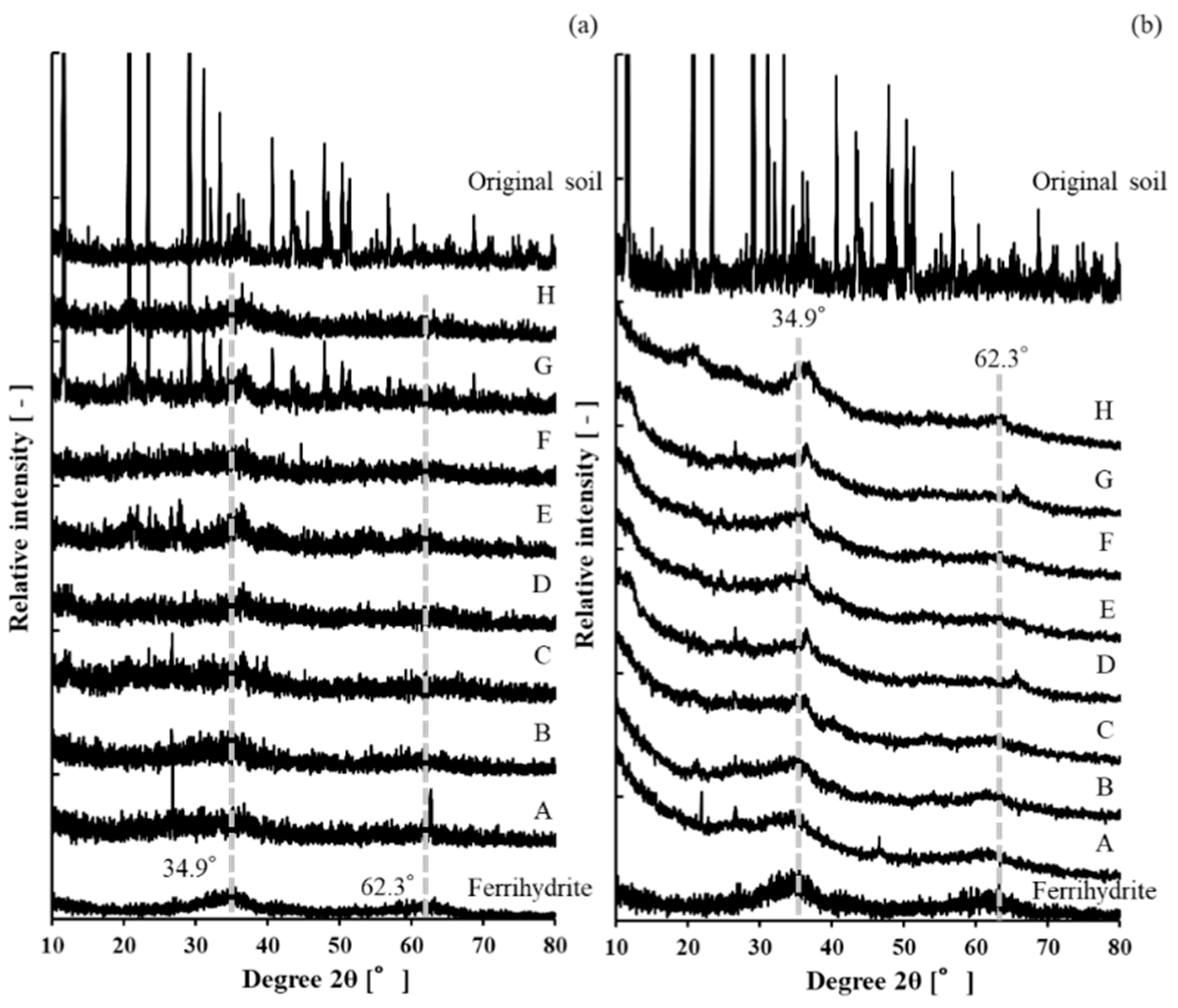
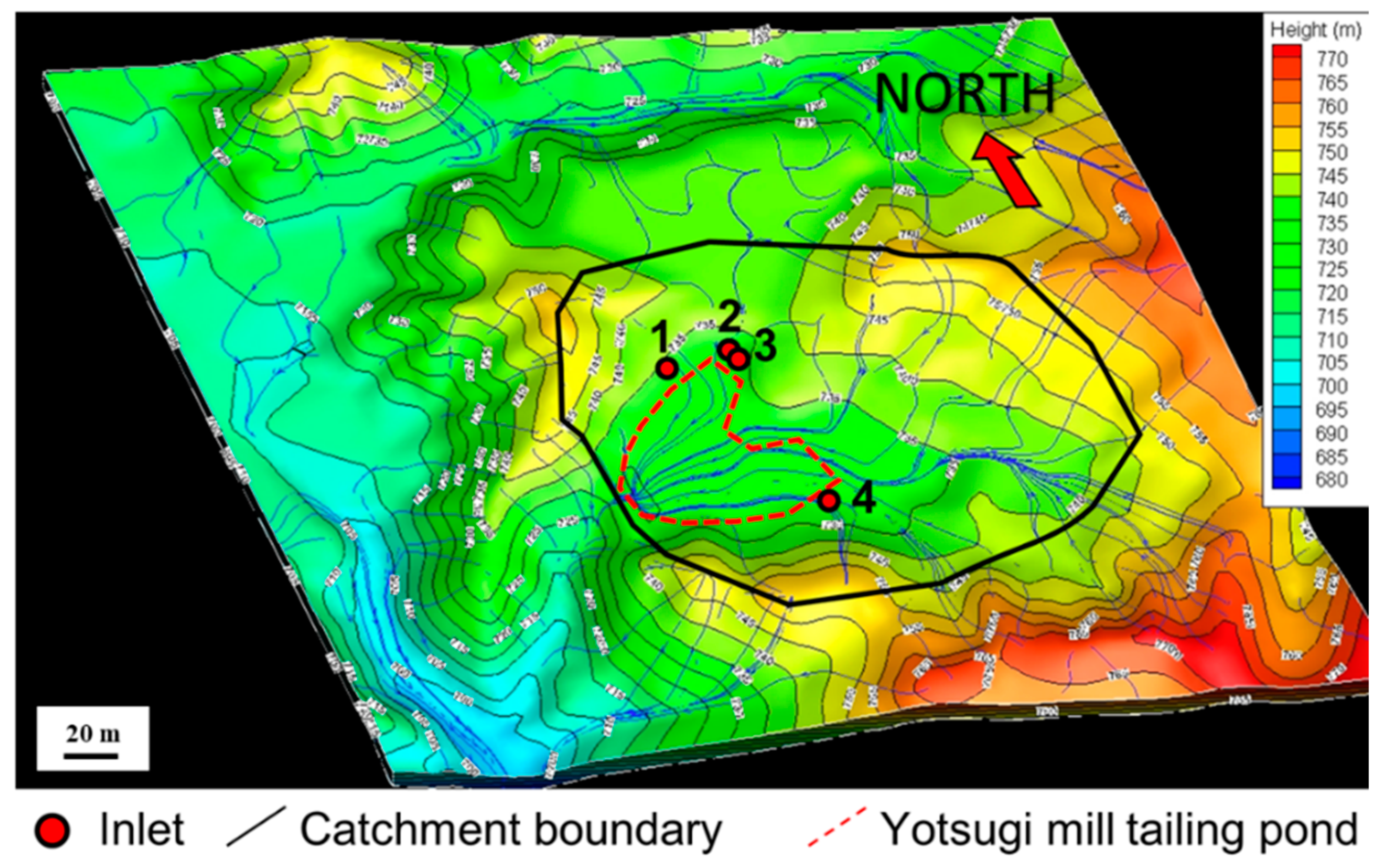
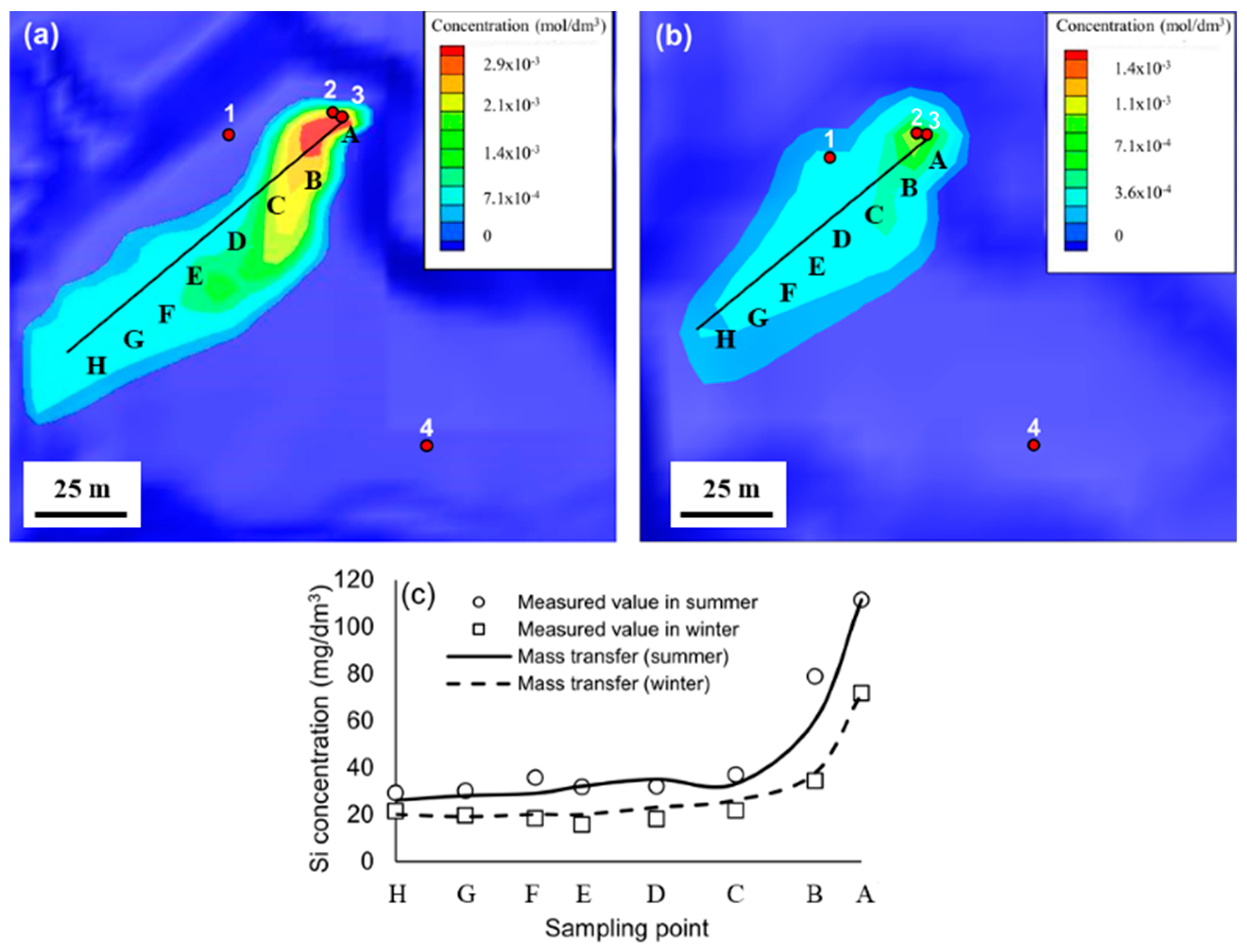
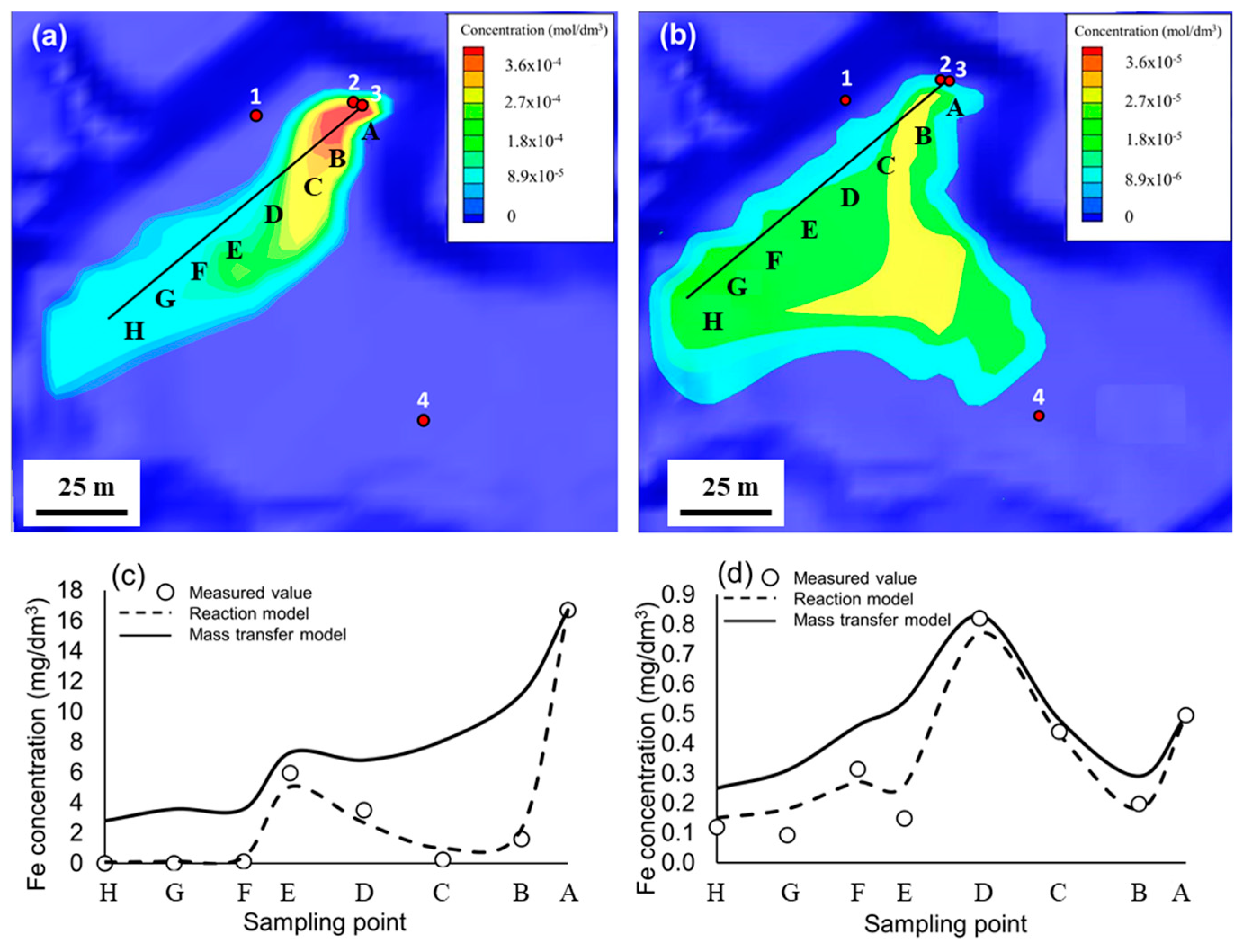
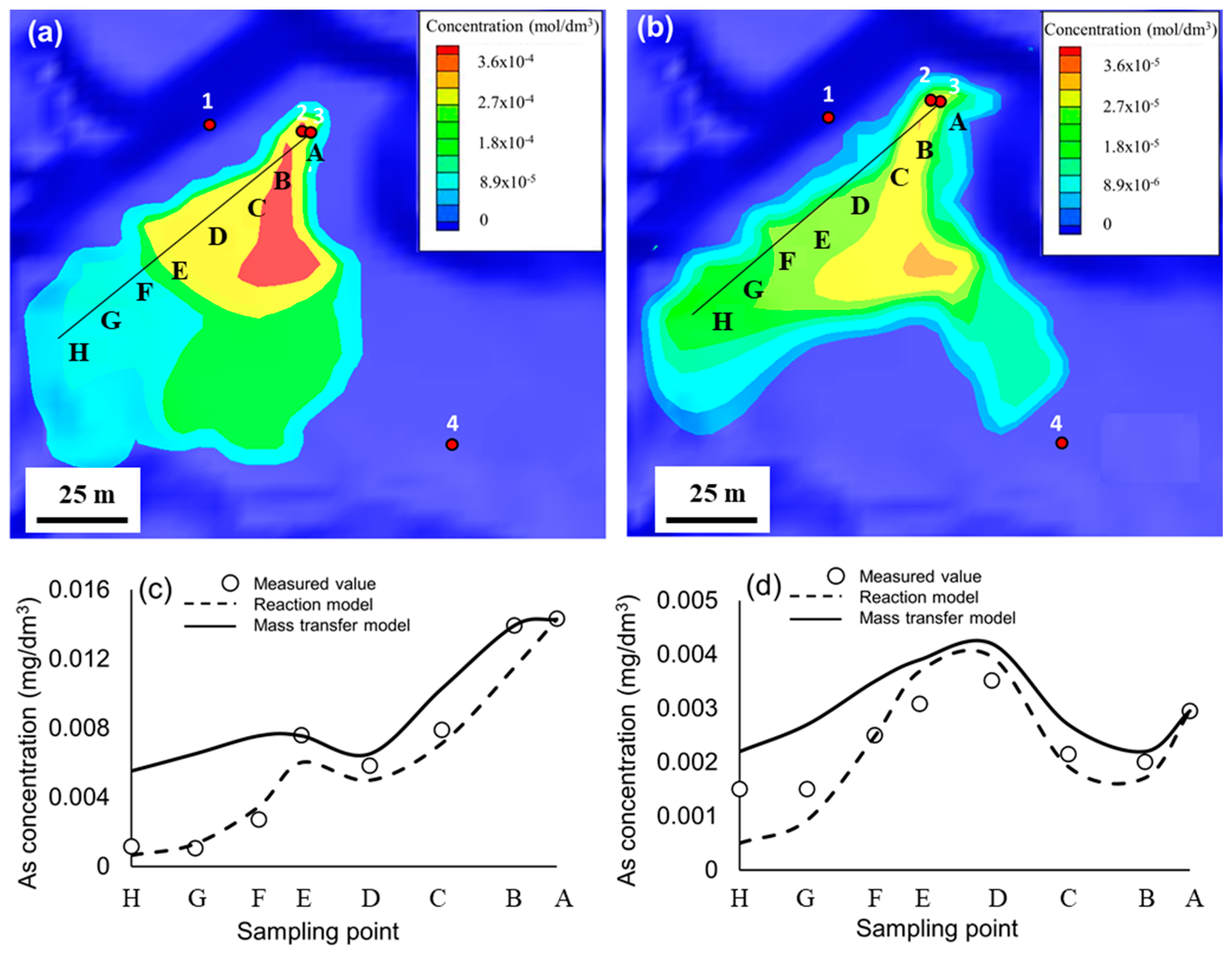
| Point | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| Distance | 0 | 10 | 27 | 44 | 60 | 70 | 85 | 100 |
| Langmuir Constant | Amount of Saturated Adsorption [mol/mol-Fe] | |
|---|---|---|
| Arsenate (As(V)) | 2.27 × 106 | 2.70 × 10−1 |
| Arsenite (As(III)) | 1.13 × 106 | 8.82 × 10−2 |
| Point | TEMP | pH (–) | DO | EC | ORP | Concentration (mg/L) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Si | Fe2+ | As | Na | K | Ca | Mg | Al | SO4 | Cl | ||||||
| I | 15.6 | 6.5 | 8.7 | 17 | 0.1 | 24 | 4.1 | 6.1 × 10−3 | 17 | 2.3 | 18 | 6.3 | 2.8 × 10−3 | 14 | 35 |
| Ii | 11.9 | 6.5 | 8.8 | 31 | 0.03 | 1.1 × 102 | 16 | 1.4 × 10−2 | 55 | 3.2 | 21 | 10 | 5.8 × 10−3 | 1.3 × 102 | 32 |
| Iii | 12.9 | 6.6 | 4.9 | 7.7 | 0.2 | 40 | 0.6 | 1.3 × 10−3 | 11 | 1.4 | 6.9 | 3.5 | 6.6 × 10−3 | 8.8 | 31 |
| Iv | 18.3 | 6.5 | 2.5 | 0.1 | 0.3 | 13 | 0.4 | 9.9 × 10−3 | 14 | 1.1 | 13 | 1.6 | 1.5 × 10−2 | 25 | 29 |
| A | 14.8 | 7.0 | 4.2 | 28 | 0.2 | 1.1 × 102 | 17 | 1.4 × 10−3 | 54 | 2.5 | 18 | 9.8 | 4.0 × 10−3 | 1.4 × 102 | 18 |
| B | 17.1 | 6.8 | 2.0 | 23 | 0.2 | 79 | 1.6 | 1.4 × 10−2 | 45 | 5.7 | 14 | 7.9 | 7.2 × 10−3 | 1.1 × 102 | 21 |
| C | 18.6 | 6.6 | 3.6 | 17 | 0.3 | 37 | 0.2 | 7.9 × 10−3 | 17 | 3.1 | 23 | 5.8 | 3.7 × 10−3 | 46 | 16 |
| D | 19.1 | 7.1 | 0.5 | 21 | 0.03 | 32 | 3.5 | 5.8 × 10−3 | 17 | 1.0 | 25 | 5.6 | 6.1 × 10−3 | 47 | 16 |
| E | 22.0 | 6.5 | 0.4 | 42 | 0.02 | 32 | 6.0 | 7.6 × 10−3 | 18 | 0.7 | 68 | 7.6 | 3.8 × 10−3 | 2.3 × 102 | 20 |
| F | 26.7 | 7.0 | 3.1 | 0.5 | 0.1 | 31 | 0.1 | 2.7 × 10−3 | 17 | 0.6 | 54 | 4.7 | 4.9 × 10−3 | 1.8 × 102 | 20 |
| G | 32.1 | 7.2 | 6.2 | 0.3 | 0.2 | 29 | 2.2× 10−3 | 1.1 × 10−3 | 16 | 0.3 | 53 | 4.4 | 2.3 × 10−3 | 1.6 × 102 | 19 |
| H | 32.4 | 7.3 | 3.1 | 0.3 | 0.3 | 28 | 2.2× 10−3 | 1.2 × 10−3 | 15 | 0.4 | 49 | 4.5 | 2.7 × 10−3 | 1.5 × 102 | 39 |
| Point | TEMP | pH (–) | DO | EC | ORP | Concentration (mg/L) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Si | Fe2+ | As | Na | K | Ca | Mg | Al | SO4 | Cl | ||||||
| I | 12.8 | 6.4 | 7.8 | 0.2 | 0.1 | 24 | 2.0 | 1.2 × 10−2 | 9.9 | 1.3 | 13 | 3.5 | 0.2 × 10−4 | 12 | 0.0 |
| Ii | 10.2 | 6.5 | 8.7 | 0.3 | 0.03 | 72 | 8.2 × 10−2 | 8.2 × 10−3 | 36 | 2.0 | 14 | 6.5 | 0.1 × 10−4 | 98 | 0.0 |
| Iii | 10.8 | 6.6 | 4.7 | 0.1 | 0.3 | 35 | 0.4 | 5.6 × 10−3 | 6.2 | 0.9 | 6.1 | 2.5 | 0.0 | 7.7 | 0.0 |
| Iv | 11.1 | 6.7 | 3.1 | 0.2 | 0.06 | 14 | 3.7 | 5.3 × 10−2 | 11 | 1.5 | 16 | 1.6 | 0.3 × 10−4 | 45 | 0.0 |
| A | 11.6 | 6.6 | 4.7 | 0.1 | 0.2 | 72 | 0.5 | 3.0 × 10−3 | 13 | 1.0 | 6.9 | 3.0 | 0.0 | 48 | 0.0 |
| B | 12.0 | 7.0 | 6.7 | 0.2 | 0.2 | 35 | 0.2 | 2.0 × 10−3 | 14 | 1.2 | 6.3 | 2.8 | 0.0 | 15 | 7.2 |
| C | 11.8 | 6.9 | 5.6 | 0.2 | 0.3 | 22 | 0.4 | 2.2 × 10−3 | 10 | 1.4 | 14 | 3.1 | 0.0 | 14 | 11 |
| D | 12.3 | 6.6 | 1.0 | 0.2 | 0.2 | 18 | 0.8 | 3.5 × 10−3 | 8.9 | 1.2 | 15 | 3.1 | 0.0 | 13 | 9.7 |
| E | 11.4 | 6.9 | 0.8 | 0.3 | 0.2 | 16 | 0.2 | 3.1 × 10−3 | 8.9 | 0.9 | 24 | 2.8 | 0.0 | 32 | 8.8 |
| F | 12.2 | 6.7 | 0.8 | 0.7 | 0.01 | 19 | 0.3 | 2.5 × 10−3 | 9.8 | 0.7 | 80 | 4.1 | 0.0 | 1.5 × 102 | 9.3 |
| G | 11.8 | 7.0 | 6.2 | 0.3 | 0.2 | 20 | 0.9 | 1.5 × 10−3 | 9.3 | 1.2 | 21 | 3.4 | 0.0 | 0.02 | 7.7 |
| H | 11.9 | 7.0 | 3.3 | 0.3 | 0.3 | 22 | 0.1 | 1.5 × 10−3 | 11 | 1.3 | 30 | 3.5 | 0.1 × 10−4 | 94 | 0.0 |
| Flow | Summer | Winter |
|---|---|---|
| Precipitation (mm/day) | 6.6 | 5.8 |
| Evaporation (mm/day) | 1.6 | 0.7 |
| Inlet flowrate point 1 (m3/day) | 169.8 | 254.1 |
| Inlet flowrate point 2 (m3/day) | 34.9 | 29.4 |
| Inlet flowrate point 3 (m3/day) | 11.6 | 16.2 |
| Inlet flowrate point 4 (m3/day) | 7.52 | 5.45 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kato, T.; Kawasaki, Y.; Kadokura, M.; Suzuki, K.; Tawara, Y.; Ohara, Y.; Tokoro, C. Application of GETFLOWS Coupled with Chemical Reactions to Arsenic Removal through Ferrihydrite Coprecipitation in an Artificial Wetland of a Japanese Closed Mine. Minerals 2020, 10, 475. https://doi.org/10.3390/min10050475
Kato T, Kawasaki Y, Kadokura M, Suzuki K, Tawara Y, Ohara Y, Tokoro C. Application of GETFLOWS Coupled with Chemical Reactions to Arsenic Removal through Ferrihydrite Coprecipitation in an Artificial Wetland of a Japanese Closed Mine. Minerals. 2020; 10(5):475. https://doi.org/10.3390/min10050475
Chicago/Turabian StyleKato, Tatsuya, Yohei Kawasaki, Masakazu Kadokura, Kohei Suzuki, Yasuhiro Tawara, Yoshiyuki Ohara, and Chiharu Tokoro. 2020. "Application of GETFLOWS Coupled with Chemical Reactions to Arsenic Removal through Ferrihydrite Coprecipitation in an Artificial Wetland of a Japanese Closed Mine" Minerals 10, no. 5: 475. https://doi.org/10.3390/min10050475
APA StyleKato, T., Kawasaki, Y., Kadokura, M., Suzuki, K., Tawara, Y., Ohara, Y., & Tokoro, C. (2020). Application of GETFLOWS Coupled with Chemical Reactions to Arsenic Removal through Ferrihydrite Coprecipitation in an Artificial Wetland of a Japanese Closed Mine. Minerals, 10(5), 475. https://doi.org/10.3390/min10050475






