Abstract
The thermoelastic properties of K0.7Na0.3AlSi3O8 hollandite and NaAlSi2O6 jadeite, synthesized from a (K, Na)-felspar (microcline), were investigated by a combination of in situ energy dispersive synchrotron X-ray radiation and multi-anvil techniques at high pressure (P) and temperature (T) up to 21 GPa and 1700 K. The second-order phase transformation was found to occur in hollandite at ~16 GPa from tetragonal I/4m (hollandite-I) to monoclinic I2/m (hollandite-II), which confirms the previous report that the incorporation of Na in the hollandite structure decreases the transformation pressure. Fitting the pressure–volume–temperature data to the Birch–Murnaghan equation of state yielded estimates of the thermoelastic parameters for jadeite as well as the K0.7Na0.3AlSi3O8 hollandite-I and -II phases, which indicate that the incorporation of Na is likely to decrease the bulk moduli of both hollandite phases. The obtained thermoelastic parameters were combined with those of other mantle minerals reported previously to estimate the density of continental materials along an average mantle geotherm. Based on our results, continental crust and sediment become, respectively, 11% and 15% denser than the pyrolitic mantle at pressure >10 GPa, suggesting that once pulled down to the critical depth of ~300 km, the continental portions of the slab can subduct further into the deep mantle, down to the lowermost part of the mantle transition region.
1. Introduction
Geological observations suggest that the subduction of continental crust may have occurred through time and transported extensive amounts of continental crust and sedimentary materials into the Earth’s mantle [], which can be traced by the diamond inclusions of minerals such as K-rich hollandite [,]. At the mantle transition region (MTR) depths, petrological works have shown that continental crust materials transform to a mixture of garnet, stishovite, pyroxene, hollandite, and Ca-rich aluminosilicate (CAS) phase [,]. Numerical simulations on the basis of the density contrasts between continental crust and mantle components have predicted that when such transformations occur, continental crust is likely to sink even deeper into the Earth’s mantle [,] where it could accumulate through time and form a thick and buoyant second continent at the bottom of the MTR []. Such a layer would have important implications for the location of alkali metals in the Earth, especially K40, which is believed to play a key role in the Earth’s internal heating and long-term evolution, by providing substantial amount of heat through its long radiogenic decay process [,].
The density estimates made by previous studies were, however, mostly based on assuming the thermoelastic properties of the endmembers of continental crust minerals [,]. To this day, there have been only a few works that addressed the effect of cationic substitutions on the elastic properties of those minerals under the relevant pressure and temperature conditions, which hampers precise estimates of the density of the continental crust in the deep mantle. (K,Na)AlSi3O8 hollandite is the solid solution in the KAlSi3O8 liebermannite [] and NaAlSi3O8 lingunite [] joint system, and jadeite is a Na-rich clinopyroxene. These two phases are very specific to continental crust compositions where they represent up to ~40 vol.% of the phase assemblages at high pressure, while they do not appear in pyrolite or mid-ocean ridge basalt (MORB) compositions at the MTR pressures [,,]. Therefore, knowledge of their elasticity at high pressure (P) and temperature (T) is of importance for estimating the density of continental crust when it is subducted in the slab to the depths of the MTR. The thermoelastic properties of liebermannite have been reported previously by in situ measurements using multi-anvil and diamond anvil techniques [,,], while those of (K,Na)AlSi3O8 hollandite have been poorly investigated. To this day, only one experimental study reported the compression curve for K0.8Na0.2AlSi3O8 hollandite at room T, based on which it was concluded that the incorporation of Na has no significant effect on the compressibility of the hollandite structure []. The elasticity of jadeite has been reported by several studies, although those works were limited to high T measurements at relatively low pressure [,] or high P measurements at room T [,], requiring large extrapolations when calculating the density of this phase under the high P and high T conditions of the mantle.
Here we investigated the thermoelastic properties of K0.7Na0.3AlSi3O8 hollandite and NaAlSi2O6 jadeite synthesized from a microcline feldspar by a combination of in situ synchrotron X-ray measurements and multi-anvil techniques at high pressures and high temperatures up to 21 GPa and 1700 K, respectively, at the beamline BL04B1 (SPring-8, Japan). This hollandite composition is comparable with those obtained in the phase relation studies on continental crust materials at high P up to ~22 GPa [,]. Our results of the thermoelastic properties of hollandite are compared with some previous studies, and the effect of Na on the compressibility of the hollandite structure is discussed. The density profiles of continental crust and sediment are estimated on the basis of a thermoelastic dataset that includes our new data on K0.7Na0.3AlSi3O8 hollandite and jadeite and compared to that of other mantle compositions.
2. Materials and Methods
2.1. Starting Material
We prepared a feldspar glass from a natural microcline (Nellore, Andhra Pradesh, India), which was melted at ~1800 K and quenched in cold water. Analysis of the resulting glass by a field emission scanning electron microscope (FE-SEM, JSM7000F, JEOL Ltd., Tokyo, Japan) equipped with an energy dispersive spectrometer (EDS, X-MaxN, Oxford Instruments plc, Oxon, UK) yielded the composition reported in Table 2. The microcline glass was powdered and cold-sealed in a gold capsule, then hot-pressed at 15 GPa and 1500 K for 30 min (OS2999, Table 1) using the 2000-ton Kawai-type multi-anvil press apparatus ORANGE2000 at the Geodynamics Research Center (Ehime University, Japan). The recovered samples appeared well sintered in a cylindrical shape (~2.0 mm diameter) and free of visible cracks. The texture analyses (Figure 1a,b) and chemical composition (Table 2) obtained from SEM–EDS analysis showed that the sample consisted of a multiphase aggregate of K0.7Na0.3AlSi3O8 liebermannite and NaAlSi2O6 jadeite intergrown with small grains (<1µm) of stishovite (Table 1).

Table 1.
Experimental conditions and run products.

Figure 1.
Electron image of (a) (b) the microcline sample before (OS2999) and (c) after (S2697) in situ measurements. (d) OD1667 show the result of an equilibrium experiment carried out for 12 h at ~21 GPa and 1700 K, corresponding to the highest pressure (P) and temperature (T) data of the in situ measurements (see Table 1). Abbreviations: Lieb, Na-rich liebermannite; Jd, jadeite; St, stishovite.

Table 2.
Composition of starting material and run products.
Micro-focused X-ray diffraction patterns collected on the recovered sample was well explained by an assemblage of Na-liebermannite (space group I4/m, Z = 2), jadeite (space group: C2/c, Z = 4), and stishovite (space group P42/mnm, Z = 2). Fitting of liebermannite peaks yielded the unit-cell parameters a = 9.3207(2) Å and c= 2.7193(1) Å; e.g., V = 236.2(2) Å3, which is ~0.3%–0.6% smaller than that of the KAl2Si3O8 endmember [,,], due to the incorporation of Na, which decreases the unit-cell volume of the hollandite structure [,]. The jadeite unit-cell parameters a = 9.431(5) Å, b = 8.569(1) Å, c = 5.219(3) Å3, and β = 107.43(3)° (e.g., V = 402.4(4) Å3) are in good agreement with those of the NaAlSi3O8 endmember [,]. The stishovite unit-cell parameters a = 4.184(2) Å and c = 2.669(1) Å (e.g., V = 46.74(1) Å3) is slightly higher than pure stishovite, which suggest the incorporation of ~1 wt.% Al2O3 [], although the exact composition could not be measured by SEM–EDS due to the small size (<1 µm) of the stishovite grains. The unit-cell parameters and volumes of all the observed phases are shown in Table 3.

Table 3.
Unit-cell volumes of Na-liebermannite and jadeite in the recovered samples.
2.2. High Pressure Synchrotron Experiments
X-ray diffraction measurements were carried out in a 1500-ton DIA-type multi-anvil press apparatus at the beamline BL04B1 at SPring-8 (Hyogo, Japan). High pressure was generated within so called 11/5 assemblies, equipped with a 20 μm thick cylindrical Re heater, which was transparent to high-energy X-rays. MgO was used to make a quasi-hydrostatic environment around the sample. A mixture of NaCl + BN + gold (10:1:0.1 wt.%) was placed at one end of the sample to enhance hydrostatic conditions and also served as a pressure standard using the EoS of NaCl and gold [,]. Temperature was monitored using a W97Re3–W75Re25 thermocouple (Type-D, Nilaco Corporation, Tokyo, Japan), which was maintained at high pressure, at the center of the cell and in contact with the pressure standard. Unit-cell volumes of the sample and pressure marker constituent phases were determined by energy dispersive X-ray diffraction (ED-XRD) at a fixed diffraction angle 2θ = 5.9757°, which was calibrated by the diffraction peaks of the gold standard at room P and T conditions. A multichannel Ge solid state detector was used to acquire photons in a range of 30–150 keV, which was calibrated with the characteristic fluorescence lines of 55Fe, 57Co, and 133Ba, yielding the precision of the energy measurements within ±30 eV per channel. The polychromatic X-ray beam was collimated to 0.05 mm horizontally and 0.2 mm vertically, while its position relative to the sample and marker was determined before each measurement by X-ray radiography imaging techniques using a high-resolution CCD camera (C11440, Hamamatsu Photonics, Iwata, Japan).
2.3. Data Reduction and EoS Procedure
The GSAS/EXPGUI software package (v1.251, Argonne National Laboratory, Lemont, IL, USA) [,] was used to analyze the diffraction data assuming the BaMn8O15 hollandite-type structure (space group I4/m, Z = 2) for the Na-liebermannite phase and the monoclinic structure (space group: C2/c, Z = 2) for the jadeite phase, respectively. The peak positions of Na-liebermannite and jadeite were refined simultaneously by a least-square fitting of the whole diffraction profile using the Le Bail technique [] for energy dispersive spectra. The extracted unit-cell volumes for each experimental P and T conditions are summarized in Supplementary Materials Table S1.
The pressure-volume relations were determined by a least-square fitting of the room T unit-cell volumes VP,300 of Na-liebermannite and jadeite as a function of the pressure (gold P-scale) to the third-order Birch–Murnaghan (BM) equation of state (EoS) with the general form given in Equation (1).
where the parameters K0,T, K’0,T, and V0,T are the isothermal bulk modulus, its pressure derivative, and the zero-pressure unit-cell volume, respectively. Because of the limited data in this study, fitting of all elastic parameters simultaneously generally yielded large errors due to the inaccuracy in determining K’0,T and V0,T from Equation (1). Therefore, we chose to fix V0,T to its experimental value at room P and T conditions, and constrain K’0,T to values varying from 3 to 5.
The thermal properties were subsequently determined by fitting all data at high P and T to Equation (1) while assuming the bulk modulus is a linear function of the zero-pressure bulk modulus K0,300 and the first temperature derivative (∂K0,T/∂T)P, e.g., Equation (2); the first pressure derivative is independent of the temperature, e.g., Equation (3); and the zero-pressure volume is an exponential function of the thermal expansion α0,T, e.g., Equation (4) and Equation (5).
When fitting the thermal parameters, the room temperature parameters K0,300 and V0,300 were fixed to the values determined by the fitting of 300 K data by Equation (1).
3. Results
Figure 2 shows selected diffraction patterns collected in situ at high P and room T as well as high P and high T up to 20.4 GPa and 1700 K. At all P and T, our sample consisted of K0.7Na0.3AlSi3O8 hollandite (e.g., Na-liebermannite) and jadeite (Figure 2). Stishovite peaks, although visible at room conditions, had too low intensities, which did not permit us to calculate its unit-cell volume at high P and T. The compression curve of Na-liebermannite along the 300 K isotherm (Figure 3) shows that our unit-cell values were generally consistent with those of K0.8Na0.2AlSi3O8 hollandite reported by Boffa-Ballaran et al. [], with differences that can be explained by the slightly higher Na-content in our hollandite phase. Similarly to Boffa-Ballaran et al. [], we also observed a discontinuous volume decrease at P > 16 GPa, which they attributed to the hollandite to hollandite-II phase transition, although in our experiments, we could not observe clearly the broadening and splitting of diffraction peaks that generally characterize the transition [,,] because of the low resolution of the present energy dispersive XRD method.
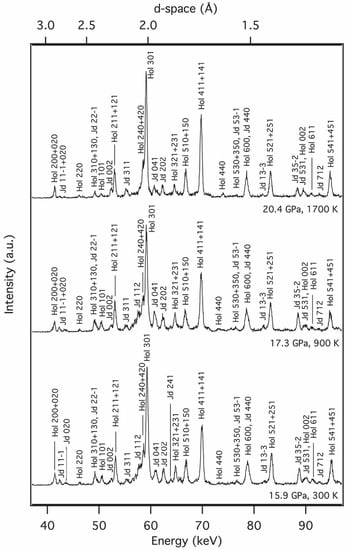
Figure 2.
X-ray diffraction pattern of the microcline aggregate at high pressure and high temperature. Abbreviations: Hol, Na-rich liebermannite; Jd, jadeite.
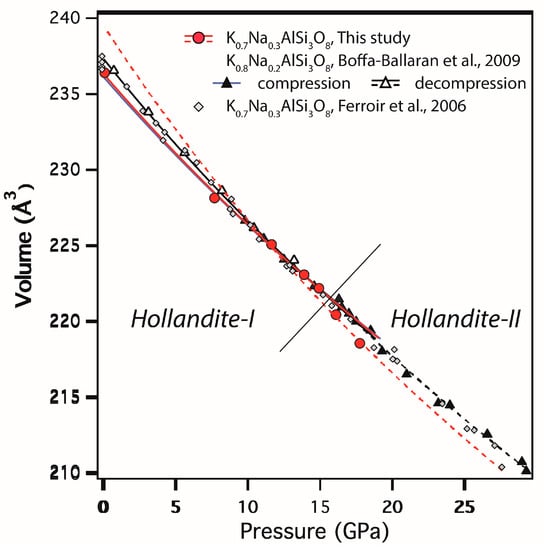
Figure 3.
Unit-cell volume of K0.7Na0.3AlSi3O8 liebermannite as a function of pressure across the hollandite-I to hollandite-II transition. Red lines represent a fitting of hollandite-I (solid line) and hollandite-II (broken line) data by a Birch–Murnaghan EoS (Equation (1)). Black lines represent a fitting of Boffa-Ballaran et al.’s [] data with (solid line) and without (broken line) decompression data.
In order to assess that the volume decrease is related to the second order transition in the hollandite phase and not to an eventual reaction between liebermannite and jadeite at high P and T, we carried out an additional experiment (OD1667, Table 1) at 21.4 GPa and 1700 K, which corresponds to the highest P and T conditions where the density was measured in situ (Figure 2, Supplementary Materials Table S1). In OD1667, the microcline glass was compressed to the target pressure and annealed at 1700 K for 12 h, which is similar to the procedure for equilibrium experiments in the KAlSi3O8-NaAlSi3O8 system []. SEM–EDS analyses of the recovered sample showed Na-liebermannite and jadeite + stishovite, with rather similar texture and composition to the multiphase aggregate, before and after the in situ experiment (Figure 1 and Table 1). The slightly lower Na-content observed in OD1667’s hollandite phase indicates that Na-content of liebermannite was unlikely to increase at P > 16 GPa, as a result of reaction with the coexisting jadeite, which is compatible with previous studies showing that the partitioning coefficient of Na in hollandite decreases with increasing P and T []. Analyses of the sample recovered after the in situ experiment (S2697, Table 1) were, however, quasi-identical to those of the starting aggregate (OS2999, Table 1) suggesting the kinetics of this reaction would be slower than the heating time required for our measurements. The volume decrease we observed at P > 16 GPa was likely to correspond to the hollandite to hollandite-II transition in K0.7Na0.3AlSi3O8 hollandite, which is consistent with Boffa-Ballaran et al.’s [] observations of the transition in between 17 GPa and 20 GPa for K0.8Na0.2AlSi3O8 hollandite. Our results also indicated that substitution of Na into the KAlSi3O8 hollandite structure decreased the transition pressure with respect to that observed for the endmember at pressures higher than 20 GPa [,,], which is generally consistent with conclusions of previous experimental and theoretical studies [,].
3.1. P–V–T EoS of K0.7Na0.3AlSi3O8 Liebermannite
A least-square fitting of the room T Na-liebermannite unit-cell volume below 16 GPa to Equation (1) yielded the isothermal bulk modulus K0 = 214(1) GPa and V0 = 236.24(5) Å3 (K’ = 4), which was 6% to 18% higher than K0 = 180–201 GPa reported for the KAlSi3O8 endmember [,,]. Fitting of Equation (1) with K’ fixed to 3 and 5 (Table 4) showed that such differences could not be explained by the tradeoff between K0 and K’, and therefore suggested that incorporation of Na had a substantial effect on the compressibility of liebermannite. In contrast, we found our bulk modulus was ~8% higher than K0 = 198 GPa for K0.8Na0.2AlSi3O8 hollandite [], despite the two phases holding a similar Na-content. Fitting our data with V0 = 237.3 Å3 as proposed by Boffa-Ballaran et al. [], however, gave a lower bulk modulus of K0 = 195.4(4) GPa, which is more in agreement with their K0 values and suggests that the discrepancy with Boffa-Ballaran et al. [] lies in the determination of the room T zero-pressure volume.

Table 4.
Thermoelastic parameters of hollandite-I and hollandite-II phases in the system KAlSi3O8–NaAlSi3O8.
Except for our study and Ferroir et al. [], previous studies did not measure directly the unit-cell volume of their hollandite phase. Instead they derived their V0 values from the fitting of the EoS, assuming the pressure derivative of the bulk modulus K’ = 4 [,,]. Comparison of previous V0 values with a recent study by Zhou et al. [], who carried out a precise investigation of the unit-cell volume of Na-bearing liebermannite as a function of Na-content, suggests that Boffa-Ballaran et al. [] likely overestimated V0 (Figure S1), which may be partly due to the use of decompression data in their EoS fitting. A second analysis of their high-pressure data, omitting decompression data, yielded K0 = 217(4) GPa and V0 = 236.1(2) Å3 (K’ = 4), which agrees well with our K0 and V0 (Table 4) and the Na-content dependence of V0 proposed by Zhou et al. []. On the other hand, it is difficult to explain the differences between K0 values of previous studies on the KAlSi3O8 endmember [,,], which may be due not only to unconstrained V0 but also limited data at high pressure [,]. Nevertheless, more recently, some theoretical works have favored higher K0 values for the KAlSi3O8 endmember [], such as K0 = 201.4 GPa reported by Ferroir et al. []. Their value is ~9% smaller than our K0 for K0.7Na0.3AlSi3O8, suggesting a substantial effect of Na-incorporation on the compressibility of liebermannite, which contrast with a previous conclusion by Boffa-Ballaran et al. [], who proposed that Na does not affect the bulk compressibility of the hollandite structure.
Data at P > 16 GPa were used to investigate the compressibility of the K0.7Na0.3AlSi3O8 hollandite-II phase. Because the transition is reversible on release of pressure, the hollandite-II phase is unquenchable to ambient conditions and therefore there was no direct measurements of its zero-pressure volume. When we chose to fix V0 = 239.4 Å3 as proposed by Boffa-Ballaran et al. [] for the K0.8Na0.2AlSi3O8 hollandite-II above 17 GPa, a least-square fitting of our hollandite-II room T unit-cell volume data yielded K0 = 163.2(3) GPa (K’ = 4). The difference between K0 in the two studies may be partly related to the use of the tetragonal BaMn8O15 hollandite-type structure to fit our high-pressure data rather than the monoclinic cell I2/m used by Boffa-Ballaran et al. []. The reason we chose this structure is because the data were analyzed close to the transition pressure and therefore splitting of the peaks may not have been large enough to identify them as separate peaks. It is, however, worth noting that the fitting of hollandite-II data in Boffa-Ballaran et al. [] also included data close to the transition, which may have led to overestimating the zero-pressure volume in their study. When we adopted a lower V0 = 237.01 as proposed by a fitting of the combined KAlSi3O8 hollandite-II volume dataset of Hirao et al. [] and Ferroir et al. [], we obtained a larger K0 = 188.2(4) GPa (K’ = 4) Å3, which is more compatible with bulk moduli proposed by experimental and theoretical works on the KAlSi3O8 endmember [,]. Our K0 estimates for the K0.8Na0.2AlSi3O8 hollandite-II were lower than previous studies on the KAlSi3O8 endmember, suggesting that the incorporation of Na in the hollandite-II structure is likely to decrease the bulk modulus of the hollandite-II phase, although more high-pressure data on Na-bearing hollandites are necessary to constrain tightly the effect of Na on the compressibility of the hollandite-II structure.
Figure 4 shows the unit-cell volume of Na-liebermannite up to ~21 GPa and 1700 K. A least-square fitting of all data below 16 GPa by Equations (1)–(5) yielded the isothermal bulk modulus KT0 = 211(2) GPa, its temperature derivative (∂KT/∂T)P = −0.043(20) GPa·K−1, and the thermal expansion αT = 2.9(7) × 10−5 K−1 (K’ = 4, V0 = 236.24 Å3) for the hollandite-I phase. Our values of (∂KT/∂T)P and αT were slightly different than that reported for the KAlSi3O8 endmember [], but the difference falls within the uncertainties of the present measurement, suggesting that the substitution of Na may not have a significant effect on the temperature derivative of the bulk modulus of liebermannite. As for the hollandite-II, a similar fitting yielded KT0 = 160(2) GPa, (∂KT/∂T)P = −0.023(16) GPa·K−1, and αT = 3.2(11) × 10−5 K−1 (K’ = 4) for V0 = 239.4 Å3 fixed after Boffa-Ballaran et al. [], while we obtained KT0 = 184(3) GPa, (∂KT/∂T)P = −0.031(19) GPa·K−1, and αT = 3.3(12) × 10−5 K−1 (K’ = 4) when we fixed V0 = 237.01 Å3 after Hirao et al. []. These are the first estimates of the thermal properties of Na-bearing hollandite-II phase, which allow for calculating the density of this phase at the P and T conditions of the deep mantle.
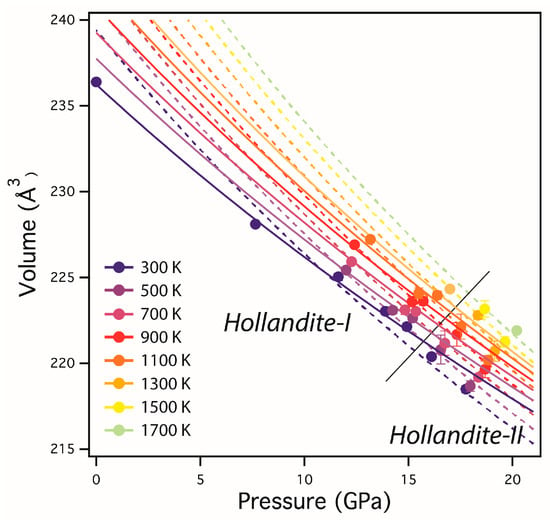
Figure 4.
Unit-cell volume of K0.7Na0.3AlSi3O8 liebermannite as a function of pressure and temperature. The color-scale represents the data at temperatures varying from 300 K to 1700 K, respectively. Pressure and volume error bars are within the size of the symbols. Solid and broken lines represent the isothermal compression curves obtained from fitting all the data to a Birch–Murnaghan EoS (Equations (1)–(5)) for the hollandite-I (plain lines) and hollandite-II (broken lines) phases, respectively.
3.2. P–V–T EoS of Jadeite
The unit-cell volumes of jadeite underwent nonlinear decreases with no discontinuity in the compression curves up to the maximum pressure, as shown in Figure 5. Because of our limited data, V0 was fixed to the value determined by ambient XRD on the starting sample (OS2999, Table 1). Fitting of the pressure–volume data at 300 K by Equation (1) yielded K0 = 129.2(2) GPa (K’ = 4, V0 = 402.4 Å3). The present K0 value was in good agreement with the former study of Zhao et al. [], while it was smaller than more recent studies [,]. The difference is, however, well explained by the tradeoff between K0 and its first pressure derivative K’ as shown by a subsequent fitting of our data with K’ = 3.3, which yielded K0 = 133.6(2) GPa, which is well consistent with the former studies of Posner et al. [] and McCarthy et al. []. On the other hand, it is difficult to explain the high value of K0 = 134.0(7) GPa reported by Nestola et al. [] for K’ = 4.4 (Table 5), although their unit-cell volume data as well as those of other studies [,,] were well explained by our compression curve (Figure 5). The difference may lie in their determination of K’ when fitting data in a relatively narrow pressure range, as pointed out by Zhao et al. [] during fitting of their own data.
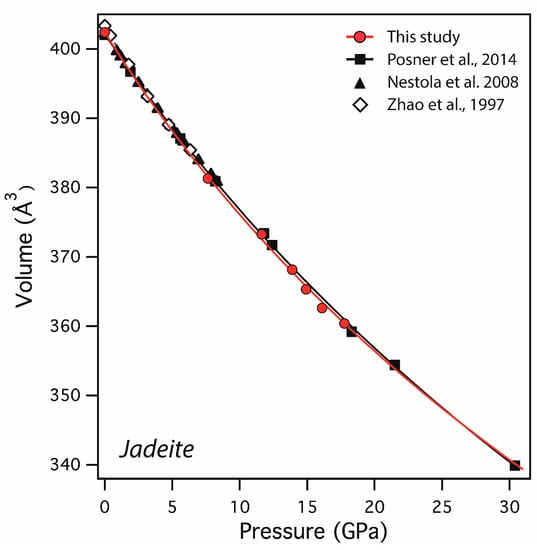
Figure 5.
Unit-cell volume of Jadeite as a function of pressure. Data are fit with a Birch–Murnaghan equation (Equation (1)).

Table 5.
Thermoelastic parameters of jadeite.
Figure 6 shows the unit-cell volume of Jadeite up to ~21 GPa and 1700 K. A least-square fitting of all data by Equations (1)–(5) yielded the isothermal bulk modulus KT0 = 127(1) GPa, its temperature derivative (∂KT/∂T)P = –0.012(11) GPa·K−1, and the thermal expansion αT = 2.6(9) × 10−5 K−1 (K’ = 4, V0 = 402.4 Å3), which are generally in good agreement with the former study of Zhao et al. []. We also noted that if we adopted K’ = 3.3 as suggested by more recent studies [,], we found KT0 = 132(1) GPa, (∂KT/∂T)P = –0.007(11) GPa·K−1, and αT = 2.3(8) × 10−5 K−1 (V0 = 402.4 Å3).
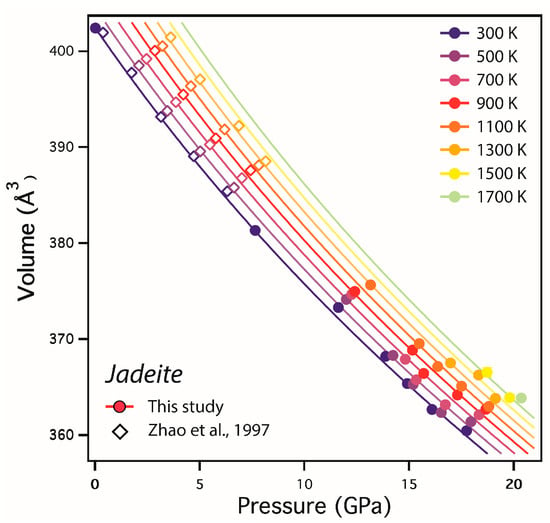
Figure 6.
Unit-cell volume of jadeite as a function of pressure and temperature. Plain circles represent our volume data while open diamonds are data taken from Zhao et al. []. The color-scale represents the data at temperatures varying from 300 K to 1700 K, respectively. Pressure and volume error bars are within the size of the symbols. Solid lines represent the isothermal compression curves obtained from fitting all data to a Birch–Murnaghan EoS (Equations (1)–(5)).
4. Discussion
Implications for the Density of Subducted Continental Crust
We combined our thermoelastic data of hollandite and jadeite with those of other mantle minerals reported by previous experimental studies (Table S2) to estimate density of continental crust and sediment along an average mantle geotherm (Figure 4). Density of pyrolite, oceanic crust, and harzburgite compositions were also calculated and presented for comparison. We used the formalism of Equations (1)–(5) to calculate densities of each mineral as a function of pressure and temperature along an adiabatic mantle geotherm []. The density of the rock aggregates were calculated by a weighted average of the density of the constituent minerals, while the proportions of each phases at depth (Figure 7a) were taken from the phase equilibrium study of Irifune et al. []. In the shallower upper mantle, continental crust consists of clinopyroxene (40%), orthoclase (30%), coesite (25%), and kyanite (5%). Here we assume that the 40% clinopyroxene is jadeite, which is supported by the experimental result that the clinopyroxene in continental crust becomes more Na-rich with increasing pressure and exists as jadeite, essentially under the MTR conditions. With increasing pressure, clinopyroxenes also gradually enter into the garnet phase, resulting in an increase of the garnet proportions up to 30% at depths of ~400 km. At these depths, garnet coexists with pyroxene (15%), stishovite (25%), hollandite (25%), and kyanite (5%). The gradual exsolution of up to 10% CaPv from garnet occurs at ~550 km []. Kyanite is present down to a depth of ~450 km where it is replaced by 10% CAS phase. The phase transformations of coesite to stishovite and orthoclase to hollandite were fixed to 10 GPa (~300 km depth) while the hollandite phase transition from hollandite-I to hollandite-II was fixed to 17 GPa (~500 km depth).
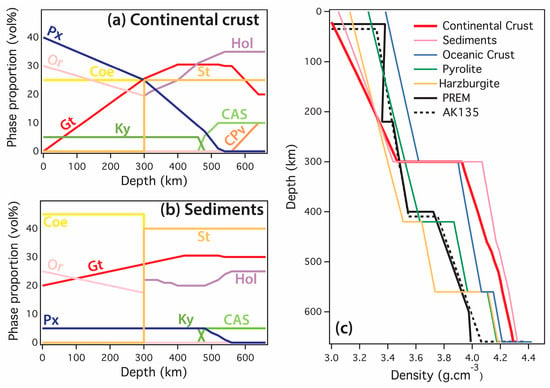
Figure 7.
Phase proportions in (a) continental crust and (b) sediment as a function of depth, derived from Irifune et al. []. (c) Calculated density of continental crust and sediment as function of depth compared to that of other mineralogical models of pyrolite, oceanic crust (mid-ocean ridge basalt), and harzburgite, and global seismic models PREM [] and AK135 []. Abbreviations: Px, pyroxene; Or, orthoclase; Coe, coesite; Gt, garnet; Ky, kyanite; St, stishovite; Hol, hollandite; CAS, Ca-rich aluminosilicate phase; CPv, CaSiO3 perovskite.
Figure 7b shows that the densities of continental crust and sediment at depth < 200 km, are lower than any other lithologies, which would provide negative buoyancy to the slab and impede its subduction at the shallower upper mantle depths. We see, however, that both continental crust and sediment densities rapidly increase, due to the increase of the garnet proportions with pressure (Figure 7a), suggesting that their negative buoyancy is likely to be canceled by the density of the oceanic crust at depths > 200 km. The high-density of the oceanic crust component is generally considered to pull the slab downward, and thus could provide a way to transport broken fragments of continental blocks or sediments down to a depth of ~270 km [,]. When the continental crust and sediment reach a critical depth of ~300 km, their density would become, respectively, 11% and 15% greater than that of the pyrolitic mantle (Figure 7b) after the transformation of orthoclase to hollandite and coesite to stishovite at ~10 GPa (Figure 7a). Consequently, if the continental crust or the sediments would decouple from the main body of the slab at depths > 300 km, their high densities compared to the mantle are likely to favor the supply of continental materials to the deeper parts of MTR. In contrast, a slab breakoff before the critical depth would impede further subduction of both continental crust and sediment.
At depths > 660 km, previous studies proposed that the continental crust may be subducted into the lower mantle owing to its higher density compared to the surrounding mantle [,] when the temperature near the slab surface is lower than ~1700 K []. The final destination of the continental crust in the lower mantle is, however, still uncertain. Some studies suggested that continental crust may be partially molten when the slab is thermally equilibrated in the lower mantle [], while others proposed that it may transform to a mineral assemblage stable at higher pressure if the subducted slab can remain cool enough in the lower mantle [,]. While recent laboratory studies favor the presence of oceanic crust in the uppermost lower mantle to explain globally the low-velocity profiles beneath subduction zones [], the recycling of continental crust and sediment in the uppermost lower mantle may provide an alternative to explain locally some seismic observations that do not conform to global seismological models. Further investigation of the elasticity of continental crust constituent minerals at the pressure and temperature relevant to the uppermost lower mantle conditions are, however, necessary, and would provide an improved understanding on the recycling of continental crust materials in the deep Earth, with implications for the Earth’s mantle internal heating and long-term evolution [,].
Supplementary Materials
The following are available online at https://www.mdpi.com/2075-163X/10/3/261/s1, Figure S1: Unit-cell volume of hollandite as a function of Na-content. The shaded area represents the uncertainties on the determination of the unit-cell volume of the KAlSi3O8 endmember on the basis of the data of Nishiyama et al. [] and Ferroir et al. [], which is translated to the other compositions., Table S1: Raw data for: Pressure (NaCl scale), Pressure (Au scale), Temperature (Kelvin), Unit-cell volume of Na-liebermannite (Angstrom cube), Unit-cell volume of Jadeite (Angstrom cube)., Table S2: Thermoelastic parameters of major mantle minerals.
Author Contributions
S.G. and T.I. conceived and designed the study. A.Y. prepared the starting glass materials. S.G. and Y.H. prepared the XRD measurement system combined with a multi-anvil apparatus and S.G. conducted experiments at SPring-8. Y.Z. conducted experiments at GRC. S.G., Y.Z. and Y.K. analyzed data. S.G. and Y.Z. wrote the manuscript. All authors discussed the content of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was carried with the support of a Grant-in-Aid for Young Scientists from the Japan Society for the Promotion of Science to S. Gréaux (Proposal No. 23740339) and the Joint Usage/Research Center PRIUS, Ehime University, Japan.
Acknowledgments
The authors thank Y. Tange, T. Kunimoto, Y. Zou, C. Zhou, and T. Arimoto for their assistance in the experiments at the beamline BL04B1 of SPring-8 (Project No. 2009A1300).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yamamoto, S.; Senshu, H.; Rino, S.; Gondwana, S.O. 2009 Granite subduction: Arc subduction, tectonic erosion and sediment subduction. Gondwana Res. 2009, 15, 443–453. [Google Scholar] [CrossRef]
- Bulanova, G.P.; Walter, M.J.; Smith, C.B.; Kohn, S.C.; Armstrong, L.S.; Blundy, J.; Gobbo, L. Mineral inclusions in sublithospheric diamonds from Collier 4 kimberlite pipe, Juina, Brazil: Subducted protoliths, carbonated melts and primary kimberlite magmatism. Contrib. Mineral. Petro. 2010, 160, 489–510. [Google Scholar] [CrossRef]
- Cid, J.P.; Nardi, L.V.S.; Cid, C.P.; Gisbert, P.E.; Balzaretti, N.M. Acid compositions in a veined-lower mantle, as indicated by inclusions of (K,Na)-Hollandite + SiO2 in diamonds. LITHOS 2014, 196–197, 42–53. [Google Scholar]
- Irifune, T.; Ringwood, A.E.; Hibberson, W.O. Subduction of continental crust and terrigenous and pelagic sediments: An experimental study. Earth Planet. Sci. Lett. 1994, 126, 351–368. [Google Scholar] [CrossRef]
- Ishii, T.; Kojitani, H.; Akaogi, M. High-pressure phase transitions and subduction behavior of continental crust at pressure–temperature conditions up to the upper part of the lower mantle. Earth Planet. Sci. Lett. 2012, 357, 31–41. [Google Scholar] [CrossRef]
- Plank, T.; van Keken, P.E. Geodynamics: The ups and downs of sediments. Nat. Geosci. 2008, 1, 17–18. [Google Scholar] [CrossRef]
- Ichikawa, H.; Kawai, K.; Yamamoto, S.; Kameyama, M. Supply rate of continental materials to the deep mantle through subduction channels. Tectonophysics 2013, 592, 46–52. [Google Scholar] [CrossRef]
- Kawai, K.; Tsuchiya, T.; Tsuchiya, J.; Maruyama, S. Lost primordial continents. Gondwana Res. 2009, 16, 581–586. [Google Scholar] [CrossRef]
- Helffrich, G.R.; Wood, B.J. The Earth’s mantle. Nature 2001, 412, 501–507. [Google Scholar] [CrossRef]
- Turcotte, D.L.; Paul, D.; White, W.M. Thorium-uranium systematics require layered mantle convection. J. Geophys. Res. 2001, 106, 4265–4276. [Google Scholar] [CrossRef]
- Li, B.; Rigden, S.M.; Liebermann, R.C. Elasticity of stishovite at high pressure. Phys. Earth Planet. Inter. 1996, 96, 113–127. [Google Scholar] [CrossRef]
- Li, B.; Neuville, D.R. Elasticity of diopside to 8 GPa and 1073K and implications for the upper mantle. Phys. Earth Planet. Inter. 2010, 183, 398–403. [Google Scholar] [CrossRef]
- Ma, C.; Tschauner, O.; Beckett, J.R.; Rossman, G.R.; Prescher, C.; Prakapenka, V.B.; Bechtel, H.A.; MacDowell, A. Liebermannite, KAlSi3O8, a new shock-metamorphic, high-pressure mineral from the Zagami Martian meteorite. Meteorit. Planet. Sci. 2017, 53, 50–61. [Google Scholar] [CrossRef]
- Liu, L.G.; El Gorsey, A. High-pressure phase transitions of the feldspars, and further characterization of lingunite. Int. Geol. Rev. 2007, 49, 854–860. [Google Scholar] [CrossRef]
- Ringwood, A.E. Phase transformations and their bearing on the constitution and dynamics of the mantle. Geochim. Cosmochim. Acta 1991, 55, 2083–2110. [Google Scholar] [CrossRef]
- Irifune, T.; Ringwood, A.E. Phase transformations in subducted oceanic crust and buoyancy relationships at depths of 600–800 km in the mantle. Earth Planet. Sci. Lett. 1993, 117, 101–110. [Google Scholar] [CrossRef]
- Ishii, T.; Kojitani, H.; Akaogi, M. Phase relations and mineral chemistry in pyrolitic mantle at 1600–2200 °C under pressures up to the uppermost lower mantle: Phase transitions around the 660-km discontinuity and dynamics of upwelling hot plumes. Phys. Earth Planet. Inter. 2018, 274, 127–137. [Google Scholar] [CrossRef]
- Nishiyama, N.; Rapp, R.P.; Irifune, T.; Sanehira, T.; Yamazaki, D.; Funakoshi, K.-I. Stability and P–V–T equation of state of KAlSi3O8-hollandite determined by in situ X-ray observations and implications for dynamics of subducted continental crust material. Phys. Chem. Miner. 2005, 32, 627–637. [Google Scholar] [CrossRef]
- Ferroir, T.; Onozawa, T.; Yagi, T.; Merkel, S.; Miyajima, N.; Nishiyama, N.; Irifune, T.; Kikegawa, T. Equation of state and phase transition in KAlSi3O8 hollandite at high pressure. Am. Mineral. 2006, 91, 327–332. [Google Scholar] [CrossRef]
- Hirao, N.; Ohtani, E.; Kondo, T.; Sakai, T.; Kikegawa, T. Hollandite II phase in KAlSi3O8 as a potential host mineral of potassium in the Earth’s lower mantle. Phys. Earth Planet. Inter. 2008, 166, 97–104. [Google Scholar] [CrossRef]
- Boffa Ballaran, T.; Liu, J.; Dubrovinsky, L.S.; Caracas, R.; Crichton, W. High-pressure ferroelastic phase transition in aluminosilicate hollandite. Phys. Rev. B 2009, 80, 214104. [Google Scholar] [CrossRef]
- Zhao, Y.; Von Dreele, R.B.; Shankland, T.J.; Weidner, D.J.; Zhang, J.; Wang, Y.; Gasparik, T. Thermoelastic equation of state of jadeite NaAlSi2O6: An energy-dispersive Reitveld Refinement Study of low symmetry and multiple phases diffraction. Geophys. Res. Lett. 1997, 24, 5–8. [Google Scholar] [CrossRef]
- Nestola, F.; Boffa Ballaran, T.; Liebske, C.; Bruno, M.; Tribaudino, M. High-pressure behaviour along the jadeite NaAlSi2O6–aegirine NaFeSi2O6 solid solution up to 10 GPa. Phys. Chem. Miner. 2006, 33, 417–425. [Google Scholar] [CrossRef]
- Posner, E.S.; Dera, P.; Downs, R.T.; Lazarz, J.D.; Irmen, P. High-pressure single-crystal X-ray diffraction study of jadeite and kosmochlor. Phys. Chem. Miner. 2014, 41, 695–707. [Google Scholar] [CrossRef]
- McCarthy, A.; Downs, R.; Thompson, R. Compressibility trends of the clinopyroxenes, and in-situ high-pressure single-crystal X-ray diffraction study of jadeite. Am. Mineral. 2008, 93, 198–209. [Google Scholar] [CrossRef]
- Zhou, Y.; Irifune, T.; Ohfuji, H.; Shinmei, T.; Du, W. Stability region of K0.2Na0.8AlSi3O8 hollandite at 22 GPa and 2273 K. Phys. Chem. Miner. 2016, 44, 33–42. [Google Scholar] [CrossRef]
- Lakshtanov, D.L.; Litasov, K.D.; Sinogeikin, S.V.; Hellwig, H.; Li, J.; Ohtani, E.; Bass, J.D. Effect of Al3+ and H+ on the elastic properties of stishovite. Am. Mineral. 2007, 92, 1026–1030. [Google Scholar] [CrossRef]
- Tsuchiya, T. First-principles prediction of the P-V-T equation of state of gold and the 660-km discontinuity in Earth’s mantle. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Matsui, M.; Higo, Y.; Okamoto, Y.; Irifune, T.; Funakoshi, K.I. Simultaneous sound velocity and density measurements of NaCl at high temperatures and pressures: Application as a primary pressure standard. Am. Mineral. 2012, 97, 1670–1675. [Google Scholar] [CrossRef]
- Larson, A.C.; Von Dreele, R.B. GSAS General Structure Analysis System. Operation Manual; LAUR 86-748; Los Alamos National Laboratory: Los Alamos, NM, USA, 2000; pp. 1–179.
- Toby, B.H. EXPGUI, a graphical user interface for GSAS. J. Appl. Crystallogr. 2001, 34, 210–213. [Google Scholar] [CrossRef]
- Le Bail, A.; Duroy, H.; Fourquet, J.L. Ab-initio structure determination of LiSbWO6 by X-ray powder diffraction. Mater. Res. Bull. 1988, 23, 447–452. [Google Scholar] [CrossRef]
- Sueda, Y.; Irifune, T.; Nishiyama, N.; Rapp, R.P.; Ferroir, T.; Onozawa, T.; Yagi, T.; Merkel, S.; Miyajima, N.; Funakoshi, K.-I. A new high-pressure form of KAlSi3O8 under lower mantle conditions. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Mookherjee, M.; Steinle-Neumann, G. Detecting deeply subducted crust from the elasticity of hollandite. Earth Planet. Sci. Lett. 2009, 288, 349–358. [Google Scholar] [CrossRef]
- Kawai, K.; Tsuchiya, T. First-principles study on the high-pressure phase transition and elasticity of KAlSi3O8 hollandite. Am. Mineral. 2012, 98, 207–218. [Google Scholar] [CrossRef]
- Zhang, J.; Ko, J.; Hazen, R.H.; Prewitt, C.T. High-pressure crystal chemistry of KAlSi3O8 hollandite. Am. Mineral. 1993, 78, 493–499. [Google Scholar]
- Brown, J.M.; Shankland, T.J. Thermodynamic parameters in the Earth as determined from seismic profiles. Geophys. J. Int. 1981, 66, 579–596. [Google Scholar] [CrossRef]
- Saikia, A.; Frost, D.J.; Rubie, D.C. Splitting of the 520-kilometer seismic discontinuity and chemical heterogeneity in the mantle. Science 2008, 319, 1515–1518. [Google Scholar]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Kennett, B.L.N.; Engdahl, E.R.; Buland, R. Constraints on seismic velocities in the Earth from traveltimes. Geophys. J. Int. 1995, 122, 108–124. [Google Scholar] [CrossRef]
- Ichikawa, H.; Gréaux, S.; Azuma, S. Subduction of the primordial crust into the deep mantle. Geosci. Front. 2017, 8, 347–354. [Google Scholar] [CrossRef]
- Ono, S.; Hirose, K.; Kikegawa, T.; Saito, Y. The compressibility of a natural composition calcium ferrite-type aluminous phase to 70 GPa. Phys. Earth Planet. 2002, 131, 311–318. [Google Scholar] [CrossRef]
- Gréaux, S.; Irifune, T.; Higo, Y.; Tange, Y.; Arimoto, T.; Liu, Z.; Yamada, A. Sound velocity of CaSiO3 perovskite suggests the presence of basaltic crust in the Earth’s lower mantle. Nature 2019, 565, 218–221. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).