Raman Study of Barite and Celestine at Various Temperatures

Abstract

The Raman spectra of barite and celestine were recorded from 25 to 600 °C at ambient pressure and both minerals were stable over the entire temperature range. Most of the Raman bands of barite decreased in wavenumber with increasing temperature with the exception of the ν₂ modes and the ν₄ band at 616 cm⁻¹, which did not exhibit a significant temperature dependence. These vibrations may be constrained by the lower thermal expansion along the a-axis and b-axis of barite. Similar to barite, most of the Raman bands of celestine also decreased in wavenumber with increasing temperature, with the exception of the ν₂ modes and the ν₄ band at 622 cm⁻¹, which showed very little variation with increasing temperature. Variations of Raman shift as a function of temperature and FWHM (full width at half maximum) as a function of Raman shift for the main, ν₁ modes of barite and celestine show that both minerals have almost identical linear trends with a slope of −0.02 cm⁻¹/°C and −0.5, respectively, which allows for the prediction of Raman shifts and FWHM up to much higher temperatures. The calculated isobaric and isothermal mode Grüneisen parameters and the anharmonicity parameters show that the M–O modes (M = Ba²⁺ and Sr²⁺) in barite and celestine exhibit much higher values of both mode Grüneisen parameters and anharmonicity than the SO₄ tetrahedra. This indicates that the S–O distances and S–O–S angles are less sensitive to pressure and temperature increase than the M–O distances in the structure. Furthermore, the generally higher anharmonicity in celestine is due to the smaller size of the Sr²⁺ cation, which causes the celestine structure to be more distorted than the barite structure.

1. Introduction

Barite (BaSO₄) and celestine (SrSO₄) are essential for many modern industries. The high density and low oil absorption properties of barite make it useful in many industrial applications [1]. Barite is used in the plastics industry to improve the stiffness, intensity, and abrasive strength of plastics and in the paper-making industry to improve the whiteness of paper products. It is used in the paint industry for increasing the stability of the paint and adding more brightness to the paint and in the rubber industry to make the rubber acid- and alkali-proof. It is also used in the pharmaceutical industry in diagnostic medical tests as barium meal is very effective in blocking x-ray and gamma-ray emissions and also in the cosmetic industry because of its mild effect on the skin. In addition, celestine is the most important chemical raw material for extracting strontium, which is widely used in producing permanent ceramic magnets and in fireworks, marine flares, and tracer ammunition because strontium burns with a brilliant red flame [2]. Therefore, investigation of the detailed variation in the structure of barite and celestine with temperature may be beneficial for industrial applications.

Natural barite and celestine occur in various evaporitic and non-evaporitic sedimentary environments [3,4]. Barite is also a common mineral in base metal sulfide deposits, associated with alkali volcanic rocks [5,6], in volcanic sequences [7], in stratiform barite deposits [8,9], and in carbonatite and rare earth element (REE) deposits [10,11]. Celestine is also found in volcanic-sedimentary environments [12] and in hydrothermal deposits, where it is commonly accompanied by fluorite, barite, calcite, lead, and zinc sulfides [13].

Barite and celestine are isostructural and their crystal structures were initially determined by James and Wood [14]. The barite structure was refined by Colville and Staudhammer [15] and the structure of celestine was refined by Garske and Peacor [16] and Hawthorne and Ferguson [17]. A further refinement of the structure of both minerals and calculation of the force constants for the SO₄ tetrahedron was later carried out by Miyake et al. [18]. The structural parameters are correlated with the effective sizes of the Ba²⁺ and Sr²⁺ cations. In celestine, the small Sr²⁺ cation forms a short average Sr–O distance, so the charge on the O atoms is less and the average S–O distance is longer. In barite, the larger Ba²⁺ cation forms a longer average Ba–O distance, and hence, the charge on the O atoms is larger and the average S–O distance is shorter. This results in the celestine structure being more distorted than the barite structure [19].

Barite was one of the first crystals to be studied shortly after the discovery of Raman spectroscopy [20,21,22,23]. More recently, studies of both barite and celestine were carried out by Buzgar et al. [24]. Raman spectroscopy has also been used to investigate the behavior of barite and celestine at high pressures [25,26,27,28]. The influence of temperature at ambient pressure on barite was first reported in 1948 by Narayanaswamy [29]. Since this preliminary investigation over 70 years ago, there appears to have been no further studies on the influence of temperature on the Raman spectra of barite or celestine at ambient pressure. Therefore, in this paper, we report the Raman spectra of barite and celestine at temperatures up to 600 °C at atmospheric pressure and consider how temperature effects the crystal structure of barite and celestine.

2. Experimental

The barite sample is from Jinkouhe, Sichuan Province, China and the celestine sample is from Sakoany, Mahajanga District, Madagascar. Both the samples were analyzed using a JEOL JXA-8530F-plus field emission electron microprobe equipped with wavelength dispersive spectrometers (WDS) at the Institute of Geochemistry, Chinese Academy of Sciences, Guiyang, China. The SPI (Structure Probe, Inc.) standards of calcite, celestine, and barite were used for Ca, Sr, Ba and S, respectively. The operating conditions were 25 kV accelerating voltage, 10 nA beam current, and a beam diameter of 10 μm. Table 1 gives a list of the analytical results for barite and celestine. The averaged results of the barite sample are as follows (wt%): BaO 64.30, SrO 0.02, SO₃ 35.78, and the calculated crystal-chemical formula is Ba_0.95S_1.02O₄. The averaged results of the celestine sample are as follows (wt%): CaO 0.01, BaO 0.02, SrO 55.58, SO₃ 43.61, and the calculated crystal-chemical formula is Sr_0.99S_1.00O₄. These results show that both barite and celestine are very pure with compositions close to the end members.

Table 1. Electron microprobe analysis results, expressed as wt.% oxide, for barite and celestine.

Barite
Oxide	Spot 1	Spot 2	Spot 3	Spot 4	Spot 5	Spot 6	Spot 7	Spot 8	Spot 9	Spot 10	Spot 11	Spot 12	Spot 13	Spot 14	Spot 15	Avg.	SD
CaO	- a	-	-	-	-	0.01	-	-	-	-	-	-	0.01	0.01	0.01	-	-
BaO	64.56	63.94	64.47	64.27	63.95	64.21	64.69	64.42	64.39	63.85	64.49	64.30	64.51	64.41	63.95	64.30	0.25
SrO	-	0.08	0.06	-	-	-	0.02	-	0.07	0.05	0.01	0.04	-	-	-	0.02	0.03
SO3	36.22	36.06	36.06	35.35	35.82	35.48	35.83	35.69	35.47	36.06	35.81	35.80	35.61	35.86	35.63	35.78	0.24
Total	100.78	100.08	100.59	99.62	99.77	99.70	100.54	100.11	99.93	99.95	100.31	100.14	100.13	100.28	99.59	100.10	0.35
Celestite
Oxide	Spot 1	Spot 2	Spot 3	Spot 4	Spot 5	Spot 6	Spot 7	Spot 8	Spot 9	Spot 10	Avg.	SD
CaO	0.02	-	-	-	0.01	0.01	0.01	-	0.02	0.01	0.01	0.01
BaO	-	0.01	0.09	-	-	0.04	-	0.01	-	0.07	0.02	0.03
SrO	55.53	55.36	55.56	55.93	55.55	55.58	55.67	55.84	55.54	55.25	55.58	0.19
SO3	43.85	43.84	43.41	43.54	43.59	43.82	43.21	43.44	43.85	43.54	43.61	0.21
Total	99.40	99.21	99.06	99.48	99.15	99.44	98.89	99.29	99.41	98.86	99.22	0.21

^a Means below detection limit.

A Renishaw inVia Reflex spectrometer system equipped with a standard confocal microscope was used for Raman spectral analysis. A Renishaw diode-pumped solid-state laser provided 532 nm laser excitation with 5 mW power at the sample. An 1800 grooves/mm grating was used giving a spectral resolution of 1.2 cm⁻¹. Depolarized Raman spectra were obtained using a 10 s integration time with 5 accumulations and a 50× Leica long working distance microscope objective, which focused the beam to a spot size of 1.6 μm. Wavenumber calibration was carried out using a silicon standard.

A Linkam MDSG600 heating stage was mounted on the microscope stage of the Renishaw Raman spectrometer. The Linkam stage was heated by a resistance heater in a silver block, and small crystals of barite and celestine (typically less than 1 mm high) were then placed on a sapphire disk which rested on top of the silver block. Sapphire was used as it has high thermal conductivity. A silver lid with a small hole to allow the laser beam to pass through was placed on top of the sample to form an enclosed homogeneous thermal oven [30]. The stage was calibrated by measuring the H₂O triple point and the H₂O critical point in synthetic fluid inclusions. A heating rate of 50 °C/minute was used to heat the crystals and then the stage was held at the desired temperature while recording the Raman spectra. Repeated measurements over a period of 30 min at constant temperature showed no changes in the Raman spectra and confirmed that the crystals reached thermal equilibrium. After heating to the maximum temperature of the stage (600 °C), the stage was allowed to cool to room temperature where further Raman spectra were acquired to check for any possible modifications or phase changes due to the heating process.

3. Results and Discussion

3.1. Ambient Raman Spectra

The Raman spectra of barite and celestine at room temperature are shown in Figure 1. The structures of barite and celestine are identical and both belong to the orthorhombic system with space group Pbnm [18]. Each S atom coordinates with four oxygen atoms and forms the SO₄ tetrahedron while the cation (Ba²⁺ or Sr²⁺) coordinates with 12 oxygen atoms. The SO₄ tetrahedron has C_s site group symmetry which theoretically has 9 degrees of vibrational freedom [31] (i.e., one nondegenerate (ν₁), one doubly degenerate (ν₂), and two triply degenerate modes (ν₃ and ν₄)). Note that, in the crystalline structure, the symmetry of the perfect tetrahedron is lowered, resulting in splitting of the ν₂, ν₃, and ν₄ modes. Furthermore, some additional modes, which arise from distortion of the SO₄ tetrahedra, remained unassigned in this study. Raman peaks below 400 cm⁻¹ were assigned to M–O₁₂ vibrations. The observed modes were in good agreement with those previously reported in the literature [32,33,34] and are listed in Table 2.

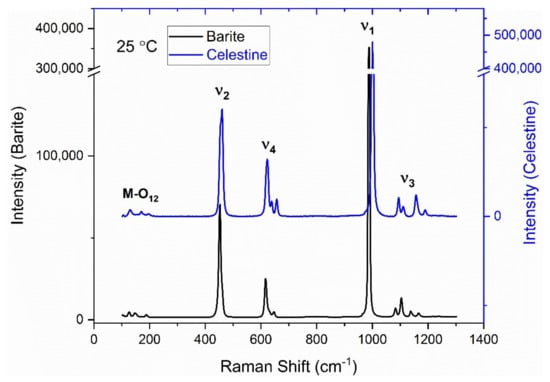
Figure 1. Raman spectra at ambient temperature of barite and celestine.

Table 2. Observed Raman vibrational modes (in cm⁻¹) of crystalline barite and celestite at room temperature.

Barite	Barite	Celestine	Celestine	Mode
This Study	Griffith [34]	This Study	Griffith [33]	Assignment
127		131		M–O12
149				M–O12
155				M–O12
169		170		M–O12
188		197	190	M–O12
			240	M–O12
452	453	454	453	ν2 SO4
461	463	461	458	ν2 SO4
616			617	ν4 SO4
623	623	622	624	ν4 SO4
646	647	639	637	ν4 SO4
		656	656	Unassigned
988	988	1000	999	ν1 SO4
1083	1083	1094	1094	ν3 SO4
1104	1105	1111	1103	Unassigned
1138				ν3 SO4
1166	1167	1158	1159	ν3 SO4
		1190	1185	ν3 SO4

3.2. Barite Temperature Dependence

Raman spectra of a barite crystal were recorded at 50 °C intervals from room temperature to 600 °C and selected spectra are shown in Figure 2. Data on the detailed variation of Raman shift with temperature are shown in Figure 3 and equations of fit are listed in Table 3. For comparison with the previous study on the effect of temperature on barite by Narayanaswamy [29], the proportional change of each observable Raman band is also shown in Table 3. There is relatively good agreement between the two studies, which verifies the current results and shows that the early studies, conducted under challenging conditions and before the advent of lasers, also produced reliable data.

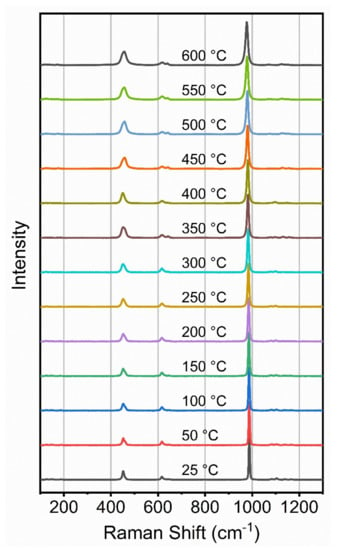
Figure 2. Raman spectra of barite as a function of temperature at atmospheric pressure.

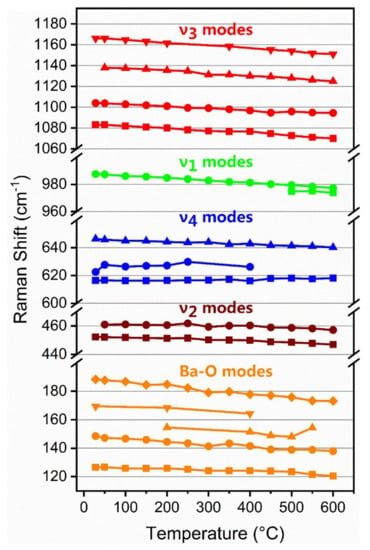
Figure 3. Temperature dependence of the wavenumber of the observed Raman bands of barite at atmospheric pressure.

Table 3. Ambient wavenumbers (ω), temperature dependencies, proportional change, and full width at half maximum (FWHM) variation of the Raman bands of barite.

ω (cm−1)	ωi = xi + yiT +ziT2 a			Proportional Change b (×106)
Room Temp.	xi	yi	zi	This Study	Narayanaswamy [29]	$\frac{\Delta \mathit{F}\mathit{W}\mathit{H}\mathit{M}}{\Delta \mathit{T}}$ This Study (cm−1/°C)
127	127.1	−0.0091		83.7	95	0.0163
148	148.5	−0.0184		125.0	117	0.0285
155	155.2	−0.0089
169	169.3	0.0034	−4.0 × 10−5
188	189.3	−0.00276				0.0138
452	452.2	−0.0021	1.0 × 10−5	141.0	177	0.0052
461	461.8	−0.0063		20.6		0.0262
616	616.0	0.0031		14.8		0.0207
623	623.8	0.0323	−7.0 × 10−5	−5.2
646	646.4	−0.0099		0.0		0.0057
988	988.3	−0.0178		16.7	14.3	0.0085
1083	1084.2	−0.0221		18.3	27.6	0.0291
1104	1104.5	−0.018		20.9	25.3	0.0125
1138	1138.0	−0.0165	−1.0 × 10−5	15.1	24.7	0.0217
1166	1167.2	−0.0272		20.0	29.4	0.0295

^a Note the units of T are Celsius; ^b Proportional change = 1/ω × (Δω/ΔT) [29].

The main ν₁ band of barite decreases in wavenumber with increasing temperature with a slope of approximately −0.02 cm⁻¹/°C (Table 3). At temperatures above 450 °C, the peak becomes slightly asymmetric in shape and is more accurately fitted by a mixed Gaussian and Lorentzian curve (Figure 4). Although this splitting is not apparent at room temperature, Kloprogge et al. [35] reported the splitting of the ν₁ band of celestine at 77 K and Girard et al. [36] reported the appearance of a shoulder on the low wavenumber side of celestine with increasing pressure. The ν₃ bands of barite all show a systematic decrease in wavenumber with increasing temperature with the 1138 cm⁻¹ band exhibiting a non-linear temperature dependence (Table 3). It is also interesting to note that the ν₂ bands at 452 and 461 cm⁻¹ and the ν₄ band at 616 cm⁻¹ are almost unaffected by temperature up to 400 °C (Figure 3) and exhibit very small slopes (Table 3).

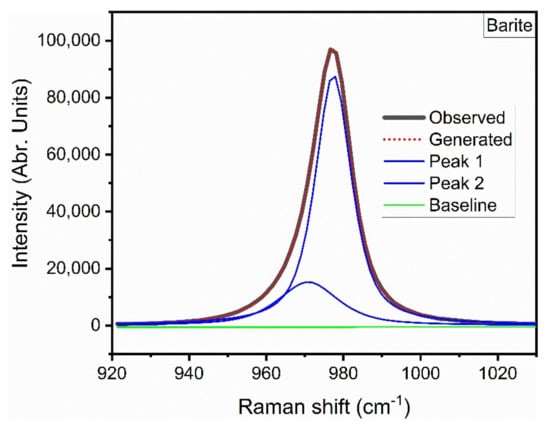
Figure 4. Results of the curve fitting of the ν₁ Raman band of barite at 600 °C. Peak 1 has a maximum at 977.4 cm⁻¹ and peak 2 has a maximum at 973.8 cm⁻¹. The dotted red curve shows the overall band fit to the observed spectrum.

The observed ν₄ bands were all assigned to the stretching and bending of the S–O bonds and appeared less sensitive to changes of Ba–O distances. Ye et al. [37] reported that the axial thermal expansion coefficients of BaSO₄ are 1.18 × 10⁻⁵ K⁻¹, 1.37 × 10⁻⁵ K⁻¹, and 1.67 × 10⁻⁵ K⁻¹ along a-, b-, and c-axes, respectively. Therefore, the behavior of the ν₄ bands may be due to vibrational restrictions arising from the lower thermal expansion along the a-axis and b-axis.

Finally, the Ba–O modes all show a decrease in wavenumber with increasing temperature (Figure 3) but the 188 cm⁻¹ band has a greater negative slope than the other bands, and hence, may vibrate parallel to the c-axis. The largest bond distance of Ba–O is parallel to the c-axis in the barite structure, and hence, the bonding force between Ba–O in this direction is the weakest and results in the fact that the c-axis is the most compressible axis [38].

It is well known that the Raman bands of minerals commonly broaden with increasing temperature [39,40,41]. Recently, Nesbitt et al. [40] expanded the theory of Balkanski et al. [42] to include Heisenberg lifetimes. In this theory, Raman shifts are dependent on thermal expansion and the Grüneisen parameter [43]. This theory predicts that FWHM plotted against Raman shift should produce a linear trend provided temperatures are greater than about 25 °C. The variation of FWHM as a function of the Raman shift of the ν₁ mode of barite is shown in Figure 5. A linear regression of the data shows that it has a slope of approximately −0.5. As discussed by Nesbitt et al. [40] this procedure allows prediction of Raman shifts and FWHM of barite up to much higher temperatures, which may find application in various industrial processes.

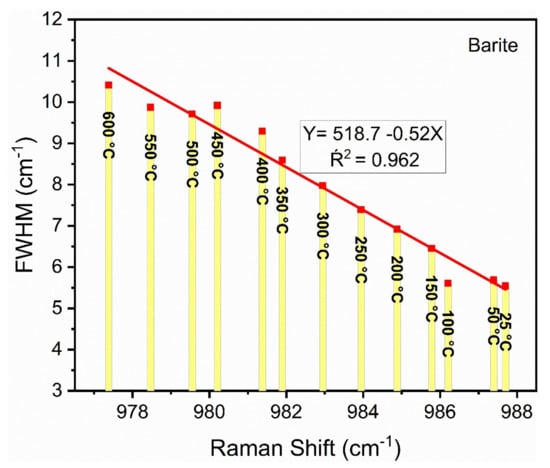
Figure 5. A plot of the FWHM versus Raman shift for the ν₁ mode of barite. The equation gives the results of a linear regression through the data. Note that the temperature increases from the far bottom right to the far upper left.

3.3. Celestine Temperature Dependence

As for barite, the Raman spectra of the celestine crystal were recorded at 50 °C intervals from room temperature to 600 °C and selected spectra are shown in Figure 6. Plots of the detailed variation with temperature are shown in Figure 7 and equations of fit are listed in Table 4.

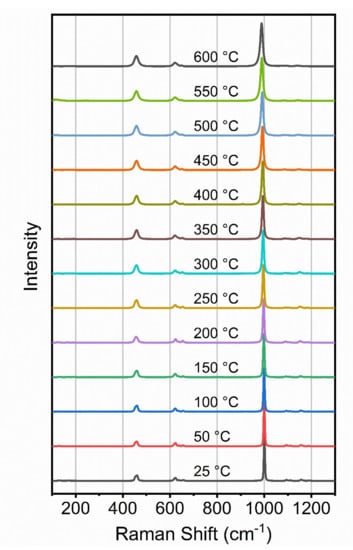
Figure 6. Raman spectra of celestine as a function of temperature at atmospheric pressure.

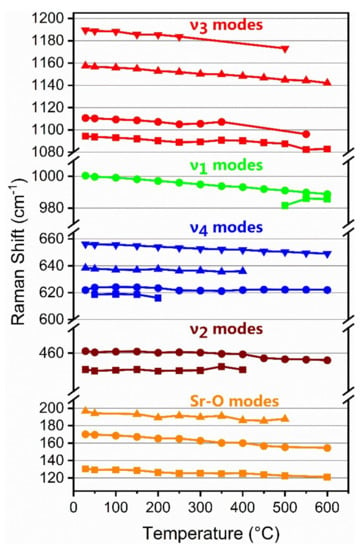
Figure 7. Temperature dependence of the observed Raman bands of celestine at atmospheric pressure.

Table 4. Ambient wavenumbers (ω) and temperature dependencies of the various Raman bands of celestine.

ω (cm−1)	ωi = xi + yiT + ziT2 a			Proportional Change b (×106)
Room Temp.	xi	yi	zi	This Study	$\frac{\Delta \mathit{F}\mathit{W}\mathit{H}\mathit{M}}{\Delta \mathit{T}}$ This Study (cm−1/°C)
131	130.7	−0.0122	−6.0 × 10−6	125.6	0.0007
170	171.7	−0.0271	−6.0 × 10−6	196.3	0.0018
197	196.7	−0.0281	2.0 × 10−5	97.4	0.0437
454	453.0	0.0016		0.6	0.0018
461	460.6	−0.0008	−1.0 × 10−5	13.6	0.0222
622	623.7	−0.006	5.0 × 10−6	−0.4	0.0606
639	638.1	−0.0062		10.5	0.0035
656	656.8	−0.0129		19.2	0.0066
1000	1001.1	−0.0202		20.3	0.0090
1094	1093.5	−0.0004	−3.0 × 10−5	18.4	0.0068
1111	1110.1	−0.0008	−4.0 × 10−5	25.0	0.0053
1158	1158.0	−0.0224	−6.0 × 10−6	23.4	0.0145
1190	1190.4	−0.027	−2.0 × 10−5	29.2	0.0274

^a Note the units of T are Celsius; ^b Proportional change = 1/ω × (Δω/ΔT) [29].

The main ν₁ band of celestine decreased in wavenumber with increasing temperature with a slope of approximately −0.02 cm⁻¹/°C (Table 4), almost the same as that of barite and the reported results of anhydrite II [44]. The ν₁ band split into two bands above 450 °C in agreement with previous observations of splitting of this band by Kloprogge et al. [35] and Girard et al. [36]. All the ν₃ bands also showed a non-linear decrease in wavenumber with increasing temperature. The ν₄, 622 cm⁻¹ band showed very little variation with increasing temperature, while the 639 cm⁻¹ and 656 cm⁻¹ bands showed a linear decrease in wavenumber with increasing temperature (Figure 7). A weak ν₄ band, also reported by Griffith [33], was observed at 618 cm⁻¹ but could not be observed at temperatures above 200 °C. The ν₂ (454 and 461 cm⁻¹) bands did not show any significant variation with temperature up to 400 °C but exhibited a slight wavenumber decrease above that temperature (Figure 7). The Sr–O₁₂ modes all decreased in wavenumber with increasing temperature.

As mentioned above, relative to the Ba²⁺ cation, the smaller size of the Sr²⁺ cation caused the celestine structure to be more distorted than the barite structure, which may be the reason why some of the Raman bands of celestine exhibited a non-linear temperature dependence. The smaller Sr²⁺ cation also results in a shorter average Sr–O bond distance than for the corresponding Ba–O bond in barite. This results in less charge on the O atoms in celestine and longer average S–O bond distances [19]. These effects lead to the observation of Raman bands at higher wavenumbers in celestine when compared with barite. Furthermore, the shorter Sr–O bond distances in celestine have a marked effect on the upper M–O₁₂ mode which shifts from 188 cm⁻¹ in barite to 197 cm⁻¹ in celestine.

The variation of the FWHM as a function of the Raman shift of the ν₁ mode of celestine is shown in Figure 8. A linear regression of the data shows that it has a slope of approximately −0.5 which is almost identical to that of barite (see Figure 5). This is in good agreement with the theory proposed by Nesbitt et al. [40] and suggests that the ν₁ mode of other M²⁺SO₄ crystals may also exhibit the same slope. The FWHM variations as a function of temperature for the other Raman modes of celestine are listed in Table 4.

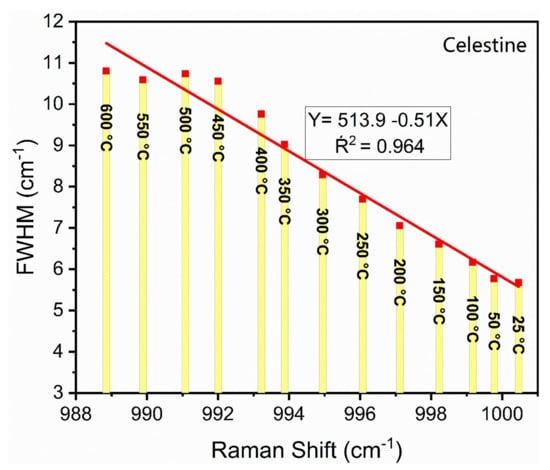
Figure 8. A plot of the FWHM versus Raman shift for the ν₁ mode of celestine. The equation gives the results of a linear regression through the data. Note that the temperature increases from the far bottom right to the far upper left.

3.4. Mode Grüneisen Parameters and Intrinsic Anharmonicity for Barite and Celestine

Gillet [45] and Mernagh [41] previously showed that logarithmic plots as a function of volume can be used to compare the effects of pressure, temperature, and volume on Raman mode frequencies. The isobaric mode Grüneisen parameter (γ_iP) measures the effect of temperature on the vibrational frequencies, and is defined by

$${\gamma }_{iP}={\left(\frac{\delta \ln \left[{\nu }_i\left(P,T\right)\right]}{\delta ln\left[V\left(P,T\right)\right]}\right)}_P$$

(1)

where ν_i is the wavenumber of the ith Raman mode, V is the molar volume and γ_iP is given by the slopes of the ln(ν) – ln(V) curves in the high-temperature region of the plots.

The isothermal mode Grüneisen parameter (γ_iT), which is a measure of the effect of pressure on vibrational frequency, is calculated following the procedure of Chopelas [46] as follows:

$${\gamma }_{iT}=\left(\frac{K_0}{{\nu }_i}\right){\left(\frac{\delta {\nu }_i}{\delta P}\right)}_T$$

(2)

where K₀ is the bulk modulus at ambient pressure and δν_i/δP is the pressure derivative at constant temperature.

The intrinsic anharmonicity parameter, a_i, in barite and celestine was determined from plots of δ lnν_i versus temperature. A list of the isobaric and isothermal mode Grüneisen parameters and the intrinsic anharmonicity for barite and celestine is given in Table 5. These results can be clearly divided into two groups: those associated with the M–O₁₂ lattice vibrations and those associated with the SO₄ tetrahedra. The lattice vibrations in barite and celestine exhibit much higher values of both mode Grüneisen parameters and anharmonicity than the SO₄ tetrahedra. This is due to the fact that the S–O distance decreases linearly with increasing cation ionic radius, the magnitude of the S–O distance variation is smaller than that of M–O distance variation, and the average of S–O–S angles of barite and celestine is nearly constant (109.46° for BaSO₄ and 109.5° for SrSO₄ [18]). Therefore, S–O distances and S–O–S angles are less sensitive to pressure and temperature increase than the M–O distances in the structure.

Table 5. Isobaric and isothermal mode Grüneisen (γ_iP and γ_iT) and anharmonic parameters (a_i) of barite and celestine.

Barite				Celestine
ω (cm−1)	γiP a	γiT b	ai (×105 K−1)	Ω (cm−1)	γiP a	γiT c	ai (×105 K−1)
127	0.02/2.92		−7.30	131	2.61		−14.26
148	3.45/1.15		−12.90
155	0.88		10.3
169	1.67		−12.36	170	3.35		−18.26
188	2.79		−15.26	197	3.12/0.28		−9.79
452	0.20/0.54	0.30	−1.97	454	0.01/0.61	0.24	−0.74
461	0.07/0.57	0.38	−1.38	461	0.33	0.30	−1.81
616		0.11	0.50	622	0.02	0.13	−1.25
623	0.09	0.19	0.60	639	0.27/0.01	0.16	−0.66
646	0.28	0.18	−1.54	656	0.47/0.26	0.19	−2.03
988	0.33	0.23	−1.81	1000	0.44/0.31	0.22	−2.06
1083	0.39		−2.11	1094	0.51/0.16	0.32	−1.90
1104	0.49/0.09		−1.64	1111	0.41		−2.13
1138	0.39	0.19	−2.14
1166	0.43	0.71	−2.34	1158	0.43	0.16	−2.39
				1190	0.55		−3.01

^a Isobaric mode Grüneisen parameter for this study. For polynomial fitting, the two values correspond to 25 °C and 600 °C, respectively. ^b Isothermal mode Grüneisen parameter. Data from Lee et al. [22]. ^c Isothermal mode Grüneisen parameter. Data from Girard et al. [29].

The corresponding intrinsic anharmonicity for celestine is generally higher than that of barite (Table 5). The intrinsic anharmonicity parameters are correlated with effective size of the cations. In celestine, the small Sr²⁺ cation forms a short average Sr–O distance, which results in the celestine structure being more distorted than the barite structure [19]. Furthermore, the results of Ye et al. [37] also inferred that bond length may be a major factor affecting the volumetric thermal expansion of barite-group minerals. The volumetric thermal expansion coefficients decrease within an increasing ionic radius (1.44 Å for Sr²⁺ and 1.61 Å for Ba²⁺) and the corresponding average M–O distances for SrSO₄ and BaSO₄ are 2.827 Å and 2.953 Å, respectively [19]. Therefore, the axial thermal expansion along the a-axis of SrSO₄ is larger than that of BaSO₄, while the corresponding axial thermal expansion along the c-axis of BaSO₄ is smaller than that of SrSO₄ [36,37]. This results in the axial thermal expansion of BaSO₄ and SrSO₄ both being slightly anisotropic.

4. Conclusions

The Raman spectra of barite and celestine have been studied from 25 to 600 °C at ambient pressure and both minerals remained stable over the entire temperature range. Plots of temperature variation of the Raman bands of barite show that most of the Raman bands decreased in wavenumber with increasing temperature with the exception of the ν₂ modes observed at 452 cm⁻¹ and 461 cm⁻¹ and the ν₄ band at 616 cm⁻¹, which did not exhibit a significant temperature dependence. This different trend suggests that the vibrations are constrained by the lower thermal expansion along the a-axis and b-axis of barite. Similarly, most of the Raman bands of celestine also decreased in wavenumber with increasing temperature, with the exception of the ν₂ modes at 454 cm⁻¹ and 461 cm⁻¹ and the ν₄ band at 622 cm⁻¹, which is the same as for barite. Variations of Raman shift as a function of temperature and FWHM as a function of Raman shift for the main ν₁ modes of barite and celestine show that both minerals have almost identical linear trends with a slope of −0.02 cm⁻¹/°C and −0.5, respectively, which allows for prediction of Raman shifts and FWHM for these minerals at much higher temperatures.

The results of this study and recent high pressure studies of barite and celestine [36,37] also allow for the determination of the isobaric and isothermal mode Grüneisen parameters and anharmonicity parameters. The calculations show that the M–O modes in barite and celestine exhibit much higher values of both mode Grüneisen parameters and anharmonicity than the SO₄ tetrahedra. This indicates that the S–O distances and S–O–S angles are less sensitive to pressure and temperature increase than the M–O distances in the structure. Furthermore, the generally higher anharmonicity in celestine is due to the smaller size of the Sr²⁺ cation, which causes the celestine structure to be more distorted than the barite structure.