Defects, Diffusion and Dopants in Sillimanite
Abstract
:1. Introduction
2. Computational Methods
3. Results
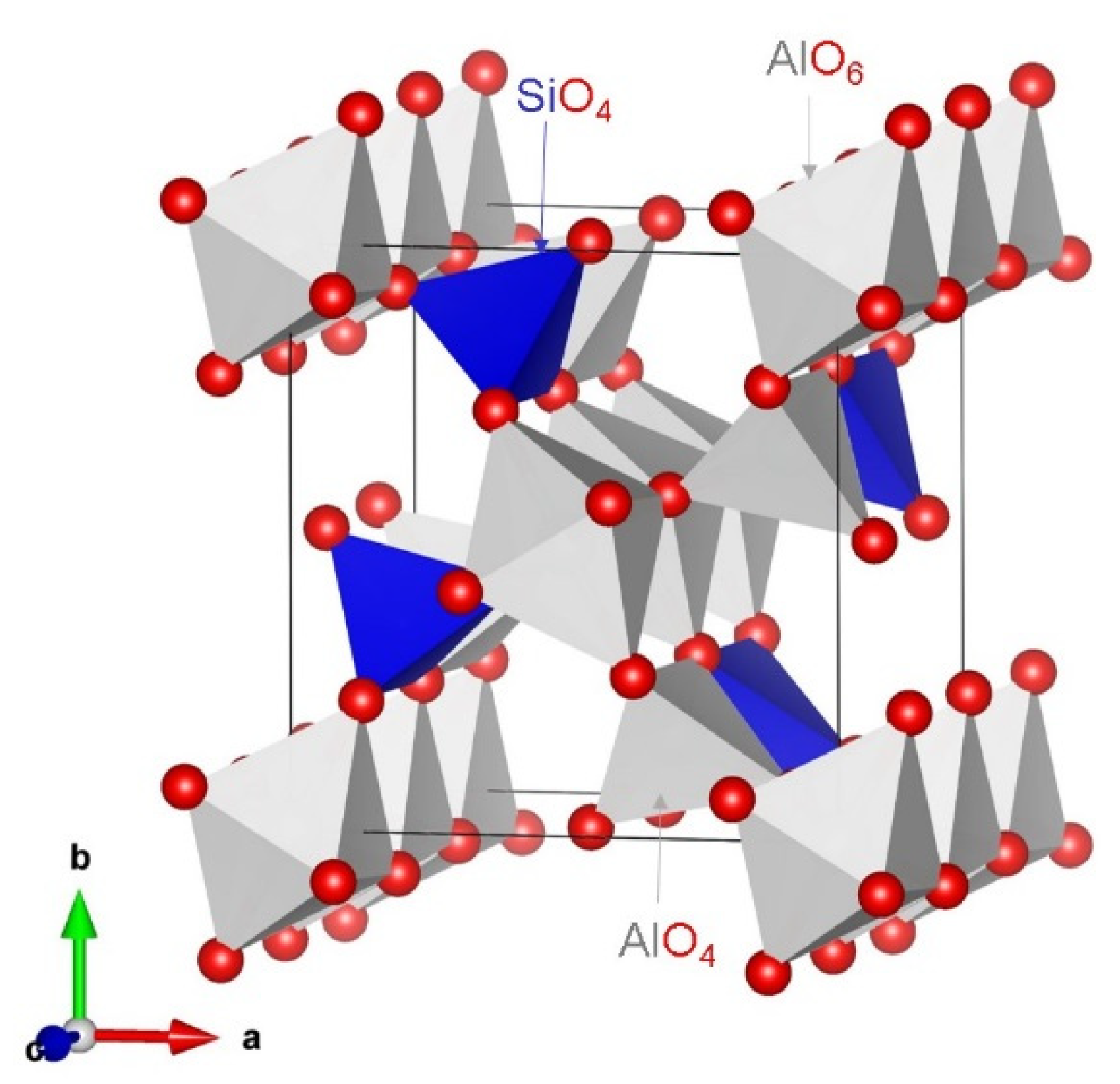
3.1. Crystal Structure of Al2SiO5
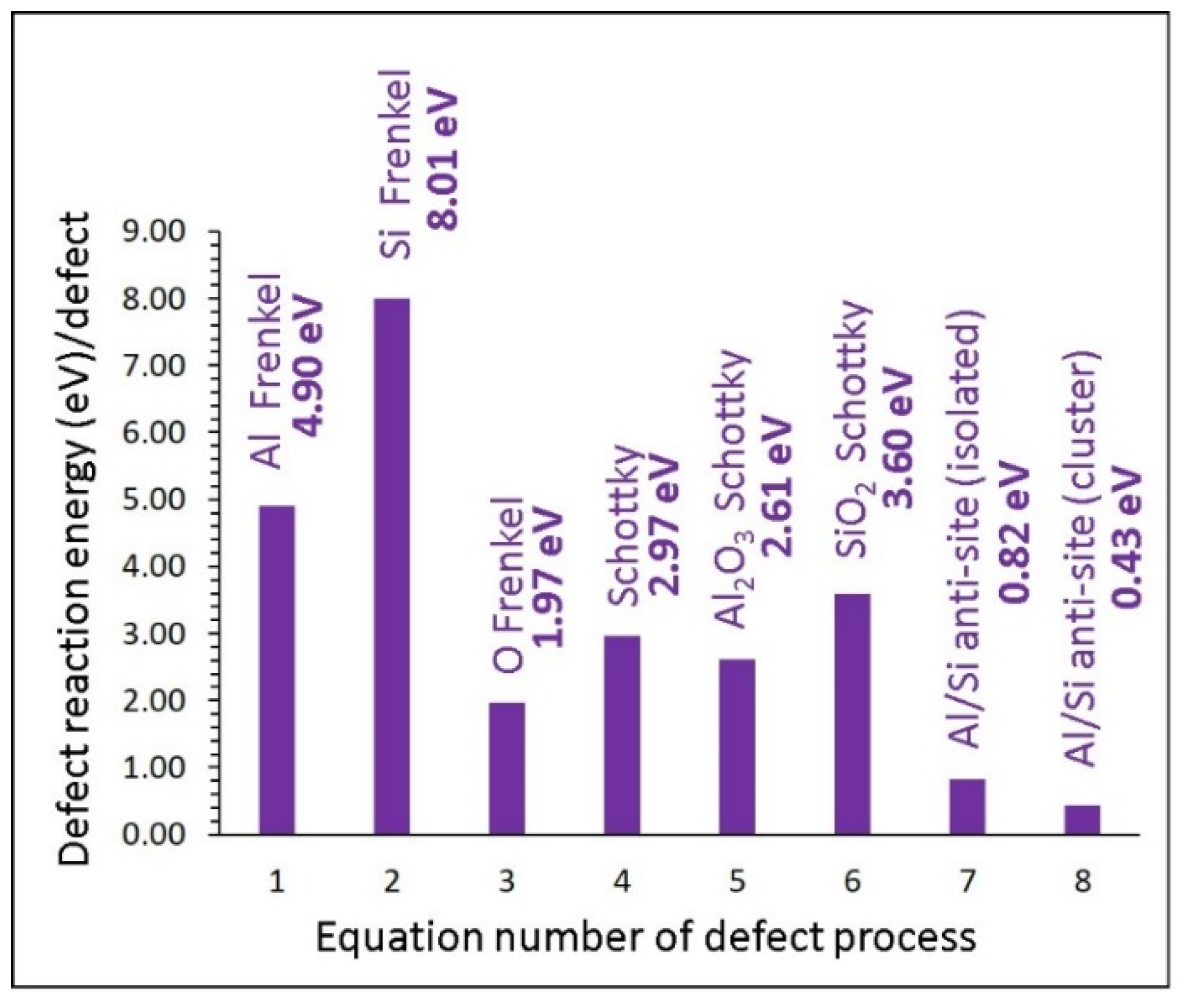
3.2. Intrinsic Defect Energetics
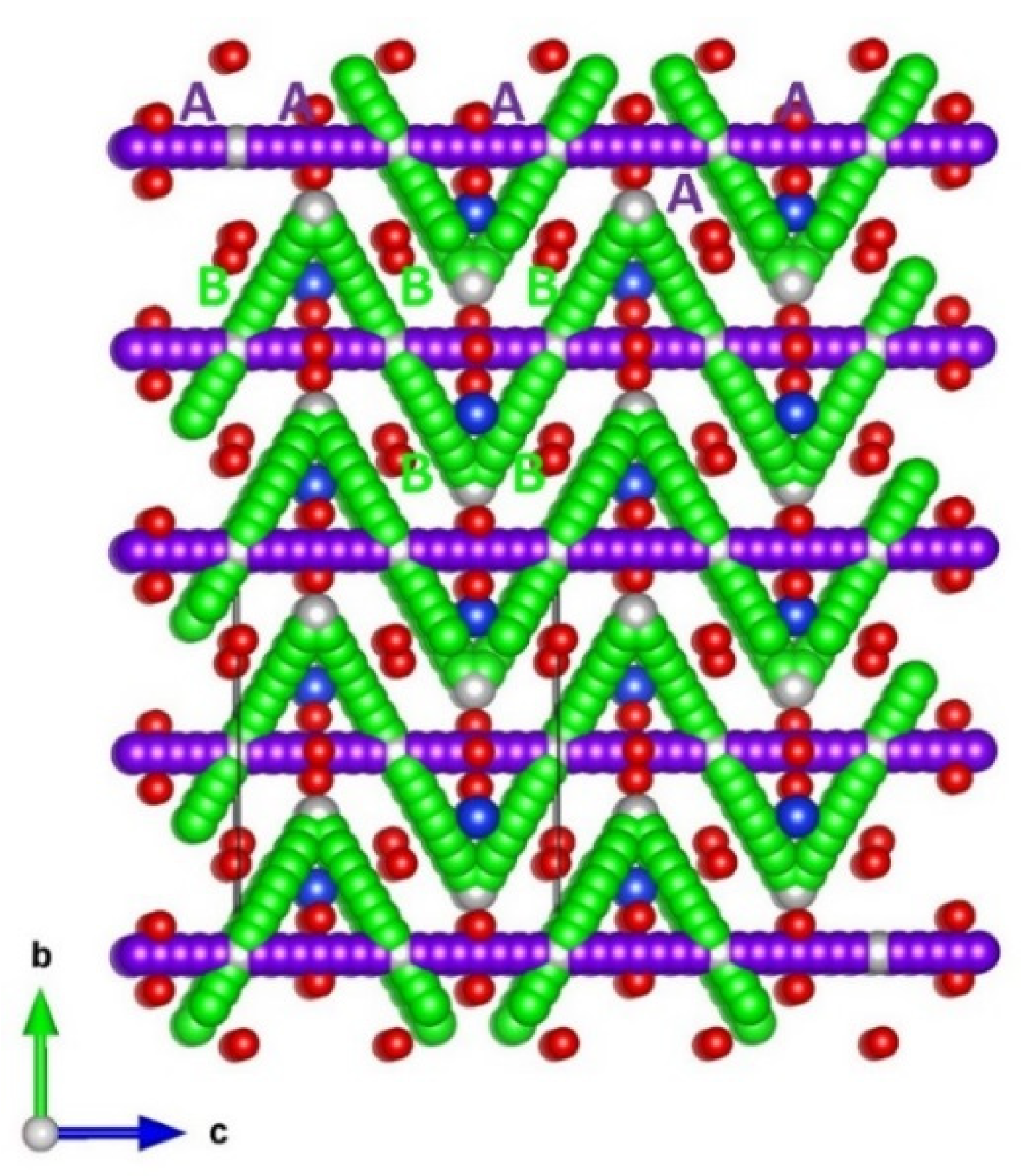
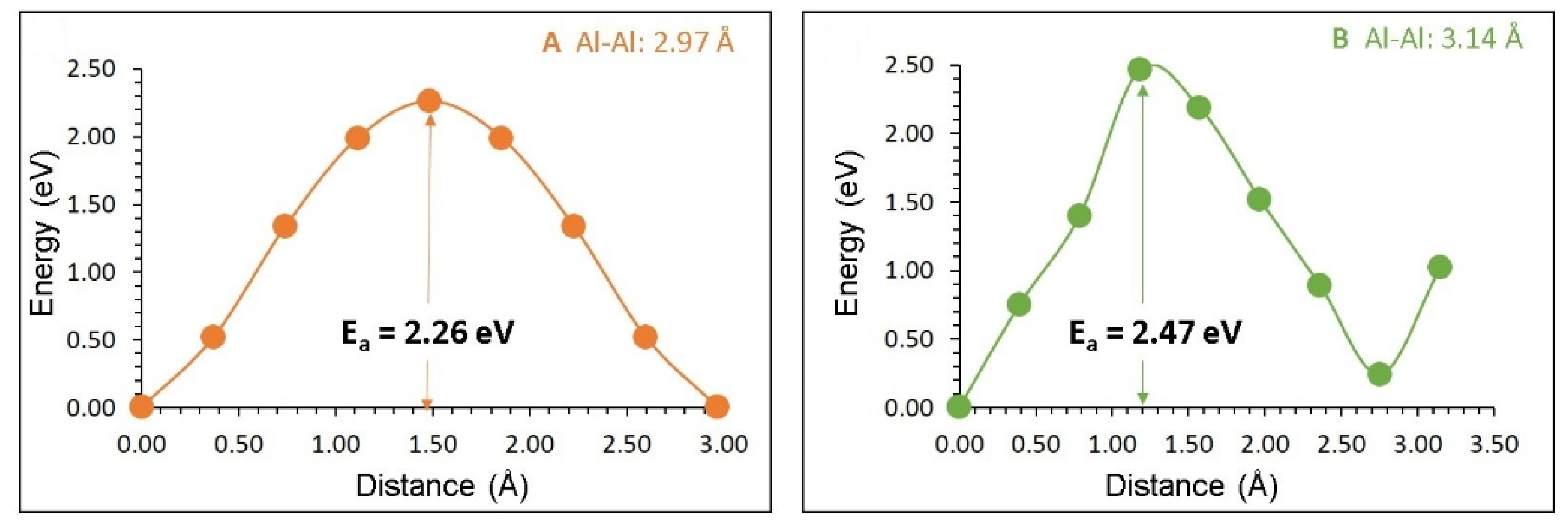
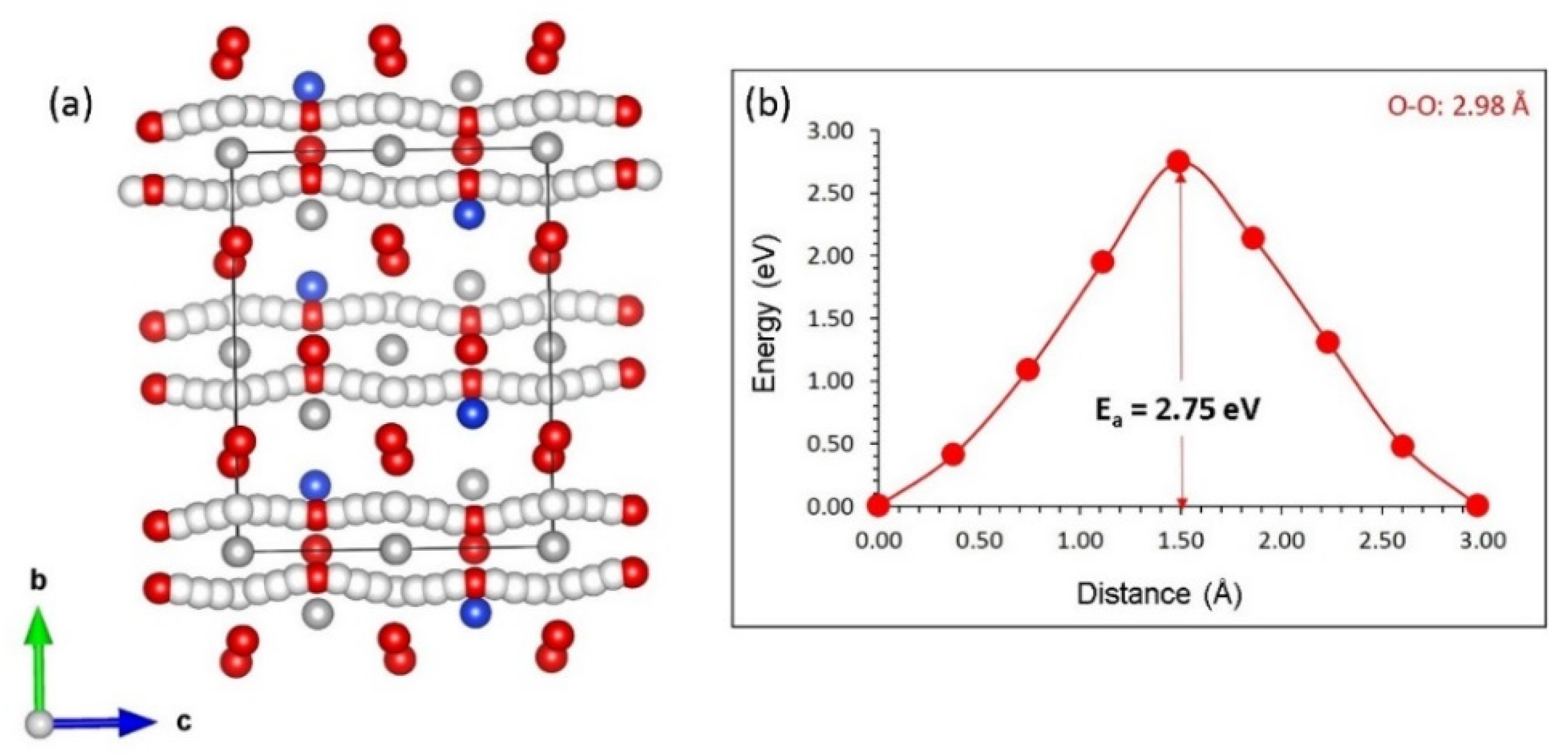
3.3. Self-Diffusion of Aluminium and Oxygen
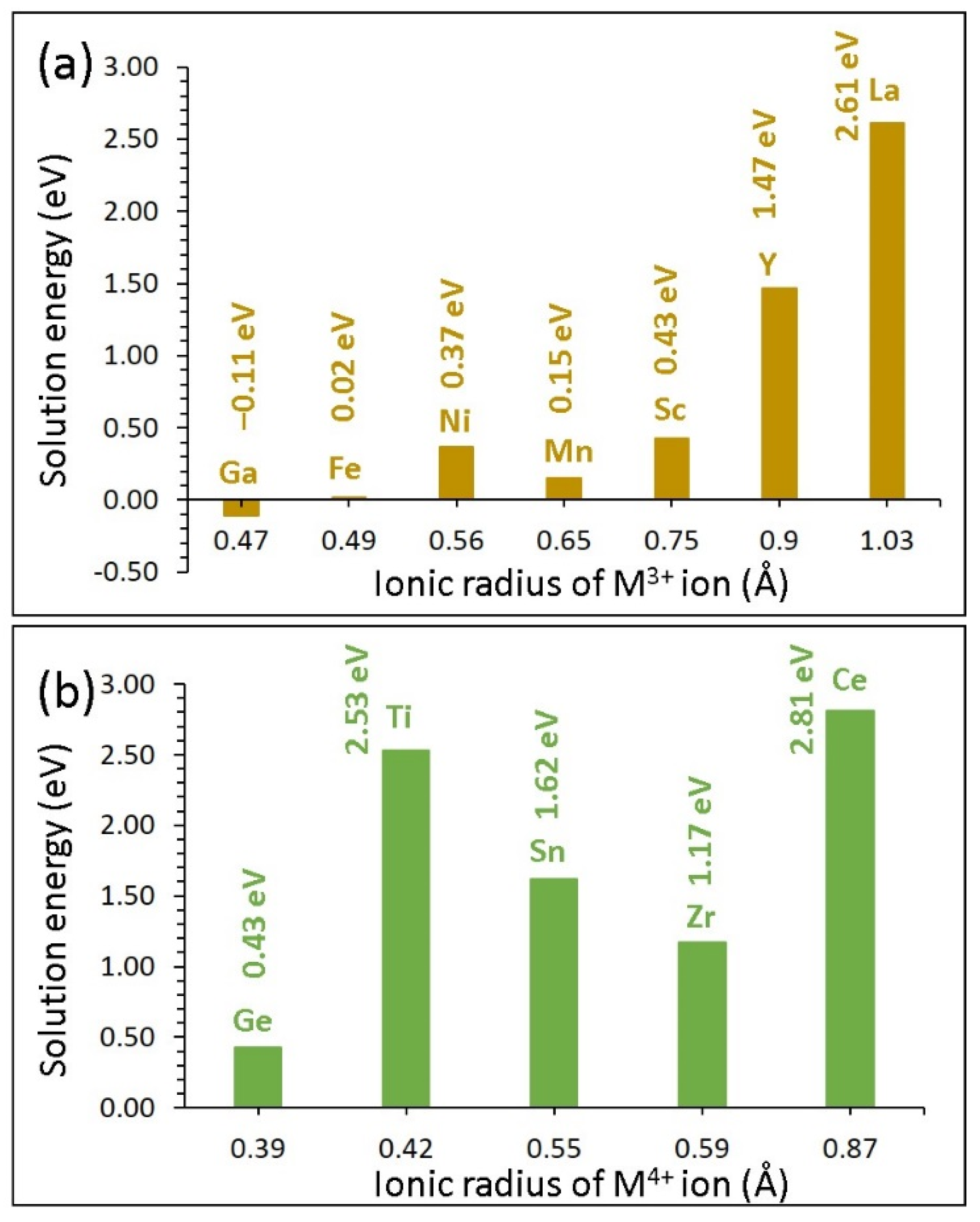
3.4. Solution of Isovalent Dopants
3.4.1. Trivalent Dopants
3.4.2. Tetravalent Dopants
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dharmapriya, P.L.; Malaviarachchi, S.P.K.; Kriegsman, L.M.; Galli, A.; Sajeev, K.; Zhang, C. New constraints on the P–T path of HT/UHT metapelites from the Highland Complex of Sri Lanka. Geosci. Front. 2017, 8, 1405–1430. [Google Scholar] [CrossRef]
- Dharmapriya, P.L.; Malaviarachchi, S.P.K.; Kriegsman, L.M.; Sajeev, K.; Galli, A.; Osanai, Y.; Subasingheh, N.D.; Dissanayakeb, C.B. Distinct metamorphic evolution of alternating silica-saturated and silica-deficient microdomains within garnet in ultrahigh-temperature granulites: An example from Sri Lanka. Geosci. Front. 2017, 8, 1115–1133. [Google Scholar] [CrossRef] [Green Version]
- Kato, M.; Mitsui, H.; Kobayashi, T.; Hiroi, Y.; Satish-Kumar, M.; Dunkley, D.J.; Hokada, T. New finding of kyanite and andalusite in sillimanite-rich pelitic granulites from the Kerala Khondalite Belt, Southern India. J. Mineral. Petrol. Sci. 2010, 105, 328–333. [Google Scholar] [CrossRef]
- Ihlen, P. Sillimanite minerals, Al2SiO5 Utilisation of sillimanite minerals, their geology, and potential occurrences in Norway—An overview. Norg. Geol. Unders Bull. 2000, 436, 113–128. [Google Scholar]
- Jin, J.; Gao, H.; Ren, Z.; Chen, Z. The Flotation of Kyanite and Sillimanite with Sodium Oleate as the Collector. Minerals 2016, 6, 90. [Google Scholar] [CrossRef] [Green Version]
- Whitney, D.L. Coexisting andalusite, kyanite, and sillimanite: Sequential formation of three Al2SiO5 polymorphs during progressive metamorphism near the triple point, Sivrihisar, Turkey. Am. Mineral. 2002, 87, 405–416. [Google Scholar] [CrossRef]
- Gilchrist, J.D. 22-Alumino-Silicate Refractories. In Fuels, Furnaces and Refractories; Gilchrist, J.D., Ed.; Pergamon: Oxfrod, UK, 1977; pp. 258–272. [Google Scholar]
- Sarkar, A.D. Chapter 9—Furane and other binders. In Mould & Core Material for the Steel Foundry; Sarkar, A.D., Ed.; Pergamon: Oxford, UK, 1967; pp. 85–98. [Google Scholar]
- Kos, S.; Dolenec, M.; Lux, J.; Dolenec, S. Raman Microspectroscopy of Garnets from S-Fibulae from the Archaeological Site Lajh (Slovenia). Minerals 2020, 10, 325. [Google Scholar] [CrossRef] [Green Version]
- Sadik, C.; El Amrani, I.-E.; Albizane, A. Recent advances in silica-alumina refractory: A review. J. Asian Ceram. Soc. 2014, 2, 83–96. [Google Scholar] [CrossRef] [Green Version]
- Grew, E.S. Sillimanite and Ilmenite from High-grade Metamorphic Rocks of Antarctica and Other Areas. J. Petrol. 1980, 21, 39–68. [Google Scholar] [CrossRef]
- Holland, T.J.B.; Carpenter, M.A. Aluminium/silicon disordering and melting in sillimanite at high pressures. Nature 1986, 320, 151–153. [Google Scholar] [CrossRef]
- Xu, L.; Xi, X.; Shui, A. Synthesis of sillimanite whiskers. Ceram. Int. 2015, 41, 10304–10307. [Google Scholar] [CrossRef]
- Igami, Y.; Ohi, S.; Miyake, A. Sillimanite-mullite transformation observed in synchrotron X-ray diffraction experiments. J. Am. Ceram. Soc. 2017, 100, 4928–4937. [Google Scholar] [CrossRef]
- Kuganathan, N.; Srikaran, R.; Fossati, C.M.P.; Chroneos, A. Theoretical Modeling of Defects, Dopants, and Diffusion in the Mineral Ilmenite. Minerals 2019, 9, 610. [Google Scholar] [CrossRef] [Green Version]
- Kuganathan, N.; Tsoukalas, L.H.; Chroneos, A. Defects, dopants and Li-ion diffusion in Li2SiO3. Solid State Ion. 2019, 335, 61–66. [Google Scholar] [CrossRef]
- Kuganathan, N.; Iyngaran, P.; Vovk, R.; Chroneos, A. Defects, dopants and Mg diffusion in MgTiO3. Sci. Rep. 2019, 9, 4394. [Google Scholar] [CrossRef] [Green Version]
- Islam, M.S.; Fisher, C.A.J. Lithium and sodium battery cathode materials: Computational insights into voltage, diffusion and nanostructural properties. Chem. Soc. Rev. 2014, 43, 185–204. [Google Scholar] [CrossRef] [Green Version]
- Kuganathan, N.; Kordatos, A.; Chroneos, A. Defect Chemistry and Li-ion Diffusion in Li2RuO3. Sci. Rep. 2019, 9, 550. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.S.; Islam, M.S.; Bates, D.R. Dopant Substitution and Ion Migration in the LaGaO3-Based Oxygen Ion Conductor. J. Phys. Chem. B 1998, 102, 3099–3104. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 93, 629–637. [Google Scholar] [CrossRef]
- Mott, N.F.; Littleton, M.J. Conduction in polar crystals. I. Electrolytic conduction in solid salts. Trans. Faraday Soc. 1938, 34, 485–499. [Google Scholar] [CrossRef]
- Kuganathan, N.; Ganeshalingam, S.; Chroneos, A. Defects, Diffusion, and Dopants in Li2Ti6O13: Atomistic Simulation Study. Materials 2019, 12, 2851. [Google Scholar] [CrossRef] [Green Version]
- Catlow, C.R.A. Solid State Chemistry—Techniques; Cheetham, A.K., Day, P., Eds.; Clarendon Press: Oxford, UK, 1987; p. 231. [Google Scholar]
- Charles, W.B. Refinement of the crystal structure of sillimanite. Z. Kristallogr. Cryst. Mater. 1963, 118, 127–148. [Google Scholar]
- Lewis, G.V.; Catlow, C.R.A. Potential models for ionic oxides. J. Phys. C Solid State Phys. 1985, 18, 1149. [Google Scholar] [CrossRef]
- Panchmatia, P.M.; Orera, A.; Kendrick, E.; Hanna, J.V.; Smith, M.E.; Slater, P.R.; Islam, M.S. Protonic defects and water incorporation in Si and Ge-based apatite ionic conductors. J. Mater. Chem. 2010, 20, 2766–2772. [Google Scholar] [CrossRef] [Green Version]
- Winkler, B.; Dove, M.T.; Leslie, M. Static lattice energy minimization and lattice dynamics calculations on aluminosilicate minerals. Am. Mineral. 1991, 76, 313–331. [Google Scholar]
- Björn, W.; Hytha, M.; Warren, M.C.; Victor, M.; Gale, J.D.; Schreuer, J. Calculation of the elastic constants of the Al2SiO5 polymorphs andalusite, sillimanite and kyanite. Z. Kristallogr. Cryst. Mater. 2001, 216, 67–70. [Google Scholar]
- Vaughan, M.T.; Weidner, D.J. The relationship of elasticity and crystal structure in andalusite and sillimanite. Phys. Chem. Miner. 1978, 3, 133–144. [Google Scholar] [CrossRef]
- Waldbaum, D.R. Thermodynamic properties of mullite, andalusite, kyanite and sillimanite. Am. Mineral. 1965, 50, 186–195. [Google Scholar]
- Kröger, F.A.; Vink, H.J. Relations between the Concentrations of Imperfections in Crystalline Solids. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: Cambridge, MA, USA, 1956; Volume 3, pp. 307–435. [Google Scholar]
- Politaev, V.V.; Petrenko, A.A.; Nalbandyan, V.B.; Medvedev, B.S.; Shvetsova, E.S. Crystal structure, phase relations and electrochemical properties of monoclinic Li2MnSiO4. J. Solid State Chem. 2007, 180, 1045–1050. [Google Scholar] [CrossRef]
- Kempaiah Devaraju, M.; Duc Truong, Q.; Hyodo, H.; Sasaki, Y.; Honma, I. Synthesis, characterization and observation of antisite defects in LiNiPO4 nanomaterials. Sci. Rep. 2015, 5, 11041. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuganathan, N.; Kordatos, A.; Anurakavan, S.; Iyngaran, P.; Chroneos, A. Li3SbO4 lithium-ion battery material: Defects, lithium ion diffusion and tetravalent dopants. Mater. Chem. Phys. 2019, 225, 34–41. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Na3V(PO4)2 cathode material for Na ion batteries: Defects, dopants and Na diffusion. Solid State Ion. 2019, 336, 75–79. [Google Scholar] [CrossRef] [Green Version]
- Jay, E.E.; Rushton, M.J.D.; Chroneos, A.; Grimes, R.W.; Kilner, J.A. Genetics of superionic conductivity in lithium lanthanum titanates. Phys. Chem. Chem. Phys. 2015, 17, 178–183. [Google Scholar] [CrossRef]
- Armstrong, A.R.; Kuganathan, N.; Islam, M.S.; Bruce, P.G. Structure and Lithium Transport Pathways in Li2FeSiO4 Cathodes for Lithium Batteries. J. Am. Chem. Soc. 2011, 133, 13031–13035. [Google Scholar] [CrossRef] [Green Version]
- Fisher, C.A.J.; Hart Prieto, V.M.; Islam, M.S. Lithium Battery Materials LiMPO4 (M = Mn, Fe, Co, and Ni): Insights into Defect Association, Transport Mechanisms, and Doping Behavior. Chem. Mater. 2008, 20, 5907–5915. [Google Scholar] [CrossRef]
- Nishimura, S.-I.; Kobayashi, G.; Ohoyama, K.; Kanno, R.; Yashima, M.; Yamada, A. Experimental visualization of lithium diffusion in LixFePO4. Nat. Mater. 2008, 7, 707. [Google Scholar] [CrossRef]
| Interaction | A/eV | ρ/Å | C/eV·Å6 | Y/e | K/eV·Å–2 |
|---|---|---|---|---|---|
| Al3+–O2− | 1114.9 | 0.3118 | 0.00 | 3.000 | 99,999 |
| Si4+−O2− | 1283.91 | 0.32052 | 10.66 | 4.000 | 99,999 |
| O2−–O2− | 22,764.00 | 0.1490 | 0.00 | −2.8481 | 74.82 |
| Parameter | Calculated | Experiment [26] | ∆|(%) |
|---|---|---|---|
| a (Å) | 7.247734 | 7.485600 | 3.18 |
| b (Å) | 7.508304 | 7.673800 | 2.16 |
| c (Å) | 5.944604 | 5.769800 | 3.03 |
| α = β = γ (°) | 90.0 | 90.0 | 0.00 |
| V (Å3) | 323.494621 | 331.434606 | 2.40 |
| Diagonal Components | This Study | Core–Shell Model [29] | DFT [30] | Experiment [31] |
|---|---|---|---|---|
| C11 | 2.53 (−12%) | 2.82 (−2%) | 3.19 (+11%) | 2.87 |
| C22 | 2.43 (+5%) | 2.94 (+27%) | 2.13 (−8%) | 2.32 |
| C33 | 5.32 (+37%) | 5.53 (+43%) | 4.14 (−17%) | 3.88 |
| C44 | 1.05 (−14%) | 1.31(+7%) | 1.23 (+1%) | 1.22 |
| C55 | 0.72 (−11%) | 0.91(+12%) | 0.76 (−6%) | 0.81 |
| C66 | 0.61 (−31%) | 0.85 (−5%) | 0.89 (0%) | 0.89 |
| Polymorphs | Relative Energy | |
|---|---|---|
| This Study (eV) | Experiment (cal/gfw) [32] | |
| Andalusite | 0 | 0 |
| Sillimanite | 0.41 | 546 |
| Kyanite | 0.86 | 1160 |
| Migration Path | Al-Al Separation (Å) | Activation Energy (eV) |
|---|---|---|
| A | 2.97 | 2.26 |
| B | 3.14 | 2.47 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sukumar, R.; Iyngaran, P.; Kuganathan, N.; Chroneos, A. Defects, Diffusion and Dopants in Sillimanite. Minerals 2020, 10, 857. https://doi.org/10.3390/min10100857
Sukumar R, Iyngaran P, Kuganathan N, Chroneos A. Defects, Diffusion and Dopants in Sillimanite. Minerals. 2020; 10(10):857. https://doi.org/10.3390/min10100857
Chicago/Turabian StyleSukumar, Raveena, Poobalasuntharam Iyngaran, Navaratnarajah Kuganathan, and Alexander Chroneos. 2020. "Defects, Diffusion and Dopants in Sillimanite" Minerals 10, no. 10: 857. https://doi.org/10.3390/min10100857
APA StyleSukumar, R., Iyngaran, P., Kuganathan, N., & Chroneos, A. (2020). Defects, Diffusion and Dopants in Sillimanite. Minerals, 10(10), 857. https://doi.org/10.3390/min10100857








