First Principles Calculation of the Stability of Iron Bearing Carbonates at High Pressure Conditions
Abstract
1. Introduction
2. Results
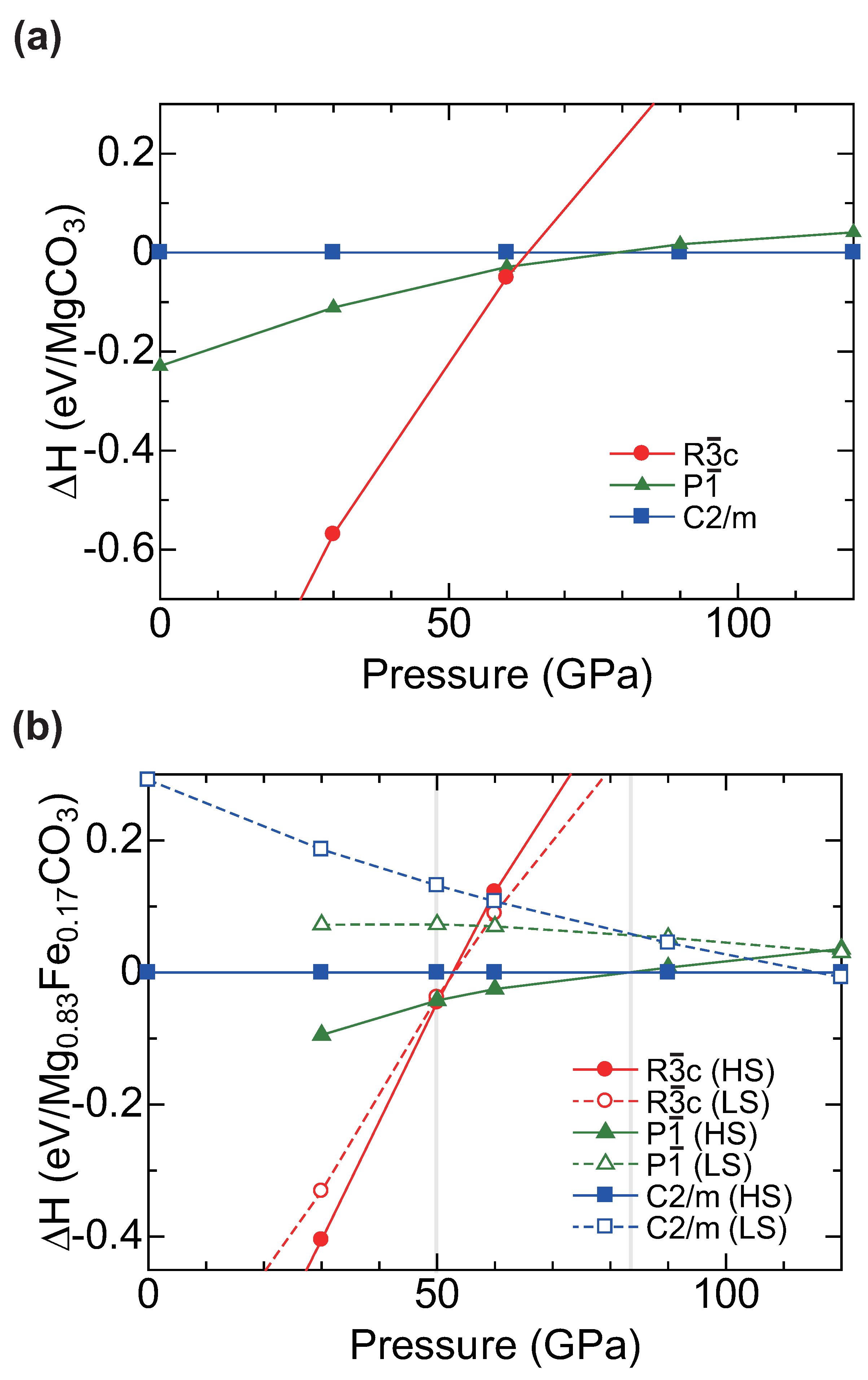
2.1. Calculation of MgCO Polymorphs under Pressure
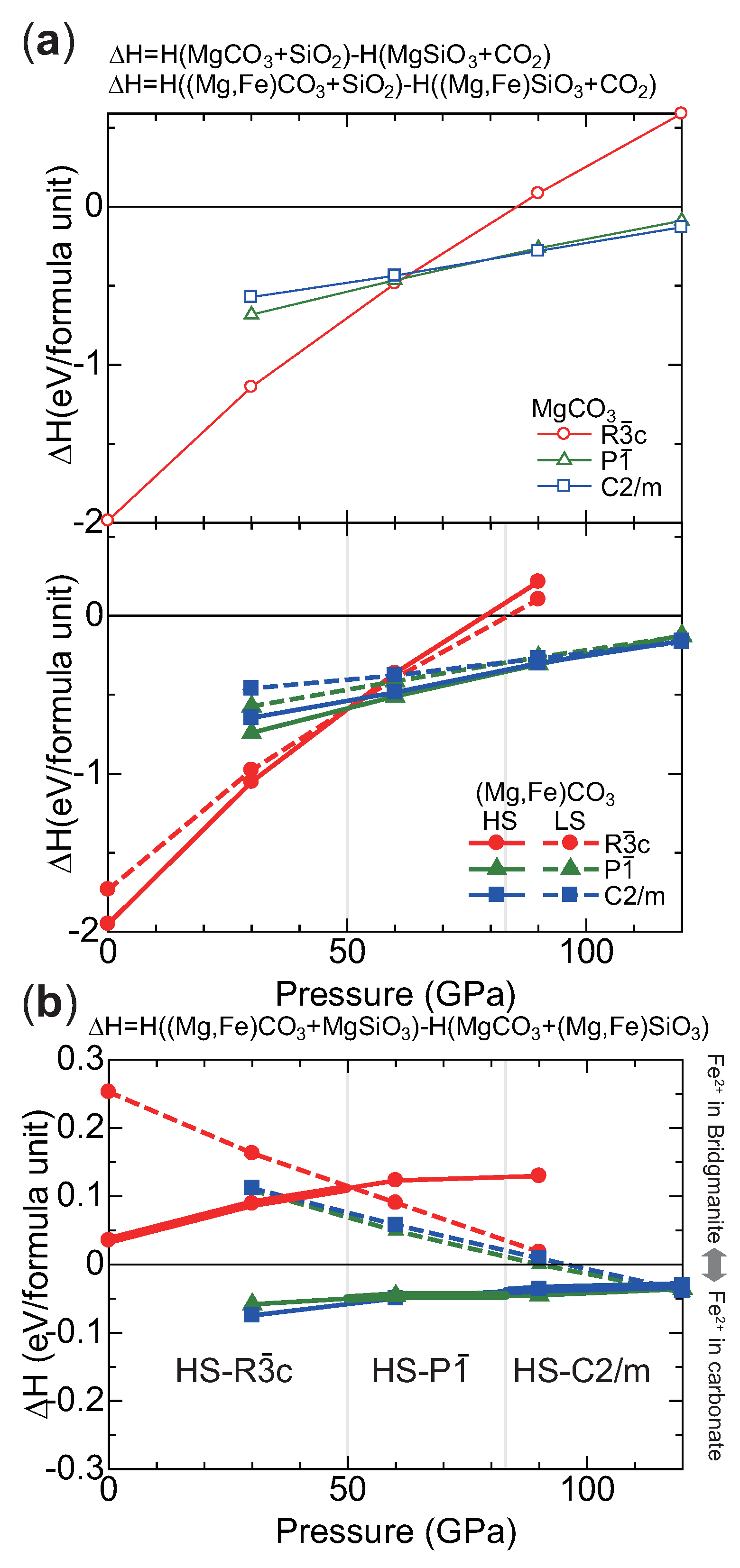
2.2. Structure Modeling of (MgFe)CO
2.3. High Pressure Transitions of MgCO and (MgFe)CO
3. Discussion
4. Conclusions
5. Methods
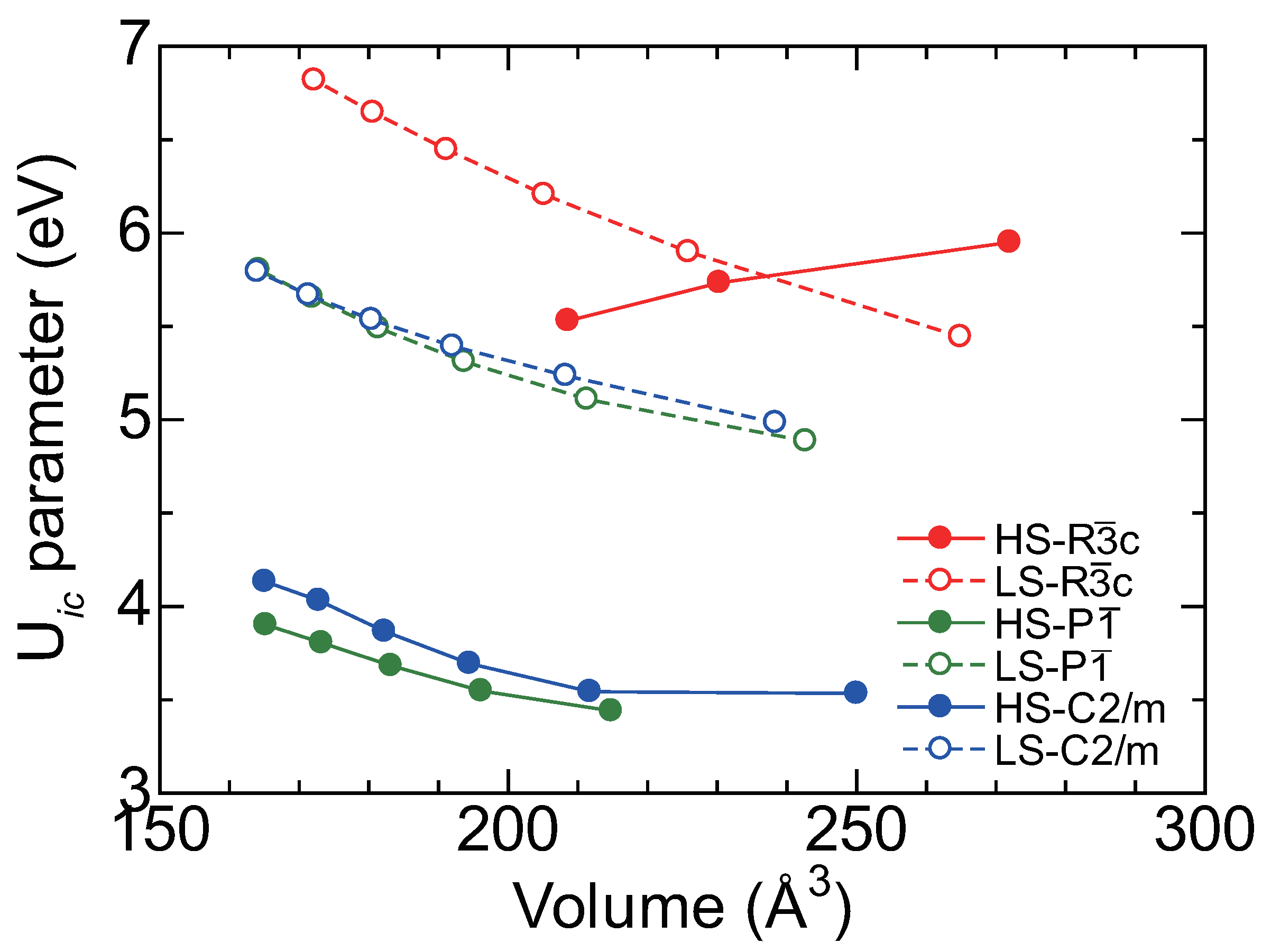
5.1. First Principles Calculation
5.2. LDA+U Calculation
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Merlini, M.; Crichton, W.A.; Hanfland, M.; Gemmi, M.; Muller, H.; Kupenko, I.; Dubrovinsky, L. Structures of dolomite at ultrahigh pressure and their influence on the deep carbon cycle. Proc. Natl. Acad. Sci. USA 2012, 109, 13509–13514. [Google Scholar] [CrossRef] [PubMed]
- Boulard, E.; Gloter, A.; Corgne, A.; Antonangeli, D.; Auzende, A.; Perrillat, J.; Guyot, F.; Fiquet, G. New host for carbon in the deep Earth. Proc. Natl. Acad. Sci. USA 2011, 108, 5184–5187. [Google Scholar] [CrossRef] [PubMed]
- Biellmann, C.; Gillet, P.; Guyot, F.; Peyronneau, J.; Reynard, B. Experimental evidence for carbonate stability in Earth’s lower mantle. Earth Planet. Sci. Lett. 1993, 118, 31–41. [Google Scholar] [CrossRef]
- Gillet, P. Stability of magnesite (MgCO3) at mantle pressure and temperature conditions: A raman spectroscopic study. Am. Miner. 1993, 78, 1328–1331. [Google Scholar]
- Fiquet, G.; Guyot, F.; Kunz, M.; Matas, J. Andrault, D.; Hanfland, M. Structural refinements of magnesite at very high pressure. Am. Miner. 2002, 87, 1261–1265. [Google Scholar] [CrossRef]
- Shatskiy, A.; Litasov, K.D.; Palyanov, Y.N.; Ohtani, E. Phase relations on the K2CO3-CaCO3-MgCO3 join at 6 GPa and 900–1400 °C: Implications for incipient melting in carbonated mantle domains. Am. Miner. 2016, 101, 437–447. [Google Scholar] [CrossRef]
- Isshiki, M.; Irifune, T.; Hirose, K.; Ono, S.; Ohishi, Y.; Watanuki, T.; Nishibori, E.; Tanaka, M.; Sakata, M. Stability of magnesite and its high-pressure form in the lowermost mantle. Nature 2004, 427, 60–63. [Google Scholar] [CrossRef]
- Maeda, F.; Ohtani, E.; Kamada, S.; Sakamaki, T.; Hirao, N.; Ohishi, Y. Diamond formation in the deep lower mantle: A high-pressure reaction of MgCO3 and SiO2. Sci. Rep. 2017, 7, 40602. [Google Scholar] [CrossRef]
- Palyanov, Y.N. Mantle-slab interaction and redox mechanism of diamond formation. Proc. Natl. Acad. Sci. USA 2013, 110, 20408–20413. [Google Scholar] [CrossRef]
- Kelemen, P.B.; Manning, C.E. Reevaluating carbon fluxes in subduction zones, what goes down, mostly comes up. Proc. Natl. Acad. Sci. USA 2015, 112, E3997–E4006. [Google Scholar] [CrossRef]
- Oganov, A.R.; Ono, S.; Ma, Y.; Glass, C.W.; Garcia, A. Novel high-pressure structures of MgCO3, CaCO3 and CO2 and their role in Earth’s lower mantle. Earth Planet. Sci. Lett. 2008, 273, 38–47. [Google Scholar] [CrossRef]
- Pickard, C.; Needs, R.J. Structures and stability of calcium and magnesium carbonates at mantle pressures. Phys. Rev. B 2015, 91, 104101. [Google Scholar] [CrossRef]
- Franzolin, E.; Schmidt, M.W.; Poli, S. Ternary Ca-Fe-Mg carbonates: subsolidus phase relations at 3.5 GPa and a thermodynamics solid solution model including order/disorder. Contrib. Miner. Petrol. 2011, 161, 213–227. [Google Scholar] [CrossRef]
- Liu, J.; Lin, J.-F.; Prakapenka, V.B. Ferromagnesite as a potential deep-mantle carbon carrier. Sci. Rep. 2015, 5, 7940. [Google Scholar] [CrossRef]
- Solomatova, N.V.; Asimow, P.D. First-principles calculations of high-pressure iron-bearing monoclinic dolomite and single-cation carbonates with internally consistent Hubbard U. Phys. Chem. Miner. 2018, 45, 293–302. [Google Scholar] [CrossRef]
- Boulard, E.; Menguy, N.; Auzende, A.L.; Bureau, H.; Antonangeli, D.; Corgne, A.; Morard, G.; Siebert, J.; Perrillat, J.P.; Guyot, F.; et al. Experimental investigation of the stability of Fe-rich carbonates in the lower mantle. J. Geophys. Res. 2012, 117, B02208. [Google Scholar] [CrossRef]
- Lavina, B.; Dera, P.; Downs, R.T.; Prakapenka, V.; Rivers, M.; Sutton, S.; Nicol, M. Siderite at lower mantle conditions and the effects of the pressure-induced spin-apiring transition. Geophys. Res. Lett. 2009, 36, L23306. [Google Scholar] [CrossRef]
- Lavina, B.; Dera, P.; Downs, R.T.; Yang, W.; Sinogeikin, S. Meng, Y.; Shen, G.; Schiferl, D. Structure of siderite FeCO3 to 56 GPa and hysteresis of its spin-pairing transition. Phys. Rev. B 2010, 82, 064110. [Google Scholar] [CrossRef]
- Mattila, A.; Pylkkanen, T.; Rueff, J.-P.; Huotari, S.; Vanko, G.; Hafland, M.; Lehtinen, M.; Hamalainen, K. Pressure induced magnetic transition in siderite FeCO3 studied by x-ray emission spectroscopy. J. Phys. Condens. Matter 2007, 19, 386206. [Google Scholar] [CrossRef]
- Farfan, G.; Wang, S.; Ma, H.; Caracas, R.; Mao, W.L. Bonding and structural changes in siderite at high pressure. Am. Miner. 2012, 97, 1421. [Google Scholar] [CrossRef]
- Lin, J.-F.; Liu, J.; Jacobs, C.; Prakapenka, V.B. Vibrational and elastic properties of ferromagnesite across the electronic spin-pairing transition of iron. Am. Miner. 2012, 97, 583. [Google Scholar] [CrossRef]
- Hsu, H.; Huang, S.C. Spin crossover and hyperfine interactions of iron in (Mg,Fe)CO3 ferromagnesite. Phys. Rev. B 2016, 94, 060404. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef]
- Wang, X.; Tsuchiya, T.; Hase, A. Computational support for a pyrolitic lower mantle containing ferric iron. Nat. Geosci. 2015, 8, 556–560. [Google Scholar] [CrossRef]
- McCammon, C. Perovskiate as a possible sink for ferric iron in the lower mantle. Nature 1997, 387, 694–696. [Google Scholar] [CrossRef]
- Zhang, F.; Oganov, A.R. Valence state and spin transitions of iron in Earth’s mantle silicates. Earth Planet. Sci. Lett. 2006, 249, 436–443. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotential for plane wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
- Tsuchiya, T.; Tsuchiya, J.; Umemoto, K.; Wentzcovitch, R.M. Phase transition in MgSiO3 perovskite in the earth’s lower mantle. Earth Planet. Sci. Lett. 2004, 224, 241–248. [Google Scholar] [CrossRef]
- Ichikawa, H.; Tsuchiya, T.; Tange, Y. The P-V-T equation of state and thermodynamic properties of liquid iron. J. Geophys. Res. Solid Earth 2013, 119, 240–252. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. Quantum ESPRESSO: A modular and open-sourcesoftware project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Tsuchiya, T.; Wentzcovitch, R.M.; da Silva, C.R.S.; de Gironcoli, S. Spin transition in magnesiowustite in earth’s lower mantle. Phys. Rev. Lett. 2006, 96, 198501. [Google Scholar] [CrossRef]
- Fukui, H.; Tsuchiya, T.; Baron, A.Q.R. Lattice dynamics calculations for ferropericlase with internally consistent LDA+U method. J. Geophys. Res. 2012, 117, B12202. [Google Scholar] [CrossRef]
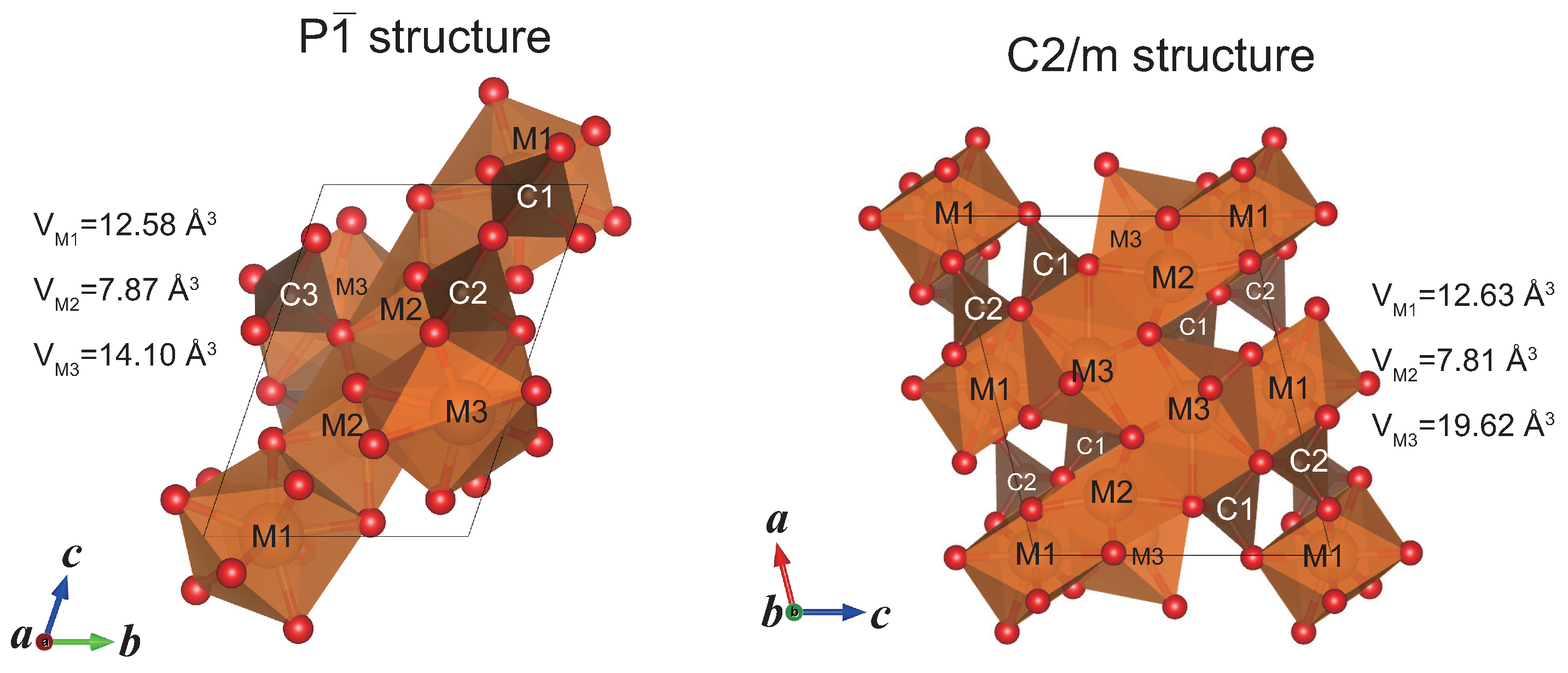
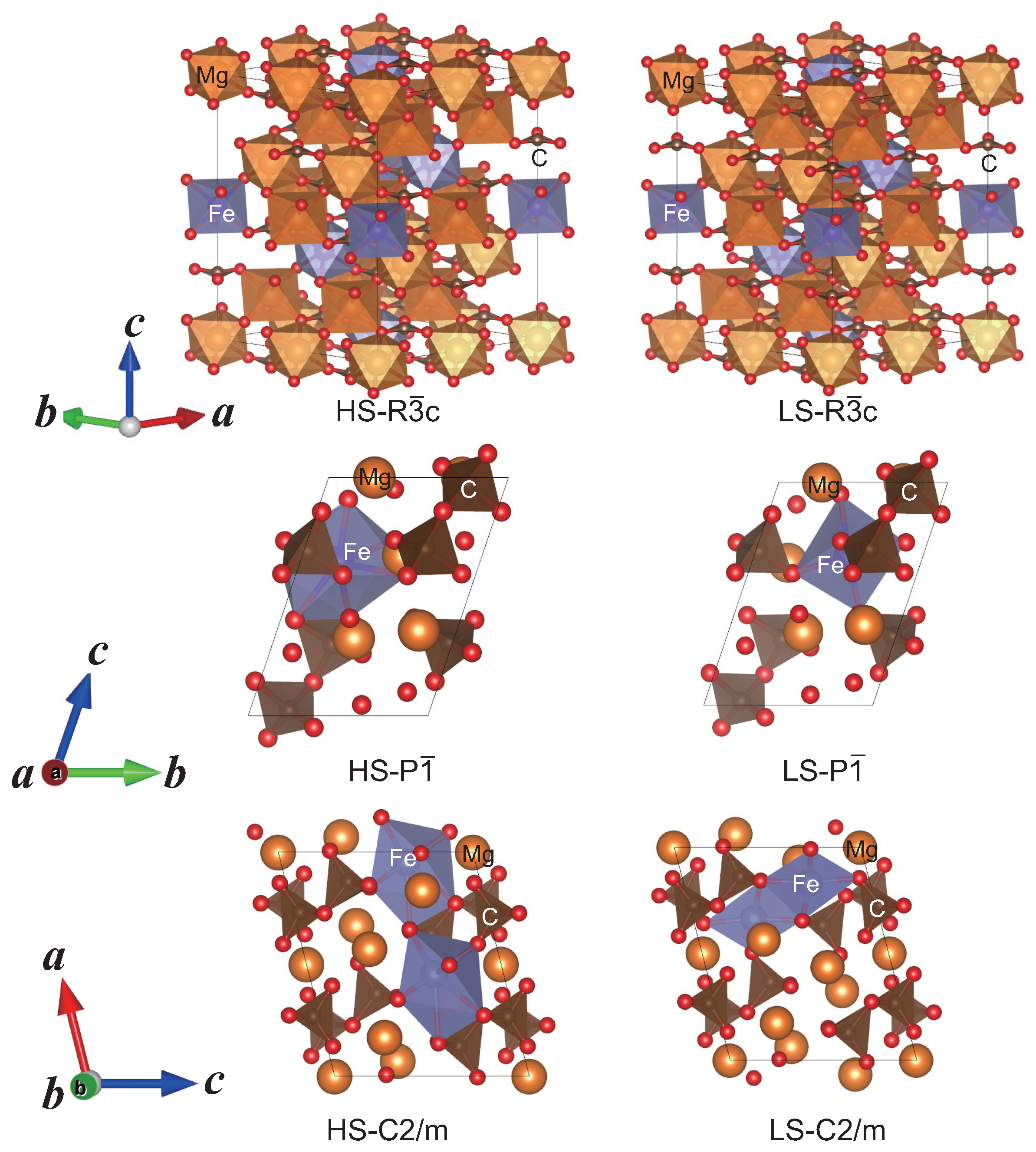
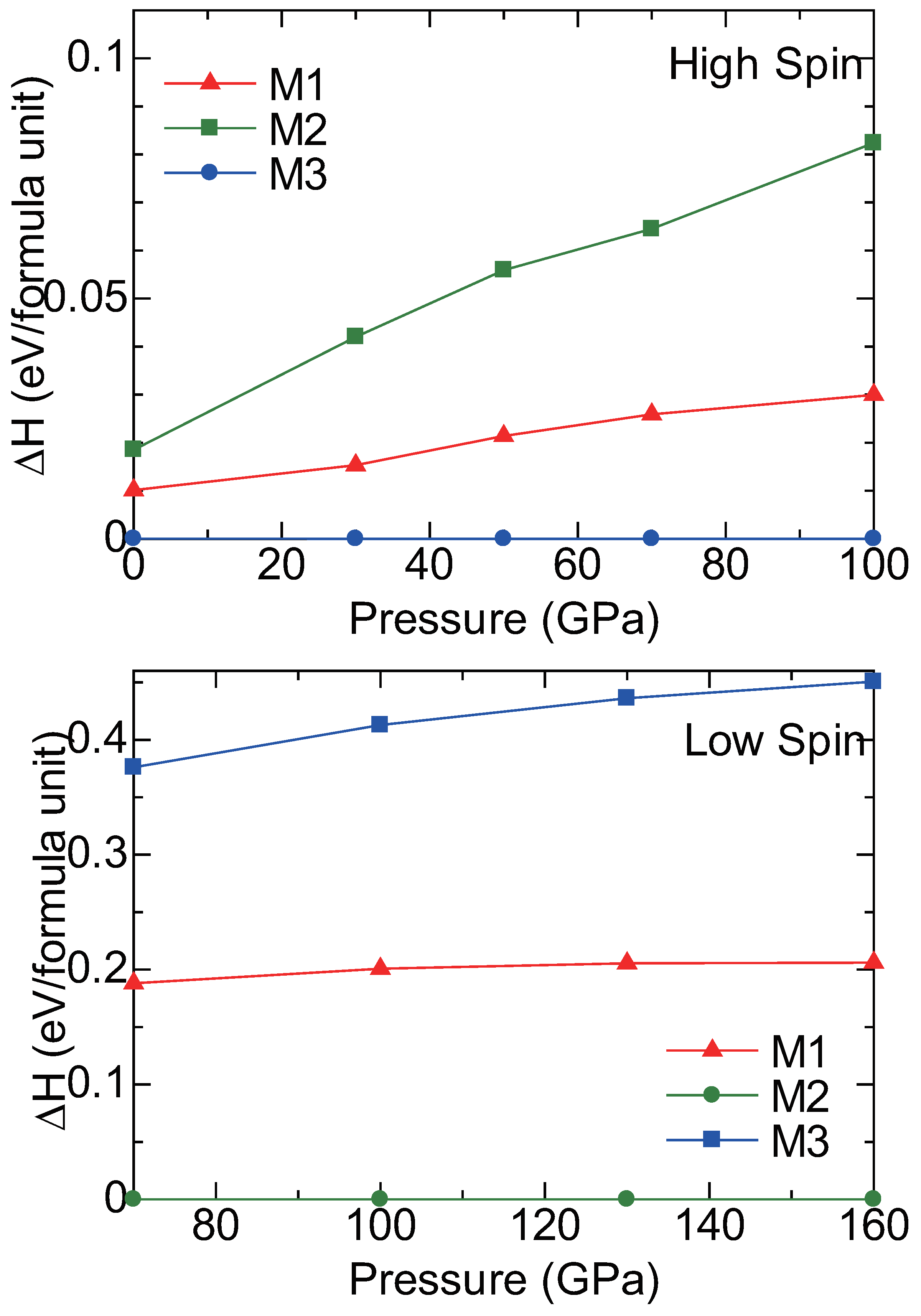
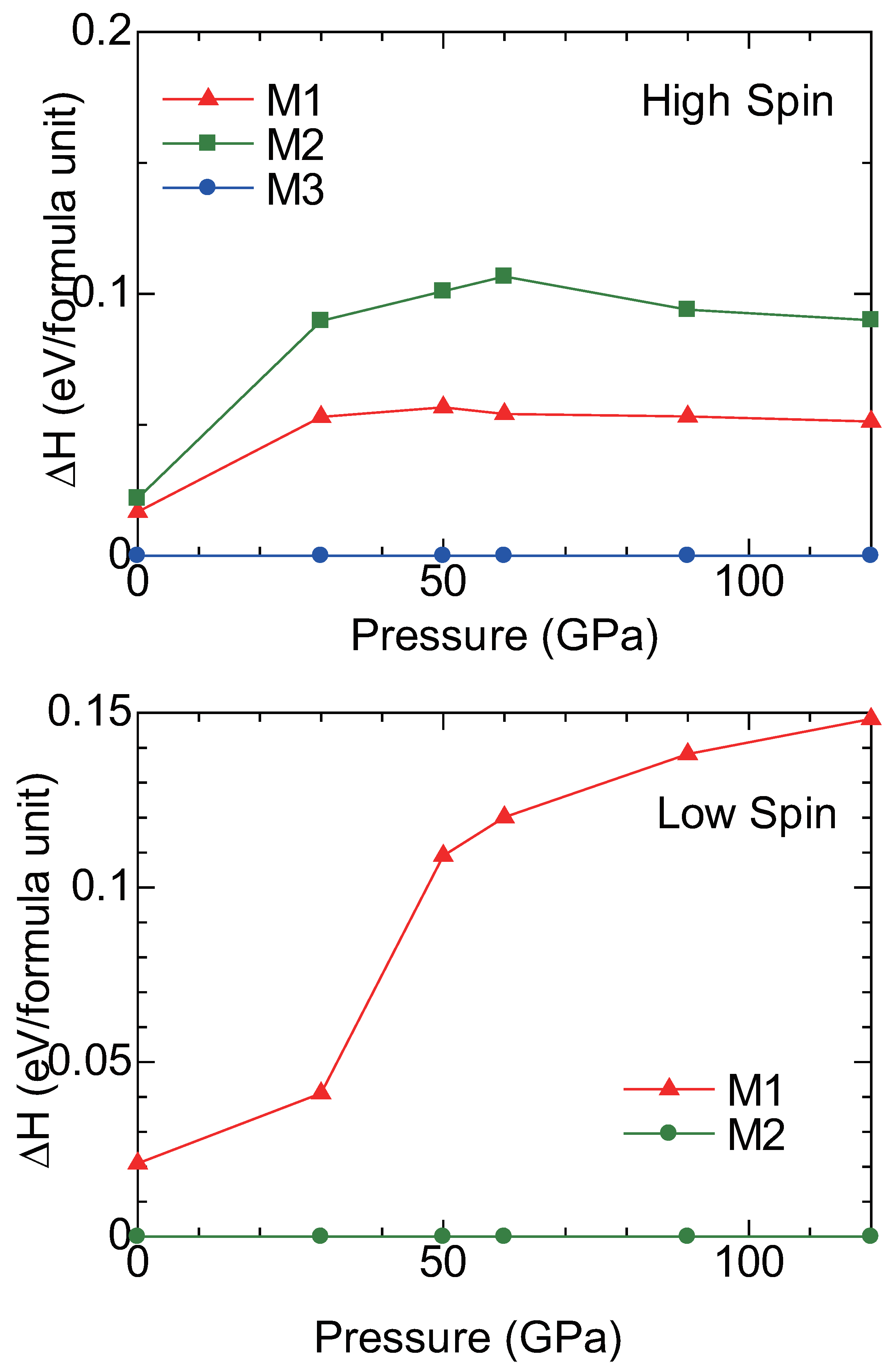
| P structureat 100 GPa | ||||
| a = 5.178 Å, b = 5.206 Å, c = 7.242 Å, | ||||
| (Pickard and Needs [12]: a = 5.211 Å, b = 5.238 Å, c = 7.268 Å, at 100 GPa) | ||||
| Atom | Wyckoff position | Atomic coordinates | ||
| x | y | z | ||
| Mg1(M1) | 2i | 0.7414 | 0.2541 | 0.0022 |
| Mg2(M2) | 2i | 0.5669 | 0.4731 | 0.3143 |
| Mg3(M3) | 2i | 0.0636 | 0.1784 | 0.6501 |
| C1 | 2i | 0.2237 | 0.2078 | 0.0295 |
| C2 | 2i | 0.0812 | 0.3351 | 0.3092 |
| C3 | 2i | 0.4398 | 0.9790 | 0.3231 |
| O1 | 2i | 0.1277 | 0.1522 | 0.8965 |
| O2 | 2i | 0.0086 | 0.2930 | 0.1470 |
| O3 | 2i | 0.8794 | 0.3896 | 0.4232 |
| O4 | 2i | 0.3461 | 0.9572 | 0.1548 |
| O5 | 2i | 0.3752 | 0.3872 | 0.9623 |
| O6 | 2i | 0.2030 | 0.0682 | 0.4149 |
| O7 | 2i | 0.2249 | 0.5252 | 0.2622 |
| O8 | 2i | 0.5465 | 0.7397 | 0.4278 |
| O9 | 2i | 0.6110 | 0.1433 | 0.2692 |
| C2/m structure at 120 GPa | ||||
| a = 8.0417 Å, b = 6.4468 Å, c = 6.8273 Å, = 103.84° | ||||
| (Oganov et al. [11]: a = 8.0945 Å, b = 6.4881 Å, c = 6.8795 Å, = 103.98° at 120 GPa) | ||||
| Atom | Wyckoff position | Atomic coordinates | ||
| x | y | z | ||
| Mg1(M1) | 4g | 0.0000 | 0.7536 | 0.0000 |
| Mg2(M2) | 4i | 0.3229 | 0.5000 | 0.6975 |
| Mg3(M3) | 4i | 0.9353 | 0.5000 | 0.6555 |
| C1 | 8j | 0.3701 | 0.3214 | 0.3273 |
| C2 | 4i | 0.2315 | 0.5000 | 0.0363 |
| O1 | 4i | 0.0926 | 0.5000 | 0.8961 |
| O2 | 8j | 0.3490 | 0.1665 | 0.4299 |
| O3 | 8j | 0.5081 | 0.3095 | 0.2675 |
| O4 | 4i | 0.3661 | 0.5000 | 0.9729 |
| O5 | 4i | 0.3522 | 0.5000 | 0.4276 |
| O6 | 8j | 0.2253 | 0.3320 | 0.1595 |
| GGA [12] | GGA (This Study) | LDA (This Study) | |
|---|---|---|---|
| Rc → P | 85 | 85 | 62 |
| P → C2/m | 101 | 95 | 80 |
| C2/m → P222 | 144 | 145 | 130 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsuchiya, J.; Nishida, R.; Tsuchiya, T. First Principles Calculation of the Stability of Iron Bearing Carbonates at High Pressure Conditions. Minerals 2020, 10, 54. https://doi.org/10.3390/min10010054
Tsuchiya J, Nishida R, Tsuchiya T. First Principles Calculation of the Stability of Iron Bearing Carbonates at High Pressure Conditions. Minerals. 2020; 10(1):54. https://doi.org/10.3390/min10010054
Chicago/Turabian StyleTsuchiya, Jun, Risa Nishida, and Taku Tsuchiya. 2020. "First Principles Calculation of the Stability of Iron Bearing Carbonates at High Pressure Conditions" Minerals 10, no. 1: 54. https://doi.org/10.3390/min10010054
APA StyleTsuchiya, J., Nishida, R., & Tsuchiya, T. (2020). First Principles Calculation of the Stability of Iron Bearing Carbonates at High Pressure Conditions. Minerals, 10(1), 54. https://doi.org/10.3390/min10010054





