Ab Initio Thermoelasticity of Liquid Iron-Nickel-Light Element Alloys
Abstract
1. Introduction
2. Results and Discussion
2.1. Effects of LE on the Thermoelasticity of Liquid Iron
2.2. Optimized Compositions
2.3. Bulk Earth Composition
3. Conclusions
4. Methods
4.1. Ab Initio Molecular Dynamics Simulations
4.2. EoS Analysis of Liquid Iron Alloys
4.3. Adiabats
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Birch, F. Density and composition of mantle and core. J. Geophys. Res. 1964, 69, 4377–4388. [Google Scholar] [CrossRef]
- Brown, J.M.; McQueen, R.G. Phase transitions, Grüneisen parameter, and elasticity for shocked iron between 77 GPa and 400 GPa. J. Geophys. Res. Solid Earth 1986, 91, 7485–7494. [Google Scholar] [CrossRef]
- Jephcoat, A.; Olson, P. Is the inner core of the Earth pure iron? Nature 1987, 325, 332–335. [Google Scholar] [CrossRef]
- Uchida, T.; Wang, Y.; Rivers, M.L.; Sutton, S.R. Stability field and thermal equation of state of e-iron determined by synchrotron X-ray diffraction in a multianvil apparatus. J. Geophys. Res. Solid Earth 2001, 106, 21799–21810. [Google Scholar] [CrossRef]
- Anderson, O.L.; Isaak, D.G. Another look at the core density deficit of Earth’s outer core. Phys. Earth Planet. Inter. 2002, 131, 19–27. [Google Scholar] [CrossRef]
- Dewaele, A.; Loubeyre, P.; Occelli, F.; Mezouar, M.; Dorogokupets, P.I.; Torrent, M. Quasihydrostatic Equation of State of Iron above 2 Mbar. Phys. Rev. Lett. 2006, 97, 215504. [Google Scholar] [CrossRef] [PubMed]
- Ichikawa, H.; Tsuchiya, T.; Tange, Y. The P-V-T equation of state and thermodynamic properties of liquid iron. J. Geophys. Res. Solid Earth 2014, 119, 240–252. [Google Scholar] [CrossRef]
- Poirier, J.-P. Light elements in the Earth’s outer core: A critical review. Phys. Earth Planet. Inter. 1994, 85, 319–337. [Google Scholar] [CrossRef]
- Morard, G.; Siebert, J.; Andrault, D.; Guignot, N.; Garbarino, G.; Guyot, F.; Antonangeli, D. The Earth’s core composition from high pressure density measurements of liquid iron alloys. Earth Planet. Sci. Lett. 2013, 373, 169–178. [Google Scholar] [CrossRef]
- Sanloup, C.; Guyot, F.; Gillet, P.; Fiquet, G.; Mezouar, M.; Martinez, I. Density measurements of liquid Fe-S alloys at high-pressure. Geophys. Res. Lett. 2000, 27, 811–814. [Google Scholar] [CrossRef]
- Sanloup, C.; Van Westrenen, W.; Dasgupta, R.; Maynard-Casely, H.; Perrillat, J.-P. Compressibility change in iron-rich melt and implications for core formation models. Earth Planet. Sci. Lett. 2011, 306, 118–122. [Google Scholar] [CrossRef]
- Huang, H.; Fei, Y.; Cai, L.; Jing, F.; Hu, X.; Xie, H.; Zhang, L.; Gong, Z. Evidence for an oxygen-depleted liquid outer core of the Earth. Nature 2011, 479, 513–516. [Google Scholar] [CrossRef]
- Huang, H.; Hu, X.; Jing, F.; Cai, L.; Shen, Q.; Gong, Z.; Liu, H. Melting behavior of Fe-O-S at high pressure: A discussion on the melting depression induced by, O and S. J. Geophys. Res. 2010, 115, B05207. [Google Scholar] [CrossRef]
- Huang, H.; Wu, S.; Hu, X.; Wang, Q.; Wang, X.; Fei, Y. Shock compression of Fe-FeS mixture up to 204 GPa. Geophys. Res. Lett. 2013, 40, 687–691. [Google Scholar] [CrossRef]
- Zhang, Y.; Sekine, T.; He, H.; Yu, Y.; Liu, F.; Zhang, M. Shock compression of Fe-Ni-Si system to 280 GPa: Implications for the composition of the Earth’s outer core. Geophys. Res. Lett. 2014, 41, 4554–4559. [Google Scholar] [CrossRef]
- Zhang, Y.; Sekine, T.; He, H.; Yu, Y.; Liu, F.; Zhang, M. Experimental constraints on light elements in the Earth’s outer core. Sci. Rep. 2016, 6, 22473. [Google Scholar] [CrossRef]
- Alfè, D. Temperature of the inner-core boundary of the Earth: Melting of iron at high pressure from first-principles coexistence simulations. Phys. Rev. B 2009, 79. [Google Scholar] [CrossRef]
- Anzellini, S.; Dewaele, A.; Mezouar, M.; Loubeyre, P.; Morard, G. Melting of iron at Earth’s inner core boundary based on fast X-ray diffraction. Science 2013, 340, 464–466. [Google Scholar] [CrossRef]
- Kamada, S.; Ohtani, E.; Terasaki, H.; Sakai, T.; Miyahara, M.; Ohishi, Y.; Hirao, N. Melting relationships in the Fe–Fe3S system up to the outer core conditions. Earth Planet. Sci. Lett. 2012, 359, 26–33. [Google Scholar] [CrossRef]
- Ma, Y.; Somayazulu, M.; Shen, G.; Mao, H.-K.; Shu, J.; Hemley, R.J. In situ X-ray diffraction studies of iron to Earth-core conditions. Phys. Earth Planet. Inter. 2004, 143, 455–467. [Google Scholar] [CrossRef]
- Nguyen, J.H.; Holmes, N.C. Melting of iron at the physical conditions of the Earth’s core. Nature 2004, 427, 339–342. [Google Scholar] [CrossRef] [PubMed]
- Terasaki, H.; Kamada, S.; Sakai, T.; Ohtani, E.; Hirao, N.; Ohishi, Y. Liquidus and solidus temperatures of a Fe–O–S alloy up to the pressures of the outer core: Implication for the thermal structure of the Earth’s core. Earth Planet. Sci. Lett. 2011, 304, 559–564. [Google Scholar] [CrossRef]
- Badro, J.; Côté, A.S.; Brodholt, J.P. A seismologically consistent compositional model of Earth’s core. Proc. Natl. Acad. Sci. USA 2014, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Pozzo, M.; Davies, C.; Gubbins, D.; Alfè, D. Transport properties for liquid silicon-oxygen-iron mixtures at Earth’s core conditions. Phys. Rev. B 2013, 87, 14110. [Google Scholar] [CrossRef]
- Brodholt, J.; Badro, J. Composition of the low seismic velocity E′ layer at the top of Earth’s core. Geophys. Res. Lett. 2017, 44, 8303–8310. [Google Scholar] [CrossRef]
- Vočadlo, L.; Alfè, D.; Gillan, M.J.; Price, G.D. The properties of iron under core conditions from first principles calculations. Phys. Earth Planet. Inter. 2003, 140, 101–125. [Google Scholar] [CrossRef]
- Umemoto, K.; Hirose, K.; Imada, S.; Nakajima, Y.; Komabayashi, T.; Tsutsui, S.; Baron, A.Q.R. Liquid iron-sulfur alloys at outer core conditions by first-principles calculations. Geophys. Res. Lett. 2014, 41, 6712–6717. [Google Scholar] [CrossRef]
- Posner, E.S.; Steinle-Neumann, G. Mass transport and structural properties of binary liquid iron alloys at high pressure. Geochem. Geophys. Geosyst. 2019, 20, 3556–3568. [Google Scholar] [CrossRef]
- Umemoto, K.; Hirose, K. Liquid iron-hydrogen alloys at outer core conditions by first-principles calculations. Geophys. Res. Lett. 2015, 42, 7513–7520. [Google Scholar] [CrossRef]
- Karato, S.; Karki, B.B. Origin of lateral variation of seismic wave velocities and density in the deep mantle. J. Geophys. Res. 2001, 106, 21771–21783. [Google Scholar] [CrossRef]
- Wentzcovitch, R.M.; Tsuchiya, T.; Tsuchiya, J. MgSiO3 post-perovskite at D” conditions. Proc. Natl. Acad. Sci. USA 2006, 103, 543–546. [Google Scholar] [CrossRef] [PubMed]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Alfè, D.; Price, G.; Gillan, M. Iron under Earth’s core conditions: Liquid-state thermodynamics and high-pressure melting curve from ab initio calculations. Phys. Rev. B 2002, 65. [Google Scholar] [CrossRef]
- Mori, Y.; Ozawa, H.; Hirose, K.; Sinmyo, R.; Tateno, S.; Morard, G.; Ohishi, Y. Melting experiments on Fe–Fe3S system to 254 GPa. Earth Planet. Sci. Lett. 2017, 464, 135–141. [Google Scholar] [CrossRef]
- Fischer, R.A.; Campbell, A.J.; Reaman, D.M.; Miller, N.A.; Heinz, D.L.; Dera, P.; Prakapenka, V.B. Phase relations in the Fe–FeSi system at high pressures and temperatures. Earth Planet. Sci. Lett. 2013, 373, 54–64. [Google Scholar] [CrossRef]
- Seagle, C.T.; Heinz, D.L.; Campbell, A.J.; Prakapenka, V.B.; Wanless, S.T. Melting and thermal expansition in the Fe-FeO syustem at high pressure. Phys. Earth Planet. Inter. 2008, 265, 655–665. [Google Scholar] [CrossRef]
- Shibazaki, Y.; Terasaki, H.; Ohtani, E.; Tateyama, R.; Nishida, K.; Funakoshi, K.; Higo, Y. High-pressure and high-temperature phase diagram for Fe0.9Ni0.1-H alloy. Phys. Earth Planet. Inter. 2014, 228, 192–201. [Google Scholar] [CrossRef]
- Kawai, K.; Tsuchiya, T. Temperature profile in the lowermost mantle from seismological and mineral physics joint modeling. Proc. Natl. Acad. Sci. USA 2009, 106, 22119–22123. [Google Scholar] [CrossRef]
- Nomura, R.; Hirose, K.; Uesugi, K.; Ohishi, Y.; Tsuchiyama, A.; Miyake, A.; Ueno, Y. Low core-mantle boundary temperature inferred from the solidus of pyrolite. Science 2014, 343, 522–525. [Google Scholar] [CrossRef]
- Ozawa, H.; Hirose, K.; Yonemitsu, K.; Ohishi, Y. High-pressure melting experiments on Fe–Si alloys and implications for silicon as a light element in the core. Earth Planet. Sci. Lett. 2016, 456, 47–54. [Google Scholar] [CrossRef]
- Kennett, B.L.N.; Engdahl, E.R.; Buland, R. Constraints on seismic velocities in the Earth from traveltimes. Geophys. J. Int. 1995, 122, 108–124. [Google Scholar] [CrossRef]
- Montagner, J.-P.; Kennett, B.L.N. How to reconcile body-wave and normal-mode reference earth models. Geophys. J. Int. 1996, 125, 229–248. [Google Scholar] [CrossRef]
- McDonough, W.F.; Sun, S.-S. The composition of the Earth. Chem. Geol. 1995, 120, 223–253. [Google Scholar] [CrossRef]
- Cottaar, S.; Heister, T.; Rose, I.; Unterborn, C. BurnMan: A lower mantle mineral physics toolkit. Geochem. Geophys. Geosyst. 2014, 15, 1164–1179. [Google Scholar] [CrossRef]
- Wang, X.; Tsuchiya, T.; Hase, A. Computational support for a pyrolitic lower mantle containing ferric iron. Nat. Geosci. 2015, 8, 556–559. [Google Scholar] [CrossRef]
- Fitoussi, C.; Bourdon, B.; Wang, X. The building blocks of Earth and Mars: A close genetic link. Earth Planet. Sci. Lett. 2016, 434, 151–160. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502–395521. [Google Scholar] [CrossRef] [PubMed]
- Usui, Y.; Tsuchiya, T. Ab initio two-phase molecular dynamics on the melting curve of SiO2. J. Earth Sci. 2010, 21, 801–810. [Google Scholar] [CrossRef]
- Ichikawa, H.; Tsuchiya, T. Atomic transport property of Fe-O liquid alloys in the Earth’s outer core P, T condition. Phys. Earth Planet. Inter. 2015, 247, 27–35. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Asada, T.; Terakura, K. Cohesive properties of iron obtained by use of the generalized gradient approximation. Phys. Rev. B 1992, 46, 13599–13602. [Google Scholar] [CrossRef] [PubMed]
- Stixrude, L.; Cohen, R.E.; Singh, D.J. Iron at high pressure: Linearized-augmented-plane-wave computations in the generalized-gradient approximation. Phys. Rev. B 1994, 50, 6442–6445. [Google Scholar] [CrossRef] [PubMed]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef] [PubMed]
- Louie, S.G.; Froyen, S.; Cohen, M.L. Nonlinear ionic pseudopotentials in spin-density-functional calculations. Phys. Rev. B 1982, 26, 1738–1742. [Google Scholar] [CrossRef]
- Tsuchiya, T.; Fujibuchi, M. Effects of Si on the elastic property of Fe at Earth’s inner core pressures: First principles study. Phys. Earth Planet. Inter. 2009, 174, 212–219. [Google Scholar] [CrossRef]
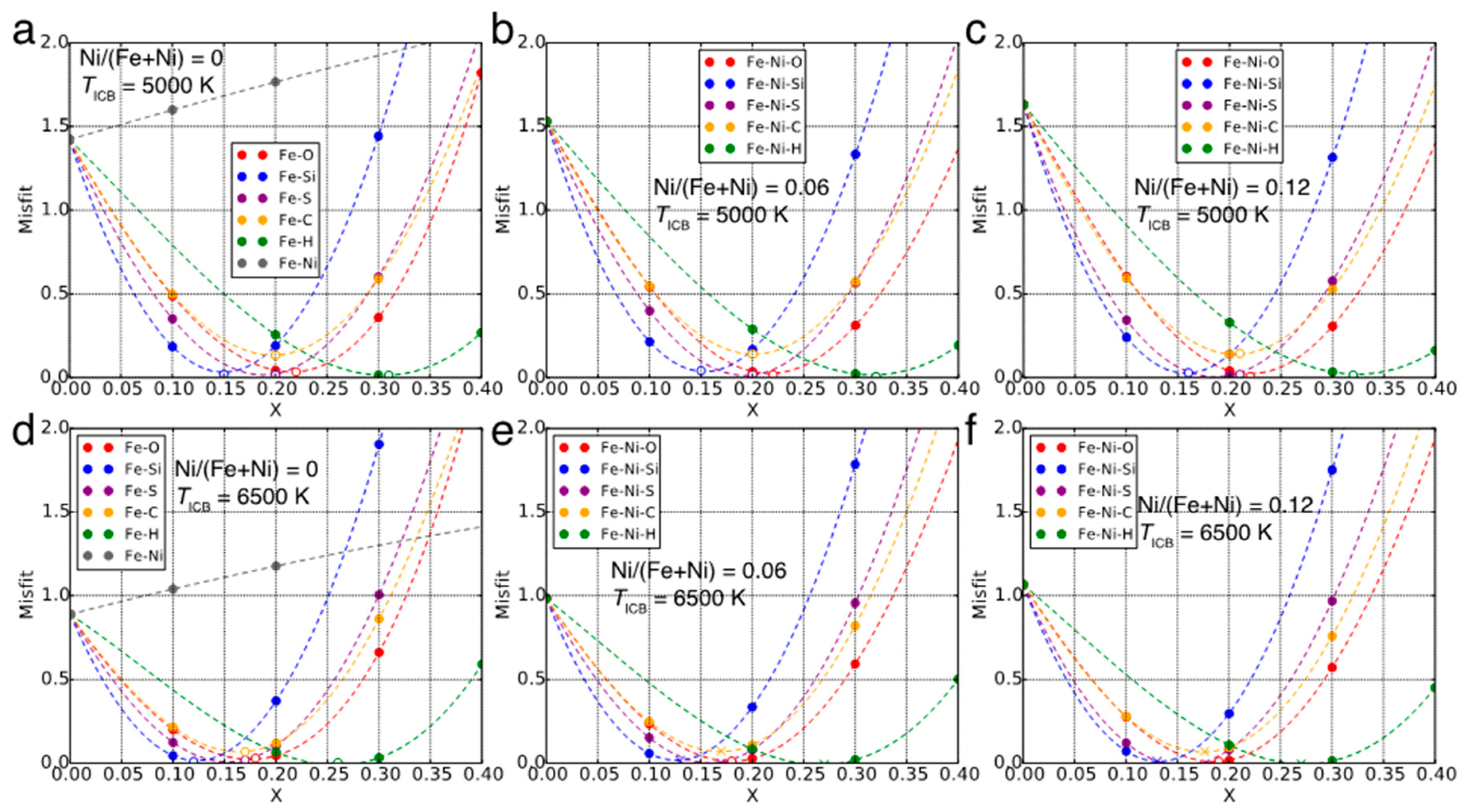
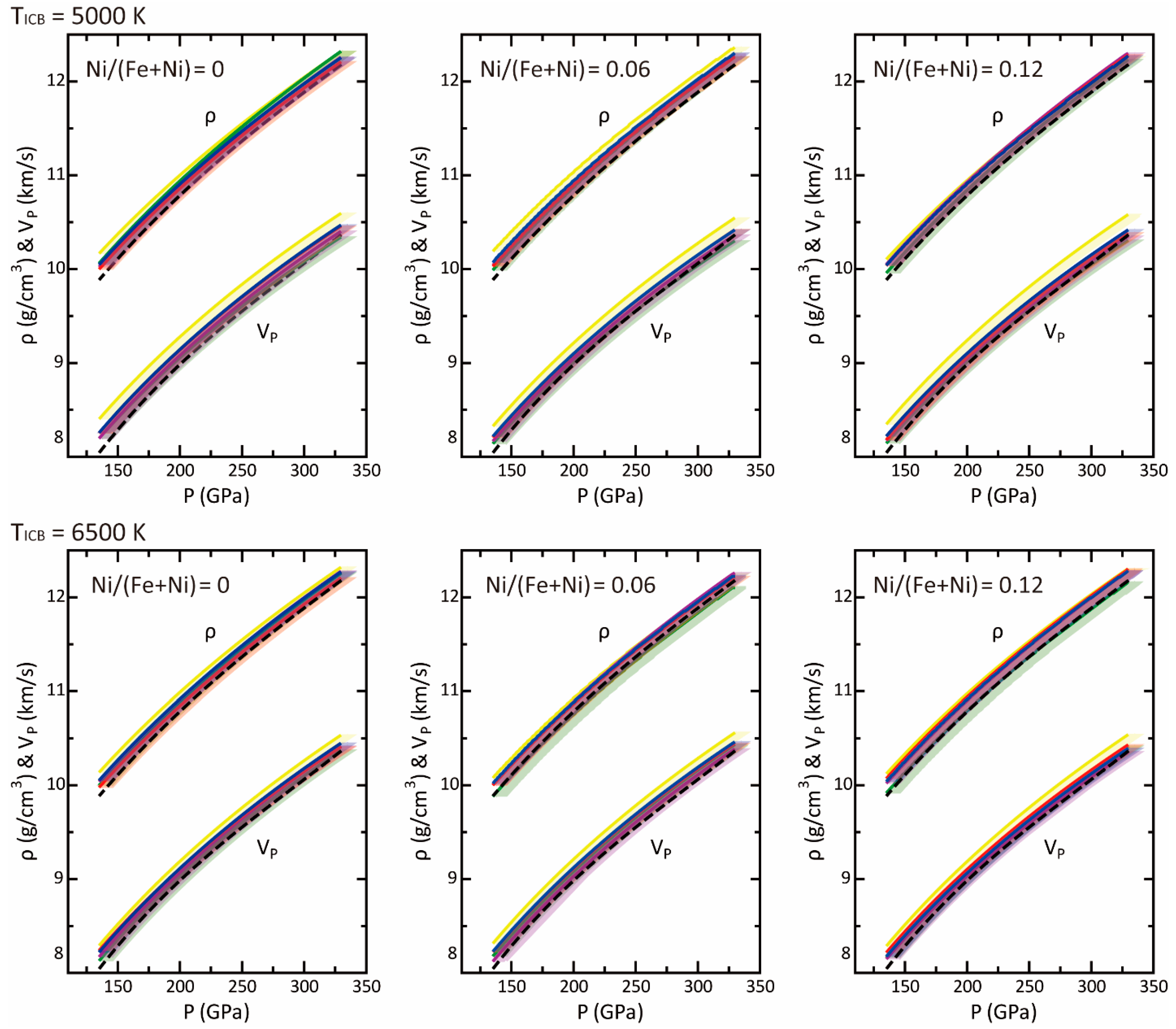
| P, T Condition | O | Si | S | C | H | |
|---|---|---|---|---|---|---|
| P = PCMB T = 4000 K | 0.05(1) | 0.13(1) | 0.06(1) | 0.16(1) | 0.02(1) | |
| −0.34(1) | −0.51(1) | −0.41(1) | −0.30(1) | −0.24(1) | ||
| −0.14(1) | −0.26(1) | −0.16(1) | −0.54(1) | −0.10(1) | ||
| P = PICB T = 5300 K | 0.09(1) | 0.21(1) | 0.16(1) | 0.20(1) | 0.07(1) | |
| −0.31(1) | −0.48(1) | −0.38(1) | −0.31(1) | −0.21(1) | ||
| −0.29(1) | −0.44(1) | −0.42(1) | −0.63(1) | −0.35(1) |
| TICB | Best-Fit Composition | Mg/Si | Mg/Fe | |
|---|---|---|---|---|
| K | Fe0.78O0.22 | 1.8(1) | 1.25(1) | 1.03(1) |
| Fe0.85Si0.15 | 2.7(1) | 1.06(1) | 1.04(1) | |
| Fe0.81S0.19 | 1.6(1) | 1.25(1) | 1.08(1) | |
| Fe0.80C0.20 | 11.2(1) | 1.25(1) | 1.01(1) | |
| Fe0.70H0.30 | 1.9(1) | 1.25(1) | 0.97(1) | |
| Fe0.73Ni0.05O0.22 | 0.8(1) | 1.25(1) | 1.10(1) | |
| Fe0.80Ni0.05Si0.15 | 1.3(1) | 1.06(1) | 1.10(1) | |
| Fe0.76Ni0.05S0.19 | 0.6(1) | 1.25(1) | 1.14(1) | |
| Fe0.75Ni0.05C0.20 | 11.8(1) | 1.25(1) | 1.07(1) | |
| Fe0.64Ni0.04H0.32 | 1.1(1) | 1.25(1) | 1.03(1) | |
| Fe0.69Ni0.09O0.22 | 0.7(1) | 1.25(1) | 1.15(1) | |
| Fe0.74Ni0.10Si0.16 | 1.4(1) | 1.05(1) | 1.17(1) | |
| Fe0.71Ni0.10S0.19 | 1.2(1) | 1.25(1) | 1.21(1) | |
| Fe0.7Ni0.09C0.21 | 10.4(1) | 1.25(1) | 1.13(1) | |
| Fe0.6Ni0.08H0.32 | 0.9(1) | 1.25(1) | 1.09(1) | |
| K | Fe0.82O0.18 | 4.8(1) | 1.25(1) | 1.02(1) |
| Fe0.88Si0.12 | 1.7(1) | 1.09(1) | 1.02(1) | |
| Fe0.85S0.15 | 0.8(1) | 1.25(1) | 1.05(1) | |
| Fe0.84C0.16 | 7.7(1) | 1.25(1) | 1.00(1) | |
| Fe0.74H0.26 | 0.1(1) | 1.25(1) | 0.97(1) | |
| Fe0.77Ni0.05O0.18 | 0.9(1) | 1.25(1) | 1.08(1) | |
| Fe0.82Ni0.05Si0.13 | 1.8(1) | 1.08(1) | 1.08(1) | |
| Fe0.79Ni0.05S0.16 | 0.2(1) | 1.25(1) | 1.12(1) | |
| Fe0.78Ni0.05C0.17 | 7.5(1) | 1.25(1) | 1.06(1) | |
| Fe0.69Ni0.04H0.27 | 2.3(1) | 1.25(1) | 1.02(1) | |
| Fe0.71Ni0.1O0.19 | 2.2(1) | 1.25(1) | 1.15(1) | |
| Fe0.77Ni0.1Si0.13 | 1.3(1) | 1.08(1) | 1.15(1) | |
| Fe0.74Ni0.1S0.16 | 0.6(1) | 1.25(1) | 1.18(1) | |
| Fe0.72Ni0.1C0.18 | 7.7(1) | 1.25(1) | 1.13(1) | |
| Fe0.64Ni0.09H0.27 | 1.0(1) | 1.25(1) | 1.09(1) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ichikawa, H.; Tsuchiya, T. Ab Initio Thermoelasticity of Liquid Iron-Nickel-Light Element Alloys. Minerals 2020, 10, 59. https://doi.org/10.3390/min10010059
Ichikawa H, Tsuchiya T. Ab Initio Thermoelasticity of Liquid Iron-Nickel-Light Element Alloys. Minerals. 2020; 10(1):59. https://doi.org/10.3390/min10010059
Chicago/Turabian StyleIchikawa, Hiroki, and Taku Tsuchiya. 2020. "Ab Initio Thermoelasticity of Liquid Iron-Nickel-Light Element Alloys" Minerals 10, no. 1: 59. https://doi.org/10.3390/min10010059
APA StyleIchikawa, H., & Tsuchiya, T. (2020). Ab Initio Thermoelasticity of Liquid Iron-Nickel-Light Element Alloys. Minerals, 10(1), 59. https://doi.org/10.3390/min10010059





