Abstract
Multiphase systems are important in minerals processing, and usually include solid–solid and solid–fluid systems, such as in wet grinding, flotation, dewatering, and magnetic separation, among several other unit operations. In this paper, the current trends in the process system engineering tasks of modeling, design, and optimization in multiphase systems, are analyzed. Different scales of size and time are included, and therefore, the analysis includes modeling at the molecular level (molecular dynamic modeling) and unit operation level (e.g., computational fluid dynamic, CFD), and the application of optimization for the design of a plant. New strategies for the modeling, design, and optimization of multiphase systems are also included, with a strong focus on the application of artificial intelligence (AI) and the combination of experimentation and modeling with response surface methodology (RSM). The integration of different modeling techniques such as CFD with discrete element simulation (DEM) and response surface methodology (RSM) with artificial neural networks (ANN) is included. The paper finishes with tools to study the uncertainty, both epistemic and stochastic, based on uncertainty and global sensitivity analyses, which is present in all mineral processing operations. It is shown that all of these areas are very active and can help in the understanding, operation, design, and optimization of mineral processing that involves multiphase systems. Future needs, such as meso-scale modeling, are highlighted.
Keywords:
computational fluid dynamic; molecular dynamics; density functional theory; discrete element simulation; smoothed particle hydrodynamics; flotation; grinding; response surface methodology; machine learning; artificial neural networks; support vector machine; hydrocyclone; global sensitivity analysis; uncertainty analysis 1. Introduction
Multiphase systems are common in mineral processing because most of the process includes the presence of particles, which are usually multiphase mineral particles, and fluids. Examples of operations in mineral processing that include solid–liquid phases are wet grinding, filtration, hydrocyclone, and thickening. An example that includes solid–gas phases is cyclone, examples that include solid–solid phases are magnetic and electrostatic separations, and an example that includes solid–liquid–gas phases is flotation. These operations are generally difficult to study because they are opaque and challenging to measure. Therefore, the modeling of these systems, like other systems, is important, because it allows us to understand their behavior, which allows us to modify them. For example, these models are applied to optimize and design unit operations or plants that depend on multiphase systems. In addition, these models can facilitate the development of new technologies such as new reagents and unit operations.
There are a growing number of tools and methods for the modeling, optimization, and design of these multiphase systems. These increases in the numbers of tools and methods are promoted by the increase in computing power and new algorithms available in the literature. On the other hand, reliable models are needed for the development of new reagents, equipment, and processes. Also, these models are necessary for the optimization of operational conditions. The lack of models increases the dependency on the experience of experts, and also increases the time and cost of scaling up from laboratory- to full-scale. Because the behavior of these systems depends on physical and chemical phenomena that occur at different time and length scales, different tools are available based on these scales. Small scales, e.g., quantum mechanical length scales of 10−13 m with time scales of 10−16 s, are of significant interest in understanding the interaction of minerals with reagents. Large scales, e.g., plants length scales of 103 m with time scales of 106 s, are important in terms of plant integration and environmental impact.
This manuscript reviews the main tools and methods for the modeling, design, and optimization of multiphase systems in mineral processing. The idea is not to produce an encyclopedic review, because there are too many tools and methods, but to highlight the most commonly used tools with greater projection. Figure 1, which is based on the work of Grossmann and Westerberg [1], shows different levels of length and time alongside the tools and methods that will be reviewed in this manuscript. First, molecular mechanics and quantum mechanics are analyzed for the purpose of understanding different mineralogical systems. Computational fluid dynamics (CFD), which consists of numerically solving equations of multiphase fluid motion, allows for quantitative predictions and analyses of multiphase fluid flow phenomena. CFD has been applied to mineral processing for both parametric studies and flow-physics investigations. Process design is analyzed next, showing the methods available, with most of them used for flotation processes. Artificial intelligence (AI) is one area with great projection and amount of research, and therefore, is analyzed from the point of view of multiphase systems in mineral processing. Most of the research on mineral processing involves experimental studies, and therefore, experimental design with response surface methodology (RSM) is an important tool to report. Uncertainty, both epistemic and stochastic, must be considered when multiphase systems are studied. The two most important methods for considering uncertainty, uncertainty analysis (UA) and global sensitivity analysis (GSA), are analyzed at the end. Finally, some conclusions and comments are presented to close this report.
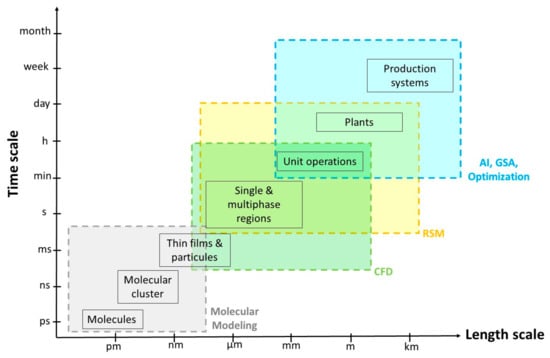
Figure 1.
Levels of length and time alongside the modeling and optimization tools analyzed in this manuscript (CFD—computational fluid dynamics; RSM—response surface methodology; AI—artificial intelligence; GSA—global sensitivity analysis).
2. Molecular Dynamic Modeling
The inherent heterogeneous nature and complexity of minerals mineralogy often make the connection between observation and theory very complicated. Additionally, industrial development promotes more and more ore deposit investigation and subsequently, transformation through mineral processing, which adds more phenomena that must be understood. All this complexity from mineralogy and geochemistry requires molecular modeling tools to understand the fundamental properties and mechanisms that control the thermodynamics and kinetics of materials. In this sense, molecular models are often used to supplement experimental observations, providing a powerful complementary tool to the researcher [2,3]. In 1998, De Villiers [4] from Miltek analyzed the potential of molecular modeling to improve mineral processes, using the South African industry as an example. He identified several potential studies including new reagents, the development of new materials, and a theoretical understanding of surface interactions.
According to the abovementioned reference, this tool can be used to understand all microscopic effects (atomic level) that occur on mineral surfaces in different field applications. For example, in the solid–fluid interactions in the flotation process (hydrophobicity and hydrophilicity), and in thickening (water absorption, hydrate minerals, layered double hydroxides, mineral interlayers, clay minerals), among other applications. All these applications have made molecular simulation an accepted approach to solve a number of mineralogical and geochemical problems in multiphase systems [5].
Molecular modeling tools consist of calculating the total energy of the molecular (isolated cluster) or periodic system (crystalline or amorphous structure) under investigation. Two fundamental approaches are typically used: molecular mechanics and quantum mechanics. Figure 2 shows a diagram of molecular mechanics and quantum mechanics methods. Both methods are related and are used to examine the structure and energy of a molecule or periodic system [2].
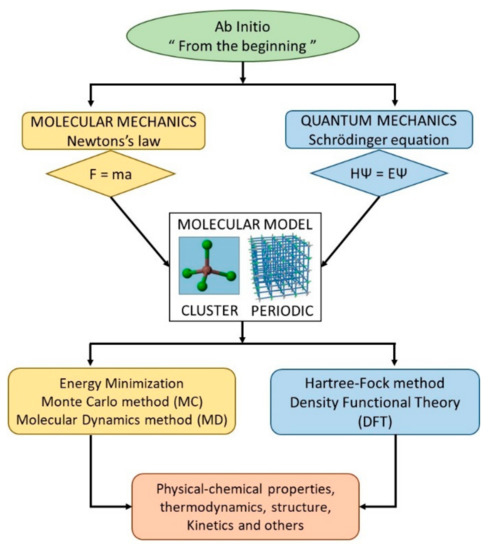
Figure 2.
Diagram of molecular mechanics and quantum mechanics methods.
To better understand this diagram, it is necessary to know some concepts regarding how molecular modeling works. According to this, firstly, ab initio refers to the quantum approach for obtaining the electronic properties of a molecule based on the Schrödinger equation (Hψ = Eψ), which describes the wave function or state function of a quantum-mechanical system. Secondly, the molecular mechanism relies on the use of analytical expressions that have been parameterized through either experimental observation or quantum calculations using an energy forcefield, based on Newtonian physics (F = ma, classical mechanics) to evaluate the interaction energies for the given structure or configuration. In contrast, in quantum mechanics, the analog of Newton’s law is Schrödinger’s equation, which does not use empirical parameters to evaluate the energy system. In this sense, in a molecular mechanics simulation, the most important requirement is the forcefield used to describe the potential energy of the system. It is essential to have an accurate energy forcefield to achieve a successful energy minimization. The energy of interaction for an assemblage of atoms in either a molecular or crystalline configuration is described by the interatomic potential, generated by the forcefield. This interatomic potential—named potential energy—can be obtained as a function of geometric variables, such as angle, distance, and other geometric measurements [2].
Therefore, it is possible to describe the potential energy for a complex multibody system by the summation of all energy interactions in the system. The energy components are the following: the coulombic energy (electrostatic energy) and the Van der Waals energy (short-range energy associated with atomic interactions), which represent the non-bonded energy components, and the bond stretching (bond energy associated with length changes), angle bending, and torsion, which represent the bonded energy components [6]. From all of these energy components, the total potential energy of a system can be calculated. These types of energies will not be explained in detail because this work provides a general overview of molecular modeling.
Thirdly, energy minimization is another concept that must be understood. This concept also refers to the geometry optimization for obtaining a stable configuration for a molecule or periodic system. This energy involves the repeated measurement of the potential energy on the surface until the minimum potential energy is obtained, which corresponds to the configuration where the forces between atoms are equal to zero. Finally, there are two molecular mechanism approaches—the Monte Carlo (MC) method and the molecular dynamics (MD) simulation—to analyze all the energies and chemical systems on mineral surfaces. The MC method is a stochastic analysis that consists of random sampling of the potential energy surface to obtain a selection of possible equilibrium configurations. The MD simulation is a deterministic molecular modeling tool that involves the calculations of forces based on Newtonian physics used to make a mathematical prediction to evaluate the time evolution of a system on the time scale of pico- and nano-seconds [2,5]. Examples of molecular modeling applications using MD and MC will be presented later, where a detailed discussion will be presented on the use of these techniques for various minerals and mineral surfaces.
The quantum mechanism is a method that evaluates the electronic structure and energy of molecular systems using the Schrödinger equation, which is based on the quantized nature of electronic configurations in atoms and molecules. This technique permits the obtainment of a detailed description of reaction mechanisms, properties of molecular and crystalline structures, electrostatic potentials, thermodynamics properties, and other phenomena that occur in a multiphasic system. The application of this method in the mineralogical and geochemical field is the most challenging task for today’s computational modeling.
Quantum chemistry methods can be divided into different classes, where the most used are the Hartree–Fock method and density functional theory (DFT). The Hartree–Fock method uses an antisymmetric determinant of one-electron orbitals to define the total wavefunction. A trial wavefunction is iteratively improved until self-consistency is attained. On the other hand, DTF is a method in which the total energy is expressed as a function of the electron density, and in which all correlation contributions are based on the Schrödinger equation for an electron gas.
Finally, a variety of molecular modeling methods have been implemented by a fair number of research works to study all the interactions between reagents and mineral surfaces, such as adsorption/desorption of reagents on mineral surfaces (collectors, depressors, frothers) in the flotation process, the interaction of water and solute species with mineral surfaces and their behavior in mineral interlayers, and the impact of clay minerals on the dewatering of coal slurry. Next, we focus on an overview of the use of molecular modeling and simulation in the last three years to address specific applications associated with mineralogical and geochemical problems [2,3,5]. Molecular modeling examples are shown following the study of solid–liquid interactions to obtain a good structural model for the material.
2.1. Collector/Depressor Adsorption on Different Mineral Surfaces in the Flotation Process
Leal Filho et al. [7] used MD to demonstrate the ability of two polysaccharides to promote the selective depression of calcite from apatite. They made a good selection of the interaction to represent the chemical and physico-chemical processes during the depression of calcite. The mineral surface of calcite and hydroxyapatite were modeled together with the corn starch and ethyl-cellulose. Firstly, measurements of the unit cell parameters were realized to study the crystal structure of calcite and hydroxy-apatite by X-ray diffraction. Later, the crystallographic orientations of particles of hydroxyapatite and particles of calcite were characterized by optical microscopy and scanning electron microscopy, respectively. The planes predominant for calcite were (101), (401), and (021), and for hydroxy-apatite it was (001). It was observed that calcium species were common active sites at the calcite/water and hydroxy-apatite/water interface, and those sites interacted with starch molecules via the hydroxyl groups existing along with the polymer structure. However, depending on partition planes (hkl), it was demonstrated that the major steric compatibility was in the calcite/starch system. The total fitting number Ft (parameter to define steric compatibility between reagents and mineral orientation) for calcite was: plane (101) Ft = 51.5, plane (401) Ft = 20.1, and plane (021) Ft = 30.3, and for hydroxy-apatite it was: plane (001) Ft = 8.5. Therefore, from these results, it was concluded that the larger the Ft, the greater the expected steric compatibility between reagent structure and crystallographic orientation [7]. Then, these results were compared with micro-flotation experiments of calcite and hydroxy-apatite with sodium oleate in the presence of starch, and it was proven, by calculating recoveries, that the Ft was calculated accurately because the recovery was less with the increase in starch concentration on the calcite surface. Finally, molecular modeling provides appropriate theoretical representations to understand the depressing ability of starch and ethyl cellulose on the mineral surface.
Similar studies using MD simulation were developed by Zhang et al. [8]. The adsorption of collectors on a coal surface was studied. The findings showed that the collector oil absorbed on the coal surface decreases the number of hydrogen bonds between the modified coal surface and contacting water molecules. This can be attributed to the improvement of coal surface hydrophobicity. The hydrophobicity occurs due to the interaction force weakening between water molecules and the coal surface [8]. The same methodology was used by Zhang et al. [9], but this time studying the adsorption behavior of methyl laurate and dodecane on the coal surface. It was determined that methyl laurate is a more successful collector to improve the hydrophobicity of the modified coal surface because the water molecule mobility in methyl laurate was greater than in dodecane. Finally, Nan et al. [10], using the DFT calculation, studied a flotation collector, N-(carboxymethyl)-N-tetradecylglycine (NCNT), in order to understand the adsorption ability of the collector on a fluorapatite (001) surface. They confirmed that the NCNT collector could be used in the fluorapatite flotation process.
2.2. Interaction of Clay Minerals, Water, and Interlayer Structures
Clay minerals such as kaolinite, montmorillonite, smectites, and others are very common in soils, sediments, and sedimentary rocks. In this sense, their properties and behavior have received considerable industrial importance. The interaction of clay minerals with water promotes the water adsorption in the interlayer structure on the clay surface, which generates complex systems. In this sense, avoiding water absorption becomes a difficult task. Hence, computational studies of clay minerals are required to understand the swelling, interlayer structure, and dynamics of water distribution on a clay surface. Today, several studies have been developed to obtain significant dynamical information about these systems. In this section, we show some of the most recent works in this area.
Ma et al. [11] studied the impact of clay minerals (kaolinite and montmorillonite) on the dewatering of coal slurry using a molecular-simulation study, followed by an experimental section to corroborate data accuracy. The molecular simulation results show different adsorptions of water on the side surfaces of kaolinite and montmorillonite. Water molecules could scarcely diffuse into kaolinite from the edge but could easily propagate into the montmorillonite layers from the edge surface because of the existence of a hydrated cation in montmorillonite and a weak interlayer connection. This means that a small amount of montmorillonite caused a major decrease in the filtration velocity and a huge rise in the moisture of the filter cake. Therefore, the efficiency of the dewatering process has a strong dependency on the interaction between kaolinite/montmorillonite and water. Figure 3 shows an equilibrium snapshot from an MD simulation of water adsorption on the side surfaces of kaolinite and montmorillonite. Another study of water absorption on a mineral surface was conducted by Wang et al. [12]. They evaluated the water adsorption on the β-dicalcium silicate (cement) surface from DFT simulations. This work studied how to improve the hydration rate on the cement surface. Then, they studied the adsorption mechanics of the water/cement system. The cement hydration is a crucial step that controls the final properties of cement materials. However, the industrial production of cement produces a large amount of CO2 emissions and energy consumption. For this reason, understanding cement hydration mechanisms was the main motivation of this study to provide an academic basis for the design of new environmentally friendly cement. Finally, Kubicki et al. [13] studied the vibrational spectra on clays by DFT approaches. Herein, they presented an overview of quantum mechanical calculations to predict vibrational frequencies of molecules and materials such as clays and silicates. For creating a realistic model, the vibrational frequencies were calculated by two analytical methods, Raman and infrared intensities.
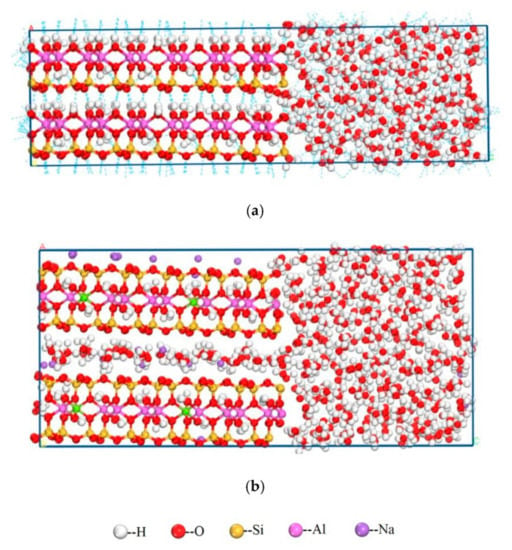
Figure 3.
Example of an equilibrium snapshot from a molecular dynamics (MD) simulation of water adsorption on the side surfaces of (a) kaolinite and (b) montmorillonite at 298 K and 1 bar [11].
The analytical methods combined with computational molecular-scale modeling studies reviewed in this paper illustrate how these methods can provide otherwise unobtainable structural, dynamical, and energetic information about mineral-fluid systems. Using modern supercomputers, molecular modeling can readily model geo-chemically relevant systems containing up to millions of atoms for times up to milliseconds. Thus, these methods can provide dynamic information at frequencies of the order of and greater than the gigahertz range. This approach will continue to play an important role in understanding different mineralogical systems. Future applications in wet grinding can help to better understand and improve this operation as, currently, it is used in nanoscale grinding [14,15]. The development of experimental methods from computational modeling can be an appropriate route for future research in this field.
3. Computational Fluid Dynamics (CFD) in Multiphase Systems
Traditional modeling in mineral processing is strongly based on empirical or semi-empirical models [16,17,18,19,20]. Typically, these models work well under the condition of the experimental data used in the fitting stage but are not reliable for new operational conditions. For new operational conditions or new equipment, new equations or parameters must be determined based on additional experimental data. Several papers have been published that review modeling in multiphase systems including the flotation process [21], either for classical mathematical models [22] or a soft computers approach [23], ball mill [24], and hydrocyclone [25]. Some of the papers are more specific, such as the review of the modeling of bubble-particle detachment [26] or entrainment [27] and water recovery [28] in flotation. These days, engineers are increasingly using CFD to analyze flow and performance in the design of new equipment and processes [29]. The secret behind the success of CFD is its ability to simulate flows, similar to those observed in practical conditions—in terms of tackling real, three-dimensional, irregular flow geometries and phenomena involving complex physics [30]. This is made possible by resorting to a numerical solution of the equations’ governing fluid flow rather than seeking an analytical solution. Usually, the equations describing the flow of fluids consist of mathematical statements of conservation of such fundamental quantities as mass, momentum, and energy during fluid flow and allied phenomena. The variables in these equations are three velocity components, pressure, and temperature of the fluid. In a typical case, each of these varies with location and time within the flow domain. Their variation is governed and determined by the conservation equations, which take the form of non-linear partial differential equations. CFD deals with the numerical solution of these equations [30]. For this, a region of space is discretized by creating what is known as a spatial mesh, dividing a region of space into small volumes of control. Then, the discretized conservation equations are solved iteratively in each of them until the residue is sufficiently small. Therefore, a CFD solution requires a large number of arithmetic computations on real numbers; hence, its rise coincided with the advent of computers and the rapid expansion of computer power that ensued in the subsequent decades. In fact, in several cases, even with simplified equations, only approximate results can be obtained. Figure 4 shows examples of CFD modeling.
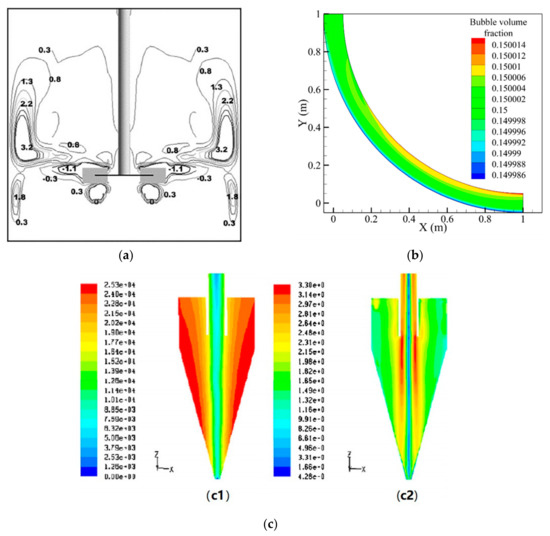
Figure 4.
Examples of computational fluid dynamics (CFD) multiphase modeling in mineral processing. (a) CFD-predicted net attachment rates after flotation time in the stirred cell [31]; (b) Bubble volume fraction (unit in vol %) distribution in a pipe for a backfill material [32]; (c) Predicted contours of (c1) pressure and (c2) tangential velocities in Renner’s cyclone [33].
Multiphase flows are usually modeled using the Euler–Lagrange (E–L) model, the Euler–Euler (E–E) model, and the mixture model. In E–L modeling, the fluid phase is modeled as a continuum, while for the dispersed phase, a large number of individual particles are modeled. The dispersed phase can exchange momentum, mass, and energy with the fluid phase. Since the particle or droplet trajectories are computed for each particle or for a bundle of particles that are assumed to follow the same trajectory, the approach is limited to systems with a low volume fraction of the dispersed phase. Typical applications are dissolved air flotation and air classification. In E–E models, the different phases are all treated as continuous phases, and momentum and continuity equations are solved for each phase. The E–E method can become computationally expensive as the number of equations increases with the number of phases present in the system. The E–E model can handle very complex flows but does not always give the best results since empirical information is needed for the momentum equations. Typical applications are flotation cells and magnetic separators. Another E–E model is the volume-of-fluid (VOF) model, whereby the interface between the different phases is tracked. This model is suitable for hydrocyclone separators. Since the interface between the fluids must be resolved, it is not applicable to a system with many small drops or bubbles. The mixture phase model shortens the E–E method, considering a single momentum equation for all the phases, assuming that they are components of a mixture. In this model, the viscosity is estimated for the mixture. The velocities of the different phases are subsequently calculated from buoyancy, drag, and other forces, giving the relative velocities in comparison with the mean velocity of the mixture [29]. Typical applications are bubble columns, fine particle suspensions, and stirred-tank reactors.
Several factors affect the selection of the most appropriate multiphase model, and the physics of the system must be analyzed and understood. For example, it must be considered whether the phases are separated or dispersed and if the particles follow the continuous phase, among several other factors.
Examples of applications of CFD in mineral processing are given below. CFD was used to improve the understanding of the influence of the geometric design of the classifier on the cut size and the resulting particle size distribution in a centrifugal air classification [34]. The E–L approach was used to investigate how the internal airflow in the second stage of the air classifier affects the classification efficiency. The simulation results show that the classification results are affected by the airflow velocity, particle shape, particle size, the geometry of the air classifier, and turbulence in the airflow. The performance of a wet, high-intensity, magnetic separator was analyzed using CFD [35]. The behavior of these systems relies on the interaction between magnetic, hydrodynamic, gravitational, and interparticle forces. These forces are controlled by the process as well as design parameters. A three-dimensional E–E approach was developed to predict the flow profile as well as the concentration profile of solid particles between two parallel plates. Three phases, i.e., one liquid and two solid phases, were considered. Simulation results agree with the results observed experimentally. Another application of CFD is the study of flow behavior in a hydrocyclone, which is a highly swirling and turbulent multiphase structure. Narasimha et al. [33] developed a multiphase CFD model to understand the particle size segregation inside a six inches hydrocyclone. The predictions were validated against experimental data, and were shown to be in good agreement. An application, outside of separators, is the study of the complex flow behavior in the pulp lifter of autogenous and semi-autogenous grinding mills as it controls the throughput, performance, and efficiency of mills. CFD modeling—the VOF approach—was used to study the efficient and effective removal of pulp/slurry from the mill by a pulp lifter design [36]. Comparison with experimental data shows that CFD can be a useful tool to understand and improve complex flow behavior. In the same direction, a CFD model, a mixture phases model, was developed to study a three-dimensional backfill pipeline transport of three-phase foam slurry backfill (TFSB) [32]. The simulation results indicate that TFSB can maintain a steady state during pipeline transport, experience a markedly reduced pipeline transport resistance, and exhibit better liquidity than conventional cement slurry. Last but not least, the flotation process is one of the most studied systems using CFD, and a comprehensive review of the published literature regarding the CFD modeling of the flotation process was presented [37]. The advances made in the modeling and simulations of the equipment were critically analyzed, and specific emphasis was given to the bubble–particle interactions and the effect of turbulence on these interactions. The simulation of flow behavior of flotation cells has been studied using multiphase E–E [38,39], mixture phase [40], and E–L [41,42] approaches. Mostly, the finite volume approach has been utilized in the reported studies, wherein local values of the flow properties are calculated by solving the governing continuity and momentum equation for each phase [37].
The combination of macroscale CFD simulation with microscale simulation can be a powerful tool in predicting complex phenomena in multiphase systems [43]. Liu and Schwarz [44,45] proposed an integrated CFD-based scheme for the prediction of bubble–particle collision efficiency in turbulent flow from a multiscale modeling perspective. The proposed model can account for changes at the macroscale in the flotation cell geometry and structure, inlet and exit configurations, impeller structure and tip speed, air nozzle structure and airflow rate, and at the microscale in turbulence and collision mechanisms. Similarly, CFD modeling can be combined with discrete element simulation (DEM) to understand the behavior of individual particles. For example, Lichter et al. [46] combined CFD with DEM to analyze the effect of cell size and inflow rate on the retention time distribution in flotation cells. Ji et al. [47] developed two numerical models to model the multiphase flow in hydrocyclones: one is a combined approach of the VOF model and DEM with the concept of the coarse-grained (CG) particle, which can be applicable to a relatively dilute flow, and the other is a combined approach of the mixture model and DEM model with the CG concept, which can be quantitatively applicable to both dilute and dense flows. Finally, Chu et al. [48] studied the coal-medium flow in a dense medium cyclone using DEM to model the motion of coal particles, while the flow of the medium was modeled using the VOF model.
Modeling of wet grinding, including autogenous grinding, semi-autogenous grinding, ball or stirred mills, has been developed using DEM because it is an adequate method to represent the movement and collision of particles. Essentially, the Newton’s equation of motion is solved together with a collision/contact law to resolve inter-particle forces. Its application has included the design, optimization, and operation of grinding devices. A complete review on DEM application to comminution, including autogenous/semi-autogenous grinding and mills, is available [49]. However, DEM is computationally intensive, which limits the number of particles that can be considered. Therefore, for a large number of small particles, the method may not be appropriate. In addition, the aqueous phase, which is added to improve the solid transportation and suppress the dust, must be considered in the simulation to obtain a realistic or complete description of the behavior of a wet grinding device. The usual approach to predict the transportation of solid particles interacting with the slurry flow is a coupled DEM and smoothed particle hydrodynamics (SPH) method [50]. SPH is a type of particle-based method, known as mesh-free methods, that employ a set of finite numbers of discrete particles to represent the state and evolution of a flow system [51]. This coupled DEM–SPH method has been successfully applied to autogenous grinding [52,53]. Figure 5 shows on example of how DEM and SPH are coupled in this type of simulation. DEM–CFD (e.g., the k–ϵ-turbulence model) methods have also been applied to wet grinding, such as stirred media and planetary ball mills [54]. Similar to DEM–SPH methods, here, CFD takes the fluid flow into account and DEM is used for modeling of the grinding media.
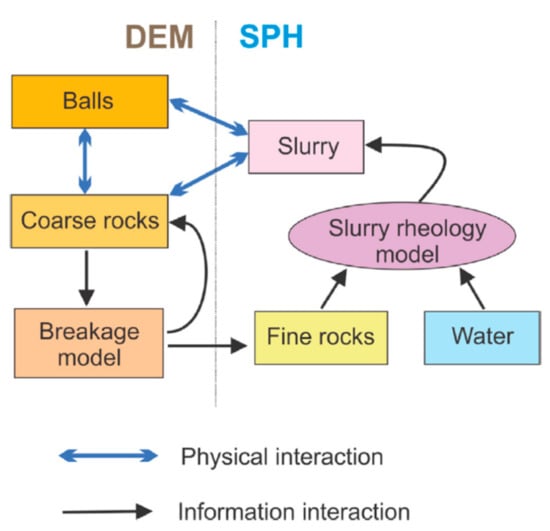
Figure 5.
Example of the physical interactions, the model components, and the data flows in discrete element simulation–smoothed particle hydrodynamics (DEM–SPH) modeling of wet grinding [53].
Since the beginning of numerical modeling in mineral processing, in the past two decades, significant advances have been made to simulate multiphase flow behavior. However, it is still far from complete due to the multiscale nature of the problem, which requires integration of the complex interplay between the molecular level and system hydrodynamics. One of the important challenges is the development of methodologies and theories for an adequate representation of the meso-scales. The meso-scales are important in linking micro and macro behaviors and in showing the complexity and diversity of phenomena that occur [55]. The meso-scales can be decisive in the modeling and understanding of multiphase systems where the behavior of the system is strongly influenced by the phenomena at that level [56]. For example, Figure 6 shows the relationship between macro and micro scales with the meso-scale of bubble behavior in flotation.
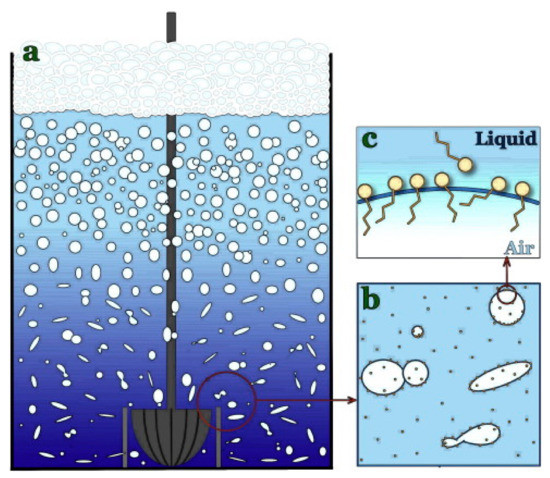
Figure 6.
Relationship between scales in bubble behavior in flotation (a) macro-scale: cell level, (b) meso-scale: bubble coalescence and breakup studies, and (c) micro/nano-scale: molecular interactions [57].
4. Design and Optimization
The development of systematic methods for process design in multiphase mineral processing has been active, but to our knowledge, has still not been applied in the industry. The development of these methods has been motived by the search to increase productivity, reduce costs, reduce the adverse environmental impact of waste, and to develop simpler, more economical processes [58]. In general, there are three methods for process design: heuristic-based methods, hybrid methods, and rigorous methods. The heuristic-based method uses rules-of-thumb to help identify process alternatives. Hybrid methods combine first principles with the insight of the designer to obtain a feasible process design. Rigorous methods use a mathematical model to represent a set of alternatives and an optimization algorithm to search for optimal solutions. As they move from heuristic to rigorous methods, the mathematical complexity of the problem increases, the probability of getting better designs increases, the importance of the designer’s experience decreases, and the design process goes from being closer to art to being closer to a science.
Most of the work published in the literature is related to the design of flotation circuits. Few works have been published based on heuristic design methods [59,60]. Chan and Price [60] presented a method to design a process for non-sharp separations based on heuristics. The process design is built up unit by unit, stopping when further addition does not increase the profit. The method was applied to flotation circuits. Because heuristic design methods do not guarantee the finding of optimal solutions, this approach to solve the design problem has lost interest from the scientific community.
The most important hybrid method for designing mineral processing facilities is linear circuit analysis (LCA). This technique provides fundamental insights into how unit operations interact and respond when arranged in multistage processing circuits [61]. The method, proposed by Meloy [62] and then developed by Meloy, Williams, and Fuerstanou over several years [63,64,65,66], consists of representing the separation yield of a process unit by a transfer function, and then expressing recoveries of the concentrate and tailing as a function of this transfer function. This mass balance approach is extended to the circuit by expressing the global recovery of the circuit as a function of the transfer function of each process unit. Figure 7 shows an example of LCA formulation.
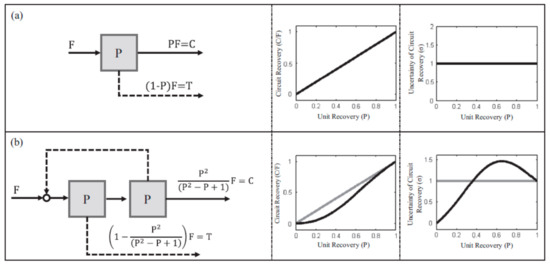
Figure 7.
Linear circuit analysis (LCA) formulation example, including uncertainty analysis: (a) individual unit, (b) two-stage circuit [71].
LCA has successfully been utilized to improve the operating performance of industrial processing circuits including magnetic separators [67] and spirals separators [68,69]. More recently, advanced versions of this tool have also been developed to include techno-economic objective functions [70] and circuit uncertainty analysis [71]—a complete review, written by Noble et al. [61], is available. Despite its applications, LCA has several disadvantages, mainly caused by the common practice of assuming that all transfer functions are equal. This simplification does not allow researchers to examine the whole behavior of a concentration circuit because it reduces a multidimensional function of the transfer functions of all the units to one dimension [72]. For example, differences of up to 10% have been observed in the overall circuit recovery for two- and three-stage circuits in the case of identical and non-identical stage recovery [73].
Rigorous methods are based on optimization procedures. The methodologies consist of developing a superstructure that represents a set of alternatives in which to search for the optimal solution. A mathematical model based on mass balance and kinetics expressions of each operation unit is developed to represent the superstructure, and then, using an objective function, it is solved to obtain the optimal solution. The mathematical model results in a mixed-integer nonlinear programming model (MINLP), which is difficult to solve due to the nonconvex nature. Most of the methodologies proposed are for flotation circuit design, but one methodology has been proposed for a dewatering system [74]. Several reviews on flotation circuit design are available [75,76,77,78,79], and therefore, a brief description is given here. Table 1 shows a list of methodologies that use optimization for the design of flotation circuits. It can be observed that most of the works use few components and/or few process units because the problem is difficult to solve. Also, some simplification of the problem has been applied so that the model is linear programming (LP), nonlinear programming (NLP), or mixed-integer linear programming (MILP). Only in the last few years can it be observed that methodologies are applied to real size plants with at least six species and five process units. The application to real size plants has been possible due to the advances in computer power, optimization algorithm improvements, and the fact that the stage recovery (unit transfer function) uncertainty has a low effect on the optimal circuit structure [80]. By now, this type of methodology can generate a set of optimal alternatives that can be subject to further study by the designer. Also, the case studies analyzed generated new knowledge that could be difficult to obtain from plant experience.

Table 1.
Flotation circuit design methodologies (adapted from Reference [84]) (LP linear programming; NLP nonlinear programming; MILP, mixed-integer linear programming; MINLP, mixed-integer nonlinear programming).
The design of concentration circuits using rigorous methods requires further development to incorporate regrinding and equipment selection, which can affect the circuit performance. A few works have considered regrinding in the design of flotation circuits [81,82,83]; however, they have used simplified models or the grinding stage was not considered in the decision problem. Therefore, strategies to incorporate grinding in the design of these systems must be considered. A major challenge is the modification of the way the design process occurs in the organizations, which is based on designer experience. Consequently, the usefulness of this type of methodology must be highlighted and adapted in the innovation of the mining sector. For example, breakthrough circuit design may not be the best option because of high capex and small research and development activities in the mining industry. Then, in-process changes of the circuit design, where one or two units or structures are changed, may be a better option.
5. Artificial Intelligence (AI) Applied to Multiphase Systems
The term AI appeared in 1955 [98]. AI is a branch of computer science dedicated to the development of computer algorithms to accomplish tasks traditionally associated with human intelligence. In recent years, the interest from the mining industry in utilizing AI techniques in areas such as geology and minerals processing has increased. This trend is repeated in the ambit of scientific research [23,99,100,101]. Among these techniques, soft computing is highlighted, which has been used in the modeling, design, and optimization of mining processes.
Soft computing is defined as the group of methodologies and tools that can assist in the design, development, and operation of intelligent systems that are capable of adaptation, learning, and operating autonomously in an environment of uncertainty and imprecision [102]. Soft computing can be divided into two groups: probability reasoning, and functional approximation and randomized search. The first group, in turn, can be divided into probabilistic models and fuzzy logic. The second group, in turn, can be divided into evolutionary computing (EC), swarm optimization (SO), and machine learning [103,104,105]. The developed tools in each group mentioned earlier are shown in Figure 8. Note that ML includes a broad set of methods used to extract useful models from empirical data. Machine learning tools are focused on endowing programs with the ability to “learn” and adapt [106]. These tools need training algorithms to learn, some of which are shown in Figure 8 (SO and EC). These algorithms, as seen later, can be used for optimizing and designing metallurgical processes [93,97].
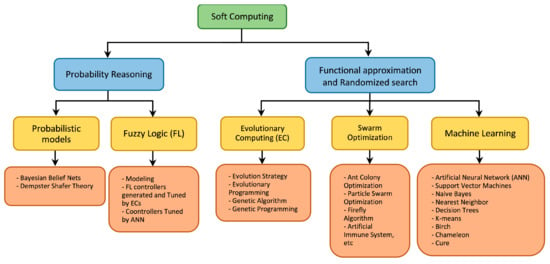
Figure 8.
Methodologies and tools considered in soft computing.
Modeling can be divided into data-driven, fault detection and/or diagnosis, and machine vision. The first considers building models for complementing or replacing physically-based models. The second involves a statistical model based on data that are considered representative of the normal operating condition (NOC) of the process. Any observations that exceed a certain limit in this NOC model are considered as faults [107]. The third considers a type of data-driven modeling that uses images or video, rather than process measurements.
Data-based modeling uses information extracted from experimental, simulated, or industrial data. At an industrial scale, these methods are applied as soft sensors for the prediction of measurements that are difficult to measure. Some applications of these methods include the modeling of metallurgical responses or subprocesses involved in integral processes: grinding [108,109,110,111,112,113,114], thickening [115], flotation [116,117,118,119,120,121], and hydrocyclones [122], among other processes. For example, Estrada-Ruiz and Pérez-Garibay [118] used multilayer perceptron, which is a type of neural network, for estimating the mean bubble diameter and bubble size distribution on the mineralized froth surface. Meanwhile, Jahedsaravani et al. [120] used multilayer perceptron for predicting the copper recovery, copper concentrate grade, mass recovery of the concentrate, and water recovery in the concentrate obtained through batch flotation. Saravani et al. [121] developed a fuzzy model for estimating the performance of an industrial flotation column. Núñez et al. [114] developed a fuzzy model for predicting the future weight of a semi-autogenous grinding (SAG) mill. Artificial neural networks (ANNs), support vector machine (SVM), and fuzzy models substantially reduce the computational cost involved in simulation, and uncertainty and sensitivity analyses [123].
Fault detection is commonly carried out using principal component analysis (PCA) or its extensions/modifications [107], and it has been used in flotation systems [124,125] and milling circuits [126,127]. Fault diagnosis, i.e., the identification of variables associated with faulty conditions, is usually achieved via the use of approaches based on PCA. Some applications of these methods include flotation [128,129,130] and grinding [126,127]. For example, Wakefield et al. [127] simulated a milling circuit for investigating faults related to particle size estimates and mill liners. They applied statistical tools (PCA) for detecting faults, in conjunction with process topology data-driven techniques (Granger causality) for root cause analysis. These authors reported that the statistical monitoring method took slightly longer to detect the mill liner fault, due to the incipient nature of the fault. However, this method is significantly faster than what has been achieved by monitoring only the economic performance of the circuit. The fault diagnosis identified the mill power as the root cause of the fault.
Machine vision is the study of techniques for extracting meaningful information from high-dimensional images, and it has been used almost exclusively in flotation [131,132,133]. Developed models were used for classifying flotation froth images, and commonly, these were based on SVM, ANNs, and decision trees [23]. For example, Zhu and Yu [132] proposed an ANN model based on features extracted from digital froth images at a hematite flotation plant. This model was used to help identify flotation conditions and to adjust the reagent’s quantity. Zhao et al. [134] estimated the bubble size distribution using image processing techniques based on decision trees.
Many of the developed models were used to optimize the process, for example, Curilem et al. [113] used ANNs and SVM models for online optimization of the energy consumption in SAG. Zhu and Yu [132] used the developed model for optimizing the reagent’s dosage. Saravani et al. [121] used a fuzzy model for optimizing and stabilizing the industrial flotation column. Note that ANN and SVM, among other tools included in machine learning, require training algorithms, which can be divided into exact and approximate algorithms. This last group considers genetic algorithms, particles swarm optimization, and differential evolution, among others, including their hybridizations. According to the related literature, these algorithms have been used for tuning the parameters of the ANN, SVM, and fuzzy models [135], and for minimizing/maximizing the objective function in optimization problems and process design.
Process optimization via approximate algorithms has been reported by several authors, for example, Tandon et al. [136] developed an ANN for predicting cutting forces in a milling process, which, in turn, was used to optimize both feed and speed through particle swarm optimization. Massinaei et al. [137] used ANN and gravitational search algorithms to model and optimize the metallurgical performance of a flotation column. Shunmugam et al. [138] used genetic algorithms to optimize the minimum production cost in a face milling operation. Here, the trend is using hybrid algorithms to explore the search space efficiently and find a global optimal solution [101,139,140].
Process design via approximate algorithms has been performed almost exclusively in froth flotation, specifically in flotation circuit design. The latter considers three ingredients: first, a superstructure for representing the alternatives for design, second, a mathematical model for modeling the alternatives for design, included goals, constraints, and objective function, and third, an optimization algorithm [76]. Lucay et al. [97] considered a stage superstructure composed of five stages of flotation, which were modeled using a bank model. Here, the single-objective function was of the economic type, and the Tabu-Search algorithm was used for solving the design problem. Hu et al. [93] used a superstructure of eight cells, which were modeled using a cell model. They used a single-objective function of the economic type and genetic algorithm for solving the problem. Ghobahi et al. [91] used genetic algorithms, a superstructure of stages, and single-objective functions of the technical type. Pirouzan et al. [95] also applied genetic algorithms but considered a multi-objective function of the technical type. Due to the multi-objective nature of the problem, the authors used the Pareto method to obtain a set of solutions. The superstructure used involved three and four flotation stages, out of all possible combinations, which were modeled using a bank model. These authors applied their methodology to improve the design of a flotation circuit processing coal. Figure 9a shows the initial flotation circuit design, and Figure 9b shows the new design of the flotation circuit. They reported that the new design provided a recovery of ash that was 6.7% higher than that of the initial design. In addition, to consider designs of four stages would increase the recovery by 3.8%, and the ash grade would be 11.2%, which is within the acceptable quality level. Here, the common factor is the use of objective functions of the economic type because objective technical functions are difficult to define, including approaches using the Pareto method to address multi-objective problems [76].
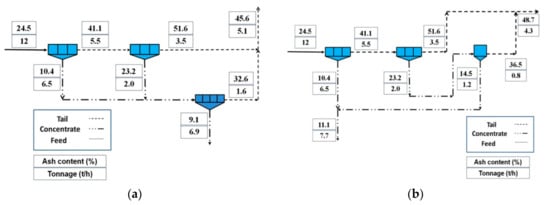
Figure 9.
Comparison of flotation circuit design: (a) design and ash contents of the initial circuit, (b) design and ash contents of the new circuit, adapted from Pirouzan et al. [95].
Obtaining data can be very expensive, so one challenge in data-based modeling is developing methodologies that allow for the attainment of robust models using a small amount of data. In addition, at an industrial scale, the data frequently exhibit as being high-dimensional, non-normally distributed, and nonstationary, with nonlinear relationships, including noise and outliers, which makes it even more difficult to develop a model capturing the true relationships between the input variables. These comments are also valid for fault detection and diagnosis and for machine vision.
6. Response Surface Methodology (RSM)
RSM is used for modeling and optimization processes. RSM involves the following three steps [141]: first, a design of experiments (DoE) for driving the experiments, second, the response surface is modeled based on empirical models, and third, the optimization of the responses is carried out using the empirical model. According to Garud et al. [142], DoE can be divided into broad families, i.e., classical and modern design of experiments. The first is based on laboratory experiments. This includes approaches such as full- and half-factorial design, central composite design, Plackett–Burman design, and Box–Behnken design, among others [143]. The second is based on computer simulations. This includes approaches such as full-factorial design [144], fractional factorial design, central composite design [145], Latin hypercube sampling [146], and symmetric Latin hypercube sampling [147], among others.
One advantage of the classical RSM is that it needs a smaller number of experiments, which means it is cheaper and requires less time. These characteristics explain the large number of applications, including flotation [148,149], grinding [150,151,152], and thickening [153], among other processes.
The related literature shows that classical RSM is commonly applied using a second-order polynomial as a prediction model [143]. For example, optimal conditions of rotation speed, solid concentration, and grinding time were obtained for wet grinding in a ball mill using central composite design with a second-order polynomial [152]. In fact, an excellent determination coefficient (R2 = 0.9989) was obtained, which indicates a good agreement with experimental values. Similar good results were observed using a Box–Bhenken design in copper sulphide ore grinding in a ball mill [150]. However, several processes do not follow a second-order polynomial behavior and, consequently, a poor adjustment of the model is obtained (see Figure 10). The immediate consequence is incorrect optimization. The related literature proposes different approaches in the modeling of surface response instead of polynomial models. For example, regression of Gaussian processes has been proposed, since these models can model complex functions [141,154]. Also, the use of SVM regression as a prediction model has been proposed [155]. However, the most popular alternative has been ANNs [156].
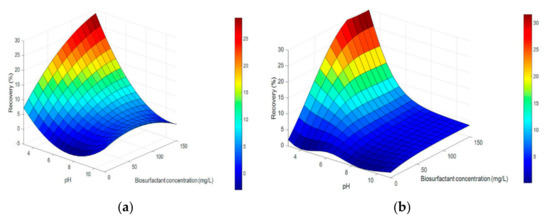
Figure 10.
(a) Quartz recovery using a second-order polynomial as a prediction model (R2 = 0.931), (b) quartz recovery using an artificial neural network as a prediction model (R2 = 0.982) [156].
On the other hand, according to Garud et al. [142], the chemical and process system engineering community has exclusively employed modern DoE techniques in the context of surrogate approximation and surrogate-assisted optimization. Modern RSM is also called response surface surrogate (RSS). Surrogate modeling techniques are grouped by some authors into two broad families, which are statistical or empirical data-driven models that emulate the high-fidelity model response, and lower-fidelity physically-based surrogates, which are simplified models of the original system [123].
Data-driven surrogates involve empirical approximations of the complex model output calibrated in a set of inputs and outputs of the complex model. Some approximate techniques proposed in the related literature are: polynomial, kriging (Gaussian process), k nearest neighbors, proper orthogonal decomposition, radial basis functions, support vector machines, multivariate adaptive regression splines, high-dimensional model representation, treed Gaussian processes, Gaussian emulator, smoothing splines analysis of variance (ANOVA) models, polynomial chaos expansions, genetic programming, Bayesian networks, and ANNs [123,157].
This approach has been applied in flotation [158], thickening [159,160], and comminution [161], among others. Usually, these works are based on CFD models, which consider several complex phenomena involved in the studied process. However, these models are computationally expensive to evaluate. This limits their application in continuous process modeling for dynamic simulation, optimization algorithms, and control purposes. Surrogate model techniques can help to overcome this disadvantage. For example, Rabhi et al. [158] developed surrogate models via a hierarchical polynomial using a dataset obtained through simulations of a CFD model of froth flotation. The surrogate model was used for estimating the bubble–particle collision probability (see Figure 11a). These authors reported that the surrogate models developed were highly accurate with a negligible CPU (central processing unit) time. This accuracy increases with an increasing number of interpolation points (see Figure 11b). Stephens et al. [159] developed surrogate models of a CDF model of flocculant adsorption in an industrial thickener because the latter is impractical for performing sensitivity analysis (SA). These authors used radial basis functions, ANNs, and least squares-support vector machines as surrogate models, and they reported that the radial angle between the flocculant sparge and feed pipe, and the distance from the feed well to the flocculant sparge, are the most important parameters in flocculant loss (output variable).
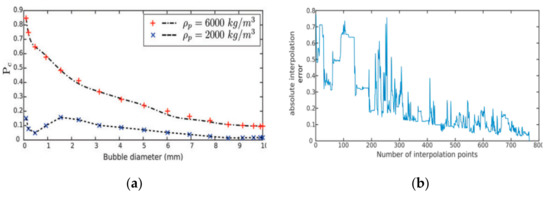
Figure 11.
(a) Bubble–particle collision probability, Pc, versus bubble diameter, (b) prediction absolute error versus number of interpolation points [158].
7. Uncertainty and Sensitivity Analyses
UA corresponds to determining the uncertainty in the output variables as a result of the uncertainty in the input variables. For performing UA, the related literature proposed several theories, such as fuzzy theory and probability theory, among other theories [162]. Meanwhile, SA can be defined as the study of how the uncertainty in the output of a model can be apportioned to different sources of uncertainty in the model input. There are two types of SA: local sensitivity analysis (LSA) and GSA. The second is the most robust because it considers the full range of uncertainty of the input variables.
According to Saltelli et al. [163], SA is an ingredient of modeling. These authors suggested that SA could considerably assist in the use of models, by providing objective criteria of judgment for different phases of the model-building process: model identification and discrimination, model calibration, and model corroboration. In line with this, Lane and Ryan [164] indicate that a well-developed model should include model verification, validation, and uncertainty quantification. Model verification is used for ensuring that the model is behaving properly, for example, the model can be compared with other models or with known analytical solutions. Model validation involves the comparison with experimental data. Uncertainty quantification (UQ) studies the effect of uncertainties on the model. UQ can be performed using uncertainty and sensitivity analyses. These provide a general overview of the effect of uncertainties. Typically, model verification, calibration, and corroboration are not applied in mineral processing, but they must be considered in future model development. The interested readers can see the model developed by Mellado et al. [165] for heap leaching, which has been validated, verified, and corroborated [166,167,168].
UA and GSA have also been used to identify the operational conditions of a mill system under uncertainty. Lucay et al. [162] applied UA for studying the effect of the distribution and magnitude of the uncertainties of input variables in the responses of the grinding process (see Figure 12a). GSA was utilized to identify influential input variables. Then, the regionalization of the influential input variables was applied to identify the operational regions (see Figure 12b). In other words, the control of the uncertainty of the significant input variables allows for the control of uncertainty in the mill system. GSA has also been applied in the design or optimization of flotation circuits under uncertainty [169,170,171,172]. Sepúlveda et al. [169] proposed a methodology for the conceptual design of flotation circuits. The methodology involved three decision levels: level I—the definition of the analysis of the problem, level II—the synthesis and screening of alternatives, and level III—the final design. This last level considers the identification of gaps and opportunities for improvement, among other aspects. Identification was performed using LSA and GSA. Figure 13a shows the flotation circuits designed using this methodology, and Figure 13b shows how the uncertainty on the recovery of each species in the flotation stages affects their global recovery. These authors reported that if the target is increasing the recovery of chalcopyrite, it is recommended that modifications should be made in cleaner 3 (see Figure 13b) because changes at this stage have a significant effect on the global recovery of chalcopyrite and little effect on the global recovery of other species (higher Sobol index values).
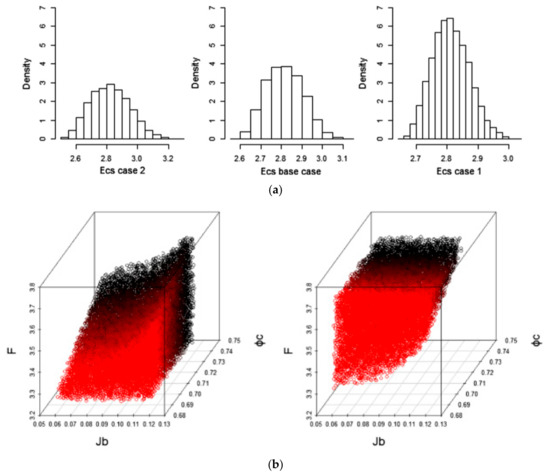
Figure 12.
(a) The comminution-specific energy histogram of a SAG (semi-autogenous grinding) mill under three uncertainty magnitudes. (b) The regionalization of fresh ore flux fed (F), percentage of mill volume occupied by steel balls (Jb), and percentage of critical speed (ϕc) [162].
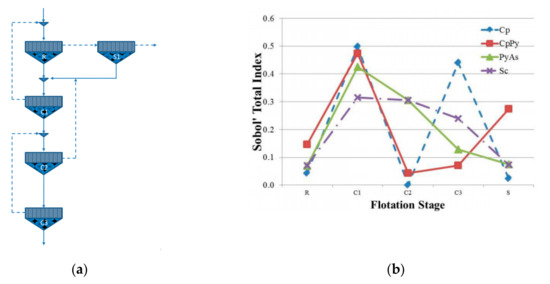
Figure 13.
(a) Designed circuit using the methodology. (b) Sobol total index for each stage and for chalcopyrite (Cp), chalcopyrite–pyrite (CpPy), pyrite–arsenopyrite, and silica (Sc) [169].
Here, the trend is using methods of GSA based on the decomposition of variance due to its versatility [173]. However, this last approach is computationally expensive. This drawback has been overcome in other engineering areas via the development of metamodels or surrogate models [123,157,174], such as ANNs. This approach has not been applied to multiphase mineral processing systems; however, we estimate that this will change due to metamodels that are not only more efficient for performing GSA and UA, but also for carrying complementary analyses, such as data classification.
8. Discussion and Conclusions
Experimentally based research is time demanding and costly, but necessary in multiphase mineral processing systems. These systems include operations and phenomena such as flotation, hydroclyclone, grinding, and magnetic separation. The need for models for these systems is not only necessary to reduce the cost and time associated with research activities but also, because if we do not have a model, we do not understand the system, and if we do not understand the system, we cannot modify it to obtain the desired conditions. The models and tools available to study multiphase systems in mineral processing depend on the length and time scales of the phenomenon that needs to be analyzed. Important advances have been developed in different tools, such as MD at the molecular level, CFD at the fluid level, and mathematical programming at the plant level. RSM can be applied to all levels to model experimental data and numerical experiments. UA and GSA are the most powerful tools to analyze uncertainty. AI can have applications at all levels and, in the future, new applications and developments are expected.
MD has recently emerged in the study of multiphase systems in mineral processing. New studies and applications will undoubtedly show the benefits of understanding phenomena at the molecular level in these systems. There are other challenges that have not been analyzed in detail in the literature, such as integration in multiscale modeling, design, and optimization. Some advances have been observed, for example, the integration of CFD modeling with DEM to integrate particle and fluid phenomena. However, new research on meso-scale modeling integrated with micro- and macro-scale modeling is essential to better describe and optimize multiphase systems. Also, some tools have been combined to increase the capabilities of these methods, for example, ANNs have been combined with RSM to be able to model complex behavior. Examples in design are the integration of process design with control design and molecular modeling with process design. The simultaneous design of process/control or process/molecular can, as a result, produce a better overall design. For example, explicit process control structures can be included in the process design problem, which allows for consideration of the operability in early stages of the design process [175]. A good understanding of molecular phenomena can aid the consideration of the properties in process design, for example, deciding the best location for stream recycling not only based on mineral concentrations, but also considering the final result in properties (such as pH, chemical potential, dissolved oxygen). A technique for property integration based on property clustering can be used for this purpose [176,177,178]. To achieve these objectives, more research and development efforts in this area are necessary.
Despite the advantages of the use of optimal design tools to identify better process structures, they have not been used in practice in mineral processing, at least to the authors’ knowledge. Therefore, the usefulness of this type of methodology must be highlighted and adapted in the innovation of the mining sector. In-process changes of the circuit design, where one or two units or structures are changed, can be explored for this purpose.
Author Contributions
Conceptualization, L.A.C.; methodology and review development, L.A.C., F.A.L. and Y.L.B.; writing—original draft preparation, L.A.C., F.A.L. and Y.L.B.; writing—review and editing, L.A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by CONICYT, PIA program grant number ACM 170005 and Fondecyt program grant number 1180826.
Acknowledgments
The authors thank financial support from Chilean National Commission for Science and Technology, CONICYT, through PIA program grant number ACM 170005 and Fondecyt program grant number 1180826. L.A.C. Thanks the supported of MINEDUCUA project, code ANT1856.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Grossmann, I.E.; Westerberg, A.W. Research challenges in process systems engineering. AIChE J. 2000, 46, 1700–1703. [Google Scholar] [CrossRef]
- Cygan, R.T. Molecular Modeling in Mineralogy and Geochemistry. Rev. Mineral. Geochem. 2010, 42, 1–35. [Google Scholar] [CrossRef]
- Kirkpatrick, R.J.; Kalinichev, A.G.; Bowers, G.M.; Yazaydin, A.Ö.; Krishnan, M.; Saharay, M.; Morrow, C.P. Review. NMR and computational molecular modeling studies of mineral surfaces and interlayer galleries: A review. Am. Mineral. 2015, 100, 1341–1354. [Google Scholar] [CrossRef]
- De Villiers, J.P.R. Minerals Processing in South Africa: Materials Modelling Opportunities. Mol. Simul. 1999, 22, 81–90. [Google Scholar] [CrossRef]
- Creton, B.; Nieto-Draghi, C.; Pannacci, N. Prediction of Surfactants’ Properties using Multiscale Molecular Modeling Tools: A Review. Oil Gas Sci. Technol. 2012, 67, 969–982. [Google Scholar] [CrossRef]
- Kirkpatrick, R.J.; Kalinichev, A.G.; Wang, J. Molecular dynamics modelling of hydrated mineral interlayers and surfaces: Structure and dynamics. Mineral. Mag. 2005, 69, 289–308. [Google Scholar] [CrossRef]
- Filho, L.S.L.; Seidl, P.R.; Correia, J.C.G.; Cerqueira, L.A.C.K. Molecular modeling of Reagents for flotation process. Miner. Eng. 2000, 13, 1495–1503. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Yan, K. Adsorption of collectors on model surface of Wiser bituminous coal: A molecular dynamics simulation study. Miner. Eng. 2015, 79, 31–39. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Xu, H.; Zhuo, Q.; Sun, X. Adsorption Behavior of Methyl Laurate and Dodecane on the Sub-Bituminous Coal Surface: Molecular Dynamics Simulation and Experimental Study. Minerals 2019, 9, 30. [Google Scholar] [CrossRef]
- Nan, N.; Zhu, Y.; Han, Y.; Liu, J. Molecular Modeling of Interactions between N-(Carboxymethyl)-N-tetradecylglycine and Fluorapatite. Minerals 2019, 9, 278. [Google Scholar] [CrossRef]
- Ma, X.; Fan, Y.; Dong, X.; Chen, R.; Li, H.; Sun, D.; Yao, S. Impact of Clay Minerals on the Dewatering of Coal Slurry: An Experimental and Molecular-Simulation Study. Minerals 2018, 8, 400. [Google Scholar] [CrossRef]
- Wang, Q.; Manzano, H.; López-Arbeloa, I.; Shen, X. Water Adsorption on the β-Dicalcium Silicate Surface from DFT Simulations. Minerals 2018, 8, 386. [Google Scholar] [CrossRef]
- Kubicki, J.; Watts, H. Quantum Mechanical Modeling of the Vibrational Spectra of Minerals with a Focus on Clays. Minerals 2019, 9, 141. [Google Scholar] [CrossRef]
- Wang, Q.; Fang, Q.; Li, J.; Tian, Y.; Liu, Y. Subsurface damage and material removal of Al–Si bilayers under high-speed grinding using molecular dynamics (MD) simulation. Appl. Phys. A 2019, 125, 514. [Google Scholar] [CrossRef]
- Ren, J.; Hao, M.; Lv, M.; Wang, S.; Zhu, B. Molecular dynamics research on ultra-high-speed grinding mechanism of monocrystalline nickel. Appl. Surf. Sci. 2018, 455, 629–634. [Google Scholar] [CrossRef]
- Safari, M.; Deglon, D. An attachment-detachment kinetic model for the effect of energy input on flotation. Miner. Eng. 2018, 117, 8–13. [Google Scholar] [CrossRef]
- Gorain, B.K.; Franzidis, J.-P.; Manlapig, E.V. The empirical prediction of bubble surface area flux in mechanical flotation cells from cell design and operating data. Miner. Eng. 1999, 12, 309–322. [Google Scholar] [CrossRef]
- Wang, L.; Runge, K.; Peng, Y.; Vos, C. An empirical model for the degree of entrainment in froth flotation based on particle size and density. Miner. Eng. 2016, 98, 187–193. [Google Scholar] [CrossRef]
- Savassi, O.N.; Alexander, D.J.; Franzidis, J.P.; Manlapig, E.V. An empirical model for entrainment in industrial flotation plants. Miner. Eng. 1998, 11, 243–256. [Google Scholar] [CrossRef]
- Kraipech, W.; Chen, W.; Dyakowski, T.; Nowakowski, A. The performance of the empirical models on industrial hydrocyclone design. Int. J. Miner. Process. 2006, 80, 100–115. [Google Scholar] [CrossRef]
- Gharai, M.; Venugopal, R. Modeling of flotation process—An overview of different approaches. Miner. Process. Extr. Metall. Rev. 2015, 37, 120–133. [Google Scholar] [CrossRef]
- Jovanović, I.; Miljanović, I. Modelling of Flotation Processes by Classical Mathematical Met—A Review. Arch. Min. Sci. 2015, 60, 905–919. [Google Scholar]
- Jovanović, I.; Miljanović, I.; Jovanović, T. Soft computing-based modeling of flotation processes—A review. Miner. Eng. 2015, 84, 34–63. [Google Scholar] [CrossRef]
- Tavares, L.M. A Review of Advanced Ball Mill Modelling. KONA Powder Part. J. 2017, 34, 106–124. [Google Scholar] [CrossRef]
- Narasimha, M.; Brennan, M.; Holtham, P.N. A Review of CFD Modelling for Performance Predictions of Hydrocyclone. Eng. Appl. Comput. Fluid Mech. 2007, 1, 109–125. [Google Scholar] [CrossRef]
- Wang, G.; Nguyen, A.V.; Mitra, S.; Joshi, J.B.; Jameson, G.J.; Evans, G.M. A review of the mechanisms and models of bubble-particle detachment in froth flotation. Sep. Purif. Technol. 2016, 170, 155–172. [Google Scholar] [CrossRef]
- Wang, L.; Peng, Y.; Runge, K.; Bradshaw, D. A review of entrainment: Mechanisms, contributing factors and modelling in flotation. Miner. Eng. 2015, 70, 77–91. [Google Scholar] [CrossRef]
- Zheng, X.; Franzidis, J.P.; Johnson, N.W. An evaluation of different models of water recovery in flotation. Miner. Eng. 2006, 19, 871–882. [Google Scholar] [CrossRef]
- Andersson, B.; Andersson, R.; Hakansson, L.; Mortensen, M.; Sudiyo, R.; Van Wachem, B. Computational Fluid Dynamics for Engineers; Cambridge University Press: Cambridge, UK, 2012; ISBN 978-1-107-01895-2. [Google Scholar]
- Jayanti, S. Computational Fluid Dynamics for Engineers and Scientists; Cambridge University Press: Cambridge, UK, 2018; ISBN 9789402412178. [Google Scholar]
- Koh, P.T.L.; Schwarz, M.P. CFD modelling of bubble—Particle attachments in flotation cells. Miner. Eng. 2006, 19, 619–626. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, J.; Chen, Q.; Shi, X.; Gou, Y. CFD Simulation of Pipeline Transport Properties of Mine Tailings Three-Phase Foam Slurry Backfill. Minerals 2017, 7, 149. [Google Scholar] [CrossRef]
- Narasimha, M.; Brennan, M.S.; Holtham, P.N. CFD modeling of hydrocyclones: Prediction of particle size segregation. Miner. Eng. 2012, 39, 173–183. [Google Scholar] [CrossRef]
- Johansson, R.; Evertsson, M. CFD simulation of a centrifugal air classifier used in the aggregate industry. Miner. Eng. 2014, 63, 149–156. [Google Scholar] [CrossRef]
- Mohanty, S.; Das, B.; Mishra, B.K. A preliminary investigation into magnetic separation process using CFD. Miner. Eng. 2011, 24, 1651–1657. [Google Scholar] [CrossRef]
- Weerasekara, N.S.; Powell, M.S. Performance characterisation of AG/SAG mill pulp lifters using CFD techniques. Miner. Eng. 2014, 63, 118–124. [Google Scholar] [CrossRef]
- Wang, G.; Ge, L.; Mitra, S.; Evans, G.M.; Joshi, J.B.; Chen, S. A review of CFD modelling studies on the flotation process. Miner. Eng. 2018, 127, 153–177. [Google Scholar] [CrossRef]
- Farzanegan, A.; Khorasanizadeh, N.; Sheikhzadeh, G.A.; Khorasanizadeh, H. Laboratory and CFD investigations of the two-phase flow behavior in flotation columns equipped with vertical baffle. Int. J. Miner. Process. 2017, 166, 79–88. [Google Scholar] [CrossRef]
- Sarhan, A.R.; Naser, J.; Brooks, G. CFD simulation on influence of suspended solid particles on bubbles’ coalescence rate in flotation cell. Int. J. Miner. Process. 2016, 146, 54–64. [Google Scholar] [CrossRef]
- Lakghomi, B.; Lawryshyn, Y.; Hofmann, R. A model of particle removal in a dissolved air flotation tank: Importance of stratified flow and bubble size. Water Res. 2015, 68, 262–272. [Google Scholar] [CrossRef]
- Xia, Y.K.; Peng, F.F.; Wolfe, E. CFD simulation of alleviation of fluid back mixing by baffles in bubble column. Miner. Eng. 2006, 19, 925–937. [Google Scholar] [CrossRef]
- Bondelind, M.; Sasic, S.; Kostoglou, M.; Bergdahl, L.; Pettersson, T.J.R. Single- and two-phase numerical models of Dissolved Air Flotation: Comparison of 2D and 3D simulations. Colloids Surf. A Physicochem. Eng. Asp. 2010, 365, 137–144. [Google Scholar] [CrossRef]
- Schwarz, M.P.; Koh, P.T.L.; Verrelli, D.I.; Feng, Y. Sequential multi-scale modelling of mineral processing operations, with application to flotation cells. Miner. Eng. 2016, 90, 2–16. [Google Scholar] [CrossRef]
- Liu, T.Y.; Schwarz, M.P. CFD-based modelling of bubble-particle collision efficiency with mobile bubble surface in a turbulent environment. Int. J. Miner. Process. 2009, 90, 45–55. [Google Scholar] [CrossRef]
- Liu, T.Y.; Schwarz, M.P. CFD-based multiscale modelling of bubble–particle collision efficiency in a turbulent flotation cell. Chem. Eng. Sci. 2009, 64, 5287–5301. [Google Scholar] [CrossRef]
- Lichter, J.; Potapov, A.; Peaker, R. The use of computational fluid dynamics and discrete element modeling to understand the effect of cell size and inflow rate on flotation bank retention time distribution and mechanism performance. In Proceedings of the 39th Annual Canadian Mineral Processors Operators Conference, Ottawa, ON, Canada, 23–25 January 2007. [Google Scholar]
- Ji, L.; Chu, K.; Kuang, S.; Chen, J.; Yu, A. Modeling the Multiphase Flow in Hydrocyclones Using the Coarse-Grained Volume of Fluid—Discrete Element Method and Mixture-Discrete Element Method Approaches. Ind. Eng. Chem. Res. 2018, 57, 9641–9655. [Google Scholar] [CrossRef]
- Chu, K.W.; Wang, B.; Yu, A.B.; Vince, A.; Barnett, G.D.; Barnett, P.J. CFD–DEM study of the effect of particle density distribution on the multiphase flow and performance of dense medium cyclone. Miner. Eng. 2009, 22, 893–909. [Google Scholar] [CrossRef]
- Weerasekara, N.S.; Powell, M.S.; Cleary, P.W.; Tavares, L.M.; Evertsson, M.; Morrison, R.D.; Quist, J.; Carvalho, R.M. The contribution of DEM to the science of comminution. Powder Technol. 2013, 248, 3–24. [Google Scholar] [CrossRef]
- Cleary, P.W. Prediction of coupled particle and fluid flows using DEM and SPH. Miner. Eng. 2015, 73, 85–99. [Google Scholar] [CrossRef]
- Ye, T.; Li, Y.A. Comparative Review of Smoothed Particle Hydrodynamics, Dissipative Particle Dynamics and Smoothed Dissipative Particle Dynamics. Int. J. Comput. Methods 2018, 15, 1850083. [Google Scholar] [CrossRef]
- Cleary, P.W.; Sinnott, M.; Morrison, R. Prediction of slurry transport in SAG mills using SPH fluid flow in a dynamic DEM based porous media. Miner. Eng. 2006, 19, 1517–1527. [Google Scholar] [CrossRef]
- Cleary, P.W.; Delaney, G.W.; Sinnott, M.D.; Morrison, R.D. Inclusion of incremental damage breakage of particles and slurry rheology into a particle scale multiphase model of a SAG mill. Miner. Eng. 2018, 128, 92–105. [Google Scholar] [CrossRef]
- Beinert, S.; Fragnière, G.; Schilde, C.; Kwade, A. Analysis and modelling of bead contacts in wet-operating stirred media and planetary ball mills with CFD–DEM simulations. Chem. Eng. Sci. 2015, 134, 648–662. [Google Scholar] [CrossRef]
- Li, J.; Ge, W.; Wang, W.; Yang, N. Focusing on the meso-scales of multi-scale phenomena—In search for a new paradigm in chemical engineering. Particuology 2010, 8, 634–639. [Google Scholar] [CrossRef]
- Li, J.; Kwauk, M. Particle-Fluid Two-Phase Flow—The Energy-Minimization Multi-Scale Method; Metallurgical Industry Press: Beijing, China, 1994. [Google Scholar]
- Jávor, Z.; Schreithofer, N.; Heiskanen, K. Multi-scale analysis of the effect of surfactants on bubble properties. Miner. Eng. 2016, 99, 170–178. [Google Scholar] [CrossRef]
- Cisternas, L.A. On the synthesis of inorganic chemical and metallurgical processes, review and extension. Miner. Eng. 1999, 12, 15–41. [Google Scholar] [CrossRef]
- Loveday, B.K.; Brouckaert, C.J. An analysis of flotation circuit design principles. Chem. Eng. J. Biochem. Eng. J. 1995, 59, 15–21. [Google Scholar] [CrossRef]
- Chan, W.K.; Prince, R.G.H. Heuristic evolutionary synthesis with non-sharp separators. Comput. Chem. Eng. 1989, 13, 1207–1219. [Google Scholar] [CrossRef]
- Noble, A.; Luttrell, G.H.; Amini, S.H. Linear Circuit Analysis: A Tool for Addressing Challenges and Identifying Opportunities in Process Circuit Design. Min. Metall. Explor. 2019, 36, 159–171. [Google Scholar] [CrossRef]
- Meloy, T.P. Analysis and optimization of mineral processing and coal-cleaning circuits—Circuit analysis. Int. J. Miner. Process. 1983, 10, 61–80. [Google Scholar] [CrossRef]
- Williams, M.C.; Meloy, T.P. Dynamic model of flotation cell banks—Circuit analysis. Int. J. Miner. Process. 1983, 10, 141–160. [Google Scholar] [CrossRef]
- Williams, M.C.; Fuerstenau, D.W.; Meloy, T.P. Circuit analysis—General product equations for multifeed, multistage circuits containing variable selectivity functions. Int. J. Miner. Process. 1986, 17, 99–111. [Google Scholar] [CrossRef]
- Williams, M.C.; Meloy, T.P. Feasible designs for separation networks: A selection technique. Int. J. Miner. Process. 1991, 32, 161–174. [Google Scholar] [CrossRef]
- Williams, M.C.; Fuerstenau, D.W.; Meloy, T.P. A graph-theoretic approach to process plant design. Int. J. Miner. Process. 1992, 36, 1–8. [Google Scholar] [CrossRef]
- Luttrell, G.H.; Kohmuench, J.; Mankosa, M. Optimization of magnetic separator circuit configurations. In Proceedings of the SME Annual Conference and Expo, Englewood, CO, USA, 23–25 February 2004. [Google Scholar]
- Luttrell, G.H.; Kohmuench, J.N.; Stanley, F.A.L.; Trump, G.D. Improving spiral performance using circuit analysis. Miner. Metall. Process. 1998, 15, 16–21. [Google Scholar] [CrossRef]
- Mckeon, T.; Luttrel, G.H. Optimization of multistage circuits for gravity concentration of heavy mineral sands. Miner. Metall. Process. 2012, 29, 1–5. [Google Scholar] [CrossRef]
- Noble, A.; Luttrell, G.H. Micro-pricing optimization: Value based partition curve analysis with applications to coal separation. In Proceedings of the 2015 SME Annual Conference and Expo and CMA 117th National Western Mining Conference—Mining: Navigating the Global Waters, Denver, CO, USA, 15–18 February 2015. [Google Scholar]
- Amini, S.H.; Noble, A. Application of linear circuit analysis in the evaluation of mineral processing circuit design under uncertainty. Miner. Eng. 2017, 102, 18–29. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Acosta-Flores, R.; Gálvez, E.D. Some Limitations and Disadvantages of Linear Circuit Analysis. In Proceedings of the 7th International Computational Modelling Symposium (Computational Modelling ’19, Falmouth, UK, 11–12 June 2019. [Google Scholar]
- Radmehr, V.; Shafaei, S.; Noaparast, M.; Abdollahi, H. Optimizing Flotation Circuit Recovery by Effective Stage Arrangements: A Case Study. Minerals 2018, 8, 417. [Google Scholar] [CrossRef]
- Cruz, R.; Cisternas, L.A.; Gálvez, E.D. Optimal Design of a Solid-Liquid Separation System. Comput. Aided Chem. Eng. 2013, 32, 907–912. [Google Scholar]
- Mehrotra, S.P. Design of optimal flotation circuits—A review. Miner. Metall. Process. 1988, 5, 142–152. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Lucay, F.A.; Acosta-Flores, R.; Gálvez, E.D. A quasi-review of conceptual flotation design methods based on computational optimization. Miner. Eng. 2018, 117. [Google Scholar] [CrossRef]
- Mendez, D.A.; Gálvez, E.D.; Cisternas, L.A. State of the art in the conceptual design of flotation circuits. Int. J. Miner. Process. 2009, 90, 1–15. [Google Scholar] [CrossRef]
- Saito, F.; Baron, M.; Dodds, J.; Muramatsu, A. Morphology Control of Materials and Nanoparticles: Chapiter I and II; Waseda, Y., Muramatsu, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 978-3-642-05671-0 (Print) 978-3-662-08863-0 (Online). [Google Scholar]
- Yingling, J.C. Parameter and configuration optimization of flotation circuits, part I. A review of prior work. Int. J. Miner. Process. 1993, 38, 21–40. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Jamett, N.; Gálvez, E.D. Approximate recovery values for each stage are sufficient to select the concentration circuit structures. Miner. Eng. 2015, 83, 175–184. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Méndez, D.A.; Gálvez, E.D.; Jorquera, R.E. A MILP model for design of flotation circuits with bank/column and regrind/no regrind selection. Int. J. Miner. Process. 2006, 79, 253–263. [Google Scholar] [CrossRef]
- Méndez, D.A.; Gálvez, E.D.; Cisternas, L.A. Modeling of grinding and classification circuits as applied to the design of flotation processes. Comput. Chem. Eng. 2009, 33, 97–111. [Google Scholar] [CrossRef]
- Schena, G.D.; Zanin, M.; Chiarandini, A. Procedures for the automatic design of flotation networks. Int. J. Miner. Process. 1997, 52, 137–160. [Google Scholar] [CrossRef]
- Acosta-Flores, R.; Lucay, F.A.; Cisternas, L.A.; Gálvez, E.D. Two phases optimization methodology for the design of mineral flotation plants including multi-species, bank or cell models. Miner. Met. Process. J. 2018, 35, 24–34. [Google Scholar]
- Mehrotra, S.P.; Kapur, P.C. Optimal-Suboptimal Synthesis and Design of Flotation Circuits. Sep. Sci. 1974, 9, 167–184. [Google Scholar] [CrossRef]
- Reuter, M.A.; van Deventer, J.S.J.; Green, J.C.A.; Sinclair, M. Optimal design of mineral separation circuits by use of linear programming. Chem. Eng. Sci. 1988, 43, 1039–1049. [Google Scholar] [CrossRef]
- Reuter, M.A.; Van Deventer, J.S.J. The use of linear programming in the optimal design of flotation circuits incorporating regrind mills. Int. J. Miner. Process. 1990, 28, 15–43. [Google Scholar] [CrossRef]
- Schena, G.; Villeneuve, J.; Noël, Y. A method for a financially efficient design of cell-based flotation circuits. Int. J. Miner. Process. 1996, 46, 1–20. [Google Scholar] [CrossRef]
- Guria, C.; Verma, M.; Mehrotra, S.P.; Gupta, S.K. Multi-objective optimal synthesis and design of froth flotation circuits for mineral processing, using the jumping gene adaptation of genetic algorithm. Ind. Eng. Chem. Res. 2005, 44, 2621–2633. [Google Scholar] [CrossRef]
- Guria, C.; Verma, M.; Gupta, S.K.; Mehrotra, S.P. Simultaneous optimization of the performance of flotation circuits and their simplification using the jumping gene adaptations of genetic algorithm. Int. J. Miner. Process. 2005, 77, 165–185. [Google Scholar] [CrossRef]
- Ghobadi, P.; Yahyaei, M.; Banisi, S. Optimization of the performance of flotation circuits using a genetic algorithm oriented by process-based rules. Int. J. Miner. Process. 2011. [Google Scholar] [CrossRef]
- Maldonado, M.; Araya, R.; Finch, J. Optimizing flotation bank performance by recovery profiling. Miner. Eng. 2011, 24, 939–943. [Google Scholar] [CrossRef]
- Hu, W.; Hadler, K.; Neethling, S.J.; Cilliers, J.J. Determining flotation circuit layout using genetic algorithms with pulp and froth models. Chem. Eng. Sci. 2013, 102, 32–41. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Lucay, F.; Gálvez, E.D. Effect of the objective function in the design of concentration plants. Miner. Eng. 2014, 63, 16–24. [Google Scholar] [CrossRef]
- Pirouzan, D.; Yahyaei, M.; Banisi, S. Pareto based optimization of flotation cells configuration using an oriented genetic algorithm. Int. J. Miner. Process. 2014, 126, 107–116. [Google Scholar] [CrossRef]
- Calisaya, D.A.; López-Valdivieso, A.; de la Cruz, M.H.; Gálvez, E.E.; Cisternas, L.A. A strategy for the identification of optimal flotation circuits. Miner. Eng. 2016, 96–97, 157–167. [Google Scholar] [CrossRef]
- Lucay, F.; Gálvez, E.; Cisternas, L. Design of Flotation Circuits Using Tabu-Search Algorithms: Multispecies, Equipment Design, and Profitability Parameters. Minerals 2019, 9, 181. [Google Scholar] [CrossRef]
- McCarthy, J.; Minsky, M.; Rochester, N.; Shannon, C. A proposal for the Dartmouth summer research project on artificial intelligence. AI Mag. 2012, 27, 12–14. [Google Scholar]
- McCoy, J.T.; Auret, L. Machine learning applications in minerals processing: A review. Miner. Eng. 2019, 132, 95–109. [Google Scholar] [CrossRef]
- Bergh, L. Artificial Intelligence in Mineral Processing Plants: An Overview. In Proceedings of the 2016 International Conference on Artificial Intelligence: Technologies and Applications, Bangkok, Thailand, 24–25 January 2016. [Google Scholar]
- Hoseinian, F.S.; Rezai, B.; Kowsari, E.; Safari, M. A hybrid neural network/genetic algorithm to predict Zn(II) removal by ion flotation. Sep. Sci. Technol. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Zadeh, L.A. Soft Computing and Fuzzy Logic. IEEE Softw. 1994, 11, 48–56. [Google Scholar] [CrossRef]
- Thyagharajan, K.K.; Vignesh, T. Soft Computing Techniques for Land Use and Land Cover Monitoring with Multispectral Remote Sensing Images: A Review. Arch. Comput. Methods Eng. 2019, 26, 275–301. [Google Scholar] [CrossRef]
- Das, S.K.; Kumar, A.; Das, B.; Burnwal, B. On Soft Computing Techniques in Various Areas. Int. J. Inform. Technol. Comput. Sci. 2013, 3, 59–68. [Google Scholar] [CrossRef]
- Sharma, D.; Chandra, P. A comparative analysis of soft computing techniques in software fault prediction model development. Int. J. Inf. Technol. 2018, 11, 1–10. [Google Scholar] [CrossRef]
- Jeffers, J.; Reinders, J.; Sodani, A. Machine learning. In Intel Xeon Phi Processor High Performance Programming; Elsevier: Amsterdam, The Netherlands, 2016; pp. 527–548. ISBN 9780128091944. [Google Scholar]
- Qin, S.J. Statistical process monitoring: Basics and beyond. J. Chemom. 2003, 17, 480–502. [Google Scholar] [CrossRef]
- Umucu, Y.; Çaǧlar, M.F.; Gündüz, L.; Bozkurt, V.; Deniz, V. Modeling of grinding process by artificial neural network for calcite mineral. In Proceedings of the INISTA 2011 International Symposium on INnovations in Intelligent SysTems and Applications, Istanbul, Turkey, 15–18 June 2011. [Google Scholar]
- Umucu, Y.; Deniz, V.; Bozkurt, V.; Çağlard, M.F. The evaluation of grinding process using artificial neural network. Int. J. Miner. Process. 2016, 146, 46–53. [Google Scholar] [CrossRef]
- Warren Liao, T.; Chen, L.J. A neural network approach for grinding processes: Modelling and optimization. Int. J. Mach. Tools Manuf. 1994, 34, 919–937. [Google Scholar] [CrossRef]
- Makokha, A.B.; Moys, M.H. Multivariate approach to on-line prediction of in-mill slurry density and ball load volume based on direct ball and slurry sensor data. Miner. Eng. 2012. [Google Scholar] [CrossRef]
- Mitra, K.; Ghivari, M. Modeling of an industrial wet grinding operation using data-driven techniques. Comput. Chem. Eng. 2006, 30, 508–520. [Google Scholar] [CrossRef]
- Curilem, M.; Acuña, G.; Cubillos, F.; Vyhmeister, E. Neural Networks and Support Vector Machine models applied to energy consumption optimization in semiautogeneous grinding. Chem. Eng. Trans. 2011, 25, 761–766. [Google Scholar]
- Núñez, F.; Silva, D.; Cipriano, A. Characterization and modeling of semi-autogenous mill performance under ore size distribution disturbances. IFAC Proc. Vol. 2011, 44, 9941–9946. [Google Scholar] [CrossRef]
- Vini, M.H. Using Artificial Neural Networks to predict rolling force and real exit thickness of steel strips. J. Mod. Process. Manuf. Prod. 2014, 3, 53–60. [Google Scholar]
- Nakhaei, F.; Irannajad, M. Comparison between neural networks and multiple regression methods in metallurgical performance modeling of flotation column. Physicochem. Probl. Miner. Process. 2013, 49, 255–266. [Google Scholar] [CrossRef]
- Hosseini, M.R.; Shirazi, H.H.A.; Massinaei, M.; Mehrshad, N. Modeling the Relationship between Froth Bubble Size and Flotation Performance Using Image Analysis and Neural Networks. Chem. Eng. Commun. 2015, 202, 911–919. [Google Scholar] [CrossRef]
- Estrada-Ruiz, R.H.; Peérez-Garibay, R. Neural networks to estimate bubble diameter and bubble size distribution of Dotation froth surfaces. J. S. Afr. Inst. Min. Metall. 2009, 109, 441–446. [Google Scholar]
- Chelgani, S.C.; Shahbazi, B.; Rezai, B. Estimation of froth flotation recovery and collision probability based on operational parameters using an artificial neural network. Int. J. Miner. Metall. Mater. 2010, 17, 526–534. [Google Scholar] [CrossRef]
- Jahedsaravani, A.; Marhaban, M.H.; Massinaei, M. Prediction of the metallurgical performances of a batch flotation system by image analysis and neural networks. Miner. Eng. 2014, 69, 137–145. [Google Scholar] [CrossRef]
- Saravani, A.J.; Mehrshad, N.; Massinaei, M. Fuzzy-Based Modeling and Control of an Industrial Flotation Column. Chem. Eng. Commun. 2014, 201, 896–908. [Google Scholar] [CrossRef]
- Karimi, M.; Dehghani, A.; Nezamalhosseini, A.; Talebi, S.H. Prediction of hydrocyclone performance using artificial neural networks. J. S. Afr. Inst. Min. Metall. 2010, 110, 207–212. [Google Scholar]
- Razavi, S.; Tolson, B.A.; Burn, D.H. Review of surrogate modeling in water resources. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Aldrich, C.; Jemwa, G.T.; Krishnannair, S. Multiscale process monitoring with singular spectrum analysis. IFAC Proc. Vol. 2007, 12, 167–172. [Google Scholar] [CrossRef]
- Bergh, L.G.; Yianatos, J.B.; León, A. Multivariate projection methods applied to flotation columns. Miner. Eng. 2005, 18, 721–723. [Google Scholar] [CrossRef]
- Groenewald, J.W.D.V.; Coetzer, L.P.; Aldrich, C. Statistical monitoring of a grinding circuit: An industrial case study. Miner. Eng. 2006, 19, 1138–1148. [Google Scholar] [CrossRef]
- Wakefield, B.J.; Lindner, B.S.; McCoy, J.T.; Auret, L. Monitoring of a simulated milling circuit: Fault diagnosis and economic impact. Miner. Eng. 2018, 120, 132–151. [Google Scholar] [CrossRef]
- Groenewald, J.W.D.; Aldrich, C. Root cause analysis of process fault conditions on an industrial concentrator circuit by use of causality maps and extreme learning machines. Miner. Eng. 2015, 74, 30–40. [Google Scholar] [CrossRef]
- Lindner, B.; Auret, L. Application of data-based process topology and feature extraction for fault diagnosis of an industrial platinum group metals concentrator plant. IFAC-PapersOnLine 2015, 48, 102–107. [Google Scholar] [CrossRef]
- Cao, B.; Xie, Y.; Gui, W.; Wei, L.; Yang, C. Integrated prediction model of bauxite concentrate grade based on distributed machine vision. Miner. Eng. 2013, 53, 31–38. [Google Scholar] [CrossRef]
- Rughooputh, H.C.S.; Rughooputh, S.D.D.V. Neural network process vision systems for flotation process. Kybernetes 2002, 31, 529–535. [Google Scholar] [CrossRef]
- Zhu, J.; Yu, K.W. Application of image recognition system in flotation process. In Proceedings of the World Congress on Intelligent Control and Automation (WCICA), Chongqing, China, 25–27 June 2008. [Google Scholar]
- Sharad, M.; Augustine, C.; Panagopoulos, G.; Roy, K. Ultra low energy analog image processing using spin based neurons. In Proceedings of the 2012 IEEE/ACM International Symposium on Nanoscale Architectures (NANOARCH), Amsterdam, The Netherlands, 4–6 July 2012. [Google Scholar]
- Zhao, L.; Peng, T.; Xie, Y.; Yang, C.; Gui, W. Recognition of flooding and sinking conditions in flotation process using soft measurement of froth surface level and QTA. Chemom. Intell. Lab. Syst. 2017, 169, 45–52. [Google Scholar] [CrossRef]
- Çinar, A. A Method for Local Tuning of Fuzzy Membership Functions. In Proceedings of the ICCS 2010: “Celebrating 10 years of Advancing Computational Thinking”, Amsterdam, The Netherlands, 31 May–2 June 2010. [Google Scholar]
- Tandon, V.; El-Mounayri, H.; Kishawy, H. NC end milling optimization using evolutionary computation. Int. J. Mach. Tools Manuf. 2002, 42, 595–605. [Google Scholar] [CrossRef]
- Massinaei, M.; Falaghi, H.; Izadi, H. Optimisation of metallurgical performance of industrial flotation column using neural network and gravitational search algorithm. Can. Metall. Q. 2013, 52, 115–122. [Google Scholar] [CrossRef]
- Shunmugam, M.S.; Bhaskara Reddy, S.V.; Narendran, T.T. Selection of optimal conditions in multi-pass face-milling using a genetic algorithm. Int. J. Mach. Tools Manuf. 2000, 40, 401–414. [Google Scholar] [CrossRef]
- Moscato, P. On evolution, search, optimization, genetic algorithms and martial arts: Towards memetic algorithms. In Caltech Concurrent Computation. Program, C3P Report; California Institute of Technology, (Caltech): Pasadena, CA, USA, 1989. [Google Scholar]
- Ojha, V.K.; Abraham, A.; Snásel, V. Metaheuristic Design of Feedforward Neural Networks: A Review of Two Decades of Research. Eng. Appl. Artif. Intell. 2017, 60, 97–116. [Google Scholar] [CrossRef]
- Tang, Q.; Lau, Y.B.; Hu, S.; Yan, W.; Yang, Y.; Chen, T. Response surface methodology using Gaussian processes: Towards optimizing the trans-stilbene epoxidation over Co2+—NaX catalysts. Chem. Eng. J. 2010, 156, 423–431. [Google Scholar] [CrossRef]
- Garud, S.S.; Karimi, I.A.; Kraft, M. Design of computer experiments: A review. Comput. Chem. Eng. 2017, 106, 71–95. [Google Scholar] [CrossRef]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef]
- Gutmann, H.M. A Radial Basis Function Method for Global Optimization. J. Glob. Optim. 2001, 19, 201–227. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Gan, Y.; Duan, Q.; Gong, W.; Tong, C.; Sun, Y.; Chu, W.; Ye, A.; Miao, C.; Di, Z. A comprehensive evaluation of various sensitivity analysis methods: A case study with a hydrological model. Environ. Model. Softw. 2014, 51, 269–285. [Google Scholar] [CrossRef]
- Ye, K.Q.; Li, W.; Sudjianto, A. Algorithmic construction of optimal symmetric Latin hypercube designs. J. Stat. Plan. Inference 2000, 90, 145–159. [Google Scholar] [CrossRef]
- Shahreza, S.; Shafaei, S.; Noaparast, M.; Sarvi, M. Optimization of Galena Flotation Process of Irankouh Complex Ore Using A Statistical Design of Experiments. Curr. World Environ. 2015, 10, 626–636. [Google Scholar] [CrossRef]
- Vieceli, N.; Durão, F.O.; Guimarães, C.; Nogueira, C.A.; Pereira, M.F.C.; Margarido, F. Grade-recovery modelling and optimization of the froth flotation process of a lepidolite ore. Int. J. Miner. Process. 2016, 157, 184–194. [Google Scholar] [CrossRef]
- Ebadnejad, A.; Karimi, G.R.; Dehghani, H. Application of response surface methodology for modeling of ball mills in copper sulphide ore grinding. Powder Technol. 2013, 245, 292–296. [Google Scholar] [CrossRef]
- Krajnik, P.; Kopac, J.; Sluga, A. Design of grinding factors based on response surface methodology. J. Mater. Process. Technol. 2005, 162, 629–636. [Google Scholar] [CrossRef]
- Chen, G.; Peng, J.H.; Chen, J. Optimizing conditions for wet grinding of synthetic rutile using response surface methodology. Miner. Metall. Process. 2011, 28, 44–48. [Google Scholar] [CrossRef]
- Alireza, A.S.; Ataallah, S.G.; Majid, E.G.; Amir, S.; Mohammad, R.; Hadi, A. Application of response surface methodology and central composite rotatable design for modeling the influence of some operating variables of the lab scale thickener performance. Int. J. Min. Sci. Technol. 2013, 23, 717–724. [Google Scholar] [CrossRef]
- Costa, N.R.; Lourenço, J. Gaussian Process Model—An Exploratory Study in the Response Surface Methodology. Qual. Reliab. Eng. Int. 2016, 32. [Google Scholar] [CrossRef]
- Charte, F.; Romero, I.; Pérez-Godoy, M.D.; Rivera, A.J.; Castro, E. Comparative analysis of data mining and response surface methodology predictive models for enzymatic hydrolysis of pretreated olive tree biomass. Comput. Chem. Eng. 2017, 101, 23–30. [Google Scholar] [CrossRef]
- Gutiérrez, A.; Olivera, C.A.C.; Hacha, R.R.; Torem, M.L.; Santos, B.F. dos Optimization of hematite and quartz BIOFLOTATION by AN artificial neural network (ANN). J. Mater. Res. Technol. 2019, 8, 3076–3087. [Google Scholar]
- Asher, M.J.; Croke, B.F.W.; Jakeman, A.J.; Peeters, L.J.M. A review of surrogate models and their application to groundwater modeling. Water Resour. Res. 2015, 51, 5957–5973. [Google Scholar] [CrossRef]
- Rabhi, A.; Chkifa, A.; Benjelloun, S.; Latifi, A. Surrogate-based modeling in flotation processes. Comput. Aided Chem. Eng. 2018, 43, 229–234. [Google Scholar]
- Stephens, D.W.; Gorissen, D.; Crombecq, K.; Dhaene, T. Surrogate based sensitivity analysis of process equipment. Appl. Math. Model. 2011, 35, 1676–1687. [Google Scholar] [CrossRef]
- Stephens, D.; Fawell, P. Optimization of Process Equipment Using Global Surrogate Models. In Proceedings of the Conference on CFD in the Minerals and Process Industries CSIRO, Melbourne, Australia, 10–12 December 2012. [Google Scholar]
- Metta, N.; Ramachandran, R.; Ierapetritou, M. A Computationally Efficient Surrogate-Based Reduction of a Multiscale Comill Process Model. J. Pharm. Innov. 2019, 2019, 1–21. [Google Scholar] [CrossRef]
- Lucay, F.A.; Gálvez, E.D.; Salez-Cruz, M.; Cisternas, L.A. Improving milling operation using uncertainty and global sensitivity analyses. Miner. Eng. 2019, 131, 249–261. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Campolongo, F. Sensitivity analysis as an ingredient of modeling. Stat. Sci. 2000, 15, 377–395. [Google Scholar]
- Lane, W.A.; Ryan, E.M. Verification, validation, and uncertainty quantification of a sub-grid model for heat transfer in gas-particle flows with immersed horizontal cylinders. Chem. Eng. Sci. 2018, 176, 409–420. [Google Scholar] [CrossRef]
- Mellado, M.E.; Cisternas, L.A.; Gálvez, E.D. An analytical model approach to heap leaching. Hydrometallurgy 2009, 95, 33–38. [Google Scholar] [CrossRef]
- Mellado, M.; Lucay, F.; Cisternas, L.; Gálvez, E.; Sepúlveda, F. A Posteriori Analysis of Analytical Models for Heap Leaching Using Uncertainty and Global Sensitivity Analyses. Minerals 2018, 8, 44. [Google Scholar] [CrossRef]
- Mellado, M.E.; Casanova, M.P.; Cisternas, L.A.; Gálvez, E.D. On scalable analytical models for heap leaching. Comput. Chem. Eng. 2011, 35, 220–225. [Google Scholar] [CrossRef]
- Mellado, M.E.; Gálvez, E.D.; Cisternas, L.A. Stochastic analysis of heap leaching process via analytical models. Miner. Eng. 2012, 33, 93–98. [Google Scholar] [CrossRef]
- Sepúlveda, F.D.; Lucay, F.; González, J.F.; Cisternas, L.A.; Gálvez, E.D. A methodology for the conceptual design of flotation circuits by combining group contribution, local/global sensitivity analysis, and reverse simulation. Int. J. Miner. Process. 2017, 164, 56–66. [Google Scholar] [CrossRef]
- Lucay, F.; Cisternas, L.A.; Gálvez, E.D. Global sensitivity analysis for identifying critical process design decisions. Chem. Eng. Res. Des. 2015, 103, 74–83. [Google Scholar] [CrossRef]
- Lucay, F.; Cisternas, L.A.; Gálvez, E.D. Retrofitting of Concentration Plants Using Global Sensitivity Analysis. Comput. Aided Chem. Eng. 2015, 37, 311–316. [Google Scholar]
- Sepúlveda, F.D.; Cisternas, L.A.; Gálvez, E.D. The use of global sensitivity analysis for improving processes: Applications to mineral processing. Comput. Chem. Eng. 2014, 66, 221–232. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Li, S.; Yang, B.; Qi, F. Accelerate global sensitivity analysis using artificial neural network algorithm: Case studies for combustion kinetic model. Combust. Flame 2016, 168, 53–64. [Google Scholar] [CrossRef]
- Sakizlis, V.; Perkins, J.D.; Pistikopoulos, E.N. Recent advances in optimization-based simultaneous process and control design. Comput. Chem. Eng. 2004, 28, 2069–2086. [Google Scholar] [CrossRef]
- Eljack, F.T.; Solvason, C.C.; Chemmangattuvalappil, N.; Eden, M.R. A Property Based Approach for Simultaneous Process and Molecular Design. Chin. J. Chem. Eng. 2008, 16, 424–434. [Google Scholar] [CrossRef]
- Kazantzi, V.; Qin, X.; El-Halwagi, M.; Eljack, F.; Eden, M. Simultaneous Process and Molecular Design through Property Clustering Techniques: A Visualization Tool. Ind. Eng. Chem. Res. 2007, 46, 3400–3409. [Google Scholar] [CrossRef]
- Eljack, F.T.; Eden, M.R.; Kazantzi, V.; Qin, X.; El-Halwagi, M.M. Simultaneous process and molecular design—A property based approach. AIChE J. 2007, 53, 1232–1239. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).