An Efficient Image Segmentation Algorithm Using Neutrosophic Graph Cut
Abstract
:1. Introduction
2. Previous Works
3. Proposed Method
3.1. Neutrosophic Image
3.2. Indeterminacy Filtering
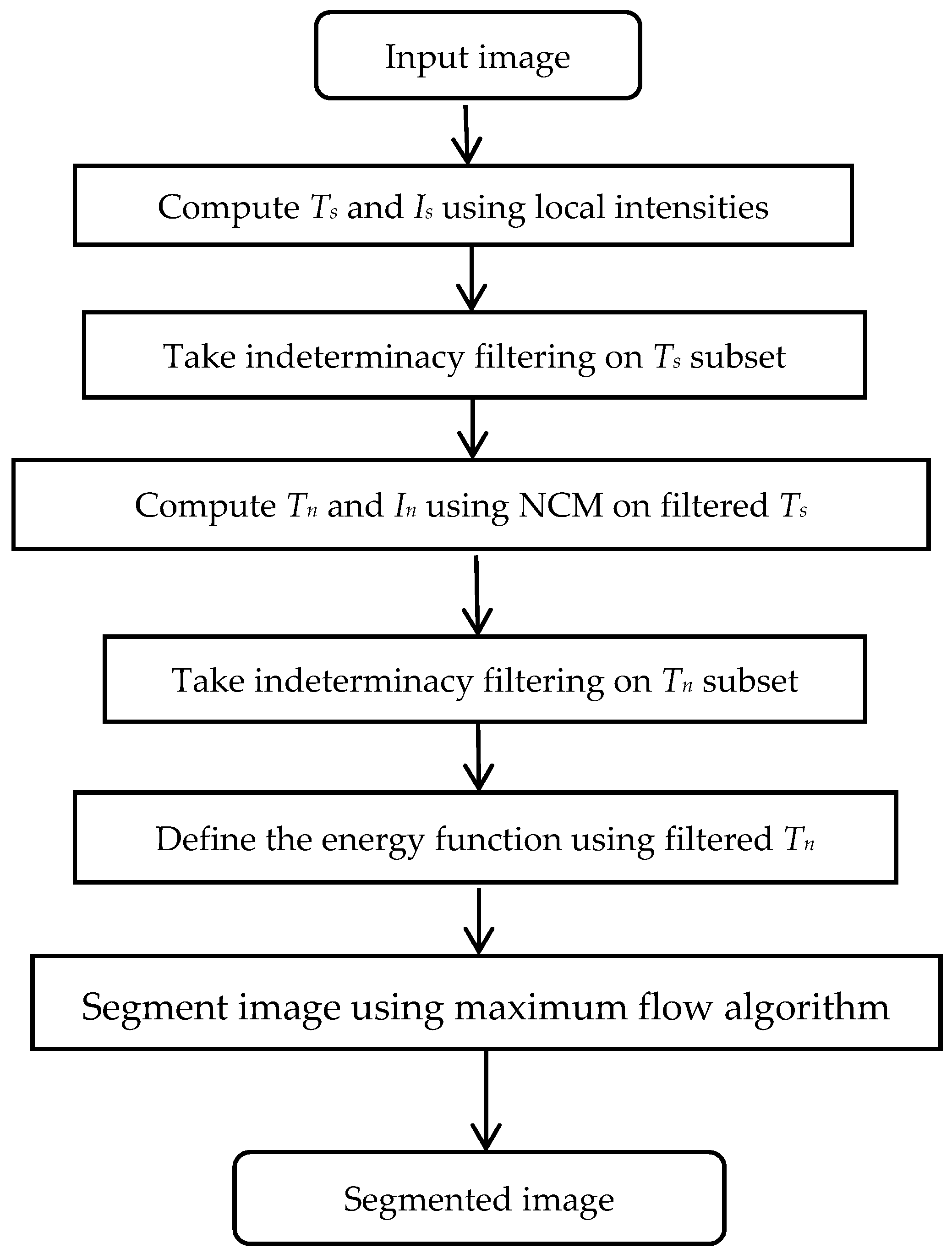
3.3. Neutrosophic Graph Cut
- Step 1: Compute the local neutrosophic value and .
- Step 2: Take indeterminate filtering on using .
- Step 3: Use NCM algorithm on the filtered subset to obtain and .
- Step 4: Filter using indeterminate filter based on .
- Step 5: Define the energy function based on the value.
- Step 6: Partition the image using the maximum flow algorithm.
4. Experimental Results
4.1. Quantitatively Evaluation
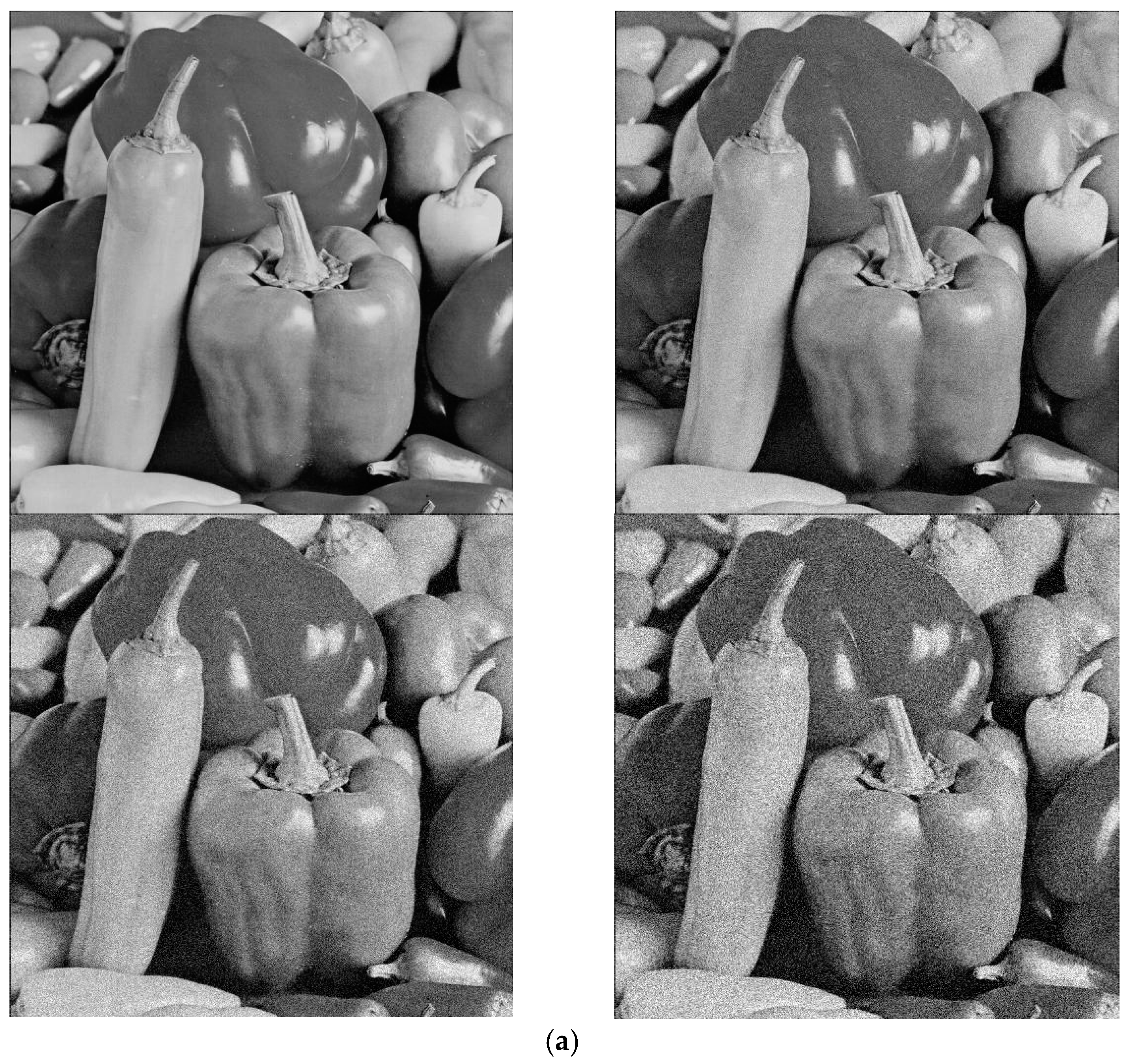
4.2. Performance on Natural Images
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pal, N.R.; Pal, S.K. A review on image segmentation techniques. Pattern Recognit. 1993, 26, 1277–1294. [Google Scholar] [CrossRef]
- Gonzalez, R.C. Digital Image Processing, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Wu, Z.; Leahy, R. An optimal graph theoretic approach to data clustering: Theory and its application to image segmentation. IEEE. Trans. Pattern Anal. Mach. Intell. 1993, 15, 1101–1113. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy. Neutrosophic Probability, Set, and Logic, ProQuest Information & Learning; Infolearnquest: Ann Arbor, MI, USA, 1998; p. 105. Available online: http://fs.gallup.unm.edu/eBook-neutrosophics6.pdf (accessed on 28 June 2017).
- Smarandache, F. A Unifying Field in Logics Neutrosophic Logic. In Neutrosophy, Neutrosophic Set, Neutrosophic Probability; American Research Press: Rehoboth, DE, USA, 2005. [Google Scholar]
- Guo, Y.; Cheng, H.-D. New neutrosophic approach to image segmentation. Pattern Recognit. 2009, 42, 587–595. [Google Scholar] [CrossRef]
- Akhtar, N.; Agarwal, N.; Burjwal, A. K-mean algorithm for Image Segmentation using Neutrosophy. In Proceedings of the ICACCI International Conference on Advances in Computing, Communications and Informatics, New Delhi, India, 24–27 September 2014; pp. 2417–2421. [Google Scholar]
- Cheng, H.; Guo, Y.; Zhang, Y. A novel image segmentation approach based on neutrosophic set and improved fuzzy c-means algorithm. New Math. Nat. Comput. 2011, 7, 155–171. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, L.; Cheng, H. A neutrosophic approach to image segmentation based on watershed method. Signal Process. 2010, 90, 1510–1517. [Google Scholar] [CrossRef]
- Hanbay, K.; Talu, M.F. Segmentation of SAR images using improved artificial bee colony algorithm and neutrosophic set. Appl. Soft Comput. 2014, 21, 433–443. [Google Scholar] [CrossRef]
- Karabatak, E.; Guo, Y.; Sengur, A. Modified neutrosophic approach to color image segmentation. J. Electron. Imaging 2013, 22, 013005. [Google Scholar] [CrossRef]
- Guo, Y.; Sengur, A. A novel color image segmentation approach based on neutrosophic set and modified fuzzy c-means. Circuits Syst. Signal Process. 2013, 32, 1699–1723. [Google Scholar] [CrossRef]
- Sengur, A.; Guo, Y. Color texture image segmentation based on neutrosophic set and wavelet transformation. Comput. Vis. Image Underst. 2011, 115, 1134–1144. [Google Scholar] [CrossRef]
- Mathew, J.M.; Simon, P. Color Texture Image Segmentation Based on Neutrosophic Set and Nonsubsampled Contourlet Transformation. In Proceedings of the ICAA 2014 First International Conference on Applied Algorithms, Kolkata, India, 13–15 January 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 164–173. [Google Scholar]
- Yu, B.; Niu, Z.; Wang, L. Mean shift based clustering of neutrosophic domain for unsupervised constructions detection. Optik-Int. J. Light Electron Opt. 2013, 124, 4697–4706. [Google Scholar] [CrossRef]
- Guo, Y.; Sengur, A. NCM: Neutrosophic c-means clustering algorithm. Pattern Recognit. 2015, 48, 2710–2724. [Google Scholar] [CrossRef]
- Guo, Y.; Şengür, A. A novel image segmentation algorithm based on neutrosophic similarity clustering. Appl. Soft Comput. 2014, 25, 391–398. [Google Scholar] [CrossRef]
- Guo, Y.; Şengür, A.; Ye, J. A novel image thresholding algorithm based on neutrosophic similarity score. Measurement 2014, 58, 175–186. [Google Scholar] [CrossRef]
- Guo, Y.; Şengür, A. A novel image edge detection algorithm based on neutrosophic set. Comput. Electr. Eng. 2014, 40, 3–25. [Google Scholar] [CrossRef]
- Guo, Y.; Şengür, A. A novel image segmentation algorithm based on neutrosophic filtering and level set. Neutrosophic Sets Syst. 2013, 1, 46–49. [Google Scholar]
- Bo, P.; Zhang, L.; Zhang, D. A survey of graph theoretical approaches to image segmentation. Pattern Recognit. 2013, 46, 1020–1038. [Google Scholar]
- Morris, O.J.; Lee, M.D.; Constantinides, A.G. Graph theory for image analysis: An approach based on the shortest spanning tree. IEE Proc. F Commun. Radar Signal Proc. 1986, 133, 146–152. [Google Scholar] [CrossRef]
- Felzenszwalb, P.F.; Huttenlocher, D.P. Efficient graph based image segmentation. Int. J. Comput. Vis. 2004, 59, 167–181. [Google Scholar] [CrossRef]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar]
- Wang, S.; Siskind, J.M. Image segmentation with ratio cut. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 675–690. [Google Scholar] [CrossRef]
- Ding, C.; He, X.; Zha, H.; Gu, M.; Simon, H. A min-max cut algorithm for graph partitioning and data clustering. In Proceedings of the First IEEE International Conference on Data Mining (ICDM), San Jose, CA, USA, 29 November–2 Devember 2001; pp. 107–114. [Google Scholar]
- Cox, I.J.; Rao, S.B.; Zhong, Y. Ratio regions: A technique for image segmentation. In Proceedings of the International Conference on Pattern Recognition, Vienna, Austria, 25–29 August 1996; pp. 557–564. [Google Scholar]
- Grady, L. Multilabel random walker segmentation using prior models. In Proceedings of the IEEE Conference of Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 763–770. [Google Scholar]
- Yuan, J.; Bae, E.; Tai, X.; Boykov, Y. A continuous max-flow approach to potts model. Comput. Vis. ECCV 2010, 6316, 379–392. [Google Scholar]
- Yasnoff, W.A.; Mui, J.K.; Bacus, J.W. Error measures for scene segmentation. Pattern Recognit. 1977, 9, 217–231. [Google Scholar] [CrossRef]
- Pratt, W.K. Digital Image Processing; John Wiley & Sons: Hoboken, NJ, USA, 1978; pp. 429–432. [Google Scholar]
- Wang, S.; Chung, F.-L.; Xiong, F. A novel image thresholding method based on Parzen window estimate. Pattern Recognit. 2008, 41, 117–129. [Google Scholar] [CrossRef]
- Salah, M.B.; Mitiche, A.; Ayed, I.B. Multiregion Image Segmentation by Parametric Kernel Graph Cuts. IEEE Trans. Image Process. 2011, 20, 545–557. [Google Scholar] [CrossRef] [PubMed]










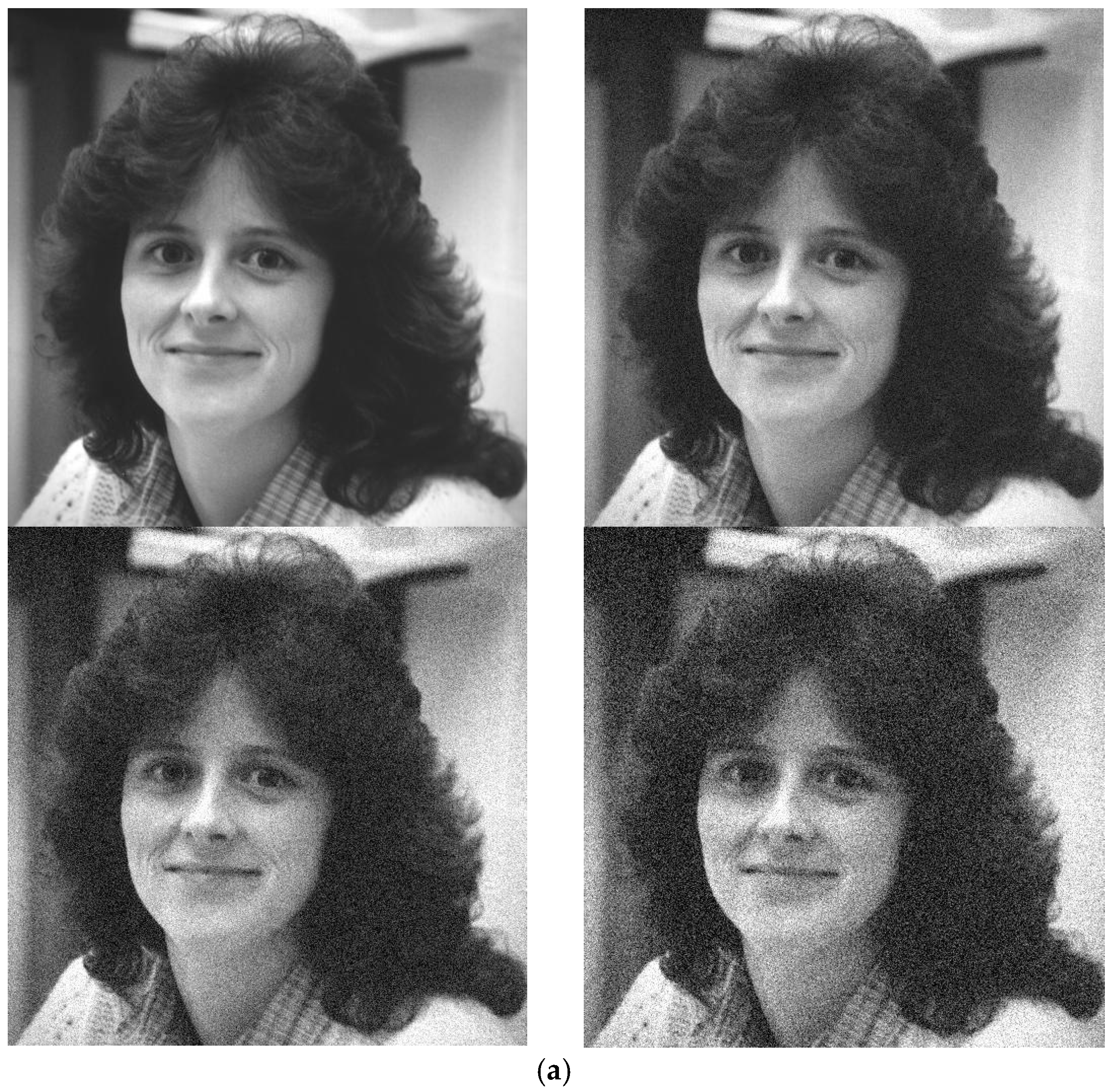








| Metrics | NSC | GC | NGC |
|---|---|---|---|
| ME | 0.247 ± 0.058 | 0.062 ± 0.025 | 0.015 ± 0.011 |
| FOM | 0.771 ± 0.025 | 0.897 ± 0.027 | 0.987 ± 0.012 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Akbulut, Y.; Şengür, A.; Xia, R.; Smarandache, F. An Efficient Image Segmentation Algorithm Using Neutrosophic Graph Cut. Symmetry 2017, 9, 185. https://doi.org/10.3390/sym9090185
Guo Y, Akbulut Y, Şengür A, Xia R, Smarandache F. An Efficient Image Segmentation Algorithm Using Neutrosophic Graph Cut. Symmetry. 2017; 9(9):185. https://doi.org/10.3390/sym9090185
Chicago/Turabian StyleGuo, Yanhui, Yaman Akbulut, Abdulkadir Şengür, Rong Xia, and Florentin Smarandache. 2017. "An Efficient Image Segmentation Algorithm Using Neutrosophic Graph Cut" Symmetry 9, no. 9: 185. https://doi.org/10.3390/sym9090185
APA StyleGuo, Y., Akbulut, Y., Şengür, A., Xia, R., & Smarandache, F. (2017). An Efficient Image Segmentation Algorithm Using Neutrosophic Graph Cut. Symmetry, 9(9), 185. https://doi.org/10.3390/sym9090185








