NS-k-NN: Neutrosophic Set-Based k-Nearest Neighbors Classifier
Abstract
:1. Introduction
2. Related works
2.1. k-Nearest Neighbor (k-NN) Classifier
- Calculate the similarity measures between test sample and training samples by using a distance function (e.g., Euclidean distance)
- Find the test sample’s k nearest neighbors in training data samples according to the similarity measure and determine the class label by the majority voting of its nearest neighbors.
2.2. Fuzzy k-Nearest Neighbor (k-NN) Classifier
3. Proposed Neutrosophic-k-NN Classifier
- Step 1:
- Initialize the cluster centers according to the labelled dataset and employ Equations (3)–(5) to calculate the T, I, and F values for each data training data point.
- Step 2:
- Compute membership grades of test data samples according to the Equations (6) and (7).
- Step 3:
- Assign class labels of the unknown test data points to the class whose neutrosophic membership is maximum.
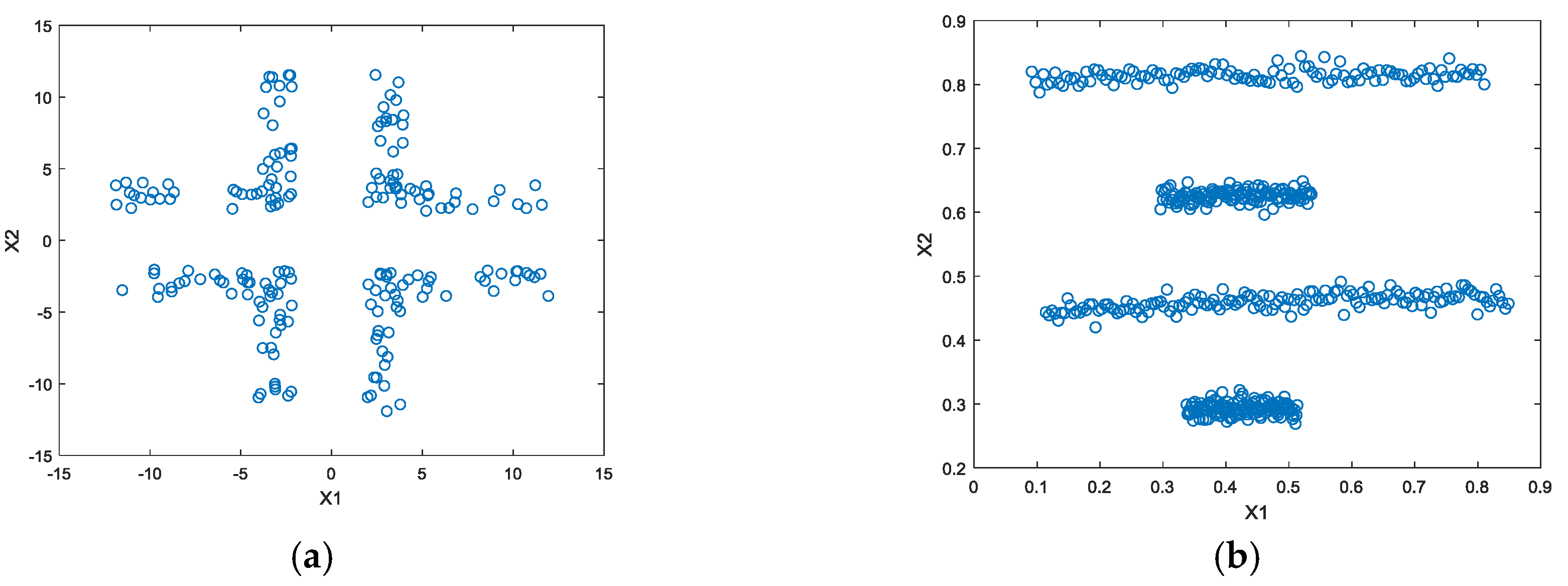
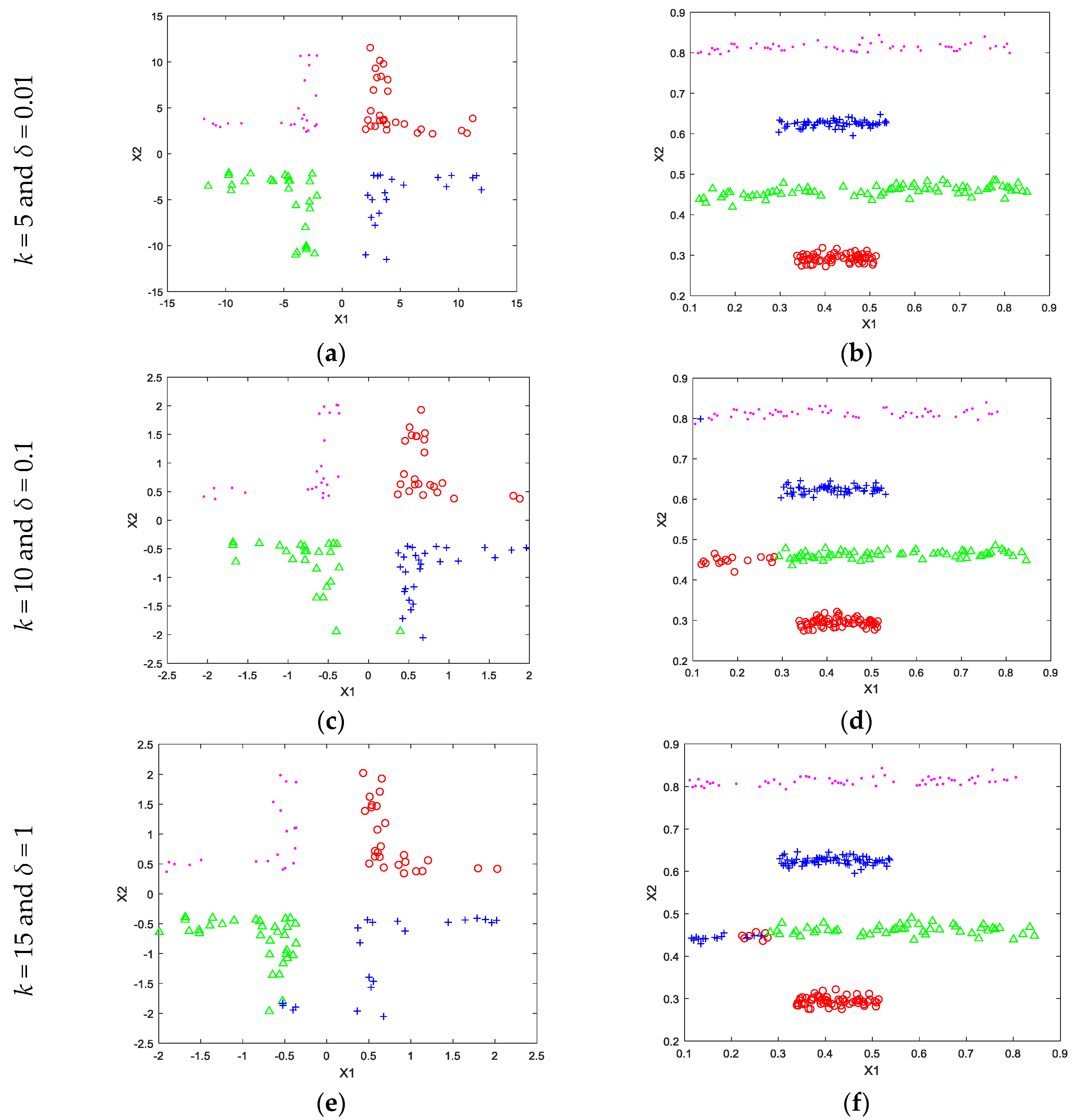
4. Experimental Works
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fix, E.; Hodges, J.L. Discriminatory Analysis, Nonparametric Discrimination: Consistency Properties; Technique Report No. 4; U.S. Air Force School of Aviation Medicine, Randolf Field Texas: Universal City, TX, USA, 1951; pp. 238–247.
- Duda, R.; Hart, P. Pattern Classification and Scene Analysis; John Wiley & Sons: New York, NY, USA, 1973. [Google Scholar]
- Cabello, D.; Barro, S.; Salceda, J.; Ruiz, R.; Mira, J. Fuzzy k-nearest neighbor classifiers for ventricular arrhythmia detection. Int. J. Biomed. Comput. 1991, 27, 77–93. [Google Scholar] [CrossRef]
- Chen, H.-L.; Yang, B.; Wang, G.; Liu, J.; Xu, X.; Wang, S.; Liu, D. A novel bankruptcy prediction model based on an adaptive fuzzy k-nearest neighbor method. Knowl. Based Syst. 2011, 24, 1348–1359. [Google Scholar] [CrossRef]
- Chikh, M.A.; Saidi, M.; Settouti, N. Diagnosis of diabetes diseases using an artificial immune recognition system2 (AIRS2) with fuzzy k-nearest neighbor. J. Med. Syst. 2012, 36, 2721–2729. [Google Scholar] [CrossRef] [PubMed]
- Aslan, M.; Akbulut, Y.; Sengur, A.; Ince, M.C. Skeleton based efficient fall detection. J. Fac. Eng. Archit. Gazi Univ. 2017, accepted (in press). [Google Scholar]
- Li, B.; Lu, Q.; Yu, S. An adaptive k-nearest neighbor text categorization strategy. ACM Trans. Asian Lang. Inf. Process. 2004, 3, 215–226. [Google Scholar]
- Keller, J.M.; Gray, M.R.; Givens, J.A. A fuzzy k-nearest neighbor algorithm. IEEE Trans. Syst. Man Cybern. 1985, 15, 580–585. [Google Scholar] [CrossRef]
- Pham, T.D. An optimally weighted fuzzy k-NN algorithm. In Pattern Recognition and Data Mining; Volume 3686 of Lecture Notes in Computer Science; Singh, S., Singh, M., Apte, C., Perner, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 239–247. [Google Scholar]
- Denoeux, T. A k-nearest neighbor classification rule based on Dempster–Shafer theory. IEEE Trans. Syst. Man Cybern. 1995, 25, 804–813. [Google Scholar] [CrossRef]
- Zouhal, L.M.; Denœux, T. An evidence-theoretic k-NN rule with parameter optimization. IEEE Trans. Syst. Man Cybern. Part C 1998, 28, 263–271. [Google Scholar] [CrossRef]
- Zouhal, L.M.; Denœux, T. Generalizing the evidence theoretic k-NN rule to fuzzy pattern recognition. In Proceedings of the 2nd International ICSC Symposium on Fuzzy Logic and Applications, Zurich, Switzerland, 12–14 February 1997; pp. 294–300. [Google Scholar]
- Liu, Z.G.; Pan, Q.; Dezert, J.; Mercier, G.; Liu, Y. Fuzzy-belief k-nearest neighbor classifier for uncertain data. In Proceedings of the Fusion 2014: 17th International Conference on Information Fusion, Salamanca, Spain, 7–10 July 2014; pp. 1–8. [Google Scholar]
- Liu, Z.; Pan, Q.; Dezert, J. A new belief-based K-nearest neighbor classification method. Pattern Recognit. 2013, 46, 834–844. [Google Scholar] [CrossRef]
- Derrac, J.; Chiclana, F.; García, S.; Herrera, F. Evolutionary fuzzy k-nearest neighbors algorithm using interval-valued fuzzy sets. Inf. Sci. 2016, 329, 144–163. [Google Scholar] [CrossRef]
- Dudani, S.A. The distance-weighted k-nearest neighbor rule. IEEE Trans. Syst. Man Cybern. 1976, 6, 325–327. [Google Scholar] [CrossRef]
- Gou, J.; Du, L.; Zhang, Y.; Xiong, T. A new distance-weighted k-nearest neighbor classifier. J. Inf. Comput. Sci. 2012, 9, 1429–1436. [Google Scholar]
- Smarandache, F. Neutrosophy. Neutrosophic Probability, Set, and Logic, ProQuest Information & Learning; Infolearnquest: Ann Arbor, MI, USA, 1998; p. 105. Available online: http://fs.gallup.unm.edu/eBook-neutrosophics6.pdf (accessed on 2 August 2017).
- Smarandache, F. Introduction to Neutrosophic Measure, Neutrosophic Integral and Neutrosophic Probability; Sitech: Craiova, Romania, 2013. [Google Scholar]
- Smarandache, F. Neutrosophy. Neutrosophic Probability, Set, and Logic; American Research Press: Rehoboth, DE, USA, 1998; p. 105. [Google Scholar]
- Smarandache, F. A Unifying Field in Logics Neutrosophic Logic. Neutrosophy, Neutrosophic Set, Neutrosophic Probability, 3rd ed.; American Research Press: Rehoboth, DE, USA, 2003. [Google Scholar]
- Guo, Y.; Sengur, A. NCM: Neutrosophic c-means clustering algorithm. Pattern Recognit. 2015, 48, 2710–2724. [Google Scholar] [CrossRef]
- Guo, Y.; Sengur, A. A novel color image segmentation approach based on neutrosophic set and modified fuzzy c-means. Circuits Syst. Signal Process. 2013, 32, 1699–1723. [Google Scholar] [CrossRef]
- Alcalá-Fdez, J.; Fernández, A.; Luengo, J.; Derrac, J.; García, S.; Sánchez, L.; Herrera, F. Keel data-mining software tool: Data set repository, integration of algorithms and experimental analysis framework. J. Mult. Valued Log. Soft Comput. 2011, 17, 255–287. [Google Scholar]
- Lichman, M. UCI Machine Learning Repository; University of California, School of Information and Computer Science: Irvine, CA, USA, 2013; Available online: http://archive.ics.uci.edu/ml (accessed on 20 July 2017).
| Data Sets | Instance (#) | Attribute (#) | Class (#) | Data Sets | Instance (#) | Attribute (#) | Class (#) |
|---|---|---|---|---|---|---|---|
| Appendicitis | 106 | 7 | 2 | Penbased | 10,992 | 16 | 10 |
| Balance | 625 | 4 | 3 | Phoneme | 5404 | 5 | 2 |
| Banana | 5300 | 2 | 2 | Pima | 768 | 8 | 2 |
| Bands | 365 | 19 | 2 | Ring | 7400 | 20 | 2 |
| Bupa | 345 | 6 | 2 | Satimage | 6435 | 36 | 7 |
| Cleveland | 297 | 13 | 5 | Segment | 2310 | 19 | 7 |
| Dermatology | 358 | 34 | 6 | Sonar | 208 | 60 | 2 |
| Ecoli | 336 | 7 | 8 | Spectfheart | 267 | 44 | 2 |
| Glass | 214 | 9 | 7 | Tae | 151 | 5 | 3 |
| Haberman | 306 | 3 | 2 | Texture | 5500 | 40 | 11 |
| Hayes-roth | 160 | 4 | 3 | Thyroid | 7200 | 21 | 3 |
| Heart | 270 | 13 | 2 | Twonorm | 7400 | 20 | 2 |
| Hepatitis | 80 | 19 | 2 | Vehicle | 846 | 18 | 4 |
| Ionosphere | 351 | 33 | 2 | Vowel | 990 | 13 | 11 |
| Iris | 150 | 4 | 3 | Wdbc | 569 | 30 | 2 |
| Mammographic | 830 | 5 | 2 | Wine | 178 | 13 | 3 |
| Monk-2 | 432 | 6 | 2 | Winequality-red | 1599 | 11 | 11 |
| Movement | 360 | 90 | 15 | Winequality-white | 4898 | 11 | 11 |
| New thyroid | 215 | 5 | 3 | Yeast | 1484 | 8 | 10 |
| Page-blocks | 5472 | 10 | 5 | - | - | - | - |
| Data Sets | k-NN | Fuzzy k-NN | Proposed Method | Data Sets | k-NN | Fuzzy k-NN | Proposed Method |
|---|---|---|---|---|---|---|---|
| Appendicitis | 87.91 | 97.91 | 90.00 | Penbased | 99.32 | 99.34 | 86.90 |
| Balance | 89.44 | 88.96 | 93.55 | Phoneme | 88.49 | 89.64 | 79.44 |
| Banana | 89.89 | 89.42 | 60.57 | Pima | 73.19 | 73.45 | 81.58 |
| Bands | 71.46 | 70.99 | 75.00 | Ring | 71.82 | 63.07 | 72.03 |
| Bupa | 62.53 | 66.06 | 70.59 | Satimage | 90.94 | 90.61 | 92.53 |
| Cleveland | 56.92 | 56.95 | 72.41 | Segment | 95.41 | 96.36 | 97.40 |
| Dermatology | 96.90 | 96.62 | 97.14 | Sonar | 83.10 | 83.55 | 85.00 |
| Ecoli | 82.45 | 83.34 | 84.85 | Spectfheart | 77.58 | 78.69 | 80.77 |
| Glass | 70.11 | 72.83 | 76.19 | Tae | 45.79 | 67.67 | 86.67 |
| Haberman | 71.55 | 68.97 | 80.00 | Texture | 98.75 | 98.75 | 80.73 |
| Hayes-roth | 30.00 | 65.63 | 68.75 | Thyroid | 94.00 | 93.92 | 74.86 |
| Heart | 80.74 | 80.74 | 88.89 | Twonorm | 97.11 | 97.14 | 98.11 |
| Hepatitis | 89.19 | 85.08 | 87.50 | Vehicle | 72.34 | 71.40 | 54.76 |
| Ionosphere | 96.00 | 96.00 | 97.14 | Vowel | 97.78 | 98.38 | 49.49 |
| Iris | 85.18 | 84.61 | 93.33 | Wdbc | 97.18 | 97.01 | 98.21 |
| Mammographic | 81.71 | 80.37 | 86.75 | Wine | 96.63 | 97.19 | 100.00 |
| Monk-2 | 96.29 | 89.69 | 97.67 | Winequality-red | 55.60 | 68.10 | 46.84 |
| Movement | 78.61 | 36.11 | 50.00 | Winequality-white | 51.04 | 68.27 | 33.33 |
| New thyroid | 95.37 | 96.32 | 100.00 | Yeast | 57.62 | 59.98 | 60.81 |
| Page-blocks | 95.91 | 95.96 | 96.34 | - | - | - | - |
| Data set | Features | Samples | Classes | Training Samples | Testing Samples |
|---|---|---|---|---|---|
| Glass | 10 | 214 | 7 | 140 | 74 |
| Wine | 13 | 178 | 3 | 100 | 78 |
| Sonar | 60 | 208 | 2 | 120 | 88 |
| Parkinson | 22 | 195 | 2 | 120 | 75 |
| Iono | 34 | 351 | 2 | 200 | 151 |
| Musk | 166 | 476 | 2 | 276 | 200 |
| Vehicle | 18 | 846 | 4 | 500 | 346 |
| Image | 19 | 2310 | 7 | 1310 | 1000 |
| Cardio | 21 | 2126 | 10 | 1126 | 1000 |
| Landsat | 36 | 6435 | 7 | 3435 | 3000 |
| Letter | 16 | 20,000 | 26 | 10,000 | 10,000 |
| Data set | WKNN (%) | DWKNN (%) | Proposed Method (%) |
|---|---|---|---|
| Glass | 69.86 | 70.14 | 60.81 |
| Wine | 71.47 | 71.99 | 79.49 |
| Sonar | 81.59 | 82.05 | 85.23 |
| Parkinson | 83.53 | 83.93 | 90.67 |
| Iono | 84.27 | 84.44 | 85.14 |
| Musk | 84.77 | 85.10 | 86.50 |
| Vehicle | 63.96 | 64.34 | 71.43 |
| Image | 95.19 | 95.21 | 95.60 |
| Cardio | 70.12 | 70.30 | 66.90 |
| Landsat | 90.63 | 90.65 | 91.67 |
| Letter | 94.89 | 94.93 | 63.50 |
| Data Sets | k-NN | Fuzzy k-NN | Proposed Method | Data Sets | k-NN | Fuzzy k-NN | Proposed Method |
|---|---|---|---|---|---|---|---|
| Appendicitis | 0.11 | 0.16 | 0.15 | Penbased | 10.21 | 18.20 | 3.58 |
| Balance | 0.15 | 0.19 | 0.18 | Phoneme | 0.95 | 1.88 | 0.71 |
| Banana | 1.03 | 1.42 | 0.57 | Pima | 0.45 | 0.58 | 0.20 |
| Bands | 0.42 | 0.47 | 0.19 | Ring | 6.18 | 10.30 | 2.55 |
| Bupa | 0.14 | 0.28 | 0.16 | Satimage | 8.29 | 15.25 | 1.96 |
| Cleveland | 0.14 | 0.18 | 0.19 | Segment | 1.09 | 1.76 | 0.63 |
| Dermatology | 0.33 | 0.31 | 0.22 | Sonar | 0.15 | 0.21 | 0.23 |
| Ecoli | 0.12 | 0.26 | 0.17 | Spectfheart | 0.14 | 0.25 | 0.22 |
| Glass | 0.10 | 0.18 | 0.18 | Tae | 0.13 | 0.12 | 0.16 |
| Haberman | 0.13 | 0.24 | 0.16 | Texture | 6.72 | 12.78 | 4.30 |
| Hayes-roth | 0.07 | 0.11 | 0.16 | Thyroid | 5.86 | 9.71 | 2.14 |
| Heart | 0.22 | 0.33 | 0.17 | Twonorm | 5.89 | 10.27 | 2.69 |
| Hepatitis | 0.06 | 0.06 | 0.16 | Vehicle | 0.17 | 0.31 | 0.27 |
| Ionosphere | 0.13 | 030 | 0.25 | Vowel | 0.47 | 0.62 | 0.31 |
| Iris | 0.23 | 0.13 | 0.16 | Wdbc | 0.39 | 0.46 | 0.26 |
| Mammographic | 0.21 | 0.22 | 0.20 | Wine | 0.08 | 0.14 | 0.17 |
| Monk-2 | 0.27 | 0.33 | 0.17 | Winequality-red | 0.28 | 0.46 | 0.34 |
| Movement | 0.16 | 0.34 | 0.35 | Winequality-white | 1.38 | 1.95 | 0.91 |
| New thyroid | 0.14 | 0.18 | 0.17 | Yeast | 0.44 | 0.78 | 0.30 |
| Page-blocks | 1.75 | 2.20 | 0.93 | Average | 1.41 | 3.17 | 0.69 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbulut, Y.; Sengur, A.; Guo, Y.; Smarandache, F. NS-k-NN: Neutrosophic Set-Based k-Nearest Neighbors Classifier. Symmetry 2017, 9, 179. https://doi.org/10.3390/sym9090179
Akbulut Y, Sengur A, Guo Y, Smarandache F. NS-k-NN: Neutrosophic Set-Based k-Nearest Neighbors Classifier. Symmetry. 2017; 9(9):179. https://doi.org/10.3390/sym9090179
Chicago/Turabian StyleAkbulut, Yaman, Abdulkadir Sengur, Yanhui Guo, and Florentin Smarandache. 2017. "NS-k-NN: Neutrosophic Set-Based k-Nearest Neighbors Classifier" Symmetry 9, no. 9: 179. https://doi.org/10.3390/sym9090179
APA StyleAkbulut, Y., Sengur, A., Guo, Y., & Smarandache, F. (2017). NS-k-NN: Neutrosophic Set-Based k-Nearest Neighbors Classifier. Symmetry, 9(9), 179. https://doi.org/10.3390/sym9090179








