Qinling: A Parametric Model in Speculative Multithreading
Abstract
:1. Introduction
2. Definitions and Motivations
2.1. Definitions
2.2. Motivations
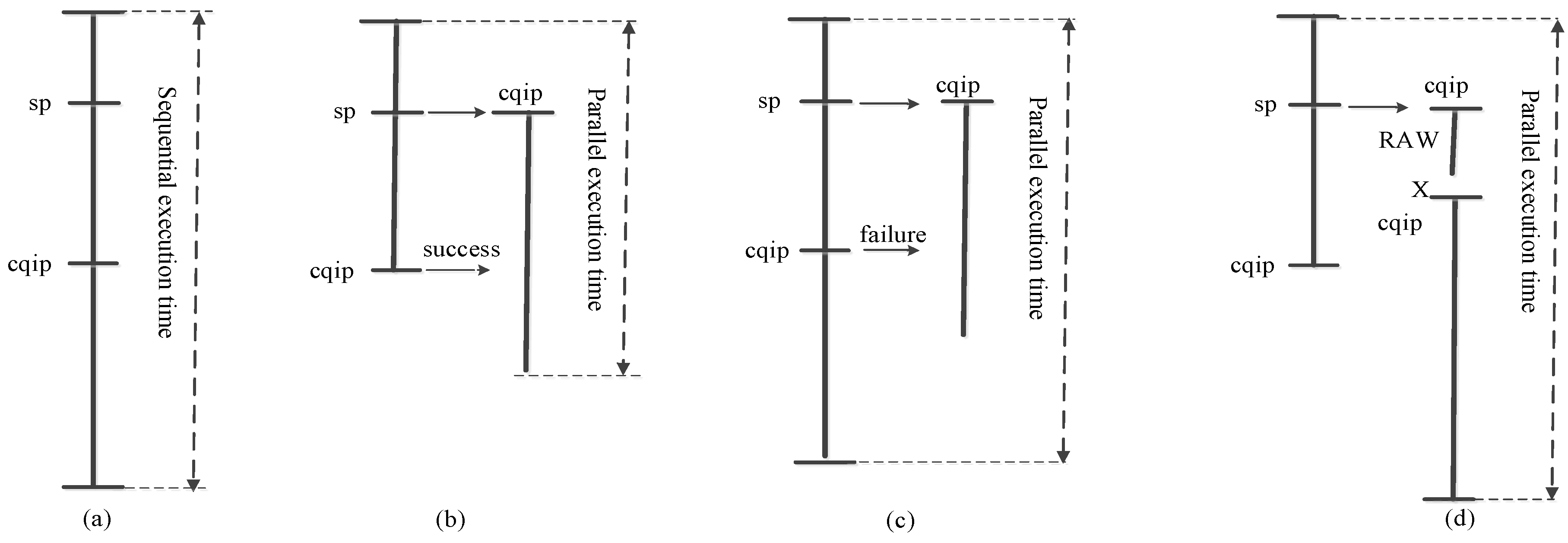
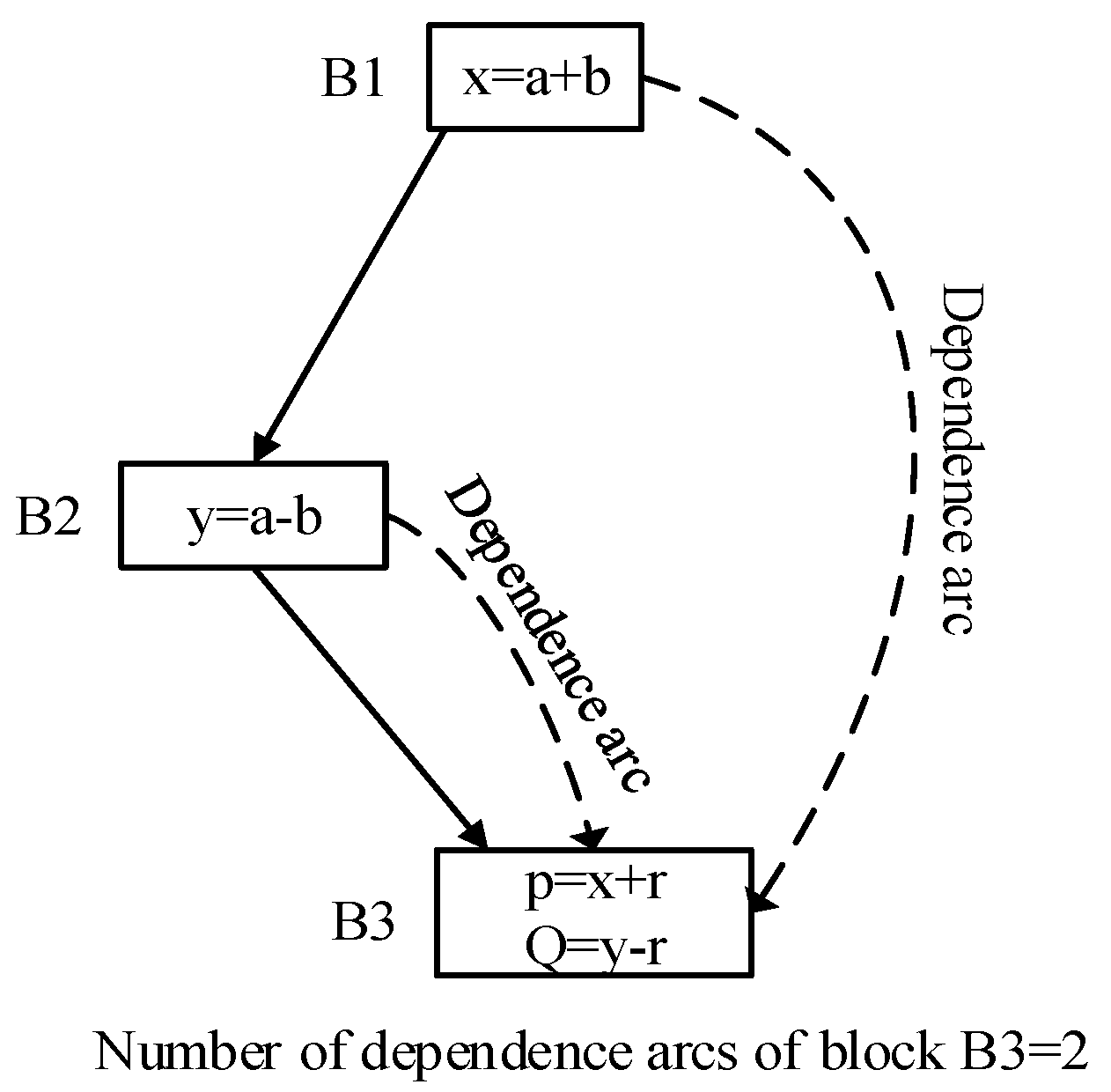
2.2.1. Motivation from Partition Algorithms
| Algorithm 1 Loop partition. |
| Input: Loop L Output: curr_thread partition_loop(loop L){ 1 start_block := entry block of loop L; 2 end_block := exit block of loop L; 3 likely_path := the most likely path from start_block to end_block; 4 opt_ddc := find_optimal_dependence(start_block, end_block, likely_path, &spawn_pos); 5 loop_size := the number of dynamic instructions in loop L; 6 if(loop_size<=THREAD_LOWER_LIMIT) 7 unroll(loop L); 8 else(opt_ddc< DEP_THRESHOLD) 9 curr_thread := create_new_thread(end_block, spawn_pos, likely_path); 10 end if 11 return curr_thread;} |
| Algorithm 2 Non-loop partition. |
| Input: start_block, end_block, curr_thread(candidate thread) Output: curr_thread partition_thread(start_block, end_block, curr_thread){ 1 if(start_block==end_block) then 2 return curr_thread; 3 end if 4 pdom_block := the nearest post dominator block of start_block; 5 likely_path:= the most likely path from start_block to pdom_block; 6 opt_ddc := find_optimal_dependence(pdom_block, curr_thread, &spawn_pos); 7 if(is_medium(thread_size) && opt_ddc<DEP_THRESHOLD) then 8 thread_size := curr_thread + sizeof (path); 9 finish_construction(curr_thread); 10 curr_thread := create_new_thread(pdom_block, spawn_pos, likely_path); 11 curr_thread = partition_thread(pdom_block, end_block, curr_thread); 12 else if(is_big(thread_size)) then 13 thread_size := curr_thread + path.first_block; 14 opt_ddc := find_optimal_dependence(path.first_block, curr_thread, null,&spawn_pos); 15 If(!is_small(thread_size) && opt_ddc< DEP_THRESHOLD) then 16 curr_thread:= curr_thread+path.first_block; 17 finish_construction(curr_thread); 18 curr_thread := create_new_thread(path.first_block,spawn_pos, likely_path); 19 curr_thread = partition_thread(path.first_block, end_block,curr_thread); 20 else 21 curr_thread := curr_thread + path; 22 curr_thread := curr_thread + pdom_block; 23 curr_thread := partition_thread(pdom_block, end_block, curr_thread); 24 end if 25 end if 26 return curr_thread;} |
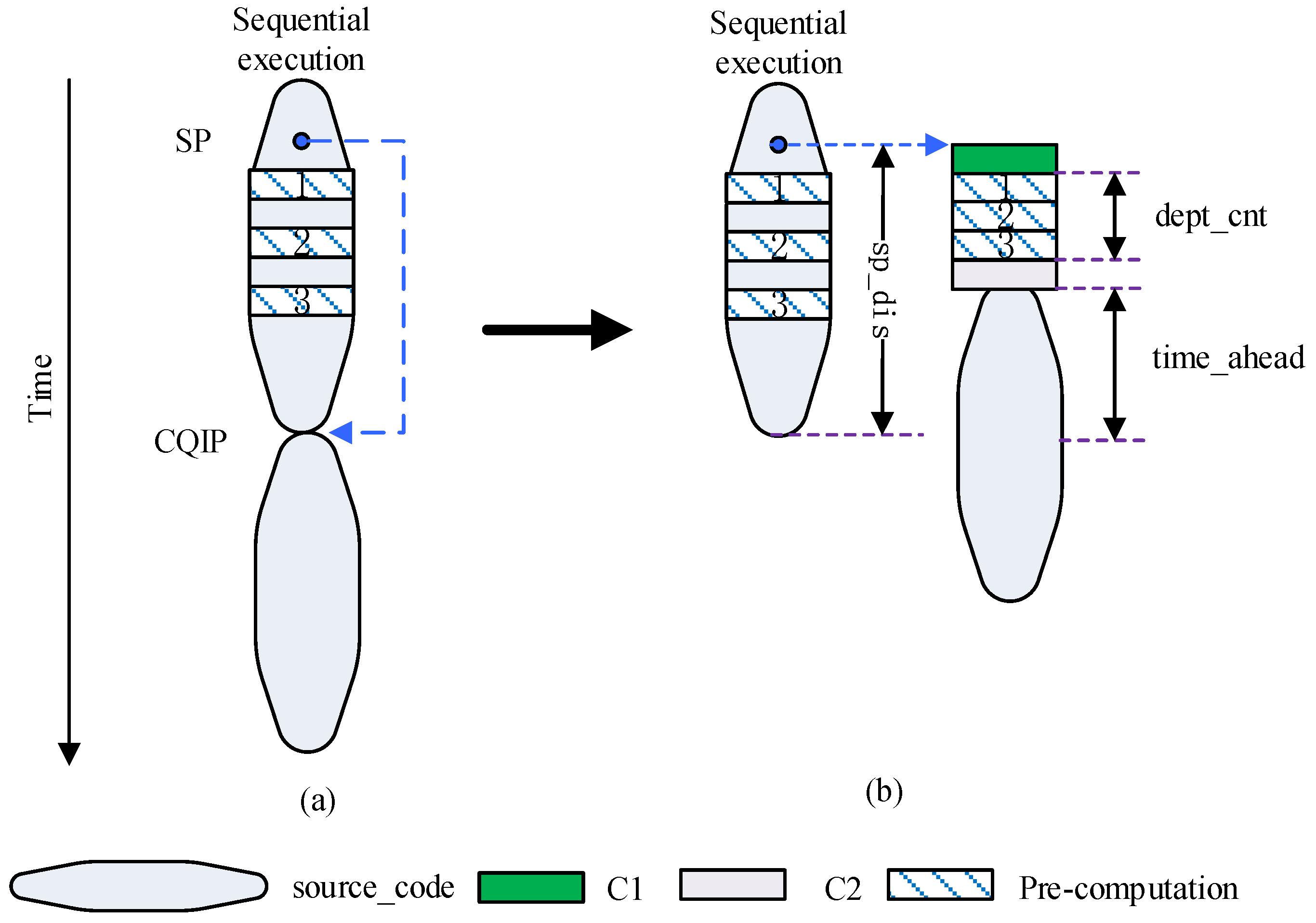
2.2.2. Motivation from Time_Ahead
2.2.3. Determination of Influencing Factors
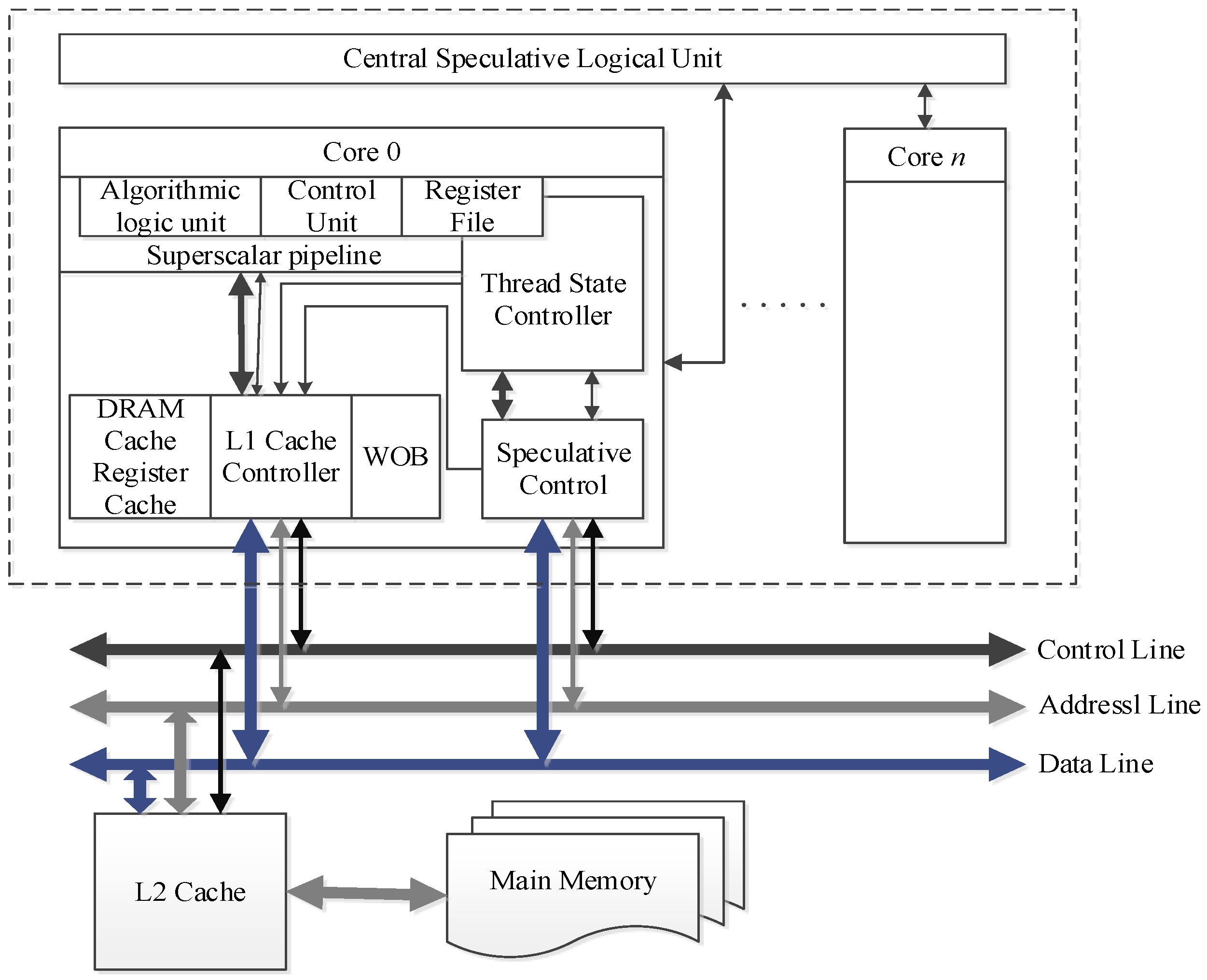
3. Speculative Multithreading
3.1. SpMT Execution Model
3.2. Pre-Computation Slices
3.3. Data Dependence Calculation
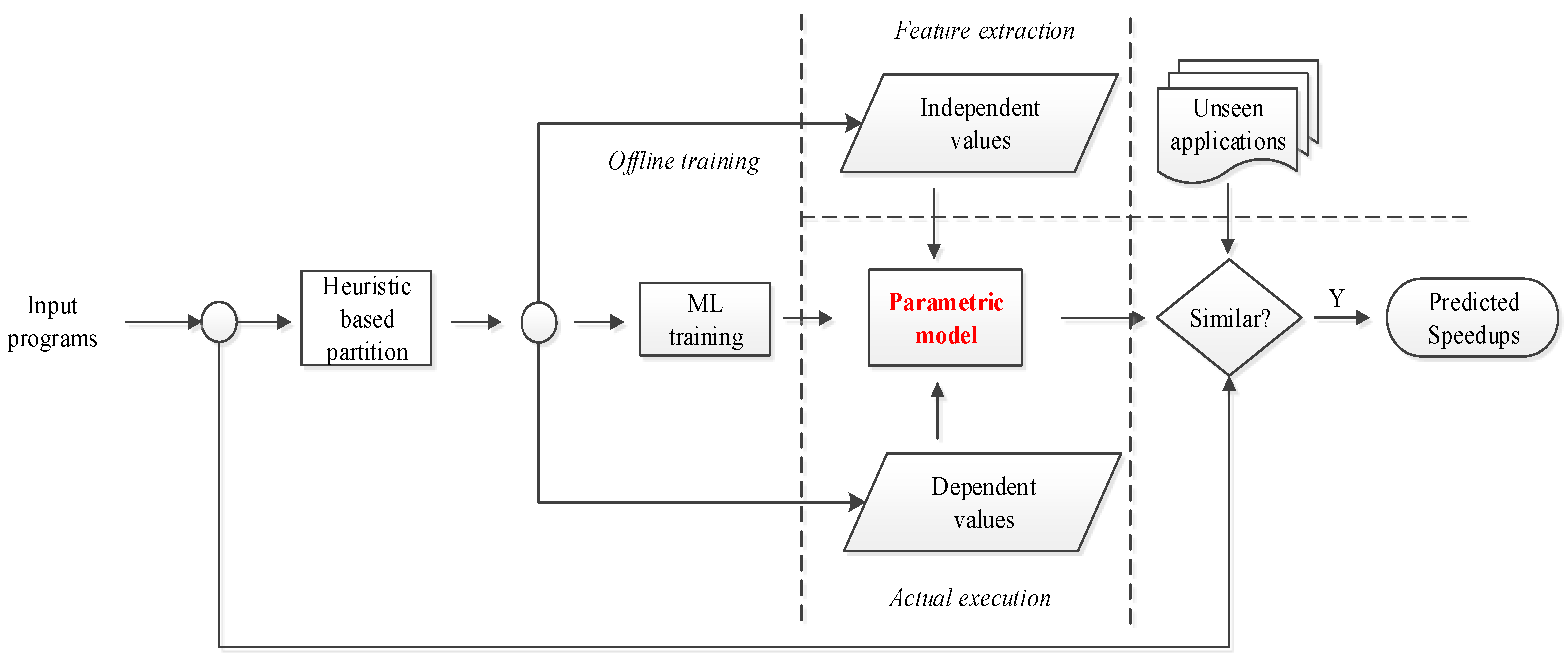
4. Model Building
4.1. Deployment
- Determination of influence factors;
- Setting of index variables;
- Gathering of statistical data;
- Determine the mathematical form of theoretical regression model;
- Estimation of model’s parameters;
- Validation and modification of model;
- Application of model.
4.2. Heuristic rules
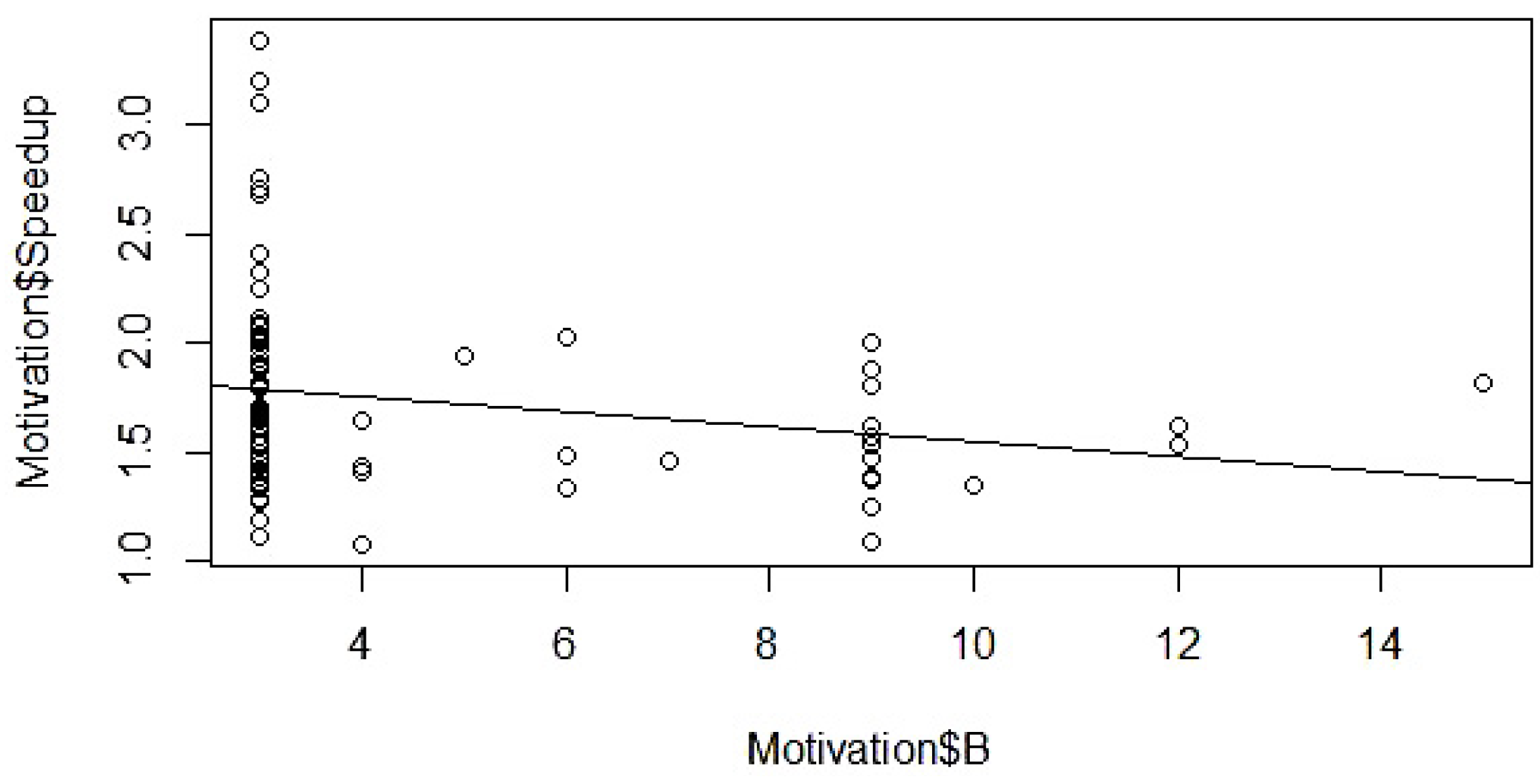
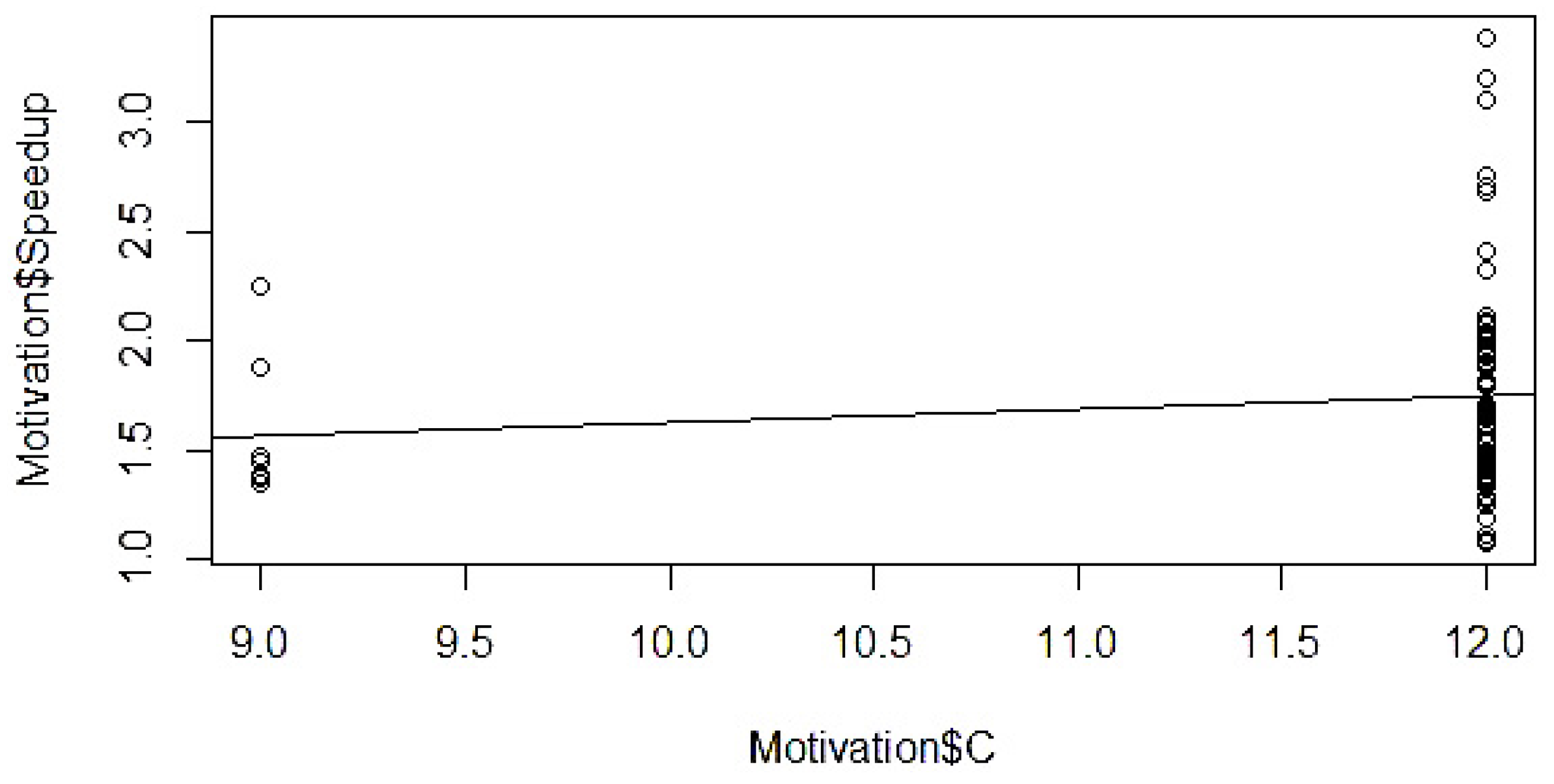
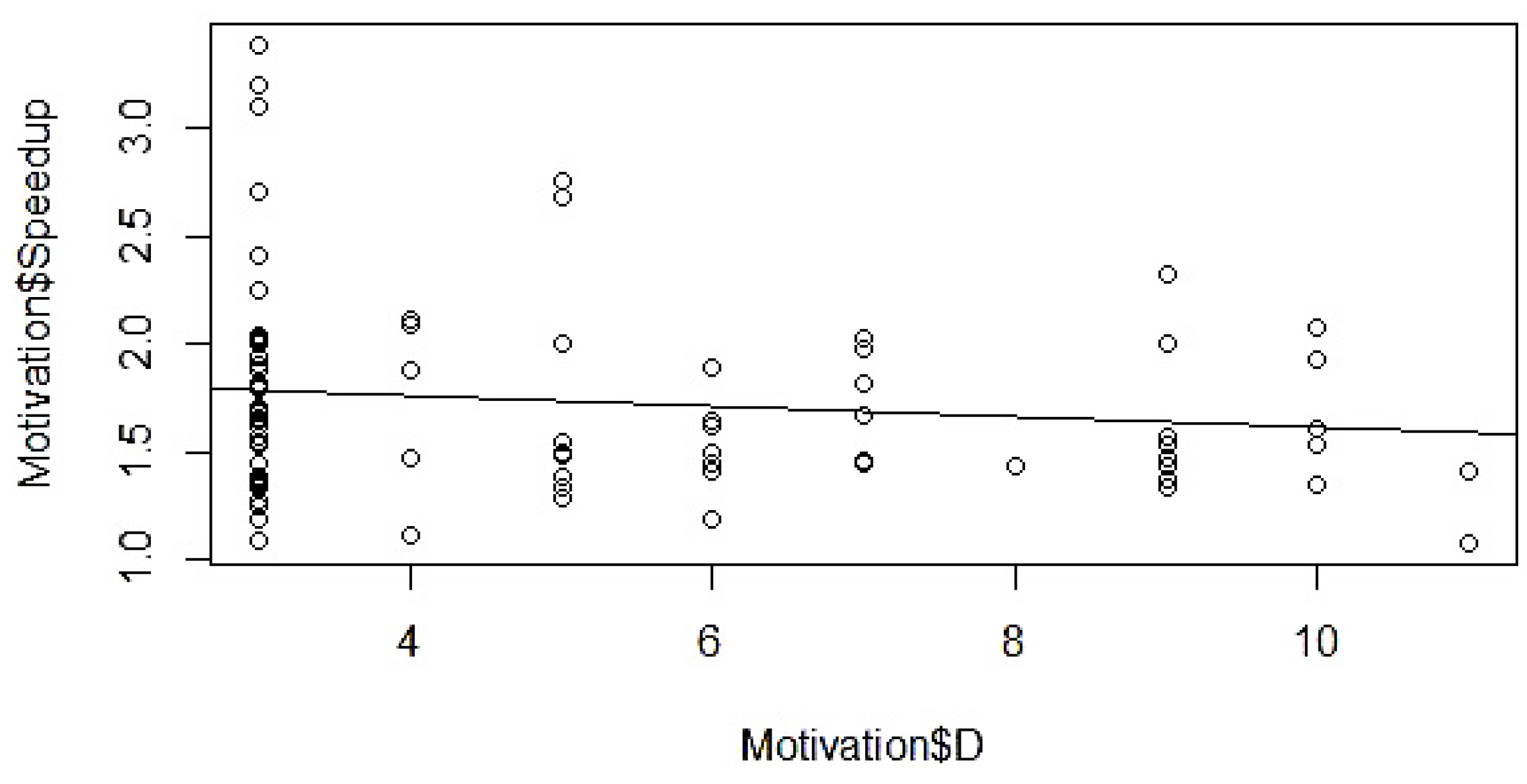
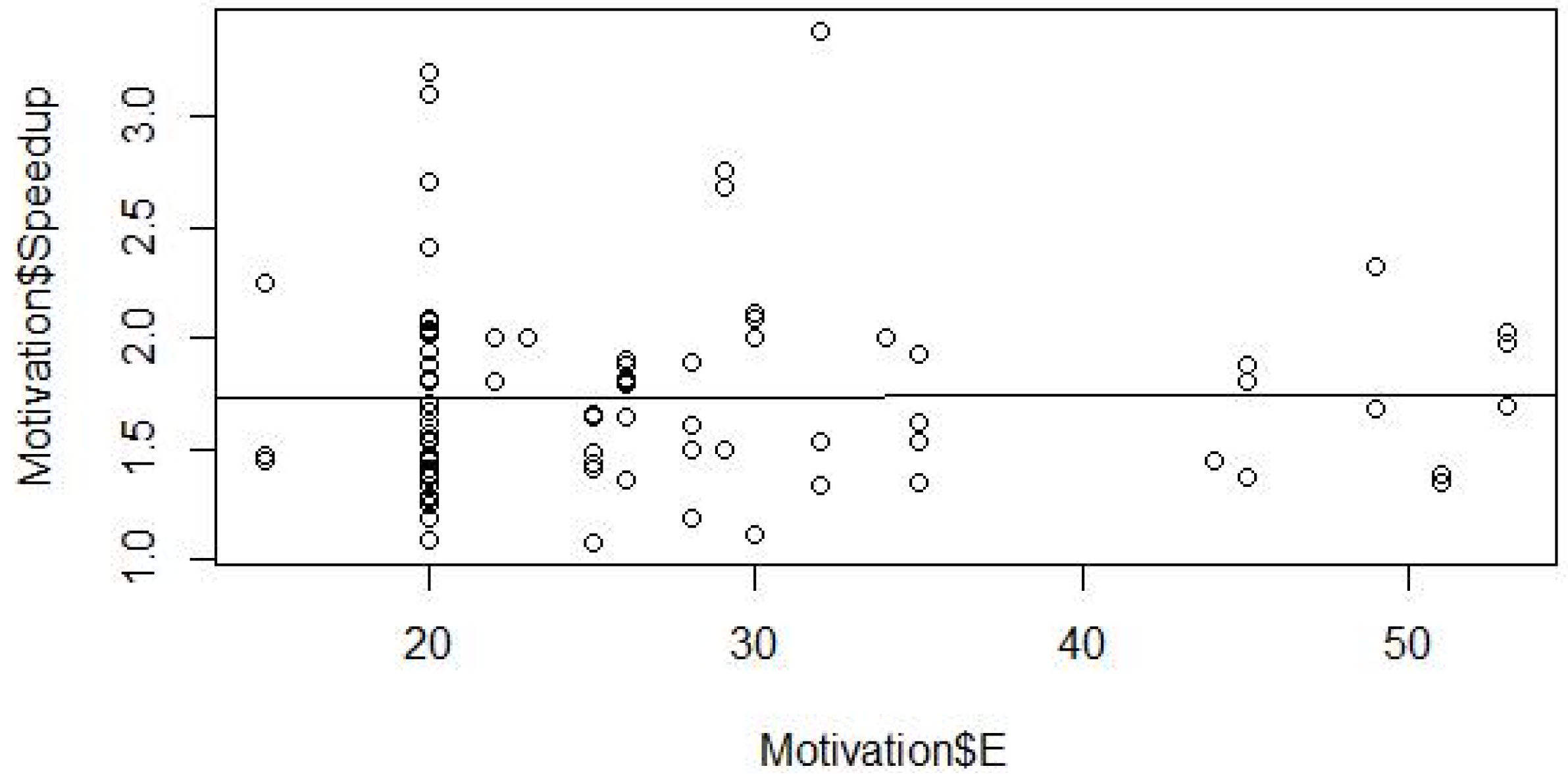
4.3. Index Variable Setting
4.4. Gathering of Statistical Data
4.5. Determination of Mathematical Form
4.6. Model Parameter Estimation
4.7. Validation and Modification
4.8. Application of Model
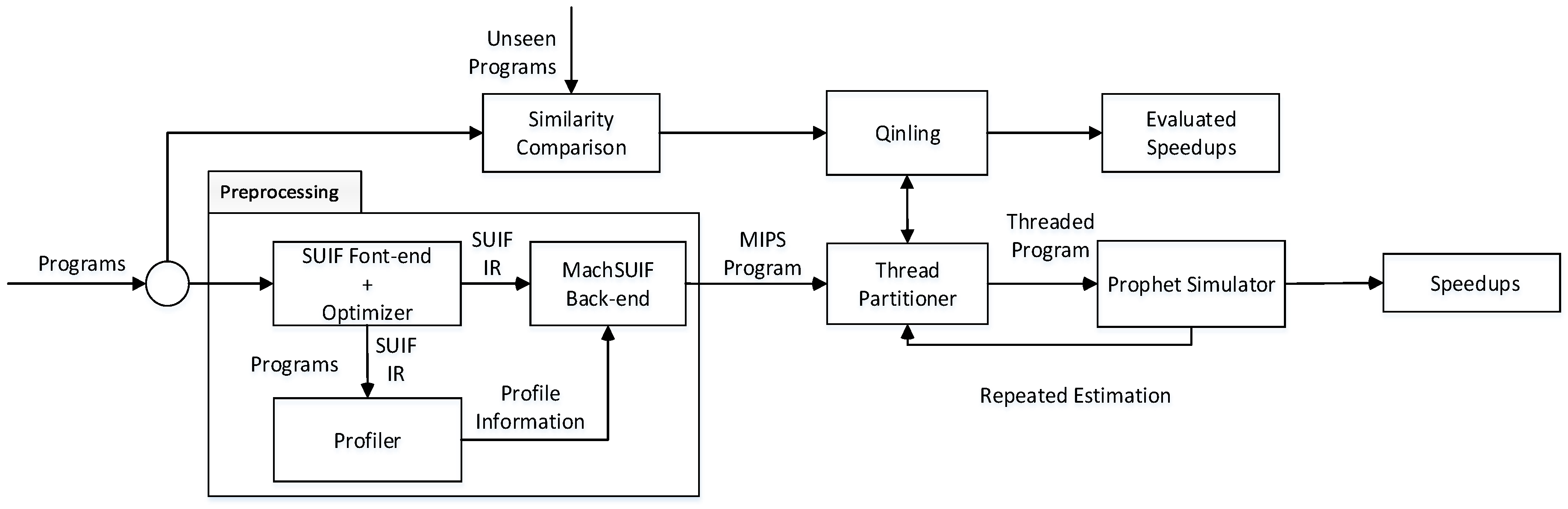
5. Experiment
5.1. Experiment Configuration
5.2. Experiment Assumption
5.3. Model Building
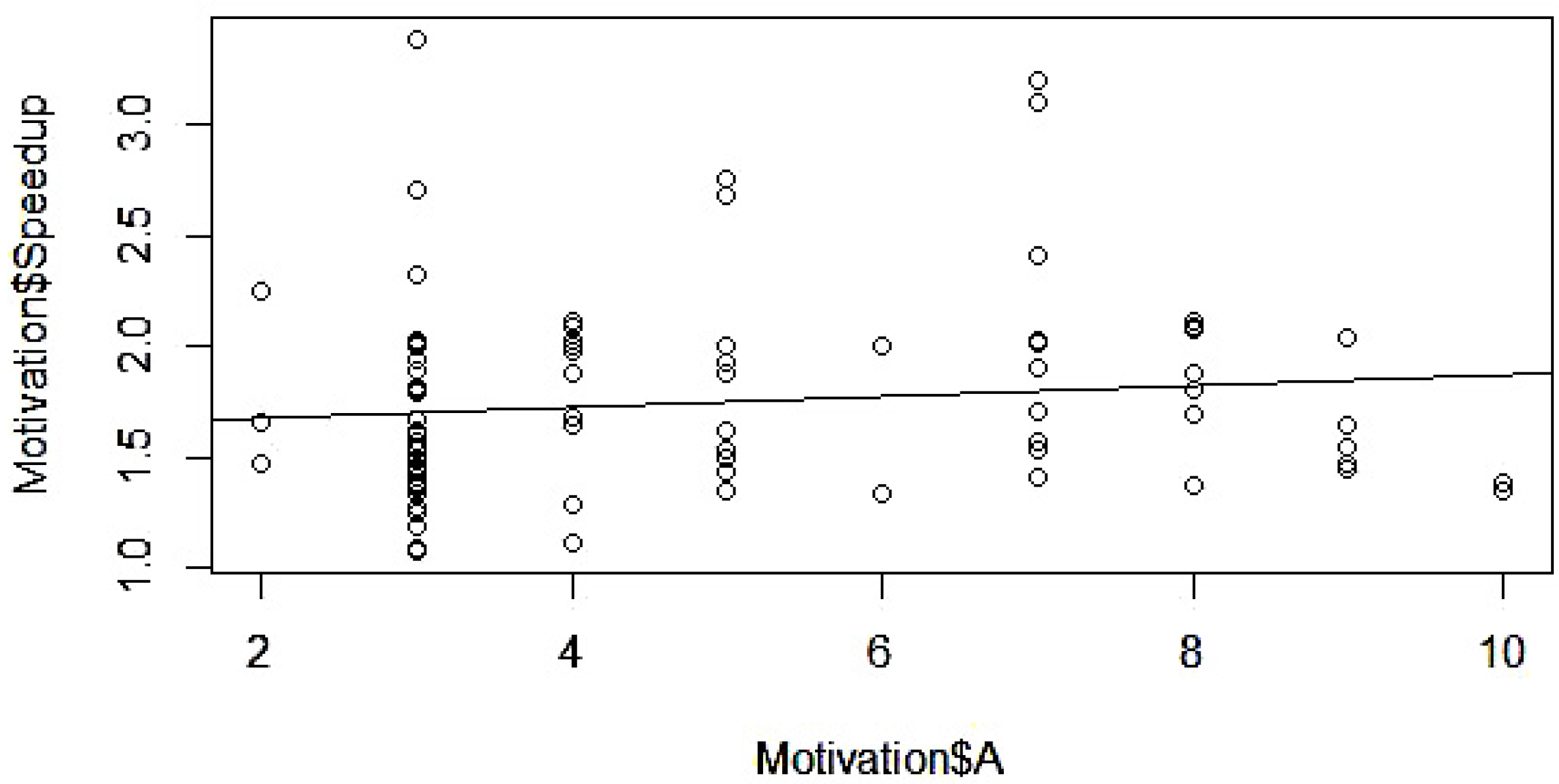
5.4. Model Validation
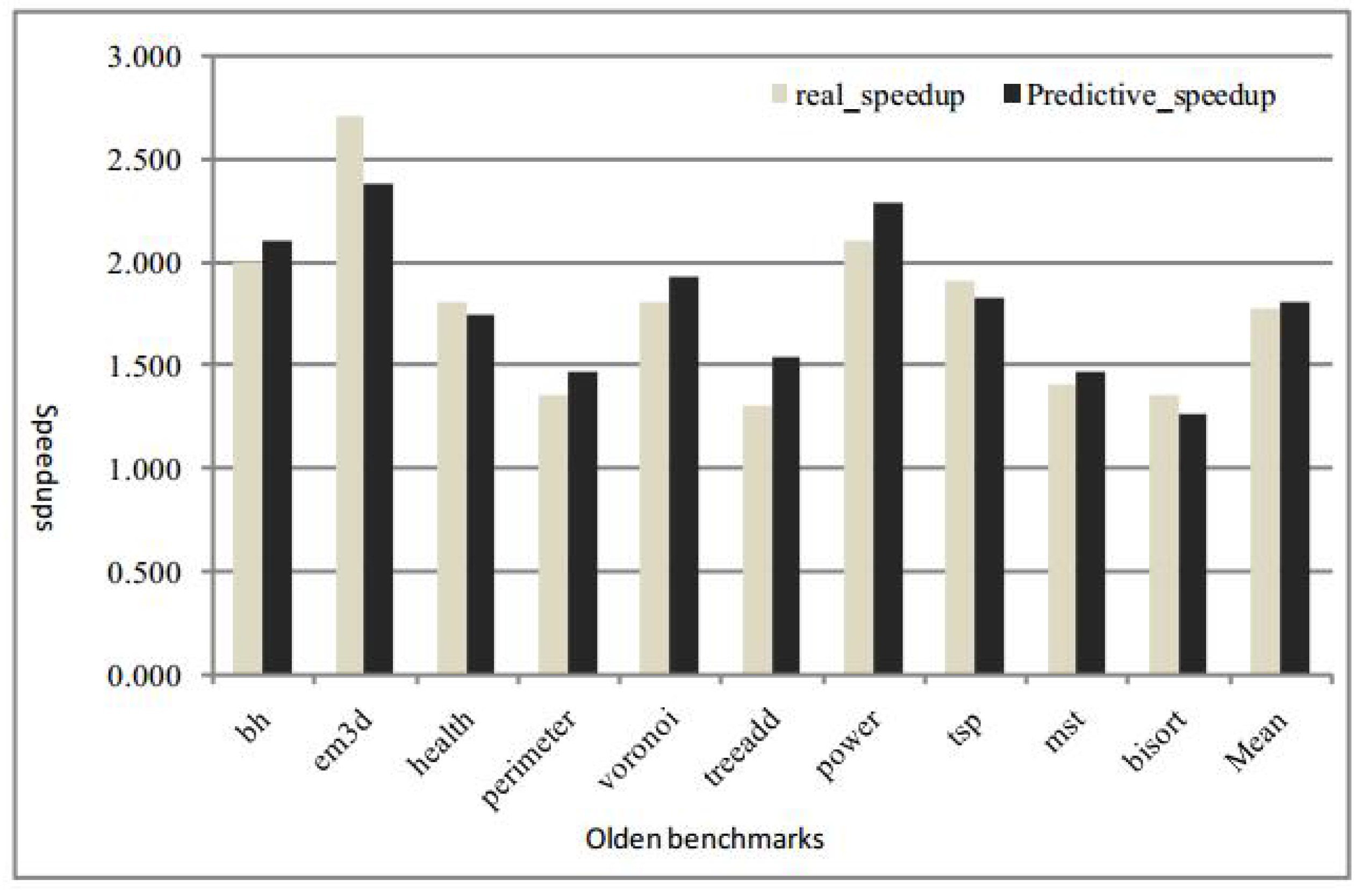
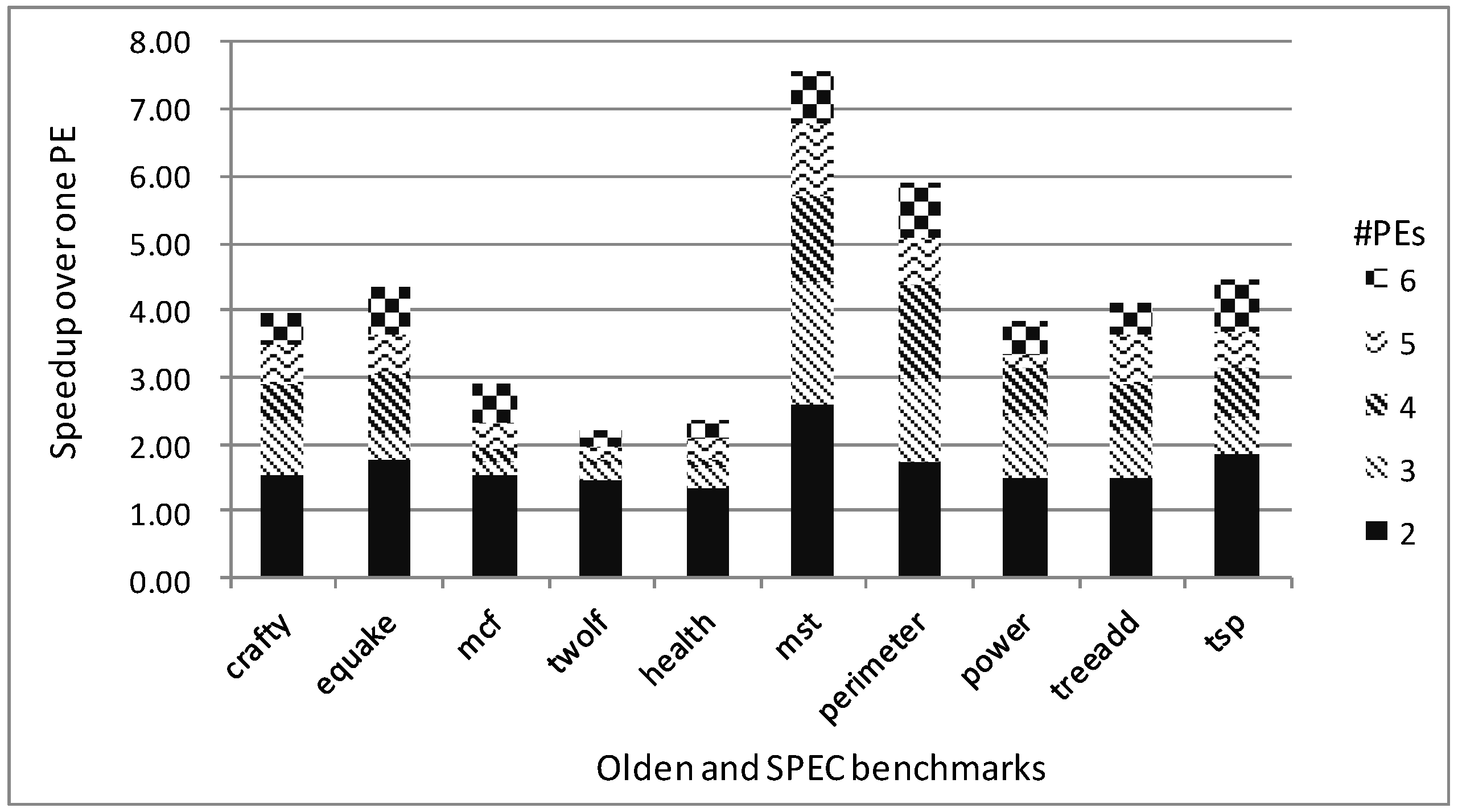
5.4.1. Speedup Prediction
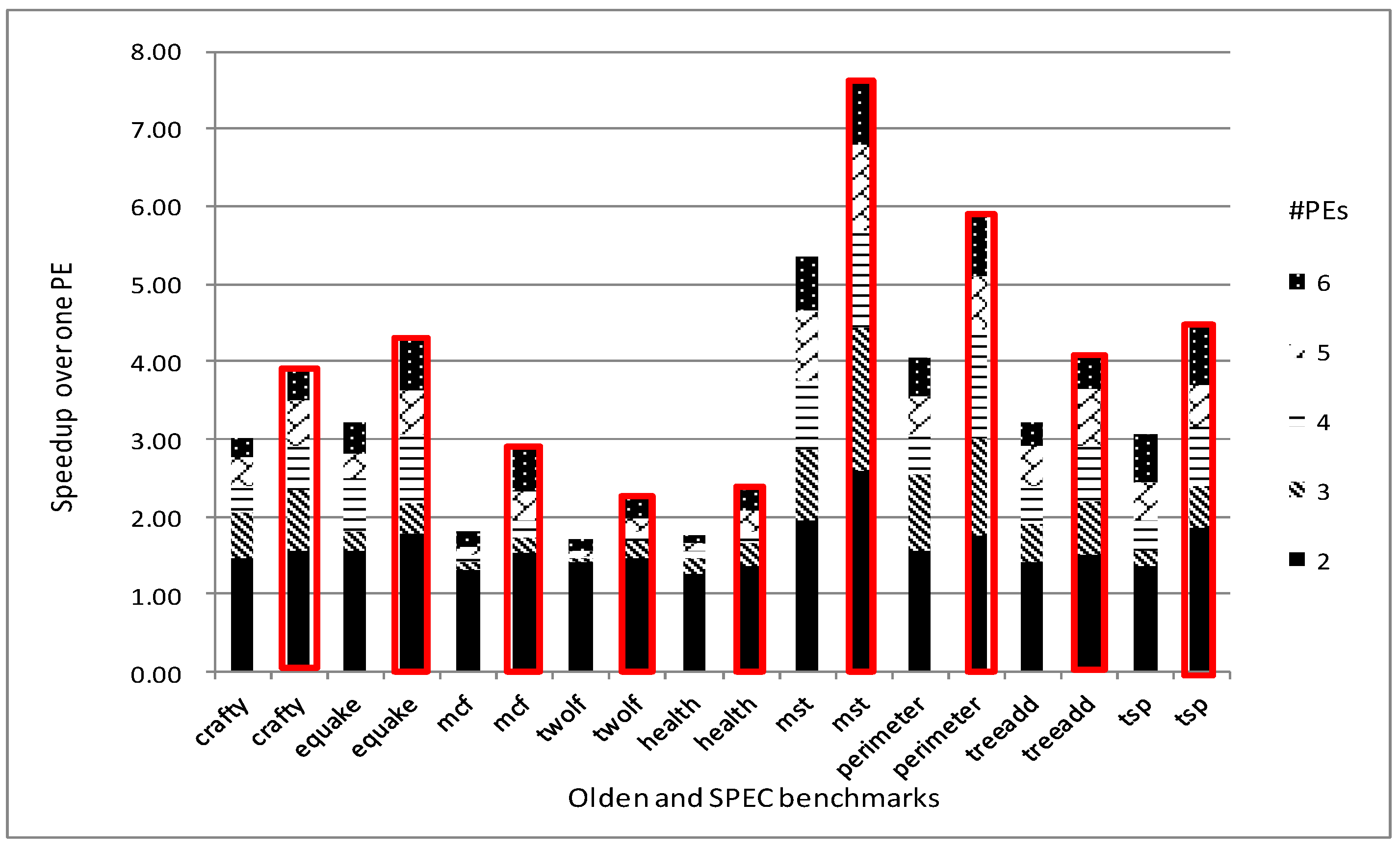
5.4.2. Feedback Guidance for Prophet
| Algorithm 3 Applying predicted results for loop partition. |
| Input: Loop L Output: curr_thread partition_loop(loop L){ 1 start_block := entry block of loop L; 2 end_block := exit block of loop L; 3 likely_path := the most likely path from start_block to end_block; 4 opt_ddc := find_optimal_dependence(start_block, end_block, likely_path, &spawn_pos); 5 loop_size := the number of dynamic instructions in loop L; 6 if(loop_size<=B) 7 unroll(loop L); 8 else((opt_ddc<A)&&(D<spawning_distance<E)&&(B<thread_size<C)) 9 curr_thread := create_new_thread(end_block, spawn_pos, likely_path); 10 end if 11 return curr_thread;} |
| Algorithm 4 Applying predicted results for nonloop partition. |
| Input: start_block, end_block, curr_thread(candidate thread) Output: curr_thread partition_thread(start_block, end_block,curr_thread){ 1 if(start_block == end_block) then 2 return curr_thread; 3 end if 4 pdom_block := the nearest post dominator block of start_block; 5 likely_path := the most likely path from start_block to pdom_block; 6 opt_ddc := find_optimal_dependence(pdom_block, curr_thread, &spawn_pos); 8 if((B+0.25(C-B)<thread_size<C-0.25(C-B)) && (opt_ddc<A)) then 9 thread_size := curr_thread + sizeof (path); 10 finish_construction(curr_thread); 11 curr_thread := create_new_thread(pdom_block, spawn_pos, likely_path); 12 curr_thread := partition_thread(pdom_block, end_block, curr_thread); 13 else if(C-0.25(C-B)<thread_size<C) then 14 thread_size := curr_thread + path.first_block; 15 opt_ddc:=find_optimal_dependence(path.first_block, curr_thread, null,&spawn_pos); 16 If((B+0.25(C-B)<thread_size<C) && (opt_ddc< A)) then 17 curr_thread := curr_thread+path.first_block; 18 finish_construction(curr_thread); 19 curr_thread := create_new_thread(path.first_block,spawn_pos, likely_path); 20 curr_thread := partition_thread(path.first_block, end_block,curr_thread); 21 else 22 curr_thread := curr_thread + path; 23 curr_thread := curr_thread + pdom_block; 24 curr_thread := partition_thread(pdom_block, end_block, curr_thread); 25 end if 26 end if 27 return curr_thread;} |
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Quiñones, C.G.; Madriles, C.; Sánchez, J.; Marcuello, P.; González, A.; Tullsen, D.M. Mitosis compiler: An infrastructure for speculative threading based on pre-computation slices. ACM Sigplan Notices 2005, 40, 269–279. [Google Scholar] [CrossRef]
- Madriles, C.; García-Quiñones, C.; Sánchez, J.; Marcuello, P.; González, A.; Tullsen, D.M.; Wang, H.; Shen, J.P. Mitosis: A speculative multithreaded processor based on precomputation slices. IEEE Trans. Parallel Distrib. Syst. 2008, 19, 914–925. [Google Scholar] [CrossRef]
- Ooi, C.L.; Kim, S.W.; Park, I.; Eigenmann, R.; Falsafi, B.; Vijaykumar, T. Multiplex: Unifying conventional and speculative thread-level parallelism on a chip multiprocessor. In Proceedings of the 15th International Conference on Supercomputing, Sorrento, Italy, 18–23 June 2001; pp. 368–380. [Google Scholar]
- Liu, W.; Tuck, J.; Ceze, L.; Ahn, W.; Strauss, K.; Renau, J.; Torrellas, J. POSH: A TLS compiler that exploits program structure. In Proceedings of the Eleventh ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, New York, NY, USA, 29–31 March 2006; pp. 158–167. [Google Scholar]
- Tournavitis, G.; Wang, Z.; Franke, B.; OBoyle, M.F. Towards a holistic approach to auto-parallelization: Integrating profile-driven parallelism detection and machine-learning based mapping. ACM Sigplan Not. 2009, 44, 177–187. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Y.; Gao, H. Using artificial neural network for predicting thread partitioning in speculative multithreading. In Proceedings of the 2015 IEEE 17th International Conference on High Performance Computing and Communications, 2015 IEEE 7th International Symposium on Cyberspace Safety and Security, and 2015 IEEE 12th International Conference on Embedded Software and Systems, New York, NY, USA, 24–26 August 2015; pp. 823–826. [Google Scholar]
- Zheng, B.; Tsai, J.Y.; Zang, B.; Chen, T.; Huang, B.; Li, J.; Ding, Y.; Liang, J.; Zhen, Y.; Yew, P.C.; et al. Designing the agassiz compiler for concurrent multithreaded architectures. In Proceedings of the International Workshop on Languages and Compilers for Parallel Computing, La Jolla, CA, USA, 4–6 August 1999; Springer: Berlin, Germany, 1999; pp. 380–398. [Google Scholar]
- Gao, L.; Li, L.; Xue, J.; Yew, P.C. SEED: A statically greedy and dynamically adaptive approach for speculative loop execution. IEEE Trans. Comput. 2013, 62, 1004–1016. [Google Scholar] [CrossRef]
- August, D.I.; Huang, J.; Beard, S.R.; Johnson, N.P.; Jablin, T.B. Automatically exploiting cross-invocation parallelism using runtime information. In Proceedings of the 2013 IEEE/ACM International Symposium on Code Generation and Optimization (CGO), Shenzhen, China, 23–27 Feburary 2013; IEEE Computer Society: Washington, DC, USA, 2013; pp. 1–11. [Google Scholar]
- Wang, S.; Yew, P.C.; Zhai, A. Code transformations for enhancing the performance of speculatively parallel threads. J. Circuits Syst. Comput. 2012, 21, 1240008. [Google Scholar] [CrossRef]
- Sohi, G. Multiscalar: Another fourth-generation processor. Computer 1997, 30, 72. [Google Scholar]
- Grewe, D.; Wang, Z.; O’Boyle, M.F. A workload-aware mapping approach for data-parallel programs. In Proceedings of the 6th International Conference on High Performance and Embedded Architectures and Compilers, Heraklion, Greece, 24–26 January 2011; pp. 117–126. [Google Scholar]
- Long, S.; Fursin, G.; Franke, B. A cost-aware parallel workload allocation approach based on machine learning techniques. In Proceedings of the IFIP International Conference on Network and Parallel Computing, Dalian, China, 18–21 September 2007; Springer: Berlin, Germany, 2007; pp. 506–515. [Google Scholar]
- Wang, Z.; O’Boyle, M.F. Partitioning streaming parallelism for multi-cores: A machine learning based approach. In Proceedings of the 19th international conference on Parallel architectures and compilation techniques, Vienna, Austria, 11–15 Sepetember 2010; pp. 307–318. [Google Scholar]
- Wang, Z.; O’Boyle, M.F.P. Mapping parallelism to multi-cores: A machine learning based approach. In Proceedings of the ACM Sigplan Symposium on Principles and Practice of Parallel Programming, PPOPP 2009, Raleigh, NC, USA, 14–18 February 2009; pp. 75–84. [Google Scholar]
- Singer, J.; Yiapanis, P.; Pocock, A.; Lujan, M.; Brown, G.; Ioannou, N.; Cintra, M. Static java program features for intelligent squash prediction. In Proceedings of the Statistical and Machine learning approaches to ARchitecture and compilaTion (SMART’10), Pisa, Italy, 24 January 2010; p. 14. [Google Scholar]
- Chen, X.; Long, S. Adaptive multi-versioning for OpenMP parallelization via machine learning. In Proceedings of the 2009 15th International Conference on Parallel and Distributed Systems (ICPADS), Shenzhen, China, 9–11 December 2009; pp. 907–912. [Google Scholar]
- Liu, B.; Zhao, Y.; Zhong, X.; Liang, Z.; Feng, B. A novel thread partitioning approach based on machine learning for speculative multithreading. In Proceedings of the 2013 IEEE 10th International Conference on High Performance Computing and Communications & 2013 IEEE International Conference on Embedded and Ubiquitous Computing, Zhangjiajie, China, 13–15 November 2013; pp. 826–836. [Google Scholar]
- Monsifrot, A.; Bodin, F.; Quiniou, R. A machine learning approach to automatic production of compiler heuristics. In Proceedings of the International Conference on Artificial Intelligence: Methodology, Systems, and Applications, Varna, Bulgaria, 4–6 September 2002; Springer: Berlin, Germany, 2002; pp. 41–50. [Google Scholar]
- Stephenson, M.; Amarasinghe, S. Predicting unroll factors using supervised classification. In Proceedings of the International Symposium on Code Generation and Optimization, San Jose, CA, USA, 20–23 March 2005; pp. 123–134. [Google Scholar]
- Agakov, F.; Bonilla, E.; Cavazos, J.; Franke, B.; Fursin, G.; O’Boyle, M.F.; Thomson, J.; Toussaint, M.; Williams, C.K. Using machine learning to focus iterative optimization. In Proceedings of the International Symposium on Code Generation and Optimization, Manhattan, NY, USA, 26–29 March 2006; IEEE Computer Society: Washington, DC, USA, 2006; pp. 295–305. [Google Scholar]
- Cavazos, J.; Dubach, C.; Agakov, F.; Bonilla, E.; O’Boyle, M.F.; Fursin, G.; Temam, O. Automatic performance model construction for the fast software exploration of new hardware designs. In Proceedings of the 2006 International Conference on Compilers, Architecture and Synthesis for Embedded Systems, Seoul, Korea, 22–27 October 2006; pp. 24–34. [Google Scholar]
- Wang, Z.; Powell, D.; Franke, B.; OBoyle, M. Exploitation of GPUs for the parallelisation of probably parallel legacy code. In Proceedings of the International Conference on Compiler Construction, Grenoble, France, 5–13 April 2014; Springer: Berlin, Germany, 2014; pp. 154–173. [Google Scholar]
- Luk, C.K.; Hong, S.; Kim, H. Qilin: Exploiting parallelism on heterogeneous multiprocessors with adaptive mapping. In Proceedings of the 2009 42nd Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), New York, NY, USA, 12–16 December 2009; pp. 45–55. [Google Scholar]
- Khan, S.; Xekalakis, P.; Cavazos, J.; Cintra, M. Using predictive modeling for cross-program design space exploration in multicore systems. In Proceedings of the 16th International Conference on Parallel Architecture and Compilation Techniques, Brasov, Romania, 15–19 September 2007; IEEE Computer Society: Washington, DC, USA, 2007; pp. 327–338. [Google Scholar]
- Lee, B.C.; Brooks, D.M. Accurate and efficient regression modeling for microarchitectural performance and power prediction. ACM SIGOPS Oper. Syst. Rev. 2006, 40, 185–194. [Google Scholar] [CrossRef]
- Yang, S.; Shafik, R.A.; Merrett, G.V.; Stott, E.; Levine, J.M.; Davis, J.; Al-Hashimi, B.M. Adaptive energy minimization of embedded heterogeneous systems using regression-based learning. In Proceedings of the 2015 25th International Workshop on Power and Timing Modeling, Optimization and Simulation (PATMOS), Bahia, Brazil, 1–4 September 2015; pp. 103–110. [Google Scholar]
- Cavazos, J.; O’boyle, M.F. Method-specific dynamic compilation using logistic regression. ACM Sigplan Not. 2006, 41, 229–240. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, Y.L.; Pan, X.Y.; Dong, Z.Y.; Gao, B.; Zhong, Z.W. An overview of Prophet. In Proceedings of the International Conference on Algorithms and Architectures for Parallel Processing, Taipei, Taiwan, 8–11 June 2009; Springer: Berlin, Germany, 2009; pp. 396–407. [Google Scholar]
- Dong, Z.; Zhao, Y.; Wei, Y.; Wang, X.; Song, S. Prophet: A speculative multi-threading execution model with architectural support based on CMP. In Proceedings of the 2009 International Conference on Scalable Computing and Communications, Eighth International Conference on Embedded Computing. Dalian, China, 25–27 September 2009; pp. 103–108. [Google Scholar]
- Liu, B.; Zhao, Y.; Li, Y.; Sun, Y.; Feng, B. A thread partitioning approach for speculative multithreading. J. Supercomput. 2014, 67, 778–805. [Google Scholar] [CrossRef]
- Bhowmik, A.; Franklin, M. A general compiler framework for speculative multithreading. In Proceedings of the Fourteenth Annual ACM Symposium on Parallel Algorithms and Architectures, Winnipeg, MB, Canada, 11–13 August 2002; pp. 99–108. [Google Scholar]
- Cao, Z.; Verbrugge, C. Mixed model universal software thread-level speculation. In Proceedings of the 2013 42nd International Conference on Parallel Processing, Lyon, France, 1–4 October 2013; pp. 651–660. [Google Scholar]
- Wilson, R.P.; French, R.S.; Wilson, C.S.; Amarasinghe, S.P.; Anderson, J.M.; Tjiang, S.W.; Liao, S.W.; Tseng, C.W.; Hall, M.W.; Lam, M.S.; et al. SUIF: An infrastructure for research on parallelizing and optimizing compilers. ACM Sigplan Not. 1994, 29, 31–37. [Google Scholar] [CrossRef]
- Holmes, G.; Donkin, A.; Witten, I.H. Weka: A machine learning workbench. In Proceedings of the 1994 Second Australian and New Zealand Conference on Intelligent Information Systems, Brisbane, Australia, 29 November–2 December 1994; pp. 357–361. [Google Scholar]
- Hammond, L.; Hubbert, B.A.; Siu, M.; Prabhu, M.K.; Chen, M.; Olukolun, K. The stanford hydra CMP. IEEE Micro 2000, 20, 71–84. [Google Scholar] [CrossRef]
- Carlisle, M.C. Olden: Parallelizing Programs with Dynamic Data Structures on Distributed-Memory Machines. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1996. [Google Scholar]
- Compiler, M.S.B. The Machine-SUIF 2.1 Compiler Documentation Set; Harvard University: Cambridge, MA, USA, 2000. [Google Scholar]
- Chen, Y. A cramer rule for solution of the general restricted linear equation? Linear Multilinear Algebra 1993, 34, 177–186. [Google Scholar] [CrossRef]
| Influencing Factors | Independent Variables | Dependent Variables |
|---|---|---|
| spawning distance, dependence count, and thread granularity | DDC, LLoTG, ULoTG, LLoSD, ULoSD. | Speedup |
| Configuration Parameter | Value |
|---|---|
| Fetch, In-order Issue and Commit bandwidth | 4 Instructions |
| Pipeline Stages | Fetch/Issue/Ex/WB/Commit |
| Architectural Registers | 32 int and 32 fp |
| Function Units | 16 int ALU (1 cycle) |
| int Mult/Div (3/12 Cycles) | |
| fp ALU (2 Cycles) | |
| fp Mult/Div (4/12 Cycles) | |
| L1-Cache(Multiversion) | 4-Way Associative 64KB (32B/Block) |
| Hit Latency 2 | |
| LRU Replacement | |
| Spec. Buffer Size | Fully Associative 2KB (1 Cycle) |
| L2-Cache(Share) | 4-Way Associative 2MB (64B/block) |
| 5 hit latency, 80 cycles(miss) | |
| LRU replacement | |
| Spawn Overhead | 5 Cycles |
| Validation Overhead | 15 Cycles |
| Local Register | 1 Cycle |
| Commit Overhead | 5 Cycles |
| Benchmark | Item Count | Speedups |
|---|---|---|
| voronoi | 17 | 1.92052 |
| treeadd | 3 | 1.33622 |
| power | 17 | 2.08553 |
| perimeter | 11 | 1.26772 |
| mst | 12 | 1.36551 |
| health | 13 | 1.64411 |
| em3d | 14 | 2.27579 |
| bh | 10 | 1.99481 |
| Testing Samples | Parameter Values | |||||
|---|---|---|---|---|---|---|
| A | B | C | D | E | Sp | |
| compute_nodes | 3 | 4 | 12 | 3 | 24 | 1.57143 |
| initialize_graph | 5 | 3 | 12 | 8 | 29 | 1.8 |
| lrand48 | 3 | 5 | 12 | 3 | 20 | 1.8 |
| drand48 | 3 | 3 | 12 | 4 | 23 | 1.25 |
| srand48 | 3 | 3 | 12 | 3 | 20 | 2.59048 |
| init_random | 3 | 3 | 12 | 3 | 20 | 1.45711 |
| gen_number | 3 | 3 | 12 | 3 | 20 | 1.34615 |
| gen_signed_number | 3 | 3 | 12 | 3 | 20 | 1.29032 |
| gen_uniform_double | 3 | 3 | 12 | 3 | 20 | 1.33333 |
| check_percent | 3 | 3 | 12 | 5 | 24 | 1.34146 |
| fill_table | 5 | 7 | 12 | 5 | 21 | 1.48148 |
| make_neighbors | 6 | 5 | 11 | 5 | 38 | 1.42958 |
| update_from_coeffs | 5 | 8 | 12 | 7 | 26 | 1.46672 |
| fill_from_fields | 5 | 4 | 12 | 3 | 24 | 1.25116 |
| dealwithargs | 6 | 3 | 12 | 3 | 25 | 2.7734 |
| print_graph | 3 | 5 | 12 | 3 | 24 | 1.26829 |
| dealwithargs | 6 | 4 | 10 | 3 | 23 | 2.75573 |
| my_rand | 4 | 3 | 12 | 6 | 34 | 2.3292 |
| generate_patient | 5 | 6 | 12 | 6 | 21 | 1.57143 |
| put_in_hosp | 3 | 3 | 12 | 3 | 22 | 1.8 |
| addList | 3 | 5 | 12 | 5 | 25 | 2.0231 |
| removeList | 3 | 4 | 12 | 5 | 25 | 1.81421 |
| sim | 6 | 3 | 12 | 3 | 32 | 2.54631 |
| check_patients_inside | 3 | 5 | 12 | 5 | 23 | 1.83007 |
| check_patients_assess | 3 | 3 | 12 | 3 | 22 | 2.70452 |
| check_patients_waiting | 7 | 3 | 12 | 3 | 24 | 2.01973 |
| get_results | 7 | 3 | 12 | 3 | 31 | 1.22222 |
| alloc_tree | 7 | 3 | 12 | 3 | 34 | 1.38029 |
| main | 3 | 3 | 12 | 6 | 21 | 1.67238 |
| Segment |
|---|
| Input:Predicted Sp |
| Output: Optimal values of B,C,D,E |
| clear; clc; |
| p = 1;T = zeros(810000,4); |
| for B = 1:1:30 for C = 1:1:30 for D = 1:1:30 |
| for E = 1:1:30 if(B<C && D<E) |
| Sp = –0.212*B + 0.582*C – 1.209*D – 0.060*E; |
| T(p,1) = B; T(p,2) = C;T(p,3) = D; T(p,4) = E; |
| p = p + 1; |
| end; end; end; end; end; |
| y = max(S) |
| T(find(y==S(:)),:) |
| Speedups | Optimal Solution | |||
|---|---|---|---|---|
| B | C | D | E | |
| 15.919 | 1 | 30 | 1 | 2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhao, Y.; Liu, B. Qinling: A Parametric Model in Speculative Multithreading. Symmetry 2017, 9, 180. https://doi.org/10.3390/sym9090180
Li Y, Zhao Y, Liu B. Qinling: A Parametric Model in Speculative Multithreading. Symmetry. 2017; 9(9):180. https://doi.org/10.3390/sym9090180
Chicago/Turabian StyleLi, Yuxiang, Yinliang Zhao, and Bin Liu. 2017. "Qinling: A Parametric Model in Speculative Multithreading" Symmetry 9, no. 9: 180. https://doi.org/10.3390/sym9090180
APA StyleLi, Y., Zhao, Y., & Liu, B. (2017). Qinling: A Parametric Model in Speculative Multithreading. Symmetry, 9(9), 180. https://doi.org/10.3390/sym9090180





