A Sparse Signal Reconstruction Method Based on Improved Double Chains Quantum Genetic Algorithm
Abstract
1. Introduction
2. Data Models of the Redundant Dictionary and FOMP Algorithm
2.1. Redundant Dictionary
2.2. OMP
2.3. The Proposed FOMP Algorithm
3. IDCQGA-Based FOMP Algorithm
3.1. The Principle of DCQGA
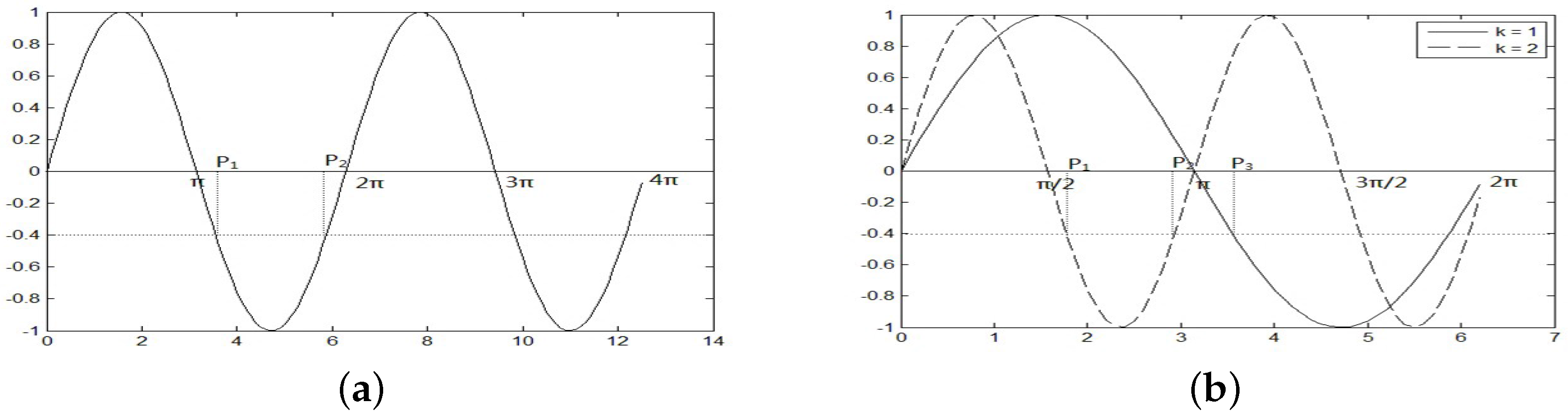
3.1.1. Double Chains Qubit Encoding
3.1.2. Quantum Rotation Gate Updating
3.1.3. Quantum Chromosome Mutation
3.2. The Proposed IDCQGA
3.2.1. High Density Qubit Encoding
3.2.2. Adaptive Step Size for Updating
3.2.3. Quantum -Gate for Mutation
3.3. FOMP Algorithm Combined with IDCQGA
4. Simulation Results and Analysis
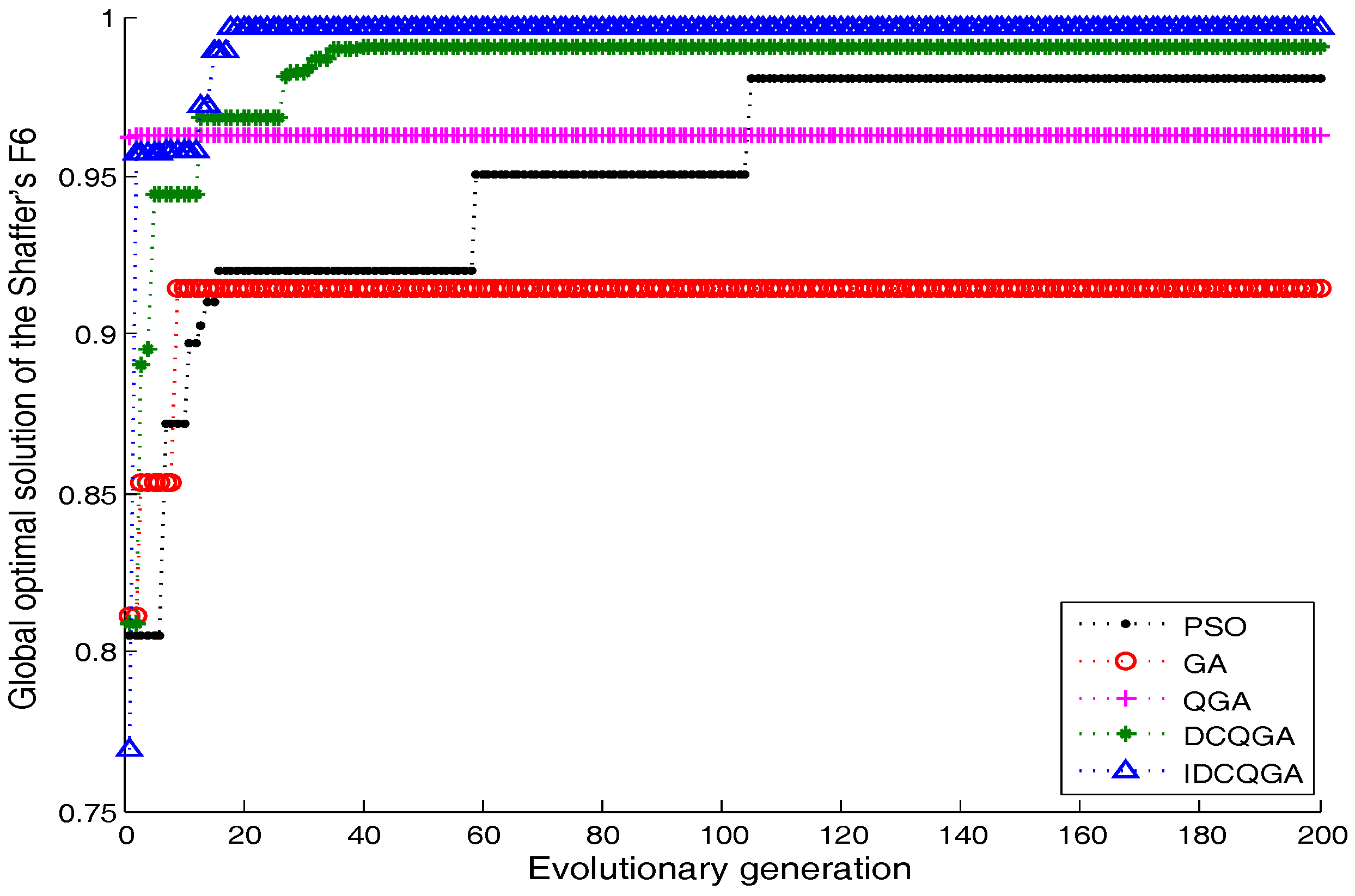
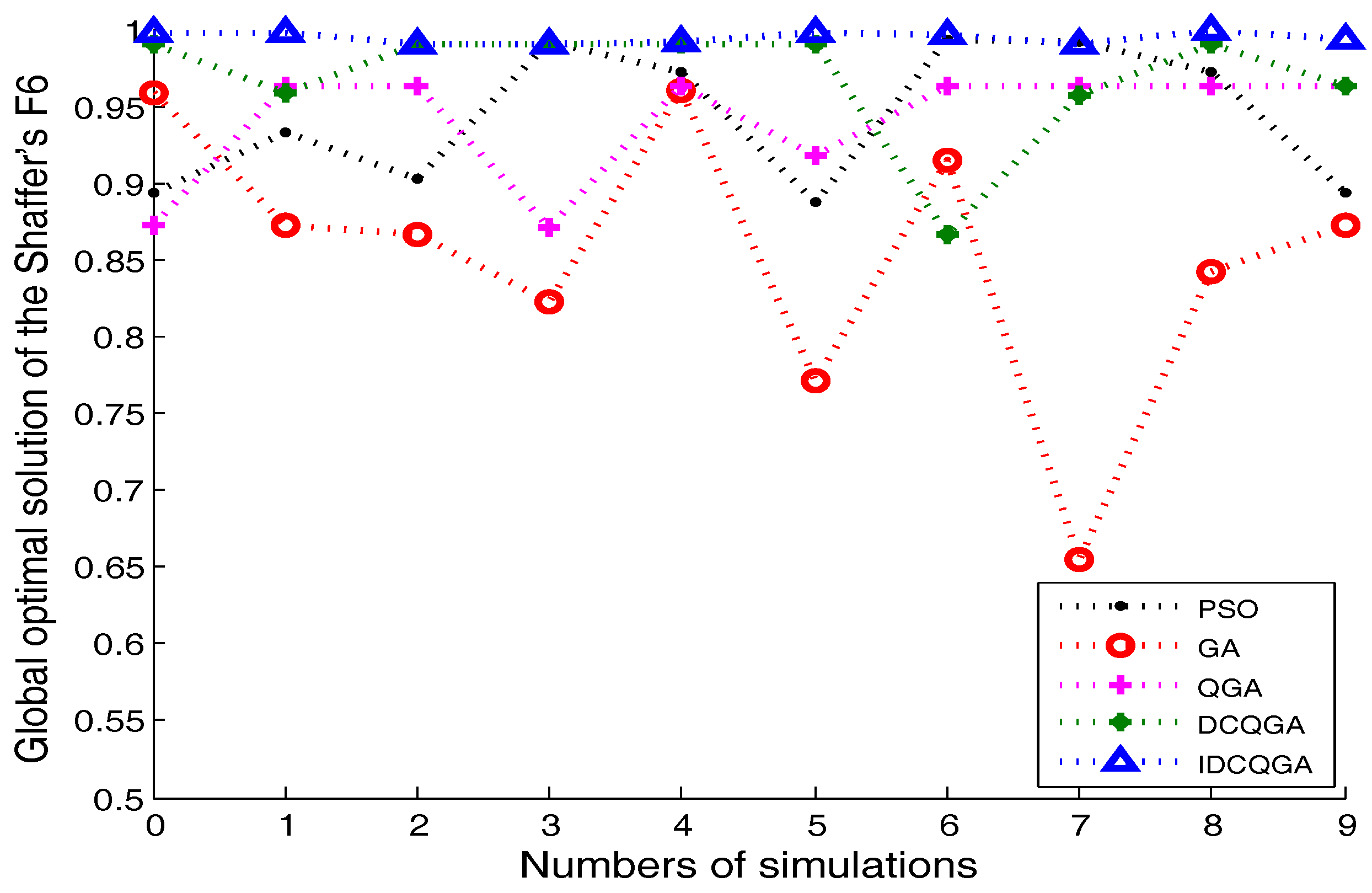
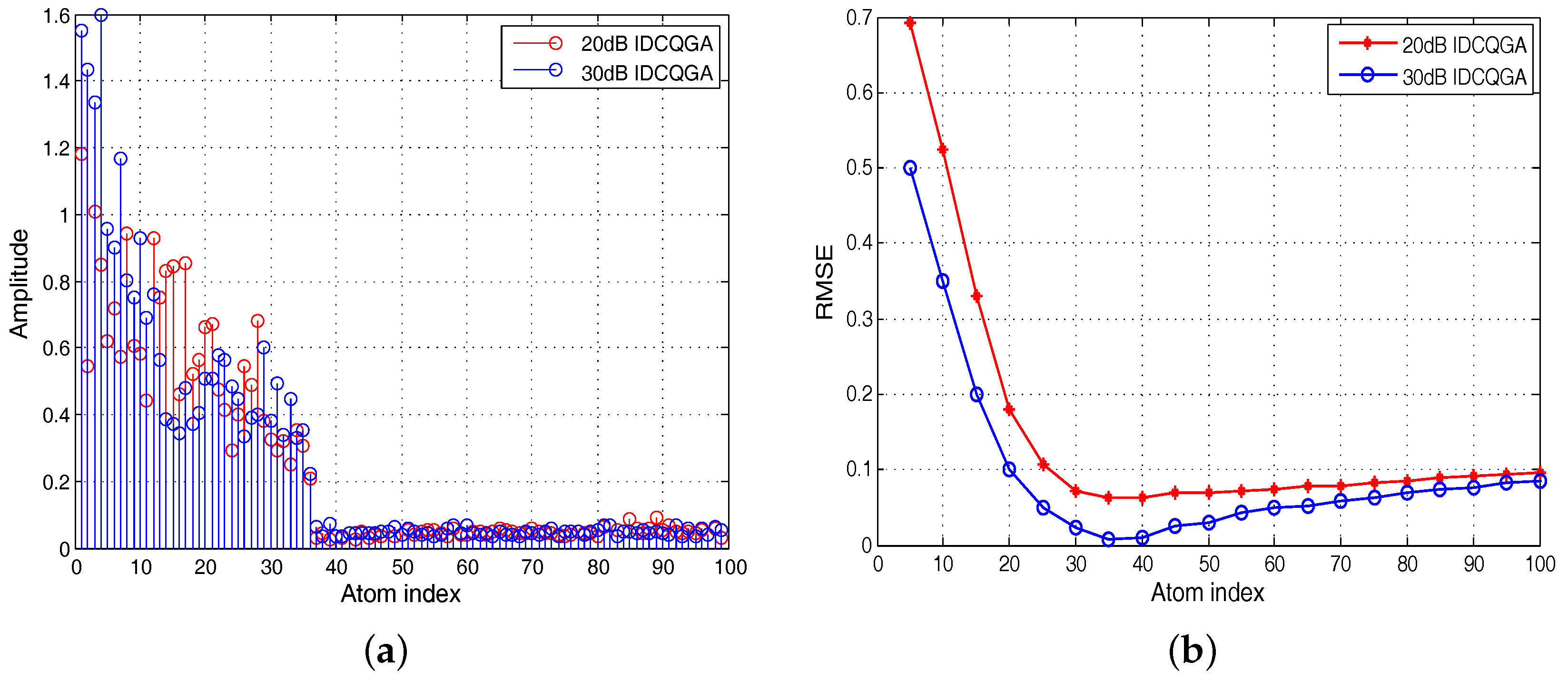
4.1. Experiment 1 and Analysis: Performance of the IDCQGA
4.2. Experiment 2 and Analysis: Performance of the OMP Based on IDCQGA
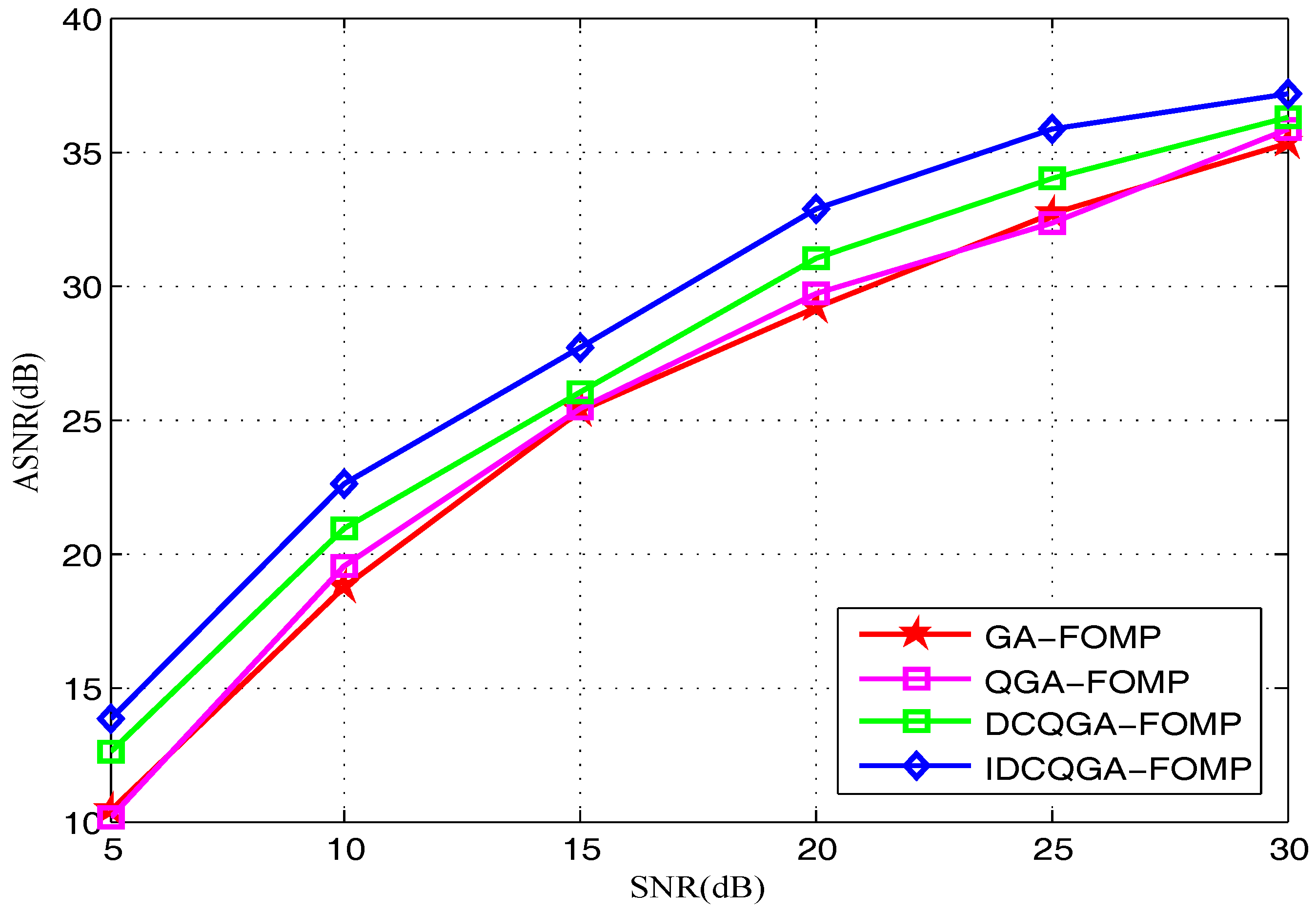
4.3. Experiment 3 and Analysis: Performance of the FOMP Based on IDCQGA
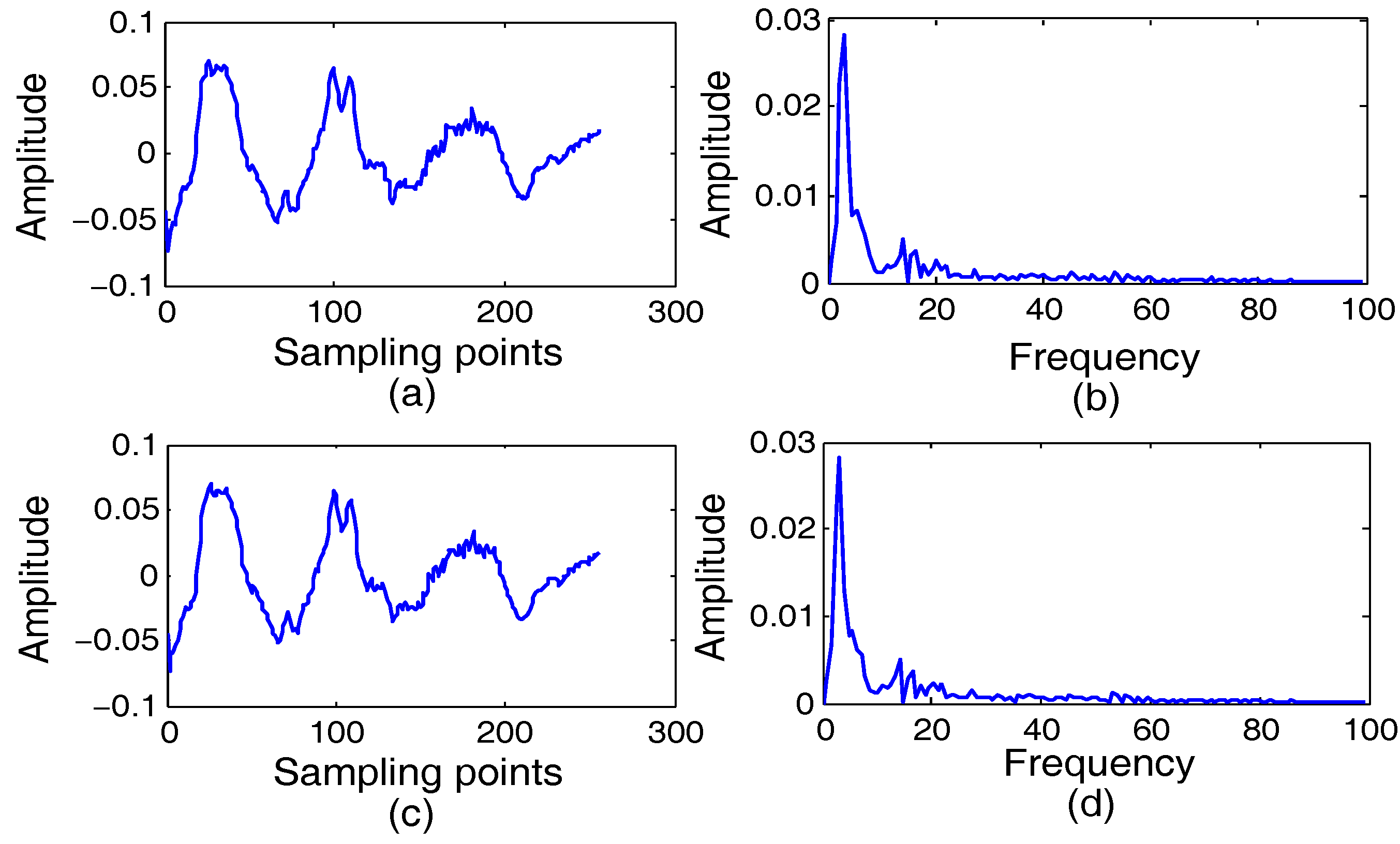
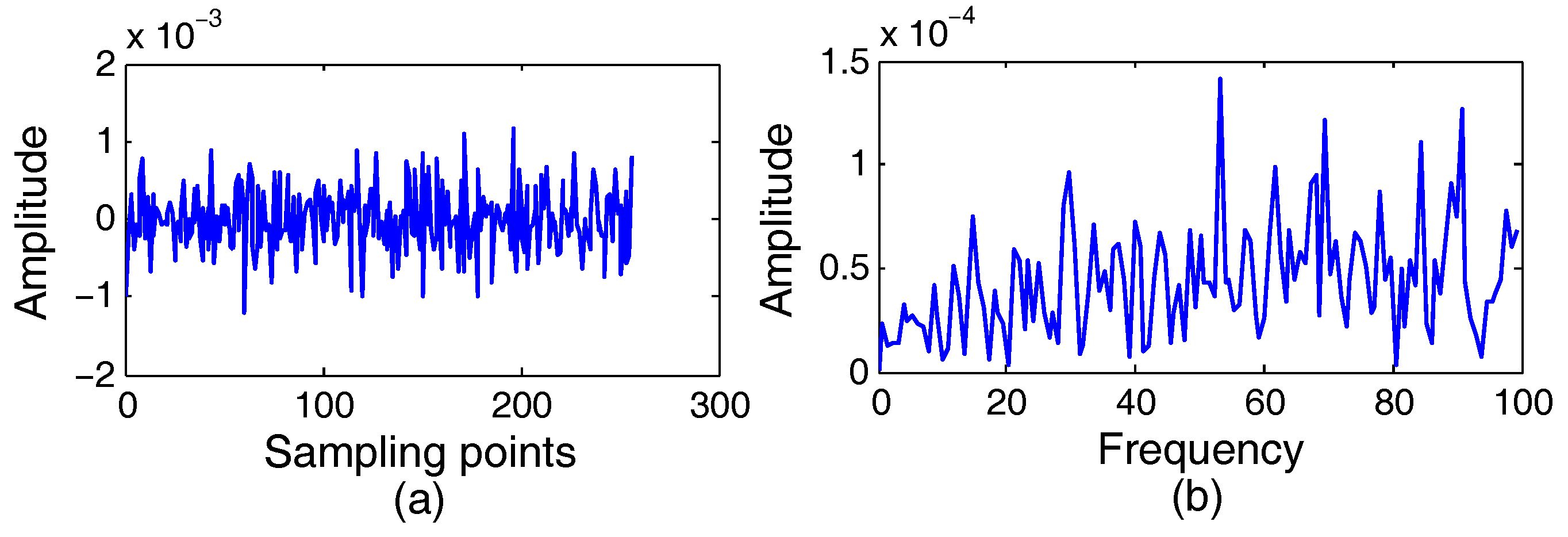
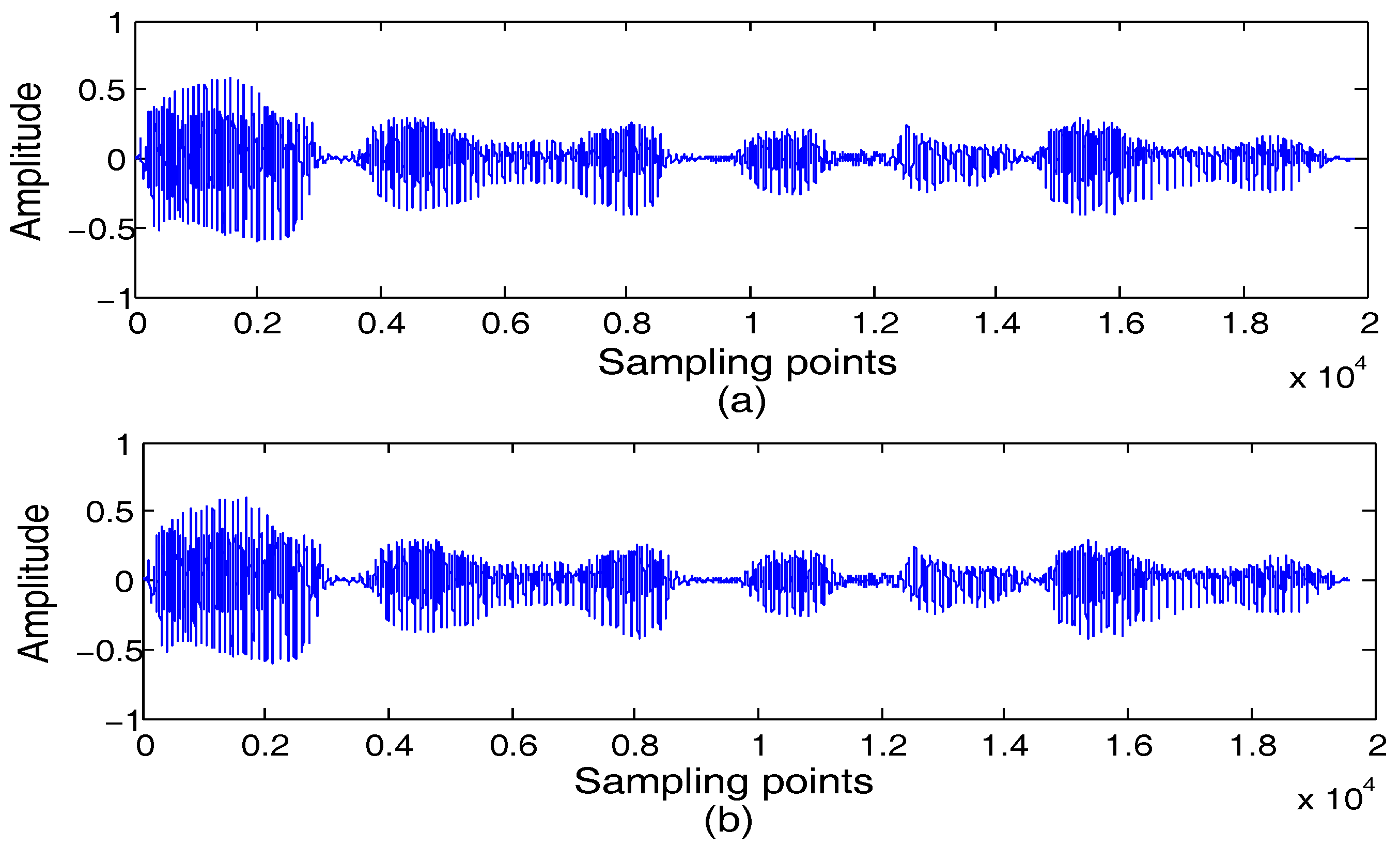
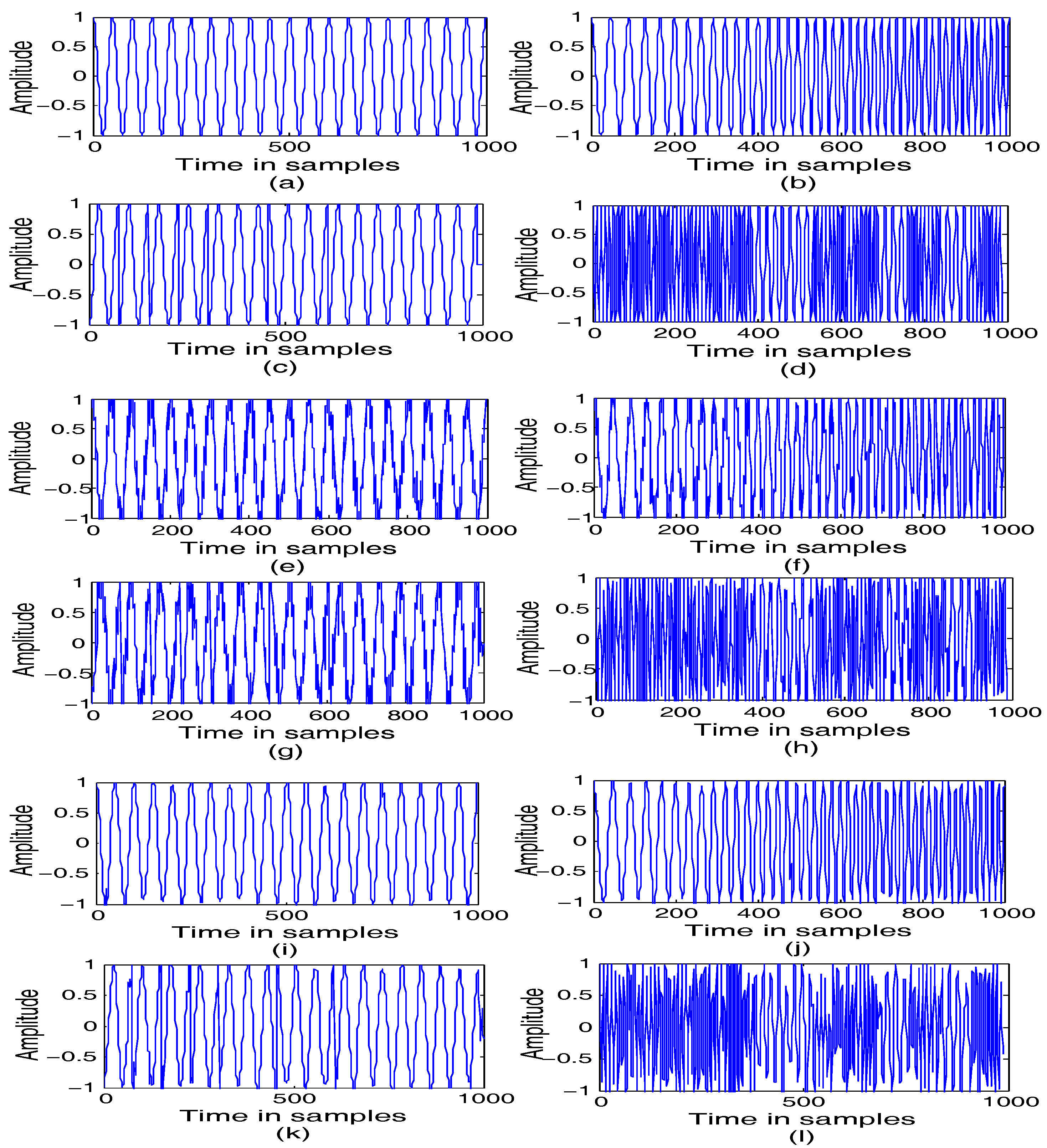
4.4. Experiment 4 and Analysis: The Applicability of the Proposed Algorithms for Radar Signals
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Goodwin, M. Adaptive Signal Models: Theory, Algorithms, and Audio Applications. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1997. [Google Scholar]
- Mallat, S.; Zhang, Z. Matching pursuit with time-frequeney dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef]
- Xu, S.; Yang, X.; Jiang, S. A fast nonlocally centralized sparse representation algorithm for image denoising. Signal Process. 2016, 31, 99–112. [Google Scholar] [CrossRef]
- Xu, K.; Minonzio, J.G.; Ta, D.; Bo, H.; Wang, W.; Laugier, P. Sparse SVD method for high resolution extraction of the dispersion curves of ultrasonic guided waves. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 1514–1524. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Chen, J.; Dong, G. Sparse representation based latent components analysis for machinery weak fault detection. Mech. Syst. Signal Process. 2014, 46, 373–388. [Google Scholar] [CrossRef]
- Wang, H.Q.; Ke, Y.L.; Song, L.Y.; Tang, G.; Chen, P. A sparsity-promoted decomposition for compressed fault diagnosis of roller bearings. Sensors 2016, 16, 1524. [Google Scholar] [CrossRef] [PubMed]
- Blumeusath, T.; Davies, M.E. Gradient pursuits. IEEE Trans. Signal Process. 2008, 56, 2370–2382. [Google Scholar] [CrossRef]
- Tropp, J.; Gilbert, A. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Donoho, D.L.; Tsaig, Y.; Drori, I.; Starck, J.L. Sparse solution of underdetermined linear equations by stage-wise rthogonal matching pursuit. IEEE Trans. Inf. Theory 2012, 58, 1094–1121. [Google Scholar] [CrossRef]
- Needell, D.; Vershynin, R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit. IEEE J. Sel. Top. Signal Process. 2010, 4, 310–316. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmonic Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef]
- Piro, P.; Sona, D.; Murino, V. Inner product tree for improved orthogonal matching pursuit. In Proceedings of the International Conference on Pattern Recognition, Tsukuba, Japan, 11–15 November 2012; pp. 429–432. [Google Scholar]
- Sun, T.Y.; Liu, C.C.; Tsai, S.J.; Hsieh, S.T.; Li, K.Y. Cluster guide particle swarm optimization (CGPSO) for underdetermined blind source separation with advanced conditions. IEEE Trans. Evolut. Comput. 2011, 15, 798–811. [Google Scholar] [CrossRef]
- Nasrollahi, A.; Kaveh, A. Engineering design optimization using a hybrid PSO and HS algorithm. Asian J. Civ. Eng. 2013, 14, 201–223. [Google Scholar]
- Nasrollahi, A.; Kaveh, A. A new hybrid meta-heuristic for structural design: Ranked particles optimization. Struct. Eng. Mech. 2014, 52, 405–426. [Google Scholar]
- Kaveh, A.; Nasrollahi, A. A new probabilistic particle swarm optimization algorithm for size optimization of spatial truss structures. Int. J. Civ. Eng. 2014, 12, 1–13. [Google Scholar]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper optimisation algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Chen, X.; Liu, X.; Dong, S.; Liu, J. Single-channel bearing vibration signal blind source separation method based on morphological filter and optimal matching pursuit (MP) algorithm. J. Vib. Control 2015, 21, 1757–1768. [Google Scholar] [CrossRef]
- Wang, J.; Wang, L.; Wang, Y. Seismic signal fast decomposition by multichannel matching pursuit with genetic algorithm. In Proceedings of the IEEE International Conference on Signal Processing, Beijing, China, 21–25 October 2012; pp. 1393–1396. [Google Scholar]
- Ventura, R.F.I.; Vandergheynst, P. Matching Pursuit through Genetic Algorithms; LTS-EPFL tech. report 01.02; Signal Processing Laboratories: Lausanne, Switzerland, 2001. [Google Scholar]
- Guldogan, M.B.; Arikan, O. Detection of sparse targets with structurally perturbed echo dictionaries. Digit. Signal Process. 2013, 23, 1630–1644. [Google Scholar] [CrossRef]
- Li, C.; Su, Y.; Zhang, Y.; Yang, H. Root imaging from ground penetrating radar data by CPSO-OMP compressed sensing. J For. Res. 2017, 28, 1–8. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, P.; Wang, H.; Li, Y.; Lv, C. Ultrasonic echo wave shape features extraction based on QPSO-matching pursuit for online wear debris discrimination. Mech. Syst. Signal Process. 2015, 60, 301–315. [Google Scholar] [CrossRef]
- Narayanan, A.; Moore, M. Quantum-inspired genetic algorithms. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 61–66. [Google Scholar]
- Yang, J.A.; Li, B.; Zhuang, Z.Q. Multi-universe parallel quantum genetic algorithm its application to blind-source separation. In Proceedings of the IEEE international conference on neural networks and signal processing, Nanjing, China, 14–17 December 2003; pp. 393–398. [Google Scholar]
- Dahi, Z.A.E.M.; Mezioud, C.; Draa, A. A quantum-inspired genetic algorithm for solving the antenna positioning problem. Swarm Evolut. Comput. 2016, 31, 24–63. [Google Scholar] [CrossRef]
- Xiong, G.; Hu, Y.X.; Tian, L.; Lan, J.L.; Jun-Fei, L.I.; Zhou, Q. A virtual service placement approach based on improved quantum genetic algorithm. Front. Inf. Technol. Electron. Eng. 2016, 17, 661–671. [Google Scholar] [CrossRef]
- Chen, P.; Yuan, L.; He, Y.; Luo, S. An improved SVM classifier based on double chains quantum genetic algorithm and its application in analogue circuit diagnosis. Neurocomputing 2016, 211, 202–211. [Google Scholar] [CrossRef]
- Li, P.C.; Song, K.P.; Shang, F.H. Double chains quantum genetic algorithm with application to neuro-fuzzy controller design. Adv. Eng. Softw. 2011, 42, 875–886. [Google Scholar] [CrossRef]
- Kong, H.; Ni, L.; Shen, Y. Adaptive double chain quantum genetic algorithm for constrained optimization problems. Chin. J. Aeronaut. 2015, 28, 214–228. [Google Scholar] [CrossRef]

| Algorithm | Population | Bits of | Encoding | Crossover | Mutation | Initial Rotation | Evolutionary |
|---|---|---|---|---|---|---|---|
| Size | Gene | Method | Probability | Probability | Angle | Generation | |
| PSO | 50 | - | - | - | - | - | 200 |
| GA | 50 | 100 | Binary | 0.7 | 0.05 | - | 200 |
| QGA | 10 | 100 | qubit | - | - | - | 200 |
| DCQGA | 10 | 2 | Double chains | - | 0.05 | 200 | |
| IDCQGA | 10 | 2 | High density | - | 0.05 | - | 200 |
| Algorithm | x | y | Best Result | Convergent Generations |
|---|---|---|---|---|
| PSO | 2.7583 | 5.01376 | 0.98327 | 105 |
| GA | 8.0283 | 4.81177 | 0.91128 | 9 |
| QGA | 2.8985 | 5.5678 | 0.96278 | 1 |
| DCQGA | −2.6202 | −1.7276 | 0.99028 | 40 |
| IDCQGA | 1.51263 | 1.39374 | 0.99793 | 22 |
| Algorithm | Best Result | Worst Result | Average Result | Number of Convergence |
|---|---|---|---|---|
| PSO | 0.9901 | 0.8925 | 0.9512 | 3 |
| GA | 0.9604 | 0.6545 | 0.8535 | 0 |
| QGA | 0.9628 | 0.8711 | 0.9402 | 0 |
| DCQGA | 0.9903 | 0.8666 | 0.9687 | 6 |
| IDCQGA | 1 | 0.9902 | 0.9946 | 10 |
| SNR | CON | LFM | BPSK | BFSK | |
|---|---|---|---|---|---|
| 5dB | Noisy signal | 0.6545 | 0.6531 | 0.6572 | 0.6496 |
| Reconstructed signal | 0.0530 | 0.0335 | 0.0402 | 0.0545 | |
| 10dB | Noisy signal | 0.5263 | 0.0372 | 0.0369 | 0.5302 |
| Reconstructed signal | 0.0324 | 0.0372 | 0.0369 | 0.0357 | |
| 15dB | Noisy signal | 0.4179 | 0.3986 | 0.3659 | 0.3982 |
| Reconstructed signal | 0.0213 | 0.0257 | 0.0315 | 0.0268 | |
| 20dB | Noisy signal | 0.3345 | 0.2856 | 0.3549 | 0.3058 |
| Reconstructed signal | 0.0197 | 0.0190 | 0.0204 | 0.0173 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Ruan, G.; Wan, J. A Sparse Signal Reconstruction Method Based on Improved Double Chains Quantum Genetic Algorithm. Symmetry 2017, 9, 178. https://doi.org/10.3390/sym9090178
Guo Q, Ruan G, Wan J. A Sparse Signal Reconstruction Method Based on Improved Double Chains Quantum Genetic Algorithm. Symmetry. 2017; 9(9):178. https://doi.org/10.3390/sym9090178
Chicago/Turabian StyleGuo, Qiang, Guoqing Ruan, and Jian Wan. 2017. "A Sparse Signal Reconstruction Method Based on Improved Double Chains Quantum Genetic Algorithm" Symmetry 9, no. 9: 178. https://doi.org/10.3390/sym9090178
APA StyleGuo, Q., Ruan, G., & Wan, J. (2017). A Sparse Signal Reconstruction Method Based on Improved Double Chains Quantum Genetic Algorithm. Symmetry, 9(9), 178. https://doi.org/10.3390/sym9090178





