Group Decision-Making for Hesitant Fuzzy Sets Based on Characteristic Objects Method
Abstract
:1. Introduction
2. Preliminaries
- 1.
- 2.
- 3.
- 1.
- The support of is
- 2.
- The core of is
- 1.
- (commutativity),
- 2.
- , if (monotonicity),
- 3.
- (associativity),
- 4.
- (neutrality of one).
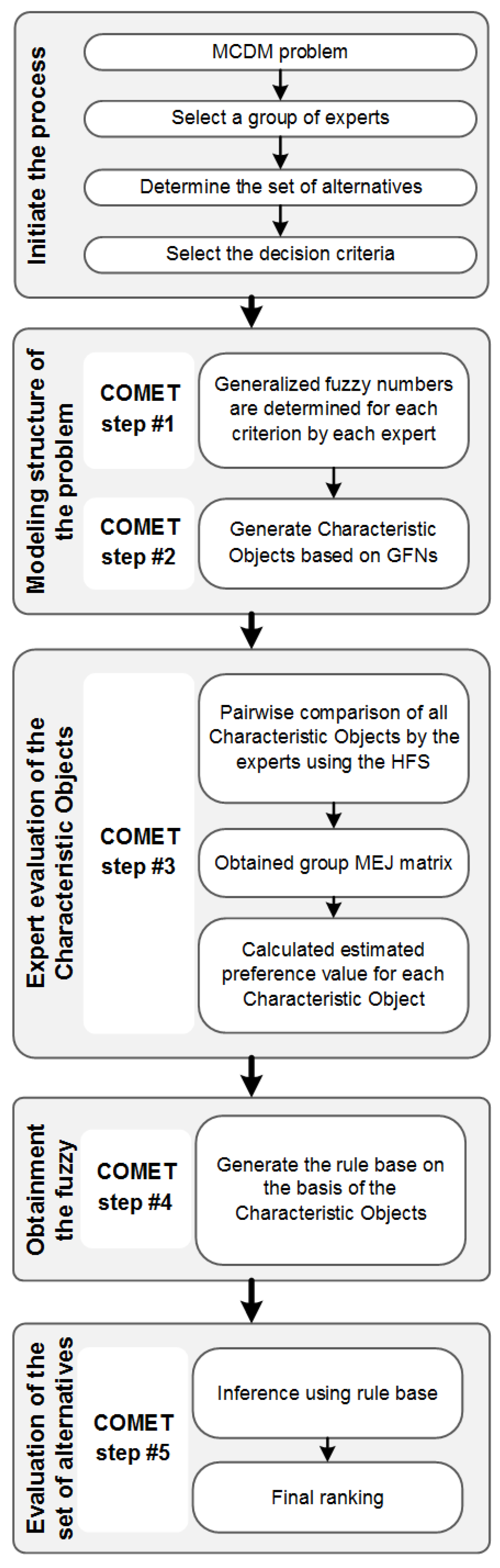
3. COMET for MCGDM Using HFS
4. An Illustrative Example
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pedrycz, W.; Ekel, P.; Parreiras, R. Fuzzy Multicriteria Decision-Making: Models, Methods and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Yeh, T.M.; Pai, F.Y.; Liao, C.W. Using a hybrid MCDM methodology to identify critical factors in new product development. Neural Comput. Appl. 2014, 24, 957–971. [Google Scholar] [CrossRef]
- Xu, Z. On consistency of the weighted geometric mean complex judgement matrix in AHP. Eur. J. Oper. Res. 2000, 126, 683–687. [Google Scholar] [CrossRef]
- Lu, N.; Liang, L. Correlation Coefficients of Extended Hesitant Fuzzy Sets and Their Applications to Decision Making. Symmetry 2017, 9, 47. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, H. A generalization of the power aggregation operators for linguistic environment and its application in group decision-making. Knowl. Based Syst. 2012, 26, 216–224. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, H.; Liu, J. Generalized power aggregation operators and their applications in group decision-making. Comput. Ind. Eng. 2012, 62, 989–999. [Google Scholar] [CrossRef]
- Sengupta, A.; Pal, T.K. Fuzzy Preference Ordering of Interval Numbers in Decision Problems; Springer: Berlin, Germany, 2009. [Google Scholar]
- Fang, Z.; Ye, J. Multiple Attribute Group Decision-Making Method Based on Linguistic Neutrosophic Numbers. Symmetry 2017, 9, 111. [Google Scholar] [CrossRef]
- Gao, J.; Liu, H. Reference-Dependent Aggregation in Multi-AttributeGroup Decision-Making. Symmetry 2017, 9, 43. [Google Scholar] [CrossRef]
- Wang, Z.-L.; You, J.-X.; Liu, H.-C. Uncertain Quality Function Deployment Using a Hybrid Group Decision Making Model. Symmetry 2016, 8, 119. [Google Scholar] [CrossRef]
- You, X.; Chen, T.; Yang, Q. Approach to Multi-Criteria Group Decision-Making Problems Based on the Best-Worst-Method and ELECTRE Method. Symmetry 2016, 8, 95. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Gitinavard, H.; Mousavi, S.M.; Vahdani, B. Soft computing-based new interval-valued hesitant fuzzy multi-criteria group assessment method with last aggregation to industrial decision problems. Soft Comput. 2017, 21, 3247–3265. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its applications to approximate reasoning-Part I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Verdegay, J.L. A model of consensus in group decision-making under linguistic assessments. Fuzzy Sets Syst. 1996, 78, 73–87. [Google Scholar] [CrossRef]
- Xu, Z.S. A method based on linguistic aggregation operators for group decision-making with linguistic preference relations. Inf. Sci. 2004, 166, 19–30. [Google Scholar] [CrossRef]
- Xu, Z.S. Deviation measures of linguistic preference relations in group decision-making. Omega 2005, 33, 249–254. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Miyamoto, S. Soft Computing and Human-Centered Machines; Springer: Berlin, Germany, 2000; pp. 9–33. [Google Scholar]
- Yager, R.R. On the theory of bags. Int. J. Gen. Syst. 1986, 13, 23–37. [Google Scholar] [CrossRef]
- Ding, Z.; Wu, Y. An Improved Interval-Valued Hesitant Fuzzy Multi-Criteria Group Decision-Making Method and Applications. Math. Comput. Appl. 2016, 21, 22. [Google Scholar] [CrossRef]
- Wibowo, S.; Deng, H.; Xu, W. Evaluation of cloud services: A fuzzy multi-criteria group decision making method. Algorithms 2016, 9, 84. [Google Scholar] [CrossRef]
- Zhang, J.; Hegde, G.G.; Shang, J.; Qi, X. Evaluating Emergency Response Solutions for Sustainable Community Development by Using Fuzzy Multi-Criteria Group Decision Making Approaches: IVDHF-TOPSIS and IVDHF-VIKOR. Sustainability 2016, 8, 291. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Jin, B. ELECTRE method for multiple attributes decision making problem with hesitant fuzzy information. J. Intell. Fuzzy Syst. 2015, 29, 463–468. [Google Scholar] [CrossRef]
- Zhang, N.; Wei, G. Extension of VIKOR method for decision making problem based on hesitant fuzzy set. Appl. Math. Model. 2013, 37, 4938–4947. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.Q.; Wu, X.H. Novel multi-criteria decision-making approaches based on hesitant fuzzy sets and prospect theory. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 621–643. [Google Scholar] [CrossRef]
- Peng, X.; Yang, Y. Interval-valued hesitant fuzzy soft sets and their application in decision making. Fundam. Inform. 2015, 141, 71–93. [Google Scholar] [CrossRef]
- Yu, D. Hesitant fuzzy multi-criteria decision making methods based on Heronian mean. Technol. Econ. Dev. Econ. 2017, 23, 296–315. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z. Extended hesitant fuzzy sets. Technol. Econ. Dev. Econ. 2016, 22, 100–121. [Google Scholar] [CrossRef]
- Wu, Y.; Xu, C.; Zhang, H.; Gao, J. Interval Generalized Ordered Weighted Utility Multiple Averaging Operators and Their Applications to Group Decision-Making. Symmetry 2017, 9, 103. [Google Scholar] [CrossRef]
- Yu, D.; Zhang, W.; Huang, G. Dual hesitant fuzzy aggregation operators. Technol. Econ. Dev. Econ. 2016, 22, 194–209. [Google Scholar] [CrossRef]
- Liu, J.; Sun, M. Generalized power average operator of hesitant fuzzy numbers and its application in multiple attribute decision-making. J. Comput. Inf. Syst. 2013, 9, 3051–3058. [Google Scholar]
- Xia, M.; Xu, Z.; Chen, N. Some hesitant fuzzy aggregation operators with their application in group decision-making. Group Decis. Negot. 2013, 22, 259–279. [Google Scholar] [CrossRef]
- Yu, D.; Wu, Y.; Zhou, W. Multi-criteria decision-making based on Choquet integral under hesitant fuzzy environment. J. Comput. Inf. Syst. 2011, 7, 4506–4513. [Google Scholar]
- Zhang, Z. Hesitant fuzzy power aggregation operators and their application to multiple attribute group decision-making. Inf. Sci. 2013, 234, 150–181. [Google Scholar] [CrossRef]
- Chen, N.; Xu, Z.; Xia, M. Interval-valued hesitant preference relations and their applications to group decision-making. Knowl. Based Syst. 2013, 37, 528–540. [Google Scholar] [CrossRef]
- Peng, D.H.; Wang, T.D.; Gao, C.Y.; Wang, H. Continuous hesitant fuzzy aggregation operators and their application to decision-making under interval-valued hesitant fuzzy setting. Sci. World J. 2014, 2014, 897304. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.J.; Wang, J.Q.; Wang, J.; Chen, X.H. Multi-criteria decision-making approach with hesitant interval-valued intuitionistic fuzzy sets. Sci. World J. 2014, 2014, 868515. [Google Scholar] [CrossRef] [PubMed]
- Wei, G.; Zhao, X.; Lin, R. Some hesitant interval-valued fuzzy aggregation operators and their applications to multiple attribute decision-making. Knowl. Based Syst. 2013, 46, 43–53. [Google Scholar] [CrossRef]
- Beg, I.; Rashid, T. Hesitant 2-tuple linguistic information in multiple attributes group decision-making. J. Intell. Fuzzy Syst. 2016, 30, 143–150. [Google Scholar] [CrossRef]
- Rashid, T.; Husnine, S.M. Multi-criteria Group decision-making by Using Trapezoidal Valued Hesitant Fuzzy Sets. Sci. World J. 2014, 2014, 304834. [Google Scholar] [CrossRef] [PubMed]
- Yu, D. Triangular hesitant fuzzy set and its application to teaching quality evaluation. J. Inf. Comput. Sci. 2013, 10, 1925–1934. [Google Scholar] [CrossRef]
- Piegat, A.; Sałabun, W. Nonlinearity of human multi-criteria in decision-making. J. Theor. Appl. Comput. Sci. 2012, 6, 36–49. [Google Scholar]
- Sałabun, W. The Characteristic Objects Method, A new distance based approach to multi-criteria decision-making problems. J. Multi Criteria Decis. Anal. 2015, 22, 37–50. [Google Scholar] [CrossRef]
- Sałabun, W. The Characteristic Objects Method: A new approach to Identify a multi-criteria group decision-making problems. Int. J. Comput. Technol. Appl. 2014, 5, 1597–1602. [Google Scholar]
- Sałabun, W. Application of the fuzzy multi-criteria decision-making method to identify nonlinear decision models. Int. J. Comput. Appl. 2014, 89, 1–6. [Google Scholar] [CrossRef]
- Sałabun, W.; Piegat, A. Comparative analysis of MCDM methods for the assessment of mortality in patients with acute coronary syndrome. Artif. Intell. Rev. 2016, 1–15. [Google Scholar] [CrossRef]
- Faizi, S.; Rashid, T.; Sałabun, W.; Zafar, S.; Wątróbski, J. Decision Making with Uncertainty Using Hesitant Fuzzy Sets. Int. J. Fuzzy Syst. 2017, 1–11. [Google Scholar] [CrossRef]
- Piegat, A.; Sałabun, W. Identification of a multicriteria decision-making model using the characteristic objects method. Appl. Comput. Intell. Soft Comput. 2014, 2014, 1–14. [Google Scholar] [CrossRef]
- Sałabun, W.; Ziemba, P.; Wątróbski, J. The Rank Reversals Paradox in Management Decisions: The Comparison of the AHP and COMET Methods. In Intelligent Decision Technologies; Springer: Berlin, Germany, 2016; pp. 181–191. [Google Scholar]
- Wątróbski, J.; Jankowski, J. Guideline for MCDA method selection in production management area. In New Frontiers in Information and Production Systems Modelling and Analysis; Springer: Berlin, Germany, 2016; pp. 119–138. [Google Scholar]
- Sałabun, W.; Ziemba, P. Application of the Characteristic Objects Method in Supply Chain Management and Logistics. In Recent Developments in Intelligent Information and Database Systems; Springer: Berlin, Germany, 2016; pp. 445–453. [Google Scholar]
- Bector, C.R.; Chandra, S. Fuzzy mathematical programming and fuzzy matrix games; Springer: Berlin, Germany, 2005; Volume 169. [Google Scholar]
- Chakeri, A.; Dariani, A.N.; Lucas, C. How can fuzzy logic determine game equilibriums better? In Proceedings of the 4th International IEEE Conference Intelligent Systems, 2008 IS’08, Varna, Bulgaria, 6–8 September 2008; Volume 1, pp. 2–51. [Google Scholar]
- Chakeri, A.; Habibi, J.; Heshmat, Y. Fuzzy type-2 Nash equilibrium. In Proceedings of the 2008 International Conference on Computational Intelligence for Modelling Control & Automation, Vienna, Austria, 10–12 December 2008; pp. 398–402. [Google Scholar]
- Chakeri, A.; Sadati, N.; Dumont, G.A. Nash Equilibrium Strategies in Fuzzy Games. In Game Theory Relaunched; InTech: Exton, PA, USA, 2013. [Google Scholar]
- Chakeri, A.; Sadati, N.; Sharifian, S. Fuzzy Nash equilibrium in fuzzy games using ranking fuzzy numbers. In Proceedings of the 2010 IEEE International Conference on Fuzzy Systems (FUZZ), Barcelona, Spain, 18–23 July 2010; pp. 1–5. [Google Scholar]
- Chakeri, A.; Sheikholeslam, F. Fuzzy Nash equilibriums in crisp and fuzzy games. IEEE Trans. Fuzzy Syst. 2013, 21, 171–176. [Google Scholar] [CrossRef]
- Garagic, D.; Cruz, J.B. An approach to fuzzy noncooperative nash games. J. Optim. Theory Appl. 2003, 118, 475–491. [Google Scholar] [CrossRef]
- Sharifian, S.; Chakeri, A.; Sheikholeslam, F. Linguisitc representation of Nash equilibriums in fuzzy games. In Proceedings of the 2010 Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS), Toronto, ON, Canada, 12–14 July 2010; pp. 1–6. [Google Scholar]
- Sharma, R.; Gopal, M. Hybrid game strategy in fuzzy Markov-game-based control. IEEE Trans. Fuzzy Syst. 2008, 16, 1315–1327. [Google Scholar] [CrossRef]
- Tan, C.; Jiang, Z.Z.; Chen, X.; Ip, W.H. A Banzhaf function for a fuzzy game. IEEE Trans. Fuzzy Syst. 2014, 22, 1489–1502. [Google Scholar] [CrossRef]
- Piegat, A.; Sałabun, W. Comparative analysis of MCDM methods for assessing the severity of chronic liver disease. In Proceedings of the 14th International Conference on Artificial Intelligence and Soft Computing, Zakopane, Poland, 14–18 June 2015; pp. 228–238. [Google Scholar]
- Wątróbski, J.; Sałabun, W. The characteristic objects method: a new intelligent decision support tool for sustainable manufacturing. In Sustainable Design and Manufacturing; Springer: Berlin, Germany, 2016; pp. 349–359. [Google Scholar]
- Jankowski, J.; Sałabun, W.; Wątróbski, J. Identification of a multi-criteria assessment model of relation between editorial and commercial content in web systems. In Multimedia and Network Information Systems; Springer: Berlin, Germany, 2017; pp. 295–305. [Google Scholar]
- Velasquez, M.; Hester, P.T. An Analysis of Multi-Criteria Decision Making Methods. Int. J. Oper. Res. 2013, 10, 56–66. [Google Scholar]
- Xia, M.; Xu, Z. Hesitant fuzzy information aggregation in decision-making. Int. J. Approx. Reason. 2011, 52, 395–407. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy Set Theory—And Its Applications; Springer Science and Business Media: Berlin, Germany, 2001. [Google Scholar]
- Chen, J.; Huang, X. Dual Hesitant Fuzzy Probability. Symmetry 2017, 9, 52. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Z.; Zhang, S. A Modification on the Hesitant Fuzzy Set Lexicographical Ranking Method. Symmetry 2016, 8, 153. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z.; Liu, M. Hesitant trapezoidal fuzzy QUALIFLEX method and its application in the evaluation of green supply chain initiatives. Sustainability 2016, 8, 952. [Google Scholar] [CrossRef]
- Piegat, A. Fuzzy Modeling and Control; Springer: New York, NY, USA, 2001. [Google Scholar]
- Wang, G.; Wang, H. Non-fuzzy versions of fuzzy reasoning in classical logics. Inf. Sci. 2001, 138, 211–236. [Google Scholar] [CrossRef]
- Ross, T.J. Fuzzy Logic with Engineering Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular Norms; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
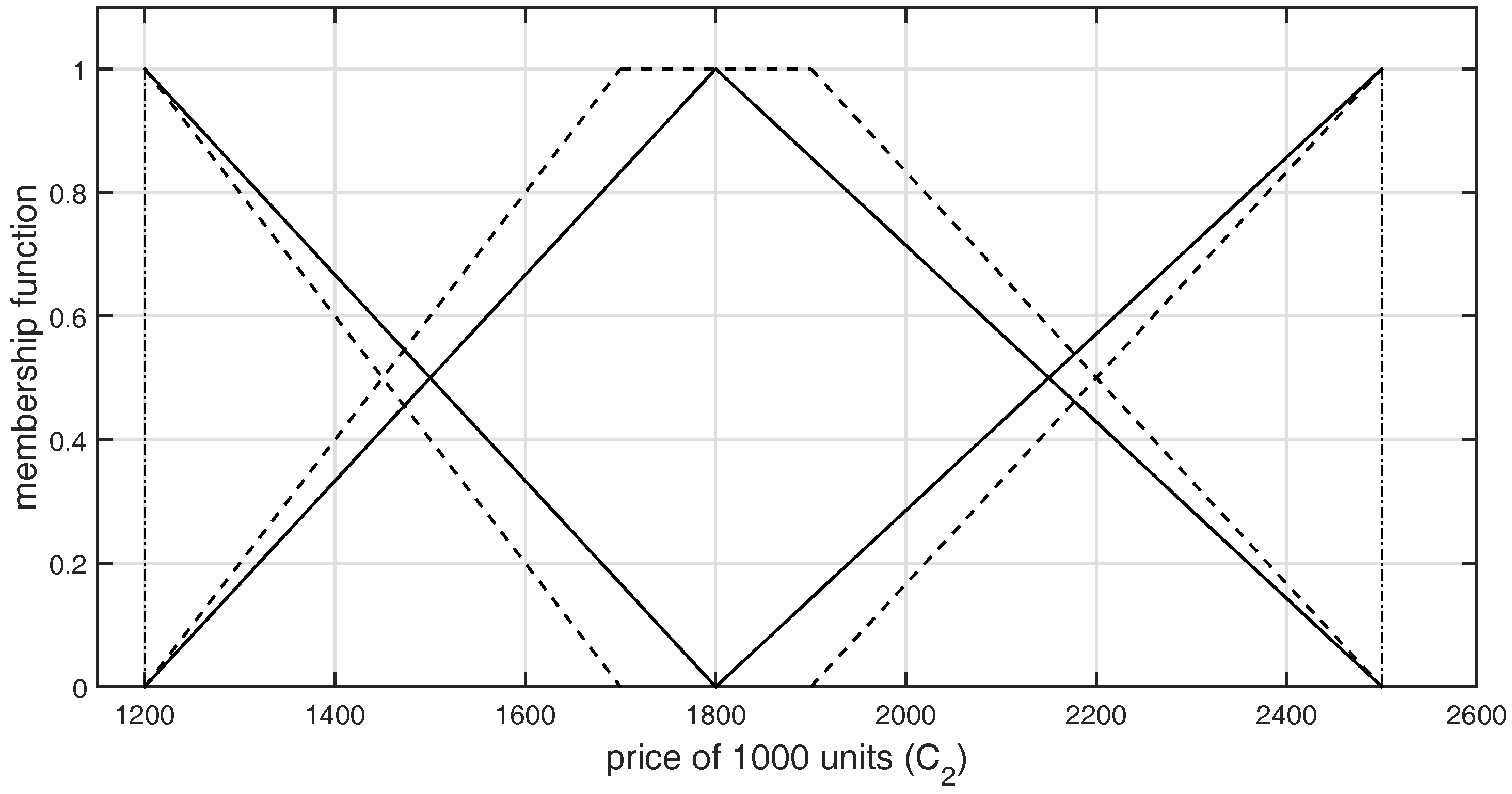
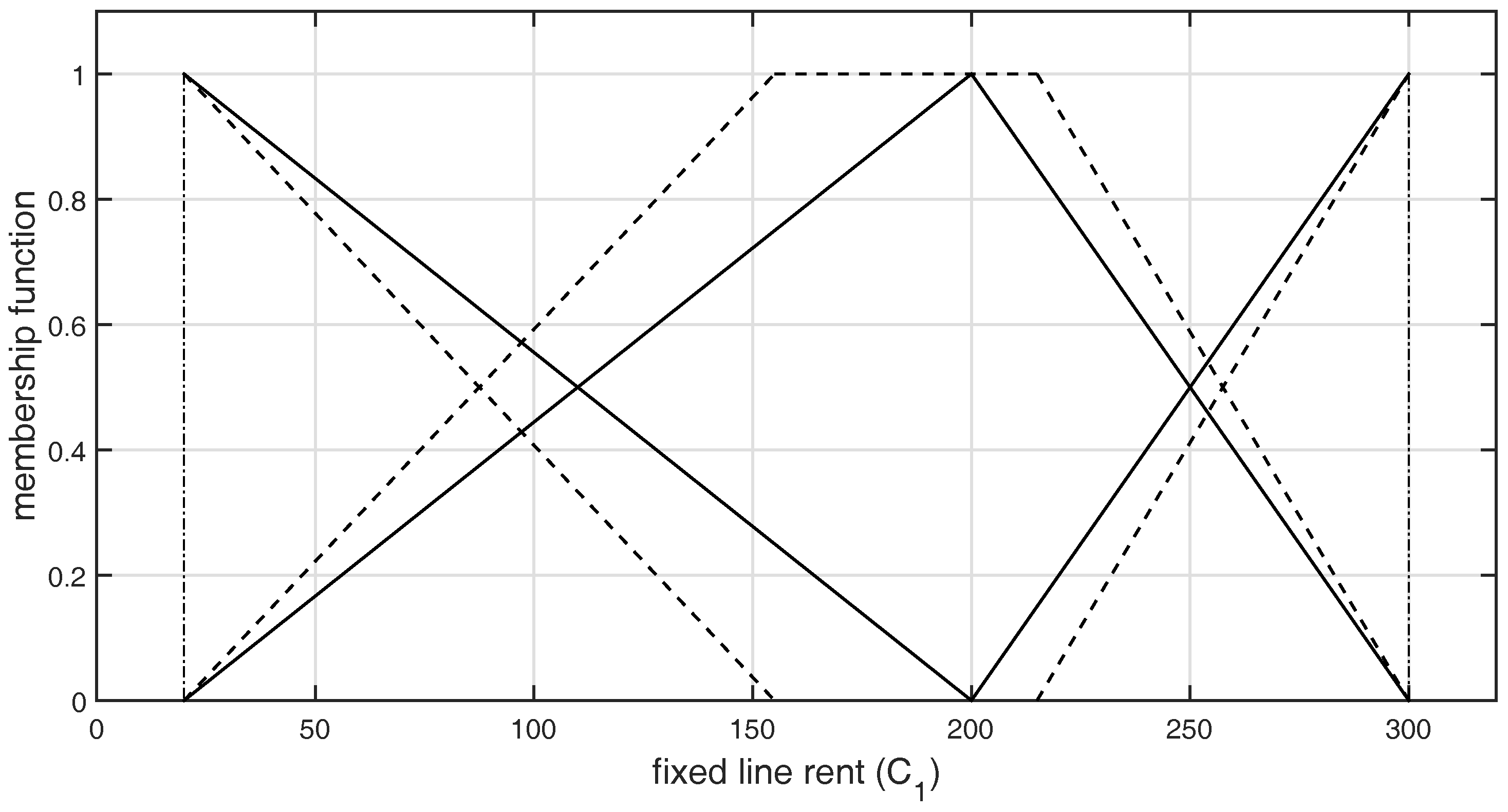
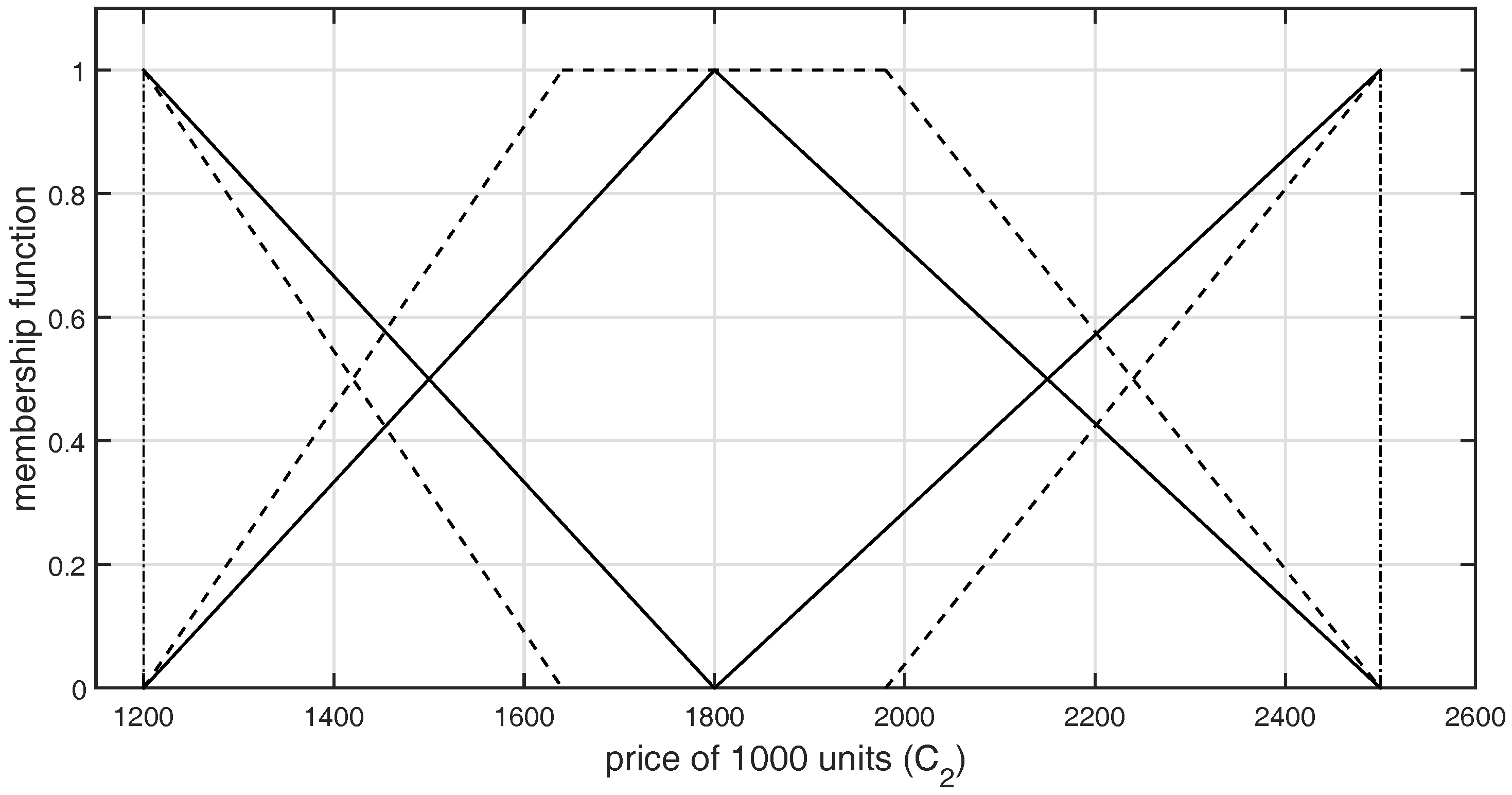
| Alternatives | (LR) | (R/U) | Bill Amount | Original Rank |
|---|---|---|---|---|
| 150 | 1500 | 1650 | 2 | |
| 50 | 2000 | 2050 | 3 | |
| 250 | 1250 | 1500 | 1 | |
| 30 | 2150 | 2180 | 4 |
| DM1 | |
| DM2 | |
| DM3 | |
| DM1 | |
| DM2 | |
| DM3 | |
| Average of the Membership Values Obtained from LR-Type GFNs for Criterion | |||
|---|---|---|---|
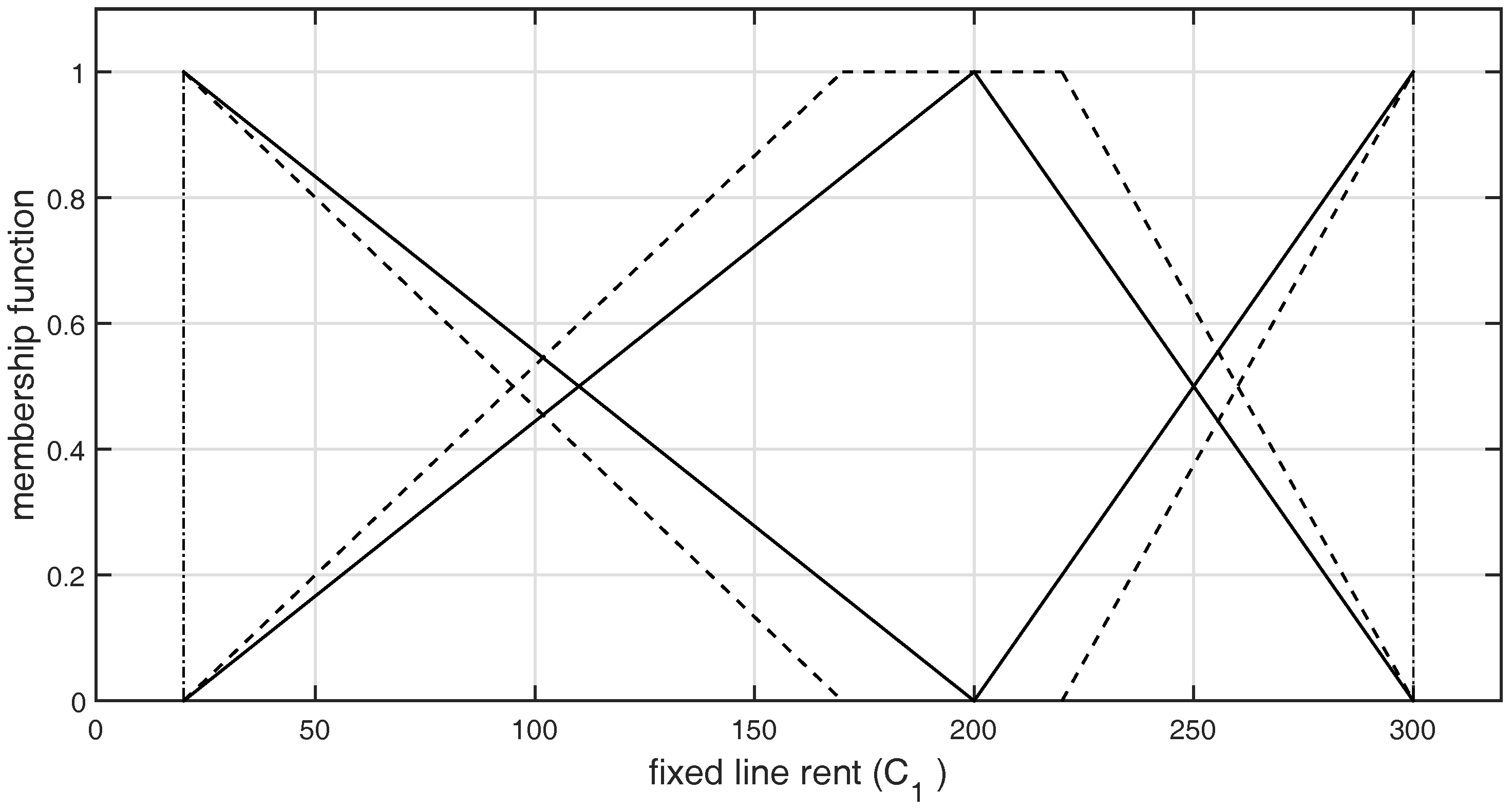
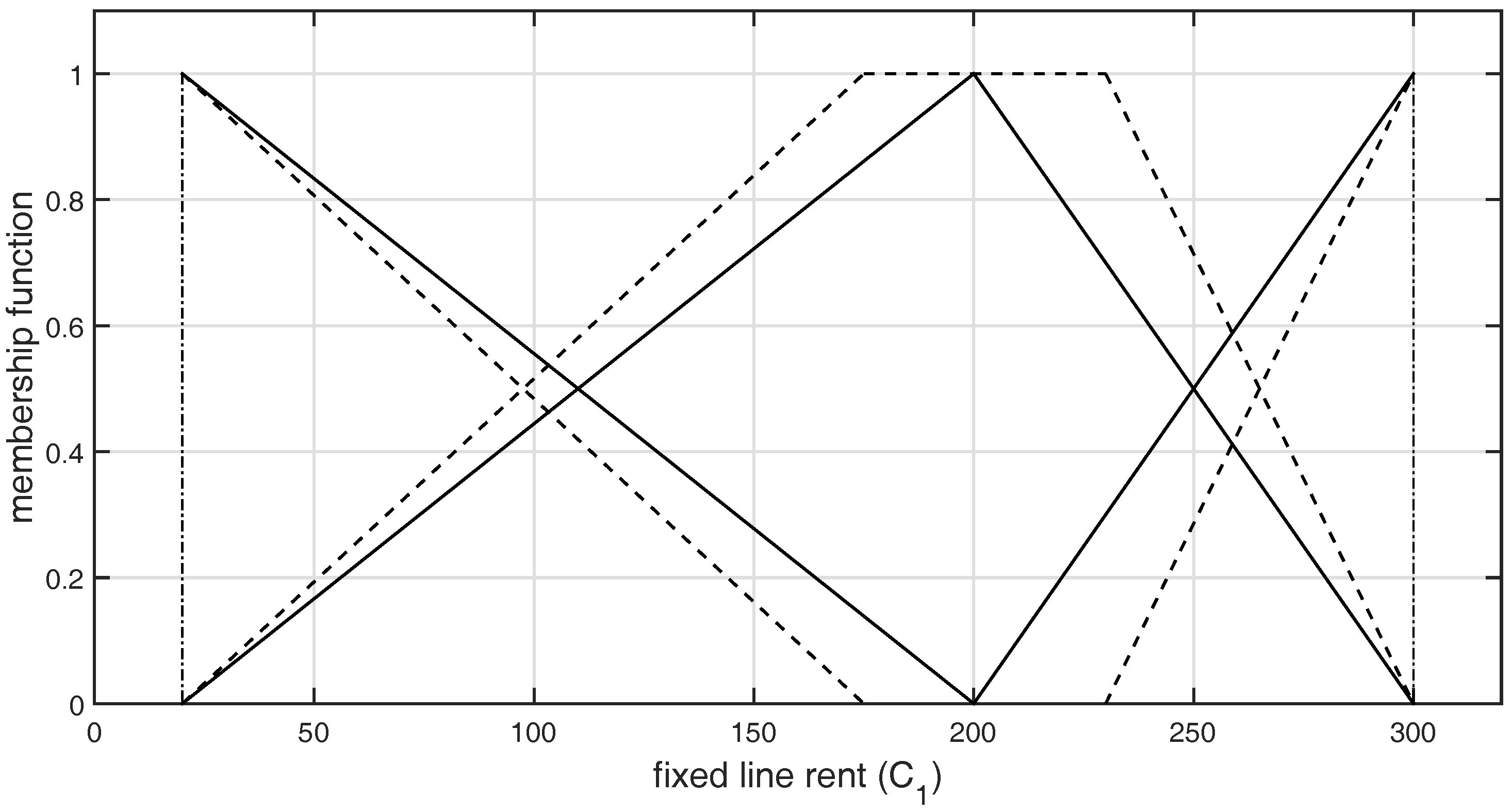
| 30 | 50 | 150 | 250 |
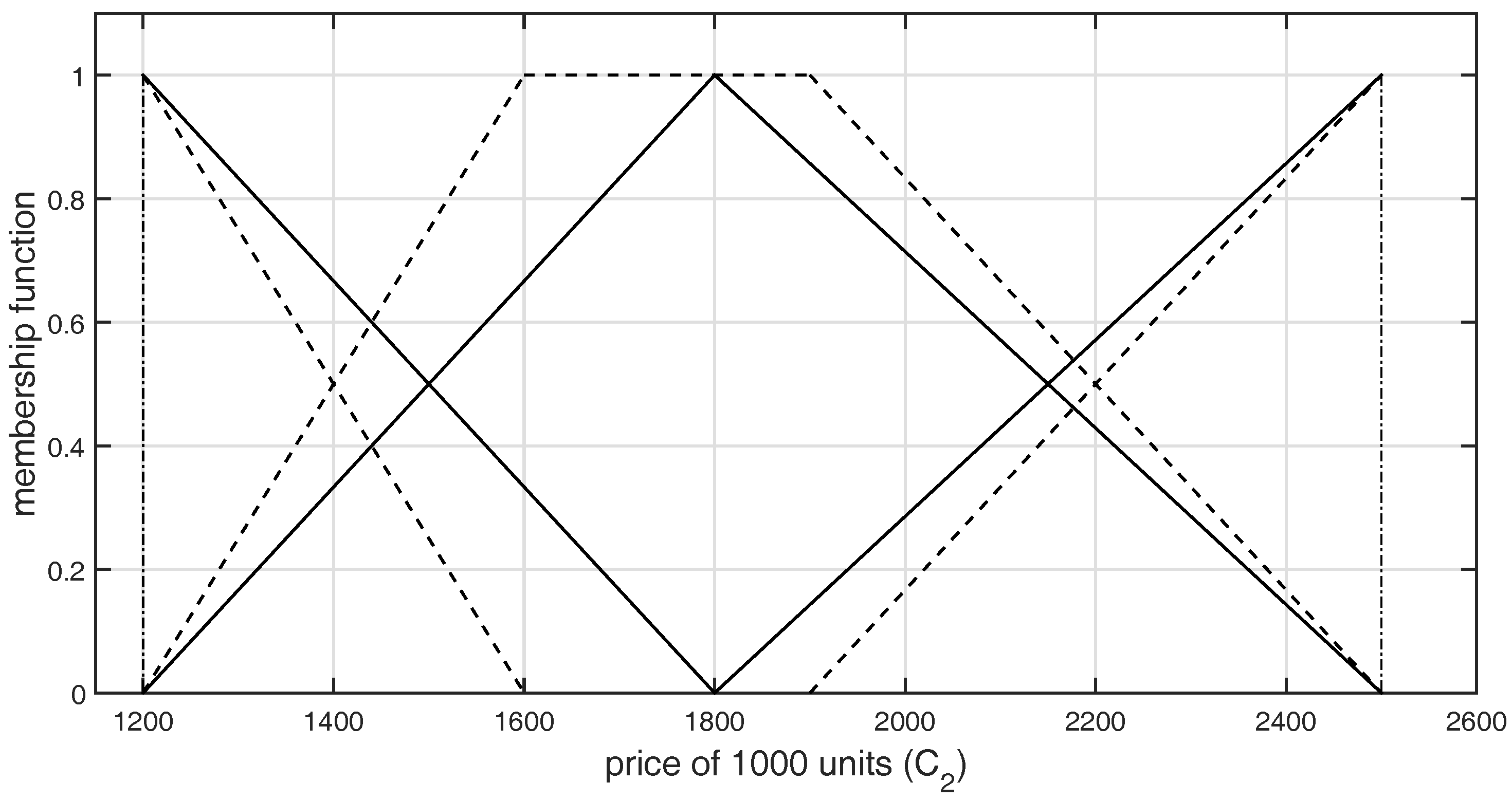
| 1250 | 1500 | 2000 | 2150 |
| Alternatives | (LR) | (R/U) | Original Ranking | Preference Values | New Ranking |
|---|---|---|---|---|---|
| 150 | 1500 | 2 | 3 | ||
| 50 | 2000 | 3 | 2 | ||
| 250 | 1250 | 1 | 1 | ||
| 30 | 2150 | 4 | 4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faizi, S.; Sałabun, W.; Rashid, T.; Wątróbski, J.; Zafar, S. Group Decision-Making for Hesitant Fuzzy Sets Based on Characteristic Objects Method. Symmetry 2017, 9, 136. https://doi.org/10.3390/sym9080136
Faizi S, Sałabun W, Rashid T, Wątróbski J, Zafar S. Group Decision-Making for Hesitant Fuzzy Sets Based on Characteristic Objects Method. Symmetry. 2017; 9(8):136. https://doi.org/10.3390/sym9080136
Chicago/Turabian StyleFaizi, Shahzad, Wojciech Sałabun, Tabasam Rashid, Jarosław Wątróbski, and Sohail Zafar. 2017. "Group Decision-Making for Hesitant Fuzzy Sets Based on Characteristic Objects Method" Symmetry 9, no. 8: 136. https://doi.org/10.3390/sym9080136
APA StyleFaizi, S., Sałabun, W., Rashid, T., Wątróbski, J., & Zafar, S. (2017). Group Decision-Making for Hesitant Fuzzy Sets Based on Characteristic Objects Method. Symmetry, 9(8), 136. https://doi.org/10.3390/sym9080136





