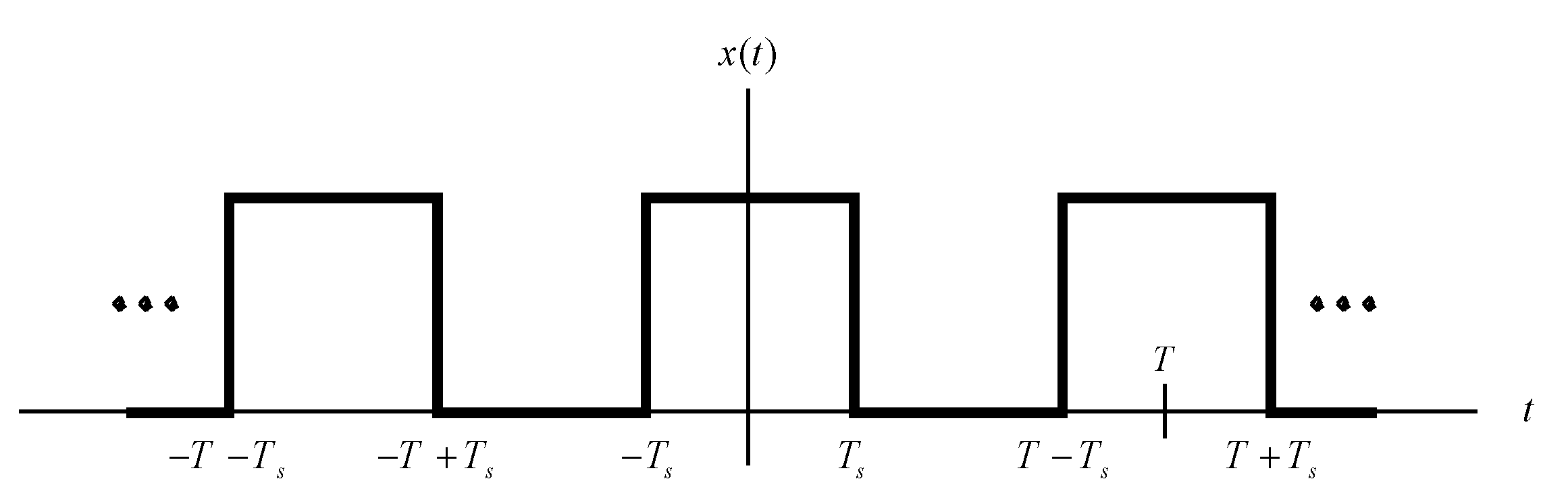High-Capacity Data-Hiding Scheme on Synthesized Pitches Using Amplitude Enhancement—A New Vision of Non-Blind Audio Steganography

Abstract

This work proposes a new and non-blind steganographic scheme for synthesized pitches. Synthesized music is popularly used to demonstrate early versions of compositions conveniently and at low-cost. They can also be utilized to pass secrets or obtain digital rights. The method consists of two procedures, of which the first is the realistic simulation of synthesized pitches using a computer and the second is the hiding of secrets during the generated simulated pitches. The first part of this paper reviews attempts to discover the fundamental patterns of synthesized pitches and to develop a strategy for generating approximate pitches using a computer. The component frequencies are used to generate a pitch in which to hide secrets. Legal receivers receive the referenced composition and frequencies, enabling them to generate the synthesized pitches according to the main frequencies of the referenced composition. Finally, the generated and received pitches are compared to identify the secret bits. As more frequencies are used to hide secret bits, more secret bits can be embedded in the synthesized pitches. The use of more frequencies makes synthesized pitches more realistic compared to real ones. The performance of the proposed method is also compared with that of competing methods and under common attacks.

1. Introduction and Related Work

The Internet is a popular environment in which people exchange personal data. Accordingly, great importance is now attached to information security. Many techniques for keeping data confidential have been developed. The field of steganography concerns hiding data that embed messages in insignificant media before a transmission. Data-hiding schemes are used to hide secrets in cover media, producing stego-media. The approach enables users to discover attempts by intruders to replace original messages with fabricated content. One of its applications is to back-up personal, private data or information on the Internet. Presently, many people frequently upload personal and secret data to cloud services, while reasonably distrusting cloud vendors. The objective of data-hiding is to increase hiding capacity while reducing the likelihood that intruders can identify anything is hidden [1]. Figure 1 displays some applications of steganography: (a) when a user backs up sensitive data on a cloud storage service, he does not want the data accessible even though it is encrypted; (b) when a user create his multimedia files, he wants to obtain his ownerships before he publishes those files; and (c) when a user wants to communicate to some, he does not want to be noticed so he makes his messages to be un-perceptual.

Popular multimedia includes images, audio, video and text [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. Audio-based data-hiding methods [3,17,18,19,20,21,22,23] can be divided into two categories. Time domain-based operations tend to replace the least significant bits [3,20], and the echo parts of a signal [3,23]. Frequency domain-based operations include directly hiding secrets in high or low frequencies and spreading the secrets throughout band frequencies. The former approach is known as psychoacoustic masking [3,21] and the latter is known as spreading the spectrum [3,22,23]. Most audio-based methods suffer from the same problems as image-based methods, that is, the issue of distortion between cover and stego-medium. Phase coding and spreading spectrum methods are safer due to they are designed to deployed secrets in un-perceptual frequencies [3], although their computation time are greater than those of other schemes.

Traditional data-hiding strategies are based on digitalized multimedia. Distortion is the most important limitation of steganography, and it must therefore be controlled to reduce awareness of the generated stego-media. Other methods for hiding data in audio are based on ideas that have been proposed by various authors [3,20,21,22,23]. They include least-significant-bit (LSB), phase coding, spread spectrum, echo data-hiding and psychoacoustic masking methods. Akhaee et al. [17] proposed a robust data-hiding algorithm to avoid statistical cracking. They found that most time-domain processing data-hiding schemes are weak and can be easily decoded by current steganalytic strategies. Their algorithm applies correlated quantization to embed data using a histogram-based detector. Huang et al. [19] presented a new steganographic scheme with variable capacity and synchronization for the secure multimedia transmission of acoustic data in real time. Atoum et al. [18] proposed a new data-hiding scheme that is based on the mp3 file format. They were concerned that human ears are very sensitive to audio features so the audio content should not be modified. Their method, therefore, hides secret data only between the frames of an mp3 file. Yamamoto and Iwakiri [24] developed a method of identifying the ownership of a digital instrumental audio. They mentioned that digital instrumental audio is now very popular on the Internet. Accordingly, the present work develops a data-hiding scheme that is based on the fundamental composition of simulated instrumental audio.

Most of the above proposed methods are based on traditional digitalized audio and are therefore restricted by distortion and exhaustion of transmission, which means the more secrets embedded in a cover media, the more differences of a cover and a stego media. They can be used simply to modify media content, but in so doing, they limit the capacity for and security of the hidden secrets. Currently, much content is transmitted through the Internet, and a fraction of it is made by computer animators, and includes text and simulated media [25,26,27,28,29,30,31,32]. Cayre and Macq [28] were the first to propose a data-hiding method that was based on 3D polygons. Their scheme is applied to 3D meshes of triangles, and extends one of the simplest data-hiding techniques, called the triangle strip peeling sequence (TSPS) technique. The basic idea of the TSPS algorithm is the insertion of bits in a path traced on the mesh. In 2009, Chao et al. [29] improved Cayre’s algorithm and increased its capacity. They redefined 3D polygons as multilayered triangles such that each layer could be used to hide secrets. They also used coordinates to define each polygon and defined a multi-layer such that the capacity of their method was 3n times that of Cayre’s method (where n is the number of layers).

Inspired by the above research works, the authors developed a new data-hiding scheme that uses synthesized musical pitches to embed more secrets and reduce distortion. The scheme reproduces a synthesized musical pitch in which it embeds secrets by amplitude enhancement. The enhancement slightly pads noises and legal receivers have only to compare the magnitude of the amplitude with that in standard patterns of synthesized pitches. The restriction is that only one pitch can be used at the same time. Sound synthesis is an important topic in the simulation of digital musical instruments. This paper is organized as follows. Section 2 first introduces the fundamental principle of the synthesis of musical notes, which is the basis of the data-hiding scheme that is presented herein. A reliable formula for synthesizing notes is introduced and some simulations are carried out. Therefore, a data-hiding scheme are presented. Section 3 displays some practical experiments to prove the feasibility and ability. Section 4 compares the performance of the proposed method with of others and presents some other evaluations and theoretical analysis. Finally, Section 5 draws conclusions. All experiments are analyzed using MATLAB (2006a, The MathWorks, Natick, MA, USA).

2. Materials and Methods

References [33,34] described efforts to describe objectively the quality of piano tones, as understood by musicians, and they tried to find synthetic tones that would be considered to be better than real piano tones. Casey showed that a two-layer feed-forward model can perform inverse mapping for a simple physical model of a string [35]. References [36,37] showed the numerical approach and the underlying physical model can be improved to simulate the motion of a piano string with a high degree of realism. This work develops a model of instruments as follows. First, a discrete Fourier transform (DFT) is utilized to transform the sampled sound data of an instrument from the time domain to the frequency domain. When a real instrumental pitch is recorded, analog acoustic is digitalized with being sampled automatically by a computer. Then the DFT could be adopted to classify and decompose the composition of the frequencies of a single pitch. Second, use the frequency domain function and the sound of an instrument is described as a pattern, which is generated using DFT and the inverse DFT, which are used to analyze sampled data using computers. Section 2.1 is the fundamental of the methodology, while Section 2.2 is the proposed scheme.

2.1. Fundamentals

This section discusses why musical instruments produce such beautiful music. Harmonics will be introduced. Fourier transformations are based on the fact that a function in the time domain can be represented as a summation of cosine functions. Consider the periodic square wave, plotted in Figure 2. The signal $x\left(t\right)$ can be represented by Equation (1) [38]:

$$x\left(t\right)=\frac{2T_s}{T}+{\displaystyle \sum }_{k=1}^{\infty }\frac{2\sin \left(2\pi k{f}_0{T}_s\right)}{\pi k}\cos \left(2\pi k{f}_{0}t\right)$$

(1)

The frequency $f_0$ is the fundamental frequency. As k increases, the coefficient of the cosine function, $\frac{2\sin \left(2\pi k{f}_0{T}_s\right)}{\pi k}$, decreases. Hence, only the coefficients for $k=2, 3, 4$ and other low values are important. The cosine function for $k=2$ is known as the second harmonic; that for $k=3$ is the third harmonic, and so on. The sound of any musical note that is produced by a musical instrument contains the fundamental frequency and a few harmonics. 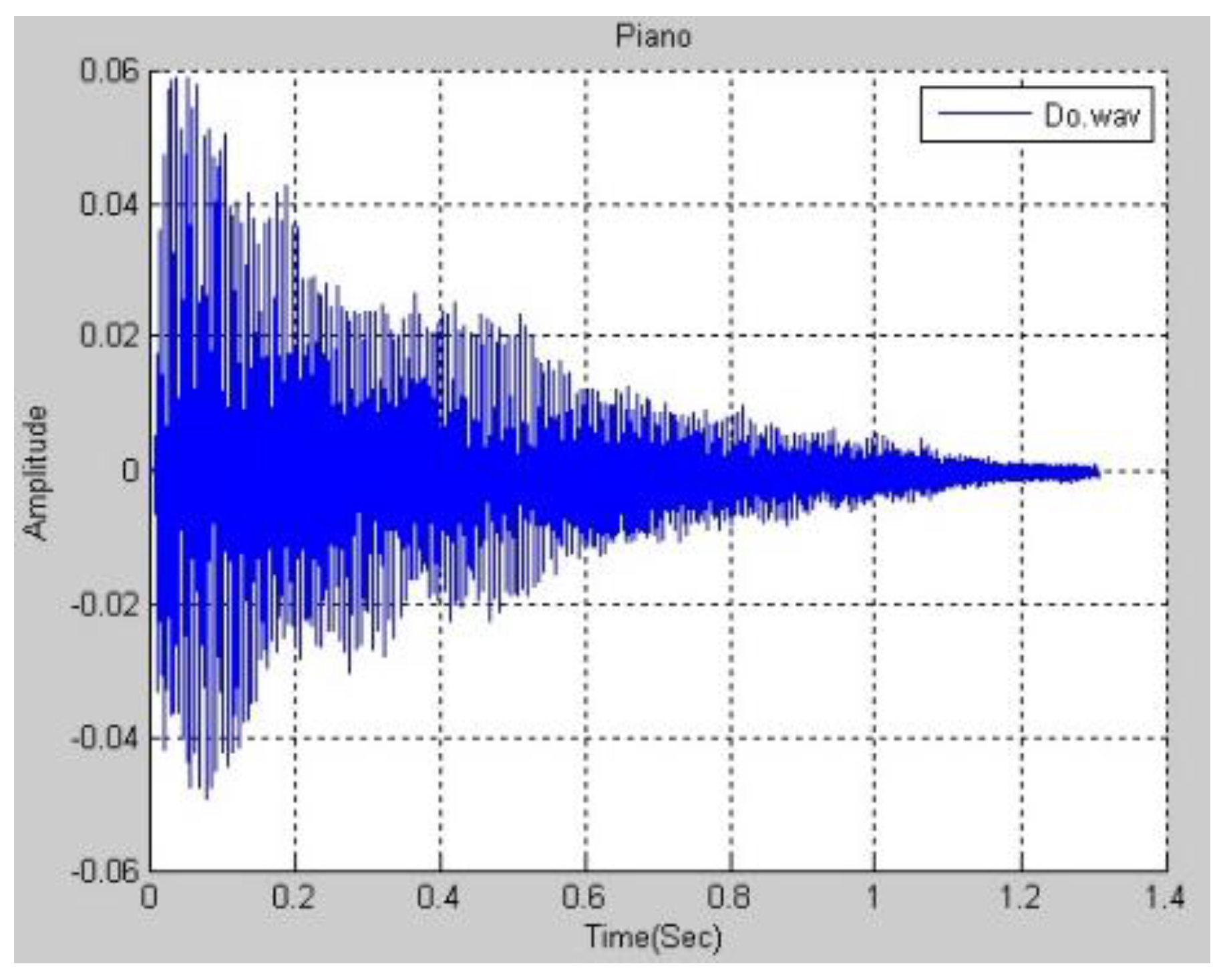Figure 3 plots the function of a real piano’s Middle C in the time domain. 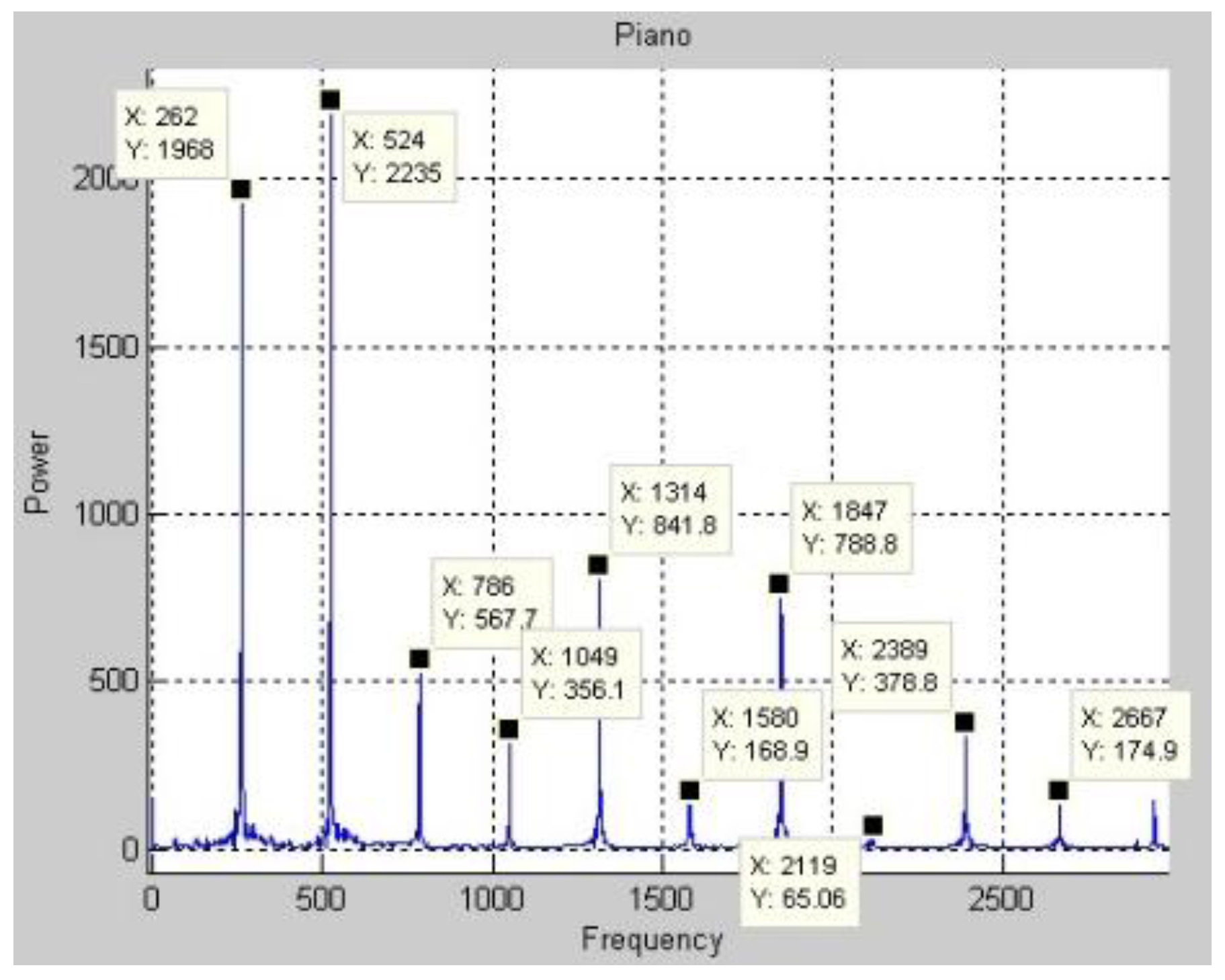The DFT is applied to the function in Figure 3 to obtain the frequency spectrum in Figure 4. Only a few of the magnitudes are marked because space is limited. After the frequency spectrum of Middle C on a real piano was obtained, the frequency spectra of all of the pitches that are produced in the middle region of a piano are found. 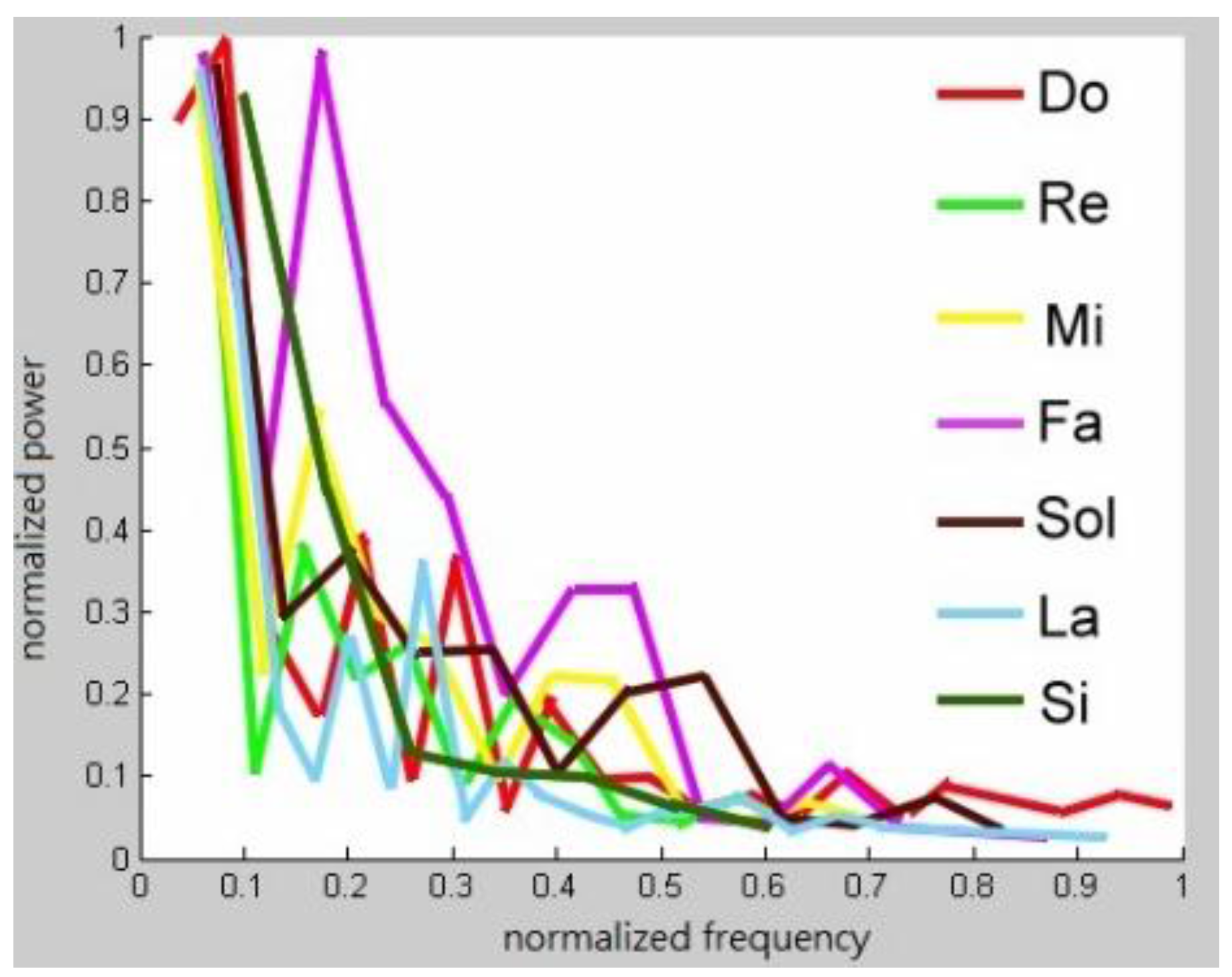Figure 5 displays these spectra.

A real music instrument produces different pitches with different frequency patterns. Consider a randomly chosen musical instrument, such as a piano and the playing of any note on it. Perform a DFT on the note. The k frequencies with the largest magnitudes are selected. Denote these frequencies as $f_1,f_2,\dots ,f_k$, where $f_1<f_2<\dots <f_k$, with magnitudes $a_1,a_2,\dots ,a_k$, $0\le a_i\le 1$. Calculate $b_i=f_i/f_1$ for $1\le i\le k$. Now suppose that the goal is to generate a frequency pattern for Middle C. The fundamental frequency of Middle C is known to be 262 Hz. Denote this frequency as $f_{ap}$. The Middle C that is generated by a real piano has frequencies $b_1{f}_{ap},b_2{f}_{ap},\dots ,b_k{f}_{ap}$ with magnitudes $a_1,a_2,\dots ,a_k$, respectively, and the inverse DFT generates the sound from these frequencies. Of course, musical sounds that are generated in this way are not expected to be the same as those produced by a piano. However, as demonstrated by the following experiment, they will be piano-like if $k$ is sufficiently large. The k frequencies with the largest magnitudes are selected using the prune and search method [39].

The following experiments involve synthesized pitches. Let $k=10$ so the ten frequencies with the largest magnitudes are obtained. The magnitudes $a_1,a_2,\dots ,a_{10}$ and respective multiples $b_1,b_2,\dots ,b_{10}$ are found and shown in

Table 1. The values of $a_i$, $b_i$ and $b_i{f}_{ap}$ of Middle C of a piano with $k=10$.

i	${\mathit{a}}_{\mathit{i}}$	${\mathit{b}}_{\mathit{i}}$	${\mathit{b}}_{\mathit{i}}{\mathit{f}}_{\mathit{a}\mathit{p}}$
1	0.2635	1.0000	262
2	0.7042	1.0038	263
3	0.5050	1.0077	264
4	0.3326	2.0038	525
5	0.8000	2.0077	526
6	0.2255	2.0115	527
7	0.3013	5.0345	1320
8	0.2823	7.0766	1854
9	0.2631	7.0805	1855
10	0.2402	7.0843	1856

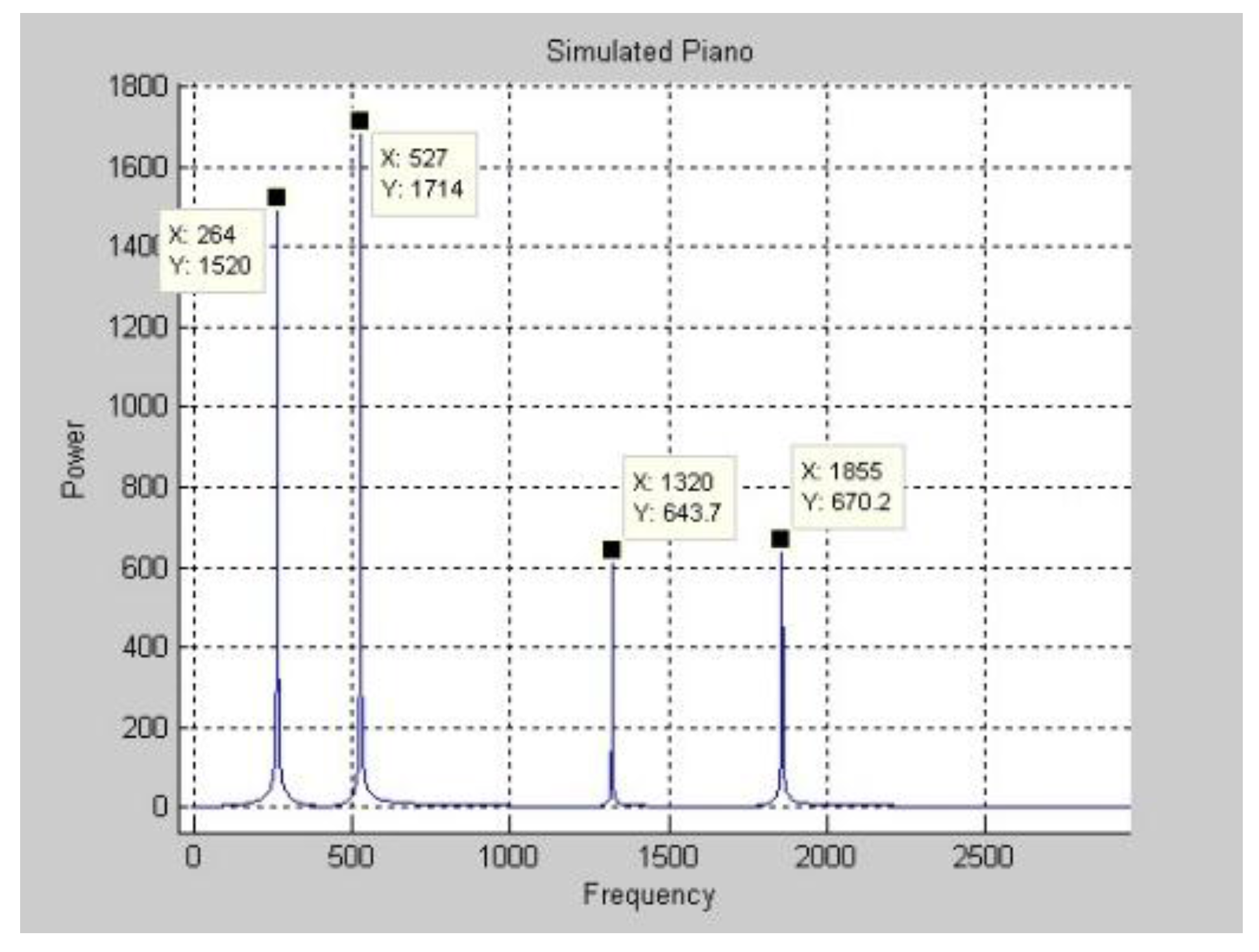
. Middle C on a piano has frequencies ($f_{ap}$, 1.0038$f_{ap}$, …, 7.0843$f_{ap}$) with respect magnitudes (0.2635, 0.7042, …, 0.2402). Let $f_{ap}=262$, yielding frequencies of (262, 263, …, 1856 Hz). Figure 6 and Figure 7 plot the experimental results in the frequency and time domains. Comparing Figure 3 and Figure 7, the waves are not similar.

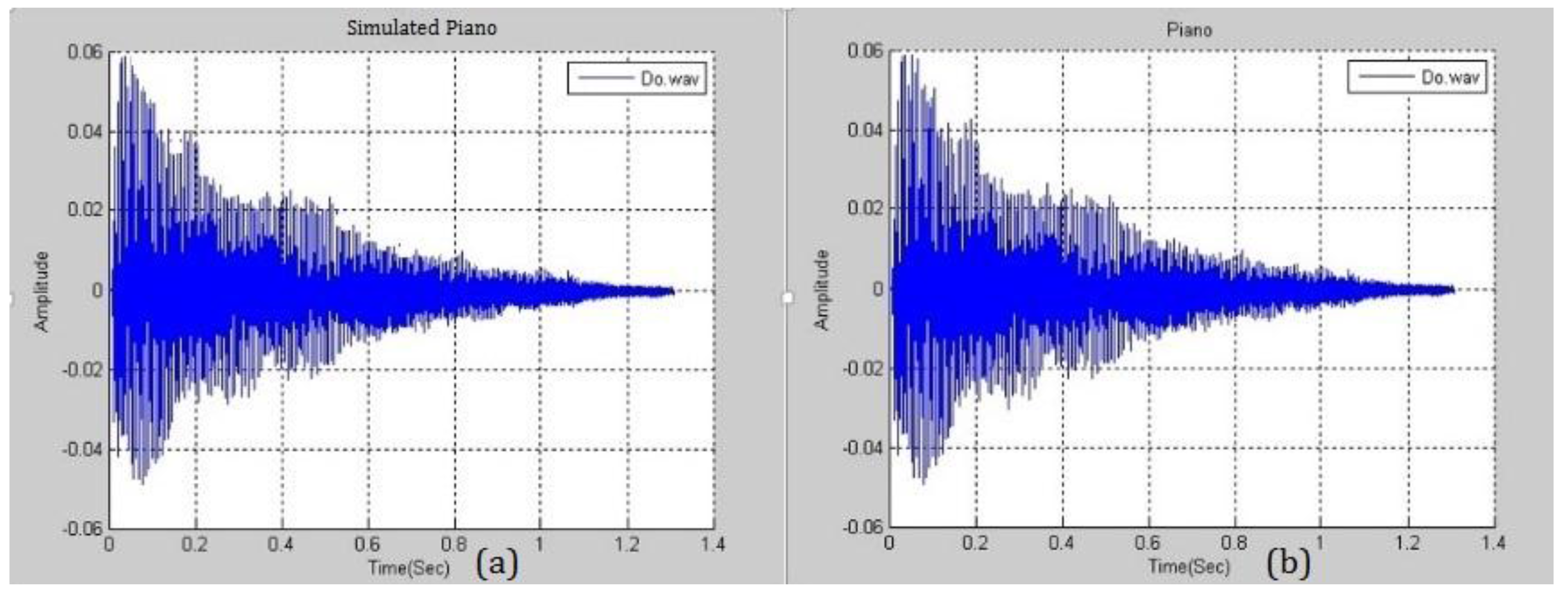
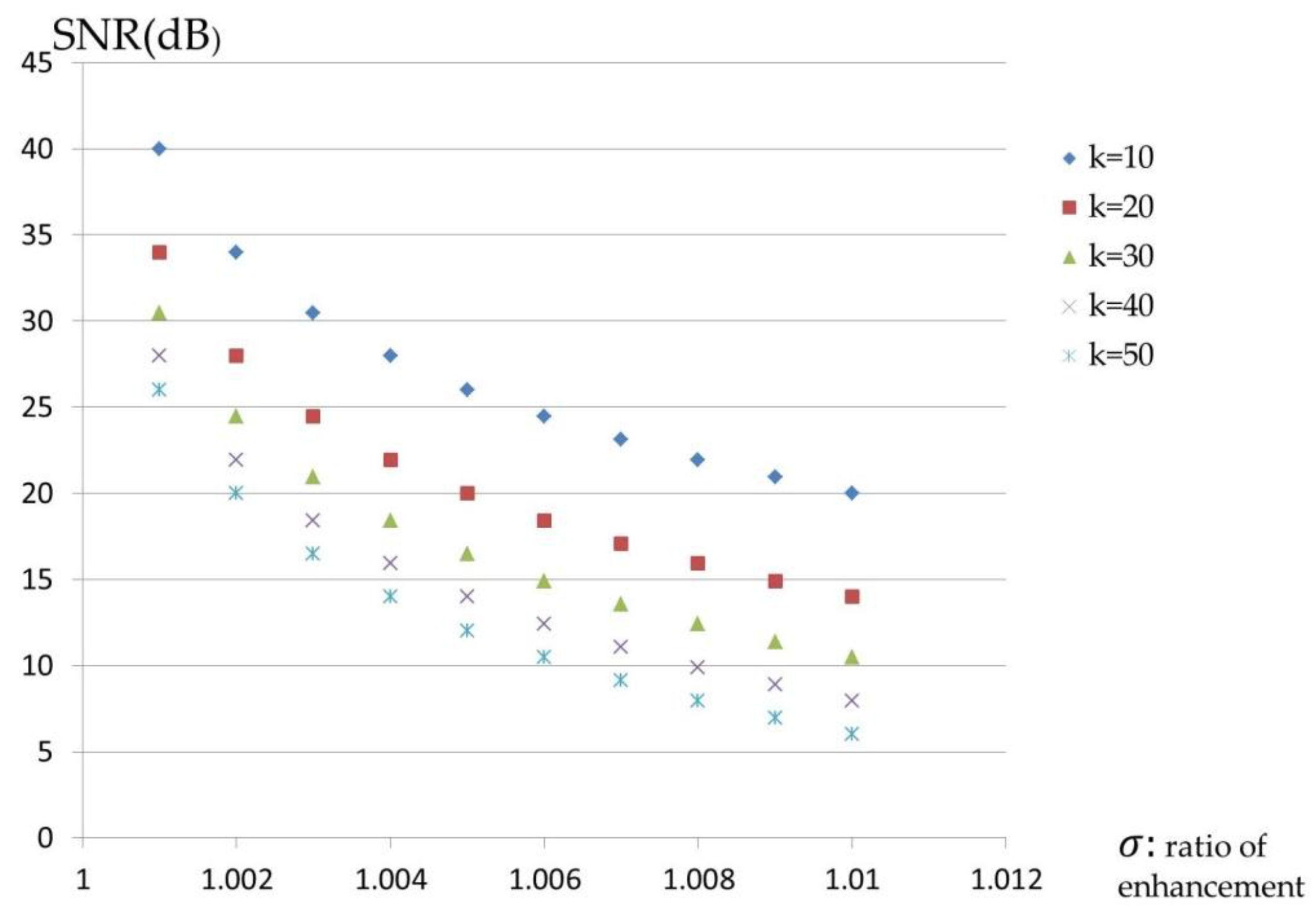
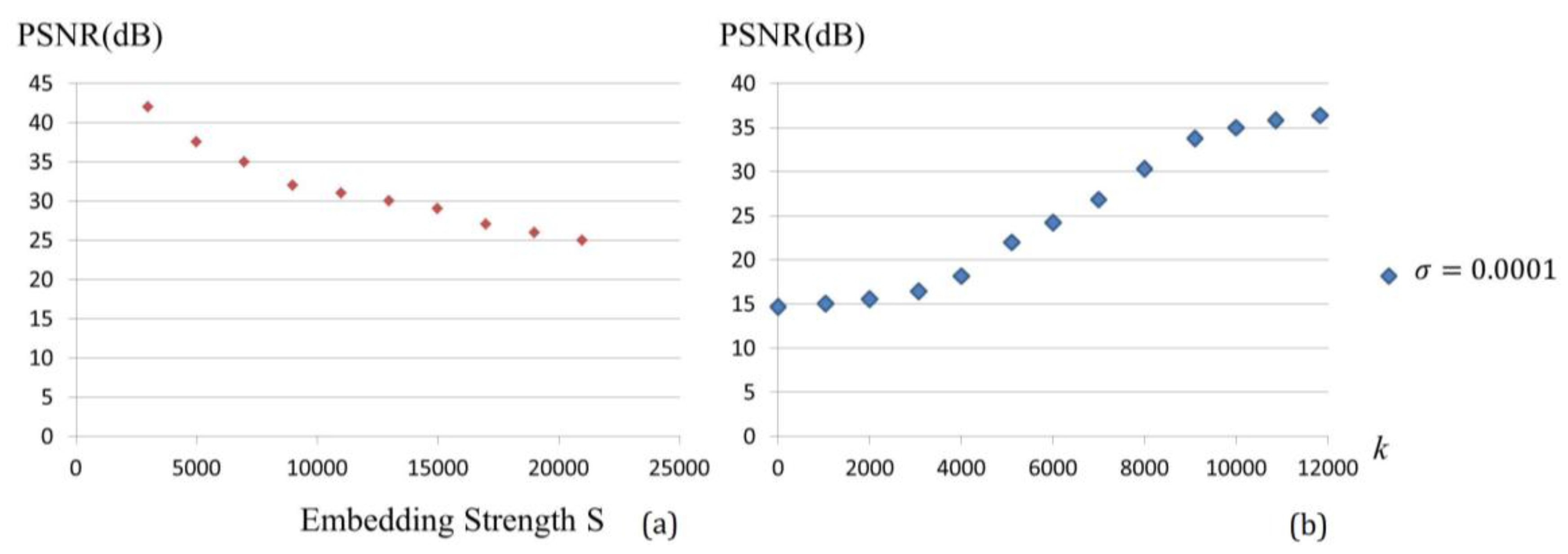
Figure 8 presents the similarity between a simulated piano note with $k=10,000$ and a real piano note. The difference between them is negligible and this fact will be exploited in the following section. A higher $k$ yields a smaller distortion and the higher ability to embed more secrets. Various pitches from different musical instruments were simulated and analyzed.

2.2. Data Hiding Scheme

The proposed data-hiding scheme involves the following steps. First, choose an instrumental pitch P to be the reference pitch. With reference to the preceding sections, all of the required parameters can be obtained. These include the magnitudes $a_i$ and the main frequencies $b_i{f}_{ap}$. 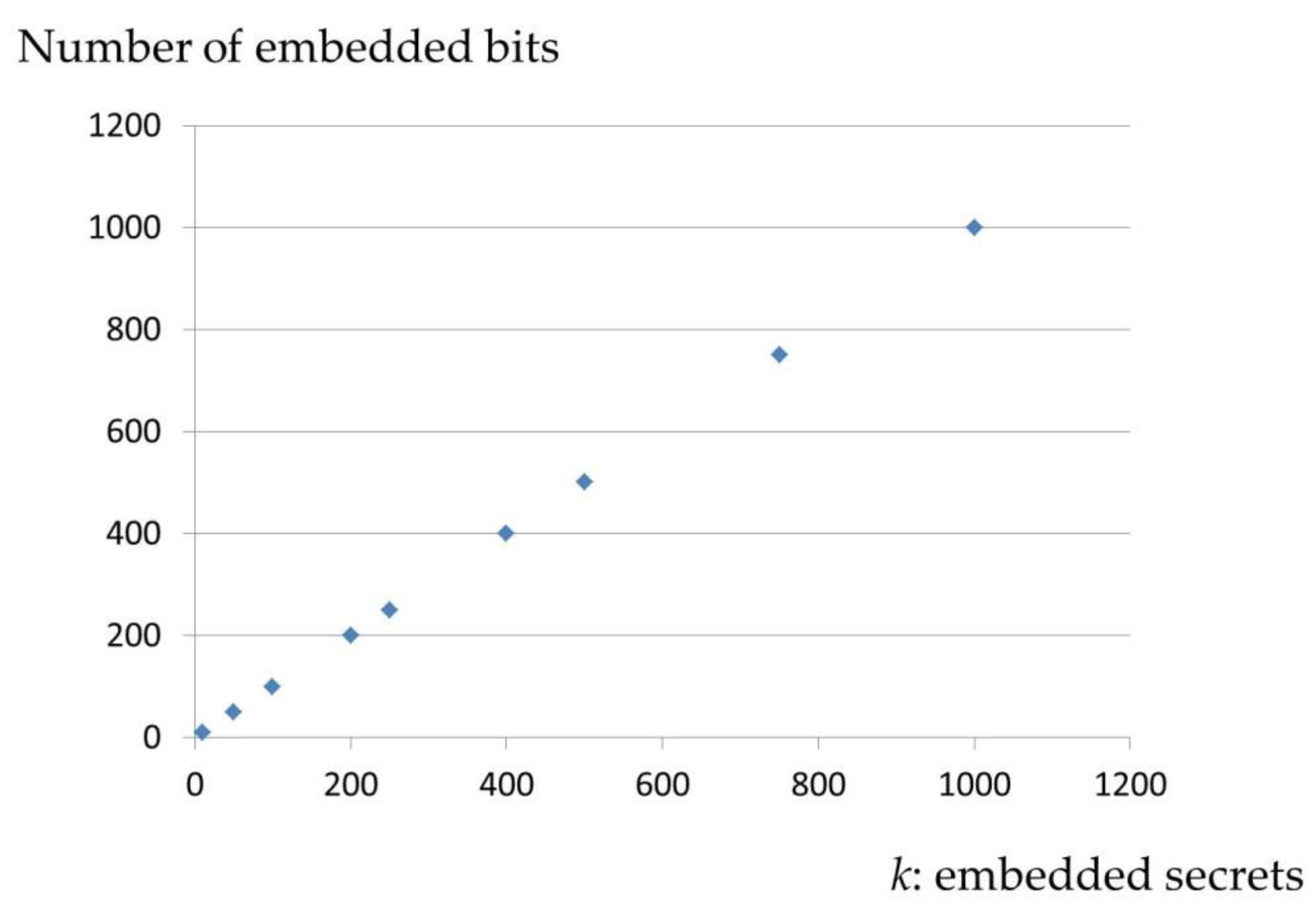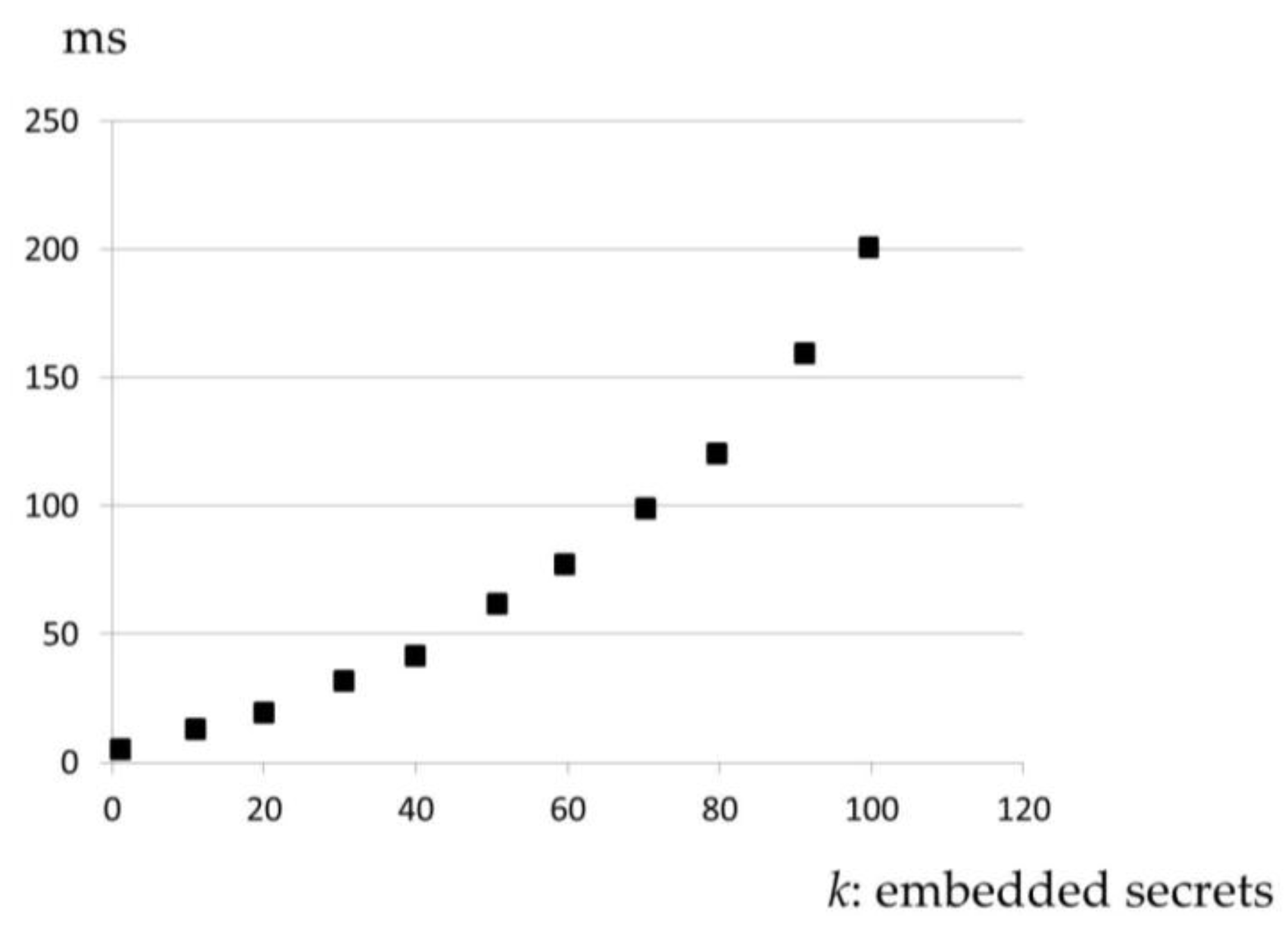The number of $a_i$ terms is k and the number of $b_i{f}_{ap}$ terms is k because the system is used only to generate the main k frequencies of the signals. Next, suppose that the length of the secret bit stream $b{t}_1,b{t}_2,\dots ,b{t}_k$ is also k. If $b{t}_1=1$, then $a_1$ is increased to $\mathsf{\sigma }{a}_1, 1<\sigma <2$; the same operation is applied to $a_2,a_3,\dots ,a_k$. 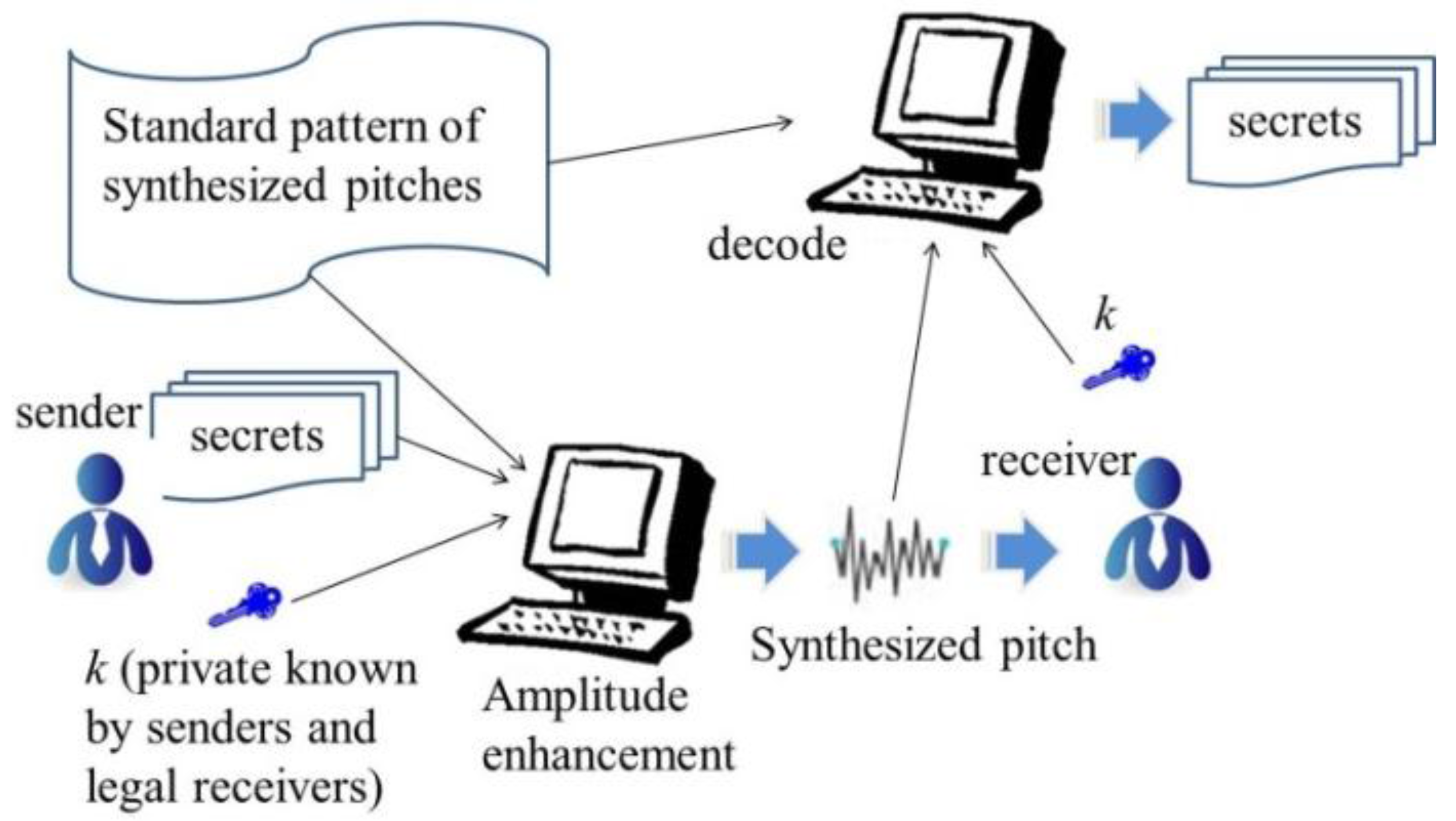Figure 9 is the overview of the scheme. The sender uses the standard pattern of synthesized pitches and k to encode the secrets to generate a synthesized pitch using amplitude enhancement. A legal receiver uses the standard pattern of synthesized pitches and k to decode the secret.

Algorithm 1 is the simple encoding procedure. Algorithm 2 is the decoding procedure.

Algorithm 1 Encoding Procedure
Input:	secret bit stream $b{t}_1,b{t}_2,\dots ,b{t}_k$ and reference instrumental pitch P
Output:	a stego-synthesized pitch
Step 1:	find $a_1,a_2,\dots ,a_k$ and $b_1{f}_{ap},b_2{f}_{ap},\dots ,b_k{f}_{ap}$ by referencing P
Step 2:	for all $a_i,1\le i\le k$, obtain $a{\prime }_1,a{\prime }_2,\dots ,a{\prime }_k$ as follows;
	if ($b{t}_i=1$)
	set $a{\prime }_i=\sigma a_i$
	else
	set $a{\prime }_i=a_i$
Step 3:	use $a{\prime }_1,a{\prime }_2,\dots ,a{\prime }_k$ and $b_1{f}_{ap},b_2{f}_{ap},\dots ,b_k{f}_{ap}$ to create a pitch p
Step 4:	return p

Algorithm 2 Encoding Procedure
Input:	length of secret k, reference pitch P and received pitch p
Output:	secret bit stream $b{t}_1,b{t}_2,\dots ,b{t}_k$
Step 1:	use standard pattern in Section 2.1 to obtain $A_1,A_2,\dots ,A_k$ of P
Step 2:	use standard pattern in Section 2.1 to obtain $a_1,a_2,\dots ,a_k$ of p
Step 3:	for each $A_i$ and $a_i$, decode secret bit $b{t}_i$ as follows.
	if ($A_i\ne a_i$)
	set $b{t}_i=1$
	else
	set $b{t}_i=0$
Step 4:	concatenate $b_1,b_2,\dots ,b_i,\dots ,b_k,1\le i\le k$ to form a bit stream B
Step 5:	return B

The value $\left(\sigma -1\right)a_1$ shall be too small to be perceived by the human ear. Consider, for example,

Table 2. The modified parameters after embedding secret 1001101101 in Middle C of a simulated piano with $\sigma =1.01$.

i	${\mathit{a}}_{\mathit{i}}$	${\mathit{b}}_{\mathit{i}}$	${\mathit{b}}_{\mathit{i}}{\mathit{f}}_{\mathit{a}\mathit{p}}$
1	0.2661	1.0000	262
2	0.7042	1.0038	263
3	0.5050	1.0077	264
4	0.3359	2.0038	525
5	0.8080	2.0077	526
6	0.2255	2.0115	527
7	0.3043	5.0345	1319
8	0.2851	7.0766	1854
9	0.2631	7.0805	1855
10	0.2426	7.0843	1856

: hiding bit stream 1001101101 in the synthesized pitch yields the enhanced magnitudes, which are shown in the first table.

Legitimate receivers obtain the reference instrumental pitch P, the length of the secret k and the method of generation of the synthesized pitches. The decoding procedure is as follows. First, identify the main frequencies that correspond to the k largest magnitudes from P and the received pitch p. The frequencies of the former are denoted as $F_1,F_2,\dots ,F_k$ and those of the latter are denoted as $f_1,f_2,\dots ,f_k$. The magnitudes of all main frequencies are obtained as $A_1,A_2,\dots ,A_k$ and $a_1,a_2,\dots ,a_k$. Each $A_i$ is compared with the corresponding $a_i$; for Algorithm 4, Step 3, if $A_i\ne a_i$, then the secret bit $b{t}_i=1$; otherwise, $b{t}_i=0$. Finally, all $b{t}_i$s are concatenated and the secret bit stream can be produced.

While the synthesis of musical pitches and the data-hiding scheme are public, the above algorithms can be designed more secure by including a parameter R, which is the real order of $a_i$ and $b_i{f}_{ap}$ during the data embedding procedure. R is generated using a random number generator and the seed of the generator is obtained by legal receivers. The formal definition of R is $R=\left\{r_i\right\}, 1\le r_i\le k,$ where all $r_i$ have different values. An example follows. Consider $R=\left\{3,1,7,9,2,10,4,6,5,8\right\}$;

Table 3. The modified parameters after embedding secret 1001101101 in Middle C of a simulated piano with $R=\left\{3,1,7,9,2,10,4,6,5,8\right\}$ and $\sigma =1.01$.

i	${\mathit{a}}_{\mathit{i}}$	${\mathit{b}}_{\mathit{i}}$	${\mathit{b}}_{\mathit{i}}{\mathit{f}}_{\mathit{a}\mathit{p}}$
1	0.2635	1.0000	262
2	0.7112	1.0038	263
3	0.5101	1.0077	264
4	0.3359	2.0038	525
5	0.8000	2.0077	526
6	0.2278	2.0115	527
7	0.3013	5.0345	1320
8	0.2851	7.0766	1854
9	0.2657	7.0805	1855
10	0.2402	7.0843	1856

is obtained after the complex version of the data embedding scheme is implemented. The red numbers indicate hidden secret “1” bits. Evidently, the positions of the secret bits differ from those in the second table. Algorithms 3 and 4 describe the complex version of the proposed scheme.

Algorithm 3 Encoding Procedure
Input:	secret bit stream $b{t}_1,b{t}_2,\dots ,b{t}_k$, secret order R and reference instrumental pitch P
Output:	a stego-synthesized pitch
Step 1:	find $a_1,a_2,\dots ,a_k$ and $b_1{f}_{ap},b_2{f}_{ap},\dots ,b_k{f}_{ap}$ by referencing P
Step 2:	for all $R_i,1\le i\le k$, obtain $a{\prime }_1,a{\prime }_2,\dots ,a{\prime }_k$ as follows.
	if ($b{t}_i=1$)
	set $a{\prime }_{R_i}=\sigma a_{R_i}$
	else
	set $a{\prime }_{R_i}=a_{R_i}$
Step 3:	use $a{\prime }_1,a{\prime }_2,\dots ,a{\prime }_k$ and $b_1{f}_{ap},b_2{f}_{ap},\dots ,b_k{f}_{ap}$ to create a pitch p
Step 4:	return p

Unlike in the first version, receivers no longer need the value of k but only the secret order R or random seed.

Algorithm 4 Encoding Procedure
Input:	secret order R, reference pitch P and received pitch p
Output:	secret bit stream $b{t}_1,b{t}_2,\dots ,b{t}_k$
Step 1:	use standard pattern in Section 2.1 to obtain $A_1,A_2,\dots ,A_k$ of P
Step 2:	use standard pattern in Section 2.1 to obtain $a_1,a_2,\dots ,a_k$ of p
Step 3:	for all $R_i,1\le i\le k$, decode secret bit $b{t}_i$ with reference to the following condition:
	if ($A_{R_i}\ne a_{R_i}$)
	set $b{t}_i=1$
	else
	set $b{t}_i=0$
Step 4:	concatenate $b_1,b_2,\dots ,b_i,\dots ,b_k,1\le i\le k$ to form a bit stream B
Step 5:	return B

The above two proposed embedding schemes focus on enhancing amplitudes when secret “1” bits are embedded. However, it shall be considered that the enhancement will be too large if there are too many “1” bits. A strengthened version is presented here called alternating current (AC) algorithm. The main idea of AC algorithm is to reduce a large enhancement caused by embedding secret “1” bits. The embedding scheme goes on alternatively enhancing each amplitude by multiply $\sigma$ and $\frac{1}{\sigma }$. For the example in Table 3, the parameters are modified as listed in

Table 4. The modified parameters after embedding secret 1001101101 in Middle C of a simulated piano using the alternating current (AC) algorithm with $R=\left\{3,1,7,9,2,10,4,6,5,8\right\}$ and $\sigma =1.01$.

i	${\mathit{a}}_{\mathit{i}}$	${\mathit{b}}_{\mathit{i}}$	${\mathit{b}}_{\mathit{i}}{\mathit{f}}_{\mathit{a}\mathit{p}}$
1	0.2635	1.0000	262
2	0.7112	1.0038	263
3	0.5101	1.0077	264
4	0.3293	2.0038	525
5	0.8000	2.0077	526
6	0.2278	2.0115	527
7	0.3013	5.0345	1320
8	0.2795	7.0766	1854
9	0.2605	7.0805	1855
10	0.2402	7.0843	1856

by adopting AC algorithm. The numbers of the even positions (9, 4, 8) of embedding secret “1” bits are modified by multiplying $\frac{1}{\sigma }$. Algorithms 5 and 6 describe the embedding and extracting procedures of the AC algorithm, respectively.

Algorithm 5 Encoding Procedure
Input:	secret bit stream $b{t}_1,b{t}_2,\dots ,b{t}_k$, secret order R and reference instrumental pitch P
Output:	a stego-synthesized pitch
Step 1:	find $a_1,a_2,\dots ,a_k$ and $b_1{f}_{ap},b_2{f}_{ap},\dots ,b_k{f}_{ap}$ by referencing P
Step 2:	initialize AC = 0
Step 3:	for all $R_i,1\le i\le k$, obtain $a{\prime }_1,a{\prime }_2,\dots ,a{\prime }_k$ as follows.
	if ($b{t}_i=1$)
	if(AC = 0)
	set $a{\prime }_{R_i}=\sigma a_{R_i}$
	set AC = 1
	else
	set $a{\prime }_{R_i}=\frac{1}{\sigma }{a}_{R_i}$
	set AC = 0
	else
	set $a{\prime }_{R_i}=a_{R_i}$
Step 4:	use $a{\prime }_1,a{\prime }_2,\dots ,a{\prime }_k$ and $b_1{f}_{ap},b_2{f}_{ap},\dots ,b_k{f}_{ap}$ to create a pitch p
Step 5:	return p

Algorithm 6 Encoding Procedure
Input:	secret order R, reference pitch P and received pitch p
Output:	secret bit stream $b{t}_1,b{t}_2,\dots ,b{t}_k$
Step 1:	use standard pattern in Section 2.1 to obtain $A_1,A_2,\dots ,A_k$ of P
Step 2:	use standard pattern in Section 2.1 to obtain $a_1,a_2,\dots ,a_k$ of p
Step 3:	for all $R_i,1\le i\le k$, decode secret bit $b{t}_i$ with reference to the following condition:
	if ($A_{R_i}\ne a_{R_i}$)
	set $b{t}_i=1$
	else
	set $b{t}_i=0$
Step 4:	concatenate $b_1,b_2,\dots ,b_i,\dots ,b_k,1\le i\le k$ to form a bit stream B
Step 5:	return B

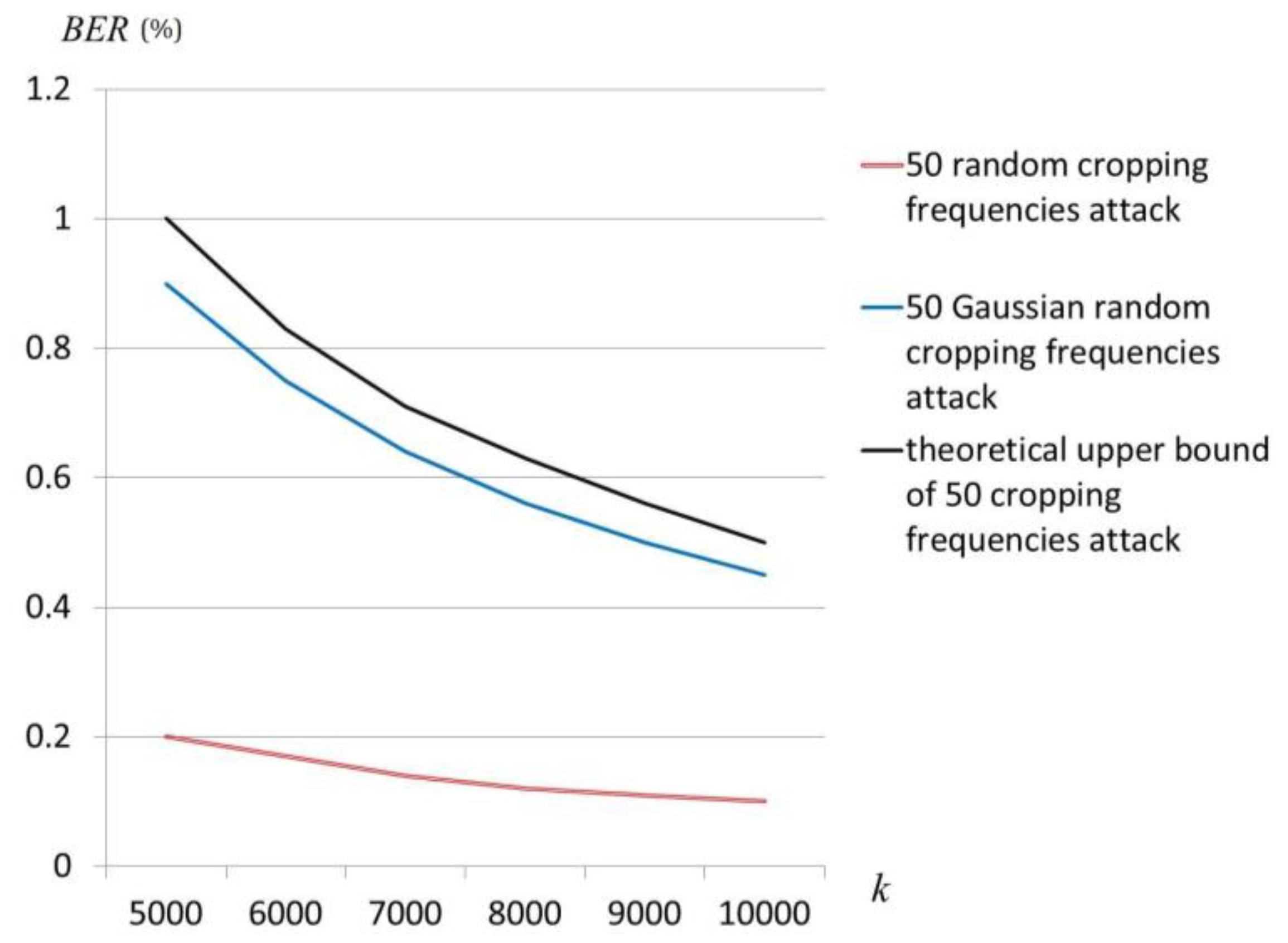
It shall be proven that even if the proposed steganographic scheme is applied twice, it is still able to get the embedded secrets. A simple proof is given as follows. The basic idea of this presented research work is the enhancement of amplitudes if embeds a secret “1” bits. Applying the embedding procedure twice makes the enhanced amplitudes multiply $\sigma$ of $\frac{1}{\sigma }$ again, that is, $a_i$ will be ${\sigma }^2{a}_i$ or $\frac{1}{{\sigma }^2}{a}_i$ but not $\sigma a_i$ or $\frac{1}{\sigma }{a}_i$. When legal receivers apply the decoding procedure, the main strategy is to compare the enhanced amplitudes to the original amplitudes of the standard patterns. The are only three possible values of $a_i$: $a_i$, ${\sigma }^2{a}_i$, and $\frac{1}{{\sigma }^2}{a}_i$. Apparently, the comparisons work and are able to obtain the embedded secrets.

3. Results

This section displays experiments of the proposed scheme. Figure 10 displays the cover and the stego-pitches with $k=10$. The red numbers indicate secret “1” bits that are hidden. Figure 11 shows that the cover and the stego-pithes when $k=10,000$ by embedding 10,000 random bits and the differences are nearly none because the enhancement of amplitudes is too small. Figure 12 plots the signal-to-noise ratio (SNR) between the embedded noise and the standard pitch as a function of $\sigma$ from 1.001 to 1.01 for k from 10 to 50. A larger $\sigma$ causes greater distortions of the cover pitches.

The performance of a data-hiding scheme is generally measured using capacity and distortion. As mentioned above, more multimedia are being produced by Internet users, so intruders have difficulty in distinguishing stego-media from cover media. This work develops a new cover medium, and comparisons can only be made between frequencies for different values of k, as selected by the standard pattern in Section 2.1. First, the capacity of the proposed scheme is discussed. Since the proposed scheme embeds a secret bit in a selected pitch, the capacity increases with the number of selected pitches. Figure 13 displays the capacity for different values of k; a larger $k$ allows more secret bits to be embedded. The value of k is linearly related to capacity.

Second, the distortions between the stego and real pitches are provided for different values of k and $\sigma$. The following experiment is conducted. The peak-signal-to-noise ratio (PSNR) function in the MATLAB library is utilized to evaluate the distortion of two plotted images of stego and real pitches. Figure 14 plots the variation of the PSNR associated with different values of k and $\sigma$. Each point represents a comparison between a stego and a real pitch; for example, the point (10,000, 35) compares a stego pitch (with 10,000 bits hidden, $\sigma =1.0001$) and a real pitch.

The above curve reveals that the proposed scheme yields a smaller distortion as more secret bits are embedded up to a limit beyond which too many secret bits are hidden. In the proposed experiment, the upper bound of the distortion is 37 dB when $\sigma =0.0001$ and 12,000 bits are embedded. In practical applications, the advantage of the present scheme is that the capacity grows and the distortion declines.

Third, the computational performance of the proposed scheme is addressed. Figure 15 plots the time consumption of the proposed scheme.

4. Discussion

This section presents the comparison with other related work, performance under other attacks and some theoretical analysis.

4.1. Comparisons with Related Work

Common attacks against an audio data-hiding scheme include the low pass filter (LPF) attack, mp3-like compression, and re-quantization. The bit error ratio (BER) is used to measure the performance of a data-hiding scheme under common attacks. The BER is defined as the ratio of exact matching of the embedded secret bit-stream and of the decoded secret bit-stream after the stego cover pitch has undergone by the above common attacks. The mathematical definition is:

$$BER=\frac{{{\displaystyle \sum }}_{i=1}^{k}B{\prime }_i\oplus B_i}{\left|B\right|}\left(\oplus \mathrm{is}\mathrm{exlusive}\mathrm{or}\right)$$

(2)

The definitions of the common attacks adopted in the proposed comparisons are as follows:

• LPF (3 kHz) filters all signals with frequencies lower than 3 kHz.
• mp3 (64 kbps) adopts an existing multimedia tool (Adobe Audition) to compress the stego-pitch (.wav file->.mp3 file) and decompress back to .wav file format.
• Re-quantization (16 to 32 bits) adopts an existing multimedia tool (Adobe Audition) to re-quantize the sampling point from 16 bits to 32 bits and then to re-quantize it back to 16 bits.
• Re-quantization (16 to 8 bits) adopts an existing multimedia tool (Adobe Audition) to re-quantize the sampling point from 16 bits to 8 bits and then to re-quantize it back to 8 bits.

Table 5. The bit error ratio (BER) of the proposed methods and related work. LPF: low pass filter; HQ: hard quantization; SQ: soft quantization.

Methods/Attacks	LPF (3 kHz)	mp3 (64 kbps)	Re-Quantization 16–32 bits	Re-Quantization 16–8 bits
Ours (k = 40)	0.0%	0.0%	0.0%	0.0%
Akhaee et al. [17]: HQ, SQ	15.0%, 15.0%	10.2%, 0.1%	$0.0\text{\%}$, 0.0%	0.0%, 0.0%
Wu et al. [40]	$\varnothing$	4.3%	$\varnothing$	$\varnothing$
Chen et al. [41]	$\varnothing$	6.5%	$\varnothing$	11.9%

$\varnothing$: Not mentioned by the corresponding authors.

compares the BERs of the proposed scheme and methods proposed elsewhere [17,40,41]. The results indicate that the methods developed herein outperform the others under the indicated attacks. In [17], the authors proposed two steganographic methods, hard quantization (HQ) and soft quantization (SQ) using correlated quantization to embed data with histogram based detector. A novel mapping denoted as point to point graph (PPG) is used to evaluate the correlation among each value of samples. PPG point radii are suggested to embed data to obtain the performances. In [40], the authors presented a self-synchronization scheme for audio watermarking. The synchronization codes are hidden into audio as the informative data, thus the embedded data have the ability of self-synchronization. The synchronization codes are hidden into low frequency coefficients in discrete wavelet transform domain. In [41], the authors proposed an echo hiding scheme. Some echoes are adequately adapted when the embedding process is executing.

The proposed scheme protects all of the hidden secrets under the specified common attacks for the following reasons.

LPF (3 kHz), by the definition of the LPF, frequencies higher than 3 kHz will be eliminated under this attack, while in the proposed scheme, the selected k-pitches are all beyond 3 kHz such that no bits are eliminated. mp3 (64 kbps), the main purpose of mp3 compression is to eliminate frequencies higher than 22 kHz, and as under the LPF attack, the proposed scheme selects all low frequencies so that no bits disappear. Re-quantization (16 to 32 bits), this attack increases the size of the binary representation of numbers and extension will not affect the sampled values of the stego-pitches. Evidently, no secret bits will be destroyed. Re-quantization (16 to 8 bits), this attack shrinks the size of the binary representation of numbers, eliminating the suffix numbers when is re-quantized to its original size. In the proposed scheme, the selected $\sigma$ does not produce long floating numbers after the enhancement of amplitudes so the scheme performs well under this attack.

Another fact of the comparison is the curve of the trend among capacity and distortion. Figure 16 demonstrates the difference of the curve between the related work [17] and the proposed work. It can be seen that the distortion decreases when the capacity increases, while, in this work, the distortion increases to a boundary value when the capacity increases. The phenomenon is because the proposed scheme is designed for breaking the bottleneck of traditional steganography, as illustrated in Figure 16a.

4.2. Performances under Other Attacks

The performances of the proposed work under other attacks like frequency cropping [42], direct current (DC) and high pass filter (HPF) [43] are discussed in this subsection. The definition of DC attack is to pad a certain power on a stego audio, then run the decoding procedure to examine the BER. The definition of HPF attack is to filter all signals whose frequencies are higher than a certain frequency, then run the decoding procedure to examine the BER. The frequency cropping attack is to randomly pad signals with certain frequencies on a stego pitch. The presented schemes are conditionally outperformed under the above three attacks.

For frequency cropping attack, if, frequencies of all randomly padded signals are exactly the same with the frequencies of the selected $b_i{f}_{ap}$s, a high BER occurs. Figure 17 presents the experiments of frequency cropping attack. In the setting of the experiment, 50 frequencies are randomly generated to replace the corresponding frequencies of a pitch with different k selected. Another 50 frequencies are generated by normal distribution. In addition, a baseline of the theoretical upper bound is also drawn in the figure.

For DC attack, all sampled values increase after padding a DC signal, and the decoding procedure will fail because the testing condition is the quality of the power of the cover and the stego pitches. However, if the decoding procedure is adequately modified to inspect all amplitudes of $b_i{f}_{ap}$s, it is possible to filter out the DC power and obtain all correct secrets. The inspection could be achieved as follows. Subtract all amplitudes of the selected $b_i{f}_{ap}$s and discover the most appeared value. The most appeared value is the power of DC, and the subtraction of the DC power from the stego pitch will successfully filter out the DC.

For HPF attack, all selected $b_i{f}_{ap}$s will be filtered out under a certain frequency $f_{HP}$, that is, only those selected $b_i{f}_{ap}$s which are larger than $f_{HP}$ can survive after exploiting HPF on the stego pitch. However, it is a trick to avoid the sabotage of HPF; selecting higher $b_i{f}_{ap}$ will outperform under HPF attack.

Table 6. The BER of the proposed methods and related work. HPF: high pass filter; DC: direct current.

Methods/Attacks	HPF (8 kHz)	DC
Ours (k = 40, all $b_i{f}_{ap}$s are larger than 8,000)	0.0%	0.0%
Akhaee et al. [17]: HQ, SQ	0.0%, 0.0%	0.0%, 0.0%
Wu et al. [40]	$\varnothing$	$\varnothing$
Chen et al. [41]	4.2%	4.5%

$\varnothing$: Not mentioned by the corresponding authors.

presents the performances under DC and HPF attacks compared with [17,40,41]. Two types of the selected $b_i{f}_{ap}$s are used.

In recent years, many steganography were proposed with considering the cracking probability [44,45,46,47,48,49,50,51] under a brute force guessing. The threating mode evaluated here is based on the intruders knowing algorithms but without the order R. In practice, R is a private key and it should be transmitted via a secure channel. If an intruder uses a computer and successfully detects all slight noises between the stego and cover pitch (the standard patterns are also public knowledge), he could dress all enhanced frequencies but without a correct order. This means that he knows which frequency is used to embed “1” or “0” but he cannot reconstruct the exact bit-stream without R. Absolutely, the only thing he can do is to try all combinations of these 1s and 0s with n 1s and $i$ 0s where $0\le n\le k$ and k is the number of selected frequencies. Denote the summation of the combinations as $S\left(n\right)$. For $n=0$, there are k possibilities of embedded bit-stream because an intruder does not obtain the length of R, so that $S\left(0\right)=k$.

For $n=1$: $S\left(1\right)=\frac{1!}{1!}+\frac{2!}{1!1!}+\dots +\frac{\left(k-1\right)!}{1!\left(k-2\right)!}+\frac{k!}{1!\left(k-1\right)!}$.

For $n=2$: $S\left(2\right)=\frac{2!}{2!}+\frac{3!}{2!1!}+\dots +\frac{\left(k-1\right)!}{2!\left(k-3\right)!}+\frac{k!}{2!\left(k-2\right)!}$.

For $n=3$: $S\left(3\right)=\frac{3!}{3!}+\frac{4!}{3!1!}+\dots +\frac{\left(k-1\right)!}{3!\left(k-4\right)!}+\frac{k!}{3!\left(k-3\right)!}$.

For $n=\frac{k}{2}$:

$$S\left(\frac{k}{2}\right)=\frac{\left(\frac{k}{2}\right)!}{\left(\frac{k}{2}\right)!}+\frac{\left(\frac{k}{2}+1\right)!}{\left(\frac{k}{2}\right)!1!}+\frac{\left(\frac{k}{2}+2\right)!}{\left(\frac{k}{2}\right)!2!}+\dots +\frac{\left(k-2\right)!}{\left(\frac{k}{2}\right)!\left(\frac{k}{2}-2\right)!}+\frac{\left(k-1\right)!}{\left(\frac{k}{2}\right)!\left(\frac{k}{2}-1\right)!}+\frac{k!}{\left(\frac{k}{2}\right)!\left(\frac{k}{2}\right)!}$$

(3)

For $n=k-3$: $S\left(k-3\right)=\frac{\left(k-3\right)!}{\left(k-3\right)!}+\frac{\left(k-2\right)!}{\left(k-3\right)!1!}+\frac{\left(k-1\right)!}{\left(k-3\right)!2!}+\frac{k!}{\left(k-3\right)!3!}$.

For $n=k-2$: $S\left(k-2\right)=\frac{\left(k-2\right)!}{\left(k-2\right)!}+\frac{\left(k-1\right)!}{\left(k-2\right)!1!}+\frac{k!}{\left(k-2\right)!2!}$.

For $n=k-1$: $S\left(k-1\right)=\frac{\left(k-1\right)!}{\left(k-1\right)!}+\frac{k!}{\left(k-1\right)!1!}$.

For $n=k$: $S\left(k\right)=\frac{k!}{k!}$.

The above equations reveal a fact that the probability is the same of [S(0), S(k)], [S(1), S(k − 1)], [S(2), S(k − 2)], …, [S($\lfloor \frac{k}{2}\rfloor -2$), S($\lceil \frac{k}{2}\rceil +2$)], [S($\lfloor \frac{k}{2}\rfloor -1$), S($\lceil \frac{k}{2}\rceil +1$)], [S($\lfloor \frac{k}{2}\rfloor$), S($\lceil \frac{k}{2}\rceil$)]. According to the above equations:

$$S\left(\frac{k}{2}\right)={{\displaystyle \sum }}_{i=0}^{k/2}\frac{\left(\frac{k}{2}+i\right)!}{\left(k/2\right)!i!}=\frac{\left(k+1\right)!}{\frac{k}{2}!\frac{k+2}{2}!}$$

(4)

It is the worst case of the successful guessing under brute force. Figure 18 performs $S\left(k/2\right)$ as an exponential function performed and the probability is then equal to $\frac{\frac{k}{2}!\frac{k+2}{2}!}{\left(k+1\right)!}$.

4.3. Theoretical Analysis

This section describes some theoretical analyses of the proposed scheme. Theorem 1 is the theoretical boundary condition of the enhancement. The lower bound is according to the limit of the floating points provided by the software. The upper bound is decided by a user with selected number of capacity and expected distortion. Theorem 2 is the theoretical evaluation of the capacity, and it is according to the selected number of hidden secrets. Theorem 3 describes the theoretical time consumption of the proposed scheme. The parameter n is the total sampled data of a pitch and k is the number of secrets. The total computations include DFT, time of data embedding and inverse DFT. Theorem 4 describes the theoretical evaluate of the limit when error bits occur. Because the least bits of the proposed re-quantization are eight bits, this indicates that each datum needs at least eight bits to represent the number. Therefore, if the bit-represent of the enhancement larger than eight, the suffix of the number will disappear when the down-re-quantization (16 to 8 bits) deployed.

Theorem 1.

The practical boundary condition of$\sigma$ is $1+{10}^{-L}<\sigma <1+\frac{1}{kSNR}$ where L is the bit length of the floating point in the corresponding software; k is the number of the selected pitches, and SNR is the set quality of the stego-pitches.

Proof. 

The value of $\sigma$ is considered here. Ideally, the range of $\sigma$ is 1 to 2 because less noises is better and embedding a signal in a cover pitch that is identical to it is meaningless. A smaller $\sigma$ is preferred because it supports lower distortion and the length of the floating point is limited such that $\lg \left(\sigma -1\right)$ cannot exceed the size of the floating point, say L, which is defined by the software. Therefore, $\lg \left(\sigma -1\right)<L,1<\sigma <2\to 1+{10}^{-L}<\sigma (\mathrm{becasue}0<\sigma -1<1)$. The practical upper bound is obtained by the setting $\frac{P_{signal}}{P_{stego}-P_{signal}}>\mathrm{SNR}$ (signal-to-noise ratio). The denominator $P_{stego}-P_{signal}$ causes the embedded noise to stisfy $\frac{1}{k\left(\sigma -1\right)}>\mathrm{SNR}$. With fixed k and SNR, the upper bound of $\sigma$ is obtained as $1+\frac{1}{k\mathrm{SNR}}$.

Theorem 2.

The capacity of the proposed data-hiding scheme is O(k), where k is the number of selected pitches.

Proof. 

According to Figure 15, the capacity complexity is related to k, the number of selected pitches.

Theorem 3.

The time complexity of the proposed scheme is O(nlgn + k(1 + lgk)).

Proof. 

The DFT and inverse DFT cause a temporal bottleneck in the scheme. The best time consumption of DFT and inverse DFT is O(nlgn), and the time consumed by the proposed scheme, for embedding secrets is O(k). Because k frequencies are selected, the inverse DFT has a time cost of O(klgk) rather than O(nlgn). The total time complexity of the proposed scheme is addressed by the following theory.

Theorem 4.

Error bits start to appear if $lg\sigma >8$.

Proof. 

The value of $\sigma$ at which the error bit of re-quantization (16 to 8 bits) begins to be caused is of interest. The key point is the bit-size of $\sigma a_i$, so $\lg \sigma$ should be smaller than 8. A theory concerning the production of the error under re-quantization (16 to 8 bits) that corresponds to $\sigma$ is provided.

5. Conclusions and Future Work

This work developed a data-hiding scheme that is based on a new cover medium, and synthesized pitches, which are popularly used to demonstrate initial versions of compositions conveniently and at low-cost. This data-hiding scheme relies on the similarity between synthesized pitches and real instrumental pitches to remove concern about the compromising of the hidden of data by audio distortion. To demonstrate the feasibility of the scheme, secret bits are embedded during the generation of simulation of instrumental pitches. Experimental results reveal that more secrets can be hidden without distortion. The proposed method differs from traditional data-hiding schemes in that the data embedding procedure causes insignificant signal distortion. Finally, comparisons of the BER values obtained herein and in related work under common attacks reveal that the scheme herein outperforms under some attacks.

The main restriction is that only one pitch can be used at the same time and it is expected that there shall be a more efficient scheme using several pitches at the same time. To achieve more applicability, multiple pitches with multiple instruments used at a single time slot shall be developed. Moreover, according to the progress of technologies of signal processing and the faster computation of computers, exploiting further robust strategies such as spread transform dither modulation is necessary to against attacks.