Abstract
To improve the accuracy of indoor pedestrian positioning, an indoor pedestrian positioning system with two-order Bayesian estimation based on Extended Kalman Filter (EKF) and Particle Filter (PF) is proposed in this paper. The presented system combines a foot-mounted inertial sensor, a Wi-Fi propagation model and building structure to make good use of these information resources. There are two updates in this system in order to limit the accumulative errors of inertial sensors. In the first update, the inertial navigation system (INS) is the main system in the calculation of pedestrian positioning, and Zero-velocity update (ZUPT) is introduced as the reference to correct the accumulative errors of INS based on EKF. To further limit the accumulative errors of inertial sensors, the estimated results obtained from the first update, including horizontal position information, are introduced as the observations based on PF in the second update; Pedestrian Dead Reckoning (PDR) is the main system in the calculation of pedestrian positioning, and the weight of particles is determined by the Wi-Fi propagation model, building structure information and output of the first update. The results show that the accuracy of positioning is effectively increased.
1. Introduction
Global Positioning System (GPS) is a widely used positioning system which can provide highly accurate outdoor position information in real-time and in all weather conditions. Due to signal attenuation, multipath interference and other factors in the indoor environment, the accuracy of GPS cannot meet the requirements of indoor positioning accuracy [1].
With the development of society, the demand for indoor positioning is growing, for example, in route planning for public places such as smart homes, airports and shopping malls, as well as positioning for emergency situations, such as fire and earthquakes. Many different indoor positioning technologies have been developed to obtain position information in different indoor environments. According to the information sources, the common technologies for indoor positioning can be divided into Wi-Fi [2,3,4], Ultra Wide Band (UWB) [5,6], Ultrasound [7], and Micro-Electro-Mechanical Systems (MEMS) [8] etc.
Indoor pedestrian positioning based on MEMS is an autonomous positioning system; it can provide position information without additional infrastructures thanks to the development of the manufacture process—the integration of MEMS devices has been improved and the volume has been greatly reduced, which make MEMS more suitable in indoor positioning applications.
There are two kinds of inertial positioning methods based on MEMS, the first one is the inertial navigation system (INS), which can provide the 3-axis position information, 3-axis velocity information and 3-axis attitude information by integrating accelerations and turn rates obtained from inertial sensors with time; the other one is Pedestrian Dead Reckoning (PDR), which can provide 2-axis horizontal position information and heading information by detecting the statement of the pedestrian and calculating the step length from step to step. The pedestrian positioning based on MEMS can work without external information; however, there are accumulative errors caused by inertial sensors and algorithms, which can greatly reduce the positioning accuracy. Hence, Zero-velocity update (ZUPT) is adopted to limit the accumulative errors of indoor positioning based on MEMS.
There are two kinds of indoor positioning methods based on a Wi-Fi signal: the first one is Wi-Fi fingerprinting positioning, and the other is Wi-Fi propagation model positioning. Normally, the average accuracy Wi-Fi propagation model is lower than the accuracy of Wi-Fi fingerprinting. In this paper, the Wi-Fi positioning is used intermittently when the pedestrian is closed to Access Points (APs) by detecting the Received Signal Strength (RSS) of Wi-Fi. The accuracy of the Wi-Fi propagation model closed to APs is higher than the average accuracy of the Wi-Fi propagation model. Compared with Wi-Fi fingerprinting positioning, the Wi-Fi propagation model positioning requires less pre-preparation. In this paper, Wi-Fi propagation model positioning is adopted to obtain position information intermittently.
The research work in [9] adopts ZUPT to limit the accumulative errors of inertial sensors based on Extended Kalman Filter (EKF); the velocity error can be effectively compensated. However, the positioning error quickly increases as the distance increases. Hence, more information sources are needed for data fusion to improve the accuracy of indoor pedestrian positioning by providing redundant data. With the development of smart device sensor integration, the wireless network covers many indoor scenes; it can be considered as an information source to provide auxiliary information. Single positioning technology cannot meet the indoor positioning accuracy; the key to improving the accuracy of indoor pedestrian positioning is the data fusion algorithm.
At present, the Bayesian estimation algorithm is widely used in indoor pedestrian positioning and EKF and Particle Filter (PF) are commonly used algorithms in the nonlinear model; EKF is used in indoor pedestrian positioning because the pedestrian movement model is weakly nonlinear; PF is applied to the nonlinear system state and measurement model and the noise can be non-Gaussian noise.
The work in [10] fuses the building structure information and Pedestrian Dead Reckoning information by backtracking the particle filter. However, this technique still lacks the compensation for inertial navigation accumulative errors. Meanwhile, the particle filter is implanted in each step of the pedestrian, which leads to heavy computation.
INS assisted by ZUPT is commonly used in the indoor pedestrian positioning system based on MEMS. The frame combines INS with ZUPT based on EKF to limit accumulative errors, and a single foot-mounted inertial sensor is used to collect pedestrian state information. Research work in [11,12] adopts the above-mentioned positioning frame; additional infrastructure is not required in this frame. In research work in [13], a positioning system adopt INS and PDR to combine the advantages of both mechanizations for micro-electro-mechanical systems (MEMS) sensors in pedestrian navigation. However, the heading error cannot be compensated for when the velocity error is introduced as an observation based on EKF.
Research work in [14] employs a cascaded extended Kalman filter to fuse the data of Wi-Fi fingerprinting, foot mounted inertial and magnetometer sensors. The research work in [15] combines the fingerprinting-based WLAN system with the INS system, and INS navigation data can speed up the construction process of the fingerprint database. The work in [16] obtains the position information of the pedestrian by combining Wi-Fi fingerprinting and inertial sensors based on PF; the three methods introduce Wi-Fi fingerprinting as additional information, which requires a pre-survey for the offline fingerprinting map.
In this paper, indoor pedestrian positioning with two-order Bayesian estimation based on EKF and PF is proposed to improve the accuracy of indoor pedestrian positioning. In the first update, INS plays a major role in the calculation of pedestrian positioning, and ZUPT is introduced as the reference to correct the accumulative errors of INS based on EKF; in the second update, the estimated results obtained from the first update, which are horizontal position information, are introduced as the observations in the second update. PDR plays a major role in the calculation of pedestrian positioning; the method of data fusion is PF, the particle weight is determined by the Wi-Fi propagation model, building structure information and output of first-order data fusion.
The paper is organized as follows. In Section 2, the principles of INS, ZUPT, PF and the Wi-Fi propagation model are investigated. Then, in Section 3, an integration approach and details of filter design are proposed. Section 4 presents experiment and error analysis. Section 5 summarizes the whole paper.
2. Algorithm Fundamentals
2.1. Inertial Navigation System
Newton mechanics is one of most important principles in INS calculation. The acceleration vector can be obtained based on the data collected from the accelerator, which is then integrated twice over time to calculate the displacement. The turn rate is provided by gyroscopes, which can be calculated to obtain the attitude of the pedestrian. Therefore, the state of the pedestrian is obtained by this method. The equation can be presented as follows:
where is the position vector that includes the position at , and axes, respectively, is the velocity vector in the geographic coordinate system. is a matrix. is the rotation matrix from the body frame to the navigation frame as a function to obtain the pedestrian’s attitude. and are the skew-symmetric matrices of angular velocity vectors and , respectively. is the gravity vector in the navigation frame. There are inertial sensor errors and integration errors in INS calculation that can lead to quick divergence [16].
2.2. Zero-Velocity Update
In order to limit the accumulative errors, ZUPT is adopted to provide velocity errors as observations during the moment that the foot of the pedestrian touches the ground, which is a static state of the pedestrian.
Zero-velocity detection (ZV detection) is a crucial part of ZUPT, and there are many methods proposed to trigger the ZUPT; most ZV detections tend to have roughly equivalent performance. In this paper, an improved ZV detection method is proposed. Firstly, we calculate the magnitude of acceleration and turn rate collected by the foot-mounted inertial sensor, and then compare the calculation value with a threshold in each step; the ZV detection will be set to one when the calculation result is less than the threshold. Secondly, the stored ZV detection values are further processed; see details from [17].
2.3. Particle Filter
The evolution of state follows the following state transition equation:
where is system noise, and are the state at time and , respectively. Measurement and state follow the following relationship:
Usually, all measurements can be obtained by sensors or measuring devices. According to Equation (3), in order to obtain the state of the pedestrian, the posterior probability density function (PDF) needs to be constructed. The construction method of the posterior PDF is achieved through the Chapman–Kolmogorov equation [18]:
where is the previous posterior PDF, is the likelihood function, and are transition PDF. and are posterior PDF at time k and k − 1, respectively.
The particle filter implements a recursive Bayesian filter based on the Sequential Monte-Carlo method. It is particularly good for dealing with nonlinear and non-Gaussian estimation problems. Particles are based on a set of random samples with weights, and the weight can represent probability density. From the Equation (6), the calculation of posterior PDF contains many integral calculations, which means a large amount of computation. To decrease the calculation, the posterior PDF can be calculated approximately using the following equation:
where is the total number of particles at time k, is the Dirac function, the i donates the number of particles, and corresponding weight , can be calculated by the following equation:
where is the proposal density, all of the particle weights need to be normalized by the following equation [18]:
2.4. Wi-Fi Propagation Model
In the indoor environment, the distance between receiver point and AP can be calculated by the relation between the signal loss and signal transmission distance. There are lots of propagation models to calculate the distance. The Keenan–Motley propagation model is one of the most common signal propagation models applied in indoor signal propagation, which fully takes into account the effect of wall, floor, human body and multipath loss on Wi-Fi signal propagation; the model can be expressed by:
where is the power loss, is the power loss at distance , when is the reference distance, and it can usually be set to 1 m, and path loss coefficient . is the distance between the location point and AP. and are the number of the walls and floors penetrated by the Wi-Fi signal, respectively. and are wall penetration loss coefficient and floor penetration loss coefficient, respectively. and are multipath loss and human body loss, respectively.
Since the work in this paper mainly involves 2-D indoor positioning, the factor of the loss caused by penetrating floors can be neglected, which means . The multipath loss can be obtained by experiments in our testbed, and it equals to 2 dB. In the testbed, all APs operate at 2.45 GHz, as can be seen from [19], the human body loss . The penetration loss for wall is about 20 dB from [20]. The Equation (10) can be simplified as:
Due to the complexity of the indoor environment, more experiments are needed in order to obtain a more local signal propagation model. The distance d can be obtained by Equation (11) and by integrating the transmission power and receiver power of APs and the antenna gain of transmit antenna and receive antenna.
3. Fusion Algorithm
An overview of the proposed indoor pedestrian positioning with two-order Bayesian estimation based on EKF and PF is illustrated in Figure 1. In the proposed method, there are four information sources in the far left of the frame diagram, including an accelerometer, a gyroscope, the Wi-Fi propagation model and building structure information. Data collected from the accelerometer and gyroscope are used to make an INS calculation and PDR calculation. In the INS calculation, the 3-axis accelerations and 3-axis turn rates are used to calculate the Euler angle, rotation matrix and quaternion, and then achieve the conversion of accelerations from the body frame to the navigation frame. The acceleration integrates once and twice over time to obtain the velocity and position of the pedestrian in the navigation frame. The ZV update based on EKF will be used to compensate for accumulated errors. The first-order data fusion output includes , , and . The 3-axis accelerations and 3-axis turn rates are also used to calculate the stride length. The second-order data fusion method is PDR based on the particle filter; the Wi-Fi propagation model, building structure information and the position output of first-order data fusion determine the weight of particles together. Finally, a horizontal position can be obtained.
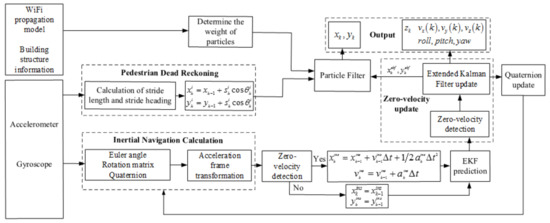
Figure 1.
Block diagram of the proposed method. EKF: Extended Kalman Filter.
3.1. First-Order Data Fusion
3.1.1. Quaternion Update
The 3-axis accelerations and 3-axis turn rates in the sensor frame can be obtained from foot-mounted inertial sensors, and an orientation is needed to obtain the 3-axis acceleration in the navigation frame. There are three equivalent ways to represent an orientation: Euler angles, rotation matrix and quaternion. In this paper, rotation matrix is used to achieve the frame conversion. Because the calculation of the rotation matrix is complex, quaternions are adopted in the iteration process; the update of the quaternion is shown in the following equation:
where is the skew-symmetric cross-product operator matrix, , and are the turn rates of the X-axis, Y-axis and Z-axis, respectively.
Then, the new rotation matrix is updated with new quaternions:
3.1.2. Pedestrian Inertial Navigation Solution
The velocity of the pedestrian can be obtained by initial velocity and integration of the acceleration in time.
where is the Z-axis acceleration that subtracts the acceleration of gravity, , and are the 3-axis velocities of the pedestrian at time k, respectively., and are the 3-axis locations of the pedestrian in time k. Through the above equations, the velocity and position of the pedestrian at time k can be obtained.
3.1.3. EKF Implantation
In the proposed system, a 9-dimension state vector is expressed as:
where , and are velocity errors, position errors and attitude errors in the navigation frame, respectively.
By the discretization of the state transition equation and measurement Formulas (2) and (3), the discrete-time state transition equation and measurement equation can be obtained.
(1) The state transition equation:
In order to obtain the state transition matrix , the skew-symmetric matrix can be expressed as:
where , and are accelerations in the navigation frame at the X-axis, Y-axis and Z-axis, respectively. Hence, the state transition matrix can be expressed as:
(2) The measurement equation:
After a linearization in measurement Equation (3), the above equation can be obtained, where and are measurement matrix and measurement noise, respectively.
When the Zero-velocity detection is triggered, the velocity of the pedestrian is zero in theory. Actually, due to the drift and accumulative errors of the inertial sensor, the velocity is usually not zero. Therefore, during each Zero-velocity update, the velocity error obtained from inertial sensors is considered as a measurement; the measurement matrix is designed as follows:
The priori estimate of the error covariance at time k is calculated by posteriori estimation of the error covariance at time k − 1:
In the subsequent update phase, the parameters of the Gaussian posterior PDF are computed recursively at each iteration.
The Kalman gain factor is calculated by the following equation:
The Posterior covariance is calculated by:
where is an error compensation term, which can be used in the following update phase.
(3) The update phase:
where , and are velocity, position and attitudes in the navigation frame, respectively. All three components include three elements at the X-axis, Y-axis and Z-axis respectively, and the final 9-state of the pedestrian compensated for by EKF can be obtained, which consists of two parts— and —that are used for second-order data fusion.
Through the estimated pedestrian state, the rotation matrix and quaternion can be updated by:
where and are the rotation matrix in time k and k − 1, respectively. is the skew-symmetric cross-product operator matrix. With the movement of the pedestrian, the attitude of the pedestrian will also change; the updating of the rotation matrix from time k to k + 1 is realized by the matrix , and the new quaternion can be calculated by Equation (15).
3.2. Second-Order Data Fusion
From the system block diagram, PF is used to fuse information; the specific implementation of the method is shown in the following.
As shown in Figure 2a, the relationship of the pedestrian’s position information between two different times, and the position of the pedestrian at time k can be calculated by the step length and the heading of the pedestrian. As shown in Figure 2b, the colors of the particle represent its weight, which is determined by the Wi-Fi propagation model, building structure information and the output of first-order data fusion.
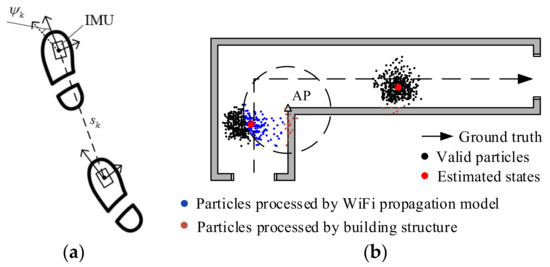
Figure 2.
(a) Pedestrian movement model; (b) the schematic of the particle filter for data fusion. IMU: Inertial Measurement Unit. AP: Access Point.
The following transition function is implemented by the Particle filter for PDR:
where is the i-th particle stride length at time k, sampled from normal Gauss distribution . and are the mean stride length and standard deviation, respectively. is obtained from numerous experiments. is the i-th particle heading, sampled from a normal distribution , and are heading and its standard deviation, respectively. is provided by the first-filter EKF. is set to a fixed percentage of the stride-to-stride heading change [21].
The stride length varies for different people. There are too many models to calculate the stride length, and the research work in [22] has proposed an empirical model, which assumes that the stride length is proportional to the vertical movement of the pedestrian hip. In this paper, the stride length is calculated by an empirical model:
where and are the maximum and minimum accelerations at the Z-axis, respectively. is a constant for unit conversion. In this paper, and are collected from a period between two ZUPT triggers.
From the transition function, particles can be obtained in time k. The weight of particles can be calculated by:
where is the location output of EKF, is the location of the i-th particle at time k. is the standard deviation. The preliminary weight of each particle and can be obtained by the Equation (36) [22].
Before the integration of Wi-Fi information, an offline map of APs’ location information needs to be constructed. The offline map can be expressed as:
where represents the i-th AP, it consists of three parts: is the ID of AP; is the mean received signal intensity where distance from the ; is the horizontal location of in a building, and the offline map can be expressed by:
In the online positioning phase, a sequence includes all APs and corresponding received signal intensity at a location point:
When , it means that the distance between the location point and the AP is less than ; the Wi-Fi propagation model can be introduced in data fusion.
From Formula (11), according to the power of the transmitting antenna, the gain of the transmitting antenna and receiving antenna, and the received Wi-Fi signal strength at the location point, the distance between the AP and location point can be obtained.
In the online positioning phase, the max received intensity value of all is used to match with the offline map :
The weight of the particle will be given by the following expression:
In order to make good use of Wi-Fi and building structure information, an off-phase map is constructed, which includes the positioning distributions of APs, and the geometric profiles of the indoor environment, which can affect the particle weights.
The building structure has a decisive influence on the particle weight, which can be expressed as , as shown in the following equations:
The final particle’s weight will be expressed by:
Normalized particle weights by following Equation (9), and the final horizontal position can be obtained by the following equations:
4. Experimental Evaluation
4.1. Text Bed Setup
To evaluate the performance of the proposed algorithm, a foot-mounted inertial sensor MTi-G710 was installed on the pedestrian shoe, which is shown in Figure 3, and the experiments were conducted on the first floor of the student activity center. The inertial sensor was connected to a laptop with MTi Application Programming Interface (API) which can preliminary output the data collected from the foot-mounted inertial sensor during walks with a visual window.

Figure 3.
The IMU tied on the left foot.
The preliminary work includes the establishment of an offline 2D map, which includes the contour information of the building structure and the distribution information of Aps; see Section 4.2 for details.
During the walk, the MTi API and Homedale software are adopted in Personal Computer (PC) to collect the inertial sensor data and RSS; the sampling rate of the inertial sensor and collecting rate of Wi-Fi are set to 50 Hz, and 1 Hz respectively. The stored data during the walk are used to estimate the pedestrian trajectory and compare with the ground truth to evaluate the proposed algorithm. The floor plans for the experiments are shown in Figure 4.
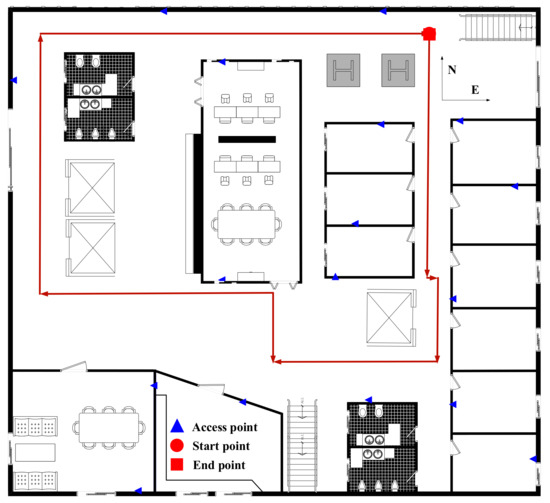
Figure 4.
Floor plans for the experiments.
4.2. Filter Parameter Initialization

Table 1.
Initialization of EKF.

Table 2.
Initialization of Particle Filter (PF).
4.3. Experimental Results
Normally, the sampling frequency of the inertial sensor will be greater than the frequency of the pedestrian walking. Thus, over a period of time, the output data of the accelerometer and gyro are approximated, and ZV detection can easily detect the state of the pedestrian. In this paper, an improved version of ZV detection is used for pedestrian state detection. There are two pedestrian conditions to detect the static state: (1) ZV detection at time k is equal to 1; (2) ZV detection at time k logic and ZV detection at time k is equal 0. The experiment results by using improved ZV detection are shown in Figure 5.
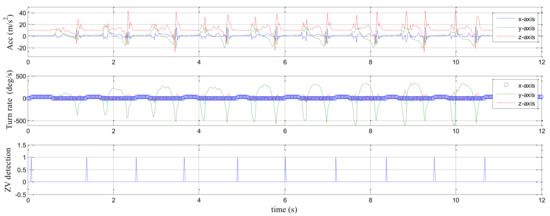
Figure 5.
Zero-velocity (ZV) detection in a waking pedestrian.
There are 16 APs in the whole experimental plane, and their distribution is not uniform. As shown by the positioning results in Figure 6a, the Wi-Fi positioning based on the propagation model is less accurate than fingerprint database positioning, which is determined by the distribution of APs and the indoor environment.
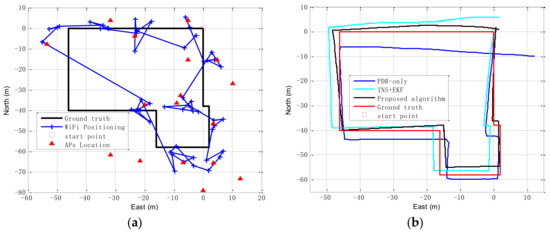
Figure 6.
(a) The trajectories of Wi-Fi positioning based on the propagation model; (b) The trajectories of pedestrian positioning of the inertial navigation system (INS) based on EKF (INS+EKF), Pedestrian Dead Reckoning (PDR)-only, proposed algorithm and ground truth.
In order to improve the reliability of the propagation model, thus enabling it to play a greater role in the integration positioning, a signal intensity threshold is set to control the use of the propagation model. In this paper, the threshold of each AP is the average of the received Wi-Fi signal strengths at a distance of 1.5 m, which is obtained by experiments. The Wi-Fi positioning based on propagation is used to further improve the position estimation, and limit the accumulative errors of the inertial sensors.
The positioning results of three algorithms are shown in Figure 6b, and the blue solid line, cyan-blue solid line, black solid line and red solid line are trajectories calculated by PDR-only, INS+EKF, the proposal algorithm and ground truth, respectively. The black solid line has a different start point because the location of the start point is provided by the Wi-Fi propagation model. It is easy to see that these trajectories do not coincide with the start point and endpoint. The positioning error is continually expanding over time, and the proposed algorithm is significantly inhibited the growth of the accumulation error.
As shown in Figure 7 and Table 3, the proposed algorithm has the best positioning performance. The more specific statistical results of pedestrian positioning are shown in Table 3; the mean error of the proposed algorithm is 1.85 m, and the mean error is decreased by about 39% by the trajectory calculated by PDR-only and decreased by about 35% by the trajectory calculated by INS+EKF.
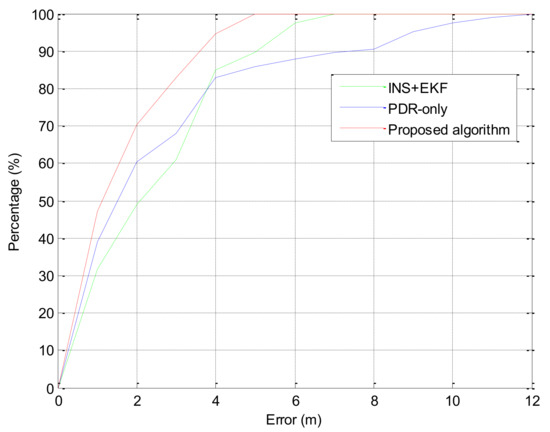
Figure 7.
Accumulative error percentages.

Table 3.
Positioning performance of different algorithms.
5. Conclusions
In this paper, a new indoor pedestrian positioning algorithm with two-order Bayesian estimation based on EKF and PF is proposed to improve the accuracy of indoor pedestrian positioning. In the first update, INS plays a major role in the calculation of pedestrian positioning, and ZUPT is introduced as the reference to correct the cumulative errors of INS based on EKF; in the second update, the estimated results obtained from the first update, which are horizontal position information, are introduced as the observations in the second update, where PDR plays a major role in the calculation of pedestrian positioning; the method of data fusion is PF, the particle weight is determined by the Wi-Fi propagation model, building structure information and output of first-order data fusion.
The proposed integrated algorithm was tested in indoor pedestrian experiments to demonstrate its performance, accuracy, and ability in providing an effective solution. By comparing with other positioning algorithms, the experiments demonstrate that mean positioning errors of the proposed two-order Bayesian estimation based on EKF and PF decrease by about 39% when compared with traditional PDR-only, and decrease by about 35% when compared with INS based on EKF. The positioning accuracy will be higher if the distribution of APs is more intensive and reasonable.
Acknowledgments
This paper is partly supported by the Science and Technology Innovative Talents Foundation of Harbin (2013RFXXJ083), the Foundational Research Funds for the Central Universities (HEUCF131602, HEUCFD1433).
Author Contributions
Xianfeng Yang and Tao Jiang conceived and designed the experiments; Xianfeng Yang performed the experiments; Xianfeng Yang and Xufei Cui analyzed the data; Tao Jiang and Xufei Cui contributed reagents/materials/analysis tools; Xianfeng Yang wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Feliz, R.; Zalama, E.; Gómez, J. Pedestrian tracking using inertial sensors. In CT and Myelography of the Spine and Cord; Springer-Verlag: Berlin, Germany, 1982; pp. 409–423. [Google Scholar]
- Mahiddin, N.A.; Safie, N.; Nadia, E.; Safei, S.; Fadzli, E. Indoor position detection using WiFi and trilateration technique. In Proceedings of the International Conference on Informatics and Applications (ICIA2012), Kuala Terengganu, Malaysia, 3–5 June 2012; pp. 362–366. [Google Scholar]
- Lim, C.H.; Ng, B.P.; Da, D. Robust methods for AOA geo-location in a real-time indoor Wi-Fi system. J. Locat. Based Serv. 2008, 2, 112–121. [Google Scholar] [CrossRef]
- Roos, T.; Myllymäki, P.; Tirri, H.; Misikangas, P.; Sievänen, J. A probabilistic approach to WLAN user location estimation. Int. J. Wirel. Inf. Netw. 2002, 9, 155–164. [Google Scholar] [CrossRef]
- Gigl, T.; Janssen, G.J.M.; Dizdarevic, V.; Witrisal, A.; Irahhauten, Z. Analysis of a UWB indoor positioning system based on received signal strength. In Proceedings of the 4th Workshop on Positioning, Navigation and Communication, Hannover, Germany, 22 March 2007; pp. 97–101. [Google Scholar]
- Denis, B.; He, L.; Ouvry, L. A flexible distributed maximum log-likelihood scheme for UWB indoor positioning. In Proceedings of the 2007 4th Workshop on Positioning, Navigation and Communication, Hannover, Germany, 22 March 2007; pp. 77–86. [Google Scholar]
- Carlos, M.; Carlos, S.J.; Ángel, D.L.T. Ultrasound indoor positioning system based on a low-power wireless sensor network providing sub-centimeter accuracy. Sensors 2013, 13, 3501–3526. [Google Scholar]
- Sy, C.; Cg, P. MEMS based pedestrian navigation system. J. Navig. 2006, 59, 135–153. [Google Scholar]
- Foxlin, E. Pedestrian tracking with shoe-mounted inertial sensors. IEEE Comput. Graph. Appl. 2005, 25, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Widyawan; Klepal, M.; Beauregard, S. A backtracking particle filter for fusing building plans with PDR displacement estimates. In Proceedings of the 5th Workshop on Positioning, Navigation and Communication, Hannover, Germany, 27 March 2008; pp. 207–212. [Google Scholar]
- Jiménez, A.R.; Seco, F.; Prieto, J.C.; Guevara, J. Indoor pedestrian navigation using an INS/EKF framework for yaw drift reduction and a foot-mounted IMU. In Proceedings of the 7th Workshop on Positioning, Navigation and Communication, Dresden, Germany, 11–12 March 2010; pp. 135–143. [Google Scholar]
- Brescianini, D.; Jung, J.-Y.; Jang, I.-H.; Park, H.S.; Riener, R. INS/EKF-based stride length, height and direction intent detection for walking assistance robots. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011. [Google Scholar]
- Atia, M.M.; Noureldin, A.; Georgy, J.; Korenberg, M. Bayesian filtering based Wi-Fi/INS integrated navigation solution for GPS-denied environments. Navigation 2011, 58, 111–125. [Google Scholar] [CrossRef]
- Frank, K.; Krach, B.; Catterall, N.; Robertson, P. Development and evaluation of a combined WLAN and inertial indoor pedestrian positioning system. In Proceedings of the 22nd International Technical Meeting of The Satellite Division of the Institute of Navigation, Savannah, GA, USA, 22–25 September 2009; pp. 538–546. [Google Scholar]
- Seitz, J.; Patino-Studencka, L.; Schindler, B.; Thielecke, J. Sensor data fusion for pedestrian navigation using WLAN and INS. In Proceedings of the Symposium Gyro technology 2007, Karlsruhe, Germany, 18–19 September 2007; pp. 1–10. [Google Scholar]
- Zhuang, Y.; Lan, H.; Li, Y.; El-Sheimy, N. PDR/INS/WiFi Integration based on handheld devices for indoor pedestrian navigation. Micromachines 2015, 6, 793–812. [Google Scholar] [CrossRef]
- Li, Y. A Pedestrian navigation system based on low cost IMU. J. Navig. 2014, 67, 1–21. [Google Scholar] [CrossRef]
- Gustafsson, F. Particle filter theory and practice with positioning applications. IEEE Aerosp. Electr. Syst. Mag. 2010, 25, 53–82. [Google Scholar] [CrossRef]
- Zhou, F.; Zhang, X.; Han, H.; Rui, Z.; Ruixin, W.; Luoyong, X.; Yan, Z. Measurement of human body penetration loss in wireless communication band. Mod. Telecom Technol. 2012, 8, 20–22. [Google Scholar]
- Mohammad, Y.E.; Abdullah, A.S.; Liu, Y. Measurement of penetration loss at 2.4 GHz frequency in indoor. J. Beijing Univ. Posts Telecom 2004, 27, 98–102. [Google Scholar]
- Widyawan; Pirkl, G.; Munaretto, D.; Fischer, C.; An, C.; Lukowicz, P.; Klepal, M.; Timm-Giel, A.; Widmer, J.; Pesch, D.; et al. Virtual lifeline: Multimodal sensor data fusion for robust navigation in unknown environments. Pervasive Mob. Comput. 2012, 8, 388–401. [Google Scholar]
- Weinberg, H. Using the ADXL202 in Pedometer and Personal Navigation Applications; Analog Devices: Norwood, MA, USA, 2002. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).