1. Introduction
Modern radars usually have low instantaneous power, called low probability of intercept (LPI) radars, which are used in electronic warfare (EW). For a radar electronic intelligence (ELINT) system (anti-radar system), analyzing and classifying the waveforms of LPI radars is one of the most effective methods to detect, track and locate the LPI radars [
1,
2]. Therefore, the second order statistics and power spectral density are utilized in the waveforms’ recognition earlier to classify phase shift keying (PSK), frequency shift keying (FSK) and amplitude shift keying (ASK) [
3]. Dudczyk presents the parameters (such as pulse repetition interval (PRI), pulse width (PW), etc.) to identify different radar signals [
4,
5,
6,
7]. Nandi introduces the decision theoretic approach to classify different types of modulated signals [
8]. Additionally, the ratio of successful recognition (RSR) is over 94% at a signal-to-noise ratio (SNR) ≥15 dB. The artificial neural network is also utilized in the recognition system. The multi-layer perceptron (MLP) recognizer reaches more than 99% recognized performance at SNR ≥0 dB [
9]. Atomic decomposition (AD) is also addressed in the detection and classification of complex radar signals. Additionally, the receiver realizes the interception of four signals (including linear frequency modulation (LFM), PSK, FSK and continuous wave (CW)) [
10]. Time-frequency techniques can increase signal processing gain for the low power signals [
11]. In [
12], López analyzes the differences among LFM, PSK and FSK based on the short-time Fourier transform (STFT). Additionally, the RSR ≥90% at SNR ≥0 dB. Lundén [
13] introduces a wide classification system to classify the intercepted pulse compression waveforms. The system achieves overall RSR ≥98% at SNR ≥6 dB. Ming improves the system of Lundén and shows the results in [
14]. The sparse classification (SC) based on random projections is proposed in [
15]. The approach improves efficiency, noise robustness and information completeness. LFM, FSK and PSK are recognized with RSR ≥90% at SNR ≥0 dB.
We investigate the convolutional neural network (CNN) for radar waveform recognition. CNN has been proposed in image recognition fields [
16,
17]. Recently, it has been applied for speech recognition [
18,
19,
20,
21], computer vision [
22,
23] and handwritten recognition [
24,
25,
26], etc. Abdel-Hamid introduces the approaches to reduce the further error rate by utilizing CNNs in [
27]. Experimental results show that CNNs reduce the error rate by 6%–10% compared with deep neural networks (DNNs) on the speech recognition tasks. In [
26], a hybrid model of two superior classifiers CNN and support vector machine (SVM) is discussed. The RSR of the model achieves more than 99.81%, in which SVM performs as a classifier and CNN works as a feature extractor.
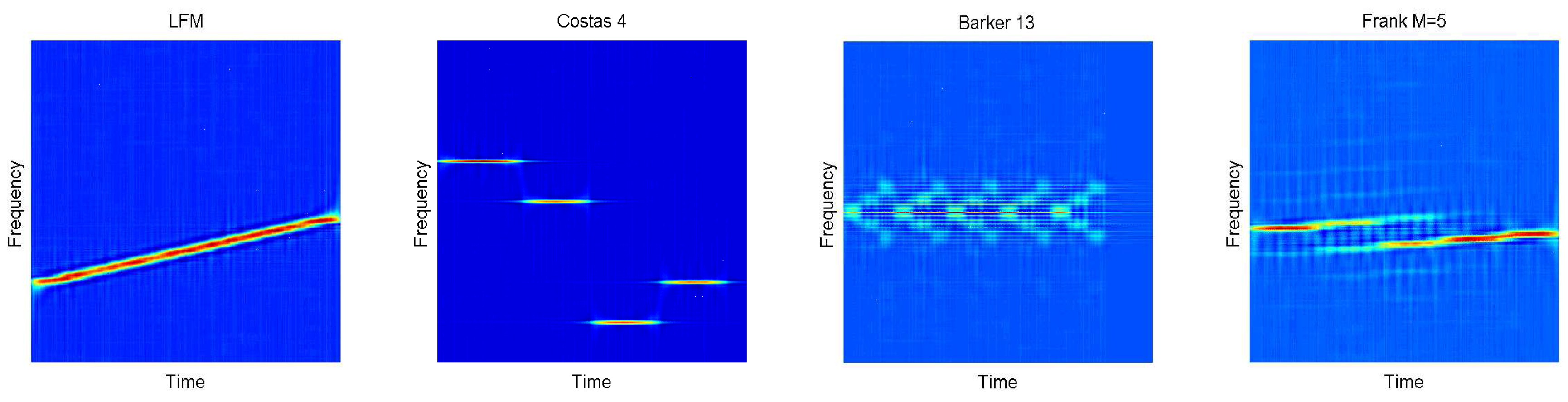
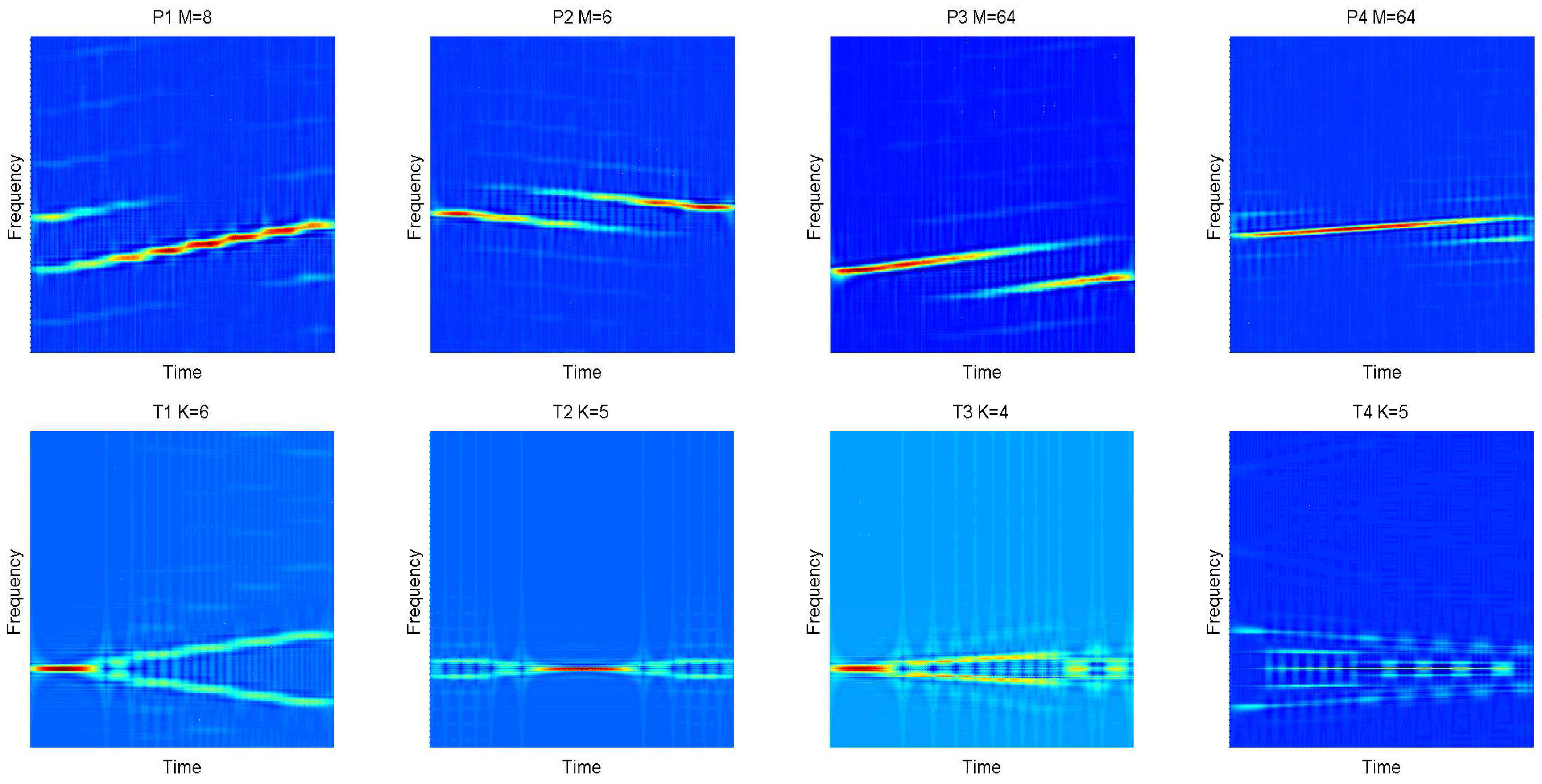
In this paper, we explore a wide radar waveform recognition system to classify, but not identify In this paper, the meaning of “classify” is that we distinguish the different types of waveforms. Additionally, “identify” is distinguishing the different individuals of the same type. Twelve types of waveforms (LFM, BPSK, Costas codes, polyphase codes and polytime codes) by using CNN and Elman neural network (ENN) are discussed. We propose time-frequency and statistical characteristic approaches to process detected signals, which transmit in the highly noisy environment. The detected signals are processed into time-frequency images with the Choi–Williams distribution (CWD). CWD has few cross terms for signals, which is a member of the Cohen classes [
28]. Time-frequency images show the three main pieces of information of signals: time location, frequency location and amplitude. In the images, time and frequency information is more robust than amplitude. To make the images more suitable for the classifier, a thresholding method is investigated. The method handles the time-frequency images as binary images. After that, binary images are addressed by noise-removing approaches. The final images are used for classification and feature extraction. However, polyphase codes (including Frank code and P1-P4 codes) and LFM are similar to each other. It is difficult to classify them through shapes individually. Therefore, we extract some effective features for further classification of them. Features extraction is from binary images through digital image processing (such as skeleton extraction, Zernike moments [
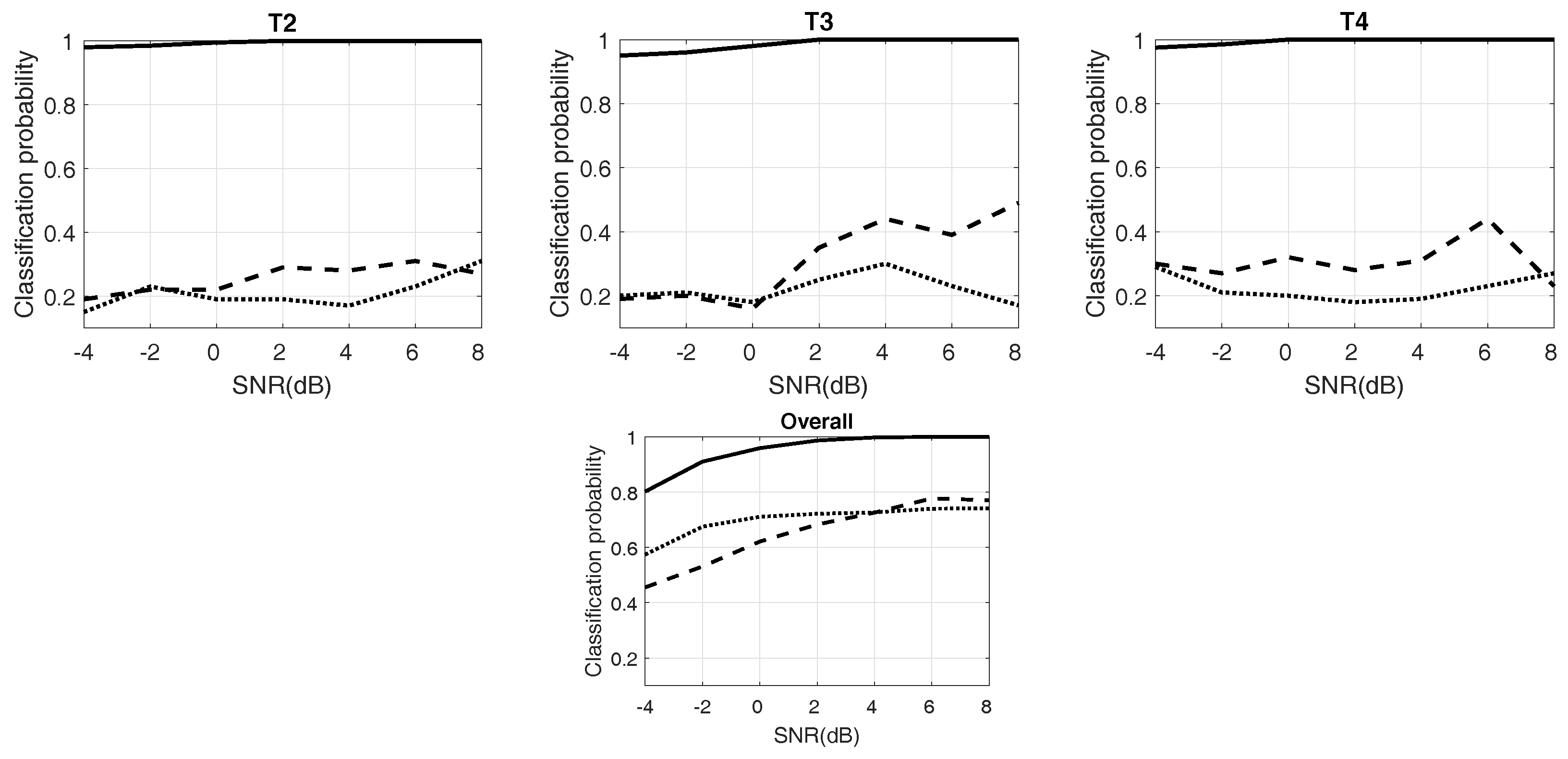
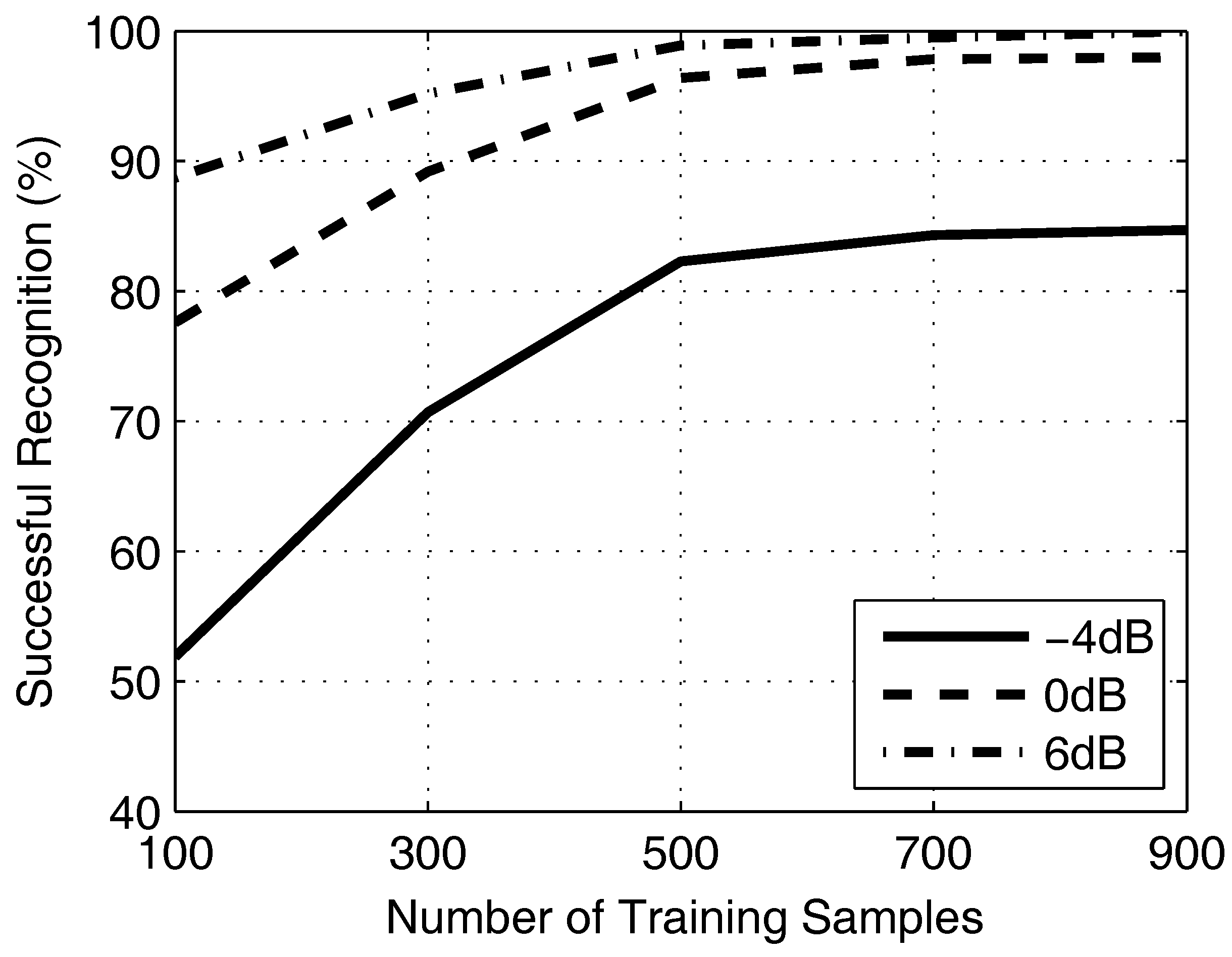
29], principal component analysis (PCA), etc.). The set of features is the input of ENN. Additionally, the output of ENN is the classification result. The entire structure of the classifier consists of two networks, CNN and ENN. CNN is the primary cell of the classifier, and ENN is auxiliary. Binary images are resized for CNN to separate polytime codes (include T1–T4) from the other eight kinds of waveforms. Additionally, we extract features for ENN, which can indicate the eight remaining codes obviously. Only if “others” are selected by the CNN, ENN starts to work (see Figure 2). In the experiments, the recognition system has overall RSR ≥94% at SNR ≥−2 dB.
In this paper, the major contributions can be summarized as follows: (1) build the framework of signals processing; additionally, establish the label data for testing the system; (2) the proposed recognition system can classify as many as 12 kinds of waveforms, which are described in the context; previous articles can seldom reach such a wide range of classification of radar signals; especially, four kinds of polytime codes are classified together for the first time in the published literature; (3) almost all interested parameters and all features will be estimated by received data without a priori knowledge; (4) propose a hybrid classifier that has two different networks (CNN and ENN).
The paper is organized as follows. The structure of the recognition system is exhibited in
Section 2.
Section 3 proposes the signal model and preprocessing.
Section 4 explores the feature extraction, including signal features and image features. Additionally, it lists all features that we need. After that,
Section 5 searches the structure of the classifier and describes it in detail.
Section 6 shows the experiments.
Section 7 draws the conclusions.
2. System View
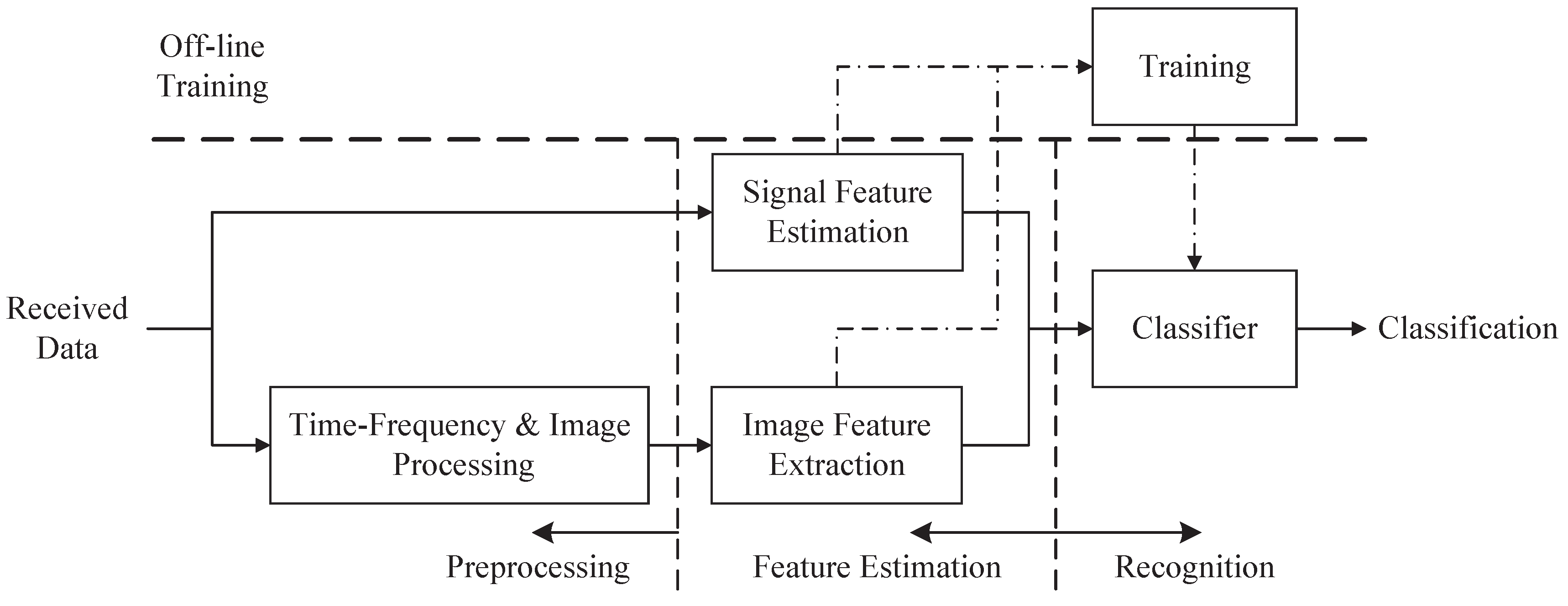
The entire classification system mainly consists of three components: preprocessing, feature estimation and recognition; see
Figure 1. It is an automatic process from the preprocessing part to the recognition part. In the preprocessing part, the received data are transformed into time-frequency images by utilizing CWD transformation. Then, the time-frequency images are transformed into the binary image through image binarization, image opening operation and noise-removing algorithms. In the feature extraction part, we extract effective features to train and test the classifier. Different kinds of waveforms have different shapes in the images. After image processing, the differences of shapes are more significant. CNN has a powerful ability of classification, which distinguishes polytime codes from others. To classify these similar waveforms (such as polyphase codes), we extract features from detected signals and binary images. In the recognition part, all of the waveforms are classified via the proposed classifier based on the extracted features.
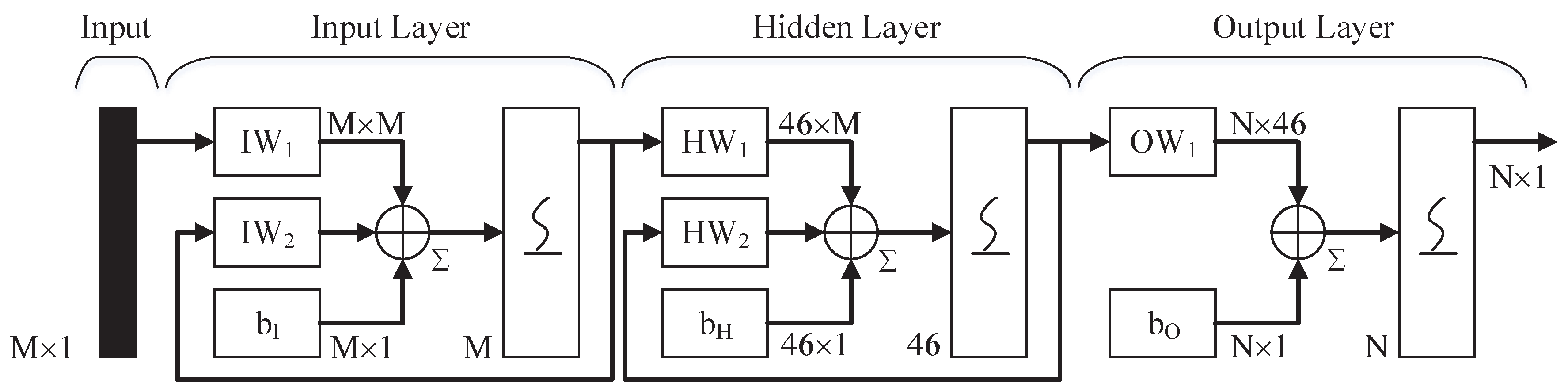
The hybrid classifier consists of two networks,
and
; see
Figure 2. The entire classifier can classify 12 different kinds of radar waveforms, which has been mentioned in the writing.
is the main network composed of CNN. Its input is a binary image after preprocessing. Additionally, the outputs are five different kinds of classification results. They are four kinds of polytime codes (T1-T4) and others (do not belong to the polytime class).
is ENN, which is an auxiliary network.
assists the main network
in classifying the eight remaining waveforms that do not belong to polytime codes. When the waveform is considered as “others” by
,
will begin to classify the waveform into one of the eight kinds of waveforms. The proposed structure of the classifier can improve the classified power.
4. Feature Extraction
In this section, we extract some useful features and build a feature vector for ENN in order to assist the CNN to complete recognition. The section consists of two parts, including signal features and image features. The features, which we can estimate or calculate from detected signals directly, belong to signal features. Similarly, image features include the features that are extract from binary images.
Table 1 lists the signal features and image features that are used in
.
4.1. Signal Features
In this part, the features are extracted from signals based on signal processing approaches.
4.1.1. Based on the Statistics
We estimate the
n-order moment of complex signals as follows:
where
is the conjugated symbol and
N is the sample number. We utilize absolute values to ensure that the estimated values are invariant constants when the signal phase rotates.
and
are calculated by Equation (
4).
The
n-order cumulant is given by [
33,
34]:
where, the same as context,
is from Equation (
4).
4.1.2. Based on the Power Spectral Density
Before estimation of Power Spectral Density (PSD), the detected signals should be normalized as follows:
where
is obtained from Equation (
4) and
is the
k-th sample. The variance of additive noise
can be obtained in [
35].
The PSD are calculated as follows:
where
is from Equation (
6).
4.1.3. Based on the Instantaneous Properties
Instantaneous properties are the essential characteristics of detected signals. They can distinguish frequency modulated signals from phase modulated signals effectively. In this paper, we estimate the instantaneous frequency and instantaneous phase from samples. The standard deviation of instantaneous phase is addressed in [
9]. For brevity,
is applied; where, Re and Im are the real and imaginary parts of complex signals, respectively. The standard deviation of instantaneous phase is given by:
where
N is the sample number.
is the instantaneous phase with the range of
.
Instantaneous frequency estimation is more complex than instantaneous phase. We describe the method in several steps to make it clear.
4.2. Image Features
In this part, we extract the features based on binary images. The number of objects () is a key feature. For instance, Costas codes have more than three objects, but Frank code and P2 have two. Additionally, P1, P4 and LFM only have one. We estimate two features and . is the number of objects, the sizes of the pixels of which are more than 20% of the size of the largest object. Likewise,
The maximum energy location in time domain is also a feature, i.e.,
where
is the resized time-frequency image and
N is the sample number.
The standard deviation of the width of signal objects () can describe the concentration of signal energy. The feature is estimated as follows.
- ●
Repeat for every object, do ;
Retain the k-th object and remove others, called ;
Estimate the principal components of ;
Rotate the until the principal components are vertical; record as ;
Sum the vertical axis, i.e.,
;
Normalize
as follows
Estimate the standard deviation of
, i.e.,
where
N is the sample number;
- ●
Output the rotation degree , which performs Step (c) at the maximum object.
- ●
Output the average of the
, i.e.,
- ★
Nearest neighbor interpolation is applied in rotation processing.
P2 has a negative slope in five types of polyphase codes. Therefore, the feature can classify P2 from others easily. The feature shows the angle between the maximum object and the vertical direction. It can be obtained from the calculation of easily.
Next, we retain the maximum object in the binary image, but others are removed. The skeleton of the object is extracted by utilizing the image morphology method. Additionally, the linear trend of the object is also estimated based on minimizing the square errors method at the same time. Subtract the linear trend from the skeleton to achieve the difference vector
. The standard deviation of
is estimated as:
where
M is the sample number of
.
Some features are extracted by using autocorrelation of
, i.e.,
,
. The autocorrelation method makes differences more significant among stepped waveforms (P1, Frank code) and linear waveforms (P3, P4, LFM). See
Figure 3 for more details.
The ratio of the maximum value and sidelobe maximum value of
is formulated as:
where
is the value corresponding to the minimum of
and
is the value corresponding to the maximum of
in the location of
.
We estimate the maximum of the absolute of FFT operation
as follows:
where
is normalized from
and
.
Pseudo-Zernike moments are invariant for topological transformation [
36], such as rotation, translation, mirroring and scaling. They are widely applied in pattern recognition [
37,
38,
39]. The
n-order image geometric moments are calculated as:
where
is from
Section 3.3. The central geometric moments for scale and translation invariant are given by:
where
and
.
The scale and translation invariant radial geometric moments are shown as:
where
and
.
Then, the pseudo-Zernike moments can be estimated as follows:
where
,
and:
At last, is estimated, i.e., . The members of pseudo-Zernike moments include , , , , , and .