Redundant Symmetry Influences Perceptual Grouping (as Measured by Rotational Linkage)
Abstract
:1. Introduction
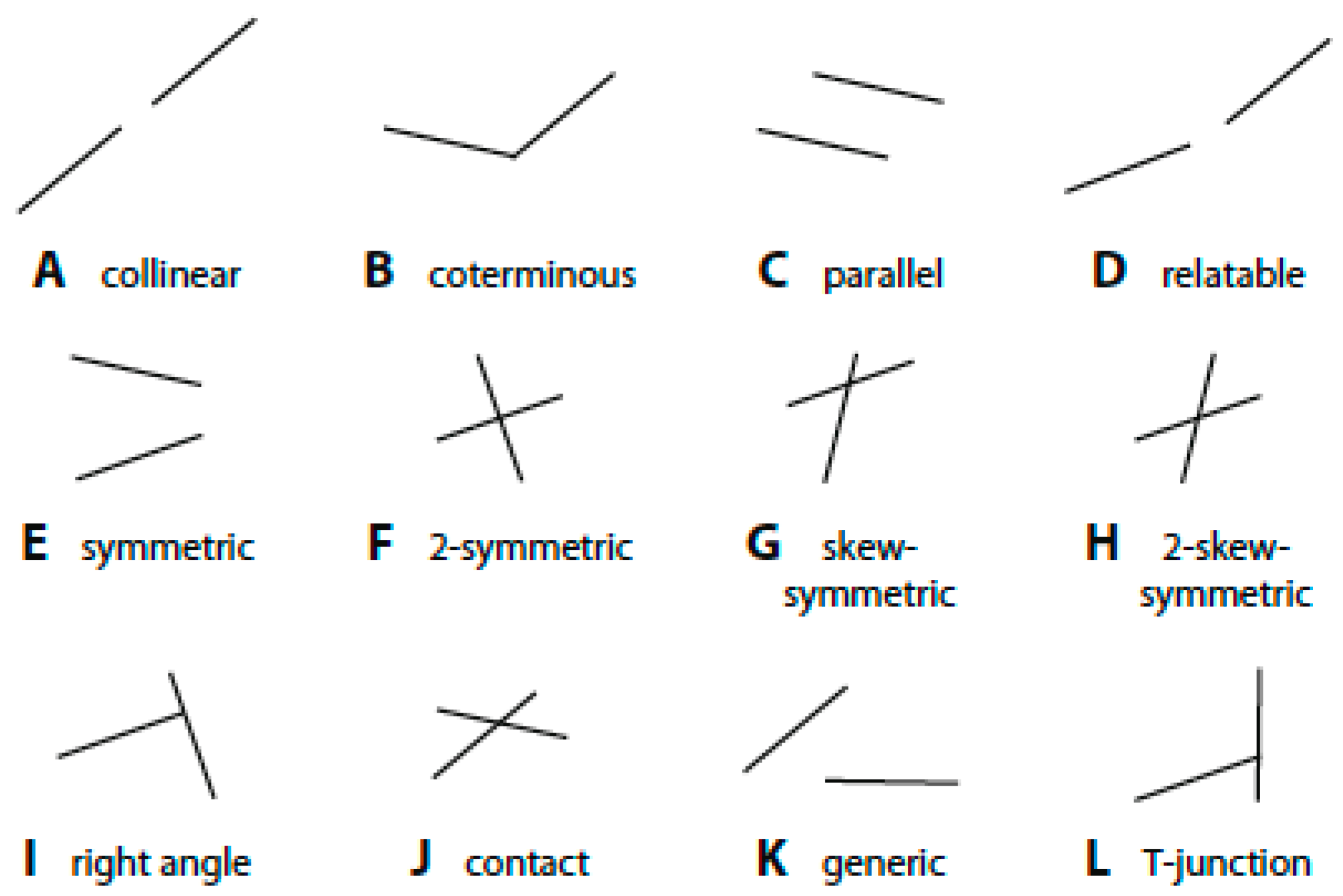
2. Experiment 1
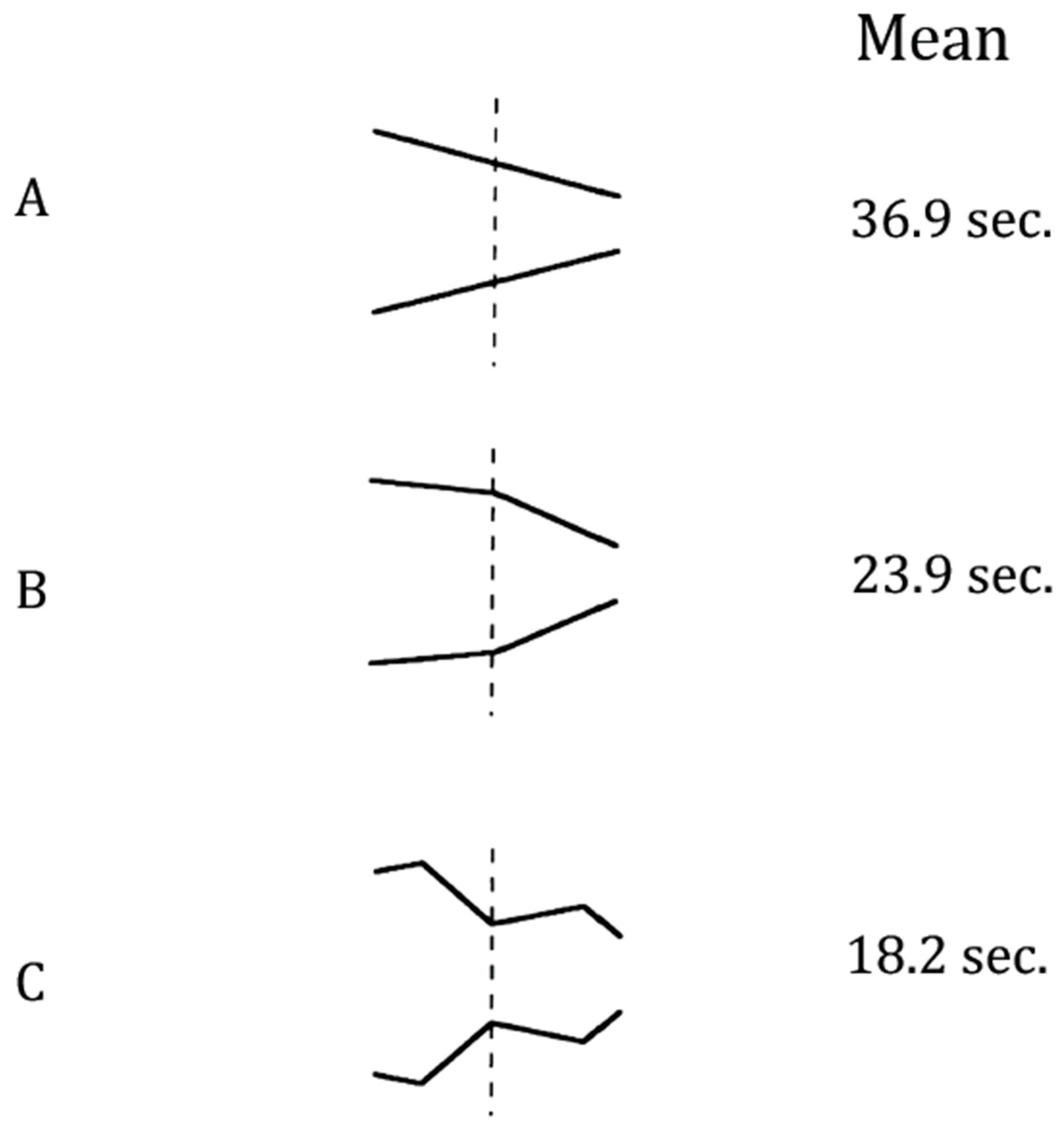
2.1. Method
2.2. Observers
2.3. Results
3. Experiment 2
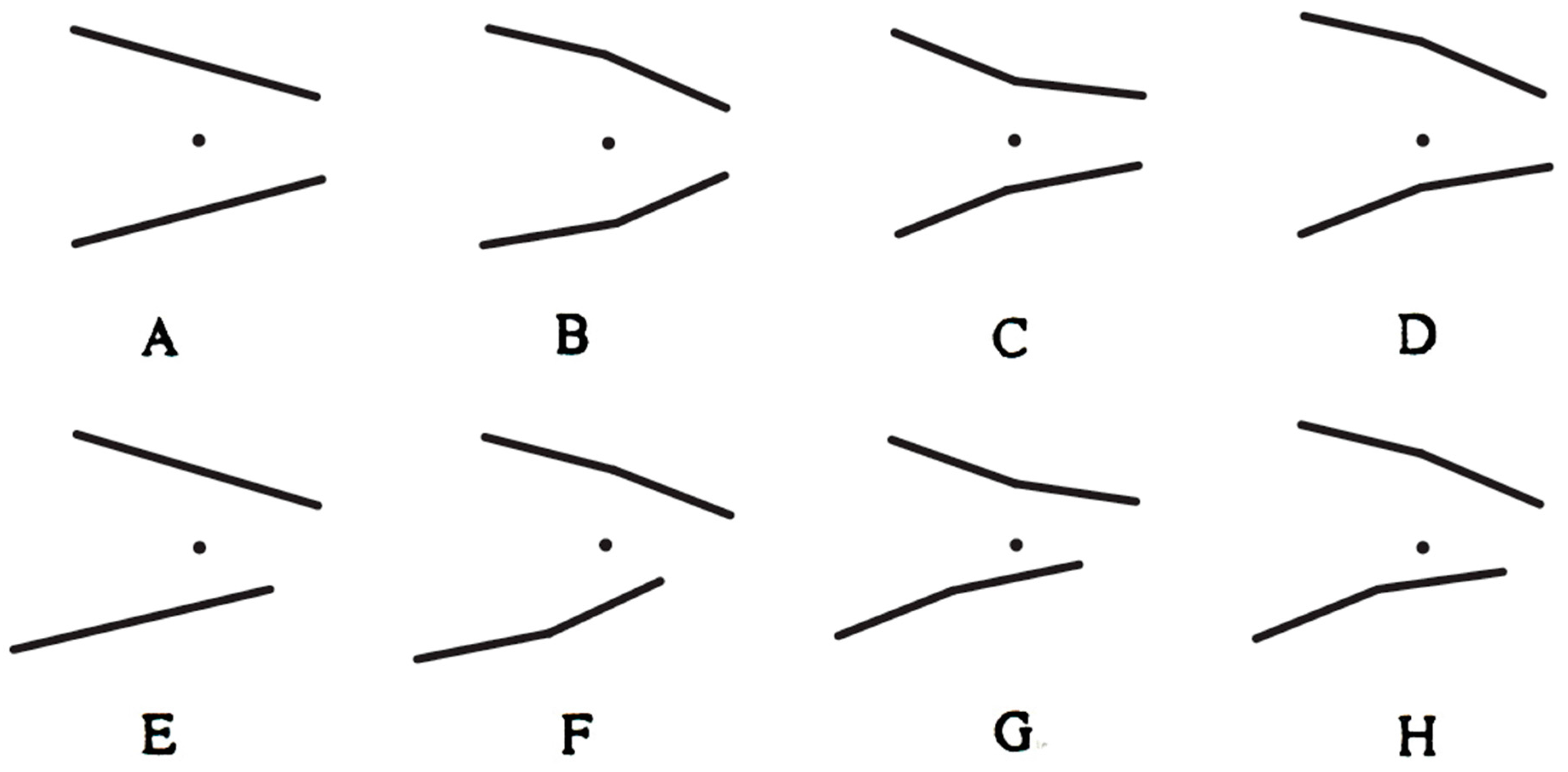
3.1. Method
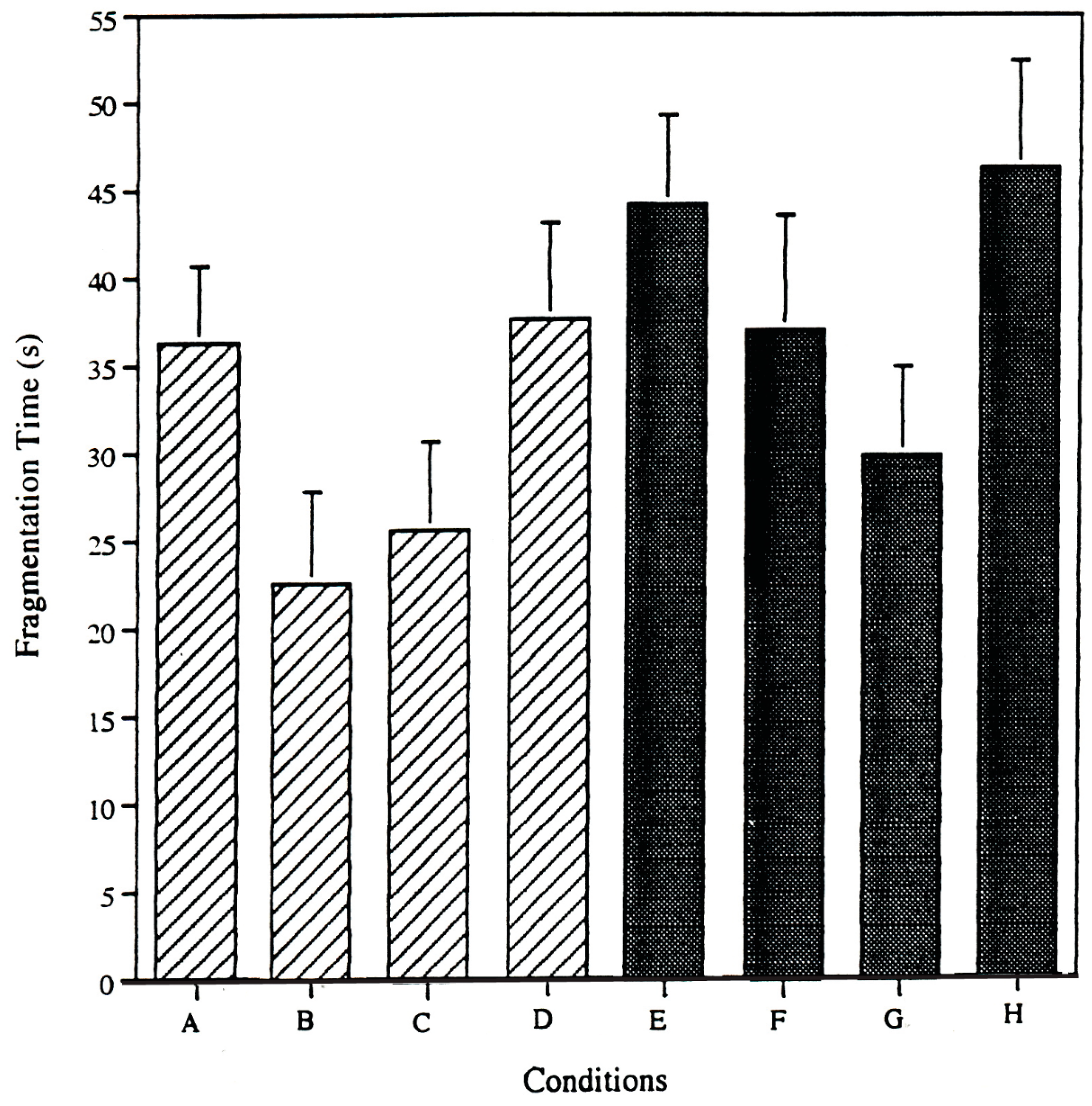
3.2. Results
3.3. Discussion
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Koffka, K. Principles of Gestalt Psychology; Harcourt, Brace & World: New York, NY, USA, 1935. [Google Scholar]
- Treder, M.S.; van der Helm, P.A. Symmetry versus repetition in cyclopean vision: A microgenetic analysis. Vis. Res. 2007, 47, 2956–2967. [Google Scholar] [CrossRef] [PubMed]
- Barlow, H.B.; Reeves, B.C. The versatility and absolute efficiency of detecting mirror symmetry in random dot displays. Vis. Res. 1979, 19, 783–793. [Google Scholar] [CrossRef]
- Royer, F. Detection of symmetry. J. Exp. Psychol. Hum. Percept. Perform. 1981, 7, 1186–1210. [Google Scholar] [CrossRef] [PubMed]
- Wenderoth, P. The salience of vertical symmetry. Perception 1984, 23, 221–236. [Google Scholar] [CrossRef] [PubMed]
- Tyler, C.W. Empirical aspects of symmetry perception. Spat. Vis. 1995, 9, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Wagemans, J. Characteristics and models of human symmetry detection. Trends Cogn. Sci. 1995, 9, 9–32. [Google Scholar] [CrossRef]
- Gurnsey, R.; Herbert, A.M.; Kenemy, J. Bilateral symmetry embedded in noise is detected only at fixation. Vis. Res. 1998, 38, 3795–3803. [Google Scholar] [CrossRef]
- Locher, P.J.; Wagemans, J. Effect of element type and spatial grouping on symmetry detection. Perception 1993, 22, 565–587. [Google Scholar] [CrossRef] [PubMed]
- Bertamini, M.; Friedenberg, J.D.; Kubovy, M. Detection of symmetry and perceptual organization: The way a lock and key process works. Acta Psychol. 1997, 95, 119–140. [Google Scholar] [CrossRef]
- Pomerantz, J.R.; Kubovy, M. Chapter 36 Theoretical Approaches to Perceptual Organization: Simplicity and Likelihood Principles. In Handbook of Perception and Performance; Boff, K.R., Kaufman, L., Thomas, J.P., Eds.; Wiley: New York, NY, USA, 1986; Volume 2. [Google Scholar]
- Bahnsen, P. Eine Untersuchung über Symmetrie und Asymmetrie bei visuellen Wahrnehmungen. Z. für Psychol. 1928, 108, 129–154. [Google Scholar]
- Rubin, E. Synsoplevede Figurer; Gyldendal: Copenhagen, Denmark, 1915. [Google Scholar]
- Peterson, M.A.; Gibson, B.S. Must figure-ground organization precede object recognition? Psychol. Sci. 1994, 5, 253–259. [Google Scholar] [CrossRef]
- Mojica, A.J.; Peterson, M.A. Display-wide influences on figure-ground perception: The case of symmetry. Attn. Percept. Psychopys. 2014, 76, 1069–1084. [Google Scholar] [CrossRef] [PubMed]
- Kanizsa, G.; Gerbino, W. Convexity and Symmetry in Figure-Ground Organization. In Vision and Artifact; Henle, M., Ed.; Springer: New York, NY, USA, 1976; pp. 25–32. [Google Scholar]
- Machilsen, B.; Pauwels, M.; Wagemans, J. The role of vertical mirror symmetry in visual shape detection. J. Vis. 2009, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Gillam, B.; McGrath, D. Orientation relative to the retina determines perceptual organization. Percept. Psychophys. 1979, 26, 177–181. [Google Scholar] [CrossRef]
- Feldman, J. Formation of visual “objects” in the early computation of spatial relations. Percept. Psychophys. 2007, 69, 816–827. [Google Scholar] [CrossRef] [PubMed]
- Gillam, B. Perceived common rotary motion of ambiguous stimuli as a criterion of perceptual grouping. Percept. Psychophys. 1972, 11, 99–101. [Google Scholar] [CrossRef]
- Eby, D.W.; Loomis, J.M.; Solomon, E.M. Perceptual linkage of multiple objects rotating in depth. Perception. 1989, 18, 427–444. [Google Scholar] [CrossRef] [PubMed]
- Wallach, H.; O’Connell, D.N. The kinetic depth effect. J. Exp. Psychol. 1953, 65, 205–217. [Google Scholar] [CrossRef]
- Gillam, B. Separation relative to length determines the organization of two lines into a unit. J. Exp. Psychol. Hum. Percept. Perform. 1981, 7, 884–889. [Google Scholar] [CrossRef] [PubMed]
- Gillam, B.; Grant, T., Jr. Aggregation and unit formation in the perception of moving collinear lines. Perception 1984, 13, 659–664. [Google Scholar] [CrossRef] [PubMed]
- Gillam, B.; Broughton, R. Motion capture by a frame: Global or local processing. Percept. Psychophys. 1991, 49, 547–550. [Google Scholar] [CrossRef] [PubMed]
- Gillam, B. Observations on associative grouping: In honor of Jacob Beck. Spat. Vis. 2005, 18, 147–157. [Google Scholar] [CrossRef] [PubMed]
- Rock, I. The Logic of Perception; MIT Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Barlow, H. Redundancy reduction revisited. Netw. Comput. Neural Syst. 2001, 12, 241–253. [Google Scholar] [CrossRef]
- Csatho, A.; van der Vloed, G.; van der Helm, P.A. Blobs strengthen repetition but weaken symmetry. Vis. Res. 2003, 43, 993–1007. [Google Scholar] [CrossRef]
- Baylis, G.C.; Driver, J. Perception of symmetry and repetition within and across visual shapes: Part-descriptions and object based attention. Vis. Cogn. 2001, 8, 163–196. [Google Scholar] [CrossRef]
- Makin, A.D.J.; Wright, D.; Rampon, G.; Palumbo, L.; Guest, M.; Sheehan, R.; Cleaver, H.; Bertamini, M. An electrophysiological index of perceptual goodness. Cereb. Cortex 2016, 26, 4416–4434. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gillam, B. Redundant Symmetry Influences Perceptual Grouping (as Measured by Rotational Linkage). Symmetry 2017, 9, 67. https://doi.org/10.3390/sym9050067
Gillam B. Redundant Symmetry Influences Perceptual Grouping (as Measured by Rotational Linkage). Symmetry. 2017; 9(5):67. https://doi.org/10.3390/sym9050067
Chicago/Turabian StyleGillam, Barbara. 2017. "Redundant Symmetry Influences Perceptual Grouping (as Measured by Rotational Linkage)" Symmetry 9, no. 5: 67. https://doi.org/10.3390/sym9050067
APA StyleGillam, B. (2017). Redundant Symmetry Influences Perceptual Grouping (as Measured by Rotational Linkage). Symmetry, 9(5), 67. https://doi.org/10.3390/sym9050067




