Abstract
The adaptive multi-rate wideband (AMR-WB) speech codec is widely used in modern mobile communication systems for high speech quality in handheld devices. Nonetheless, a major disadvantage is that vector quantization (VQ) of immittance spectral frequency (ISF) coefficients takes a considerable computational load in the AMR-WB coding. Accordingly, a binary search space-structured VQ (BSS-VQ) algorithm is adopted to efficiently reduce the complexity of ISF quantization in AMR-WB. This search algorithm is done through a fast locating technique combined with lookup tables, such that an input vector is efficiently assigned to a subspace where relatively few codeword searches are required to be executed. In terms of overall search performance, this work is experimentally validated as a superior search algorithm relative to a multiple triangular inequality elimination (MTIE), a TIE with dynamic and intersection mechanisms (DI-TIE), and an equal-average equal-variance equal-norm nearest neighbor search (EEENNS) approach. With a full search algorithm as a benchmark for overall search load comparison, this work provides an 87% search load reduction at a threshold of quantization accuracy of 0.96, a figure far beyond 55% in the MTIE, 76% in the EEENNS approach, and 83% in the DI-TIE approach.
1. Introduction
With a 16 kHz sampling rate, the adaptive multi-rate wideband (AMR-WB) speech codec [1,2,3,4] is one of the speech codecs applied to modern mobile communication systems as a way to remarkably improve the speech quality on handheld devices. The AMR-WB is a speech codec developed on the basis of an algebraic code-excited linear-prediction (ACELP) coding technique [4,5], and provides nine coding modes with bitrates of 23.85, 23.05, 19.85, 18.25, 15.85, 14.25, 12.65, 8.85, and 6.6 kbps. The ACELP-based technique is developed as an excellent speech coding technique, having a double advantage of low bit rates and high speech quality, but a price paid is a high computational complexity required in an AMR-WB codec. Using an AMR-WB speech codec, the speech quality of a smartphone can be improved but at the cost of high battery power consumption.
In an AMR-WB encoder, a vector quantization (VQ) of immittance spectral frequency (ISF) coefficients [6,7,8,9,10] occupies a significant computational load in various coding modes. The VQ structure in AMR-WB adopts a combination of a split VQ (SVQ) and a multi-stage VQ (MSVQ) techniques, referred to as split-multistage VQ (S-MSVQ), to quantize the 16-order ISF coefficient [1]. Conventionally, VQ uses a full search to obtain a codeword best matched with an arbitrary input vector, but the full search requires an enormous computational load. Therefore, many studies [11,12,13,14,15,16,17,18,19] have made efforts to simplify the search complexity of an encoding process. These approaches are classified into two types in terms of the manner the complexity is reduced: triangular inequality elimination (TIE)-based approaches [11,12,13,14] and equal-average equal-variance equal-norm nearest neighbor search (EEENNS)-based algorithms [15,16,17,18,19].
As in [11], a TIE algorithm is proposed to address the computational load issue in a VQ-based image coding. Improved versions of TIE approaches are presented in [12,13] to reduce the scope of a search space, giving rise to further reduction in the computational load. However, there exists a high correlation between ISF coefficients of neighboring frames in AMR-WB, that is, ISF coefficients evolve smoothly over successive frames. This feature benefits TIE-based VQ encoding, according to which a considerable computational load reduction is demonstrated. Yet, a moving average (MA) filter is employed to smooth the data in advance of VQ encoding of ISF coefficients. It means that the high correlation feature is gone, resulting in a poor performance in computational load reduction. Recently, a TIE algorithm equipped with a dynamic and an intersection mechanism, named DI-TIE, is proposed to effectively simplify the search load, and this algorithm is validated as the best candidate among the TIE-based approaches so far. On the other hand, an EEENNS algorithm was derived from equal-average nearest neighbor search (ENNS) and equal-average equal-variance nearest neighbor search (EENNS) approaches [15,16,17,18,19]. In contrast to TIE-based approaches, the EEENNS algorithm uses three significant features of a vector, i.e., mean, variance, and norm, as a three-level elimination criterion to reject impossible codewords.
Furthermore, a binary search space-structured VQ (BSS-VQ) is presented in [20] as a simple as well as efficient way to quantize line spectral frequency (LSF) coefficients in the ITU-T G.729 speech codec [5]. This algorithm demonstrated that a significant computational load reduction is achieved with a well maintained speech quality. In view of this, this paper will apply the BSS-VQ search algorithm to the ISF coefficients quantization in AMR-WB. This work aims to verify whether the performance superiority of the BSS-VQ algorithm remains, for the reason that the VQ structure in AMR-WB is different from that in G.729. On the other hand, another major motivation behind this is to meet the energy saving requirement on handheld devices, e.g. smartphones, for an extended operation time period.
The rest of this paper is outlined as follows. Section 2 gives the description of ISF coefficients quantization in AMR-WB. The BSS-VQ algorithm for ISF quantization is presented in Section 3. Section 4 demonstrates experimental results and discussions. This work is summarized at the end of this paper.
2. ISF Coefficients Quantization in AMR-WB
In a quantization process of AMR-WB [1], a speech frame of 20 ms is firstly applied to evaluate linear predictive coefficients (LPCs), which are then converted into ISF coefficients. Subsequently, quantized ISF coefficients are obtained following a VQ encoding process, which is detailed below.
2.1. Linear Prediction Analysis
In a linear prediction, a Levinson–Durbin algorithm is used to compute a 16th order LPC, ai, of a linear prediction filter [1], defined as:
Subsequently, the LPC parameters are converted into the immittance spectral pair (ISP) coefficients for the purposes of parametric quantization and interpolation. The ISP coefficients are defined as the roots of the following two polynomials:
and are symmetric and antisymmetric polynomials, respectively. It can be proven that all the roots of such two polynomials lie and alternate successively on a unit circle in the z-domain. Additionally, has two roots at z = 1 (ω = 0) and z = −1 (ω = π). Such two roots are eliminated by introducing the following polynomials, with eight and seven conjugate roots respectively on the unit circle, expressed as:
where the coefficients qi are referred to as the ISPs in the cosine domain, and a[16] is the last predictor coefficient. A Chebyshev polynomial is used to solve Equations (4) and (5). Finally, 16th order ISF coefficients ωi can be obtained by taking the transformation ωi = arccos(qi).
2.2. Quantization of ISF Coefficients
Before a quantization process, a mean-removed and first order MA filtering are performed on the ISF coefficients to obtain a residual ISF vector [1], that is:
where z(n) and p(n) respectively denote the mean-removed ISF vector and the predicted ISF vector at frame n by a first order MA prediction, defined as:
where is the quantized residual vector at the previous frame.
Subsequently, S-MSVQ is performed on r(n). As presented in Table 1 and Table 2, S-MSVQ is categorized into two types in terms of the bit rate of the coding modes. In Stage 1, r(n) is split into two subvectors, namely, a 9-dimensional subvector r1(n) associated with codebook CB1 and a 7-dimensional subvector r2(n) associated with codebook CB2, for VQ encoding. As a preliminary step of Stage 2, the quantization error vectors are split into three subvectors for the 6.60 kbps mode or five for the modes with bitrates between 8.85 and 23.85 kbps, symbolized as , respectively. For instance, r(2)1,1–3 in Table 1 represents the subvector split from the 1st to the 3rd components of r1, and then VQ encoding is performed thereon over codebook CB11 in Stage 2. Likewise, r(2)2,4–7 stands for the subvector split from the 4th to the 7th components of r2, after which VQ encoding is performed over codebook CB22 in Stage 2. Finally, a squared error ISF distortion measure, that is, Euclidean distance, is used in all quantization processes.

Table 1.
Structure of S-MSVQ in AMR-WB in the 8.85–23.85 kbps coding modes.

Table 2.
Structure of S-MSVQ in AMR-WB in the 6.60 kbps coding mode.
3. BSS-VQ Algorithm for ISF Quantization
The basis of the BSS-VQ algorithm is that an input vector is efficiently assigned to a subspace where a small number of codeword searches is carried out using a combination of a fast locating technique and lookup tables, as a prerequisite of a VQ codebook search. In this manner, a significant computational load reduction can be achieved.
At the start of this algorithm, each dimension is dichotomized into two subspaces, and an input vector is then assigned to a corresponding subspace according to the entries of the input vector. This idea is illustrated in the following example. There are 29 = 512 subspaces for a 9-dimensional subvector r1(n) associated with codebook CB1, and an input vector can then be assigned to one of the 512 subspaces by means of a dichotomy according to each entry of the input vector. Finally, VQ encoding is performed using a prebuilt lookup table containing the statistical information on sought codewords.
In this proposal, the lookup table in each subspace is pre-built in a way that requires lots of data for training purposes. A training as well as an encoding procedure in BSS-VQ is illustrated with the example of a 9-dimensional codebook CB1 with 256 entries in AMR-WB.
3.1. BSS Generation with Dichotomy Splitting
As a preliminary step of a training procedure, each dimension is dichotomized into two subspaces, and a dichotomy position is defined as the mean of all the codewords contained in a codebook, formulated as:
where represents the jth component of the ith codeword ci, dp(j) the mean value of all the jth components. Taking the codebook CB1 as an instance, CSize = 256, Dim = 9. As listed in Table 3, all the dp(j) values are saved and then presented in a tabular form.

Table 3.
Dichotomy position for each dimension in the codebook CB1.
Subsequently, for vector quantization on the nth input vector xn, a quantity νn(j) is defined as:
where xn(j) denotes the jth component of xn. Then xn is assigned to subspace k (bssk), with k given as the sum of νn(j) over the entire dimensions, formulated as:
In this study, 0 ≤ k < BSize and BSize = 29 = 512 represents the total number of subspaces. Taking an input vector xn = {20.0, 20.1, 20.2, 20.3, 20.4, 20.5, 20.6, 20.7, 20.8} as an instance, νn(j) = {20, 21, 22, 0, 0, 0, 0, 0, 28} for each j, 0 ≤ j ≤ 8, and k = 263 can be obtained by Equations (9) and (10) respectively. Thus, the input vector xn is assigned to the subspace bssk with k = 263.
By means of Equations (9) and (10), it is noted that this algorithm requires a small number of basic operations, i.e., comparison, shift and addition, such that an input vector is assigned to a subspace in a highly efficient manner.
3.2. Training Procedure of BSS-VQ
Following the determination of the dichotomy position for each dimension, a training procedure is performed to build a lookup table in each subspace. The lookup tables give the probability that each codeword serves as the best-matched codeword in each subspace, referred to as the hit probability of a codeword in a subspace for short.
A training procedure is stated below as Algorithm 1. With more than 1.56 GB of memory, a duration longer than 876 min and a total of 2,630,045 speech frames, a large speech database, covering a diversity of contents and multiple speakers, is employed as the training data in a training procedure.
| Algorithm 1: Training procedure of BSS-VQ |
|
A lookup table is built for each subspace, following the completion of a training procedure. The lookup table gives the hit probability of each codeword in a subspace. For sorting purposes, a quantity , 1 ≤ m ≤ CSize, is defined as the m ranked probability that a codeword hits the best-matched codeword in subspace bssk. Taking m = 1 as an instance, , namely, the highest hit probability in bssk. As it turns out, the lookup table in each subspace gives the ranked hit probability in descending order and the corresponding codeword.
3.3. Encoding Procedure of BSS-VQ
In the encoding procedure of BSS-VQ, the cumulative probability is firstly defined as the sum of the top M in bssk, that is:
Subsequently, given a threshold of quantization accuracy (TQA), a quantity Mk(TQA) represents the minimum value of M that satisfies the condition in bssk, that is:
For a given TQA, a total of 512 Mk(TQA)s are evaluated by Equation (14) for all the subspaces, and the mean value is then given as:
Illustrated in Figure 1 is a plot of the average number of searches corresponding to the values of TQA ranging between 0.90 and 0.99. Given a TQA = 0.95 as an instance, a mere average of 14.58 codeword searches is required to reach a search accuracy as high as 95%. In simple terms, the search performance can be significantly improved at the cost of a small drop in search accuracy. Furthermore, a trade-off can be made instantly between the quantization accuracy and the search load according to Figure 1. Hence, a BSS-VQ encoding procedure is described below as Algorithm 2.
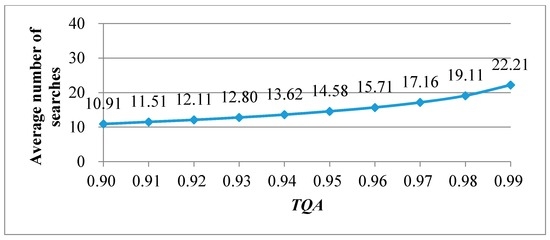
Figure 1.
A plot of the average number of searches versus TQA.
| Algorithm 2: Encoding procedure of BSS-VQ |
|
The BSS-VQ algorithm is briefly summarized as follows. Table 3 is the outcome by performing Equation (8) and is saved as the first lookup table. Subsequently, the second lookup table concerning and the corresponding codeword is built for each subspace according to the training procedure. Accordingly, the VQ encoding can be performed using Algorithm 2.
4. Experimental Results
There are three experiments conducted in this work. The first is a search load comparison among various search approaches. The second is a quantization accuracy (QA) comparison among a full search and other search approaches. The third is a performance comparison among various approaches in terms of ITU-T P.862 perceptual evaluation of speech quality (PESQ) [21] as an objective measure of speech quality. A speech database, completely different from all the training data, is employed for outside testing purposes. With one male and one female speaker, the speech database in total takes up more than 221 MB of memory, occupies more than 120 min, and covers 363,281 speech frames.
Firstly, Table 4 lists a comparison on the average number of searches among full search, multiple TIE (MTIE) [13], DI-TIE, and EEENNS, while Table 5 gives the search load corresponding to TQA values of the BSS-VQ algorithm. Moreover, with the search load required in the full search algorithm as a benchmark, Table 6 and Table 7 present comparisons on the load reduction (LR) with respect to Table 4 and Table 5. A high value of LR reflects a high search load reduction. Table 6 indicates that DI-TIE provides a higher value of LR than MTIE and EEENNS search approaches among all the codebooks. It is also found that most LR values of BSS-VQ are higher than the DI-TIE approach by an observation in Table 6 and Table 7. For example, the LR values of BSS-VQ are indeed higher than DI-TIE in case the TQA is equal to or smaller than 0.99, 0.98, 0.96, and 0.99 in codebooks CB1, CB2, CB21, and CB22, respectively. Accordingly, a remarkable search load reduction is reached by the BSS-VQ search algorithm.

Table 4.
Average number of searches among various algorithms in the 8.85–23.85 kbps modes.

Table 5.
Search load of the BSS-VQ algorithm versus TQA values in the 8.85–23.85 kbps modes.

Table 6.
LR percentage representation of Table 4.

Table 7.
LR percentage representation of Table 5.
In the QA aspect, a 100% QA is obtained by the MTIE, DI-TIE, and EEENNS algorithms as compared with a full search approach. Thus, only the QA experiment of BSS-VQ is conducted. The QA corresponding to TQA values of the BSS-VQ algorithm is given in Table 8. It reveals that QA is an approximation of TQA in either inside or outside testing cases. Moreover, this algorithm provides an LR between 77.78% and 93.98% at TQA = 0.90 as well as an LR between 67.23% and 88.39% at TQA = 0.99, depending on the codebooks. In other words, a trade-off can be made between the quantization accuracy and the search load.

Table 8.
Comparison of QA percentage of the BSS-VQ algorithm versus TQA values in the 8.85–23.85 kbps modes among codebooks.
Furthermore, an overall LR is evaluated to observe the total search load of an entire VQ encoding procedure of an input vector. The overall LR refers to the total search load, defined as the sum of the average number of searches multiplied by the vector dimension in each codebook. Thus, an overall LR comparison with the full search as a benchmark is presented as a bar graph in Figure 2. As clearly indicated in Figure 2, the overall LR of BSS-VQ is higher than MTIE, DI-TIE, and EEENNS approaches, but at the same time the QA is as high as 0.98. Moreover, Table 9 gives a PESQ comparison, including the mean and the STD, among various approaches. Since MTIE, DI-TIE, and EEENNS provide a 100% QA, they both share the same PESQ with a full search, meaning that there is no deterioration in the speech quality. A close observation reveals little difference between PESQs obtained in a full search and in this search algorithm, that is, the speech quality is well maintained in BSS-VQ at TQA not less than 0.90. This BSS-VQ search algorithm is experimentally validated as a superior candidate relative to its counterparts.
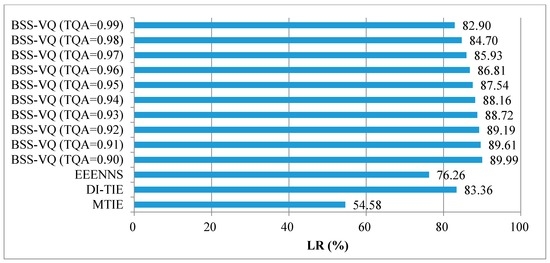
Figure 2.
Comparison of overall search load reduction among various approaches.

Table 9.
Comparison on mean opinion score (MOS) values using the PESQ algorithm among various methods.
5. Conclusions
This paper presents a BSS-VQ codebook search algorithm for ISF vector quantization in the AMR-WB speech codec. Using a combination of a fast locating technique and lookup tables, an input vector is efficiently assigned to a search subspace where a small number of codeword searches is carried out and the aim of remarkable search load reduction is reached consequently. Particularly, a trade-off can be made between the quantization accuracy and the search load to meet a user’s need when performing a VQ encoding. This BSS-VQ search algorithm, providing a considerable search load reduction as well as nearly lossless speech quality, is experimentally validated as superior to MTIE, DI-TIE, and EEENNS approaches. Furthermore, this improved AMR-WB speech codec can be adopted to upgrade the VoIP performance on a smartphone. As a consequence, the energy efficiency requirement is achieved for an extended operation time period due to computational load reduction.
Acknowledgments
This research was financially supported by the Ministry of Science and Technology under grant number MOST 105-2221-E-167-031, Taiwan. The author felt deeply indebted as well to the co-authors of two cited papers, including Tzu-Hung Lin, Shaw-Hwa Hwang, Shun-Chieh Chang and Bing-Jhih Yao, for their contribution as the basis of this work.
Conflicts of Interest
The author declares no conflict of interest.
References
- 3rd Generation Partnership Project (3GPP). Adaptive Multi-Rate—Wideband (AMR-WB) Speech Codec; Transcoding Functions; TS 26.190; 3GPP: Valbonne, France, 2012. [Google Scholar]
- Ojala, P.; Lakaniemi, A.; Lepanaho, H.; Jokimies, M. The adaptive multirate wideband speech codec: System characteristics, quality advances, and deployment strategies. IEEE Commun. Mag. 2006, 44, 59–65. [Google Scholar] [CrossRef]
- Varga, I.; De Lacovo, R.D.; Usai, P. Standardization of the AMR wideband speech codec in 3GPP and ITU-T. IEEE Commun. Mag. 2006, 44, 66–73. [Google Scholar] [CrossRef]
- Bessette, B.; Salami, R.; Lefebvre, R.; Jelínek, M.; Rotola-Pukkila, J.; Vainio, J.; Mikkola, H.; Järvinen, K. The adaptive multirate wideband speech codec (AMR-WB). IEEE Trans. Speech Audio Process. 2002, 10, 620–636. [Google Scholar] [CrossRef]
- Salami, R.; Laflamme, C.; Adoul, J.P.; Kataoka, A.; Hayashi, S.; Moriya, T.; Lamblin, C.; Massaloux, D.; Proust, S.; Kroon, P.; et al. Design and description of CS-ACELP: A toll quality 8 kb/s speech coder. IEEE Trans. Speech Audio Process. 1998, 6, 116–130. [Google Scholar] [CrossRef]
- Linde, Y.; Buzo, A.; Gray, R.M. An algorithm for vector quantizer design. IEEE Trans. Commun. 1980, 28, 84–95. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Z.; Yin, F. A novel hierarchical decomposition vector quantization method for high-order LPC parameters. IEEE Trans. Audio Speech Lang. Process. 2015, 23, 212–221. [Google Scholar] [CrossRef]
- Ramirez, M.A. Intra-predictive switched split vector quantization of speech spectra. IEEE Signal Process. Lett. 2013, 20, 791–794. [Google Scholar] [CrossRef]
- Han, W.J.; Kim, E.K.; Oh, Y.H. Multicodebook split vector quantization of LSF parameters. IEEE Signal Process. Lett. 2002, 9, 418–421. [Google Scholar]
- Chatterjee, S.; Sreenivas, T.V. Optimum switched split vector quantization of LSF parameters. Signal Process. 2008, 88, 1528–1538. [Google Scholar] [CrossRef]
- Hwang, S.H.; Chen, S.H. Fast encoding algorithm for VQ-based image coding. Electron. Lett. 1990, 26, 1618–1619. [Google Scholar]
- Choi, S.Y.; Chae, S.I. Incremental-search fast vector quantiser using triangular inequalities for multiple anchors. Electron. Lett. 1998, 34, 1192–1193. [Google Scholar] [CrossRef]
- Hsieh, C.H.; Liu, Y.J. Fast search algorithms for vector quantization of images using multiple triangle inequalities and wavelet transform. IEEE Trans. Image Process. 2000, 9, 321–328. [Google Scholar] [CrossRef] [PubMed]
- Yao, B.J.; Yeh, C.Y.; Hwang, S.H. A search complexity improvement of vector quantization to immittance spectral frequency coefficients in AMR-WB speech codec. Symmetry 2016, 8, 1–8. [Google Scholar] [CrossRef]
- Lu, Z.M.; Sun, S.H. Equal-average equal-variance equal-norm nearest neighbor search algorithm for vector quantization. IEICE Trans. Inf. Syst. 2003, 86, 660–663. [Google Scholar]
- Chu, S.C.; Lu, Z.M.; Pan, J.S. Hadamard transform based fast codeword search algorithm for high-dimensional VQ encoding. Inf. Sci. 2007, 177, 734–746. [Google Scholar] [CrossRef]
- Chen, S.X.; Li, F.W.; Zhu, W.L. Fast searching algorithm for vector quantisation based on features of vector and subvector. IET Image Process. 2008, 2, 275–285. [Google Scholar] [CrossRef]
- Chen, S.X.; Li, F.W. Fast encoding method for vector quantisation of images using subvector characteristics and Hadamard transform. IET Image Process. 2011, 5, 18–24. [Google Scholar] [CrossRef]
- Xia, S.; Xiong, Z.; Luo, Y.; Dong, L.; Zhang, G. Location difference of multiple distances based k-nearest neighbors algorithm. Knowl.-Based Syst. 2015, 90, 99–110. [Google Scholar] [CrossRef]
- Lin, T.H.; Yeh, C.Y.; Hwang, S.H.; Chang, S.C. Efficient binary search space-structured VQ encoder applied to a line spectral frequency quantisation in G.729 standard. IET Commun. 2016, 10, 1183–1188. [Google Scholar] [CrossRef]
- ITU-T Recommendation P.862. Perceptual Evaluation of Speech Quality (PESQ): An Objective Method for End-to-End Speech Quality Assessment of Narrow-Band Telephone Networks and Speech Codecs; ITU (International Telecommunication Union): Geneva, Switzerland, 2001. [Google Scholar]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).