Methods for solving optimization problems like heuristics do not guarantee obtaining the result identical with analytical solution. Depending on the initial population, we might expect faster or slower convergence to analytical solutions. However as the research show these methods give very precise results. Therefore it is important to constantly work on new efficient algorithms. Heuristics simulate phenomena that occur in nature into optimization algorithms. Different approaches make use of various selective strategies implemented into optimization algorithms. There are many propositions to simulate the way animals hunt and breed. Selecting a right place to settle is also a very important strategy, in which an animal adapts to environmental conditions to achieve the best possible result. Hunting is inevitably linked to the prey and local environment. Different conditions involve a lonely hunting behavior or hunting in a herd. In the first, an animal uses various aspects of smell, hearing, sight which are altogether combined into efficient actions for optimal hunting strategy. On the other hand, while hunting in a group the animals depend on other members of the herd, which all cooperate to corner the prey. Similarly other phenomena from the nature can inspire optimization methods. Water running on the surface of the ocean is adapting to weather conditions in which a cylindrical shape gives to the waves optimal strength of action. These are very similar to optimization, where the algorithm must adapt to given criterion for the best possible solution. We can find many models based on animals strategies and nature phenomena composed into optimization strategies.
Simulated Annealing (SA) is one of the first proposed meta-heuristics [
7]. In this method annealing process is simulated in the search space to find the optimum for modeled functions. In [
8] was presented an idea of Genetic Algorithm (GA), which is simulating processes of genetic evolution into optimization purposes. Particle Swarm Optimization (PSO) was presented in [
9]. This method is based on a model of the swarm of individuals that cooperate together to optimize the strategy for development. Another interesting example of the swarm intelligence is Artificial Bee Colony Algorithm (ABCA) presented in [
10]. This method simulates the behavior of ants while traversing the habitat in search for food. One of heuristics based on stochastic theory is Cuckoo Search Optimization Algorithm (CSA) described by [
11]. Proposed model simulates behavior of cuckoos while tossing their eggs into nests of other birds. The movement of individuals in the search for the optimal location is described using Lévy flight approach. The phenomenon of echolocation used by bats have been modeled in Bat Algorithm (BA) by [
12]. This algorithm simulates hunting bats, which are using natural radar to trace the prey. Firefly Algorithm (FA) was introduced in [
13], where the author presented an idea to model relations between individuals in a swarm of fireflies. In that heuristic a model of communication between bugs searching for an optimal partner is implemented into optimization algorithm. Not only behavior of animals has been subjected to mathematical analysis, but also phenomenon of plants growth. Flowers Pollination Algorithm (FPA) presented by [
14] brings a model of flower pollen raised by the wind. Recent years brought other models sourced in nature phenomena. In [
15] was shown a model of breaking sea waves called Water Wave Optimization Algorithm (WWO). The particles of the wave inspired optimization strategy, which simulates the cylindrical movements of the water on the surface of the ocean. In [
16] was proposed the model of moths movements to the light based on spiral trajectory formulated in Moth-Flame Optimization Algorithm (MFO). Predation of dragonflies was formulated in Dragon-Fly Algorithm (DA) in [
17].
These algorithms have presented a dedicated modeling of various aspects taken from the nature of living species and weather phenomena. Some of the strategies present a swarm communication models, the other use single individual actions to simulate optimization. Among them we have models of organisms on various levels of evolution and also various families of fauna and flora. We have models of birds, models of bugs, models of cell evolutions but at the same time we have models of flowers and water waves. Some of these methods have clearly visible two stages of modeling: global and local search. Depending on the proposed model the algorithms can have fast convergence to the optimum. However still important aspect is the location of the initial population. The starting points may influence the final results. Therefore the best option to compose a meta-heuristic algorithm is to define a composition of efficient approaches that will support the highest performance for each of the optimization stages. The algorithm shall be efficient in the global search, since this phase makes it possible to search the entire model space. A precision of the results depends on the local search, in which the algorithm is correcting the final values in the local sub domain. Each of the methods must be possibly low complex for fast computations. Therefore one of the possible aspects is to efficiently control the number of individuals in the population.
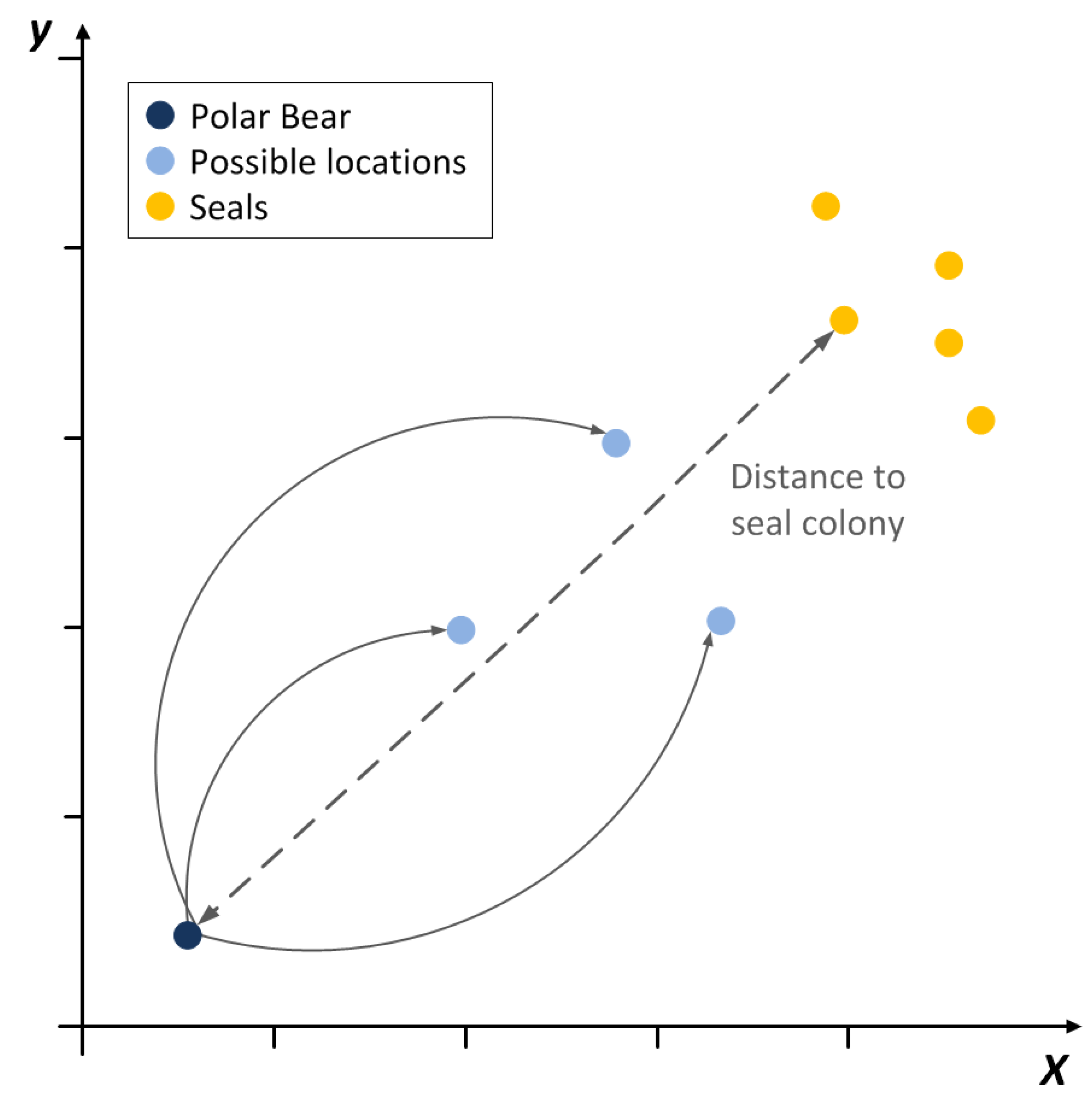
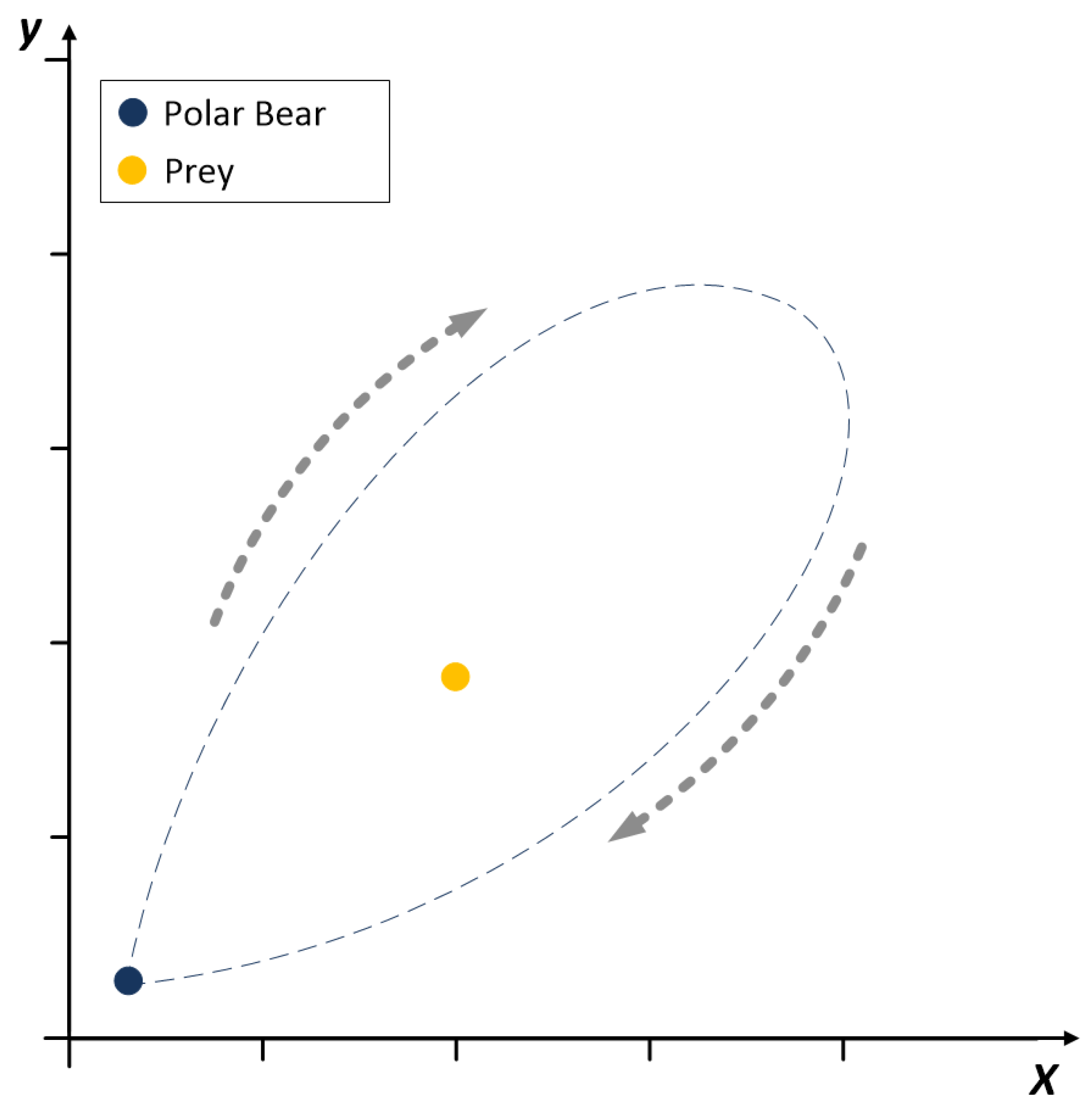
In this article, we propose to model behavior of polar bears while searching for food over frosty arctic land and sea into optimization strategy, see
Figure 1. Polar bears have a very difficult environment for their development, yet these animals achieved optimal results becoming rulers of the arctic. This gave us an inspiration for the research on possible modeling of their behavior into heuristic algorithm. In the model we assume that the domain for the optimization is very similar to arctic conditions. We do not know where the optimums are. Similarly polar bears do not know where to find seals or other food. In the search we can be trapped in local optima, what can prevent us from global optimization. Moreover the nature of optimized objects and functions can be difficult and so the optimization needs some specific strategies to avoid mistakes. Polar bears search for food but the arctic conditions can make them trapped and even die, so they developed very efficient mechanisms that help them to succeed. We have distinguished two phases of the hunting strategy. One we simulate for a global search, the other for a local search. A model of searching for food through the arctic lands and waters gave a very promising global search. We adopted travel through the arctic for a search of sub domains with possible optimum. While in each iteration of the algorithm local search is simulated using model of specific hunting. Additionally the proposed model introduces a mechanism to control birth and death processes, which stimulates the number of individuals similarly to the nature conditions.
The novelty of the proposed method is in the efficient composition of these three nature-inspired mechanisms into one heuristic algorithm. Each of them represents some important aspect of the adaptation of polar bears to the arctic conditions that help them to succeed. Proposed model makes use of these actions implemented into optimization strategy, in which we can efficiently search through the entire domain. The model prevents blocking in the sub spaces of the local minima. While proposed birth and death strategy enables dynamic adaptation to the optimized model, without using large population of individuals in each iteration.