1. Introduction
Symmetries have since a long time played an important role in the analysis of physical systems. The insight gained can be either calculational, in that a recognised symmetry becomes useful in simplifying calculations, or else conceptual, in that the identification of symmetries can lead to new level of understanding. In the statistical physics of equilibrium second-order phase transitions in two dimensions,
conformal invariance has ever since the pioneering work of Belavin, Polyakov and Zamolodchikov [
1] created considerable progress, both computationally as well as conceptually. It then appears natural to ask if one might find extensions of conformal invariance which apply to time-dependent phenomena. Here, we shall inquire about dynamical symmetries of the following stochastic Langevin equation, to be called
diffusion-limited erosion (dle) Langevin equation, which reads in momentum space [
2]
and describes the Fourier-transformed height
. Because of the (Fourier-transformed) standard brownian motion
, with the variance
, this is a stochastic process, called
diffusion-limited erosion (dle) process. Herein,
are non-negative constants and
is the Dirac distribution. Since we shall be interested in deriving linear responses, an external infinitesimal source term
is also included, to be set to zero at the end. Inverting the Fourier transform in order to return to direct space, Equation (1) implies spatially long-range interactions. The conformal invariance of equilibrium critical systems with long-range interactions has been analysed recently [
3]. Equation (1) arises in several distinct physical contexts.
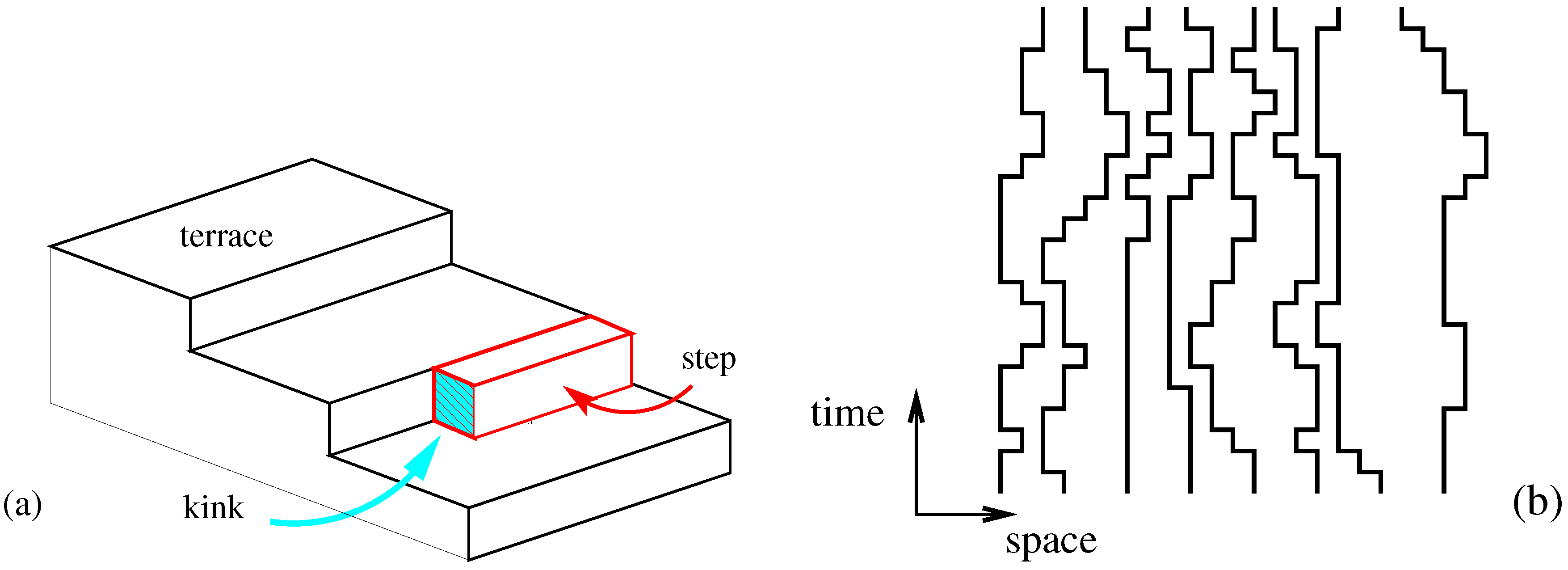
Example 1. For the original definition of the (dle) process [2], one considers how an initially flat interface is affected by the diffusive motion of corrosive particles. A single corrosive particle starts initially far away from the interface. After having undergone diffusive motion until the particle finally arrives at the interface, it erodes a particle from that interface. Repeating this process many times, an eroding interface forms which is described in terms of a fluctuating height , see Figure 1. It can be shown that this leads to the dle Langevin Equation (1) [2,4]. Several lattice formulations of the model [2,5,6,7] confirm the dynamical exponent . Example 2. A different physical realisation of Equation (1) invokes vicinal surfaces. Remarkably, for space dimension, the Langevin Equation (1) has been argued [8] to be related to a system of non-interacting fermions, conditioned to an a-typically large flux. Consider the terrace-step-kink model
of a vicinal surface, and interpret the steps as the world lines of fermions, see Figure 2. Its transfer matrix is the matrix exponential of the quantum hamiltonian H of the asymmetric XXZ chain [8]. Use Pauli matrices , attached to each site n, such that the particle number at each site is .
On a chain of N sites, consider the quantum hamiltonian [8,9,10]where , and . Herein, describe the left/right bias of single-particle hopping and are the grand-canonical parameters conjugate to the current and the mean particle number. In the continuum limit, the particle density is related to the height h which in turn obeys (1), with a gaussian white noise
η [8]. This follows from the application of the theory of fluctuating hydrodynamics, see [11,12] for recent reviews. The low-energy behaviour of H yields the dynamical exponent [8,9,10]. If one conditions the system to an a-typically large current, the large-time, large-distance behaviour of (2) has very recently been shown [10] (i) to be described by a conformal field-theory with central charge and (ii) the time-space scaling behaviour of the stationary structure function has been worked out explicitly, for . Therefore, one may conjecture that the so simple-looking Equation (1) should furnish an effective continuum description of the large-time, long-range properties of quite non-trivial systems, such as (2). The physical realisation of Equation (1) in terms of the
dle process makes it convenient to discuss the results in terms of the physics of the growth of interfaces [
13,
14,
15], which can be viewed as a paradigmatic example of the emergence of non-equilibrium collective phenomena [
16,
17]. Such an interface can be described in terms of a time-space-dependent height profile
. This profile depends also on the eventual fluctuations of the set of initial states and on the noise in the Langevin equation, hence
h should be considered as a random variable. The degree of fluctuations can be measured through the interface width. If the model is formulated first on a hyper-cubic lattice
of
sites, the interface width is defined by
where the generically expected scaling form, for large times/lattice sizes
,
, is also indicated. Physicists call this
Family-Vicsek scaling [
18]. Implicitly, it is assumed here that one is
not at the ‘upper critical dimension
’, where this power-law scaling is replaced by a logarithmic scaling form, see also below. Herein,
denotes an average over many independent samples and
is the spatially averaged height. Furthermore,
β is called the
growth exponent,
is the
dynamical exponent and
is the
roughness exponent. When
, one speaks of the
saturation regime and when
, one speaks of the
growth regime. We shall focus on the growth regime from now on.
Definition 1. On a spatially infinite substrate, an interface with a width for large times is called rough. If is finite, the interface is called smooth.
This definition permits a first appreciation of the nature of the interface: if in (
3)
, the interface is rough.
In addition, dynamical properties of the interface can be studied through the two-time correlators and responses. In the growth regime (where effectively
), one considers the double scaling limit
with
fixed and expects the scaling behaviour
where
j is an external field conjugate to the height
h. Throughout, all correlators are calculated with
. In the context of Janssen-de Dominicis theory,
is the conjugate response field to
h, see [
17]. Spatial translation-invariance was implicitly admitted in (4). This defines the
ageing exponents . The
autocorrelation exponent and the
autoresponse exponent are defined from the asymptotics
as
. For these non-equilibrium exponents, one has
[
15] and the bound
[
19,
20].
For the
dle process, these exponents are readily found form the exact solution of (1) [
2,
4,
21]. For an initially flat interface
, the two-time correlator and response are in Fourier space
In direct space, this becomes, for
and with
where the Heaviside function Θ expresses the causality condition
. In particular, in the growth regime, the interface width reads (where
is a known constant and a high-momentum cut-off Λ was used for
)
Hence
is the upper critical dimension of the
dle process. It follows that at late times the
dle-interface is smooth for
and rough for
. On the other hand, one may consider the
stationary limit
with the time difference
being kept fixed. Then one finds a fluctuation-dissipation relation
. The similarity of this to what is found for equilibrium systems is unsurprising, since several discrete lattice variants of the
dle process exist and are formulated as an equilibrium system [
5]. Lastly, the exponents defined above are read off by taking the scaling limit, and are listed in
Table 1. In contrast to the interface width
, which shows a logarithmic growth at
, logarithms cancel in the two-time correlator
C and response
R, up to
additive logarithmic corrections to scaling. This is well-known in the physical ageing at
of simple magnets [
22,
23] or of the Arcetri model [
20].
For comparison, we also list in
Table 1 values of the non-equilibrium exponents for several other universality classes of interface growth. In particular, one sees that for the Edwards-Wilkinson (
ew) [
24] and Arcetri classes, the upper critical dimension
, while it is still unknown if a finite value of
exists for the Kardar-Parisi-Zhang (
kpz) class, see [
13,
14,
25,
26,
27,
28]. Clearly, the stationary exponents
are the same in the
ew and Arcetri classes, but the non-equilibrium relaxation exponents
are different for dimensions
. This illustrates the independence of
from those stationary exponents, in agreement with studies in the non-equilibrium critical dynamics of relaxing magnetic systems. On the other hand, for the
kpz class, a perturbative renormalisation-group analysis shows that
for
[
29]. For
, a new strong-coupling fixed point arises and the relaxational properties are still unknown. Even for
, the results of different numerical studies in the
kpz class are not yet fully consistent, but recent simulations suggest that precise information on the shape of the scaling function, coming from a dynamical symmetry [
30], may improve the quality of the extracted exponents [
31].
Here, we are concerned with the dynamical symmetries of the dle process. Our main results are as follows.
Theorem 1. The dynamical symmetry
of the dle process, in space dimension and with , is a meta-conformal algebra, in a sense to be made more precise below, and is isomorphic to the direct sum of three Virasoro algebras without central charge (or loop-Virasoro algebra
). The Lie algebra generators will be given below in Equation (29), they are non-local in space. The general form of the co-variant two-time response function is (with )where are real parameters and are normalisation constants. Remark 1. The exact solution (6b) of the dle-response in is reproduced by (8) if one takes , , and . This illustrates the importance of non-local generators in a specific physical application.
Remark 2. The symmetries so constructed are only dynamical symmetries of the so-called ‘deterministic part’ of Equation (1), which is obtained by setting . We shall see that the co-variant two-time correlator . This agrees with the vanishing of the exact dle-correlator (6a) in the limit (fix and let first and only afterwards ).
This paper presents an exploration of the dynamical symmetries of
dle process for
and is organised as follows. In
Section 2, we introduce the distinction of ortho-conformal and meta-conformal invariance and illustrate these notions by several examples, see
Table 2. In
Section 3, we explain why none of these local symmetries can be considered as a valid candidate of the dynamical symmetry of the
dle process.
Section 4 presents some basic properties on the Riesz-Feller fractional derivative which are used in
Section 5 to explicitly construct the
non-local dynamical symmetry of the
dle process, thereby generalising and extending earlier results [
21].
Section 6 outlines the formulation of time-space Ward identities for the computation of covariant
n-point functions and in
Section 7 the two-point correlator and response are found for the dynamical symmetry of the
dle process. The propositions proven in
Section 5 and
Section 7 make the Theorem 1 more precise and constitute its proof. The Lie algebra contraction, in the limit
, and its relationship with the conformal Galilean algebra is briefly mentioned. This is summarised in
Table 3.
2. Local Conformal Invariance
Can one explain the form of the two-time scaling functions of the dle process in terms of a dynamical symmetry? To answer such a question, one must first formulate it more precisely.
Definition 2. The deterministic part of the Langevin Equation (1) is obtained when formally setting .
Our inspiration comes from Niederer’s treatment [
38] of the dynamical symmetries of the free diffusion equation. The resulting Lie algebra, called
Schrödinger algebra by physicists, was found by Lie (1882) [
39]. The corresponding continuous symmetries, however, were already known to Jacobi (1842/43) [
40]. For growing interfaces, the Langevin equation of the
ew class is the noisy diffusion equation. Hence its deterministic part, the free diffusion equation, is obviously Schrödinger-invariant. In this work, we seek dynamical symmetries of the deterministic part of the
dle process, that is, we look for dynamical symmetries of the non-local equation
, where the non-local Riesz-Feller derivative
will be defined below, in
Section 4.
Since we see from Equation (1), or the explicit correlators and responses (5), that the dynamical exponent
, conformal invariance appears as a natural candidate, where one spatial direction is re-labelled as ‘time’. However, one must sharpen the notion of conformal invariance. For notational simplicity, we now restrict to the case of
time-space dimensions, labelled by a ‘time coordinate’
t and a ‘space coordinate’
r. Our results on the dynamical symmetries of the
dle process, see Propositions 3 and 4, require us to present here a more flexible definition than given in [
21,
41].
Definition 3. (a) A set of meta-conformal transformations is a set of maps , which may depend analytically on several parameters and form a Lie group. The corresponding Lie algebra is isomorphic to the conformal algebra such that the maximal finite-dimensional Lie sub-algebra is semi-simple and contains at least a Lie algebra isomorphic to . A physical system is meta-conformally invariant if its n-point functions transform covariantly under meta-conformal transformations; (b) A set of ortho-conformal transformations is a set of meta-conformal transformations , such that (i) the maximal finite-dimensional Lie algebra is isomorphic to and that (ii) angles in the coordinate space of the points are kept invariant. A physical system is ortho-conformally invariant if its n-point functions transform covariantly under ortho-conformal transformations.
The names ortho- and meta-conformal are motivated by the greek prefixes
: right, standard and
: of secondary rank. Ortho-conformal transformations are usually simply called ‘conformal transformations’. We now recall simple examples to illustrate these definitions. See
Table 2 for a summary.
Example 3. In , ortho-conformal transformations are analytic or anti-analytic maps, or , of the complex variables , . The Lie algebra generators are and with . The conformal Lie algebra is a pair of commuting Virasoro algebras with vanishing central charge [42,43], viz. . In an ortho-conformally invariant physical system, the act on physical ‘quasi-primary’ [1] scaling operators and contain terms describing how these quasi-primary operators should transform, namelywhere are the conformal weights of the scaling operator ϕ. The scaling dimension is . Laplace’s equation is a simple example of an ortho-conformally invariant system, because of the commutator This shows that for a scaling operator ϕ with , the space of solutions of the Laplace equation is conformally invariant, since any solution ϕ is mapped onto another solution (or
) in the transformed coordinates. The maximal finite-dimensional sub-group is given by the projective conformal transformations with ; its Lie algebra is . Two-point functions of quasi-primary scaling operators read Their ortho-conformal covariance implies the projective Ward identities for [1]. For scalars, such that , this gives, up to the normalisation [44] Below, we often use the basis and , see also Table 2. Example 4. An example of meta-conformal transformations in reads [45]with . Herein, are the scaling dimension and the ‘rapidity’ of the scaling operator on which these generators act. The constant has the dimensions of a velocity. The Lie algebra is isomorphic to the conformal Lie algebra [46], see Table 2, where it is called meta-1 conformal invariance
. If , the generators (13) act as dynamical symmetries on the equation . This follows from the only non-vanishing commutators of the Lie algebra with , namely and . The formulation of the meta-1 conformal Ward identities does require some care, since already the two-point function turns out to be a non-analytic function of the time- and space-coordinates. It can be shown that the covariant two-point correlator is [41] Although both examples have
and isomorphic Lie algebras, the explicit two-point functions (12) and (14), as well as the invariant equations
, are different, see also
Table 2. That the form of two-point functions depends mainly on the representation and not so much on the Lie algebra, is not a phenomenon restricted to the conformal algebra. Similarly, for the so-called
Schrödinger algebra at least three distinct representations with different forms of the two-point function are known [
47].
The representation (13) can be extended to produce dynamical symmetries of the
Vlasov equation [
48].
Example 5. Taking the limit in the meta-conformal representation (13) produces the generatorsof the conformal Galilean algebra
(cga) in [49,50,51,52,53,54,55,56,57,58,59,60]. Its Lie algebra is obtained by standard contraction of the conformal Lie algebra, see Table 2. Hence the cga is not
a meta-conformal algebra, although . About cga-
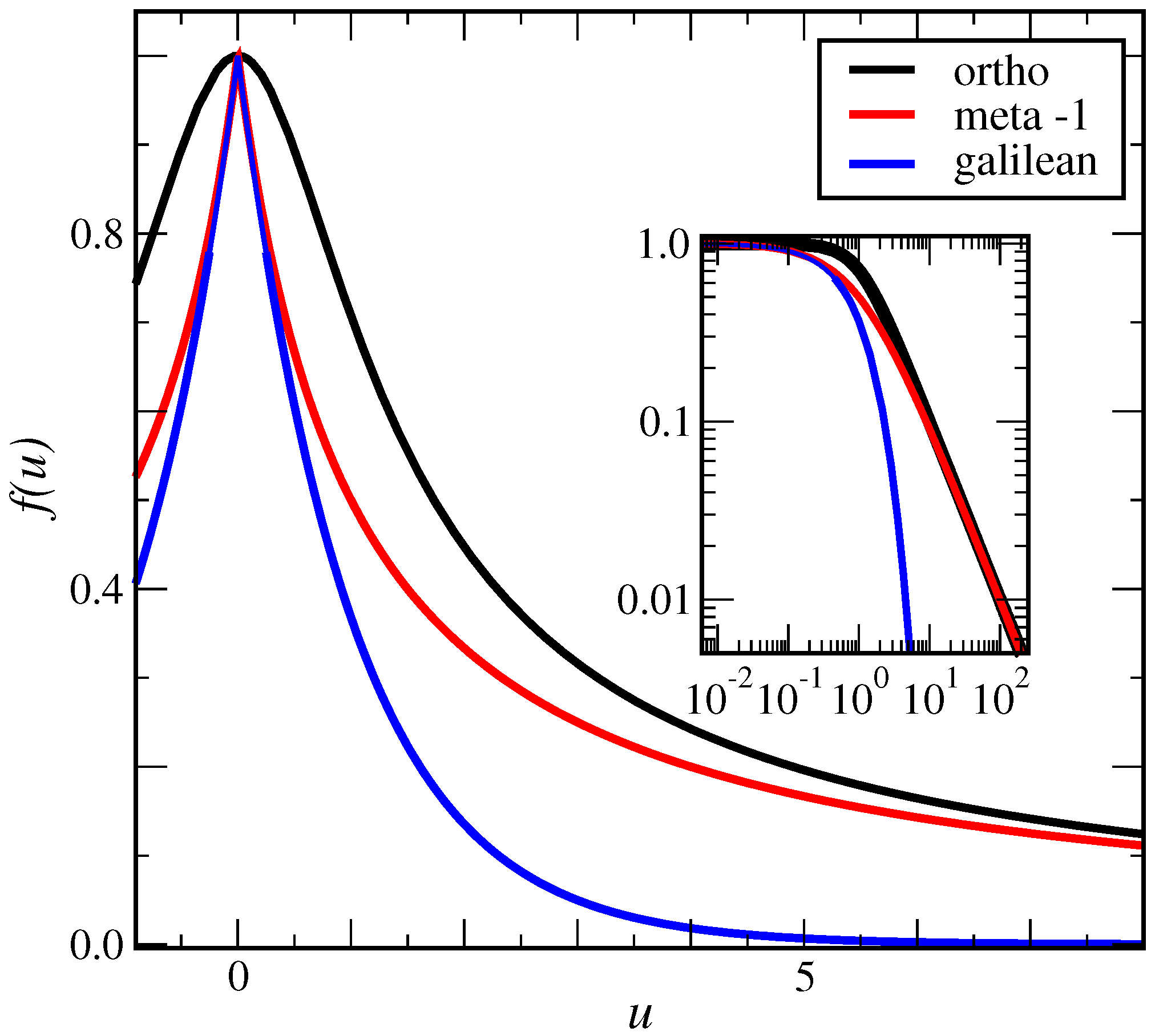
covariant equations, see [61]. The co-variant two-point correlator can either be obtained from the generators (15), using techniques similar to those applied in the above example of meta-conformal invariance [46,68], or else by letting in (14). Both approaches giveClearly, this form is different from both ortho- and meta-1-conformal invariance. The non-analyticity of the correlators (14), and especially (16), in general overlooked in the literature, is required in order to achieve for large time- or space-separations, viz. or .
All two-point functions (12), (14) and (16) have indeed the symmetries
and
, under permutation
of the two scaling operators, as physically required for a correlator. The shape of the scaling function of these three two-point function is compared in
Figure 3. In particular, the non-analyticity of the meta- and Galilean conformal invariance at
is clearly seen, in contrast to ortho-conformal invariance, while for
, the slow algebraic decay of ortho- and meta-conformal invariance is distinct from the exponential decay of conformal Galilean invariance. This illustrates the variety of possible forms already for
. Below, we shall find another form of (meta-)conformal invariance, different from all forms displayed in
Figure 3.
5. Non-Local Meta-Conformal Generators
The deterministic part of (1) becomes
, where
. Following earlier studies [
45], it seems physically reasonable that the Lie algebra of dynamical symmetries should at least contain the generators of time translations
, dilatations
and space translations
. It turns out, however, if one wishes to construct a generator of generalised Galilei transformations as a dynamical symmetry, the non-local generator
automatically arises, see below and ([
16], Chapter 5.3). It is still an open problem how to close these generators into a Lie algebra, for
and beyond the examples listed above in
Section 2.
This difficulty motivates us to start with the choice of a non-local spatial translation operator . Here indeed, a closed Lie algebra can be found.
Proposition 1. [21] Define the following generatorswhere the constants and , respectively, are the scaling dimension and rapidity of the scaling operator on which these generators act. The six generators (22) obey the commutation relations of a meta-conformal Lie algebra, isomorphic to Proposition 2. [21] The generators (22) obey the commutatorswith the operator and thus form a Lie algebra of meta-conformal dynamical symmetries (of the deterministic part) of the dle Langevin Equation (1), if only . The non-local generators
in (22) do not generate simple local changes of the coordinates
, in contrast to all examples of
Section 2. Finding a clear geometrical interpretation of the generators (22) remains an open problem.
This meta-conformal symmetry algebra can be considerably enlarged.
Proposition 3. Consider the generators (22) and furthermore defineThese generators are dynamical symmetries of the dle Langevin equation, since and they extend the meta-conformal Lie algebra (23) as follows Although generates local spatial translations, the transformations obtained from are non-local. In what follows, we write for the second, independent scaling dimension of φ.
Corollary 2. Define the generators , . Then the non-vanishing commutators of the Lie algebra (23) and (26) take the form The are dynamical symmetries of thedleprocess, since .
Corollary 3. Define the generators , . Then the non-vanishing commutators of the Lie algebra (27) are This Lie algebra of dynamical symmetries of the deterministic part of the dle Langevin Equation (1) is isomorphic to the direct sum .
In this last choice of basis, all generators contain non-local terms. Their form, in Corollary 3, is suggestive for the explicit construction of an infinite-dimensional extension of the above Lie algebra.
Proposition 4. Construct the generators, for all and constants Their non-vanishing commutators are given by (28), for . Their Lie algebra is isomorphic to the direct sum of three Virasoro algebras with vanishing central charges. They are also dynamic symmetries of the deterministic equation of dle process, provided that , because of the commutators Proof. For
, the generators (29) are those given above in (22) and (25), using
and rescaling
. One generalises the first identity (20) in the Corollary 1 to the following form, with
where
α is a constant. The assertions now follow by direct formal calculations, using (18) and (20). ☐
This is the
dle-analogue of the ortho- and meta-1 conformal invariances, respectively, of the Laplace equation and of simple ballistic transport, as treated in Examples 3 and 4. In
Table 3, it is called “meta-2 conformal”. It clearly appears that both local and non-local spatial translations are needed for realising the full dynamical symmetry of the
dle process, which we call
erosion-Virasoro algebra and denote by
. The infinite-dimensional Lie algebra
is built from
three commuting Virasoro algebras (obviously, the maximal finite-dimensional Lie sub-algebra is
). The scaling operators
on which these generators act are characterised by two independent
scaling dimensions and
. By analogy with conformal Galilean invariance [
76], one expects that three independent central charges of the Virasoro type should appear if the algebra (28) will be quantised. Additional physical constraints (e.g. unitarity) may reduce the number of independent central charges.
6. Ward Identities for Co-Variant Quasi-Primary n-Point Functions
A basic application of dynamic time-space symmetries is the derivation of co-variant
n-point functions. Adapting the corresponding definition from (ortho-)conformal invariance [
1], a scaling operator
is called
quasi-primary, if it transforms co-variantly under the action of the generators of the maximal finite-dimensional sub-algebra of
. A
primary scaling operator transforms co-variantly under the action of all generators of
. In this work, we consider examples of
n-point functions of quasi-primary scaling operators.
In the physical context of non-equilibrium dynamics, such
n-point functions can either be correlators, such as
, or response functions
, which can be formally rewritten as a correlator by using the formalism of Janssen-de Dominicis theory [
17] which defines the response operator
conjugate to the scaling operator
φ.
Proceeding in analogy with ortho-conformal and Schrödinger-invariance [
1,
16,
43,
44,
77], the quasi-primary
-Ward identities are obtained from the explicit form of the Lie algebra generators (22) and (25), generalised to
n-body generators. In order to do so, we assign a
signature to each scaling operator [
21]. We choose the convention that
for scaling operators
and
for response operators
. In order to prepare a later application to the conformal Galilean algebra, to be obtained from a Lie algebra contraction, we also multiply the generators
by the scale factor
μ. The
n-body generators then read
with the short-hands
,
and
. It can be checked that the generators (31) obey the meta-conformal Lie algebra of the
dle process. Define the
-point function
of quasi-primary scaling and response operators. Their co-variance is expressed through the quasi-primary Ward identities, for
The solution of this set of (linear) differential equations gives the sought -point function .
7. Co-Variant Two-Time Correlators and Responses
In order to illustrate the procedure outlined in section 6, we shall apply it to the two-point functions.
Proposition 5. Any two-point correlator , built from -quasi-primary scaling operators , vanishes.
Proof. Time-translation-invariance, expressed by
, implies that
, with
. Invariance under both non-local and local space-translations gives
. In Fourier space, this becomes
where the signatures are both positive, viz.
. The only solution is
. ☐
Recall that the dynamical symmetry of the
algebra is only a symmetry of the
deterministic part of the
dle Langevin equation (1), which corresponds to
. The vanishing of
is seen explicitly in the exact
dle-correlator (5a,6a), which indeed vanishes as
. This result of the
dle process is analogous to what is found for Schrödinger-invariant systems [
16,
77], where it follows from a Bargman superselection rule [
69]. Still, this does not mean that symmetry methods could only predict vanishing correlators. For example, in Schrödinger-invariant systems, correlators with
can be found from certain integrals of higher
n-point responses [
16,
70]. For a simple illustration in the noisy Edwards-Wilkinson equation, see [
78]. We conjecture that an analogous procedure might work for the
dle process and hope to return to this elsewhere.
We now concentrate on the two-time
response function . Time-translation-invariance, which imposes
, implies that
, with
. Invariance under non-local and local space-translations now give (in Fourier space)
since the signatures are now
. Here, a non-vanishing solution is possible and we can write
, with
.
Proposition 6. The -covariant two-point response function from (32) satisfies the scaling form , with the scaling variable . If the scaling function obeys the following two conditions, with the abbreviations and ,and the constraint holds true, then all quasi-primary Ward identities are satisfied. The conditions (34) come from the deterministic part of the
dle Langevin Equation (1) and do not contain
T. This is consistent with the
T-independence of the exact
dle-response function (5b) and (6b). A fuller justification, analogous to the derivation of the Bargman superselection rules of Schrödinger-invariance [
70,
77], is left as an open problem, for future work.
Proof. Denote by
and
(with
), the two scaling dimensions of the scaling operator
and of the response operator
, respectively. Time-translation-invariance and non-local and local space-translation-invariances produced the form
, with
,
and the signatures
. The other six Ward identities lead to the conditions, using (18)
Herein, Equation (35d) is obtained by using Equations (35a) and (35c), and Equations (35e) and (35f) are obtained by using (35b) and (35c). Actually, because of the identity
the condition
, Equation (35b), implies
, Equation (35c). Since
, see the Corrollary 1, the converse also holds true. Next, Equation (35d) can be simplified further: multiply Equation (35a) with
t and subtract it from (35d), which gives
Then multiply (35c) with
r and substract it from (36). This gives the condition
Similarly, simplify Equation (35e): multiply (35b) by
t and subtract from (35e), then multiply (36) by
μ and subtract as well. This gives
Unless
is a distribution, this gives the constraint
. Finally, Equation (35f) is simplified by multiplying first (35c) with
t and subtracting and then multiplying (35b) with
r and subtracting as well. This leads to
. Since in the proof of the Corollary 1, we have seen that
, this can be rewritten as follows:
. Taking the constraint into account, the last condition can be combined with (37) into the single equation
The form of F is now fixed by the three equations (35a,35b,38) and the constraint has to be obeyed.
Equation (35a) implies the scaling form
. Inserting this into (35b) produces, with the help of (18), the first of the Equations (34). Finally, inserting the scaling form for
F into (38) gives
. Since it is not immediately obvious if that condition is consistent with the first Equation (34), we rephrase it as follows: use the commutator
to write formally
. Then, apply
to the last condition on
derived from (38), in order to rewrite it as follows
and this equation is obeyed if the second Equation (34) holds true. We have found a sufficient set of conditions to satisfy all nine
dle-quasi-primary Ward identities for
. ☐
The two conditions in Equation (34) are compatible in two distinct cases:
- Case A:
. Then and is still possible.
- Case B:
. Then and .
We must also compare the differential operator with the dle Langevin Equation (1). Taking into account the normalisation in the definition of the Riesz-Feller derivative, we find . Physically, one should require in order that the correlators and responses vanish for large momenta .
Proposition 7. The -co-variant two-time response function has the form
where is assumed real, are normalisation constants and the convention is admitted. Proof. Both cases can be treated in the same way. The first Equation (34) becomes in Fourier space
In case A, the constant term vanishes, while it is non-zero in case B. The solution reads
where
is a normalisation constant and we can now adopt
. We also introduced the constant
ν from the
dle Langevin Equation (1) to illustrate that
for
large when
ν is positive. Both cases A and B produce valid solutions of the linear Equations (34). Therefore, the general solution should be a linear superposition of both cases. Carrying out the inverse Fourier transforms is straightforward. ☐
Remark 3. Propositions 4 and 7 contain the assertions in the Theorem 1, which are also listed in Table 3. Proposition 5 proves the statement in Remark 2. We had already mentioned in Section 1 (Remark 1), that if we restrict to case A and take and , the resulting two-time response , with and , reproduces the exact solution (6b). We stress that no choice of will make the ortho-conformal prediction (12) compatible with (6b). This is the main conceptual point of this work: The non-local representation (29) of the meta-conformal algebra is necessary to reproduce the correct scaling behaviour of the non-stationary response of the dle process.
The non-local meta-2 conformal invariance produces the response function , whereas all local ortho-, Galilean and meta-conformal invariances yielded a correlator .
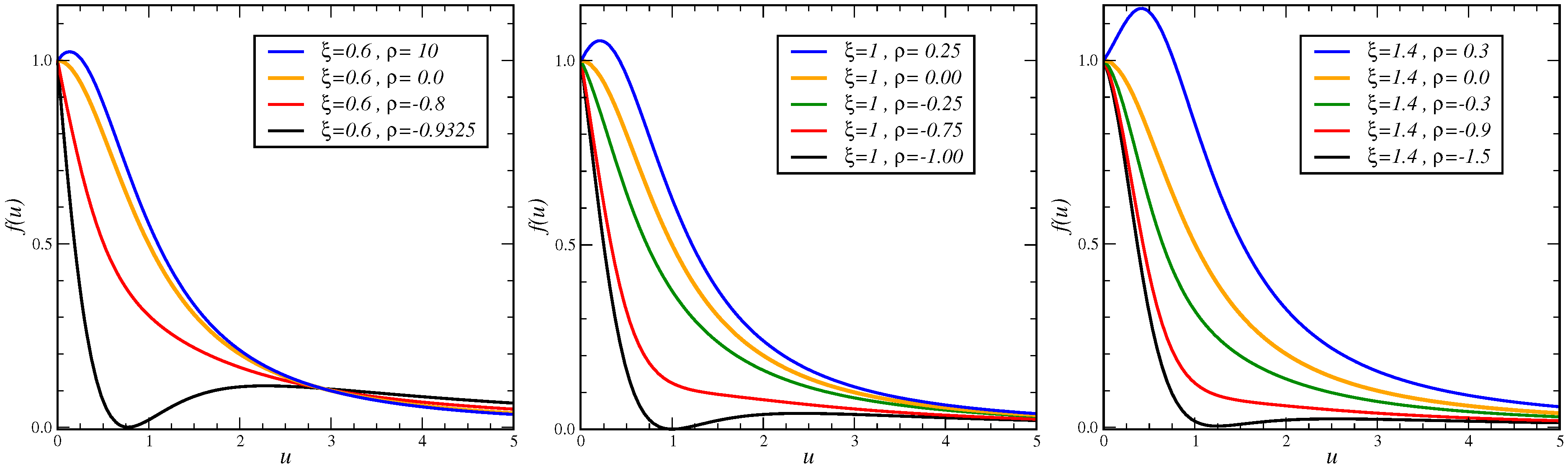
The main result (8) and (39) on the shape of the meta-2-conformal response can be cast into the scaling form
, with the explicit scaling function
We see that the first scaling dimensions
merely arrange the data collapse, while the form of the scaling functions only depends on the second scaling dimension
and the amplitude ratio
ρ (the exact solution (6b) of the
dle-process corresponds to
). The normalisation is chosen such that
. For
, we simply have
. In
Figure 4, several examples of the shape of
are shown. Clearly, these are quite distinct from all the examples of ortho-, meta-1- and Galilean-conformal invariance, displayed above in
Figure 3.
Remark 4. By analogy with Schrödinger-invariance, we conjecture that the fluctuation-dominated correlators should be obtained from certain time-space integrals of higher n-point responses [16,70]. Working with the quantum chain representation of the terrace-step-kink model, Karevski and Schütz have calculated the stationary two-point correlator of the densities, which in our terminology correspond to the slopes . They find [10]with the scaling variable , where is the global velocity of the interface, is a real parameter and are normalisation constants. The structure of their result is qualitatively very close to the form (8) and (39) for the two-time response of the -algebra, in the sense that it contains a dominant and monotonous term and a non-dominant and oscillatory one. Indeed, it can be checked that from the exact height-height correlator (5a) and (6a) this first term in (41) is recovered by computing the correlator of the densities . We interpret this as an encouraging signal that it should be possible to find the correlators from the as well, by drawing on the analogies with Schrödinger-invariance. The first step in this direction would be the derivation of an analogue of a Bargman superselection rule, which is work in progress. Remark 5. The consequences of the choice of the fractional derivative are difficult to appreciate in advance and largely remain a matter of try and error. Our choice of the Riesz-Feller derivative was suggested that in this way the Lie algebra becomes a dynamical symmetry of the dle process. In the past, we had also worked [16,45] with an extension of the Riemann-Liouville derivative by distributional terms [74]. For dynamical exponents , this leads to a strong oscillatory behaviour of the response functions which appears to be physically undesirable. We consider the success of the simple case study of the dle process treated here as suggestive for future investigations. Corollary 4. In the limit (or ) the Lie algebra can be contracted into the algebrawith and with the explicit generatorswhere is the signature and and are the scaling dimension and the rapidity of the scaling operator on which these generators act. The co-variant quasi-primary two-point correlator , whereas the co-variant quasi-primary two-point response is, with the normalisation constant The algebra (42), which one might call meta-conformal Galilean algebra, contains the conformal Galilean algebra as a sub-algebra, although the generators (43) are in general non-local, in contrast with those in Equation (15). However, the co-variant two-point function is here a response, and not a correlator.
Proof. In order to carry out the contraction on the generators (29), where
, we first change coordinates
, let
and rescale the generators
. Then the last commutator in (27) becomes
. Taking the limit
produces the generators (43) and the commutators (42) immediately follow. The Ward identities for the finite-dimensional sub-algebra are written down as before and
follows. For the response function, going again through the proof of the proposition 7 and recalling that
, we see that case A in (39) does not have a non-vanishing limit as
. For case B, consider the scaling form
, with the scaling function
written as
and
. If
, the first term
, and where
is a constant, to be absorbed into the overall normalisation. The second term vanishes, since
as
. On the other hand, if
, one divides
by
, and redefines the normalisation constant. Now, the second term produces
and the first one vanishes in the
limit. Both cases are combined into
. Alternatively, one derives from the Ward identities the two constraints
and
. Global dilation-invariance gives the scaling form
where the scaling function
must satisfy the equation
which leads to the asserted form, modulo a dualisation procedure, analogous to [
41,
46] to guarantee the boundedness for large separations. ☐
Our results on non-local meta-conformal algebras are summarised in
Table 3.