Abstract
A simplified Keller–Segel model is studied by means of Lie symmetry based approaches. It is shown that a (1 + 2)-dimensional Keller–Segel type system, together with the correctly-specified boundary and/or initial conditions, is invariant with respect to infinite-dimensional Lie algebras. A Lie symmetry classification of the Cauchy problem depending on the initial profile form is presented. The Lie symmetries obtained are used for reduction of the Cauchy problem to that of (1 + 1)-dimensional. Exact solutions of some (1 + 1)-dimensional problems are constructed. In particular, we have proved that the Cauchy problem for the (1 + 1)-dimensional simplified Keller–Segel system can be linearized and solved in an explicit form. Moreover, additional biologically motivated restrictions were established in order to obtain a unique solution. The Lie symmetry classification of the (1 + 2)-dimensional Neumann problem for the simplified Keller–Segel system is derived. Because Lie symmetry of boundary-value problems depends essentially on geometry of the domain, which the problem is formulated for, all realistic (from applicability point of view) domains were examined. Reduction of the the Neumann problem on a strip is derived using the symmetries obtained. As a result, an exact solution of a nonlinear two-dimensional Neumann problem on a finite interval was found.
Keywords:
Keywords; Lie symmetry; algebra of invariance; nonlinear boundary-value problem; Keller–Segel model; Cauchy problem; exact solution MSC:
35K5; 22E70
1. Introduction
Nonlinear partial differential equations describe various processes in society and nature. The well-known principle of linear superposition cannot be applied to generate new exact solutions to nonlinear partial differential equations (PDEs). Therefore, the classical methods for solving linear PDEs are not applicable for solving nonlinear PDEs. It means that finding exact solutions of most nonlinear PDEs generally requires new methods. Finding exact solutions that have a physical, chemical or biological interpretation is of fundamental importance. The most popular method for construction of exact solutions to nonlinear PDEs is the Lie method, which was created by Sophus Lie, the famous Norwegian mathematician, in 1880s–1890s and published in his papers and books. His most important work in this direction is [1] (see also [2]). Nowadays, the Lie symmetry method is widely applied to study partial differential equations (including multi-component systems of PDEs), notably for their reductions to ordinary differential equations (ODEs) and for constructing exact solutions. There are a huge number of papers and many excellent books [3,4,5,6,7] devoted to such applications.
In real world applications, mathematical models are typically based on PDEs with the relevant boundary and/or initial conditions. As a result, one needs to investigate boundary value problems (BVPs) and initial problems (Cauchy problems). In the case of nonlinear BVPs and initial problems, a fundamental difficulty arises in solving such problems using analytical methods. One may note that the Lie method has not been widely used for solving BVPs and initial problems. A natural reason follows from the following observation: the relevant boundary and initial conditions are usually not invariant under transformations, which are generated by Lie symmetry of the governing PDE. Nevertheless, there are some classes of BVPs that can be solved by means of the Lie symmetry algorithm. A brief history concerning first attempts to apply Lie symmetries for solving BVPs are discussed in the recent papers [8,9,10,11] and the relevant papers cited therein.
In this work, we continue study of a simplified (1+2)-dimensional Keller–Segel model, initiated in the first part of this work [12]. This model is a particular case of the classical Keller–Segel model [13,14] used for modeling a wide range of processes in biology, ecology, medicine, etc. The basic equations of the simplified Keller–Segel model that we are interested in have the form (see more details about these equations in [15,16,17,18]):
where unknown functions and describe the densities of cells (species) and chemicals, respectively; t and x denote the time and space variables; the parameters and β are non-negative constants, (otherwise, the model loses its biological meaning) and the operators , . We start from the nonlinear System (1) supplied by initial profiles for unknown functions, i.e. the Cauchy problem, and continue by examination of System (1) with Neumann boundary conditions (including zero flux conditions as an important particular case).
The paper is organized as follows. In Section 2, the Lie symmetry classification of the Cauchy problem for a simplified Keller–Segel (SKS) system is derived. In Section 3, the exact solutions of the (1 + 1) and (1 + 2)-dimensional Cauchy problems were constructed including a nontrivial example of the exact solution for the correctly-specified initial profiles. In Section 4, Lie symmetry of BVPs with the Neumann boundary conditions is studied. Because Lie symmetry of BVPs essentially depends on geometry of the domain, which the problem is formulated on, all realistic (from applicability point of view) domains were examined. In Section 5, a Lie symmetry operator was used in order to reduce the (1 + 2)-dimensional Neumann problem for SKS and to construct the exact solution of the corresponding (1 + 1)-dimensional Neumann problem. The results obtained are summarized in the Conclusions section.
2. Lie Symmetry of the Cauchy Problem
It was shown in [12] that the SKS System (1) can be further simplified provided . In this case, one may reduce SKS System (1) to the form:
Of course, the system derived is still nonlinear; however, one admits infinite-dimensional Lie algebra of invariance generated by the operators [12]:
where , and are arbitrary smooth functions.
Now, we consider the Cauchy problem for the nonlinear System (2), which can be formulated as follows:
where is an arbitrary smooth function. In the most general case, this function may depend also on the variable y; however, here we restricted ourselves in this case, in order to avoid cumbersome calculations. To guarantee existence of a classical solution of the Cauchy Problem (4), the initial profile for the component ρ should be specified as above.
Obviously, the Lie algebra (3) cannot be maximal algebra of invariance (MAI) of the Cauchy Problem (4) for the arbitrary given Function . To determine which of the operators listed in (3) are Lie symmetry operators of the Cauchy problem in question, we use the well-known criteria [4]. According to the criteria, one should examine whether initial conditions from Equation (4) are invariant under the operator in question. In order to check this for all the operators listed in Equation (3), we take their linear combination (hereafter, are arbitrary parameters):
Applying operator X to the manifold generated by the initial conditions, one arrives at the restriction and two equations:
Because Equation (8) is a differential consequence of (7), we need to analyze (7) only. Obviously, the restriction means (6) that the Cauchy problem is not invariant w.r.t. time translation.
Equation (7) implies certain limitations on the function . This function can only be arbitrary when both sides of equation vanish. When the multiplier on the left-hand-side is non-zero, then one obtains a linear ordinary differential equation (ODE) to find . This ODE has been solved depending on the values of the parameters . As a result, four different profiles for the function were derived. One of them, namely, (this function springs up if ), was exempted from the further examination because the function possesses singularity. The other three cases are presented in Table 1 together with the relevant MAIs.
Theorem 1.

All possible MAIs of the (1+2)-dimensional Cauchy Problem (4), depending on the form of initial profiles (up to translations w.r.t. the space variable x), are presented in Table 1.

Table 1.
maximal algebra of invariances (MAIs) of the Cauchy Problem (4).
Remark 1.
Because and contain arbitrary functions on time (see Formulae (3)), one notes corresponding restrictions on these functions in Table 1, which reduce their arbitrariness. For instance, MAI in case 4 differs from that in case 1 because there is only a single restriction on the function , while there are two restrictions on in case 1.
3. Application of Lie Symmetry for Constructing Exact Solutions of Cauchy Problems
The Cauchy Problem (4) can be reduced to a set of (1 + 1)-dimensional ones by using the Lie symmetry operators. Nowadays, it is a standard routine in the case of application of symmetry operators to PDEs in the case of Lie algebras of low dimensionality. In the case of BVPs with a wide Lie symmetry, classification of inequivalent subalgebras of MAI and its application for reducing can be highly nontrivial (see examples in [8]). One notes that all MAIs listed in Table 1 are infinite-dimensional, hence here we restrict ourselves on the operator from case 1 of Table 1.
Because the operator contains an arbitrary function with the property , we consider two cases, namely: (i) i.e., , and (ii) is an arbitrary non-constant function.
3.1. Exact Solutions of the (1 + 1)-Dimensional Cauchy Problem
In case (i), one easily construct the ansatz:
Substituting ansatz (9) into Equation (4), the (1 + 1)-dimensional Cauchy problem,
is obtained. Thus, the same problem is derived, however, in the case of a single spacial variable. Let us reduce the governing system to a single equation, extracting from the second equation of Equation (10) and substituting it into the first. Hence, the 4th order differential equation:
is obtained, which is equivalent to the 3rd order equation:
where is an arbitrary function. The obvious substitution:
transforms the last equation to the nonlinear 2nd order equation:
The Burgers equation is linearizable via the famous Cole–Hopf substitution [19,20]:
to the linear heat equation:
All the substitutions mentioned above could be combined as follows:
It should be stressed that the Substitution (13) reduces the nonlinear Cauchy Problem (10) to the linear problem for the heat Equation (12), which can be exactly solved. In fact, having the specified initial profiles in (10), we find the initial condition for Equation (12) as follows:
i.e.,
Thus, calculating the derivatives and , and using Substitution (13), one can construct the solution of the Cauchy Problem (10):
Because the Cole–Hopf substitution in non-local transform (i.e., involves derivatives), we need to examine the behavior of the solution as :
Hence, having chosen the function with the property , we obtain , i.e., the function is continuous at .
In order to prove that , one needs to show that and . The proof of the first equality can be found in [19]. We have proved that under the restriction (here, the relevant calculations are omitted). Thus, the following statement can be formulated.
Theorem 2.
The classical solution of the Cauchy Problem (10), in the case when is differentiable twice and can be presented as:
where
Obviously, the exact Solution (16) is not unique because one contains two arbitrary functions and . To specify these functions, one needs additional biologically motivated restrictions. We remind the reader that function describing the density of chemicals should be bounded in space. Therefore, functions must vanish (in this case, function , which depends on , also vanishes). In order to specify both functions and one needs, for example, to assume that the quantity of the chemical is finite in space and time, i.e., for . This assumption immediately leads to the unique solution of Cauchy Problem (10) in the form:
In order to present a non-trivial exact Solution of (10) in terms of elementary functions, we consider the initial profiles:
where γ is an arbitrary constant.
Using Formula (17), one obtains:
To calculate the integral , the Mellin transformation (see, e.g., [21]) has been used:
Here, is a parabolic cylinder function. Using the known properties of such functions, the integral in question can be explicitly calculated:
Now, we find the function:
Because , one also finds the function . Thus, the exact solution of the Cauchy Problems (10) and (18) has the form:
Plots of this solution with are presented in Figure 1 and Figure 2. Both functions, and , have attractive properties. For example, they are periodic, bounded and tend to some constants if . However, one notes that the function , which usually describes the densities of cells or species (see Introduction), are not non-negative for . It turns out that this unrealistic behavior (for real world applications) is a natural property of each non-constant solution of the (1 + 1)-dimensional Cauchy Problem (10) with an arbitrary non-negative function .
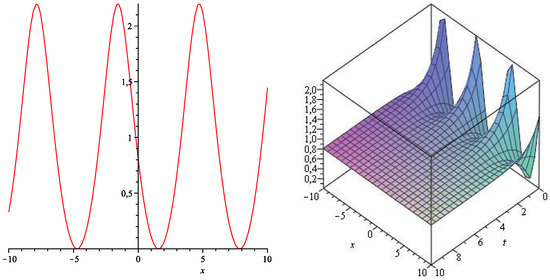
Figure 1.
Plots of the functions and using Formulae (19) with .
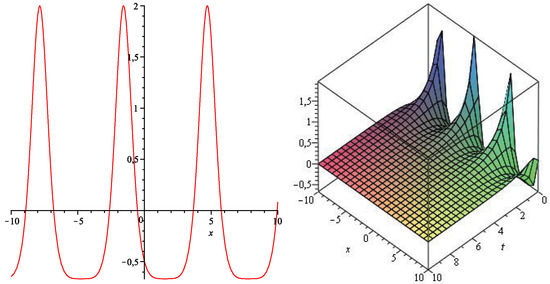
Figure 2.
Plots of the functions and using Formulae (19) with .
Let us show this assuming that there is a Solution of (10) with a non-negative function , such that the functions and are non-negative for . Let us fix an arbitrary . Because , the second derivative is non-positive for all x. It means the continues function is convex upwards for all x (otherwise, one is a constant). Now, one realizes that any function with such property (like , , etc.) cannot be non-negative for all x.
3.2. Reduction and Exact Solutions of (1 + 2)-Dimensional Cauchy Problem
Now, we apply the operator with an arbitrary non-constant function . In order to reduce System (4), we need to construct an ansatz by solving the corresponding system of characteristic equations for this operator. After rather standard calculations, the ansatz:
is obtained. Ansatz (20) reduces Cauchy Problem (4) to the (1 + 1)-dimensional Cauchy problem:
The function can be easily found by using the second equation:
Substituting this expression into the first Equation of (21), one arrives at the fourth order partial differential equation:
which can be integrated twice w.r.t. the variable x. Thus, the second order nonlinear equation:
is obtained ( and are arbitrary smooth functions).
In contrast to the nonlinear Equation (11), we were unable to linearize Equation (22) (we remind the reader that ). To find particular solutions, we used a non-Lie ansatz (see [22] for an example):
in order to reduce the partial differential Equation (22) to a system of ODEs. In fact, Substituting (23) into Equation (22), the system of three ODEs:
is obtained to find unknown functions and . Because System (24) has the same structure as (38) [22], one is integrable. In fact, the first equation can be solved for arbitrary function . By substituting the known function into the second equation, one obtains the first order linear ODE to find the function . Finally, having the known functions and , the third equation of System (24) can be easily solved. As a result, the general Solution of (24) has the form:
Taking into account that and are arbitrary smooth functions, we may simplify the general Solution (25) to the form:
by introducing new notations and , which are arbitrary smooth functions, while is an arbitrary parameter.
Thus, using Equations (20), (23) and (26), we construct the exact solution:
of Cauchy Problem (4) with the correctly-specified initial profile .
Obviously, this solution blows up for the finite time , which makes its immediate biological interpretation unlikely. On the other hand, it is in agreement with [18] (see also the references cited therein) because the global solution of this problem requires the constraint , which does not take place for . Notably, blow-up solutions occur in some physical models, and they have been intensively studied since the 1980s (see, e.g., [23] and references therein).
4. Lie Symmetry of the Neumann Problems
In this section, we study Lie symmetry of BVPs with the Neumann boundary conditions. Because the result depends essentially on geometry of the domain Ω, where BVP in question is defined, one needs to examine different cases. In [12], the simplest case, when Ω is a half-plane, was under study. In principle, Ω can be an arbitrary (bounded or unbounded) domain with smooth boundaries. However, it was established in [10] that geometry of Ω is predicted by the Lie symmetry of the governing equations of BVP in question. In particular, all possible domains were established if the projection of MAI of the governing equations on the space gives the Lie algebra with the basic operators:
Now, one notes that such projection of MAI (3) is exactly the Lie algebra (28) (the projections of and are the operators and , which are equivalent to X and Y because the time variable is now a parameter). It means that all generic domains leading to non-trivial Lie symmetry of any Neumann problem for the SKS System (2) are already known [10]. Here, we consider the most important (from an applicability point of view) of them, and the first one is a strip.
4.1. Neumann Problem on the Strip
The Neumann problem on the strip can be formulated as follows:
where and are arbitrary smooth functions. We note that BVP on an arbitrary strip can be reduced to BVP (29) by the translation and scaling transformation w.r.t. the variable y.
In contrast to the previous problem, BVP (29) does not involve boundary conditions at infinity; hence, the standard definition of invariance can be applied in order to find Lie symmetry of Problem (29). Let us apply the operator X (5) to the manifolds , , :
A simple analysis of the conditions obtained above immediately leads to . Now, one needs to apply the first prolongation to the manifolds , , and . Taking into account the restrictions , one may easily check that the expressions:
are fulfilled automatically. Thus, there are no any restrictions on the functions and . Finally, we apply operator X with to the initial profiles:
One notes that the second equation in these formulae is a differential consequence of the first. Thus, we need solve only the equation:
Obviously, it is the linear ODE for the function (variable y should be treated as a parameter). A simple analysis of Equation (30) leads two different cases, and . As a result, the following statement can be formulated.
Theorem 3.
MAI of the Neumann Problem (29) does not depend on the form of the functions and . If the initial profile is an arbitrary smooth function, then MAI is the infinite-dimensional Lie algebra generated by the operators:
with and . In the case,
where is an arbitrary smooth function, this algebra is extended by operators of the form:
with .
There are no other initial profiles , leading to extensions of the Lie algebra (31).
It is worth noting that Lie symmetry of the Neumann problem on the strip (29) is essentially different than one for the same problem on the half-plane. In particular, there is no any dependence on the form of flux (i.e., the functions and ) in contrast to case of the half-plane (see Theorem 2 in [12]).
4.2. Neumann Problem on Interior/Exterior of a Circle
Now, we turn to the case of a bounded domain. As it was pointed out in [10], the interior of the circle is the simplest case of such domain, which may occur for the system in question. It should be noted that the circle interior is a two-dimensional analog of the ball in the 3D space. On the other hand, the ball is a typical approximation of the domains arising in biomedical applications (for instance, when the Keller–Segel model is applied for tumour growth).
The Neumann problem in Ω can be formulated as follows:
where and are again arbitrary smooth functions, while is the outer normal to the boundary (the circus of the radius R) of the domain. Now, we formulate the theorem presenting the Lie symmetry classification of this BVP.
Theorem 4.
MAI of the Neumann Problem (33) does not depend on the form of the functions and . If the initial profile is an arbitrary smooth function, then MAI is the infinite-dimensional Lie algebra generated by the operator with .
In the case:
this algebra is extended by operator of the form:
where ψ and h are arbitrary smooth functions of their arguments, the function h additionally satisfies the condition with a fixed constant .
There are no other initial profiles leading to extensions of the above Lie algebras.
The proof of the theorem is similar to that of Theorem 3 and is based on applying the invariance criteria to the operator X (5). It is worth noting that the relevant calculations can be essentially simplified if one applies the polar coordinates instead of the Cartesian of those . In particular, one may see that Formula (34) is much simpler in the polar coordinates, and the operator takes the form .
Another possible bounded domain is the annulus only [10]. In the case of the annulus, the corresponding Neumann problem has the form (33) with the additional boundary conditions:
and being arbitrary smooth functions. It turns out that the result of the Lie symmetry classification for such BVP will be the same as presented in Theorem 4.
Finally, the case of the domain, which is the interior of the circle , is also interesting. The Neumann Problem (33) in such domain should be supplied by the boundary conditions at infinity. Typically, they have the form:
i.e., zero-flux at infinity. In order to establish Lie symmetry of the nonlinear BVPs (33) and (37), one needs to examine separately the boundary Conditions (37). Because Formula (37) presents conditions at infinity, we cannot apply the standard invariance criteria [3]; however, we may use Definition 2 [10]. In fact, applying the transformation:
to Equation (37) in the polar coordinates, one may easily calculate that the manifold , corresponding to Equation (37) is mapped into . At the final step, one checks invariance of the manifold w.r.t. the operators and Equation (35), taking into account transformation (38).
5. Exact Solutions of the Neumann Problem
This section is devoted to the application of the Lie symmetry operators obtained in the previous section in order to reduce BVP (29) to BVPs of lower dimensionality and to find exact solutions.
Let us consider the case of the specified initial profile from Theorem 3:
and apply operator (32). This operator generates ansatz:
which reduces BVP (29) to the (1 + 1)-dimensional BVP:
This (1 + 1)-dimensional BVP is still nonlinear, and it is a difficult task to construct its exact solution in an explicit form. We are interested in the special case when (then, automatically, ), when Problem (40) is nothing else but the (1 + 1)-dimensional case of BVP (29), i.e., the Neumann problem on the interval for the simplified Keller–Segel system.
Nevertheless, the corresponding BVP can be solved for arbitrary smooth functions , , and we take , in order to avoid cumbersome formulae. In this case, the nonlinear Problem (40) takes the form:
First of all, we reduce System (41) to the 3rd order PDE in a similar way as it was done in Section 3; hence, we arrive at:
Setting , one notes that it is the Burgers equation w.r.t. the function . Thus, using the celebrated Cole–Hopf Substitution [20]:
and taking into account the Conditions (42), one obtains the Neumann problem for heat equation:
where . We will use Fourier method to solve Problems (44) and (45).
Let , by substituting it into (44), we obtain:
Now, we can calculate the general solution for Equations (44) and (45):
where are the roots of Equation (46) and:
for . Thus, using Substitution (43) and the second equation from (41), one constructs the exact solution of the nonlinear BVPs (41) and (42):
where is an arbitrary function.
Because the Cole–Hopf substitution in non-local transform (i.e., involves derivatives) we need to check whether this solution satisfies the initial and boundary conditions. Setting , we note that:
Therefore, provided . Simple calculations show that the second initial condition is also fulfilled.
It can be easily checked that the functions and constructed above also satisfy zero Neumann conditions from Equation (42).
Finally, our result can be formulated as the following theorem.
Theorem 5.
Obviously, the exact Solution (48) is not unique because one contains the arbitrary function and a parameter C. To specify this function, one needs additional biologically motivated restrictions; however, it lies outside of the scope of this paper.
6. Conclusions
In this paper, the simplified Keller–Segel model has been studied by means of Lie symmetry based approaches. It is shown that (1 + 2)-dimensional Keller–Segel type System (2), together with the relevant boundary and initial conditions, is invariant with respect to infinite-dimensional Lie algebras. A classification of Lie symmetries for the Cauchy problem and the Neumann problem for this system is derived and presented in Theorems 1, 3 and 4, which say that the Cauchy (initial) problem and some Neumann problems for this system are still invariant w.r.t. infinite-dimensional Lie algebras (with the relevant restrictions on the structure of arbitrary functions arising in Equation (3)). It should be stressed that Lie symmetry of a boundary-value problem depends essentially on geometry of the domain, which the problem is formulated on. All possible domains, which may lead to nontrivial Lie symmetry of BVPs with the governing System (2), have been identified using the result of the recent paper [10]. All realistic from applicability point of view domains (a strip, an interior and exterior of the circle, an annulus) were examined (the case of a half-plane was studied earlier in [12]).
The results obtained, in particular infinite-dimensional Lie algebras of invariance, seem to be very interesting because initial and boundary-value problems usually demonstrate a full scale breaking Lie symmetry of the governing equation(s). For example, the classical example of the Cauchy problem for the linear heat equation says that this problem can be invariant only w.r.t. finite-dimensional Lie algebra [3]. Finite-dimensional Lie algebras of invariance occur also for boundary-value problems involving the linear heat equation [3,24] and nonlinear heat equations [8,9]. However, one cannot claim that the result obtained here is unique because infinite-dimensional Lie algebras of invariance may occur for BVPs with the governing equation(s) possessing infinite-dimensional MAI. A non-trivial example can be found in [10] (see case 11 in Table 2).
The Lie symmetries obtained are used for reduction of the problems in question to two-dimensional those. Exact solutions of some two-dimensional problems are constructed. In particular, we have proven that the Cauchy problem for the (1 + 1)-dimensional Keller–Segel type system can be linearized and solved in an explicit form (see Theorem 2). Because the exact solution involves two arbitrary functions, the relevant biologically motivated restrictions were proposed in order to obtain a unique solution. A non-trivial example of the solution in terms of elementary functions was also derived (see Formulae (19)). It should be stressed that exact solutions of Cauchy problems with nonlinear governing PDEs can be derived only in exceptional cases because there are no constructive methods for solving such nonlinear problems (in contrast to linear Cauchy problems).
Symmetry operators were applied also for reduction of the Neumann problems on the strip. As a result, the exact solution of the Neumann problem for the (1 + 1)-dimensional simplified Keller–Segel system has been constructed (see Theorem 5). The work is in progress for finding exact solutions of the Neumann problem on bounded domains.
Acknowledgments
This research was supported by a Marie Curie International Incoming Fellowship to the first author within the 7th European Community Framework Programme (Project BVP symmetry 912563).
Author Contributions
The authors contributed equally to this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lie, S. Uber integration durch bestimmte integrale von einer Klasse lineare partiellen differentialgleichungen. Arch. Math. 1881, 8, 328–368. [Google Scholar]
- Engel, F.; Heegaard, P. Gesammelte Abhandlungen, Band 3; Benedictus Gotthelf Teubner: Leipzig, Germany, 1922. [Google Scholar]
- Bluman, G.W.; Anco, S.C. Symmetry and Integration Methods for Differential Equations; Springer: New York, NY, USA, 2002. [Google Scholar]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations; Springer: Berlin, Germany, 1989. [Google Scholar]
- Fushchych, W.I.; Shtelen, W.M.; Serov, M.I. Symmetry Analysis and Exact Solutions of Equations of Nonlinear Mathematical Physics; Kluwer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Ovsiannikov, L.V. The Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Cherniha, R.; Kovalenko, S. Lie symmetries and reductions of multi-dimensional boundary value problems of the Stefan type. J. Phys. A Math. Theor. 2011, 44. [Google Scholar] [CrossRef]
- Cherniha, R.; Kovalenko, S. Lie symmetries of nonlinear boundary value problems. Commun. Nonlinear Sci. Numer. Simulat. 2012, 17, 71–84. [Google Scholar] [CrossRef]
- Cherniha, R.; King, J.R. Lie and conditional symmetries of a class of nonlinear (1 + 2)-dimensional boundary value problems. Symmetry 2015, 7, 1410–1435. [Google Scholar] [CrossRef]
- Abd-el Malek, M.B.; Amin, A.M. Lie group method for solving the generalized Burgers’, Burgers’-KdV and KdV equations with time-dependent variable coefficients. Symmetry 2015, 7, 1816–1830. [Google Scholar] [CrossRef]
- Didovych, M. A (1 + 2)-dimensional simplified Keller–Segel model: Lie symmetry and exact solutions. Symmetry 2015, 7, 1463–1474. [Google Scholar] [CrossRef]
- Keller, E.K.; Segel, L.A. Initiation of slime mold aggregation viewed as an instability. J. Theor. Biol. 1970, 26, 399–415. [Google Scholar] [CrossRef]
- Keller, E.K.; Segel, L.A. Traveling bands of chemotactic bacteria: A theoretical analysis. J. Theor. Biol. 1971, 30, 235–248. [Google Scholar] [CrossRef]
- Horstmann, D. From 1970 until present: The Keller–Segel model in chemotaxis and its consequences. Jahresber. Deutsch. Math.-Verein 2013, 105, 103–165. [Google Scholar]
- Calvez, V.; Dolak-Strub, Y. Asymptotic behavior of a two-dimensional Keller–Segel model with and without density control. Math. Model. Biol. Syst. 2007, 2, 323–329. [Google Scholar]
- Nagai, T. Convergence to self-similar solutions for a parabolic-elliptic system of drift-diffusion type in R2. Adv. Differ. Equ. 2011, 9, 839–866. [Google Scholar]
- Nagai, T. Global existence and decay estimates of solutions to a parabolic-elliptic system of drift-diffusion type in R2. Differ. Integral Equ. 2011, 1, 29–68. [Google Scholar]
- Hopf, E. The partial differential equation Ut + UUx = μUxx. Comm. Pure Appl. Math. 1950, 3, 201–230. [Google Scholar] [CrossRef]
- Burgers, J.M. The Nonlinear Diffusion Equation; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1973. [Google Scholar]
- Bateman, H.; Erdelyi, A. Tables of Integral Transforms; McGraw-Hill Book Company: New York, NY, USA, 1954. [Google Scholar]
- Cherniha, R. New non-Lie ansatze and exact solutions of nonlinear reaction-diffusion-convection equations. J. Phys. A Math. 1998, 31, 8179–8198. [Google Scholar] [CrossRef]
- Samarskii, A.A.; Galaktionov, V.A.; Kurdyumov, S.P.; Mikhailov, A.P. Blow-up in quasilinear parabolic equations. In de Gruyter Expositions in Mathematics; Walter de Gruyter & Co.: Berlin, Germany, 1995; Volume 19. [Google Scholar]
- Bluman, G.W. Application of the general similarity solution of the heat equation to boundary value problems. Q. Appl. Math. 1974, 31, 403–415. [Google Scholar] [CrossRef]
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).