Abstract
Optics has proved a fertile ground for the experimental simulation of quantum mechanics. Most recently, optical realizations of -symmetric quantum mechanics have been shown, both theoretically and experimentally, opening the door to international efforts aiming at the design of practical optical devices exploiting this symmetry. Here, we focus on the optical -symmetric dimer, a two-waveguide coupler where the materials show symmetric effective gain and loss, and provide a review of the linear and nonlinear optical realizations from a symmetry-based point of view. We go beyond a simple review of the literature and show that the dimer is just the smallest of a class of planar N-waveguide couplers that are the optical realization of the Lorentz group in 2 + 1 dimensions. Furthermore, we provide a formulation to describe light propagation through waveguide couplers described by non-Hermitian mode coupling matrices based on a non-Hermitian generalization of the Ehrenfest theorem.
1. Introduction
The desire to create an optical directional coupler, a device composed of parallel optical waveguides close enough that leaked energy is transferred between them, led to the exploration of waveguide creation in semi-conductors via proton bombardment [1]. At the time, power losses played an interesting role, and the nascent mode coupling theory [2] allowed the theoretical description of linear loses in such devices [3],
where the real numbers α and K are the effective linear loss, identical in all implanted waveguides, and the effective waveguide coupling strength, also identical for the whole system, in that order. This, to the best of our knowledge, was the first theoretical description of an experimental N-waveguide coupler including losses in the form of a Schrödinger-like equation involving a non-Hermitian Hamiltonian. Almost twenty years later, the desire to create an intensity-dependent switch working at low power levels took another team of researchers to explore twin core nonlinear couplers with gain and loss. Again, coupled mode theory allowed the description of such devices [4],
where we have kept the notation used before and introduce the effective real part of the refractive index, , and the real function that describes an effective Kerr nonlinearity-induced change in the refractive index of the j-th core, positive for self-focusing and negative for self-defocusing materials. At this point in history, there existed experimental and theoretical work describing an optical dimer where the waveguides present effective loss and gain and a nonlinearity, but a little something was missing. A couple of years later, a theory exploring a particular type of non-Hermitian Hamiltonians with real spectra was brought forward in quantum mechanics [5]. These Hamiltonians were invariant under space-time reflection, received the name of -symmetric and opened new avenues of research in quantum mechanics, as well as other areas of physics and mathematics, cf. [6,7] and the references therein.
In optics, it took a few years more to propose two seminal ideas. The first one regarded single elements and showed, in particular, that an optical planar slab waveguide composed of two media with linear gain and loss can be described by a Schrödinger-like equation under dynamics dictated by a -symmetric Hamiltonian, where the optical refractive index played the role of quantum-like potential and propagation distance that of time [8]. The second one dealt with composite systems, where a mature mode coupling theory produced a theory of coupled optical -symmetric structures [9]. In the ten years following those first proposals for an optical realization of -symmetry, work has been reported on slab waveguides [10,11], Bragg scatterers [12,13,14,15,16,17], as well as linear [18,19,20,21,22,23,24,25,26] and nonlinear [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45] coupled waveguides, to mention just a few. Research in this field is slowly getting to information technologies applications with recent proposals of all-optical -symmetric logic gates [46] and amplitude-to-phase converters [47].
Here, we will provide a review of the optical -symmetric dimer. First, in Section 2, we will introduce a two-waveguide coupler where component waveguides show effective complex refractive indices with an identical real part. Starting from this device, we will recover the effective mode coupling differential equation set for the linear -symmetric dimer, which describes a nonunitary optical device showing symmetric effective loss and gain feasible for passive and active optical realizations. Then, we will recover the dispersion relation for the dimer that shows three regimes, one with real eigenvalues, the -symmetric regime, another with fully-degenerate eigenvalues equal to zero, the fully-degenerate regime, and a third one with purely imaginary eigenvalues, the broken symmetry regime. We will construct an analytic propagator that will show asymmetric amplifying oscillator, power amplification and exponential amplification behaviors in each of these regimes. We will also show that it is possible to uncouple the mode coupling differential equation set of the -symmetric dimer. The resulting second order differential equations and boundary conditions for the field amplitudes propagating through each waveguides take the form of nonlocal oscillators with positive potential, a free particle traveling through a nonlocal medium and nonlocal oscillators with inverted potential, in each of the regimes. In the final part of Section 2, we will bring forward the renormalized field approach that helps us cast the linear -symmetric dimer as a nonlinear dimer with imaginary Kerr nonlinearity, either in a self- or a cross-modulation scheme, and allowing us to realize an asymptotic behavior that depends just on the gain to coupling strength ratio of the device. In Section 3, we will discuss the linear -symmetric dimer when both waveguides show the same effective self-focusing Kerr nonlinearity. We will show the stable nonlinear modes of the device, discuss its dynamics in terms of the passive Kerr two-waveguide coupler that allows for coherent and localized oscillations between the waveguide field modes and show that the inclusion of symmetric gain and loss breaks these dynamics, producing localization in the gain waveguide without showing an asymptotic behavior. In Section 4, we will extend the linear -symmetric dimer to planar N-waveguide couplers using finite dimensional matrix representations of a complexified version of . We have previously shown [48] that the -symmetric dimer and its extensions to planar N-waveguide couplers possess an symmetry realized in a finite dimensional non-unitary irreducible representation. This representation is accomplished through complexification of , , and it allows us to provide the dispersion relation and a closed form analytic propagator, which have the same regimes and dynamics found for the dimer. We will show that the renormalized field approach provides us with an asymptotic behavior that is independent of the initial field distribution and depends just on the waveguide number and the effective gain to coupling ratio. Then, in Section 5, we will introduce a modified version of the Ehrenfest theorem suitable for non-Hermitian Hamiltonians and show how it can help us define the dynamics of an -dimensional generalized Stokes vector for the planar N-waveguide couplers discussed in Section 4. In Section 6, we will go back to the dimer, but consider the propagation of quantum fields. In the quantum regime, spontaneous generation and absorption of electromagnetic radiation should be considered when using media with linear gain or loss. We will show the solution for the quantum linear -symmetric dimer and discuss the generation of light from a vacuum due to spontaneous processes in the absence of fields impinging at the device. Finally, we will produce a brief summary and discuss future avenues regarding non-Hermitian optical systems.
2. Linear -Symmetric Dimer
A two-waveguide coupler can be described by the following differential equation system via mode coupling theory,
where the complex numbers are the field amplitudes at each waveguide, the parameters and g, which in the most general case can be complex, are the effective refractive indices and waveguide coupling (the latter will be assumed real from now on, in that order) and the operator stands for the derivative with respect to the propagation distance z. Note that using field amplitudes of the form:
with , reduces the system to an effective mode coupling matrix,
The mode coupling matrix has eigenvalues:
The eigenvalues are real for the case of the identical real part of the effective refractive indices, , and the imaginary part less than the value of the effective coupling, . The eigenvalues degenerate in the case and . They are purely imaginary for and and, finally, complex elsewhere. This general non-Hermitian dimer has a rich structure that deserves further attention, but right now, we are interested in just the -symmetric case.
In quantum mechanics, -symmetry refers to space-time reflection symmetry [6]. In discrete optical couplers, we can consider waveguide permutation and propagation inversion as equivalent to space and time reflection, respectively. Then, in order to recover the standard linear -symmetric dimer, we need to work with waveguides that have the same effective refractive indices, , such that is purely imaginary, and we can write a differential set [48],
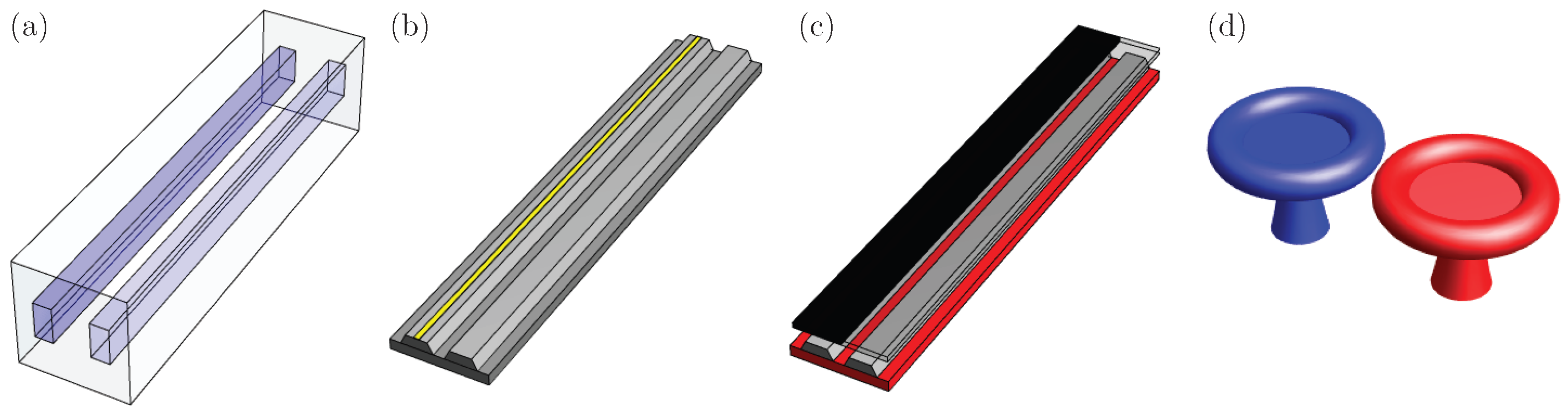
where the permutation of the waveguides, , and propagation reversal, , leaves the system invariant. Note that we have used the effective coupling parameter to scale the propagation distance, , such that we deal with a single parameter given by the effective refractive index to coupling ratio, with . This mathematical model is equivalent to considering waveguides with effective pure linear loss and gain, and , in that order. In optics, the linear -symmetric dimer has been experimentally demonstrated in passive lossy waveguides [49,50] (Figure 1a,b), as well as active, pumped waveguides [51] (Figure 1c) and pumped whispering-gallery mode microcavities [52,53] (Figure 1d) with linear gain. The experimental demonstration of -symmetric devices is not limited to optical resonators; they have also been realized with operational amplifiers in electronics [54].
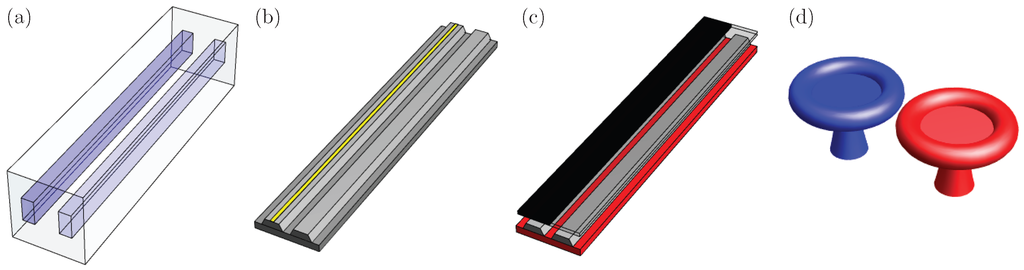
Figure 1.
Schematics of the experimental realizations of the linear -symmetric dimer. (a) Passive laser-engraved waveguides; (b) passive waveguides with metallic scatterers; (c) pumped active waveguides; (d) pumped active whispering-gallery mode microcavities.
2.1. Quantum Mechanics, Linear Algebra Approach
Let us try to address propagation in the linear -symmetric dimer. First, note that we can cast its coupled differential equation system, Equation (8), in a vector form,
similar to Schrödinger equation. Now, the coupling matrix takes the role of a Hamiltonian,
where the operators with are Pauli matrices. We will keep the standard sign convention used in classical optics, although this Hamiltonian may confuse those working in quantum mechanics, as it implies that a parallel spin-field configuration is the most energetic configuration. In any given case, it is straightforward to find the propagator for this ζ-independent Schrödinger-like equation [48],
such that the propagated fields through the device are given in terms of the initial field configuration,
with the dispersion relation given by:
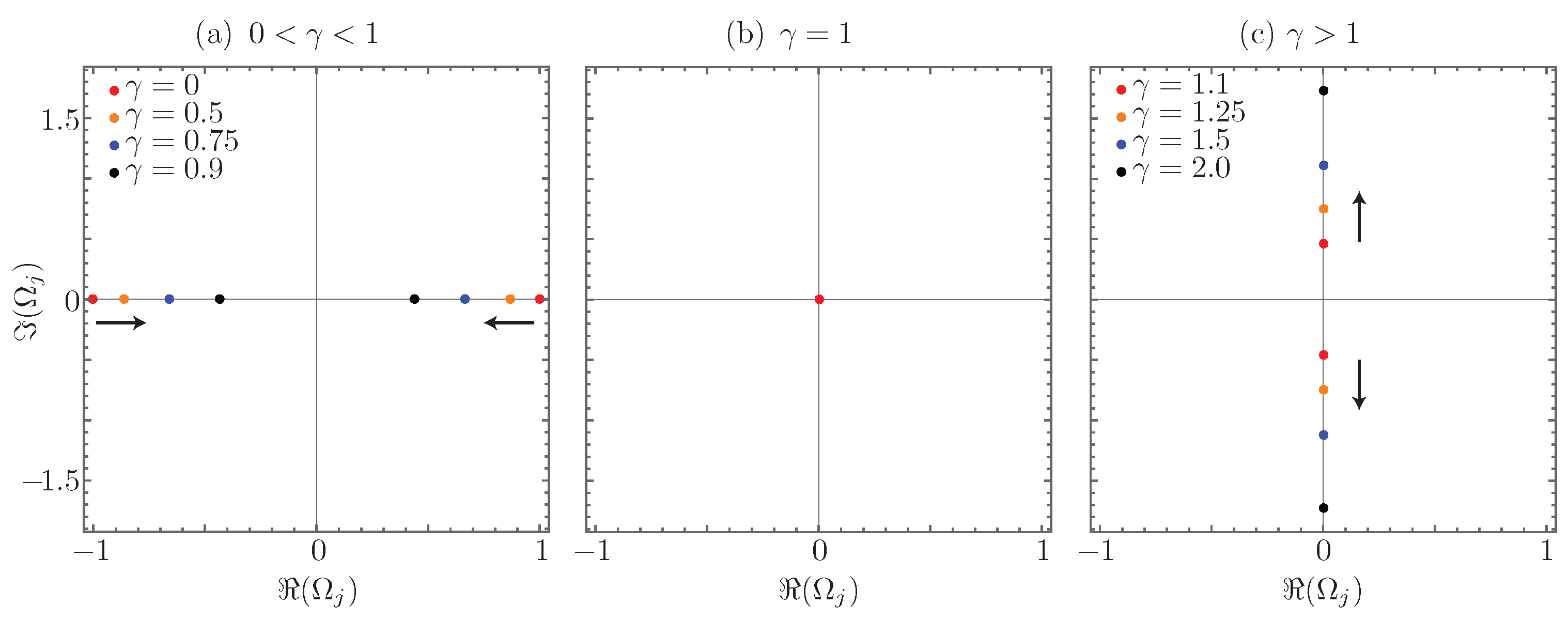
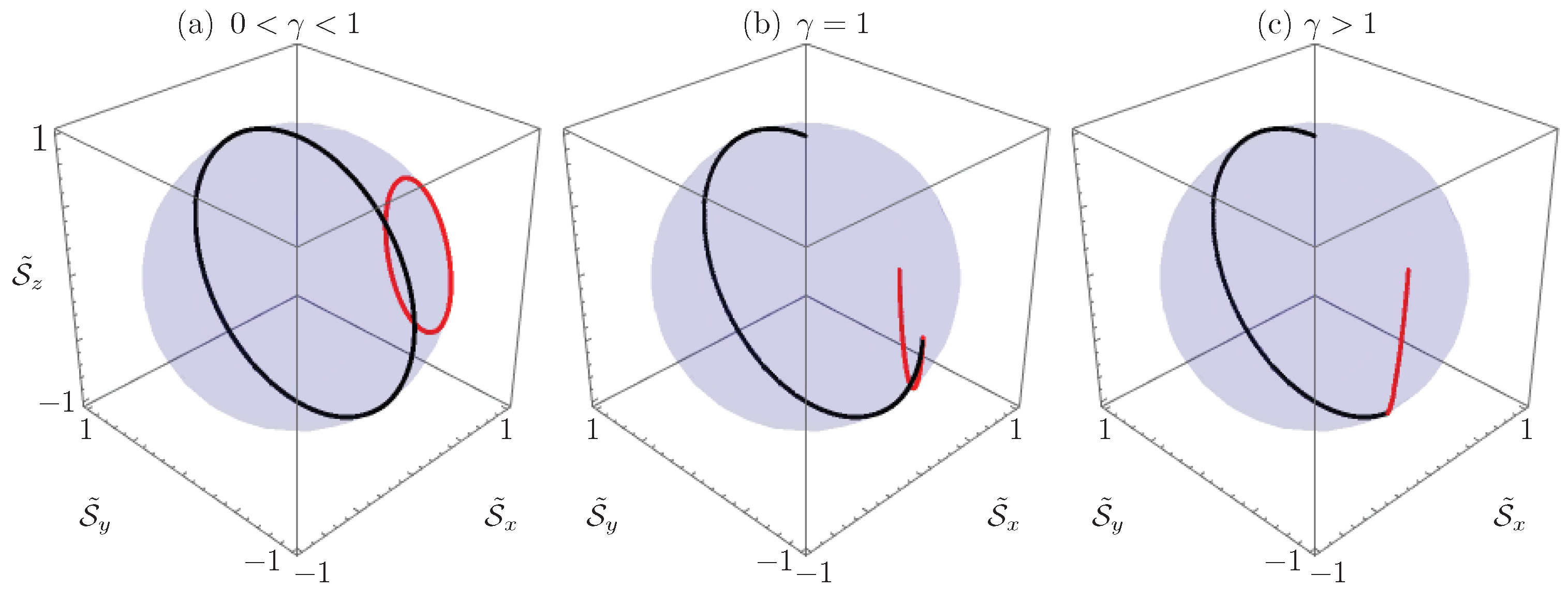
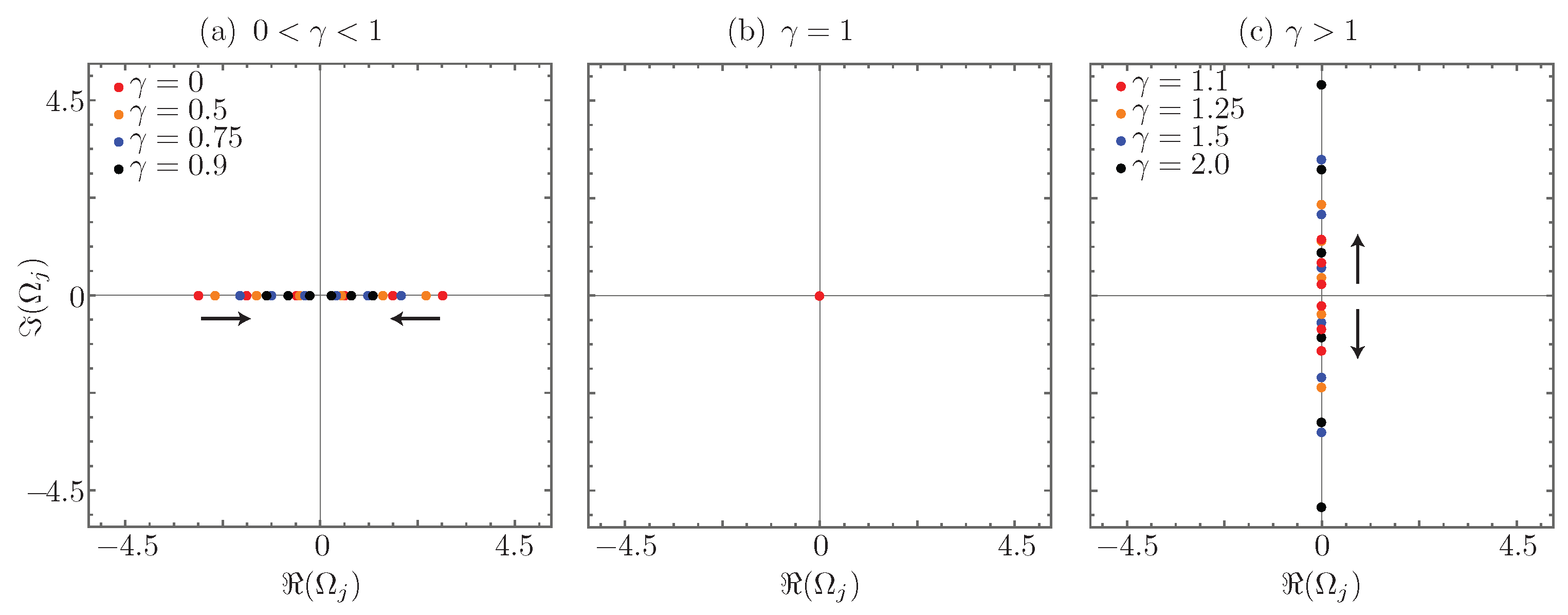
which can be real for , zero for or purely imaginary for . Note that the eigenvalues of the coupling matrix are given by , and they become fully degenerate at . Note that this degeneracy is different from that in Hermitian systems; here, the actual dimension of the system becomes one at this point known in the theory of linear operators as the Kato exceptional point [55]. Figure 2 shows the behavior of the coupling matrix eigenvalues as a function of the gain to coupling ratio as they go from purely real, Figure 2a, degenerate to zero, Figure 2b, and become purely imaginary, Figure 2c.
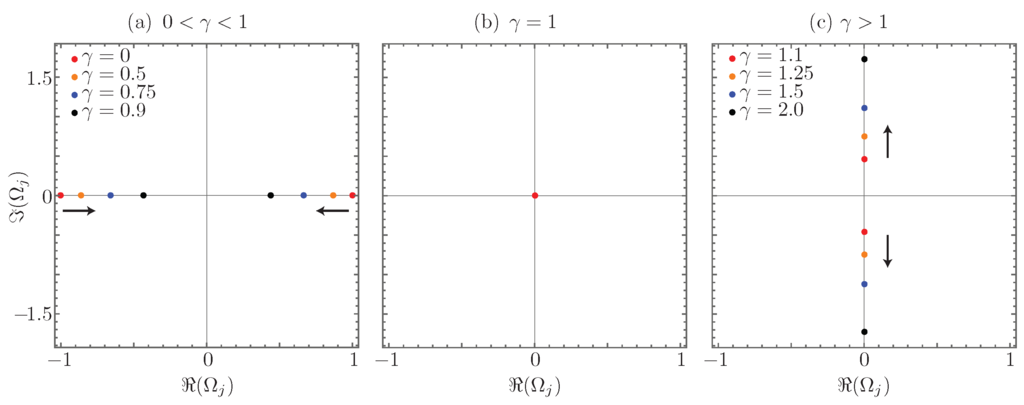
Figure 2.
Coupling matrix eigenvalue dynamics: (a) -symmetric regime; (b) fully-degenerate regime; and (c) broken symmetry regime. The black arrows show the direction of the eigenvalues as the gain to coupling ratio increases.
It is straightforward to show that in the -symmetric regime, where the eigenvalues of the mode coupling matrix are real, the device behaves as an asymmetric oscillator with amplification,
Once the -symmetry is broken, we have two distinct cases, the fully-degenerate one where both eigenvalues are zero and the device shows amplification ruled by a power law,
and the case of purely imaginary eigenvalues, where the amplification is exponential,
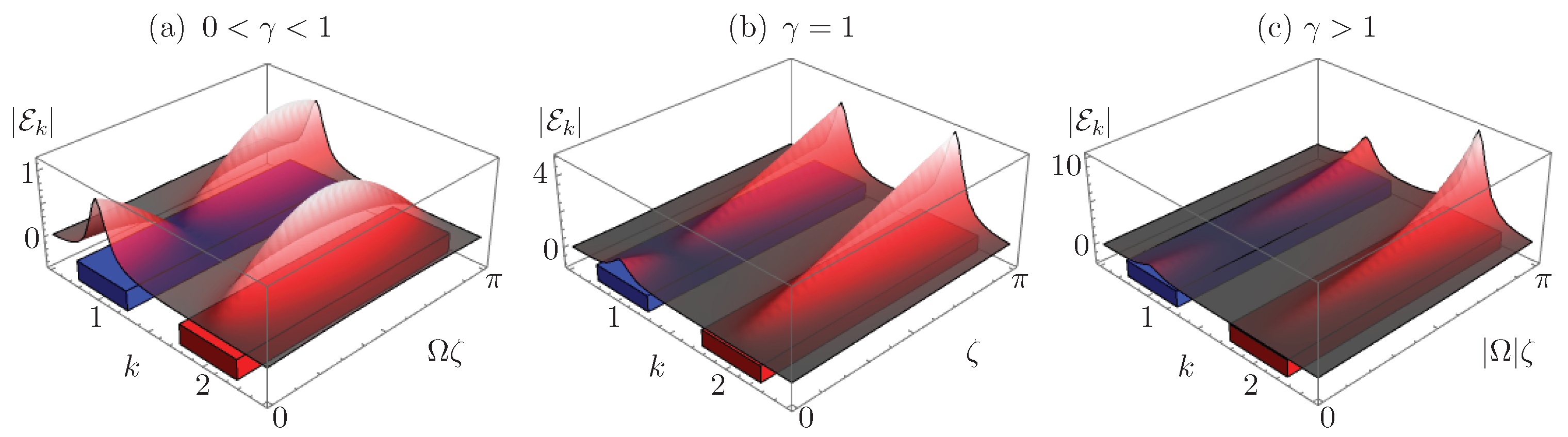
Figure 3 shows the absolute field amplitude propagating through a -symmetric dimer when light impinges just at the first waveguide in a device with parameters in the regime with real eigenvalues, Figure 3a, fully degenerate eigenvalues, Figure 3b, and imaginary eigenvalues, Figure 3c. Now, while we find this algebraic approach short, elegant and elucidating, it is not the only available method to infer the properties of the -symmetric dimer.
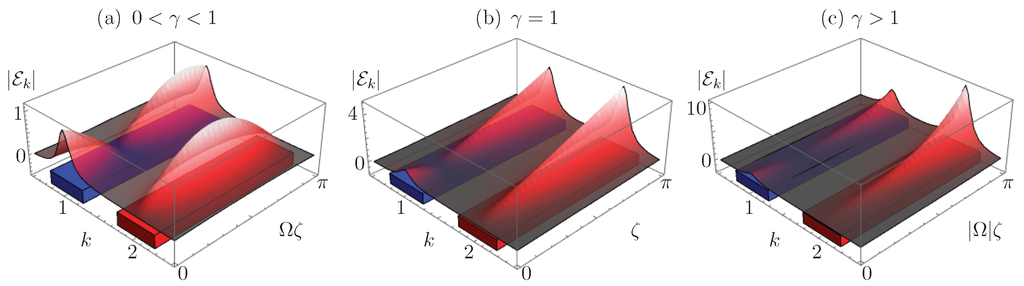
Figure 3.
Absolute field amplitude propagation in a coupler with effective symmetric loss, blue waveguide, and gain, red waveguide, in the: (a) -symmetric regime, ; (b) fully-degenerate regime, ; and (c) broken symmetry regime, .
2.2. Nonlocal Oscillator, Partial Differential Equation Approach
It is also possible to decouple the dimer differential equation set, Equation (8), into two second order differential equations that have the same form of the one-dimensional wave equation [48],
The boundary conditions are given by the initial fields impinging the device, , and their first derivatives,
obtained from the dimer mode coupling equation, Equation (8). Note that the latter takes us far from the standard one-dimensional wave equation, because it refers to nonlocal media involving linear loss and gain. Nevertheless, we can follow the standard partial differential equation approach.
In the -symmetric case, the characteristic equation is positive, , and we can write the second order differential equation as that of a standard oscillator,
thus, we can use its well-known solution plus our particular boundary conditions to obtain the propagated fields,
These fields allow us to describe the dimer as an asymmetric periodic oscillator with amplification. It is not a harmonic oscillator due to the boundary condition on the first derivatives. In the fully-degenerate case, where the characteristic equation is equal to zero, ,
we can think of light propagating through the dimer as a free particle through some nonlocal media with linear unitary gain and loss, which yields amplification following a power law,
Finally, in the broken symmetry case, the characteristic equation is negative, , and we can write the second order differential equation as an inverted oscillator,
that provides us with a device that amplifies initial fields following an exponential law,
All of these solutions are just the explicit form of the propagated field found earlier by a purely algebraic approach, Equations (13)–(17), and tap into the well-known one-dimensional wave equation with the difference that an effective nonlocal active medium is provided by the first derivative boundary conditions.
2.3. Nonlinear Oscillator, Renormalized Fields Approach
So far, we have managed to provide an algebraic propagator and to describe the field behavior in the three possible regimes of the linear -symmetric dimer. Now, we can bring forward a complementary view that can give us asymptotic information of the broken symmetry phases. Let us define instantaneous renormalized fields [48],
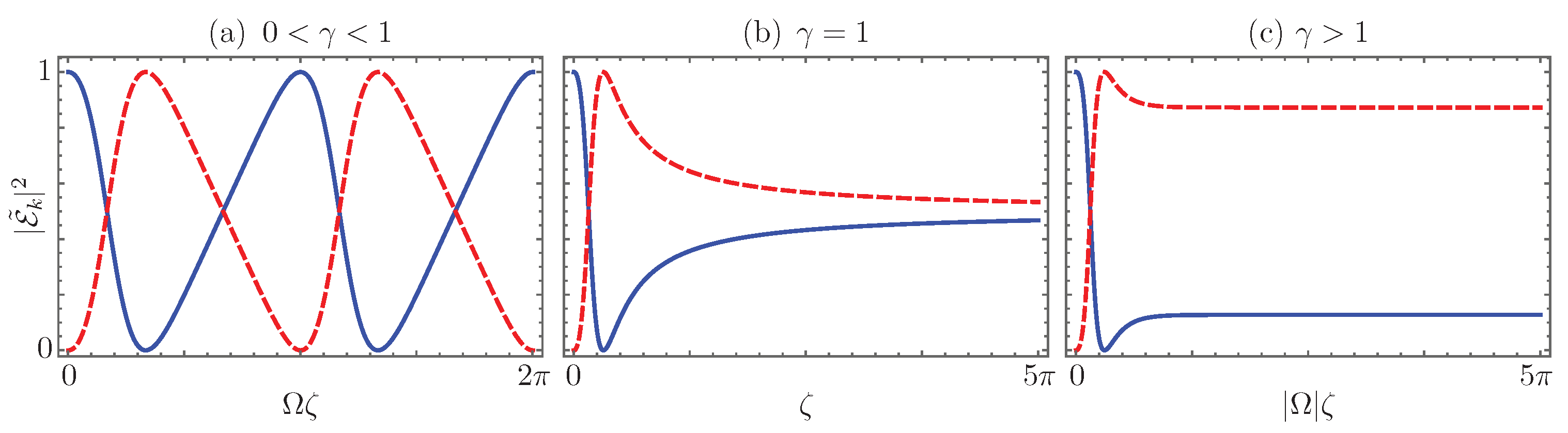
such that the total renormalized field intensity at each propagation distance is always the unit, . In this picture, it is easier to realize that light intensity through the -symmetric device behaves like a non-harmonic oscillator, Figure 4a. Furthermore, this allows us to conduct asymptotic analysis in the broken symmetry phases. In the fully-degenerate phase, , such that , it is possible to calculate the asymptotic behavior of the fields’ intensity as the scaled propagation distance goes to infinity and to find out that the renormalized optical power is balanced in both waveguides, independent of the initial field distribution,
as shown in Figure 4b. In the broken symmetry regime, where the eigenvalues are purely imaginary, the asymptotic intensity distribution depends on the effective gain to coupling ratio, and we can include the previous result,
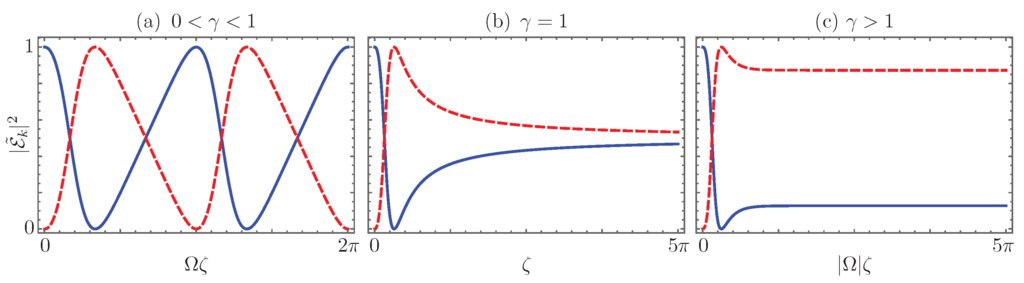
Figure 4.
Renormalized field intensity propagation in the waveguides with effective loss, , solid blue line, and gain, , dashed red line, in the (a) -symmetric regime, ; (b) fully-degenerate regime, ; and (c) broken symmetry regime, , for an initial field impinging just at the first waveguide.
In other words, for a device long enough, in the broken symmetry region, the input field distribution has no effect on the output field intensity distribution. The latter is governed only by the gain to coupling ratio of the device, γ (Figure 4c).
Furthermore, this approach also allows us to show that the linear -symmetric dimmer is the irreducible form of two equivalent reducible nonlinear models, one with linear loss and gain, as well as an imaginary nonlinearity [48],
that has a form reminiscent of van der Pol oscillators [56] in the sense that there is a change of sign dependent on the intensity for the self-modulation of the waveguide fields. Actual -symmetric-coupled van der Pol oscillators have been implemented in the laboratory, as well as their optical realizations [57]. The other form corresponds to an imaginary cross-nonlinearity,
We can follow a standard approach from non-Hermitian Bose–Hubbard dimers [58,59,60,61] used to deal with optical nonlinear -symmetric dimers [28], and introduce a Stokes vector, , with components given by,
Again, the matrices are Pauli matrices; the notation is a column vector containing the renormalized field amplitudes equivalent to that defined in Section 2 for the field amplitudes; and the new conjugate transpose notation is a row vector with the conjugate renormalized field amplitudes as components. In terms of the renormalized field amplitudes,
In the case at hand, where the nonlinearity is reducible, the Stokes vector norm is the unit and a constant of motion,
The Stokes vector components verify the following set of coupled differential equations:
Note that these equations have a set of stable points only outside the -symmetric regime, , given by . It is also possible to describe the asymptotic behavior of the renormalized Stokes vector components,
The Stokes vector approach allows us to visualize the field propagation as a trajectory on a unit sphere. Any initial condition, in the fully-degenerate and broken symmetry regimes, will converge asymptotically to the same stable point on the sphere of the differential equation, , in a dimer described by the gain to coupling ratio γ. Figure 5 shows the Stokes vector propagation related to the examples given in Figure 4 and an additional initial condition set to show that the asymptotic behavior is independent of the initial conditions. This asymptotical behavior suggest the use of this device as an unidirectional variable amplitude coupler.
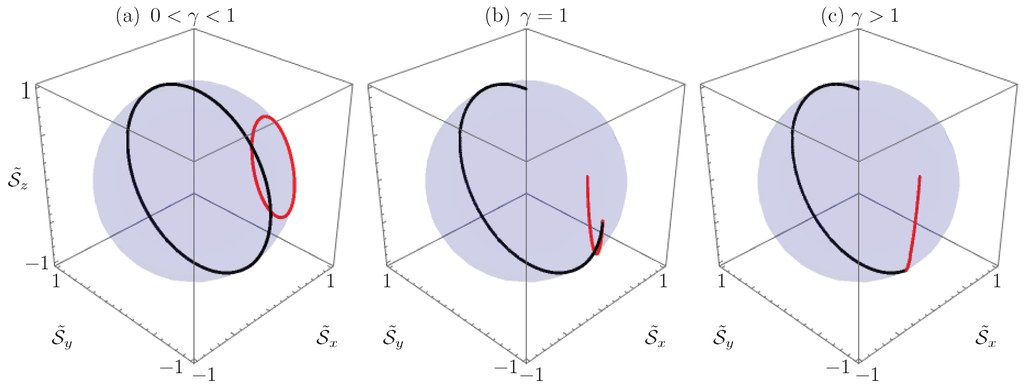
Figure 5.
Stokes vector propagation in the waveguide coupler with effective symmetric loss and gain, in the (a) -symmetric regime, ; (b) fully-degenerate regime, ; and (c) broken symmetry regime, , for the initial conditions and in black and and in red.
3. Nonlinear -Symmetric Dimer
Now, we will discuss a variation of the -symmetric dimer where the waveguides have an additional Kerr nonlinearity,
For the sake of simplicity, we will consider the effective Kerr nonlinearity to coupling strength ratio, κ, to be equal in both waveguides. Stability in this system has been formally discussed in the case of , and it was found that the zero equilibrium state is neutrally stable in the -symmetric regime, , and that the total light intensity at the waveguides is bounded from above by the initial intensity amplified by an exponential gain, [35]. In order to deal with the dynamics, it is possible to introduce a Stokes vector defined, now, in terms of the field amplitudes [28],
Thus, the norm of the redefined Stokes vector, the total intensity at the waveguides, is no longer a constant of motion,
and its dynamics,
will not be restricted to the unit sphere. These dynamics have been shown to be an optical simulation of a relativistic massless particle of negative charge in a pseudo-electromagnetic field [28]. Note that there is a set of stable points, , for the effective gain to coupling ratio ,
All of these stable nonlinear modes are waveguide fields of the form with and phase difference constricted by the relation,
There are no stable points outside the -symmetric regime, .
In order to create intuition, let us start with the passive self-focusing two-waveguide coupler, , that has two constants of motion in the form of the Stokes vector norm, , such that , and the Hamiltonian-like quantity,
Note that the system is integrable, and the conservation of the Stokes vector norm allows for the parametrization and , such that we can write a Hamilton–Jacobi model,
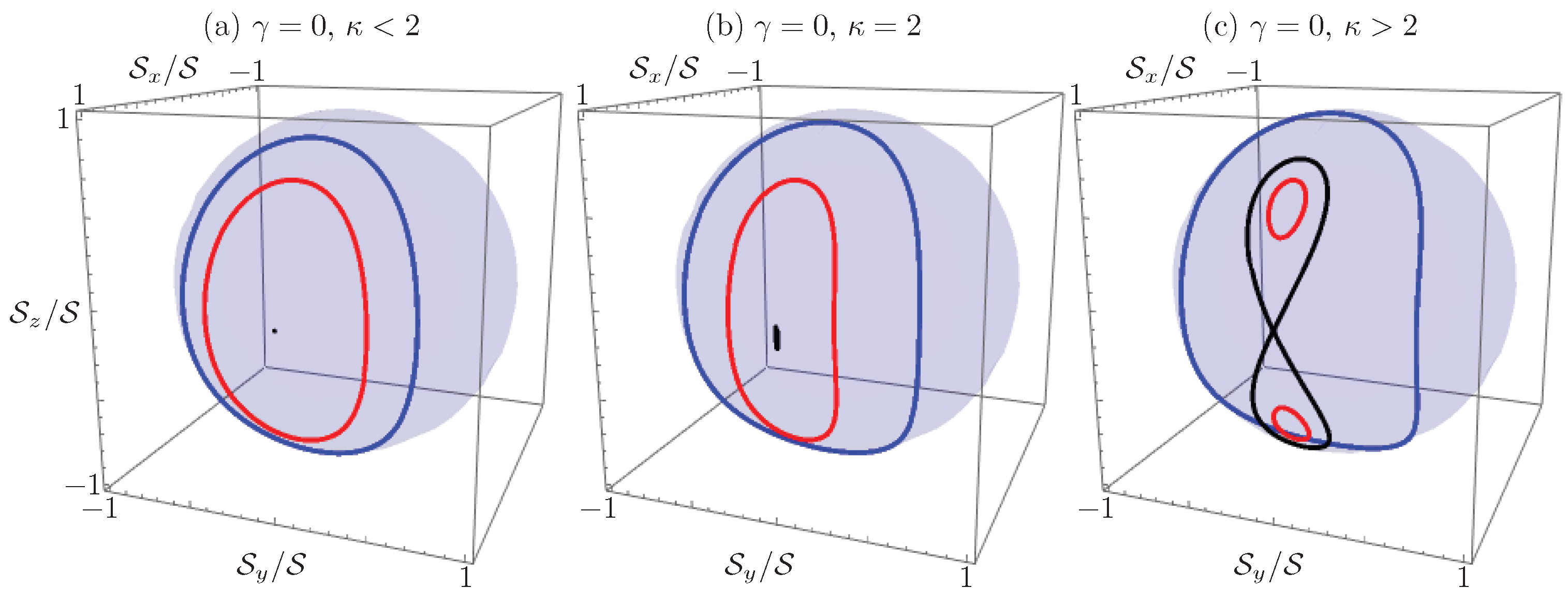
equivalent to that of a nonrigid pendulum or a Bose–Josephson junction [62,63]. This particular configuration allows for Rabi oscillations (Figure 6a) below the critical effective Kerr nonlinearity to coupling ratio, (Figure 6b); above this critical value, the system can show both Rabi and Josephson oscillations (Figure 6c). In other words, the initial field amplitudes either coherently oscillate between the waveguides or localize at the waveguide where they were originally prepared, depending on both the initial field distribution and the effective Kerr nonlinearity of the device.
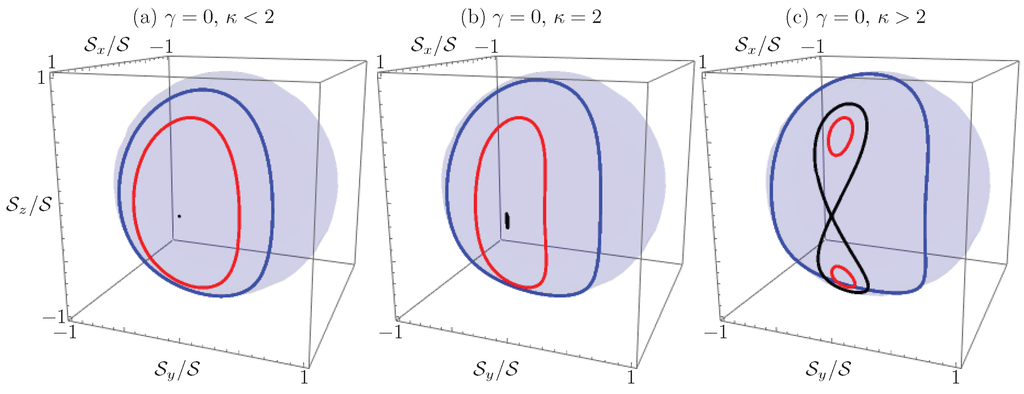
Figure 6.
Stokes vector propagation in the passive two-waveguide coupler, , with nonlinearities (a) below, ; (b) at, ; and (c) above, , the critical Kerr nonlinearity to coupling strength ratio, . The figure shows: (a) stationary point; (b) trajectory infinitesimally near the stationary point; and (c) separatrix in black; (a,b) Rabi and (c) Josephson oscillations in red; and (a)–(c) Rabi oscillations in blue.
If we now include the symmetric gain and loss, , the system is still integrable, as we can write two constants of motion [28],
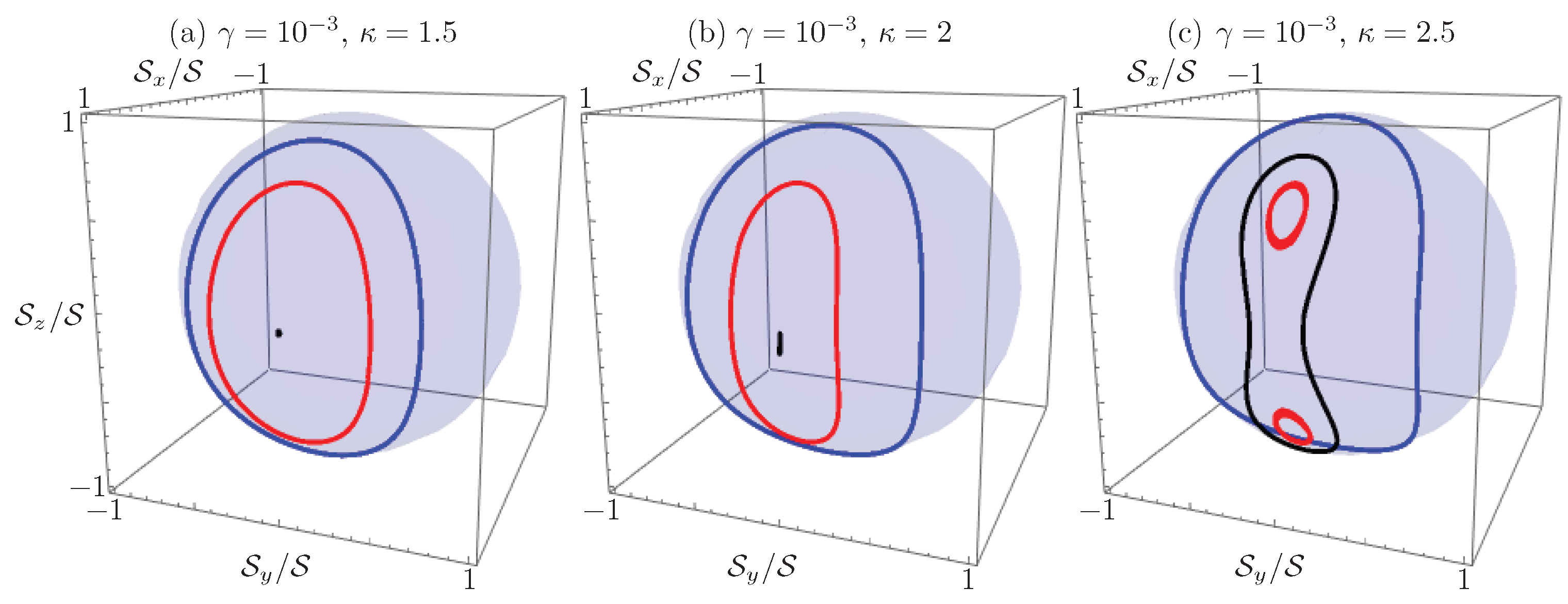
In the literature, it has been found that the system is stable in the interval for effective nonlinearity [35], and numerical arguments have been given in the most general case [28]. Figure 7 shows how the dynamics of the passive nonlinear dimer are affected by the addition of a small effective gain to coupling ratio to the system. Below the critical nonlinearity for the passive system (Figure 7a), we can still find the coherent oscillation behavior of the linear -symmetric dimer, but the former stable point is no longer a fixed point of the system. As the nonlinearity increases, we can see how device parameters and initial conditions start having an effect on the dynamics (Figure 7b), until a point where it is possible to have unstable light localization at the waveguide where light originally impinged (Figure 7c). Here, the constant of motion plays an important role as an accuracy test for the process of numerically solving the coupled nonlinear system.
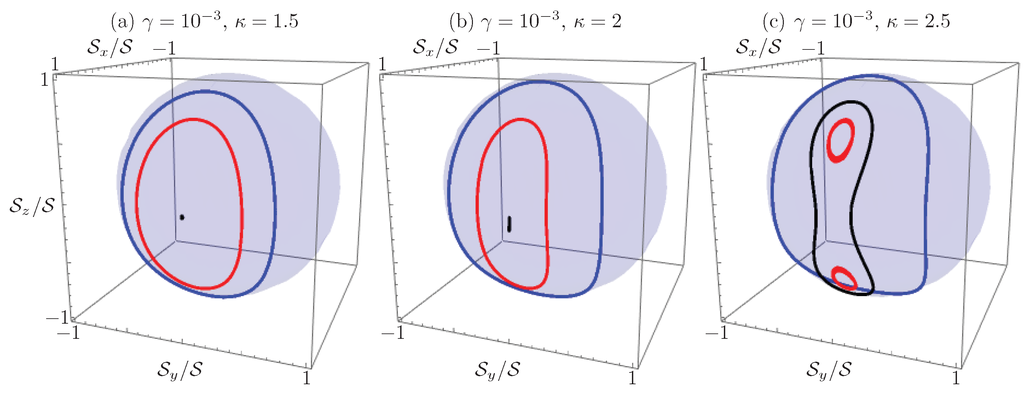
Figure 7.
Renormalized Stokes vector propagation in the waveguide coupler with a fixed gain to coupling ratio and variable effective nonlinearity to coupling ratio (a) ; (b) ; and (c) , for the same initial conditions as Figure 6.
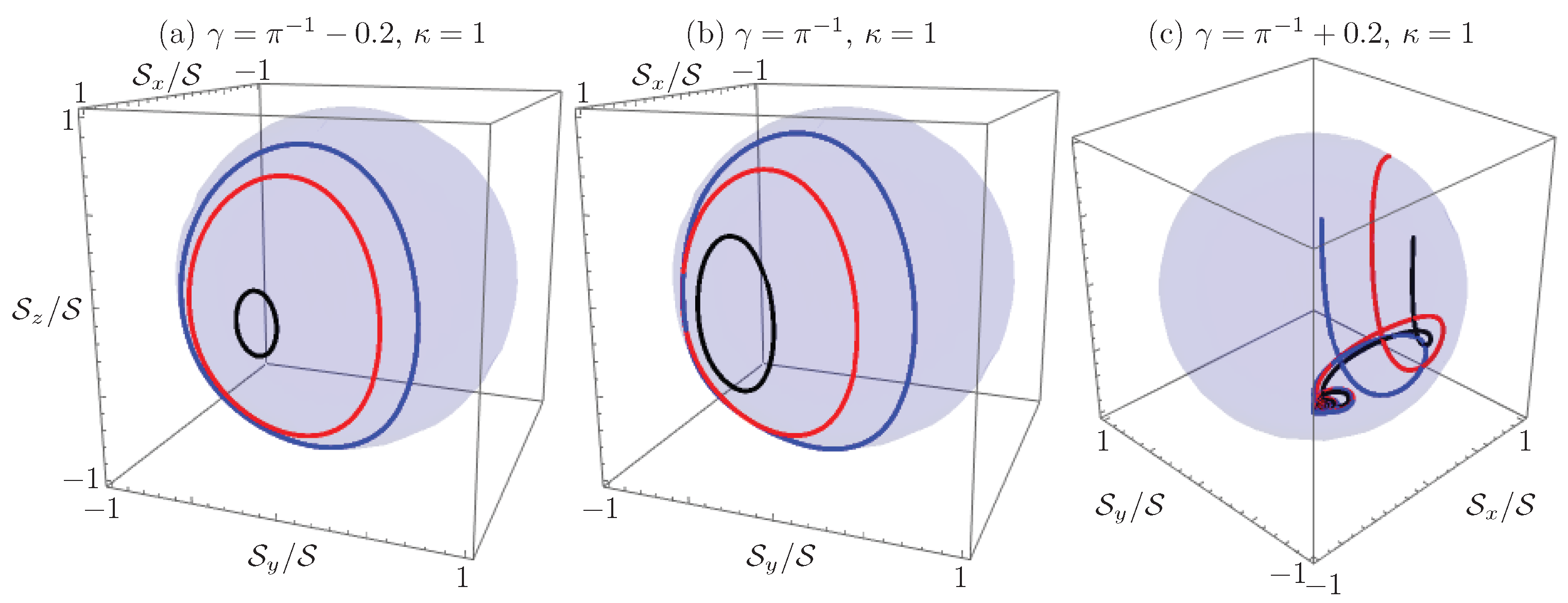
Now, for a given effective Kerr nonlinearity to coupling ratio, , we can approximate a critical effective gain to coupling ratio, , where a change of dynamics occur. First, the reciprocity condition regarding the exchange of waveguides for a given initial field distribution breaks as we get closer to the approximate critical gain to coupling ratio (note the shift to the left in Figure 8a,b), then, after we cross the critical value, the field intensity at the gain waveguide gets localized and experiences an exponential gain, while the field in the lossy waveguide diminishes independently of the initial field amplitude distribution (Figure 8c). Note, the dynamics above the critical gain to coupling ratio do not tend to the fixed point of the system as in the linear device; the fields do not seem to show a constant behavior in the asymptotic limit. This localization with amplification in the gain waveguide suggests the use of these devices as optical diodes [28].
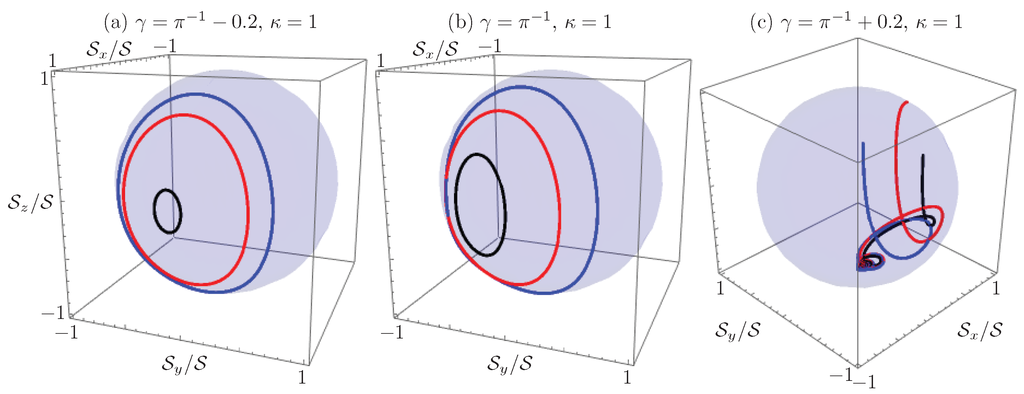
Figure 8.
Renormalized Stokes vector propagation in the waveguides’ waveguide coupler with a fixed effective Kerr nonlinearity to coupling ratio and variable effective gain to coupling ratio (a) ; (b) ; and (c) , for the same initial conditions as Figure 7.
4. Linear -Symmetric Planar -Waveguide Coupler
As we said before, the linear dimer is the device with the smallest dimension showing -symmetry. Its algebraic structure, Equation (10), and the fact that Pauli matrices are the two by two scaled matrix representation of the group in dimension two, , suggest that a larger class of N-waveguide devices can be constructed with higher dimensional matrix representations of . Therefore, we can construct a mode coupling equation set describing a device of N waveguides following Equation (8),
Now, we choose to introduce a different scaled propagation, , to recover a single parameter Schrödinger-like equation with the form,
where the effective refractive index to coupling ratio is the same as in the standard dimer, . This mode coupling matrix with describes planar N-waveguide couplers with identical real effective refractive indices and underlying symmetry that show harmonic oscillator behavior [64]. These devices have been used to produce perfect state transfer in both the classical [65,66,67,68] and quantum regimes [69]. In order to deal with a linear -symmetric N-waveguide coupler, we must consider pure imaginary effective refractive indices, , and thus, the realization of higher finite-dimensional non-unitary representation of , implemented as a complexified version of , is involved. In matrix form, the group generators have the following elements,
with the Kronecker delta given by and the Bargmann parameter by . These matrices fulfill the commutation relation , where is the Levi–Civita symbol, and commute with the Casimir operator , . In the standard differential form, this is equivalent to the coupled mode set,
Following the vector notation, we can construct a field vector as,
where we can define the n-th element of the standard basis as:
such that we can define more helpful generators with their corresponding actions,
where we have defined the ladder operators that fulfill . Following the Gilmore–Perelomov approach for [48,64], we can find the n-th eigenvalue of the mode coupling matrix,
and obtain the same structure found for the dimer. All of the eigenvalues will be real numbers for (Figure 9a), completely degenerate and equal to zero for (Figure 9b) and imaginary for (Figure 9c). This so-called collapse of the eigenvalues is a direct consequence of the underlying symmetry [70].
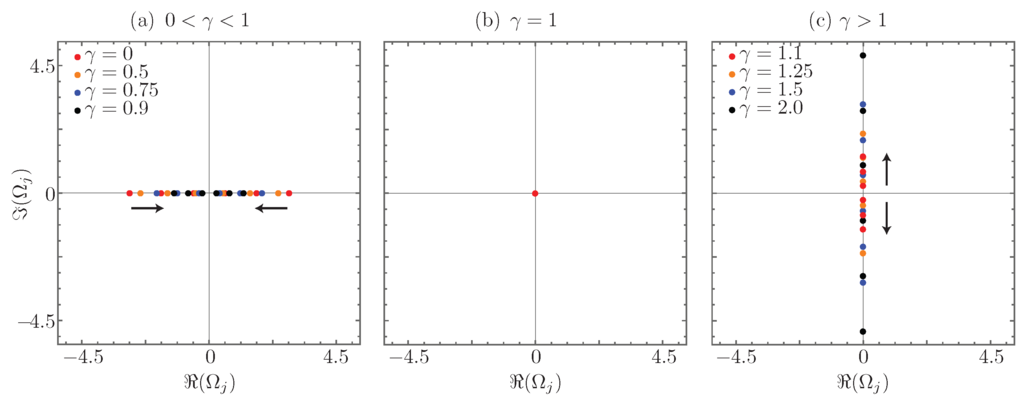
Figure 9.
Coupling matrix eigenvalue dynamics: (a) -symmetric regime; (b) fully-degenerate regime; and (c) broken symmetry regime. The black arrows show the direction of the eigenvalues as the gain to coupling ratio increases. Theses cases show the results for a waveguide coupler that provides a Bargmann parameter .
Furthermore, we can provide the propagation matrix elements,
where the notations and stand for the binomial coefficient and Gauss hypergeometric function, in that order. Again, we will have three distinct propagation behaviors as demonstrated for the dimer. These behaviors are simpler to visualize if we define renormalized field amplitudes,
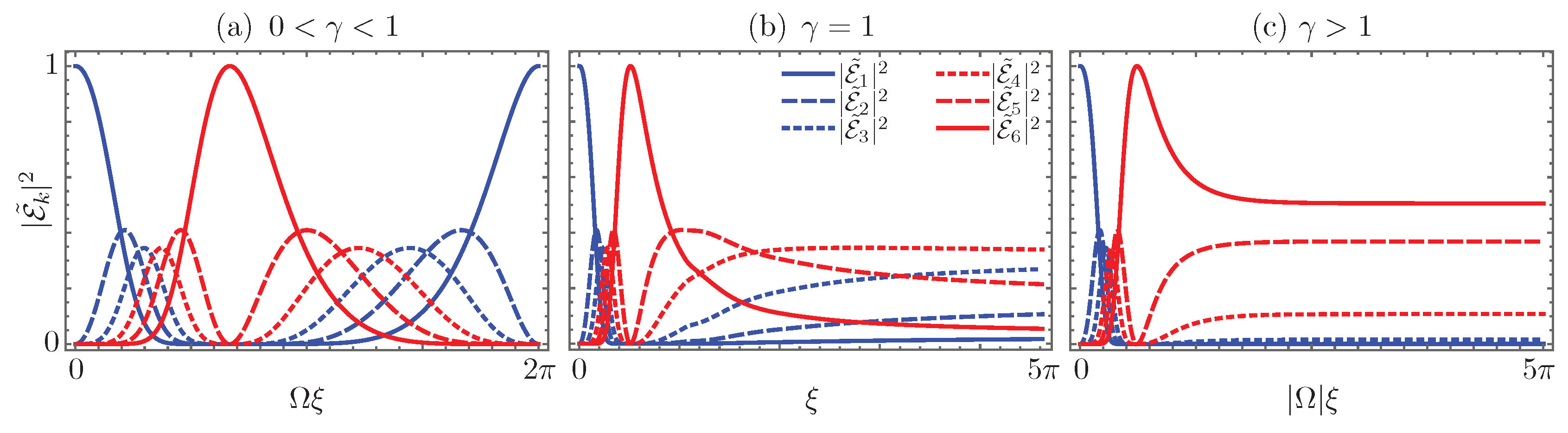
Now, we can see periodic amplified oscillations in the -symmetric regime, (Figure 10a), amplification following a power law in the fully-degenerate regime, (Figure 10b), and asymmetric amplification following an exponential law in the broken symmetry regime, (Figure 10c).
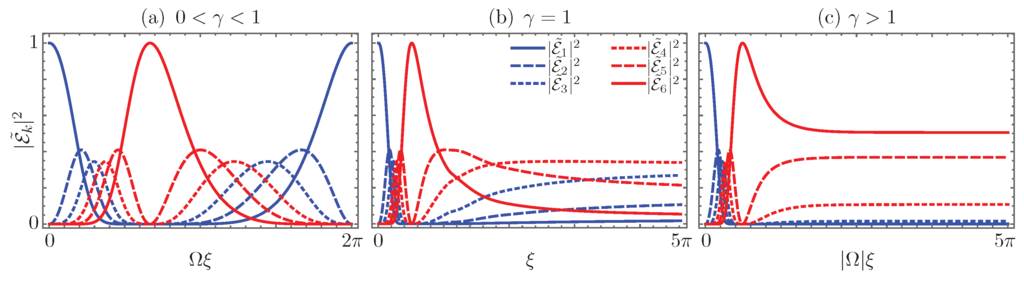
Figure 10.
Renormalized field intensity propagation for a waveguide coupler, Bargmann parameter , in the (a) -symmetric regime, ; (b) fully-degenerate regime, ; and (c) broken symmetry regime, , for an initial field impinging just the first waveguide.
Furthermore, we can derive the set of reducible coupled nonlinear equations for the renormalized field amplitudes,
It is cumbersome, but possible to show that the asymptotic response of an N-waveguide coupler in the fully-degenerate and broken symmetry regimes is independent of the input field amplitude distribution,
which can be seen in Figure 10b for and Figure 10c for . As expected from the mathematical description, in the fully-degenerate regime (Figure 10b), the extremal waveguides, those with major effective losses and gain, will transmit fields with smaller amplitudes than those in the central waveguides, because the asymptotic intensity distribution follows the binomial coefficient. In the broken symmetry regime (Figure 10c), the field intensity correlates with the strength of the gain or loss; the most intense field will travel through the waveguide with the larger effective gain and the less intense through the one with the larger effective loss.
The equivalent three-dimensional formulation of the Stokes vector for renormalized fields,
yields components of the following form,
Here, the conserved variable is the Casimir operator,
and it is important to emphasize that the norm of this three-dimensional Stokes vector is no longer a constant of motion,
The reason behind this is that a complex vector of dimension N with unit norm can be represented as a point on the surface of a ball of unit radius in dimension . For example, the renormalized fields through a two-waveguide coupler, two-dimensional complex vector of unit norm, can be represented on the surface of a three-dimensional ball; in other words, a two-dimensional sphere, where the Stokes vector norm is a constant of motion,
In general, we should use the surface of a -ball of unit radius in order to describe properly the field amplitudes propagating through an N-waveguide coupler. This does not make it simpler to visualize the dynamics, so we favor a projection from -dimensional to three-dimensional space with the price of loosing the unit norm for all cases, but , where we can write with . Note that this projection also allows us to derive an asymptotic expression for the z-component of the Stokes vector via Equation (82), and heuristically propose the rest,
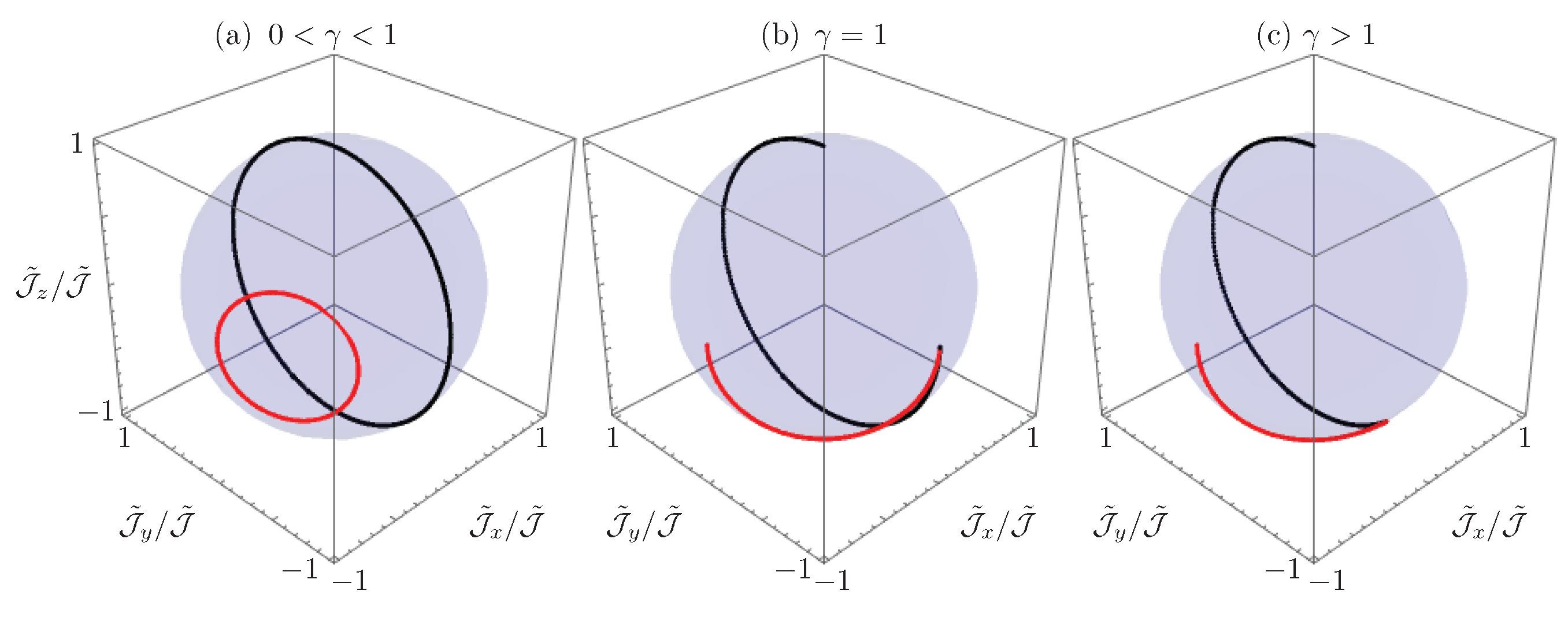
this was confirmed numerically over a random sample of initial states and gain to coupling ratios outside the -symmetric regime, and . Figure 11 shows the propagation of the renormalized Stokes vector in a six-waveguide coupler, , with parameters in the -symmetric, (Figure 11a), fully-degenerate, (Figure 11b), and broken symmetry, (Figure 11c), regimes for light impinging the first waveguide of the coupler in black. Furthermore, the renormalized Stokes vector propagation for an initial field amplitude distribution corresponding to the eigenstate of with eigenvalue is plotted in red to show the asymptotic behavior outside the -symmetric regime.
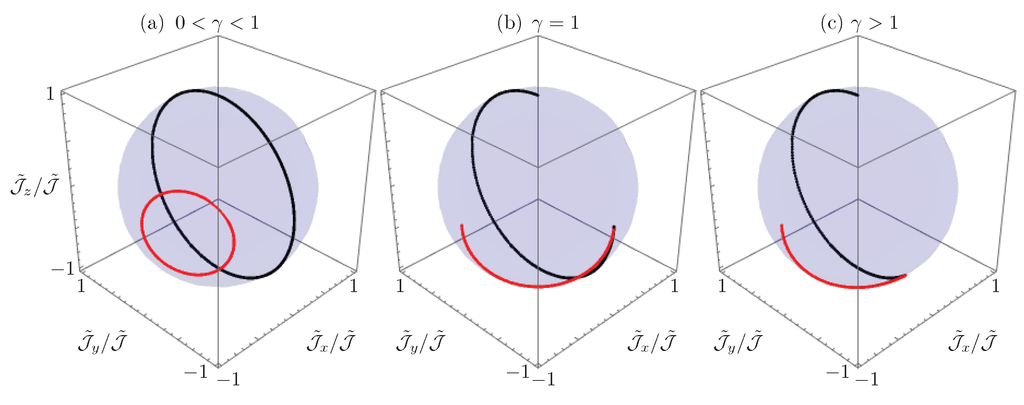
Figure 11.
Renormalized Stokes vector propagation in a six-waveguide coupler, , in the (a) -symmetric regime, ; (b) fully-degenerate regime, ; and (c) broken symmetry regime, , for the initial conditions in black and the eigenstate of with eigenvalue , in red.
5. Non-Hermitian Ehrenfest Theorem and Generalized Stokes Vector
So far, we have studied the propagation of classical light through a class of -symmetric devices with underlying symmetry that includes the linear and nonlinear -symmetric dimer. We have seen that propagation on these linear and nonlinear devices is more involved than in the passive case, , but the linear algebra approach has helped us produce closed form propagators for the lineal case, and the renormalized fields approach and its Stokes vector representation have allowed us to find stationary states and to visualize the propagation dynamics. Here, we shall try to understand the underlying reasons for this more complex propagation behavior.
As we mentioned earlier, the propagation of light through tight-binding N-waveguide couplers can be modeled by mode coupling theory in a form similar to the Schrödinger equation, Equation (9). Thus, finding a propagator, Equation (13), provides us with the information of the complex field amplitudes as they propagate through each waveguide. In quantum mechanics, we can also ask about the propagation of the expectation value, which in the optical picture translates to the following,
for the operator , which can vary with propagation. This is exactly what has been done when studying the propagation of the Stokes vector defined as the expectation value of the generators, Equations (38) and (83), with the peculiarity that we used renormalized field amplitudes instead of just the field amplitudes in the linear cases. The Ehrenfest theorem relates the variation with the propagation of the mean value with the dynamics of the model,
In standard Hermitian quantum mechanics, the Heisenberg equation provides the equation of motion for the operator, but in our non-Hermitian model, we need to go beyond this. Any non-Hermitian operator can be decomposed,
into Hermitian, , and skew-Hermitian, , parts. Thus, we can define a commutator between non-Hermitian operators,
such that we can write a Heisenberg-like equation of motion ruled by a non-Hermitian Hamiltonian,
and recover a non-Hermitian generalization of the Ehrenfest theorem for tight binding non-Hermitian waveguide couplers,
Note that equivalent modified Heisenberg equations of motion have been derived following alternate methods in non-Hermitian quantum mechanics [71]. Let us consider, as an example, the N-waveguide coupler of the last section, Equation (67), where the effective mode-coupling matrix acting as the Hamiltonian has a Hermitian part, , and a skew-Hermitian part, . Here, the Ehrenfest theorem can be simplified to the expression,
where the standard commutator, , and anti-commutator, , have been used. We can see that the anti-commutator term in this expression will be proportional to the gain to coupling strength ratio, γ, and this is the culprit behind the more complex behavior of our general class of N-waveguide lattices with underlying complexified symmetry. Note that we can also use this result to derive the conserved quantities of the model by solving .
As a practical example, let us derive the equations of motion for the Stokes vector for the linear -symmetric dimer, with , where is the identity matrix, given by Equations (52)–(55). Here, the Hermitian and skew-Hermitian parts of the mode coupling matrix are and . Now, any linear Hermitian operator for this system can be written as the linear superposition of the matrices ,
and the propagation of its expectation values, according to the non-Hermitian Ehrenfest theorem, are given by the following expression,
Thus, noting that for the Stokes vectors, the coefficients are constant, , we can write the evolution for the components of the Stokes vector without field renormalization,
which are in complete agreement with what we obtain from the nonlinear -symmetric dimer, Equations (56)–(59), if we kill the effective nonlinearity to coupling strength ratio, . Note that the total intensity, , is not conserved as expected from non-Hermitian dynamics. Note that, in this case, the total intensity, , coincides with the norm of the Stokes vector, , and we can recover the renormalized Stokes vector dynamics, Equations (43)–(46), if we define a renormalized Stokes vector, , and use the equations of motion found here. If we were to find a constant of motion, , then its components should satisfy,
A particular solution to this set of equation is in agreement with Equation (105)
For the general case of the planar N-waveguide coupler, the situation is far more complex as we are dealing with square matrices of dimension N. In order to construct any given Hermitian operator of this dimension, we need a basis with a total of matrices; these are provided by the standard unitary group of degree N, , plus the identity. This way, we will work with a set of operators where the first four elements are the representation of in dimension N plus the unity, with , that form ,
where we have just implicitly made the change , , . Thus, if we define a generalized Stokes vector for the planar N-waveguide coupler, it will have dimension , and the zeroth component will be the total intensity in the system,
but in this case, the zeroth component of the generalized Stokes vector, , is still the total intensity, but does not coincide with the norm of the generalized Stokes vector, . Thus, a graphical representation on the sphere will just be a projection of the propagation dynamics occurring on a -dimensional hypersphere as mentioned before. Note that for passive devices, , the propagation equations for the Stokes vectors do not involve any other functions, and the propagation dynamics is restricted to the subgroup of , recovering the results of [64].
6. Quantum -Symmetric Dimer
Let us turn our attention now to the propagation of nonclassical light. In the quantum regime, it is possible to describe two-waveguide couplers with the following effective Hamiltonian [72],
where we have kept the notation for the effective refractive indices and evanescent coupling strength, with and g, in that order. At this point, we can use the Schwinger two-boson representation of [73],
to write an effective Hamiltonian with underlying symmetry,
that answers to the effective Schrödinger equation,
In the single photon regime,
we recover the differential equation set describing the standard two-waveguide coupler,
This approach suffices for the analysis of ideal dimers without gain or loses, , where the total photon number,
of the initial state, , determines the dimension of the representation to be used, , with the eigenbasis of given by the following,
such that we can use the results proposed for classical waveguides’ couplers with underlying symmetry [64] to calculate relevant quantities, like the mean photon number at each waveguide.
The inclusion of linear loses and gain is not a trivial matter, and it is simpler to discuss in the Heisenberg picture [74],
where we have accounted for the change from time to distance propagation. Let us go straight to the -symmetric dimer, with the identical real part of the refractive index and moving into a rotating frame,
such that, again, we can define a scaled propagation, , and include spontaneous processes arising from the quantum description of materials with linear loss or gain processes [74],
where the first term in the right-hand side is related to propagation through the quantum two-waveguide coupler with linear loss and gain, , and the second term describes the Gaussian random processes of emission and absorption, a result arising from the linear materials in an equivalent treatment to that used in the quantum description of the laser [75],
The formal solution for this differential equation yields the propagation of the annihilation operators,
where we have obviated the common phase factor that does not play any important role. Note that we can use the propagator we already found for the classical dimer, in Equation (11), for the first term in the right-hand side.
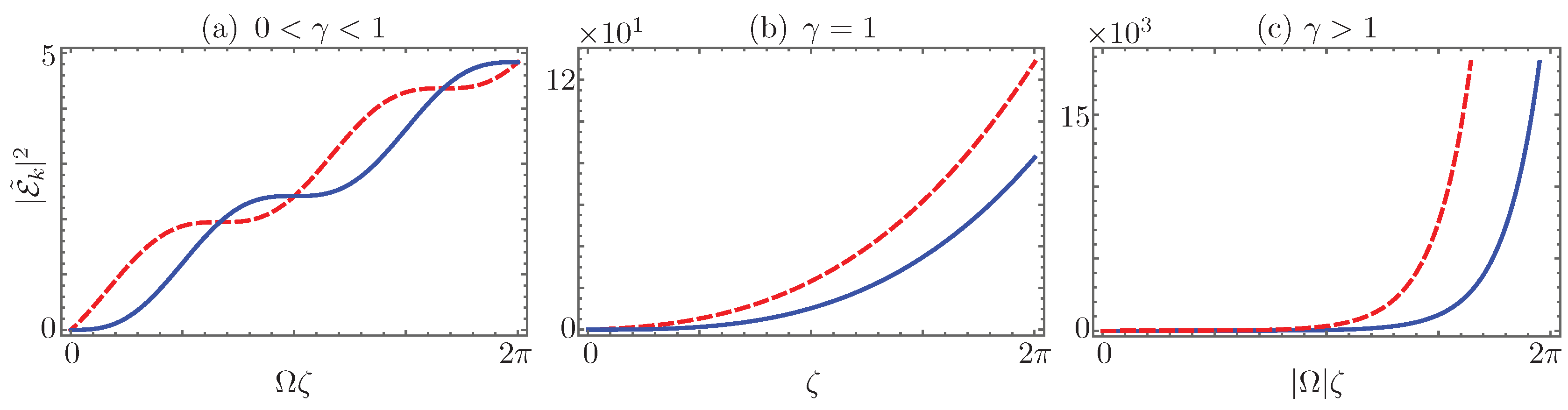
Now, in order to realize the effect of processes induced by the linear materials, let us focus on spontaneous generation in the absence of fields in both waveguides. In the classical case, there will be no light at all propagating through the waveguides, but in the quantum case, even with an initial vacuum state, we can calculate the spontaneous generation at each waveguide [74],
It shows in the symmetric regime, ,
a linear increase with a periodic modulation (Figure 12a). In the fully-degenerate case, , the spontaneous generation,
follows a cubic polynomial (Figure 12b), and in the broken symmetry regime, ,
it shows exponential amplification (Figure 12c). Further discussion regarding the effect of spontaneous processes on the propagation of diverse nonclassical fields through a linear -symmetric dimer can be found in Ref. [74].
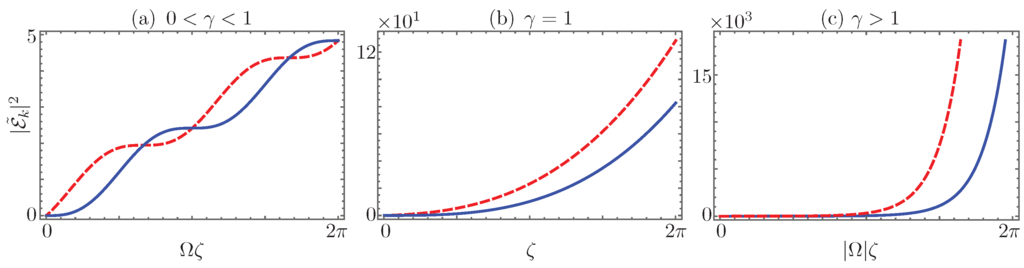
Figure 12.
Spontaneous generation of radiation in the waveguides with effective loss, solid blue line, and gain, dashed red line, in the (a) -symmetric regime, ; (b) fully-degenerate regime, ; and (c) broken symmetry regime, , for quantum vacuum fields in both waveguides.
7. Conclusions
We have presented a review of the -symmetric dimer in its linear, nonlinear and quantum versions and show that it belongs to a symmetry class with underlying symmetry, realized as a complexification of the group, that allows the description of N-waveguide couplers. We have aimed to present a coherent narrative of the different approaches to the optical -symmetric dimer and relate them to the underlying symmetry of the model. In doing this, we introduce the idea of using a non-Hermitian version of the Ehrenfest theorem to approach the propagation dynamics of waveguide couplers described by non-Hermitian mode coupling matrices.
The field is young, and there still exist fundamental open questions on the subject, such as the analytic determination of critical effective nonlinearity to coupling ratios for the Kerr nonlinear -symmetric dimer; the need for a deeper understanding of the non-unitary finite dimensional representations of , realized without resorting to the complexified representations; the generalization to propagation-dependent photonic systems together with the possible applications; just to mention a few that we hope to address in future work.
Acknowledgments
José Delfino Huerta Morales acknowledges financial support from the CONACYT #294921 Ph.D. grant. Julio Guerrero acknowledges financial support from Spanish projects DPI2015-47100-C2-1-P and FIS2014-57387-C3-3-P. Servando Lopez-Aguayo acknowledges financial support from CONACYT #243284 grant.
Author Contributions
All authors contributed equally to this work.
Conflicts of Interest
B.M.R.-L. is the guest editor for the Symmetry Special Issue on -symmetry in optics and photonics. The rest of the authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript; nor in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
Real and imaginary parts of x, in that order | |
Parity-Time | |
| , , | Unitary group, special unitary group, special orthogonal group of degree N |
Pseudo orthogonal group, Lorentz group, in 2+1 dimension. |
References
- Garmire, E.; Stoll, H.; Yariv, A.; Hunsperger, R.G. Optical waveguiding in proton-implanted GaAs. Appl. Phys. Lett. 1972, 21, 87–88. [Google Scholar] [CrossRef]
- Marcatili, E.A.J. Dielectric rectangular waveguide and directional coupler for integrated optics. Bell Syst. Tech. J. 1969, 48, 2071–2102. [Google Scholar] [CrossRef]
- Somekh, S.; Garmire, E.; Yariv, A.; Garvin, H.L.; Hunsperger, R.G. Channel optical waveguide directional couplers. Appl. Phys. Lett. 1973, 22, 46–47. [Google Scholar] [CrossRef]
- Chen, Y.; Snyder, A.W.; Payne, D.N. Twin core nonlinear couplers with gain and loss. IEEE J. Quantum Elect. 1992, 28, 239–245. [Google Scholar] [CrossRef]
- Bender, C.M. Real spectra in non-Hermitian Hamiltonians having -symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- Bender, C.M. Introduction to -symmetric quantum theory. Contemp. Phys. 2005, 46, 277–292. [Google Scholar] [CrossRef]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947–1018. [Google Scholar] [CrossRef]
- Ruschhaupt, A.; Delgado, F.; Muga, J.G. Physical realization of -symmetric potential scattering in a planar slab waveguide. J. Phys. A Math. Gen. 2005, 38, L171–L176. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Makris, K.G.; Christodoulides, D.N.; Musslimani, Z.H. Theory of coupled optical -symmetric structures. Opt. Lett. 2007, 32, 2632–2634. [Google Scholar] [CrossRef] [PubMed]
- Klaiman, S.; Günther, U.; Moiseyev, N. Visualization of branch points in -symmetric waveguides. Phys. Rev. Lett. 2008, 101, 080402. [Google Scholar] [CrossRef] [PubMed]
- Mostafazadeh, A. Spectral singularities of complex scattering potentials and infinite reflection and transmission coefficients at real energies. Phys. Rev. Lett. 2009, 102, 220402. [Google Scholar] [CrossRef] [PubMed]
- Berry, M.V. Optical lattices with -symmetry are not transparent. J. Phys. A Math. Theor. 2008, 41, 244007. [Google Scholar] [CrossRef]
- Longhi, S. -symmetric laser absorber. Phys. Rev. A 2010, 82, 031801. [Google Scholar] [CrossRef]
- Longhi, S.; Valle, G.D.; Staliunas, K. Goos-Hänchen shift in complex crystals. Phys. Rev. A 2011, 84, 042119. [Google Scholar] [CrossRef]
- Lin, Z.; Ramezani, H.; Eichelkraut, T.; Kottos, T.; Cao, H.; Christodoulides, D.N. Unidirectional Invisibility Induced by -Symmetric Periodic Structures. Phys. Rev. Lett. 2011, 106, 213901. [Google Scholar] [CrossRef] [PubMed]
- Miri, M.A.; Heinrich, M.; Christodoulides, D.N. Supersymmetry-generated complex optical potentials with real spectra. Phys. Rev. A 2013, 87, 043819. [Google Scholar] [CrossRef]
- Kozlov, M.; Tsironis, G.P. Control of power in parity-time symmetric lattices. New J. Phys. 2015, 17, 105004. [Google Scholar] [CrossRef]
- Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Musslimani, Z.H. Beam dynamics in -symmetric optical lattices. Phys. Rev. Lett. 2008, 100, 103904. [Google Scholar] [CrossRef] [PubMed]
- Longhi, S. Bloch Oscillations in Complex Crystals with Symmetry. Phys. Rev. Lett. 2009, 103, 123601. [Google Scholar] [CrossRef] [PubMed]
- Joglekar, Y.N.; Thompson, C.; Vemuri, H. Tunable waveguide lattices with nonuniform parity-symmtrey tunneling. Phys. Rev. A 2011, 83, 063817. [Google Scholar] [CrossRef]
- Vemuri, H.; Vavilala, V.; Bhamidipati, T.; Joglekar, Y.N. Dynamics, disorder effects, and -symmetry breaking in waveguide. Phys. Rev. A 2011, 84, 043826. [Google Scholar] [CrossRef]
- Ramezani, H.; Kottos, T.; Kovanis, V.; Christodoulides, D.N. Exceptional-point dynamics in photonic honeycomb lattices with symmetry. Phys. Rev. A 2012, 85, 013818. [Google Scholar] [CrossRef]
- Vemuri, H.; Joglekar, Y.N. -Symmetric lattices with local degree of freedom. Phys. Rev. A 2013, 87, 044101. [Google Scholar] [CrossRef]
- Joglekar, Y.N.; Thompson, C.; Scott, D.D.; Vemuri, G. Optical waveguide arrays: quantum effects and symmetry breaking. Eur. Phys. J. Appl. Phys. 2013, 63, 30001. [Google Scholar] [CrossRef]
- Longhi, S. Bound states in the continuum in -symmetric optical lattices. Opt. Lett. 2014, 39, 1697–1700. [Google Scholar] [CrossRef] [PubMed]
- Chern, G.W.; Saxena, A. -symmetric phase in Kagome-based photonic lattices. Opt. Lett. 2015, 40, 5806–5809. [Google Scholar] [CrossRef] [PubMed]
- Musslimani, Z.H.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N. Optical solitons in periodic potentials. Phys. Rev. Lett. 2008, 100, 030402. [Google Scholar] [CrossRef] [PubMed]
- Ramezani, H.; Kottos, T.; El-Ganainy, R.; Christodoulides, D.N. Unidirectional nonlinear -symmetric optical structures. Phys. Rev. A 2010, 82, 043803. [Google Scholar] [CrossRef]
- Sukhorukov, A.A.; Xu, Z.; Kivshar, Y.S. Nonlinear suppression of time reversals in -symmetric optical couplers. Phys. Rev. A 2010, 82, 043818. [Google Scholar] [CrossRef]
- Driben, R.; Malomed, B.A. Stability of solitons in parity-time-symmetric couplers. Opt. Lett. 2011, 36, 4323–4325. [Google Scholar] [CrossRef] [PubMed]
- Regensburger, A.; Bersch, C.; Miri, M.A.; Onishchukov, G.; Christodoulides, D.N.; Peschel, U. Parity-time synthetic photonic lattices. Nature 2012, 488, 167–171. [Google Scholar] [CrossRef] [PubMed]
- Sukhorukov, A.A.; Dmitriev, S.V.; Suchkov, V.; Kivshar, Y.S. Nonlocality in -symmetric waveguide arrays with gain and loss. Opt. Lett. 2012, 37, 2148–2150. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Kevrekidis, B.A.; Malomed, B.A.; Günther, U. Nonlinear -symmetric plaquettes. J. Phys. A Math. Theor. 2012, 45, 444201. [Google Scholar] [CrossRef]
- Li, K.; Kevrekidis, B.A.; Malomed, B.A. Nonlinear modes and symmetries in linearly-coupled pairs of -invariant dimers. Stud. Appl. Math. 2014, 133, 281–297. [Google Scholar] [CrossRef]
- Kevrekidis, P.G.; Pelinovsky, D.E.; Tyugin, D.Y. Nonlinear dynamics in -symmetric lattices. J. Phys. A Math. Theor. 2013, 46, 365201. [Google Scholar] [CrossRef]
- Barashenkov, I.V.; Jackson, G.S.; Flach, S. Blow-up regimes in the -symmetric coupler and the actively coupled dimer. Phys. Rev. A 2013, 88, 053817. [Google Scholar] [CrossRef]
- Khawaja, U.A.; Al-Marzoug, S.M.; Bahlouli, H.; Kivshar, Y.S. Unidirectional soliton flows in -symmetric potentials. Phys. Rev. A 2013, 88, 023830. [Google Scholar] [CrossRef]
- Lumer, Y.; Plotnik, Y.; Rechtsman, M.C.; Segev, M. Nonlinearly induced transition in photonic systems. Phys. Rev. Lett. 2013, 111, 263901. [Google Scholar] [CrossRef] [PubMed]
- Barashenkov, I.V. Hamiltonian formulation of the standard -symmetric nonlinear Schrödinger dimer. Phys. Rev. A 2014, 90, 045802. [Google Scholar] [CrossRef]
- Zhang, X.; Chai, J.; Huang, J.; Chen, Z.; Li, Y.; Malomed, B.A. Discrete solitons and scattering of lattice waves in guiding arrays with a nonlinear -symmetric defect. Opt. Express 2014, 22, 13927–13939. [Google Scholar] [CrossRef] [PubMed]
- Barashenkov, I.V.; Pelinovsky, D.E.; Dubard, P. Dimer with gain and loss: Integrability and -symmetry restoration. J. Phys. A Math. Theor. 2015, 48, 325201. [Google Scholar] [CrossRef]
- Martínez, A.J.; Molina, M.I.; Turitsyn, S.K.; Kivshar, Y.S. Nonlinear multicore waveguiding structures with balanced gain and loss. Phys. Rev. 2015, 91, 023822. [Google Scholar] [CrossRef]
- Walasik, W.; Litchinitser, N.M. Phase transition in multimode nonlinear parity-time-symmetric Dimer. Sci. Rep. 2015, 6, 19826. [Google Scholar] [CrossRef] [PubMed]
- Cole, J.T.; Makris, K.G.; Musslimani, Z.H.; Christodoulides, D.N.; Rotter, S. Twofold -symmetry in doubly exponential optical lattices. Phys. Rev. A 2016, 93, 013803. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Vysloukh, V.A.; Konotop, V.V.; Torner, L. Diffraction control in -symmetric photonic lattices: From beam rectification to dynamic localization. Phys. Rev. A 2016, 93, 013841. [Google Scholar] [CrossRef]
- Ding, S.; Wang, G.P. All-optical transistors and logic gates using a parity-time-symmetric Y-junction: Design and simulation. J. Appl. Phys. 2015, 118, 123104. [Google Scholar] [CrossRef]
- Zaragoza Gutiérrez, O.I.; Salinas Mendoza, L.F.; Rodríguez-Lara, B.M. All-optical -symmetric conversion of amplitude (phase) modulation to phase (amplitude) modulation. Opt. Express 2015, 24, 3989–3998. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Lara, B.M.; Guerrero, J. Optical finite representation of the Lorentz group. Opt. Lett. 2015, 40, 5682–5685. [Google Scholar] [CrossRef] [PubMed]
- Guo, A.; Salamo, G.J.; Duchesne, D.; Morandotti, R.; Volatier-Ravat, M.; Aimez, V.; Siviloglou, G.A.; Christodoulides, D.N. Observation of -symmetric breaking in complex optical potentials. Phys. Rev. Lett. 2009, 103, 093902. [Google Scholar] [CrossRef] [PubMed]
- Ornigotti, M.; Szameit, A. Quasi -symmetry in passive photonic lattices. J. Opt. 2014, 16, 065501. [Google Scholar] [CrossRef]
- Rüter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Kip, D. Observation of parity-time symmetry in optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef]
- Peng, B.; Ozdemir, S.K.; Lei, F.C.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.H.; Nori, F.; Bender, C.M.; Yang, L. Parity-time-symmetric whispering-gallery microcavities. Nat. Phys. 2014, 10, 394–398. [Google Scholar] [CrossRef]
- Hodaei, H.; Miri, M.A.; Heinrich, M.; Christodoulides, D.N.; Khajavikhan, M. Parity-time–symmetric microring lasers. Science 2014, 346, 975–978. [Google Scholar] [CrossRef] [PubMed]
- Schindler, J.; Lin, Z.; Lee, J.M.; Ramezani, H.; Ellis, F.M.; Kottos, T. -symmetric electronics. J. Phys. A Math. Theor. 2012, 45, 444029. [Google Scholar] [CrossRef]
- Kato, T. Perturbation Theory for Linear Operators; Springer-Verlag: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Van der Pool, B. The nonlinear theory of electric oscillations. Proc. Inst. Radio Eng. 1934, 22, 1051–1086. [Google Scholar] [CrossRef]
- Bender, N.; Factor, S.; Bodyfelt, J.D.; Ramezani, H.; Christodoulides, D.N.; Kottos, T. Observation of asymmetric transport in structures with active nonlinearities. Phys. Rev. Lett. 2013, 110, 234101. [Google Scholar] [CrossRef] [PubMed]
- Graefe, E.M.; Korsch, H.J.; Niederle, A.E. Mean-field dynamics of a non-Hermitian Bose-Hubbard dimer. Phys. Rev. Lett. 2008, 101, 150408. [Google Scholar] [CrossRef] [PubMed]
- Graefe, E.M.; Günther, U.; Korsch, H.J.; Niederle, A.E. A non-Hermitian -symmetric Bose-Hubbard model: eigenvalue rings from unfolding higher-order exceptional points. J. Phys. A Math. Theor. 2008, 41, 255206. [Google Scholar] [CrossRef]
- Graefe, E.M.; Korsch, H.J.; Niederle, A.E. Quantum-classical correspondence for a non-Hermitian Bose-Hubbard dimer. Phys. Rev. A 2010, 82, 013629. [Google Scholar] [CrossRef]
- Graefe, E.M. Stationary states of a -symmetric two-mode Bose-Einstein condensate. J. Phys. A Math. Theor. 2012, 45, 444015. [Google Scholar] [CrossRef]
- Smerzi, A.; Fantoni, S.; Giovanazzi, S.; Shenoy, S.R. Quantum coherent atomic tunneling between two trapped Bose-Einstein condensates. Phys. Rev. Lett. 1997, 79, 4950–4953. [Google Scholar] [CrossRef]
- Rodríguez-Lara, B.M.; Lee, R.K. Classical dynamics of a two-species condensate driven by a quantum field. Phys. Rev. E 2011, 84, 016225. [Google Scholar] [CrossRef] [PubMed]
- Villanueva Vergara, L.; Rodríguez-Lara, B.M. Gilmore-Perelomov symmetry based approach to photonic lattices. Opt. Express 2015, 23, 22836–22846. [Google Scholar] [CrossRef] [PubMed]
- Bellec, M.; Nikolopoulos, G.M.; Tzortzakis, S. Faithful communication Hamiltonian in photonic lattices. Opt. Lett. 2012, 37, 4504–4506. [Google Scholar] [CrossRef] [PubMed]
- Perez-Leija, A.; Keil, R.; Kay, A.; Moya-Cessa, H.; Nolte, S.; Kwek, L.C.; Rodríguez-Lara, B.; Szameit, A.; Christodoulides, D. Coherent quantum transport in photonic lattices. Phys. Rev. A 2013, 87, 012309. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Eisfeld, A.; Levy, M.; Christodoulides, D.N. On-chip non-reciprocal optical devices based on quantum inspired photonic lattices. Appl. Phys. Lett. 2013, 103, 161105. [Google Scholar] [CrossRef]
- Rodríguez-Lara, B.M.; Moya-Cessa, H.M.; Christodoulides, D.N. Propagation and perfect transmission in three-waveguide axially varying couplers. Phys. Rev. A 2014, 89, 013802. [Google Scholar] [CrossRef]
- Chapman, R.J.; Santadrea, M.; Huang, Z.; Corrielli, G.; Crespi, A.; Yung, M.H.; Osellame, R.; Peruzzo, A. Experimental perfect quantum state transfer. Nat. Commun. 2016, 7, 11339. [Google Scholar] [CrossRef] [PubMed]
- Teimourpour, M.H.; El-Ganainy, R.; Eisfeld, A.; Szameit, A.; Christodoulides, D.N. Light transport in -invariant photonic structures with hidden symmetries. Phys. Rev. A 2014, 90, 053817. [Google Scholar] [CrossRef]
- Dattoli, G.; Torre, A.; Mignani, R. Non-Hermitian evolution of two-level quantum systems. Phys. Rev. A 1990, 42, 1467–1475. [Google Scholar] [CrossRef] [PubMed]
- Politi, A.; Cryan, M.J.; Rarity, J.G.; Yu, S.; O’Brien, J.L. Silica-on-Silicon waveguide quantum circuits. Science 2008, 320, 646–649. [Google Scholar] [CrossRef] [PubMed]
- Sattinger, D.H.; Weaver, O.L. Lie Groups and Algebras with Applications to Physics, Geometry and Mechanics; Springer-Verlag: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Agarwal, G.S.; Qu, K. Spontaneous generation of photons in transmission of quantum fields in -symmetric optical systems. Phys. Rev. A 2012, 85, 031802. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).