Decoration of the Truncated Tetrahedron—An Archimedean Polyhedron—To Produce a New Class of Convex Equilateral Polyhedra with Tetrahedral Symmetry
1
California NanoSystems Institute, Mailcode 722710, University of California, Los Angeles (UCLA), Los Angeles, CA 90095, USA
2
Brain Research Institute, Mailcode 951761, University of California, Los Angeles (UCLA), Los Angeles, CA 90095, USA
3
Department of Psychology, Mailcode 951563, University of California, Los Angeles (UCLA), Los Angeles, CA 90095, USA
4
Department of Chemistry and Biochemistry, Mailcode 951569, University of California, Los Angeles (UCLA), Los Angeles, CA 90095, USA
5
Department of Applied Mathematics, Computer Science and Statistics, Ghent University, Krijgslaan 281-S9, B-9000 Gent, Belgium
6
Department of Psychology, Mailcode 951563, University of California, Los Angeles (UCLA), Los Angeles, CA 90095, USA
*
Author to whom correspondence should be addressed.
Symmetry 2016, 8(8), 82; https://doi.org/10.3390/sym8080082
Submission received: 27 July 2016
/
Revised: 12 August 2016
/
Accepted: 16 August 2016
/
Published: 20 August 2016
(This article belongs to the Special Issue Polyhedral Structures)
Abstract
:The Goldberg construction of symmetric cages involves pasting a patch cut out of a regular tiling onto the faces of a Platonic host polyhedron, resulting in a cage with the same symmetry as the host. For example, cutting equilateral triangular patches from a 6.6.6 tiling of hexagons and pasting them onto the full triangular faces of an icosahedron produces icosahedral fullerene cages. Here we show that pasting cutouts from a 6.6.6 tiling onto the full hexagonal and triangular faces of an Archimedean host polyhedron, the truncated tetrahedron, produces two series of tetrahedral (Td) fullerene cages. Cages in the first series have 28n2 vertices (n ≥ 1). Cages in the second (leapfrog) series have 3 × 28n2. We can transform all of the cages of the first series and the smallest cage of the second series into geometrically convex equilateral polyhedra. With tetrahedral (Td) symmetry, these new polyhedra constitute a new class of “convex equilateral polyhedra with polyhedral symmetry”. We also show that none of the other Archimedean polyhedra, six with octahedral symmetry and six with icosahedral, can host full-face cutouts from regular tilings to produce cages with the host’s polyhedral symmetry.
1. Introduction
Known to the ancient Greeks, the five Platonic polyhedra and 13 Archimedean polyhedra are the first two classes of convex equilateral polyhedra with polyhedral symmetry (icosahedral, octahedral or tetrahedral) [1]. In 1611, Johannes Kepler added a third class, the rhombic polyhedra [2]. A fourth class, the “Goldberg polyhedra”, was recently described [3]. These are primarily icosahedral fullerene cages transformed into geometrically convex equilateral polyhedra—which necessarily have convex planar faces [4,5].
Preceding the work on icosahedral viruses by Caspar and Klug [6], Goldberg’s construction of icosahedral fullerene cages employed decoration of the full equilateral triangular faces of a host icosahedron (Figure 1a, left) with equilateral triangular cutouts from a tiling of regular hexagons (Figure 1b, left) [7,8,9]. The resulting cages have the same symmetry as the host icosahedron. They also have 3-valent vertices, hexagons and 12 pentagons (Figure 1c, left). Of the other of the five Platonic (or regular) polyhedra (Figure 2a), the octahedron (Figure 1a, middle) and the tetrahedron (Figure 1a, right) also have equilateral triangular faces and can serve as hosts that can be decorated similarly (Figure 1b) to produce octahedral cages with hexagons and six squares (Figure 1c, middle) and tetrahedral cages with hexagons and four triangles (Figure 1c, right) [7].
The triangular cutouts of the tiling of hexagons can be different sizes and orientations, with the pattern still neatly continuing across the borders of adjacent triangular faces and across the gaps that span 1, 2 or 3 triangles (Figure 1b). These size and orientation variants can be expressed by indices (h,k) that characterize one side of the equilateral triangular cutout, where h indicates steps (from the center of one hexagon to the center of next) along one axis of the tiling of hexagons and k indicates steps along a second axis at 60 degrees to the first [6,7,8,9]. For example, the indices in Figure 1b are (2,1). These indices also make it easy to calculate the number T = h2 + hk + k2 of vertices in each equilateral triangle [6,7,8,9]. In Figure 1, there are thus 22 + 1 × 1 + 12 = 7 vertices in each triangle. Similarly, square cutouts in a variety of sizes and orientations from a tiling of squares can decorate the full square faces of a cube to produce octahedral cages with 4-gons and eight triangles [10].
Here, we show that just one of the Archimedean polyhedra (Figure 2b–d), the truncated tetrahedron (Figure 2b), can be similarly decorated. Specifically, we paste regular hexagonal and triangular patches cut out of a 2D tiling of hexagons onto the full hexagonal and triangular faces of a truncated tetrahedron. This “re-tiling” of the truncated tetrahedron produces 3D cages with the same symmetry as the host polyhedron, in this case tetrahedral (Td) symmetry. For a subset of these new Td cages we can produce geometrically convex equilateral polyhedra with Td symmetry, thus creating another class of convex equilateral polyhedra with polyhedral symmetry.
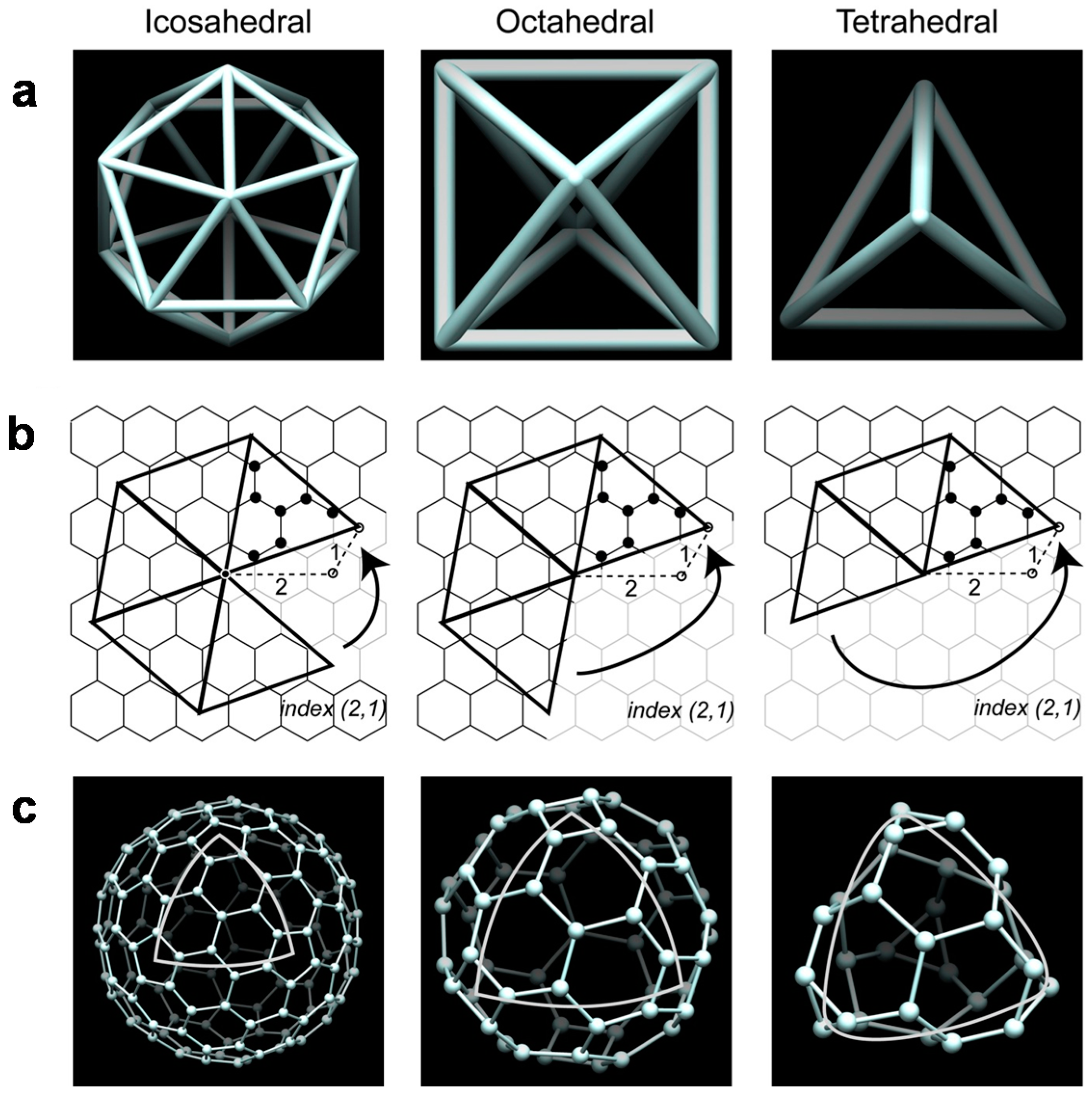
2. Materials and Methods
We used Carbon Generator (CaGe) software [11] (https://caagt.ugent.be/CaGe/) to produce cages, specifically Schlegel diagrams, w3d files and spinput files. We used the Equi program (http://caagt.ugent.be/equi/) to read the w3d files and make the cages equilateral (with edges of 5 units) and with planar faces, producing w3d and spinput files for the resulting equilateral polyhedra. We used Spartan software (Wavefunction, Inc., Irvine, CA, USA) [12] to read spinput files and produce the data in the supplementary tables and the pdb files that can by read by UCSF (University of California, San Francisco) Chimera [13].
3. Results
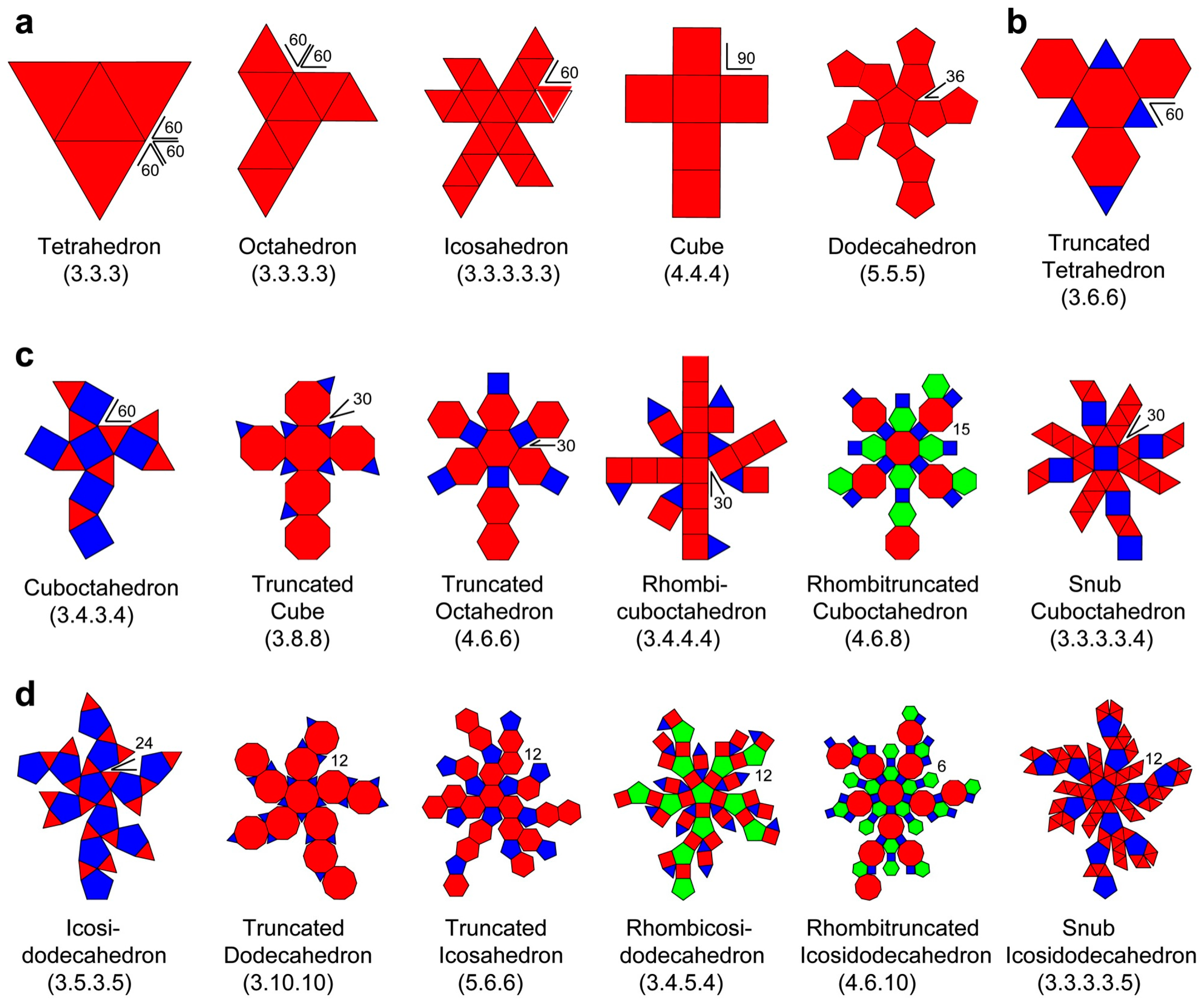
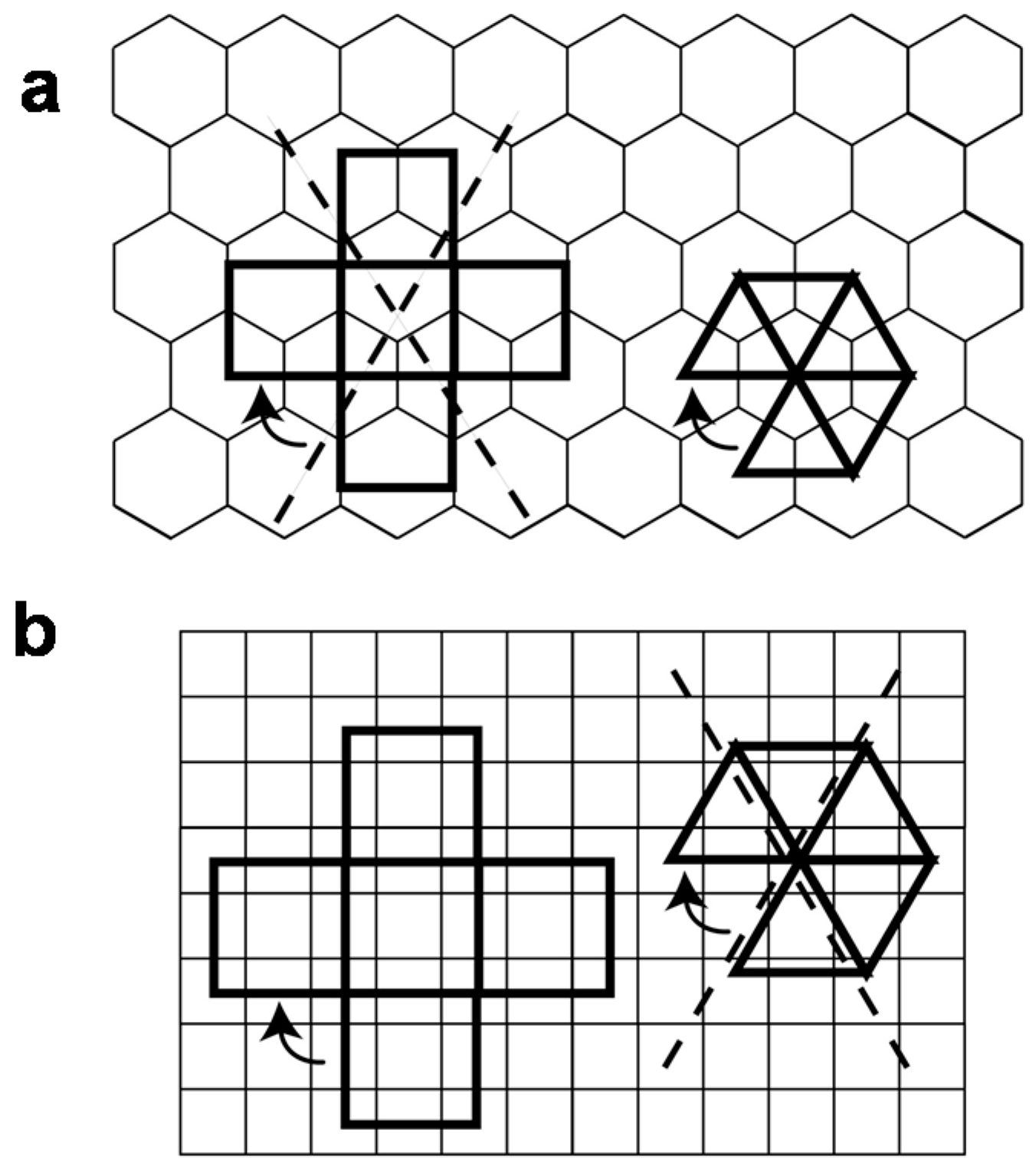
3.1. Decoration of an Archimedean Polyhedron to Produce New Cages
We ask if we can produce cages by decorating any of the 13 Archimedean polyhedra (Figure 2b–d), each with more than one type of regular face, with cutouts of a regular tiling. Although the truncated icosahedron—or soccer ball—is the most famous of the Archimedean polyhedra [14], the first one we consider is the truncated tetrahedron, which has four regular hexagons and four equilateral triangles (Figure 2b and Figure 3a). We can decorate its eight full faces with contiguous hexagonal and triangular cutouts from a 2D tiling of hexagons (top of Figure 3b, labeled (3,0 and 1,1)), with the pattern of the tiling neatly annealing across the borders of all the faces, as indicated by the dashed arrows. Only two orientations and certain sizes of hexagonal and triangular cutouts neatly fit the full faces of the truncated tetrahedron, one group (e.g., (3,0 and 1,1) and (6,0 and 2,2)) illustrated in Figure 3b, the other group (e.g., (1,1 and 1,0), (2,2 and 2,0) and (3,3 and 3,0)) in Figure 3c. By contrast, cutouts from a tiling of squares would not fit neatly into hexagons or triangles (Figure 4).
The new cages based on decoration of the full faces of the truncated tetrahedron have tetrahedral symmetry, specifically the point group Td of the host, 3-valent vertices, hexagons and 12 pentagons. They are therefore a subset of the tetrahedral (Th, Td and T) fullerene cages, even a subset of the Td fullerene cages, the construction of which was described in 1988 [15]. The latter construction created tetrahedral fullerenes from four sets of five triangles (Figure 3d), each set containing a large equilateral triangle (α), three scalene triangles (β) and a small equilateral triangle (γ), all decorated with a tiling of hexagons. (To show the 3-fold axis centered on the large equilateral triangle (α) in Figure 3d, each small equilateral triangle (γ) is divided into three thirds.) Our new Td cages, with four hexagons and four triangles, can be similarly described, with each hexagonal cutout providing the large equilateral triangle (α) and the three scalene—isosceles in this case—triangles (β), and each triangular cutout providing the small equilateral triangle (γ) (Figure 3b,c).
The equilateral triangles assembled to produce icosahedral fullerene cages can be described by Goldberg indices (h,k) that characterize one edge of the triangle (e.g., 2,1 in Figure 1b). Likewise, for the tetrahedral fullerenes, the large equilateral triangle in the construction can be described by indices (i,j) (containing i2 + ij + j2 vertices), and the small equilateral triangle can be described by its own indices (k,l) (containing k2 + kl + l2 vertices) [15]. The isosceles triangles contain the same number of vertices as the small equilateral triangle (Figure 3b,c). Therefore, for most of the cutouts in Figure 3b,c, we show just one regular hexagon (with its large equilateral triangle and three isosceles triangles) and one equilateral triangle (that becomes the small equilateral triangle).
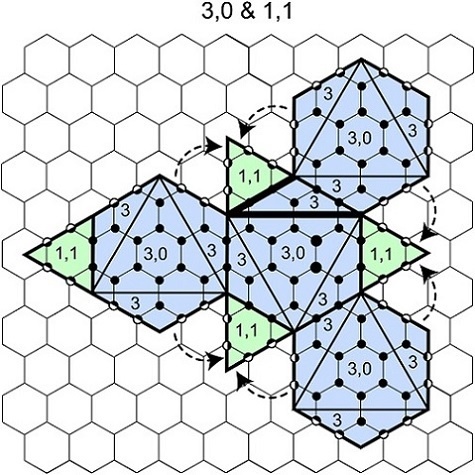
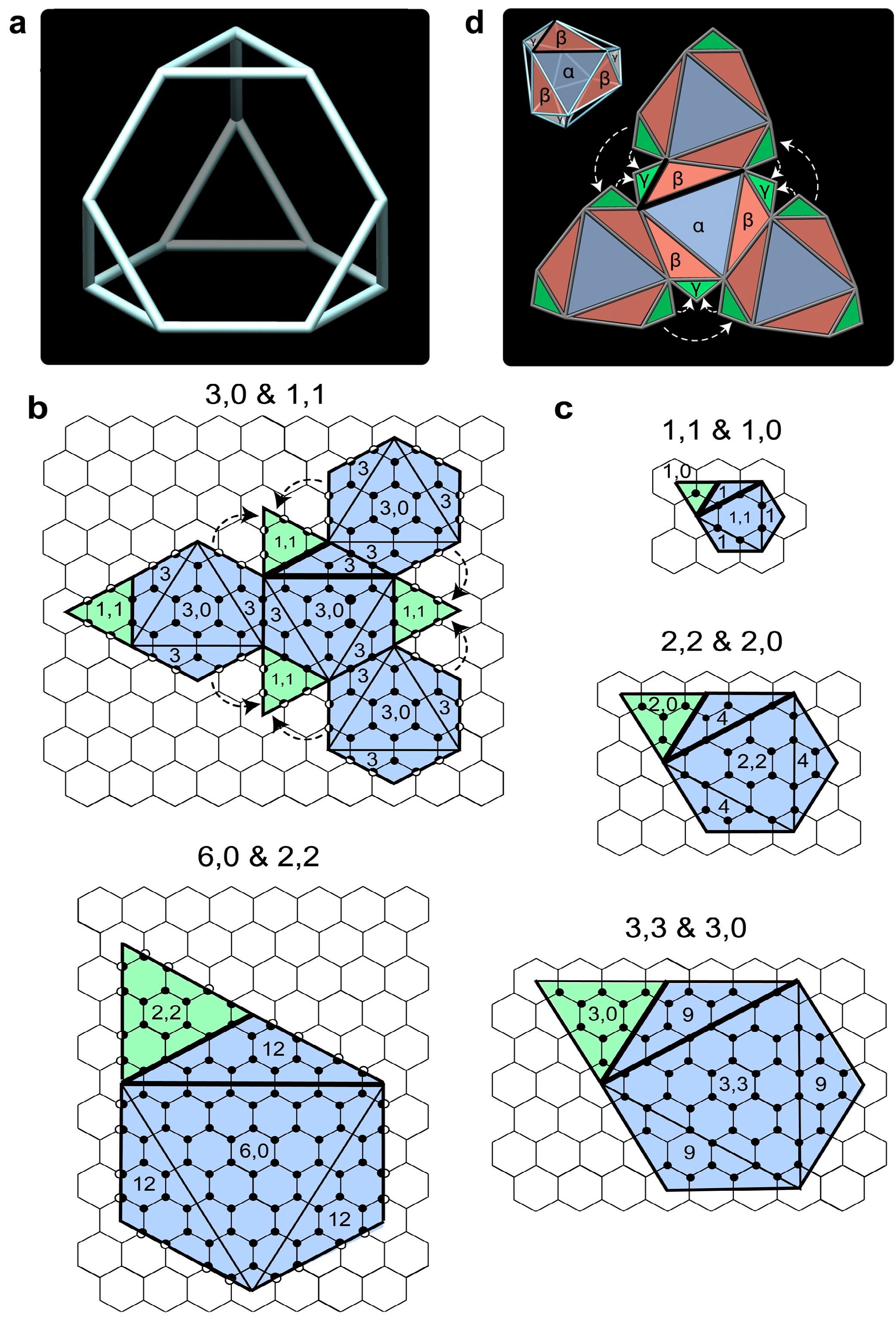
3.2. Two Series of the New Td Cages
One series of the new cages have large and small equilateral triangles with indices (1,1 and 1,0), (2,2 and 2,0), (3,3 and 3,0), etc. (Figure 3c) The other series are leapfrogs [9] of the first, with indices (3,0 and 1,1), (6,0 and 2,2), (9,0 and 3,3), etc. (Figure 3b). Arranging the indices and calculating the total numbers of vertices (Table 1) shows that the cages in the first series have 28n2 vertices (n ≥ 1), whereas the cages in the second series have 3 × 28n2, the triplication expected for leapfrogs. These new Td fullerene cages represent only a few of the possible Td fullerene cages [15].
We make these Td cages with Carbon Generator (CaGe) software [11]. Figure 5 shows two-dimensional (Schlegel) diagrams of the first four of the first series and the first two of the second (leapfrog) series. A geometric “cage” may have nonplanar faces, as can be seen in the equilateral cages in Figure 1c [3].
3.3. Production of Equilateral Polyhedra from the New Td Cages
Geometrically “convex polyhedra” are also cages, but they must have planar faces and point outward at every vertex [4,5]. Thus, if one were to place a flat plane on any face of a convex polyhedron, the plane would not intersect any of the other faces [4,5]. With two exceptions—the dodecahedron and the truncated icosahedron—equilateral icosahedral Goldberg cages with internal angles in hexagons near 120° have nonplanar faces and are therefore not polyhedra [3] (e.g., Figure 1c). However, it is possible to make the faces of these cages planar and produce convex equilateral icosahedral polyhedra by adjusting internal angles in the faces [3].
We attempted to transform all of the new Td cages into equilateral tetrahedral polyhedra with Equi, a program that is able to numerically solve equations for equal edge lengths and for planarity of faces. Equi uses a numerical method to obtain x, y and z coordinates of the V vertices by solving a system of multivariate nonlinear equations in 3V-6 variables (3 coordinates for each vertex minus 6 degrees of freedom corresponding to translation and rotation of the solution in 3-dimensional space). The system consists of two types of equations: There are 3V/2 quadratic “edge length equations” (1 for each edge) and 3V “face planarity equations” (n for each n-gonal face). The system is over-determined—n-3 equations for each n-gonal face would suffice—but using more equations makes the algorithm more stable. The numerical method is a variant of the well-known Gauss-Newton algorithm for finding a minimum of a function [16] with an added symmetrization step after each iteration to ensure the tetrahedral symmetry (Td) of the result. The coordinates we obtain are accurate to 8 digits, but we could improve the accuracy further if there were reason to do so. The current version of the algorithm can handle cages of up to 2800 vertices within a reasonable time frame on a conventional computer. In the future it might be possible to increase this limit by taking full advantage of the tetrahedral symmetry, requiring a major redesign of the algorithm.
Although the program is not yet able to solve for the coordinates and angles in very large cages, we can transform all of the first nine cages in the first series into geometrically convex equilateral polyhedra with Td symmetry (“+” symbols in Table 1). Figure 6a shows the first five. (Details are provided in Figure S1 and Tables S1–S3.) We suggest that all of the new Td cages in the first series, including larger ones, can be so transformed.
However, for the cages in the second (leapfrog) series, only the smallest with 84 vertices could be transformed into a convex equilateral polyhedron (Figure 6b; Table 1; Figure S1; Tables S1–S3). None of the larger ones, with 336, 756, 1344, and 2100 vertices, could be so transformed. We suggest that none of new leapfrog Td cages with more than 84 vertices can be transformed into geometrically convex equilateral polyhedra.
We reported that all achiral icosahedral fullerenes with T (= h2 + hk + k2) ≤ 49 (980 vertices) and all chiral fullerenes with T ≤ 37 (740 vertices) can be transformed into geometrically convex equilateral icosahedral polyhedra [3]. Here, we add that with Equi we have been able to so transform all 40 of the icosahedral fullerenes with T ≤ 108 (2160 vertices)—all of the (h,0) ones from (1,0) to (10,0), all of the (h,h) ones from (1,1) to (6,6) and all of the (h,k) ones from (2,1) to (9,2). Therefore, we suggest that the failure of the larger leapfrog Td cages to transform into convex equilateral polyhedra is real and not a failure of our methods.
4. Discussion
Above, we suggest that all of the first class of new Td cages can be transformed into geometrically convex equilateral polyhedra with Td symmetry. By contrast, only the smallest of their leapfrogs can be so transformed. There are precedents for this situation among the Goldberg cages. On the one hand, we can produce convex equilateral icosahedral polyhedra from all 40 of the icosahedral Goldberg cages that we have tried. On the other hand, among the octahedral Goldberg cages, beyond h,k = 1,0 (the Platonic octahedron) and h,k = 1,1 (the Archimedean truncated octahedron), we are able to make just one more convex equilateral polyhedron, h,k = 2,0. Larger ones have coplanar 4-gonal faces and are thus not convex; correspondingly, for a few of these we are able to show that the only equilateral planar solutions require some vertices with internal angles that sum to 360° [3]. Likewise, among the tetrahedral Goldberg cages, beyond h,k = 1,0 (the Platonic tetrahedron) and h,k = 1,1 (the Archimedean truncated tetrahedron), we are able to transform just one into a convex equilateral polyhedron, also h,k = 2,0 [3], but none of the larger ones.
Could we use any other of the Archimedean polyhedra as hosts? Is it possible to fit cutouts from a two-dimensional tiling of regular hexagons (6.6.6) or from a tiling of regular squares (4.4.4.4) onto the full faces of some other Archimedean polyhedron and have the tiling pattern knit across the edges of the host polyhedron’s faces [17]. To see what cutouts are needed, we list the faces (e.g., regular 5-gons, 8-gons, etc.) at each vertex in the remaining 12 Archimedean polyhedra, six with octahedral symmetry (3.4.3.4; 3.4.4.4; 3.8.8; 4.6.6; 4.6.8; 3.3.3.3.4) and six with icosahedral (3.4.5.4; 3.5.3.5; 3.10.10; 4.6.10; 5.6.6; 3.3.3.3.5) (Figure 2). From a 4.4.4.4 tiling, 3-gonal or 6-gonal cutouts do not exhibit 3-fold or 6-fold symmetry and do not permit knitting of the 4.4.4.4 tiling across the edges of the 3-gonal or 6-gonal faces of a host (Figure 4), thus eliminating all of the octahedral Archimedean polyhedra as potential hosts. Likewise, from a 6.6.6 tiling, 4-gonal, 5-gonal or 10-gonal cutouts do not exhibit 4-fold, 5-fold or 10-fold symmetry, respectively, and do not permit knitting of the 6.6.6 tiling across the edges of the 4-gonal, 5-gonal or 10-gonal faces of a host (Figure 4), thus eliminating all of the icosahedral Archimedean polyhedra as potential hosts. Therefore, the only admissible combination of a regular tiling and an Archimedean polyhedron as host is a tiling of hexagons and the truncated tetrahedron.
5. Conclusions
The Platonic and Archimedean polyhedra have tetrahedral, octahedral and icosahedral symmetry, lumped together as “polyhedral symmetry” [1]. The polyhedra in these two classes of “convex equilateral polyhedra with polyhedral symmetry” have regular faces. A third class of convex equilateral polyhedra with polyhedral symmetry is comprised of the rhombic polyhedra discovered by Kepler, the rhombic dodecahedron and the rhombic triacontahedron [2]. Like the rhombic polyhedra, members of a fourth class called “Goldberg polyhedral” [3] have faces, the 6-gons, that are not regular. (Because axes of 5-fold, 4-fold and 3-fold symmetry pass through the centers of their 3-gons, 4-gons and 5-gons, the smaller faces of these tetrahedral, octahedral and icosahedral polyhedra are regular.) Here we report another new class, constructed by decorations of the full faces of an Archimedean polyhedron, the truncated tetrahedron, with cutouts from a 6.6.6 tiling of regular hexagons. Although neither the 5-gons nor the 6-gons are regular, they are equilateral and planar.
Supplementary Materials
The following are available online at www.mdpi.com/2073-8994/8/8/82/s1. Figure S1: Vertex numbers for the first series of new Td polyhedra with 28, 112, 252, 448 and 700 vertices and for the other (leapfrog) series with 84 vertices; Table S1: Coordinates of vertices in the new Td polyhedra, the first series with 28, 112, 252, 448 and 700 vertices, the second (leapfrog) series with 84 vertices. Vertex numbering is shown in Figure S1. Edge lengths are 5 units; Table S2: Internal angles in faces in the new polyhedra. Vertex numbering is shown in Figure S1. The data come directly from Spartan, which provides three angles per vertex, but approximately one angle in each face is duplicated, leaving one other missing. However, the missing angles can be found by taking advantage of the symmetry of the polyhedron and in particular its Schlegel representation in Figure S1; Table S3: Dihedral angles across edges in the new polyhedra. Vertex numbering is shown in Figure S1.
Acknowledgments
We thank Gunnar Brinkmann (Department of Applied Mathematics, Computer Science and Statistics, University of Ghent, Belgium) for help with use of the CaGe software to make cages [11]. Molecular graphics in Figure 1a,c, Figure 3a,d and Figure 6 used the UCSF Chimera package [13]. Chimera is developed by the Resource for Biocomputing, Visualization, and Informatics at the UCSF (supported by NIGMS P41-GM103311). The nets in Figure 2 were produced with PolyPro (Pedagoguery Software, Terrace, BC, Canada). All of the other figures were made with Adobe Illustrator in Adobe CS4 (Adobe Systems, Inc., San Jose, CA, USA).
Author Contributions
The authors contributed equally to the work.
Conflicts of Interest
The University of California, Los Angles has applied for a patent for this work.
References
- Cromwell, P.R. Polyhedra; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Kepler, J. Strena, seu de Nive Sexangula Tthe Six-Cornered Snowflake; Godefridum Tambach: Francofurti ad Moenum, UK, 1611; English translation: Hardie, C. The Six-Cornered Snowflake; Clarendon Press: Oxford, UK, 1966. [Google Scholar]
- Schein, S.; Gayed, J. A new class of convex equilateral polyhedra with polyhedral symmetry related to fullerenes and viruses. Proc. Natl. Acad. Sci. USA 2014, 111, 2920–2925. [Google Scholar] [CrossRef] [PubMed]
- Coxeter, H.S.M. Introduction to Geometry, 2nd ed.; Wiley: New York, NY, USA, 1969. [Google Scholar]
- Grünbaum, B. Convex Polytopes, 2nd ed.; Springer: New York, NY, USA, 2003. [Google Scholar]
- Caspar, D.L.; Klug, A. Physical Principles in the Construction of Regular Viruses. Cold Spring Harb. Symp. Quant. Biol. 1962, 27, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, M. A Class of Multi-Symmetric Polyhedra. Tohoku Math. J. 1937, 43, 104–108. [Google Scholar]
- Coxeter, H.S.M. Virus Macromolecules and Geodesic Domes. In A Spectrum of Mathematics; Forder, H.G., Butcher, J.C., Eds.; Auckland University Press/Oxford University Press: Oxford, UK, 1971; pp. 98–107. [Google Scholar]
- Fowler, P.W.; Manolopoulos, D.E. An Atlas of Fullerenes; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- Dutour, M.; Deza, M. Goldberg–Coxeter construction for 3- and 4-valent plane graphs. Electron. J. Comb. 2004, 11, 20–68. [Google Scholar]
- Brinkmann, G.; Friedrichs, O.D.; Lisken, S.; Peeters, A.; Van Cleemput, N. CaGe—A Virtual Environment for Studying Some Special Classes of Plane Graphs—An Update. Match-Commun. Math. Comput. 2010, 63, 533–552. [Google Scholar]
- Hehre, W.; Ohlinger, S. Spartan’10 for Windows, Macintosh and Linux: Tutorial and User’s Guide; Wavefunction, Inc.: Irvine, CA, USA, 2011. [Google Scholar]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef] [PubMed]
- Fowler, P.W.; Cremona, J.E.; Steer, J.I. Systematics of bonding in non-icosahedral carbon clusters. Theor. Chim. Acta 1988, 73, 1–26. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Björck, A. Numerical Methods for Least Squares Problems; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar]
- Pawley, G.S. Plane Groups on Polyhedra. Acta Crystallogr. 1962, 15, 49–53. [Google Scholar] [CrossRef]
Figure 1.
Decoration of Platonic polyhedra with a tiling of hexagons. (a) The icosahedron, the octahedron and the tetrahedron, Platonic polyhedra with equilateral triangular faces; (b) a tiling of hexagons with cutouts with 5 triangular sectors (left), suitable for decorating the full triangular faces of an icosahedron with 5-valent vertices, 4 triangular sectors (middle) for the octahedron with 4-valent vertices, and 3 triangular sectors (right) for the tetrahedron with 3-valent vertices. The dashed arrows show some of the edges that anneal to one another in the cage. The edge of each triangle can be described by indices (h,k), here (2,1) in all three cases, corresponding to two steps in one direction in the tiling and one step after a turn of 60°, and containing T = 7 vertices; (c) icosahedral, octahedral and tetrahedral equilateral cages with indices (2,1) and nonplanar faces. The triangle from the tiling, which contains 7 vertices, becomes a spherical triangle with 7 vertices on the cage. These geometrically icosahedral, octahedral or tetrahedral cages are equilateral, with regular small faces (5-gons, 4-gons or 3-gons) but nonplanar 6-gons.
Figure 1.
Decoration of Platonic polyhedra with a tiling of hexagons. (a) The icosahedron, the octahedron and the tetrahedron, Platonic polyhedra with equilateral triangular faces; (b) a tiling of hexagons with cutouts with 5 triangular sectors (left), suitable for decorating the full triangular faces of an icosahedron with 5-valent vertices, 4 triangular sectors (middle) for the octahedron with 4-valent vertices, and 3 triangular sectors (right) for the tetrahedron with 3-valent vertices. The dashed arrows show some of the edges that anneal to one another in the cage. The edge of each triangle can be described by indices (h,k), here (2,1) in all three cases, corresponding to two steps in one direction in the tiling and one step after a turn of 60°, and containing T = 7 vertices; (c) icosahedral, octahedral and tetrahedral equilateral cages with indices (2,1) and nonplanar faces. The triangle from the tiling, which contains 7 vertices, becomes a spherical triangle with 7 vertices on the cage. These geometrically icosahedral, octahedral or tetrahedral cages are equilateral, with regular small faces (5-gons, 4-gons or 3-gons) but nonplanar 6-gons.
Figure 2.
Platonic and Archimedean polyhedra and their angle deficits. Five Platonic polyhedra (a); one tetrahedral Archimedean polyhedron (b); six octahedral Archimedean polyhedra (c) and six icosahedral Archimedean polyhedra (d). Polyhedra with angle deficits of 60°, 120° and 180° are compatible with decoration by a 6.6.6 tiling, the one with 90° by a 4.4.4.4 tiling. However, a 6.6.6 tiling of the square faces in the cuboctahedron—with an angle deficit of 60°—cannot knit across the boundaries of the squares.
Figure 2.
Platonic and Archimedean polyhedra and their angle deficits. Five Platonic polyhedra (a); one tetrahedral Archimedean polyhedron (b); six octahedral Archimedean polyhedra (c) and six icosahedral Archimedean polyhedra (d). Polyhedra with angle deficits of 60°, 120° and 180° are compatible with decoration by a 6.6.6 tiling, the one with 90° by a 4.4.4.4 tiling. However, a 6.6.6 tiling of the square faces in the cuboctahedron—with an angle deficit of 60°—cannot knit across the boundaries of the squares.
Figure 3.
Decoration of the full hexagonal and triangular faces of a truncated tetrahedron with a tiling of hexagons. (a) The truncated tetrahedron, an Archimedean polyhedron; (b) patterns of cutouts for the new Td cages in the leapfrog series. For (3,0 and 1,1), the cutout consists of four regular hexagons (blue) and four equilateral triangles (green). The dashed arrows show a few of the edges that anneal to one another when the cutout is folded to create the cage. The regular hexagon may be subdivided into a large equilateral triangle and three isosceles triangles. The index (3,0) characterizes one (bolded) edge of the large equilateral triangle that contains 9 vertices, and the index (1,1) characterizes one (bolded) edge of the small equilateral triangle that contains 3 vertices. The isosceles triangles have the same number of internal vertices, 3, as the small equilateral triangle. For the other cage in this series, (6,0 and 2,2), only one regular hexagon (containing a large equilateral triangle and three isosceles triangles) and one small equilateral triangle are shown; (c) patterns of cutouts for the new Td cages in the first series. Only one hexagon (blue) and one small equilateral triangle (green) are shown; (d) the construction of a general tetrahedral fullerene [15] includes 20 triangles, composed of 4 sets of 5 triangles, with one set shown in the inset. Each set contains a large equilateral triangle (α), three scalene triangles (β) and three thirds (=one whole) of one small equilateral triangle (γ)—in thirds to illustrate the symmetry. The dashed arrows show a few of the edges that anneal to one another when the cutout is folded to create the cage.
Figure 3.
Decoration of the full hexagonal and triangular faces of a truncated tetrahedron with a tiling of hexagons. (a) The truncated tetrahedron, an Archimedean polyhedron; (b) patterns of cutouts for the new Td cages in the leapfrog series. For (3,0 and 1,1), the cutout consists of four regular hexagons (blue) and four equilateral triangles (green). The dashed arrows show a few of the edges that anneal to one another when the cutout is folded to create the cage. The regular hexagon may be subdivided into a large equilateral triangle and three isosceles triangles. The index (3,0) characterizes one (bolded) edge of the large equilateral triangle that contains 9 vertices, and the index (1,1) characterizes one (bolded) edge of the small equilateral triangle that contains 3 vertices. The isosceles triangles have the same number of internal vertices, 3, as the small equilateral triangle. For the other cage in this series, (6,0 and 2,2), only one regular hexagon (containing a large equilateral triangle and three isosceles triangles) and one small equilateral triangle are shown; (c) patterns of cutouts for the new Td cages in the first series. Only one hexagon (blue) and one small equilateral triangle (green) are shown; (d) the construction of a general tetrahedral fullerene [15] includes 20 triangles, composed of 4 sets of 5 triangles, with one set shown in the inset. Each set contains a large equilateral triangle (α), three scalene triangles (β) and three thirds (=one whole) of one small equilateral triangle (γ)—in thirds to illustrate the symmetry. The dashed arrows show a few of the edges that anneal to one another when the cutout is folded to create the cage.
Figure 4.
Compatibility between regular tilings and face type. (a) The 6.6.6 tiling has 6-fold symmetry about the centers of hexagonal faces, with the pattern repeated every 60°. The edges of an icosahedron neatly anneal because of its 60°-angle deficit at each vertex, whereas the edges of a cube do not anneal, as indicated by the X, because of the cube’s 90°-angle deficit at each vertex; (b) the 4.4.4.4 tiling has 4-fold symmetry about the centers of square faces, with the pattern repeated every 90°. The edges of a cube neatly anneal because of the cube’s 90°-angle deficit at each vertex, whereas the edges of an icosahedron do not anneal, as indicated by the X, because of its 60°-angle deficit at each vertex.
Figure 4.
Compatibility between regular tilings and face type. (a) The 6.6.6 tiling has 6-fold symmetry about the centers of hexagonal faces, with the pattern repeated every 60°. The edges of an icosahedron neatly anneal because of its 60°-angle deficit at each vertex, whereas the edges of a cube do not anneal, as indicated by the X, because of the cube’s 90°-angle deficit at each vertex; (b) the 4.4.4.4 tiling has 4-fold symmetry about the centers of square faces, with the pattern repeated every 90°. The edges of a cube neatly anneal because of the cube’s 90°-angle deficit at each vertex, whereas the edges of an icosahedron do not anneal, as indicated by the X, because of its 60°-angle deficit at each vertex.
Figure 5.
Schlegel diagrams of the new cages, each with a (blue) hexagon (containing a large triangle with a bolded edge and three small isosceles triangles around the large triangle), and a (green) triangle (also with a bolded edge). Indices for the equilateral triangles can be obtained for the bolded edges. (a) The first four Td fullerene cages in the first series, with 28, 112, 252 and 448 vertices; (b) the first two Td fullerene cages in the leapfrog series with 84 and 336 vertices.
Figure 5.
Schlegel diagrams of the new cages, each with a (blue) hexagon (containing a large triangle with a bolded edge and three small isosceles triangles around the large triangle), and a (green) triangle (also with a bolded edge). Indices for the equilateral triangles can be obtained for the bolded edges. (a) The first four Td fullerene cages in the first series, with 28, 112, 252 and 448 vertices; (b) the first two Td fullerene cages in the leapfrog series with 84 and 336 vertices.
Figure 6.
Convex equilateral Td polyhedra from new Td cages. (a) The convex equilateral Td polyhedra from the first series of Td cages with 28, 112, 252, 448 and 700 vertices; (b) the convex equilateral Td polyhedron in the leapfrog series of Td cages with 84 vertices. Figure S1 shows vertex numbers for the polyhedra in (a) and (b), and Tables S1–S3 show coordinates, internal angles in faces and dihedral angles, respectively, for these polyhedra.
Figure 6.
Convex equilateral Td polyhedra from new Td cages. (a) The convex equilateral Td polyhedra from the first series of Td cages with 28, 112, 252, 448 and 700 vertices; (b) the convex equilateral Td polyhedron in the leapfrog series of Td cages with 84 vertices. Figure S1 shows vertex numbers for the polyhedra in (a) and (b), and Tables S1–S3 show coordinates, internal angles in faces and dihedral angles, respectively, for these polyhedra.
| Large Equilateral | Small Equilateral | Scalene | Total Vertices | Equilateral | |||||
|---|---|---|---|---|---|---|---|---|---|
| Triangle | Triangle | Triangle | Polyhedron | ||||||
| i | j | Vertices | k | l | Vertices | Vertices | + or − | ||
| 1 | 1 | 3 | 1 | 0 | 1 | 1 | 28 | 1 × 28 | + |
| 2 | 2 | 12 | 2 | 0 | 4 | 4 | 112 | 4 × 28 | + |
| 3 | 3 | 27 | 3 | 0 | 9 | 9 | 252 | 9 × 28 | + |
| 4 | 4 | 48 | 4 | 0 | 16 | 16 | 448 | 16 × 28 | + |
| 5 | 5 | 75 | 5 | 0 | 25 | 25 | 700 | 25 × 28 | + |
| 6 | 6 | 108 | 6 | 0 | 36 | 36 | 1008 | 36 × 28 | + |
| 7 | 7 | 147 | 7 | 0 | 49 | 49 | 1372 | 49 × 28 | + |
| 8 | 8 | 192 | 8 | 0 | 64 | 64 | 1792 | 64 × 28 | + |
| 9 | 9 | 243 | 9 | 0 | 81 | 81 | 2268 | 81 × 28 | + |
| 10 | 10 | 300 | 10 | 0 | 100 | 100 | 2800 | 100 × 28 | too large |
| 3 | 0 | 9 | 1 | 1 | 3 | 3 | 84 | 1 × 3 × 28 | + |
| 6 | 0 | 36 | 2 | 2 | 12 | 12 | 336 | 4 × 3 × 28 | − |
| 9 | 0 | 81 | 3 | 3 | 27 | 27 | 756 | 9 × 3 × 28 | − |
| 12 | 0 | 144 | 4 | 4 | 48 | 48 | 1344 | 16 × 3 × 28 | − |
| 15 | 0 | 225 | 5 | 5 | 75 | 75 | 2100 | 25 × 3 × 28 | − |
| 18 | 0 | 324 | 6 | 6 | 108 | 108 | 3024 | 36 × 3 × 28 | too large |
| 21 | 0 | 441 | 7 | 7 | 147 | 147 | 4116 | 49 × 3 × 28 | too large |
| 24 | 0 | 576 | 8 | 8 | 192 | 192 | 5376 | 64 × 3 × 28 | too large |
| 27 | 0 | 729 | 9 | 9 | 243 | 243 | 6804 | 81 × 3 × 28 | too large |
| 30 | 0 | 900 | 10 | 10 | 300 | 300 | 8400 | 100 × 3 × 28 | too large |
1 Each of the new Td fullerene cages is composed of four regular hexagonal patches and four equilateral triangular patches. Each hexagonal patch can be subdivided into a large equilateral triangle and three isosceles triangles. The table shows the pairs of indices (i,j) and (k,l) for the equilateral triangles and the number of vertices for each of the triangles. The total number of vertices is 4× the number in the large equilateral triangle, 4× the number in the small equilateral triangle, and 12× the number in the isosceles triangle. The total numbers of vertices in the new cages are all multiples of 28. The symbols “+” and “−“ mean definite success or failure by Equi to produce a convex equilateral polyhedron from the cage. Cages with ≥2800 vertices are “too large” for the current version of the Equi program to equiplanarize on a conventional computer.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Schein, S.; Yeh, A.J.; Coolsaet, K.; Gayed, J.M. Decoration of the Truncated Tetrahedron—An Archimedean Polyhedron—To Produce a New Class of Convex Equilateral Polyhedra with Tetrahedral Symmetry. Symmetry 2016, 8, 82. https://doi.org/10.3390/sym8080082
AMA Style
Schein S, Yeh AJ, Coolsaet K, Gayed JM. Decoration of the Truncated Tetrahedron—An Archimedean Polyhedron—To Produce a New Class of Convex Equilateral Polyhedra with Tetrahedral Symmetry. Symmetry. 2016; 8(8):82. https://doi.org/10.3390/sym8080082
Chicago/Turabian StyleSchein, Stan, Alexander J. Yeh, Kris Coolsaet, and James M. Gayed. 2016. "Decoration of the Truncated Tetrahedron—An Archimedean Polyhedron—To Produce a New Class of Convex Equilateral Polyhedra with Tetrahedral Symmetry" Symmetry 8, no. 8: 82. https://doi.org/10.3390/sym8080082
APA StyleSchein, S., Yeh, A. J., Coolsaet, K., & Gayed, J. M. (2016). Decoration of the Truncated Tetrahedron—An Archimedean Polyhedron—To Produce a New Class of Convex Equilateral Polyhedra with Tetrahedral Symmetry. Symmetry, 8(8), 82. https://doi.org/10.3390/sym8080082
Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.
