Massless Majorana-Like Charged Carriers in Two-Dimensional Semimetals

Abstract

The band structure of strongly correlated two-dimensional (2D) semimetal systems is found to be significantly affected by the spin-orbit coupling (SOC), resulting in SOC-induced Fermi surfaces. Dirac, Weyl and Majorana representations are used for the description of different semimetals, though the band structures of all these systems are very similar. We develop a theoretical approach to the band theory of two-dimensional semimetals within the Dirac–Hartree–Fock self-consistent field approximation. It reveals partially breaking symmetry of the Dirac cone affected by quasi-relativistic exchange interactions for 2D crystals with hexagonal symmetry. Fermi velocity becomes an operator within this approach, and elementary excitations have been calculated in the tight-binding approximation when taking into account the exchange interaction of $\pi ({\mathrm{p}}_z)$-electron with its three nearest $\pi ({\mathrm{p}}_z)$-electrons. These excitations are described by the massless Majorana equation instead of the Dirac one. The squared equation for this field is of the Klein–Gordon–Fock type. Such a feature of the band structure of 2D semimetals as the appearance of four pairs of nodes is shown to be described naturally within the developed formalism. Numerical simulation of band structure has been performed for the proposed 2D-model of graphene and a monolayer of Pb atoms.

1. Introduction

Strongly correlated materials, such as two-dimensional (2D) complex oxides of transition metals, graphene, oxides with a perovskite structure, and IV–VI semiconductors being three-dimensional (3D) analogues of graphene, can demonstrate unusual electronic and magnetic properties, such as e.g., half-metallicity. The linear dispersion law for such materials is stipulated by the simultaneous existence of positively and negatively charged carriers [1]. Conical singularities are generic in the quantum crystals having honeycomb lattice symmetry [2]. Bipolarity of the material suggests that the state of an excitonic insulator is possible for it. Since an electron-hole pair is at the same time its own antiparticle, the Majorana representation has been used [3,4] to describe the interaction of pseudospins with the valley currents in a monolayer graphene.

The electron is a complex fermion, so if one decomposes it into its real and imaginary parts, which would be Majorana fermions, they are rapidly re-mixed by electromagnetic interactions. However, such a decomposition could be reasonable for a superconductor where, because of effective electrostatic screening, the Bogoliubov quasi-fermions behave as if they are neutral excitations [5].

A helical magnetic ordering (commensurate magnetism) occurs due to strong spin-orbit coupling (SOC) between Fe and Pb atoms in the system where a chain of ferromagnetic Fe atoms is placed on the surface of conventional superconductor composed of Pb atoms [6]. In this case, the imposition of SOC results in the appearance of Majorana-like excitations at the ends of the Fe atom chain.

The discovered p-wave function pairing in this Fe-chain is allowed to assume that there exists a new mechanism of superconductivity in high-temperature superconductors through the exchange of Majorana particles rather than phonons in the Bardeen–Cooper–Schrieffer theory. Such a novel superconducting state emerges, for example, in compound CeCoIn${}_5$ in strong magnetic fields in addition to ordinary superconducting state, [7]. It has been shown [8,9,10] that the coupling of electrons into Cooper pairs in pnictides (LiFeAs with slabs FeAs) is mediated by the mixing of d-electron orbitals surrounding the atomic cores of transition metal. The new state is mediated by an anti-ferromagnetic order, and its fluctuations appear due to strong spin-orbit coupling [8,9,11]. It has been experimentally confirmed in [10] for LiFeAs. For antiferromagnetic itinerant-electron system LaFe${}_{12}$B${}_6$, ultrasharp magnetization steps have been observed [12]. The last can be only explained by the existence of anti-ferromagnetic order, and its fluctuations appear due to strong spin-orbit coupling.

Thus, there is a strong evidence that SOC may control the spin ordering in the absence of external magnetic fields. However, the mechanism that leads to such, commensurate magnetism has not been yet established.

The phenomenon of the contraction of electron density distribution in one direction is called nematicity. It is observed in pnictides BaFe${}_2$(As${}_{1-x}$P${}_x$)${}_2$ placed in a magnetic field, and such a phenomenon remains in the superconducting state [13]. The nematicity is coupled with considerable stripe spin fluctuations in FeSe [14]. The very strong spin orbit coupling leads to contraction in a factor of about 10% and rotation on 30${}^{\circ }$ of the hexagonal Brillouin zone of delafossite oxide PtCoO${}_2$, belonging to yet another class of topological insulators in which atoms of metal are in layers with triangular lattices [15].

Other topological insulators, namely so-called Weyl materials with a linear dispersion law, are close in properties with layered perovskite-like materials (see [16] and references therein). Currently, the first candidate for such a material has been found, namely TaAs, whose Brillouin zone has Weyl-like nodes and Fermi arcs [17,18,19].

Moreover, the experimental evidence of the similarities between the Fermi surfaces of insulator SmB${}_6$ and metallic rare earth hexaborides (PrB${}_6$ and LaB${}_6$) has been presented in [20]. To explain the accompanying ordering phenomena, each associated with different symmetry breaking, it is necessary to develop a unified theory as it has been pointed out in [9].

Electrically charged carriers in the strongly correlated semimetallic systems with half-filled bands are massless fermions [15,21,22].

In a low-dimensional system, the exciton binding energy turns out to be high [23] and, respectively, the transition to the state of excitonic insulator is possible. Therefore, the Majorana rather than Weyl representation is preferable for the description of 2D semimetals. An attempt to represent the transition to the state of excitonic insulator as the appearance of Majorana zero-modes solution in graphene with trigonal warping [24] contradicts experimental data on the absence of a gap in band structure of graphene [25] and on diminishing of charged carriers mobility [26] and minimal conductivity [27]. However, at the present time, there exist experimental signatures of graphene Majorana states in graphene-superconductor junctions without the need for spin-orbit coupling [28]. However, modern Quantum Field Theory of pseudo-Dirac quasiparticles in random phase approximation predicts a strong screening that destroys the excitonic pairing instability if the fermion dynamic mass $m(p)$ dependent on momentum p is small in comparison with the chemical potential μ: $m(p)\le \mu$ [29].

In the paper, we would like to show how the above described features of the layered materials can be formalized in 2D models, where the charged carriers are the quasiparticles of Majorana rather than of the Weyl type. We also show that, under certain conditions, these quasiparticles reveal themselves as Weyl-like states or massless Dirac pseudofermions.

However, the use of the well-known Majorana representations to describe a semimetal as a massless-quasiparticle system is encountered with such a puzzle as the absence of harmonic oscillatory solutions in ultrarelativistic limit for Majorana particles of zero mass [30]. The equations are known for massive Majorana particles only [31,32,33].

In the paper, we reveal different aspects of appearance of Majorana-like quasiparticle states in the band structure of semimetals. 2D Hartree–Fock approximation for graphene, however, predicts experimentally observable increase of the Fermi velocity value $v_F(\overrightarrow{p})$ at small momenta p [25] but leads to logarithmically divergent $v_F(\overrightarrow{p})$ at $p\to 0$ [34]. To take into account this effect of long range Coulomb interactions correctly, our calculation is based on the quasi-relativistic Dirac–Hartree–Fock self-consistent field approach developed earlier [35,36].

The goal is to construct a 2D-semimetal model in which a motion equation is a pseudo-relativistic massless Majorana-like one. We show that the squared equation for this field is of a Klein–Gordon–Fock type, and therefore the charged carriers in such 2D-semimetal models can be assumed massless Majorana-like quasiparticles.

We study quasiparticle excitations of the electronic subsystem of a hexagonal monoatomic layer (monolayer) of light or heavy atoms in tight-binding approximation. The simulations are performed for the atoms of C and Pb on the assumption that sp${}^2$-hybridization for s- and p-electron orbitals is also possible for the atoms of Pb.

We demonstrate that the band-structure features for the hexagonal monolayers are similar to each other due to the similarity of external electronic shells of their atoms. Despite the similarity of the band structure, the charged carriers in such 2D-semimetal models can possess different features, e.g., the charged carriers in the monolayer of the atoms of C can be thought of as massless Dirac pseudofermions, whereas in the monolayer from the atoms of Pb, they reveal themselves as Weyl-like states.

The paper is organized as follows. In Section 2, we propose a semimetal model with coupling between pseudospin and valley currents and prove the pseudo-helicity conservation law. In Section 3, we briefly introduce the approach [3,35,36,37] and use it in a simple tight-binding approximation to obtain the system of equations for a Majorana secondary quantized field. In Section 4, we support the statement that the squared equation for the constructed field is of the Klein–Gordon–Fock type for different model exchange operators. We also discuss features of our model manifesting in the band structure of real semimetals. In Section 5, we discuss the proposed approximations for the exchange interactions in 2D semimetals and summarize our findings.

2. Monolayer Semimetal Model with Partial Unfolding of Dirac Bands

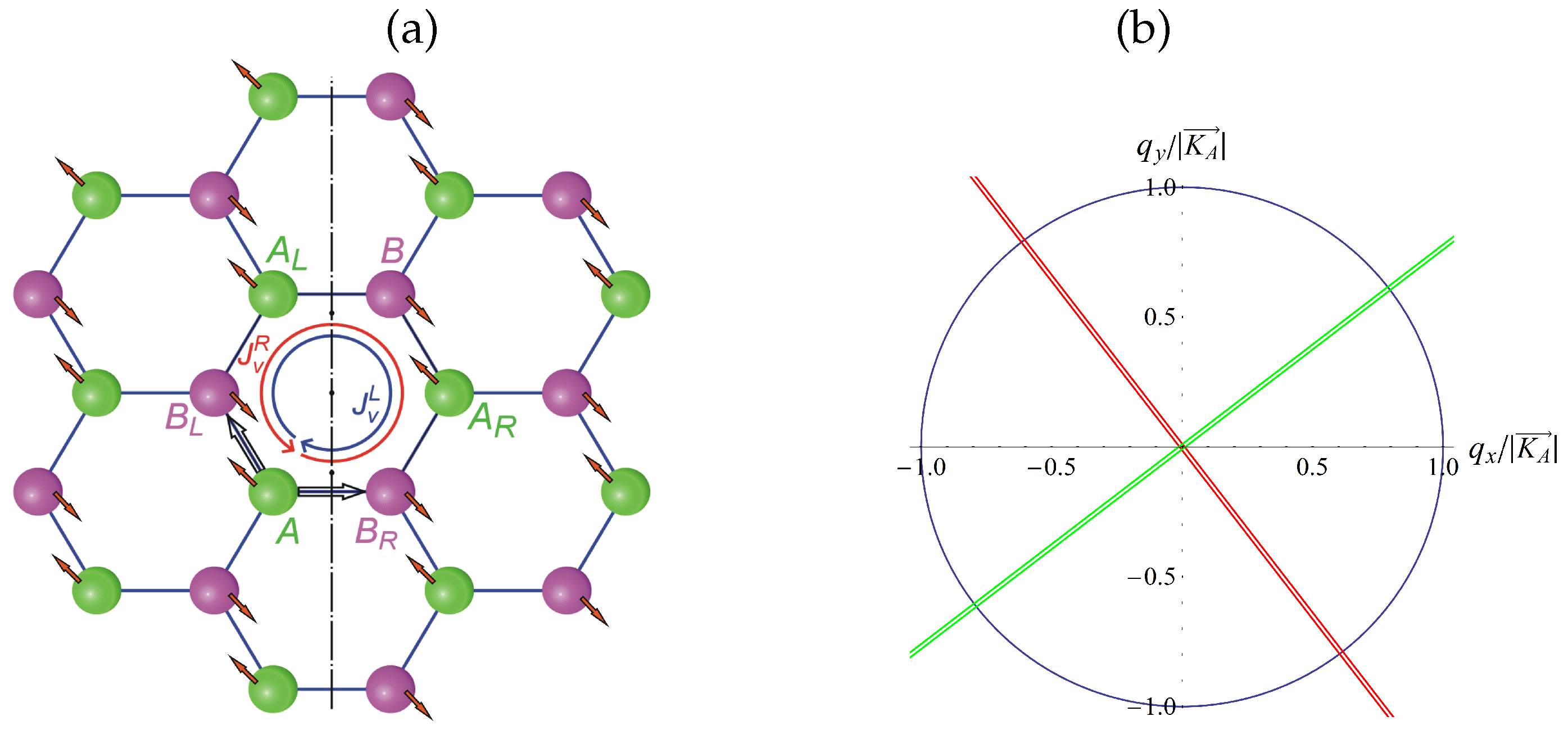
Semimetals are known to be bipolar materials with half-filled valence and conduction bands. A distinctive feature of the graphene band structure is the existence of Dirac cones in the Dirac points (valleys) $K,K^{\prime }$ of the Brillouin zone. In the present paper, these Dirac points are designated as $K_A,K_B$. We assume that pseudo-spins of hexagonally packed carbon atoms in the monoatomic layer (monolayer) graphene are anti-ordered, as it is shown schematically in Figure 1a. The fact that the pseudo-helicity (chirality) conservation law forbids massless charged carriers to be in lattice sites with the opposite signs of pseudo-spin, makes possible the existence of valley currents due to jumps through the forbidden sites. This is shown schematically in Figure 1a. Coupling between the pseudo-spin and the valley current in the Majorana representation of bispinors can be determined in the following way.

According to Figure 1a, a particle can travel from a lattice site A to e.g., a lattice site $A_R$ through right or left sites $B_R$ or $B_L$, respectively. Since the particle is symmetrical, its description in the right and left reference frames has to be equivalent. Therefore, a bispinor wave function ${\mathsf{\Psi }}^{\prime }$ of graphene has to be chosen in the Majorana representation, and its upper and lower spin components ${\psi }^{\prime }$, ${\dot{\psi }}^{\prime }$ are transformed by left and right representations of the Lorentz group:

$$\begin{array}{c}\hfill {\mathsf{\Psi }}^{\prime }=\left(\begin{array}{c}{\psi }_{\sigma }^{\prime }\\ {\dot{\psi }}_{-\sigma }^{\prime }\end{array}\right)=\left(\begin{array}{c}{e}^{\frac{\kappa }{2}\overrightarrow{\sigma }·\overrightarrow{n}}{\psi }_{\sigma }\\ e^{\frac{\kappa }{2}(-\overrightarrow{\sigma })·\overrightarrow{n}}{\dot{\psi }}_{-\sigma }\end{array}\right).\end{array}$$

(1)

The wave-function $\widehat{{\chi }_{\sigma }^{†}}({\overrightarrow{r}}_A)\left|0,+\sigma \right.〉$ of a particle (in our case of an electron-hole pair) located on the site A, behaves as a component ${\psi }_{\sigma }$, while the wave-function $\widehat{{\chi }_{-\sigma }^{†}}({\overrightarrow{r}}_B)\left|0,-\sigma \right.〉$ of a particle located on the site B behaves as a component ${\dot{\psi }}_{-\sigma }$ of the bispinor (1).

Relativistic particles with non-zero spin possess the helicity h, which is the projection of the particle’s spin to the direction of motion [32]:

$$\begin{array}{c}\hfill h\equiv \overrightarrow{p}·\overrightarrow{S}=\frac{1}{2}{p}_i\left(\begin{array}{cc}{\sigma }_i& 0\\ 0& {\sigma }_i\end{array}\right),\end{array}$$

(2)

where $\overrightarrow{p}$ is the particle momentum, $\overrightarrow{S}$ is the spin operator for a particle, $\overrightarrow{\sigma }$ is the vector of the Pauli matrices ${\sigma }_i$, and $i=x,y$. In quantum relativistic field theory, the value of the helicity of a massless particle is preserved in the transition from one reference frame moving with the velocity $v_1$, to another one moving with the velocity $v_2$ [32,38].

Let us designate the two-dimensional spin of the quasi-particle in valleys $K_A$ and $K_B$ as ${\overrightarrow{S}}_{AB}=\hslash {\overrightarrow{\sigma }}_{AB}/2$ and ${\overrightarrow{S}}_{BA}=\hslash {\overrightarrow{\sigma }}_{BA}/2$, respectively.

Let us introduce two-dimensional pseudospin ${\overrightarrow{S}}_{AB}$ and ${\overrightarrow{S}}_{BA}$ of quasi-particles in valleys $K_A$ and $K_B$ through the transformed vector $\overrightarrow{\sigma }$ of the Pauli matrices ${\sigma }_i$, $i=x,y$ as ${\overrightarrow{S}}_{AB}=\hslash {\overrightarrow{\sigma }}_{AB}/2$ and ${\overrightarrow{S}}_{BA}=\hslash {\overrightarrow{\sigma }}_{BA}/2$. The explicit form of this transformation is given in Section 3.

A valley current $J_v^R$ or $J_v^L$, on the right or left closed contour $\{A\to B_R\to A_R\to B\to A_L\to B_L\to A\}$ or $\{A\to B_L\to A_L\to B\to A_R\to B_R\to A\}$, respectively, in Figure 1, is created by an electron (hole) with pseudo-angular momentum ${\overrightarrow{l}}_{A{B}_R}$ and momentum ${\overrightarrow{p}}_{A{B}_R}$ or by an electron (hole) with ${\overrightarrow{l}}_{A{B}_L}$ and ${\overrightarrow{p}}_{A{B}_L}$. Pseudo-helicity of bispinors (1), describing the particles right or left the from lattice site A, is defined by the expressions, which are analogous to (2):

$$\begin{array}{c}\hfill h_{B_{R}A}\equiv {\overrightarrow{p}}_{A{B}_R}·{\overrightarrow{S}}_{B_{R}A},\end{array}$$

(3)

$$\begin{array}{c}\hfill h_{B_{L}A}\equiv {\overrightarrow{p}}_{A{B}_L}·{\overrightarrow{S}}_{B_{L}A}.\end{array}$$

(4)

Let us use the parity operator P, which mirrors the bispinor (1) with respect to the line passing through the points A and B. Pseudo-helicity of the mirrored bispinor is defined by the expression:

$$\begin{array}{c}\hfill P{h}_{B_R{A}_R}P=h_{A_L{B}_L}={\overrightarrow{p}}_{B_L{A}_L}·{\overrightarrow{S}}_{A_L{B}_L}.\end{array}$$

(5)

Pseudo-helicity $h_{AB}$ does not change its value while the valley momentum and the pseudo-spin change signs: ${\overrightarrow{p}}_{A_L{B}_L}=-{\overrightarrow{p}}_{B_R{A}_R}$ and ${\overrightarrow{S}}_{A_L{B}_L}=-{\overrightarrow{S}}_{B_R{A}_R}$.

The pseudo-helicity $h_{AB}$ is expressed through the projection ${\tilde{\mathcal{M}}}_{AB}={\overrightarrow{\sigma }}_{BA}·\left({\overrightarrow{l}}_{AB}+\hslash {\overrightarrow{\sigma }}_{BA}/2\right)$ of the total angular momentum on the direction of the spin ${\overrightarrow{\sigma }}_{BA}$ as [39,40]:

$$\begin{array}{c}\hfill {\overrightarrow{\sigma }}_{BA}·{\overrightarrow{p}}_{AB}={\sigma }_{BA}^r\left(p_{r,BA}+\mathit{ı}\frac{{\tilde{\mathcal{M}}}_{AB}}{r}-\hslash /2\right)={\sigma }_{BA}^r\left(p_{r,BA}+\mathit{ı}\frac{{\overrightarrow{\sigma }}_{BA}·{\overrightarrow{l}}_{AB}}{r}\right),\end{array}$$

(6)

where ${\sigma }_{BA}^r$ and $p_{r,BA}$ are radial components of the spin and the momentum, respectively. According to Equation (6), the pseudo-spin-orbit scalar ${\overrightarrow{\sigma }}_{BA}·{\overrightarrow{l}}_{AB}$ describes the coupling (interaction) of the spin with the valley currents flowing along a closed loop clockwise or in opposite directions, as is shown in Figure 1a. Hence, there exists a preferred direction along which the spin projection of the bispinor (1) is not changed after transition from one moving reference frame into another. At this, the spin of a particle precesses. Transformation of the electron and hole into each other in an exciton is a pseudo-precession.

As a result, the coupling of pseudo-spin and valley currents stipulates the spin precession of exciton charged carriers in graphene. In our model, the orientation of non-equilibrium spin of the states of monolayer graphene in electromagnetic fields may be retained for a long time due to prohibition of change for exciton pseudo-helicity. Pseudo-precession is possible, if spins of p${}_z$ -electrons are anti-ordered (pseudo-antiferromagnetic ordering). Therefore, the pseudo-spin precession of the exciton can be implemented through the exchange interaction. Furthermore, we determine the operators ${\overrightarrow{\sigma }}_{BA(AB)}$, ${\overrightarrow{p}}_{AB(BA)}$ and describe the effects of pseudo-spin and valley current coupling.

3. Effects of Coupling between Pseudo-Spin and Valley Current

In quasi-relativistic approximation ($c^{-1}$ expansion), the eigenproblem for the equation of motion of the secondary quantized field ${\widehat{\chi }}_{-{\sigma }_A}^{†}$ in the model shown in Figure 1a has the form: [35,36,37]

$$\begin{array}{c}\hfill \left\{\overrightarrow{\sigma }·\overrightarrow{p}{\widehat{v}}_F^{qu}-\frac{1}{c}{\left(i{\Sigma }_{rel}^x\right)}_{AB}{\left(i{\Sigma }_{rel}^x\right)}_{BA}\right\}\widehat{{\chi }_{-{\sigma }_{{}_A}}^{†}}(\overrightarrow{r})\left|0,-\sigma \right.〉\\ \hfill =E_{qu}(p)\widehat{{\chi }_{-{\sigma }_{{}_A}}^{†}}(\overrightarrow{r})\left|0,-\sigma \right.〉,\end{array}$$

(7)

where the Fermi velocity operator ${\widehat{v}}_F^{qu}$ is defined as

$${\widehat{v}}_F^{qu}=\left[{\left({\Sigma }_{rel}^x\right)}_{BA}+c\hslash \overrightarrow{\sigma }·({\overrightarrow{K}}_A+{\overrightarrow{K}}_B)\right].$$

${\left({\Sigma }_{rel}^x\right)}_{BA},{\left({\Sigma }_{rel}^x\right)}_{AB}$ are determined through an ordinary exchange interaction contribution, for example [39,40]:

$$\begin{array}{c}\hfill {\left({\Sigma }_{rel}^x\right)}_{AB}{\widehat{\chi }}_{{\sigma }_{{}_B}}^{†}(\overrightarrow{r})\left|0,\sigma \right.〉=\sum _{i=1}^{N_{v}N}\int d{\overrightarrow{r}}_i{\widehat{\chi }}_{{\sigma }_i{}^B}^{†}(\overrightarrow{r})\left|0,\sigma \right.〉\\ \hfill \times \langle 0,-{\sigma }_i|{\widehat{\chi }}_{-{\sigma }_i^A}^{†}({\overrightarrow{r}}_i)V({\overrightarrow{r}}_i-\overrightarrow{r}){\widehat{\chi }}_{-{\sigma }_B}({\overrightarrow{r}}_i)|0,-{\sigma }_{i^{\prime }}\rangle .\end{array}$$

$V({\overrightarrow{r}}_i-\overrightarrow{r})$ is the Coulomb interaction between two valent electrons with radius-vectors ${\overrightarrow{r}}_i$ and $\overrightarrow{r}$; N is a total number of atoms in the system, $N_v$ is a number of valent electrons in an atom, c is the speed of light.

After applying the non-unitary transformation to the wave function in the form

$$\widehat{{\tilde{\chi }}_{-{\sigma }_{{}_A}}^{†}}\left|0,-\sigma \right.〉={\left({\Sigma }_{rel}^x\right)}_{BA}\widehat{{\chi }_{-{\sigma }_{{}_A}}^{†}}\left|0,-\sigma \right.〉,$$

we obtain (neglecting mixing of the states for the Dirac points) the equation that is similar to the one in 2D quantum field theory (QFT) [41,42,43], but it describes the motion of a particle with pseudo-spin ${\overrightarrow{S}}_{AB}=\hslash {\overrightarrow{\sigma }}_{AB}/2$:

$$\begin{array}{c}\hfill \left\{{\overrightarrow{\sigma }}_{2D}^{AB}·{\overrightarrow{p}}_{BA}-c^{-1}\widetilde{{\Sigma }_{BA}{\Sigma }_{AB}}\right\}\widehat{{\tilde{\chi }}_{-{\sigma }_{{}_A}}^{†}}(\overrightarrow{r})\left|0,-\sigma \right.〉={\tilde{E}}_{qu}(p)\widehat{{\tilde{\chi }}_{-{\sigma }_{{}_A}}^{†}}(\overrightarrow{r})\left|0,-\sigma \right.〉,\end{array}$$

(8)

with a transformed 2D vector ${\overrightarrow{\sigma }}_{2D}^{AB}$ of the Pauli matrices, which are determined as ${\overrightarrow{\sigma }}_{2D}^{AB}={\left({\Sigma }_{rel}^x\right)}_{BA}\overrightarrow{\sigma }{\left({\Sigma }_{rel}^x\right)}_{BA}^{-1}$. The following notions are introduced: ${\overrightarrow{p}}_{BA}\widehat{{\tilde{\chi }}_{-{\sigma }_A}^{†}}={\left({\Sigma }_{rel}^x\right)}_{BA}\overrightarrow{p}{\left({\Sigma }_{rel}^x\right)}_{BA}^{-1}\widehat{{\tilde{\chi }}_{-{\sigma }_A}^{†}}\equiv \left[{\left({\Sigma }_{rel}^x\right)}_{BA}\overrightarrow{p}\right]\widehat{{\chi }_{-{\sigma }_A}^{†}}$, ${\tilde{E}}_{qu}=E_{qu}/{\widehat{v}}_F^{BA}$, ${\widehat{v}}_F^{BA}={\left({\Sigma }_{rel}^x\right)}_{BA}$, $\widetilde{{\Sigma }_{BA}{\Sigma }_{AB}}\equiv {\left({\Sigma }_{rel}^x\right)}_{BA}{\left(i{\Sigma }_{rel}^x\right)}_{AB}{\left(i{\Sigma }_{rel}^x\right)}_{BA}{\left({\Sigma }_{rel}^x\right)}_{BA}^{-1}={\left(i{\Sigma }_{rel}^x\right)}_{BA}{\left(i{\Sigma }_{rel}^x\right)}_{AB}$; and the product of two capital sigma, as one sees from the last chain of formulas, behaves like a scalar mass term.

Further simulations are performed in nearest neighbor tight-binding approximation [44,45]. This approximation correctly predicts the graphene band structure in the energy range $\pm 1$ eV [46]. This turns out to be sufficient for our purposes. We use the expressions for the exchange between $\pi (p_z)$-electrons only. One can find the explicit form of these expressions in [4].

The action of the matrices ${\left({\Sigma }_{rel}^x\right)}_{BA},{\left({\Sigma }_{rel}^x\right)}_{AB}$ in the momentum space is shown in Figure 1b. As ${\left({\Sigma }_{rel}^x\right)}_{BA}\ne {\left({\Sigma }_{rel}^x\right)}_{AB}$, the vector ${\overrightarrow{p}}_{BA}$ is rotated with respect to ${\overrightarrow{p}}_{AB}$ and stretched. According to Figure 1b, ellipses in momentum spaces of electrons and holes are rotated 90${}^{\circ }$ with respect to each other. With an account of the hexagonal symmetry of the system, the last explains the experimentally observed rotation in 30${}^{\circ }$ of the hexagonal Brillouin zone of PtCoO${}_2$ [15].

Thus, the sequence of exchange interactions ${\left({\Sigma }_{rel}^x\right)}_{AB}{\left({\Sigma }_{rel}^x\right)}_{BA}{\left({\Sigma }_{rel}^x\right)}_{AB}$ for valley currents makes rotation initially of the electron Brillouin zone and Dirac band into the hole Brillouin zone and Dirac band, and then vice-versa. Thus, the exchange ${\left({\Sigma }_{rel}^x\right)}_{AB(AB)}\equiv {\Sigma }_{AB(BA)}$ changes the sublattices wave functions:

$$\left|{\psi }_{AB}\right.〉={\Sigma }_{AB}\left|{\psi }_{BA}^{*}\right.〉.$$

Owing to it and neglecting a very small mass term $c^{-1}\widetilde{{\Sigma }_{BA}{\Sigma }_{AB}}$, the equation in which the operator of the Fermi velocity enters, can be rewritten as follows:

$$\begin{array}{c}\hfill {\overrightarrow{\sigma }}_{2D}^{BA}·{\overrightarrow{p}}_{AB}\left|{\psi }_{AB}\right.〉=E_{qu}\left|{\psi }_{BA}^{*}\right.〉.\end{array}$$

(9)

Taking into account that $E\to i\frac{\partial }{\partial t}$ and $\overrightarrow{\widehat{p}}=-i\overrightarrow{\nabla }$, we transform the system of equations for the Majorana bispinor $({\psi }_{AB}^{†},{({\psi }_{BA}^{*})}^{†})$:

$$\begin{array}{c}\hfill {\overrightarrow{\sigma }}_{2D}^{BA}·{\overrightarrow{p}}_{AB}\left|{\psi }_{AB}\right.〉=i\frac{\partial }{\partial t}\left|{\psi }_{BA}^{*}\right.〉,\end{array}$$

(10)

$$\begin{array}{c}\hfill {\overrightarrow{\sigma }}_{2D}^{AB}·\overrightarrow{p}{}_{BA}^{*}\left|{\psi }_{BA}^{*}\right.〉=-i\frac{\partial }{\partial t}\left|{\psi }_{AB}\right.〉,\end{array}$$

(11)

into the wave equation of the form:

$$\begin{array}{c}\hfill ({\overrightarrow{\sigma }}_{2D}^{AB}·\overrightarrow{\widehat{p}}{}_{BA}^{*})({\overrightarrow{\sigma }}_{2D}^{BA}·{\overrightarrow{\widehat{p}}}_{AB})\left|{\psi }_{AB}\right.〉=\frac{{\partial }^2}{\partial t^2}\left|{\psi }_{AB}\right.〉.\end{array}$$

(12)

Equation (12) describes an oscillator with the energy operator $\widehat{\omega }(\overrightarrow{p})$

$$\begin{array}{c}\hfill \widehat{\omega }(\overrightarrow{p})=\frac{1}{\sqrt{2}}{\left[({\overrightarrow{\sigma }}_{2D}^{AB}·{\overrightarrow{p}}_{BA})({\overrightarrow{\sigma }}_{2D}^{BA}·{\overrightarrow{p}}_{AB})+({\overrightarrow{\sigma }}_{2D}^{BA}·{\overrightarrow{p}}_{AB})({\overrightarrow{\sigma }}_{2D}^{AB}·{\overrightarrow{p}}_{BA})\right]}^{1/2}.\end{array}$$

(13)

Now, one can really see that the obtained equation is the equation of motion for a Majorana bispinor wave function of the semimetal charged carriers.

Thus, the Fermi velocity becomes an operator within this approach, and elementary excitations are fermionic excitations described by the massless Majorana-like equation rather than Dirac-like one.

4. Harmonic Analysis of the Problem

Equation (13) can be rewritten in the following form:

$$\begin{array}{c}\hfill {\widehat{\omega }}^2(\overrightarrow{p})=\frac{1}{2}\left({\widehat{H}}_{AB}{\widehat{H}}_{BA}+{\widehat{H}}_{BA}{\widehat{H}}_{AB}\right).\end{array}$$

(14)

In order to describe the proposed secondary quantized field by a set of harmonic oscillators, it is necessary to show that the squared Equation (14), obtained by the symmetrization of the product of the Hamiltonians ${\widehat{H}}_{AB}$ and ${\widehat{H}}_{BA}$, is the Klein–Gordon–Fock operator. This will be the case if the non-diagonal matrix elements of the operator vanish identically, and therefore the components of the equation are independent. Then, ${\widehat{\omega }}^2(\overrightarrow{p})$ can be considered as a “square of energy operator”.

Unfortunately, because of the complex form of the exchange operator, the statement is difficult to prove in the general case. Therefore, we do this for several approximations of the exchange interaction and demonstrate that the Equation (14) is a Klein–Gordon–Fock one.

As a first particular case, when the proposed Majorana-like field is proven to be a harmonic oscillators set, we consider ϵ-neighborhood ($ϵ\to 0$) of the Dirac point $K_A(K_B)$.

Let us designate the momentum of a particle in a valley as $\overrightarrow{q}$. The momentum $\overrightarrow{q}$ is determined as $\overrightarrow{q}=\overrightarrow{p}-\hslash {\overrightarrow{K}}_A$. In the case of very small values of $\overrightarrow{q}$, $q\to 0$ the exchange operator ${\Sigma }_{AB(BA)}$ is approximated by a power series expansion up to the fourth order in q. Then, an analytical calculation of non-diagonal elements of the operator ${\widehat{\omega }}^2(\overrightarrow{p})$ performed in the Mathematica system proves that they are identically zero.

Band structures for monolayer graphene and monolayer of atoms of Pb are shown in Figure 2a,b. One can see that the Weyl nodes in graphene are located far enough from the Dirac point. The Weyl nodes are shifted to the Dirac point for the Pb-monolayer. Therefore, Weyl-like character in the behavior of charged carriers may be exhibited for the Pb-monolayer under the condition that the contributions up to 4-th order in q are prevailing in the exchange. In accordance with Figure 1b, the exchange operator matrices transform a circumference in the momentum space into a highly stretched ellipse that allows us to assume the presence of nematicity in the model.

For a given $\overrightarrow{q}$, where the eigenfunction of Equation (9) represents 2D spinor Ψ, we choose its normalization in the form $\mathsf{\Psi }(\overrightarrow{q})={(\psi (\overrightarrow{q}),1)}^{†}$ with lower component equal to unity. Then, as it can be easily shown for the massless Dirac pseudo-fermion model [47], the absolute value of the upper component $|\psi (\overrightarrow{q})|$ does not depend upon the wave vector $\overrightarrow{q}$, demonstrating the equivalence of all directions in $\overrightarrow{q}$ space. We construct $|\psi (\overrightarrow{q}){|}^2$ for Equation (9) in $q^4$-approximation for the exchange. The results are shown in Figure 2c. The isotropy of $|\psi (\overrightarrow{q}){|}^2$ is broken for our model due to the appearance of the preferable directions in the momentum space.

As one can see from Figure 2c, the existence of almost one-dimensional regions with sharp jump in $|\psi (\overrightarrow{q}){|}^2$ should probably lead to some anisotropy already in the configuration space for the carriers that we consider as manifestation of nematicity.

The approximation $q^4$ for the exchange operator expression presents a particular interest for systems with strong damping of quasi-particle excitations.

The second approximation of the exchange, for which we can prove the harmonic origin of the proposed Majorana-like field, is the model exchange with full exponential factors taken into account, but with the phase-difference between π(p)${}_z$-electrons wavefunction chosen to be identically zero (see Ref. [4] for detail). Numeric simulation of ${\widehat{\omega }}^2(\overrightarrow{p})$ with this model exchange has been performed on a discrete lattice in the Brillouin zone. It has been demonstrated that the operator ${\widehat{\omega }}^2(\overrightarrow{p})$ is always diagonal in this case.

Now, we perform the simulations with the exact expression for the exchange term.

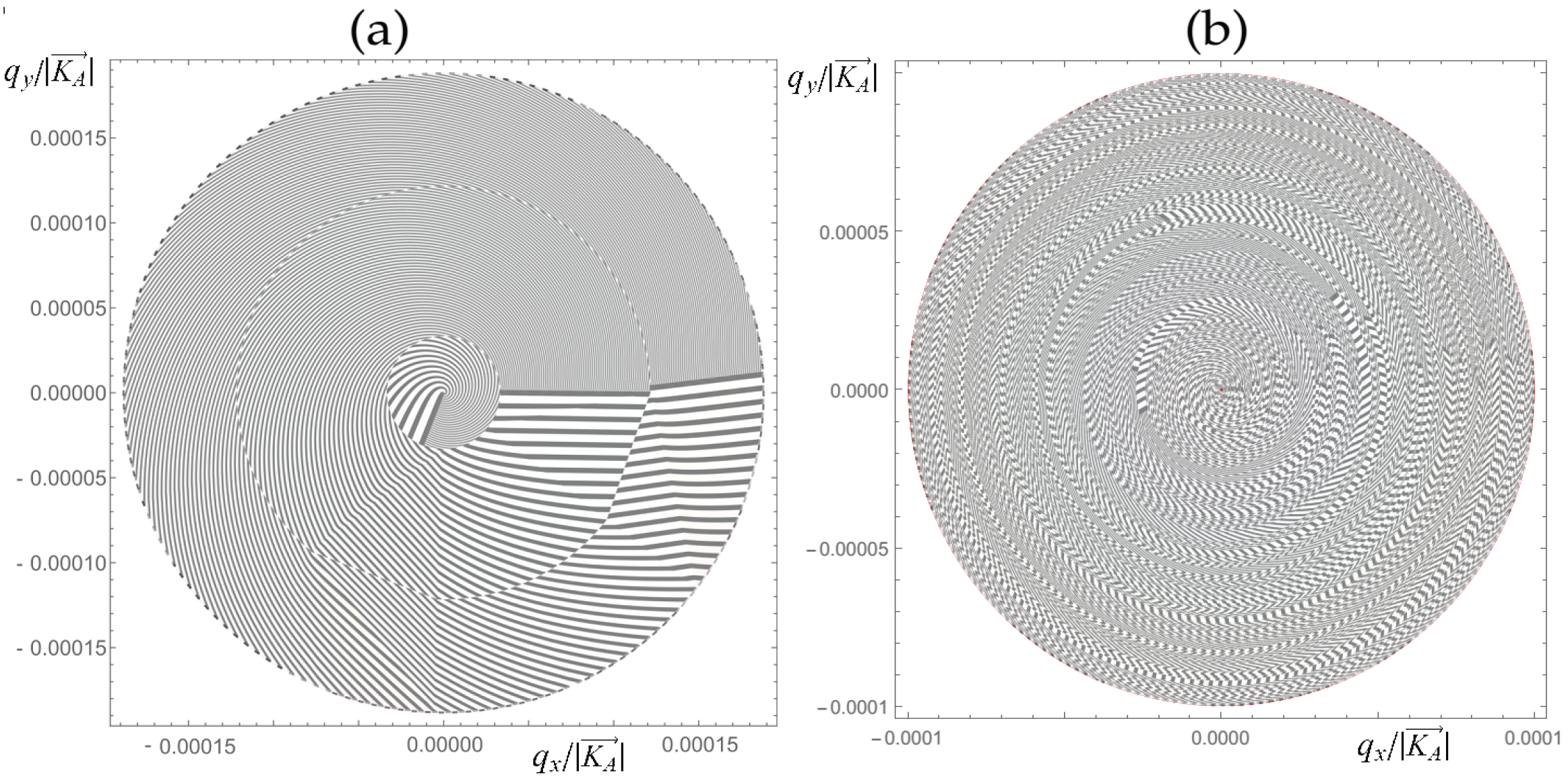
In this general case, the exchange between π(p${}_z$)-electron and its three nearest π(p${}_z$)-electrons has been calculated based on the method proposed in [4]. Band structure of the 2D semimetal has the form of a degenerated Dirac cone in the neighborhood of the Dirac point. Then, the emergence of unfolding leads to replica appearance, and further splitting of these replicas gives the octagonal symmetry of the problem, as one can see in Figure 3. Hyperbolic points (saddle points) are located between nodes and at the apex of the Dirac cone (Van-Hove singularities) as one can see in Figure 2a,b [3,48,49,50]. Therefore, a fractal-like set of Fermi arcs which are shown in Figure 4, is formed in the absence of damping in the system. Contrary to the graphene case, the splitting of the Dirac bands for the Pb-monolayer occurs at sufficiently small q, and therefore, can be observed experimentally. In addition, for the Pb-monolayer, there exist regions with huge numbers of Fermi arcs, and, respectively, regions with strong fluctuations of antiferromagnetic ordering.

Thus, the secondary quantized field described by Equation (9) represents a field in which quanta manifest themselves as Dirac pseudo-fermions in the apex of the Dirac cone and as Weyl-like particles for sufficiently large q at the presence of the dumping in the system. For an ideal system ($\Im mϵ(\overrightarrow{q})=0$), such a behavior is similar to that of the mathematical pendulum in the vicinity of the separatrix [51,52].

5. Discussion

Discussing the obtained results, we have to point out, firstly, that the excitations of the constructed secondary-quantized pseudo-fermionic field are Majorana-like massless quasiparticles.

The set of Fermi arcs in our model shows that the splitting of Dirac replicas on a huge number of Weyl-like states occurs in the momentum space except for the Dirac cone apex.

In contrast to known massless Dirac and Weyl models, in the proposed model, there is a partial removing of the degeneracy of the Dirac cone, and the octagonal symmetry of the bands emerges for sufficiently large q. Thus, Majorana particles in our model can be represented as a wave package of infinitely large number of Weyl-like states.

Secondly, the Dirac cone for the proposed 2D-semimetal model is degenerated in a very small neighborhood of the Dirac point $K_A(K_B)$ at $q\to 0$.

Thirdly, the first-approximation with damping demonstrates that sufficiently strong decay leads to diminishing the number of the Weyl states and formation of bands having hexagonal symmetry. In accordance with the obtained results, in the system with strong damping, only six pairs of Weyl nodes survive. In this case, each Dirac hole (electron) cone is surrounded by three electron (hole) bands relating to three Weyl pairs. Provided the lifetime of the Weyl-like states is sufficiently large (small but finite damping) to preserve the octagonal symmetry of the bands, each Dirac hole (electron) cone will be surrounded by four electron (hole) bands relating to four Weyl pairs.

Important features of the proposed model are that the fractal set of Fermi arches manifests pseudospin fluctuations and the phenomenon of nematicity is possible.

6. Conclusions

In conclusion, contrary to known Dirac and Weyl models, the constructed 2D-semimetal model allows for description, in a general formalism, the band structure of a wide class of existing strongly.